Как найти высоту пирамиды с основанием ромб

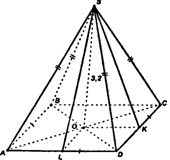
Основание пирамиды — ромб. Диагонали ромба взаимно перпендикулярны и в точке пересечения делятся пополам. Тогда из прямоугольного треугольника, образованного  половинами диагоналей (катеты) и стороной ромба (гипотенуза) по Пифагору находим сторону ромба: DC = √(15² + 20²) = √625 =25см.
Площадь ромба (основания) равна полупроизведению его диагоналей, то есть Sр=(1/2)*30*40 = 600см². С другой стороны, площадь ромба равна произведению высоты на сторону, откуда высота ромба равна 600:25 = 24см. Точка пересечения диагоналей делит пополам и высоту ромба, тогда из прямоугольного треугольника, образованного половиной высоты ромба, высотой пирамиды (катеты) и апофемой грани пирамиды (гипотенуза) по Пифагору находим высоту пирамиды. Н = √(13² -12²) = √25 = 5см.
Ответ: высота пирамиды равна 5см.

Объем пирамиды рассчитывается по формуле:

V = S*h/3, где h — высота пирамиды, S — площадь основания (в нашем примере ромба);

площадь ромба рассчитаем по формуле

S= d1*d2/2, где d1 и d2 — длины диагоналей

Таким образом, объем пирамиды составит:

S = 6 см * 8 см/2 = 24 см2

V = 24 см2 *5 см /3 = 40 см3

Надеюсь формулы для расчета объема и площади в этом примере выводить не нужно

Для решения задачи нам нужно найти высоту треугольной призмы, образованной основанием пирамиды и ее высотой, а затем разделить эту высоту пополам, чтобы получить высоту пирамиды.

Для начала найдем площадь ромба по формуле: S = (d1 * d2) / 2, где d1 и d2 — диагонали ромба.

S = (10 * 15) / 2 = 75 кв.см.

Затем найдем периметр основания пирамиды, который равен 4 * a, где a — длина стороны ромба. Для этого нам нужно найти a, используя теорему Пифагора, так как мы знаем диагонали ромба и расстояние от вершин до сторон основания.

Пусть x — половина длины одной из сторон ромба. Тогда по теореме Пифагора:

x^2 + 8^2 = 5^2 + (15/2)^2

x^2 = 25/4

x = 5/2

Таким образом, сторона ромба равна a = 2x = 5 см.

Периметр основания пирамиды равен 4 * a = 20 см.

Теперь мы можем найти высоту призмы, используя формулу V = S * h, где V — объем призмы, S — площадь основания призмы, h — высота призмы.

Объем пирамиды равен V = (1/3) * S * h, так как объем пирамиды равен трети объема призмы.

Таким образом,

V = (1/3) * 75 * h

V = 25 * h

Высота призмы равна h = V / 25

h = (1/3) * S * h / 25

h = 3 км.

Высота пирамиды равна половине высоты призмы, то есть h/2 = 3/2 = 1.5 см.

Ответ: высота пирамиды равна 1.5 см.

Привет, вот она
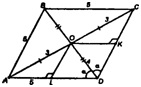
Пусть ABCDS — данная пирамида. О — точка пересечения диагоналей  ромба  ABCD. Построим  отрезки KS и LS. По теореме о 3-х перпендикулярах имеем: 

BD — меньшая диагональ (т.к. она лежит против острого утла ромба). ΔLOD=ΔKOD, следовательно, OL=OK. Значит, ΔSOL=ΔSOK и SK=SL.
Следовательно, высоты всех 4-х боко­вых граней равны.

Из ΔAOD по теореме Пифагора име­ем:
= 4 (см),
cos α тогда sin а 
Из ΔODL: OL = OD ∙ sin α = 2,4 (см).
Из ΔSOK:
Ответ: 4 см, 4 см, 4 см, 4 см.

Пирамида

Пирамида – многогранник, основание которого — многоугольник , а остальные грани — треугольники, имеющие общую вершину.

По числу углов основания различают пирамиды треугольные , четырёхугольные и т. д.

Вершина пирамиды — точка, соединяющая боковые рёбра и не лежащая в плоскости основания.

Основание — многоугольник, которому не принадлежит вершина пирамиды.

Апофема — высота боковой грани правильной пирамиды, проведенная из ее вершины.

Высота — отрезок перпендикуляра, проведённого через вершину пирамиды к плоскости её основания (концами этого отрезка являются вершина пирамиды и основание перпендикуляра).

Диагональное сечение пирамиды — сечение пирамиды, проходящее через вершину и диагональ основания.

Некоторые свойства пирамиды

1) Если все боковые ребра равны, то

– около основания пирамиды можно описать окружность, причём вершина пирамиды проецируется в её центр

– боковые ребра образуют с плоскостью основания равные углы

Верно и обратное.

Если боковые ребра образуют с плоскостью основания равные углы, то все боковые ребра пирамиды равны.

Если около основания пирамиды можно описать окружность, причём вершина пирамиды проецируется в её центр, то все боковые ребра пирамиды равны.

2) Если все грани пирамиды наклонены к плоскости основания под одним углом , то в основание пирамиды можно вписать окружность, причём вершина пирамиды проецируется в её центр

Верно и обратное.

Виды пирамид

Пирамида называется правильной , если основанием её является правильный многоугольник, а вершина проецируется в центр основания.

Для правильной пирамиды справедливо:

– боковые ребра правильной пирамиды равны;

– в правильной пирамиде все боковые грани — равные равнобедренные треугольники;

– в любую правильную пирамиду можно вписать сферу;

– около любой правильной пирамиды можно описать сферу;

– площадь боковой поверхности правильной пирамиды равна половине произведения периметра основания на апофему.

Пирамида называется прямоугольной , если одно из боковых рёбер пирамиды перпендикулярно основанию. Тогда это ребро и есть высота пирамиды.

Усечённой пирамидой называется многогранник, заключённый между основанием пирамиды и секущей плоскостью, параллельной её основанию.

Тетраэдр – треугольная пирамида. В тетраэдре любая из граней может быть принята за основание пирамиды.

Решение задач с использованием свойств различных видов пирамид

Разделы: Математика

Изучение пирамиды и ее элементов представляет широкие возможности для составления и решения задач на различных видах пирамид по следующим темам:

• Пирамиды, в которых основание высоты является центром описанной или вписанной окружности основания пирамиды.
• Пирамиды, в которых одна или две боковые грани перпендикулярны плоскости основания.
• Пирамиды, в которых заданы расстояния между точками и элементами пирамиды.

Действующие учебники геометрии либо не содержат , либо содержат в недостаточном количестве задачи по этим темам.

Как показала практика, учащиеся с большим интересом принимают участие не только в решении данных задач, но и в их составлении. Они с удовольствием предлагают различные решения придуманных ими задач.

К этому учащихся необходимо подводить хорошо продуманной системой теоретических положений и практических упражнений.

Учебники Л.С. Атанасяна и др. “Геометрия 10–11” и А.В.Погорелова “Геометрия 10–11” содержат опорный теоретический материал по теме “Пирамида и ее элементы”.

В дополнение к нему можно рассмотреть следующие свойства часто встречающихся видов пирамид.

Теория.

Теоремы о пирамидах, в которых основание высоты является центром описанной или вписанной окружности основания пирамиды.

• Если все боковые ребра пирамиды составляют с плоскостью основания равные углы, то:

а) основание высоты пирамиды совпадает с центром окружности, описанной около основания пирамиды;

б) все боковые ребра пирамиды равны между собой.

• Если основание высоты пирамиды совпадает с центром окружности, описанной около ее основания, то:

а) все боковые ребра пирамиды образуют с плоскостью основания равные углы;

в) все боковые ребра пирамиды равны между собой.

• Если все боковые ребра пирамиды равны, то:

а) основание высоты пирамиды совпадает с центром окружности, описанной около основания пирамиды;

б) все боковые ребра пирамиды составляют с плоскостью ее основания равные между собой углы.

• Если высота пирамиды пересекает ее основание и все боковые грани пирамиды образуют с плоскостью основания равные двугранные углы, то основание высоты пирамиды совпадает с центром окружности, вписанной в ее основание.
• Если вершина пирамиды проектируется в центр окружности, вписанной в основание пирамиды, то боковые грани пирамиды образуют с плоскостью основания равные двугранные углы.
• Если у треугольной пирамиды все боковые ребра равны, а в основании лежит прямоугольный треугольник, то грань, содержащая его гипотенузу, перпендикулярна основанию. Основание высоты данной пирамиды является середина гипотенузы.

Теоремы о пирамидах, в которых одна или две боковые грани перпендикулярны плоскости основания.

• Если пирамида содержит ровно одну боковую грань, которая перпендикулярна плоскости основания, то высота такой пирамиды лежит в этой боковой грани.
• Если пирамида содержит две смежные боковые грани, перпендикулярные плоскости основания, то высотой такой пирамиды является боковое ребро, общее для этих граней.
• Если в пирамиде две не смежные боковые грани перпендикулярны плоскости основания, то высота такой пирамиды лежит на прямой пересечения плоскостей этих граней.
• Если боковое ребро пирамиды перпендикулярно основанию, то и боковые грани, содержащие это ребро, перпендикулярны основанию.
• Если в четырехугольной пирамиде в основании ромб, и две смежные боковые грани перпендикулярны основанию, то боковые грани данной пирамиды – две пары равных треугольников.

Задачи для решения.

Задания из книги “Самостоятельные и контрольные работы по геометрии для 11-го класса” Ершовой А.П., Голобородько В.В.

Пирамиды, в которых основание высоты является центром описанной или вписанной окружности основания пирамиды.

Вариант А.

1. Основание пирамиды SABCD – прямоугольник АВСД со сторонами 6 и 8 см. Все боковые ребра пирамиды равны 13 см.

а) Опишите построение высоты пирамиды SO.

б) Докажите равенство отрезков АО, ВО, СО и ДО.

в) Обоснуйте положение точки О в прямоугольнике АВСД и найдите длину высоты SO.

1. Основание пирамиды – равнобедренный треугольник с основанием а и углом при вершине . Все двугранные углы при основании пирамиды равны .

а) Опишите построение высоты пирамиды, высот боковых граней и их проекций на плоскость основания. Обоснуйте двугранные углы при основании пирамиды.

б) обоснуйте положение основания высоты пирамиды в данном равнобедренном треугольнике.

в) Найдите высоту пирамиды.

Вариант Б.

1. Основание пирамиды – равнобедренный треугольник с боковой стороной b и углом при основании . Все боковые ребра пирамиды наклонены к плоскости основания под углом .

а) Обоснуйте положение основания высоты пирамиды в данном равнобедренном треугольнике.

б) Определите, при каких значениях ? высота пирамиды будет находиться вне пирамиды.

в) Найдите высоту пирамиды.

1. Основание пирамиды – ромб с большей диагональю d и острым углом . Все двугранные углы при основании пирамиды равны .

а) Обоснуйте данные двугранные углы и положение основания высоты пирамиды в ромбе.

б) Найдите высоту пирамиды.

в) Двумя способами – путем вычисления площадей боковых граней и с помощью теоремы об ортогональной проекции многоугольника – найдите боковую поверхность пирамиды. Сравните полученные результаты.

Вариант В.

1. Основание пирамиды – треугольник с углами и . Точка высоты пирамиды, удаленная от плоскости основания на расстояние d, равноудалена от концов бокового ребра. Все боковые ребра пирамиды наклонены к плоскости основания под углом .

а) Обоснуйте положение основания высоты пирамиды.

б) При каких условиях высота пирамиды лежит внутри пирамиды?

в) Найдите высоту пирамиды.

г) Найдите площадь основания пирамиды.

1. В основании пирамиды лежит равнобокая трапеция с острым углом . Высота пирамиды равна Н, а все двугранные углы при основании равны .

а) обоснуйте положение основания высоты пирамиды.

б) Найдите высоту трапеции, лежащей в основании пирамиды.

в) Не вычисляя площадей боковых граней, найдите боковую поверхность пирамиды.

Пирамиды, в которых одна или две боковые грани перпендикулярны плоскости основания.

Вариант А.

1. Основание пирамиды – равнобедренный треугольник с боковой стороной b и углом при вершине . Боковые грани пирамиды, содержащие стороны данного угла перпендикулярны плоскости основания, а третья боковая грань наклонена к ней под углом .

а) Обоснуйте положение высоты пирамиды.

б) Обоснуйте угол .

в) Найдите площадь третьей боковой грани.

г) Найдите боковую поверхность пирамиды.

1. Основание пирамиды – правильный треугольник со стороной а. Одна из боковых граней пирамиды перпендикулярна плоскости основания, а две другие – наклонены к ней под углом .

а) Из вершины пирамиды в плоскости грани, перпендикулярной основанию, проведите перпендикуляр к ребру основания и обоснуйте, почему он будет высотой пирамиды.

б) Обоснуйте углы наклона, равные .

в) Докажите, что основание высоты пирамиды равноудалено от двух сторон правильного треугольника, и обоснуйте положение основания высоты на стороне правильного треугольника.

г) Найдите боковую поверхность пирамиды.

Вариант Б.

1. Основание пирамиды – квадрат со стороной а, две смежные боковые грани пирамиды перпендикулярны плоскости основания, а две другие – наклонены к ней под углом .

а ) Обоснуйте положение высоты пирамиды.

б ) Обоснуйте углы, равные .

в ) Докажите, что боковые грани пирамиды попарно равны.

г ) Найдите боковую поверхность пирамиды.

1. Основание пирамиды – прямоугольный треугольник с гипотенузой с и острым углом . Боковая грань, содержащая катет, противолежащий данному углу , перпендикулярна плоскости основания, а две другие грани наклонены к ней под углом .

а) Обоснуйте положение высоты пирамиды.

б) Обоснуйте положение основания высоты пирамиды.

в) Найдите высоту пирамиды.

г) Найдите боковую поверхность пирамиды.

Вариант В.

1. Основание пирамиды – ромб с тупым углом . Две боковые грани, содержащие стороны этого угла, перпендикулярны плоскости основания, а две другие – наклонены к ней под углом . Высота пирамиды равна Н.

а) Обоснуйте положение высоты пирамиды.

б) Обоснуйте углы, равные .

в) Найдите боковую поверхность пирамиды.

1. Основание пирамиды – прямоугольная трапеция с острым углом ? и прилежащей к нему боковой стороной . Боковая грань, содержащая большее основание трапеции, перпендикулярна плоскости основания, а три другие грани наклонены к ней под углом .

а ) Обоснуйте положение высоты пирамиды.

б) Обоснуйте положение основания высоты пирамиды.

в) Найдите площадь основания пирамиды.

г) Найдите боковую поверхность пирамиды.

Пирамиды, в которых заданы расстояния между точками и элементами пирамиды.

Вариант А.

1. В правильной треугольной пирамиде боковое ребро наклонено к плоскости основания под углом . Расстояние от середины высоты пирамиды до середины бокового ребра равно d.

б ) Найдите площадь основания пирамиды.

1. В правильной четырехугольной пирамиде двугранный угол при основании равен . Расстояние от середины высоты пирамиды до ее апофемы равно l . Найдите боковую поверхность пирамиды.

Вариант Б.

1. В правильной четырехугольной пирамиде двугранный угол при основании равен . Расстояние от основания высоты пирамиды до середины апофемы равно l . Найдите полную поверхность пирамиды.
2. Основание пирамиды – равнобедренный треугольник с углом при вершине. Все боковые ребра пирамиды наклонены к плоскости основания под углом . Биссектриса этого угла пересекает высоту пирамиды в точке, удаленной от бокового ребра на расстояние d.

б ) Найдите площадь основания пирамиды.

Вариант В.

1. Основание пирамиды – равнобедренный треугольник с углом при основании . Все двугранные углы при основании пирамиды равны . Отрезок, соединяющий точки пересечения медиан боковых граней, содержащих боковые стороны треугольника, равен m. Найдите боковую поверхность пирамиды.
2. Основание пирамиды – прямоугольный треугольник с острым углом . Боковые грани пирамиды, содержащие катеты треугольника, перпендикулярны плоскости основания, а третья боковая грань наклонена к ней под углом . Расстояние от основания высоты пирамиды до этой грани равно l. Найдите боковую поверхность пирамиды.

Указанный в статье перечень задач может быть расширен Вами и вашими учениками.

Пирамиды с высотой в центре вписанной или описанной окружности основания

Этот видеоурок доступен по абонементу

У вас уже есть абонемент? Войти

Данный урок поможет получить представление о теме «Пирамиды, у которых высота проектируется в центр описанной или вписанной окружности основания». На этом занятии мы научимся решать задачи на пирамиды, в которых высота проектируется в центр описанной или вписанной окружности.