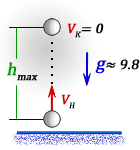
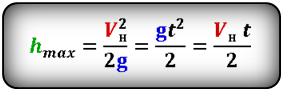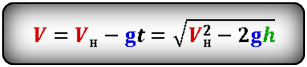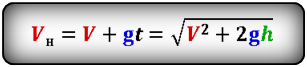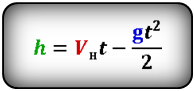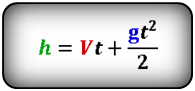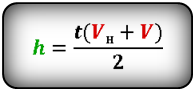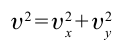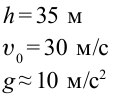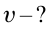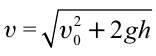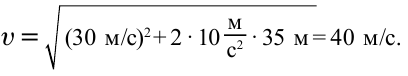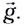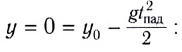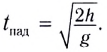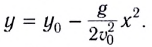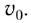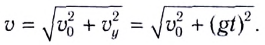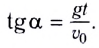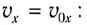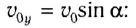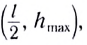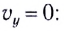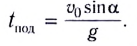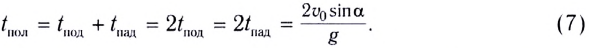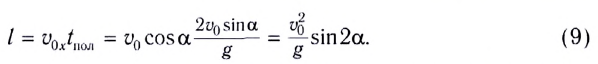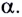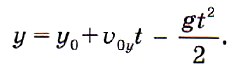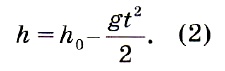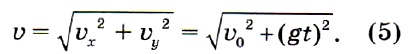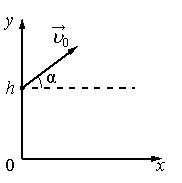1. Формулы максимальной высоты и времени за которое тело поднялось на максимальную высоту
h max
— максимальная высота достигнутая телом за время t
Vк — конечная скорость тела на пике, равная нулю
Vн — начальная скорость тела
t — время подъема тела на максимальную высоту h
g ≈ 9,8 м/с2 — ускорение свободного падения
Формула максимальной высоты (h max):
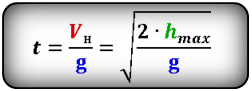
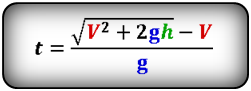
Формула времени за которое тело достигло максимальную высоту (t):
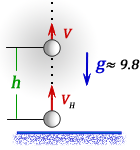
2. Формулы скорости, высоты и времени тела брошенного вертикально вверх под воздействием силы тяжести
h — расстояние пройденное телом за время t
Vн — начальная скорость тела
V — скорость тела в момент времени t
t — время подъема за которое тело пролетело расстояние h
g ≈ 9,8 м/с2 — ускорение свободного падения
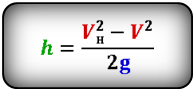
Формула скорости тела в момент времени t (V):
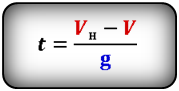
Формула начальной скорости тела (Vн):
Формулы высоты тела в момент времени t (h):
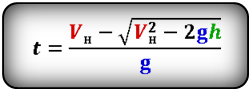
Формулы времени, за которое тело достигло высоту h (t):
- Подробности
-
Опубликовано: 04 августа 2015
-
Обновлено: 13 августа 2021
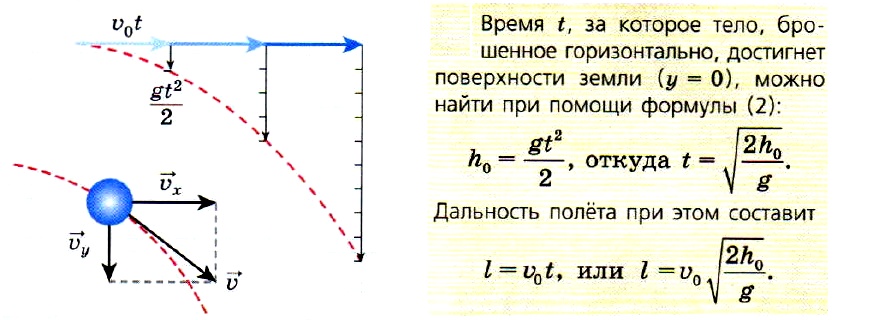
Движение горизонтально брошенного тела:
Рассмотрим движение шара, движущегося прямолинейно по поверхности стола с высотой
При достаточно малом сопротивлении воздуха, которым можно пренебречь, тело будет двигаться в горизонтальном направлении равномерно со скоростью 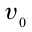
в горизонтальном направлении в любой момент времени 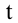
Проекции скорости тела на оси 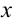
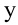
В вертикальном же направлении, двигаясь равноускоренно без начальной скорости, тело будет свободно падать с высоты 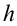
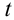
Из соотношений (1.21) и (1.22) уравнение траектории движения горизонтально брошенного тела на плоскости 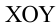
Выражение (1.24) является уравнением параболы. Значит, горизонтально брошенное тело будет двигаться по параболической линии. Время полета тела, брошенного горизонтально с высоты 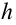
В этом случае формула для расчета длины полета тела будет иметь вид:
Горизонтально брошенное тело, одновременно двигаясь в горизонтальном направлении равномерно и в вертикальном направлении равноускоренно, свободно падает. К концу движения (после истечения времени 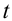
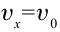
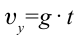
или
Перемещение и траектория тела при криволинейном движении неравны между собой. Модуль вектора и направление движения горизонтально брошенного тела на протяжении движения меняются непрерывно.
Образец решения задачи:
Тело брошено горизонтально на высоте 35 м со скоростью 30м/с. Найти скорость тела при падении на землю.
Дано:
Найти:
Формула:
Решение:
Ответ: 40 м/c.
Движение тела, брошенного горизонтально и под углом к горизонту
Если материальная точка участвует одновременно в нескольких движениях, то такое движение называют сложным.
Примером сложного движения является движение под действием силы тяжести в том случае, если падающему телу сообщена начальная скорость, непараллельная вектору ускорения свободного падения.
Рассмотрим движение тела, брошенного горизонтально со скоростью 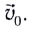
Это сложное движение можно представить в виде суммы двух независимых движений — равномерного с постоянной скоростью 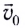
Движение тела в горизонтальном направлении будет описываться уравнением
а в вертикальном — уравнением
Здесь 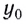
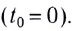
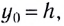
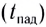
условия
Для получения уравнения траектории движения у(х) необходимо исключить время из уравнений движения (1) и (2). Из уравнения (1) выражаем время t и подставляем в уравнение (2). Получаем
Это уравнение параболы, ветви которой направлены вниз, так как коэффициент перед множителем 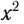
Скорость вдоль направления оси Ох остается неизменной и равной
Вдоль оси Оу движение равноускоренное. В начальный момент времени вертикальная составляющая скорости равна нулю 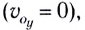
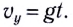
Угол между начальной скоростью 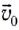
В приведенных формулах сопротивление воздуха не учитывается.
Рассмотрим теперь движение тела, брошенного со скоростью 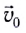
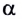
Это сложное движение можно представить в виде суммы двух независимых движений — равномерного в горизонтальном направлении со скоростью
и равноускоренного в вертикальном направлении с ускорением 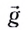
скоростью
В том случае, если система координат выбрана так, что начальные координаты 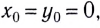
Как и при движении тела, брошенного горизонтально, траектория представляет собой параболу, ветви которой направлены вниз, поскольку коэффициент перед 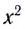
где l — дальность полета тела, 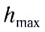
Модули горизонтальной 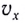
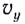
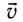
Мгновенную скорость 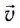
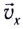
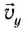
Время подъема тела можно найти из условия
Если сопротивление воздуха при движении не учитывается, то время подъема равно времени падения: 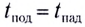
Таким образом, время полета тела можно найти как
Определив вертикальную составляющую скорости 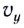
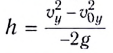
Максимальная высота подъема тела 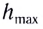
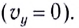
Дальность полета l — расстояние, пройденное телом за время полета 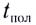
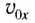
Таким образом, дальность полета определяется модулем начальной скорости 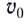
Заметим, что согласно формуле (9) при неизменном модуле начальной скорости тела максимальная дальность 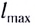
- Движение тела, брошенного под углом к горизонту
- Принцип относительности Галилея
- Движение в гравитационном поле
- Зависимость веса тела от вида движения
- Вертикальное движение тел в физик
- Неравномерное движение по окружности
- Равномерное движение по окружности
- Взаимная передача вращательного и поступательного движения
Конспект по физике для 9 класса «Движение тела, брошенного горизонтально». Как движется тело, брошенное горизонтально. Как найти дальность и высоту полёта тела, брошенного горизонтально. Как найти модуль скорости тела, брошенного горизонтально.
Конспекты по физике Учебник физики Тесты по физике
Движение тела,
брошенного горизонтально
Мы рассмотрели самые простые случаи движения тела под действием силы тяжести: свободное падение и движение тела, брошенного вертикально вверх. Теперь рассмотрим случай, когда тело, движущееся под действием силы тяжести, имеет начальную скорость, направленную горизонтально. Примерами такого движения могут быть: движение мяча, брошенного горизонтально; движение стрелы, выпущенной из лука горизонтально, и т. п.
ПРИНЦИП СЛОЖЕНИЯ ДВИЖЕНИИ
До сих пор мы рассматривали только прямолинейное движение, для описания которого было достаточно одной координатной оси. При этом сила тяжести, действующая на тело, была параллельна этой оси.
Пусть шарик движется без трения по горизонтальной поверхности со скоростью ʋ0. Согласно первому закону Ньютона в горизонтальном направлении никакие силы на шарик не действуют (он движется равномерно). При движении по плоскости сила тяжести, действующая на шарик, компенсируется силой реакции опоры, т. е. равнодействующая этих сил равна нулю. В момент, когда шарик достигает края горизонтальной поверхности, сила реакции опоры исчезает. При этом в горизонтальном направлении шарик продолжает своё движение по инерции с той же скоростью ʋ0. А в вертикальном направлении на него теперь действует только сила тяжести (силой сопротивления воздуха мы пренебрегаем), поэтому он начинает равноускоренное движение вниз с ускорением свободного падения g.
Таким образом, движение шарика можно представить как сложение двух независимых движений: движения вдоль горизонтальной оси ОХ и движения вдоль вертикальной оси OY.
Изучением движения тел, брошенных горизонтально, занимался Галилей. В своих трудах этот вид движения он описал как сумму двух движений: по горизонтали и по вертикали, введя тем самым в механику принцип сложения движений.
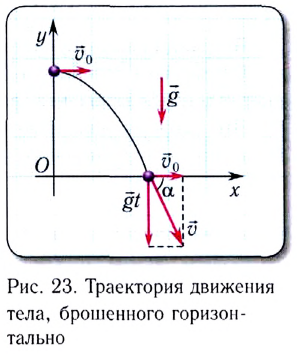
ТРАЕКТОРИЯ ДВИЖЕНИЯ ТЕЛА, БРОШЕННОГО ГОРИЗОНТАЛЬНО
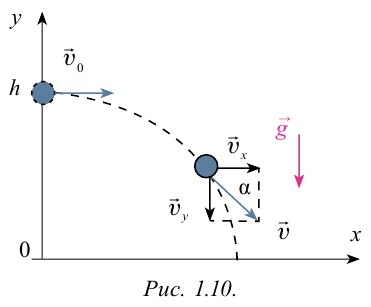
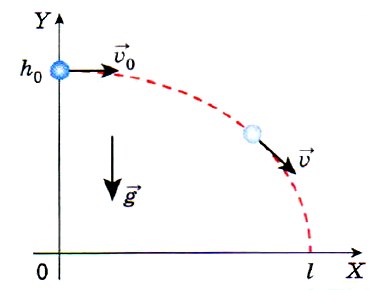
Рассмотрим движение тела, брошенного с высоты h0 и имеющего начальную скорость ʋ0. Для описания этого движения направим координатную ось ОХ горизонтально, а ось ОY направим вертикально вверх. Траектория этого движения имеет вид плавной кривой, называемой параболой. Движение, при котором траектория не является прямой линией, называют криволинейным.
ДВИЖЕНИЕ ВДОЛЬ ВЕРТИКАЛЬНОЙ ОСИ
Проекция ускорения свободного падения на ось OY отрицательна и равна gy = -g. Направление начальной скорости ʋ0 совпадает с направлением оси ОХ, поэтому ʋ0у = 0.
Поскольку скорость тела, движущегося равноускоренно, в момент времени t можно найти по формуле
Найдём высоту h, на которой находится тело в момент времени t. Для этого воспользуемся уравнением движения тела:
Обозначим начальную высоту у0 как h0. Получим
Проведём на листе клетчатой бумаги вертикальную и горизонтальную линии. Так как движения в горизонтальном и вертикальном направлениях происходят независимо друг от друга, то через время t с тело переместится на отрезок ʋ0t вправо и на отрезок gt2/2 вниз. Если отложить по горизонтали отрезок ʋ0t, а из его конца вертикальный отрезок gt2/2, то получится точка, в которой тело окажется через t с. Сделав подобное построение для нескольких промежутков времени и соединив эти точки плавной линией, получим ветвь параболы.
СКОРОСТЬ ТЕЛА, БРОШЕННОГО ГОРИЗОНТАЛЬНО
Мы уже знаем, что движение тела, брошенного горизонтально, можно рассматривать как сложение движений вдоль горизонтальной и вертикальной осей. В каждый момент времени такое тело имеет мгновенную скорость ʋ, проекции которой можно найти по формулам (1) и (3).
Если обозначить скорость движения тела вдоль оси ОХ через ʋx, а его скорость вдоль оси OY через ʋу, то можно записать:т. е. вектор скорости тела можно найти как сумму векторов скоростей тела вдоль осей.
Для того чтобы изобразить вектор, являющийся суммой двух векторов, используют правило параллелограмма: для векторов с общим началом их сумма изображается диагональю параллелограмма, построенного на этих векторах.
В нашем случае векторы ʋx и ʋу перпендикулярны друг другу, поэтому их сумма — диагональ прямоугольника. Значение (модуль) скорости тела в любой момент времени можно найти по теореме Пифагора:
Вы смотрели Конспект по физике для 9 класса «Движение тела, брошенного горизонтально».
Вернуться к Списку конспектов по физике (Оглавление).
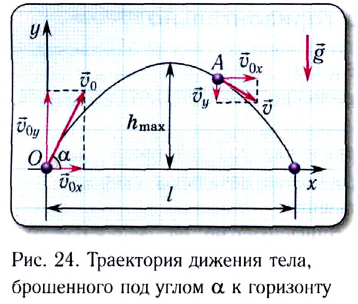
Когда тело бросают вверх под углом к горизонту, оно сначала равнозамедленно поднимается, а затем равноускорено падает. При этом оно перемещается относительно земли с постоянной скоростью.
Важные факты!График движения тела, брошенного под углом к горизонту:
α — угол, под которым было брошено тело
- Вектор скорости тела, брошенного под углом к горизонту, направлен по касательной к траектории его движения.
- Так как начальная скорость направлена не вдоль горизонтальной линии, обе ее проекции отличны от нуля. Проекция начальной скорости на ось ОХ равна v0x = v0cosα. Ее проекция на ось ОУ равна v0y = v0sinα.
- Проекция мгновенной скорости на ось ОХ равна: vx = v0 cosα. Ее проекция на ось ОУ равна нулю: vy = v0 sinα – gt.
- Проекция ускорения свободного падения на ось ОХ равна нулю: gx = 0. Ее проекция на ось ОУ равна –g: gy = –g.
Кинематические характеристики
Модуль мгновенной скорости в момент времени t можно вычислить по теореме Пифагора:
Минимальной скорости тело достигает в верхней точке траектории. Она выражается формулой:
vmin = v0 cosα = vh
Максимальной скоростью тело обладает в момент начала движения и в момент падения на землю. Начальная и конечная скорости движения тела равны:
vmax = vo = v
Время подъема — время, которое требуется телу, чтобы достигнуть верхней точки траектории. В этой точке проекция скорости на ось ОУ равна нулю: vy = 0. Время подъема определяется следующей формулой:
Полное время — это время всего полета тела от момента бросания до момента приземления. Так как время падения равно времени подъема, формула для определения полного времени полета принимает вид:
Дальность полета — перемещение тела относительно ОХ. Обозначается буквой l. Так как относительно ОХ тело движется с постоянной скоростью, для вычисления дальности полета можно использовать формулу перемещения при равномерном прямолинейном движении:
l = sx = v0x tполн = v0 cosα tполн
Подставляя в выражение формулу полного времени полета, получаем:
Горизонтальное смещение тела — смещение тела вдоль оси ОХ. Вычислить горизонтальное смещение тела в любой момент времени t можно по формуле координаты x:
Учитывая, что x0 = 0, и проекция ускорения свободного падения на ось ОХ тоже равна нулю, а проекция начальной скорости на эту ось равна v0 cosα, данная формула принимает вид:
x = v0 cosα t
Мгновенная высота — высота, на которой находится тело в выбранный момент времени t. Она вычисляется по формуле координаты y:
Учитывая, что начальная координата равна 0, проекция начальной скорости на ось ОУ равна v0 sinα, а проекция ускорения свободного падения на эту ось равна –g, эта формула принимает вид:
Наибольшая высота подъема — расстояние от земли до верхней точки траектории. Наибольшая высота подъема обозначается h и вычисляется по формуле:
Пример №1. Небольшой камень бросили с ровной горизонтальной поверхности под углом к горизонту. На какую максимальную высоту поднялся камень, если ровно через 1 с после броска его скорость была направлена горизонтально?
Скорость направляется горизонтально в верхней точке полета. Значит, время подъема равно 1 с. Из формулы времени подъема выразим произведение начальной скорости на синус угла, под которым было брошено тело:
v0 sinα = gtпод
Подставим полученное выражение в формулу для определения наибольшей высоты подъема и сделаем вычисления:
Тело, брошенное под углом к горизонту с некоторой высоты
Когда тело бросают под углом к горизонту с некоторой высоты, характер его движения остается прежним. Но приземлится оно дальше по сравнению со случаем, если бы тело бросали с ровной поверхности.
Важные факты!
График движения тела, брошенного под углом к горизонту с некоторой высоты:
Время падения тела больше времени его подъема: tпад > tпод.
Полное время полета равно:
tполн = tпад + tпод
Уравнение координаты x:
x = v0 cosα t
Уравнение координаты y:
Пример №2. С балкона бросили мяч под углом 60 градусов к горизонту, придав ему начальную скорость 2 м/с. До приземления мяч летел 3 с. Определить дальность полета мяча.
Косинус 60 градусов равен 0,5. Подставляем известные данные в формулу:
x = v0 cosα t = 2 ∙ 0,5 ∙ 3 = 3 м.
Задание EF17562
С высоты Н над землёй начинает свободно падать стальной шарик, который через время t = 0,4 c сталкивается с плитой, наклонённой под углом 30° к горизонту. После абсолютно упругого удара он движется по траектории, верхняя точка которой находится на высоте h = 1,4 м над землёй. Чему равна высота H? Сделайте схематический рисунок, поясняющий решение.
Алгоритм решения
1.Записать исходные данные.
2.Построить на чертеже начальное и конечное положения тела. Выбрать систему координат.
3.Выбрать нулевой уровень для определения потенциальной энергии.
4.Записать закон сохранения энергии.
5.Решить задачу в общем виде.
6.Подставить числовые значения и произвести вычисления.
Решение
Запишем исходные данные:
• Время падения стального шарика: t = 0,4 c.
• Верхняя точка траектории после абсолютно упругого удара о плиту: h = 1,4 м.
• Угол наклона плиты: α = 30о.
Построим чертеж и укажем на нем все необходимое:
Нулевой уровень — точка D.
Закон сохранения энергии:
Ek0 + Ep0 = Ek + Ep
Потенциальная энергия шарика в точке А равна:
EpA = mgH
Кинетическая энергия шарика в точке А равна нулю, так как скорость в начале свободного падения нулевая.
В момент перед упругим ударом с плитой в точке В потенциальная энергия шарика минимальна. Она равна:
EpB=mgl1
Перед ударом кинетическая энергия шарика равна:
EkB=mv22
Согласно закону сохранения энергии:
EpA=EpB+EkB
mgH=mgl1+mv22
Отсюда высота H равна:
H=mgl1mg+mv22mg=l1+v22g
Относительно точки В шарик поднимется на высоту h – l1. Но данный участок движения можно рассматривать как движение тела, брошенного под углом к горизонту. В таком случае высота полета определяется формулой:
h−l1=v2sin2β2g=v2sin2(90−2α)o2g
Отсюда:
l1=h−v2sin2(90−2α)o2g
Шарик падал в течение времени t, поэтому мы можем рассчитать высоту шарика над плитой и его скорость в точке В:
v=gt
Следовательно:
H=l1+v22g=h−(gt)2sin2(90−2α)o2g+(gt)22g
H=h−gt2sin2(90−2α)2+gt22=h−gt22(sin2(90−2α)o−1)
H=1,4−10·0,422(sin2(90−60)o−1)
H=1,4−5·0,16(sin230o−1)
H=1,4−0,8((12)2−1)=1,4−0,8(14−1)
H=1,4+0,6=2 (м)
Ответ: 20
pазбирался: Алиса Никитина | обсудить разбор
Задание EF17980
В момент t=0 мячик бросают с начальной скоростью v0 под углом α к горизонту с балкона высотой h (см. рисунок).
Графики А и Б представляют собой зависимости физических величин, характеризующих движение мячика в процессе полёта, от времени t. Установите соответствие между графиками и физическими величинами, зависимости которых от времени эти графики могут представлять. (Сопротивлением воздуха пренебречь. Потенциальная энергия мячика отсчитывается от уровня y=0).
К каждой позиции графика подберите соответствующую позицию утверждения и запишите выбранные цифры в порядке АБ.
Алгоритм решения
- Установить вид механического движения, исходя из условий задачи.
- Записать формулы для физических величин, указанных в таблице, в соответствии с установленным видом механического движения.
- Определить, как зависят эти величины от времени.
- Установить соответствие между графиками и величинами.
Решение
Исходя из условия задачи, мячик движется неравномерно. Этот случай соответствует движению тела, брошенного под углом к горизонту.
Записываем формулы для физических величин из таблицы, учитывая, что речь идет о движении тела, брошенного под углом к горизонту.
Координата x меняется согласно уравнению координаты x:
Так как начальная координата нулевая, а проекция ускорения свободного падения тоже равна нулю, это уравнение принимает вид:
Проекция скорости мячика на ось ОХ равна произведению начальной скорости на время и косинус угла, под которым мячик был брошен. Поэтому уравнение координаты x принимает вид:
В этом уравнении начальная скорость и угол α — постоянные величины. Меняется только время. И оно может только расти. Поэтому и координата x может только расти. В этом случае ей может соответствовать график, представляющий собой прямую линии, не параллельную оси времени. Но графики А и Б не могут описывать изменение этой координаты.
Формула проекции скорости мячика на ось ОХ:
Начальная скорость и угол α — постоянные величины. И больше ни от чего проекция скорости на ось ОХ не зависит. Поэтому ее может охарактеризовать график в виде прямой линии, параллельной оси времени. Такой график у нас есть — это Б.
Кинетическая энергия мячика равна половине произведения массы мячика на квадрат его мгновенной скорости. По мере приближения к верхней точке полета скорость тела уменьшается, а затем растет. Поэтому кинетическая энергия также сначала уменьшается, а затем растет. Но на графике А величина наоборот — сначала увеличивается, потом уменьшается. Поэтому он не может быть графиком зависимости кинетической энергии мячика от времени.
Остается последний вариант — координата y. Уравнение этой координаты имеет вид:
Это квадратическая зависимость, поэтому графиком зависимости координаты y от времени может быть только парабола. Так как мячик сначала движется вверх, а потом — вниз, то и график должен сначала расти, а затем — убывать. График А полностью соответствует этому описанию.
Теперь записываем установленные соответствия в порядке АБ: 42.
Ответ: 42
pазбирался: Алиса Никитина | обсудить разбор
Задание EF18741
Мальчик бросил стальной шарик вверх под углом к горизонту. Пренебрегая сопротивлением воздуха, определите, как меняются по мере приближения к Земле модуль ускорения шарика и горизонтальная составляющая его скорости?
Для каждой величины определите соответствующий характер изменения:
- увеличивается
- уменьшается
- не изменяется
Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
Алгоритм решения
- Сделать чертеж, иллюстрирующий ситуацию.
- Записать формулы, определяющие указанные в условии задачи величины.
- Определить характер изменения физических величин, опираясь на сделанный чертеж и формулы.
Решение
Выполняем чертеж:
Модуль ускорения шарика |g| — величина постоянная, так как ускорение свободного падения не меняет ни направления, ни модуля. Поэтому модуль ускорения не меняется (выбор «3»).
Горизонтальная составляющая скорости шарика определяется формулой:
vx = v0 cosα
Угол, под которым было брошено тело, поменяться не может. Начальная скорость броска тоже. Больше ни от каких величин горизонтальная составляющая скорости не зависит. Поэтому проекция скорости на ось ОХ тоже не меняется (выбор «3»).
Ответом будет следующая последовательность цифр — 33.
Ответ: 33
pазбирался: Алиса Никитина | обсудить разбор
Алиса Никитина | Просмотров: 43.4k

На все тела в воздухе, как и в жидкости, действует выталкивающая, или архимедова силаЧтобы найти архимедову (выталкивающую) силу, действующую на тело в газе, надо плотность газа умножить на ускорение свободного падения ((g=9,8Н/кг)) и на объём тела, находящегося в газе: FАρгазаgVтела.
Обрати внимание! Для того чтобы летательный аппарат поднялся в воздух, необходимо, чтобы архимедова сила, действующая на шар, была больше силы тяжести.
На этом основано воздухоплавание.
None Подъёмная сила воздушного шара равна разности между архимедовой силой и действующей на шар силой тяжести: FFАFтяж.
Чем меньше плотность газа, заполняющего воздушный шар данного объёма, тем меньше действующая на него сила тяжести, и поэтому тем больше подъёмная сила. Чтобы аэростат поднимался вверх, его нужно наполнить газом, плотность которого меньше, чем у воздуха. Это может быть водород, гелий, нагретый воздух.
Водород обладает одним большим недостатком — он горит и вместе с воздухом образует взрывчатую смесь. Негорючим и в то же время лёгким газом является гелий. Поэтому многие аэростаты в наше время наполняют гелием.
Тёплый воздух удобен тем, что его температуру (а значит, и его плотность, и подъёмную силу) можно регулировать с помощью газовой горелки, расположенной под отверстием, находящимся в нижней части шара. При увеличении пламени горелки — шар поднимается выше, при уменьшении пламени горелки — шар опускается вниз. Можно подобрать такую температуру, при которой сила тяжести, действующая на шар вместе с кабиной, оказывается равной выталкивающей силе. Тогда шар повисает в воздухе, и с него легко проводить наблюдения.
Плотность воздуха уменьшается с увеличением высоты. Поэтому по мере поднятия аэростата вверх действующая на него архимедова сила становится меньше. После того, как архимедова сила достигает значения, равного силе тяжести, подъём аэростата прекращается. Чтобы подняться выше, с шара сбрасывают специально взятый для этого балласт (высыпают песок из мешков). При этом сила тяжести уменьшается, и выталкивающая сила вновь оказывается преобладающей. Для того чтобы опуститься на землю, выталкивающую силу, наоборот, следует уменьшить. Это достигается путём уменьшения объёма шара. В верхней части шара открывают клапан, часть газа из шара выходит, и он начинает опускаться вниз.
Источники: Громов С. В. Физика: Учеб.
для 7 кл. общеобразоват. учреждений/ Громов С.
В. Родина Н. А.
— 4-е изд. — М. : Просвещение, 2002.
— 158 с. : ил.
Подъемная сила гелия. Сколько гелиевых шаров нужно чтобы поднять игрушку, открытку, шоколадку? Эти вопросы очень часто задают наши заказчики.
Рассчитать кол-во шаров достаточно просто, нужно знать точный вес изделия, которое необходимо поднять с помощью гелиевых шаров. Еще нужно четко понимать задачу : изделие нужно поднять в помещении или на улице, как долго нужно чтобы вся конструкция находилась в воздухе?
Первый примерный расчет такой: 1м3 гелия поднимает примерно 1 КГ. Или 1 стандартный шарик 27см в диаметре поднимает всего 3-4 грамма. Так например, чтобы поднять игрушку весом 250 грамм понадобиться 250/4 = примерно 62 шарика, на практике хватит и 50 шт.
, т. к даже лента на шарике имеет вес и ее можно укоротить. Когда вы покупаете подарок, то как правило не сложно где-то рядом найти весы и взвесить его, чтобы понять реальна ли Ваша задумка.
Большие веса дешевле поднимать с помощью больших гелиевых шаров, т. к вес одного большого шара меньше, чем вес большого кол-ва маленьких гелиевых шариков при одном и том же объеме гелия. Рассчитать подъемную силу большого шара можно условно рассчитав объем гелия в таком шаре по формуле 4/3 пr3 и дальше применив принцип 1 м3 гелия примерно 1 кг веса.
Например берем шар 1 м в диаметре. Получаем по формуле объема шара 4/3*3,14*0,53 = 0,522м3 что соответственно равно примерно 0,5 кг. От этого веса необходимо вычесть вес самого шарика и вес ленточки за которую он зацеплен, это и будет расчетный вес, который можно поднять с помощью этого шара в помещении.
На улице такие расчеты сделать сложно, т. к на гелиевый шарик постоянно могут воздействовать погодные условия: снег, дождь, ветер, солнце или наоборот низкая температура. Эти факторы, особенно ветер и осадки сильно влияют на подъемную силу шара.
Так например, затея с летающим возле окон любимой сердцем из воздушных шариков, иногда может просто провалиться если будет сильный ветер. Дата: 17. 01.
2018Сайт автора: https://zeppelin. kz
! Пометить как спам
Статьи рубрики Отдых и развлечения
| Правила зимнего фитнеса или Как не впасть в спячку, когда холодно? Раздел справочника: Красота и здоровье Дата: Зимой природа отдыхает… на сонях. Наш организм так же, как и все живое, подчиняется сезонным биоритмам. С первыми холодами обмен веществ постепенно замедляется, и запасы жира в самых неподходящих местах увеличиваются. Понятно, что такие “заготовки” нужны организму, чтобы защитить от мороза внутренние органы. Но каждый из нас предпочел бы, чтобы без ущерба для фигуры грели нас не “валики” на талии, а шубы, шапки, перчатки и шарфы. Увы и ах, природу нелегко уговорить на такой компромисс. Единственное, что остается – не клевать носом и продолжать вести активный образ жизни! Как это сделать, и какие правила нужно соблюдать зимой, чтобы не набрать лишний вес? 1. Не делайте из еды культа! Литературная цитата Ильфа и Петрова вполне может стать девизом по жизни. И не только зимой. |
| Сноркелинг на Ко Тао Раздел справочника: Отдых и развлечения Дата: Кораллы начинаются прямо от песчаного берега. «На что это похоже? – играю я в игру, проплывая c маской над кораллами. Все они на что-то похожи. . . . на бледные поганки, на перевернутые пластинчатые сыроежки, на древесную чагу, на строчки, сморчки и на переросшие грузди. На розы и капусту. На плесень. На коровью лепешку. На лопоухие кактусы. На сталагмиты, на муравейник, на горы с самолета. На лосиные замшевые рожки. На головки иван-чая, качающиеся под ветром, на мелкие цветочки мать-и-мачехи на холме. На заиндевевшие веточки деревьев, на ледяные горки, на морозные узоры на стекле. На боровой мох. На выкопанную картошку. На торт со взбитыми сливками. На пустые напольные вазы. На мозг со всеми извилинами и полушариями. . . А все вместе похоже на сновидение. Вроде все как в реальности, но что-то не так. Размеры не совпадают. Цвета, как в преисподней. К примеру – роза как роза. Но бледно-зеленая… Иван-чай, но грязно-коричневый… Клубни картошки, но голубые… Человеческий. |
| Евпатория Раздел справочника: Отдых и развлечения Дата: Крым – одно из лучших мест на Земле – постоянно привлекает к себе множество туристов. Обладая великолепными природными ресурсами, этот участок суши, расположенный в северной части Чёрного моря, может предложить туристам многочисленные возможности хорошо провести свой отпуск, поэтому отдых в Крыму пользуется большим спросом у граждан Украины, ближнего и дальнего зарубежья. Миллионы туристов приезжают ежегодно сюда, чтобы совместить пляжный морской отдых с различными видами активного отдыха, и их ожидания полностью оправдываются: они возвращаются домой отдохнувшими, полными сил и набравшимися новых впечатлений. Лучшие курорты Крыма расположены вдоль южного берега полуострова, и многие из них имеют всемирную известность. Один из таких курортов – Евпатория, которая расположена в западной части крымского побережья, на берегу обширного Каламитского залива. Отдых в Евпатории пользуется большой популярностью у туристов, и они приезжают сюда с конца весны и до середины осени. Евпатория – признанный климатический и бальнеологический курорт. Кроме того, она давно стала центром детского отдыха, и туристы приезжают сюда отдыхать. |
| Заработать на карточной игре “дурак” вполне реально Раздел справочника: Отдых и развлечения Дата: Если вы решите начать зарабатывать в сети интернет, то для этого вы найдете множество способов, но, как правило, все они требуют от желающего заработать наличие каких-либо специальных знаний. В связи с чем прежде, чем вы положите на свой счет первые сто долларов, вам придется приложить немало усилий направленных на то, чтобы приобрести некоторые навыки, которые помогут вам получить заработок в сети. Тем не менее, среди способов заработка существуют такие, которые потребуют от вас только проявления личностных качеств и уже имеющихся навыков. Одним из таких способов заработка является игра дурак. В повседневной жизни вы наверняка не раз играли в эту игру. Практически невозможно встретить человека, который не знал бы правил данной игры, в связи с этим изучать правила, знакомится со стратегией указанной игры, вам наверняка не потребуется. Поэтому достаточно зарегистрироваться на сайте http://www. fartu. ru и вы получите возможность улучшить свое материальное благополучие. |
Основной принцип работы воздушного шара заключается в использовании горячего воздуха для создания подъемной силы. Основные компоненты шара – оболочка, гондола или плетеная корзина, подвешенная под ним. Горелка, установленная в корзине, используется для нагрева воздуха через отверстие.
Горячий воздух (внутри оболочки) менее плотный, чем холодный (окружающий воздух). Разница в плотности вызывает подъемную силу. Выталкивающая сила, создаваемая окружающим воздухом, равна весу охладителя, вытесняемого при подъеме шара.
При этом, подъемная сила больше веса нагретого воздуха внутри оболочки, а точнее больше суммы веса: нагретого воздуха, оболочки, гондолы (корзины), пассажиров и оборудования на борту. В результате, воздушный шар испытывает достаточно высокую выталкивающую силу, обеспечивающую отрыв шара от земли.
Вес летательного аппарата сконцентрирован вблизи дна баллона (в месте нахождения пассажиров и оборудования), так что центр его веса всегда ниже центра плавучести. Таким образом, воздушный шар всегда устойчив во время полета, то есть всегда остается в вертикальном положении.
Определение высоты и направления воздушного шара.
Для уменьшения подъемной силы, отключается горелка, что приводит к охлаждению воздуха в оболочке. Уменьшение силы подъема обеспечивается и при помощи фала управления отверстием, расположенным в верхней части воздушного шара. Частичный выход горячего воздуха из отверстия, уменьшает вес воздуха в шаре, а значит, уменьшает выталкивающую силу, что также приводит к опусканию летательного аппарата.
Для того, чтобы найти подъемную силу воздушного шара и поддерживать устойчивую высоту, обеспечивается периодическое выключение горелки, когда аппарат достигает нужной высоты. Это приводит к тому, что шар то спускается, то поднимется, сохраняя высоту полета на почти одном уровне. Это единственный способ, позволяющий поддерживать приблизительно постоянную высоту, так как, поддержание строго постоянной высоты путем поддержания чистой нулевой выталкивающей силы, практически невозможно.
Для движения в горизонтальном направлении, необходимо заранее знать направление ветра, которое меняется с высотой. Поэтому просто поднимая или опуская летательный аппарат с горячим воздухом, с учетом направления ветра, обеспечивается его движение в нужное направление.
Так как, оболочка имеет отверстие в нижней области (выше местоположения горелки), расширяющийся горячий воздух, частично с этого отверстия выходит из оболочки, предотвращая перепады давления. Это означает, что давление нагретого воздуха внутри баллона лишь немного выше, давления воздуха охладителя (окружающего оболочку воздуха).
Эффективным летательным аппаратом называют тот, который «сводит к минимуму вес компонентов воздушного шара» (относительное понятие). Это обеспечивает снижение требуемой температуры воздуха внутри оболочки, необходимой для создания подъемной силы. Сведение к минимуму температуры воздуха, приводит к уменьшению расхода топлива.
[custom_ads_shortcode1]
Как рассчитать подъемную силу воздушного шара.
Нагретый воздух внутри оболочки давит на стенки приблизительно с таким же давлением, как наружный. Зная это, можно вычислить плотность нагретого воздуха при данной температуре, используя закон идеального газа: P = ρ R T , где
- P – абсолютное давление газа в Па
- ρ – плотность, в кг/м3
- R – газовая постоянная, в Дж/(кг·К) (отношение теплоемкости к массе при абсолютной температуре газа в градусах Кельвина)
- T – абсолютная температура газа в градусах Кельвина (К)
Нормальное атмосферное давление приблизительно составляет 101300 Па. Газовая постоянная для сухого воздуха равна 287 Дж/(кг·К). Воздух внутри оболочки обычно нагревают до средней температуры около 100 градусов Цельсия, что составляет 373 K101300 = ρ*287*373 ρ = 101300/287*373 = 0,946 кг/м 3Подставляя вышеуказанные три значения в уравнение, получаем плотность нагретого воздуха внутри оболочки. Затем, сравнивая эту величину с плотностью окружающего воздуха, которая приблизительно равна – 1,2 кг/м 3, вычисляем подъемную силу летательного аппарата.
Объем оболочки среднего воздушного шара равен 2800 м3. Зная это, можно определить подъемную силу. Она определяется как разница между плотностью окружающего и нагретого воздуха, умноженного на объем оболочки. Таким образом, чистая подъемная сила равна:
None На данном примере, мы постарались предоставить полную и понятную информацию о том, как вычислить подъемную силу воздушного шара.
В тепловом воздушном шаре горячий воздух используется для создания подъемной силы. Внутри оболочки нагретый воздух имеет меньшую плотность, чем окружающий, благодаря чему создается выталкивающая сила. Принцип этого лифта называется принципом Архимеда, суть которого заключается в том, что на любой объект (независимо от его формы) в жидкости воздействует выталкивающая сила, равная массе вытесненной жидкости.
[custom_ads_shortcode2]
Чему равна подъемная сила воздушного шара и как ее определить?
Нагретый в оболочке воздух имеет меньшую плотность, чем окружающий. Поэтому, подъемная сила больше массы нагретого в оболочке воздуха. Чтобы найти подъемную силу воздушного шара, необходимого помнить, что выталкивающая сила должна быть больше веса нагретого воздуха и аэростата.
Вес аэростата сконцентрирован в нижней его части (в месте нахождения пассажиров и оборудования). Центр массы ниже центра плавучести, за счет чего обеспечивается устойчивый вертикальный полет.
[custom_ads_shortcode3]
Какова подъемная сила воздушного шара – управление!
Снижение аэростата производится с помощью включения/выключения горелки, или открытия верхнего небольшого отверстия. Выход горячего воздуха из шара, приводит к уменьшению выталкивающей силы. А для плавучести шара в горизонтальном направлении, пилоту приходится заранее узнавать о направлении ветра.
[custom_ads_shortcode1]
Как вычислить подъемную силу воздушного шара – физика!
На горячий воздух в оболочке действует почти такое же давление, что и на наружный. Зная это, вычислим плотность внутреннего воздуха при заданной температуре, по формуле: Р = ρ R Tгде:
- Р – абсолютное давление, измеряемое в Па (Паскаль);
- ρ – плотность, в кг/м3;
- R – универсальная постоянная, в Дж/кг*К;
- T – абсолютная температура.
None Постоянная универсальная величина для сухого воздуха – 287 Дж/кг*К.
None ρ = Р/RT = 101300:(287*373) = 0,946 кг/м3Средняя плотность окружающего воздуха – 1,2 кг/м3 .
Узнать, какова подъемная сила воздушного шара, объемом V = 2800 м3, можно по формуле:
F чистая выталкивающая сила = (ρ внешнего воздуха – ρ внутреннего воздуха)* VF = (1.2-0.946)*2800 = 711 кг = 711*9.8 = 6967.8 Н (1 кг = 9.8 Н)Следует отметить, что тепловые воздушные шары довольно большие, для обеспечения высокой выталкивающей силы.
Источники:
- www.yaklass.ru
- belarus.bestru.ru
- magicflight.ru
- magicflight.ru