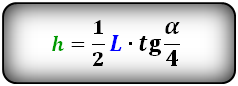Как найти высоту полуокружности формула

Формула высоты сегмента круга

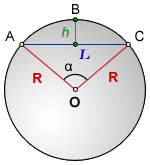
Сегмент — часть круга ABC, отсеченная хордой AC

h — высота сегмента ABC

L — хорда AC

R — радиус кружности

O — центр окружности

α — центральный угол AOC

Формула высоты через радиус и центральный угол, ( h ):

Формула высоты через хорду и центральный угол, ( h ):

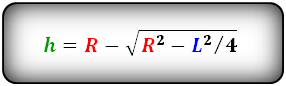
Формула высоты через радиус и хорду, ( h ):

Дополнительные формулы для окружности:

Радиус и высота сегмента круга

Свойства

Зная радиус и высоту сегмента, можно найти центральный угол α, через который становится возможным рассчитать все остальные измерения сегмента, такие как длина дуги, длина хорды и площадь сегмента круга. Из формулы высоты следует, что косинус половинного угла равен разности единицы и отношения высоты к радиусу. cos⁡〖α/2〗=1-h/r

Вычислив таким образом центральный угол сегмента круга, подставляем его в следующие формулы для длины дуги и длины хорды. Длина дуги вычисляется как произведение угла на радиус, а длина хорды находится из прямоугольного треугольника как удвоенное произведение радиуса на синус половинного угла (рис.141). P=αr c=2r sin⁡〖α/2〗

Площадь сегмента круга наряду с площадью равнобедренного треугольника, образованного двумя радиусами и хордой, является составляющей площади сектора круга. Поэтому, чтобы найти площадь сегмента необходимо вычесть из последней площадь треугольника. Упростив такое выражение, получаем половину квадрата радиуса, умноженную на разность угла α и его синуса. S=S_сек-S_тр=(r^2 α)/2-r^2 sin⁡α=1/2 r^2 (α-sin⁡α )

Длина окружности

О чем эта статья:

6 класс, 9 класс, ЕГЭ/ОГЭ

Если вы не знаете, как обозначается длина окружности, то знак окружности выглядит вот так — l

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат (в правом нижнем углу экрана).

Как найти длину окружности через диаметр

Хорда — это отрезок, который соединяет две точки окружности.

Диаметр — хорда, которая проходит через центр окружности. Формула длины окружности через диаметр:

π— число пи — математическая константа, примерно равная 3,14

d — диаметр окружности

Как найти длину окружности через радиус

Радиус окружности — отрезок, который соединяет центр окружности с точкой на окружности. Формула длины окружности через радиус:

π — число пи, примерно равное 3,14

r — радиус окружности

Это две основные формулы для вычисления длины окружности. Ниже мы покажем еще несколько формул, которые вы сможете доказать самостоятельно, пользуясь основными формулами и свойствами геометрических фигур.

Как вычислить длину окружности через площадь круга

Если вам известна площадь круга, вы также можете узнать длину окружности:

π — число пи, примерно равное 3,14

S — площадь круга

Как найти длину окружности через диагональ вписанного прямоугольника

Как измерить окружность, если в нее вписан прямоугольник:

π — число пи, примерно равное 3,14

d — диагональ прямоугольника

Как вычислить длину окружности через сторону описанного квадрата

Давайте рассмотрим, как найти длину окружности, если она вписана в квадрат и нам известна сторона квадрата:

π — математическая константа, примерно равная 3,14

a — сторона квадрата

Как найти длину окружности через стороны и площадь вписанного треугольника

Можно найти, чему равна длина окружности, если в нее вписан треугольник и известны все три его стороны, а также известна его площадь:

π — математическая константа, она примерно равна 3,14

a — первая сторона треугольника

b — вторая сторона треугольника

c — третья сторона треугольника

S — площадь треугольника

Как найти длину окружности через площадь и полупериметр описанного треугольника

Можно определить, чему равна длина окружности, если круг вписан в треугольник, и известны следующие параметры: площадь треугольника и его полупериметр.

Периметр — это сумма всех сторон треугольника. Полупериметр равен половине этой суммы, то есть чтобы его найти, вам нужно рассчитать периметр и поделить его на два.

π — математическая константа, примерно равная 3,14

S — площадь треугольника

p — полупериметр треугольника

Как вычислить длину окружности через сторону вписанного правильного многоугольника

Разбираемся, как в этом случае измерить окружность. Для этого необходимо посчитать, сколько сторон у многоугольника, а также знать длину стороны многоугольника. Напомним, что у правильного многоугольника все стороны равны, как у квадрата.

Формула вычисления длины окружности:

π — математическая константа, примерно равная 3,14

a — сторона многоугольника

N — количество сторон многоугольника

Задачи для решения

Давайте тренироваться! Двигаемся от простого к сложному:

Задача 1. Найти длину окружности, диаметр которой равен 5 см.

Решение. Итак, нам известен диаметр окружности, значит для вычисления длины заданной окружности берем формулу:

Подставляем туда известные переменные и получается, что длина окружности равна

Задача 2. Чему равна длина окружности, описанной около правильного треугольника со стороною a = 4√3 дм

Решение. Радиус окружности равен Подставим туда наши переменные и получим

Теперь, когда нам известен радиус окружности и есть формула длины окружности через радиус l=2πr, мы можем подставить наши данные и получить решение задачи.

Обучение на курсах по математике поможет закрепить полученные знания на практике.

Формула высоты сегмента круга

Круговой сегмент — часть круга ограниченная дугой и секущей (хордой).

На рисунке:
L — длина дуги сегмента
c — хорда
R — радиус
a — угол сегмента
h — высота

Первый калькулятор рассчитывает параметры сегмента, если известен радиус и угол по следующим формулам:

Формулы вычисления параметров сегмента

Площадь сегмента:
[1]
Длина дуги:

Длина хорды:

Высота сегмента:

Однако, как справедливо заметил наш пользователь:«на практике часто случается, что как радиус дуги, так и угол неизвестны» (см. длина дуги ). Для этого случая для расчета площади сегмента и длины дуги можно использовать следующий калькулятор:

Калькулятор вычисляет радиус круга по длине хорды и высоте сегмента по следующей формуле:

Далее, зная радиус и длину хорды, легко найти угол сегмента по формуле:

Остальные параметры сегмента вычисляются аналогично первому калькулятору, по формулам, приведенным в начале статьи.

Следующий калькулятор вычисляет площадь сегмента по высоте и радиусу:

Этот калькулятор вычисляет угол из высоты и радиуса по следующей формуле:

далее используется формула [1] для получения площади.

15 вычислений по сегменту круга в одной программе

Последний калькулятор включает в себя все оставшиеся вычисления параметров кругового сегмента:

• длина дуги
• угол
• хорда
• высота
• радиус
• площадь

Выберите два известных аргумента и калькулятор выдаст вам все оставшиеся.

Содержание

• Элементы и меры полукруга
• Периметр полукруга
• Площадь полукруга
• Центроид полукруга
• Момент инерции полукруга
• Вписанный угол
• Решенные упражнения
• Упражнение 1
• Решение
• Упражнение 2.
• Решение
• Упражнение 3.
• Решение
• Упражнение 4.
• Решение
• Упражнение 5.
• Решение
• Ссылки

В полукруг это плоская фигура, ограниченная диаметром окружности и одной из двух плоских дуг окружности, определяемых указанным диаметром.

Таким образом, полукруг окаймлен полуокружность, который состоит из плоской дуги окружности и прямого сегмента, соединяющего концы плоской дуги окружности. Полукруг охватывает полукруг и все точки внутри него.

Мы можем видеть это на рисунке 1, где показан полукруг радиуса R, размер которого вдвое меньше диаметра AB. Обратите внимание, что в отличие от круга, в котором есть бесконечные диаметры, в полукруге только один диаметр.

Как мы видим на следующем изображении, полукруг — это геометрическая фигура, которая широко используется в архитектуре и дизайне:

Элементы и меры полукруга

Элементами полукруга являются:

1.- Плоская дуга окружности A⌒B

2.- Отрезок [AB]

3.- Внутренняя часть указывает на полукруг, составленный из дуги A⌒B и отрезка [AB].

Периметр полукруга

Периметр — это сумма контура дуги и прямого сегмента, поэтому:

Периметр = длина дуги A⌒B + длина сегмента [AB]

В случае полукруга радиуса R его периметр P будет задан формулой:

P = π⋅R + 2⋅R = (π + 2) ⋅R

Первый член представляет собой половину периметра окружности радиуса R, а второй — длину диаметра, который в два раза больше радиуса.

Площадь полукруга

Поскольку полукруг — это один из плоских угловых секторов, которые остаются при проведении диаметра по окружности, его площадь A будет равна половине площади круга, содержащего полукруг радиуса R:

A = (π⋅R²) / 2 = ½ π⋅R²

Центроид полукруга

Центр тяжести полукруга находится на его оси симметрии на высоте, измеренной от его диаметра, умноженного на 4 / (3π) радиуса R.

Это соответствует приблизительно 0,424⋅R, измеренному от центра полукруга и на его оси симметрии, как показано на рисунке 3.

Момент инерции полукруга

Момент инерции плоской фигуры относительно оси, например оси x, определяется как:

Интеграл от квадрата расстояния между точками, принадлежащими фигуре, до оси, дифференциал интегрирования является бесконечно малым элементом площади, взятой в положении каждой точки. 

На рисунке 4 показано определение момента инерции I_Икс полукруга радиуса R относительно оси X, проходящей через его диагональ:

Момент инерции относительно оси x определяется выражением:

я_Икс = (π⋅R⁴) / 8

А момент инерции относительно оси симметрии y равен:

Iy = (π⋅R⁴) / 8

Следует отметить, что оба момента инерции совпадают в своей формуле, но важно отметить, что они относятся к разным осям.

Вписанный угол

Угол, вписанный в полукруг, всегда равен 90 °. Независимо от того, где находится точка на дуге, угол между сторонами AB и BC фигуры всегда правильный.

Решенные упражнения

Упражнение 1

Определите периметр полукруга радиусом 10 см.

Решение

Помните, что периметр как функция радиуса определяется формулой, которую мы видели ранее:

P = (2 + π) ⋅R

P = (2 + 3,14) ⋅ 10 см = 5,14 ⋅ 10 см = 51,4 см.

Упражнение 2.

Найдите площадь полукруга радиусом 10 см.

Решение

Формула площади полукруга:

А = ½ π⋅R² = ½ π⋅ (10 см)² = 50π см² = 50 х 3,14 см² = 157 см².

Упражнение 3.

Определите высоту h центра тяжести полукруга радиусом R = 10 см, измеренную от его основания, при том же диаметре полукруга.

Решение

Центроид — это точка равновесия полукруга, и его положение находится на оси симметрии на высоте h от основания (диаметр полукруга):

h = (4⋅R) / (3π) = (4⋅10 см) / (3 x 3,14) = 4,246 см

Упражнение 4.

Найдите момент инерции полукруга относительно оси, совпадающей с его диаметром, зная, что полукруг состоит из тонкого листа. Его радиус 10 см, а масса 100 грамм.

Решение

Формула, которая дает момент инерции полукруга:

я_Икс = (π⋅R⁴) / 8

Но поскольку задача говорит нам, что это материальный полукруг, то предыдущее соотношение необходимо умножить на поверхностную плотность массы полукруга, которую мы будем обозначать σ.

я_Икс = σ (π⋅R⁴) / 8

Затем мы переходим к определению σ, которое представляет собой не что иное, как массу полукруга, деленную на его площадь.

Площадь была определена в упражнении 2, и результат составил 157 см.². Тогда поверхностная плотность этого полукруга будет:

σ = 100 грамм / 157 см² = 0,637 г / см²

Тогда момент инерции по отношению к диаметру будет рассчитываться следующим образом:

я_Икс = (0,637 г / см²) [3,1416 ⋅ (10 см)⁴] / 8

Результат:

я_Икс = 2502 г⋅см²

Упражнение 5.

Определить момент инерции полукруга радиусом 10 см из листа материала с поверхностной плотностью 0,637 г / см.² вдоль оси, проходящей через его центр тяжести и параллельной его диаметру.

Решение

Чтобы решить это упражнение, необходимо вспомнить теорему Штейнера о моментах инерции параллельных осей, которая гласит:

Момент инерции I относительно оси, находящейся на расстоянии h от центроида, равен сумме момента инерции I_c относительно оси, которая проходит через центроид и параллельна первой, плюс произведение массы на квадрат расстояния между двумя осями.

Я = Я_c+ М ч²

В нашем случае I известен как момент инерции по отношению к диаметру, который уже был вычислен в упражнении 4. Также известно расстояние h между диаметром и центроидом, которое было вычислено в упражнении 3.

Нам нужно только очистить Ic:

я_c = Я — М ч²

я_c= 2502 г⋅см² — 100 г ⋅ (4,246 см)² в результате чего момент инерции по оси, параллельной диаметру и проходящей через центроид, равен:

я_c = 699,15 г⋅см²

Ссылки

1. Александр, Д. 2013. Геометрия. 5-е. Издание. Cengage Learning.
2. Открытый справочник по математике. Полукруг. Получено с: mathopenref.com.
3. Полукруг формул Вселенной. Получено с: universaloformulas.com.
4. Формулы Вселенной. Площадь полукруга. Получено с: universaloformulas.com.
5. Википедия. Полукруг. Получено с: en.wikipedia.com.