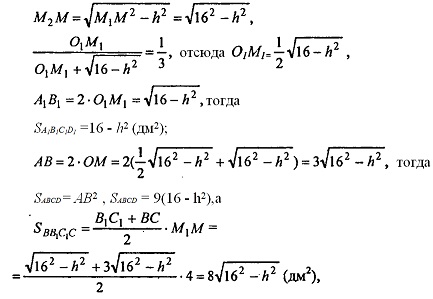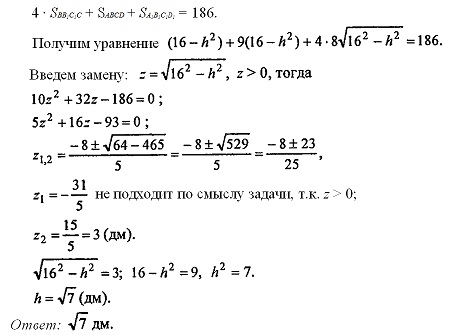Основания правильной усеченной пирамиды представляют собой правильные многоугольники, зная стороны которых можно найти все остальные параметры, такие как внутренний угол, периметр, площадь, радиусы вписанной и описанной окружностей.
γ=180°(n-2)/n
P=n(a+b+d)
S_a=(na^2)/(4 tan〖(180°)/n〗 )
S_b=(nb^2)/(4 tan〖(180°)/n〗 )
r_a=a/(2 tan〖(180°)/n〗 )
r_b=b/(2 tan〖(180°)/n〗 )
R_a=a/(2 sin〖(180°)/n〗 )
R_b=a/(2 sin〖(180°)/n〗 )
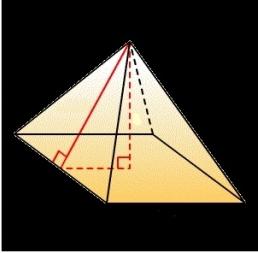
Зная высоту усеченной пирамиды, можно найти ее боковое ребро и апофему, рассмотрев прямоугольные трапеции, соединяющие их через радиусы вписанной и описанной окружностей в основаниях. Из прямоугольных трапеций построив дополнительный прямоугольный треугольник, легко вычислить боковое ребро или апофему как гипотенузу, а также найти углы при основаниях. (рис. 50.3, 50.4)
f=√(h^2+(b/2-a/2)^2 )=√(h^2+(b-a)^2/4)
cosβ=(r_b-r_a)/f
α=180°-β
d=√(h^2+(R_b-R_a )^2 )
cosδ=(R_b-R_a)/d
ε=180°-δ
Чтобы найти площадь боковой поверхности, нужно вычислить площадь каждой грани усеченной пирамиды, а затем умножить полученное значение на количество сторон в основаниях. Вычислить площадь полной поверхности усеченной пирамиды, зная стороны и высоту, нужно, преобразовав высоту в апофему по приведенным выше формулам, и сложив площадь боковой поверхности с площадями оснований.
S_(б.п.)=nf (a+b)/2
S_(п.п.)=S_(б.п.)+S_(осн.1,2)=n(f (a+b)/2+a^2/(4 tan〖(180°)/n〗 )+b^2/(4 tan〖(180°)/n〗 ))
Объем усеченной пирамиды, зная стороны и высоту, равен одной трети высоты умноженной на сумму площадей оснований с радикалом из их произведения.
V=1/3 h(S_осн1+S_осн2+√(S_осн1 S_осн2 ))
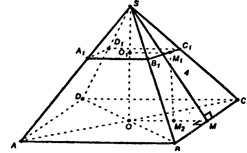
Боковые грани усеченной пирамиды — трапеции. Т.к. данная усеченная пирамида получена из правильной 4-угольной пирамиды, то ее боковые грани — равные равнобедренные трапеции.
Построим OM┴BC, M1M1┴B1C1, и отрезок M1M. По теореме о 3-х перпендикулярах имеем: M1M┴BC (M1M┴B1C1), т.е. M1M — апофема усеченной пирамиды, M1M=4 дм.
Δ SB1C1 ~ Δ SBC , и Δ SO1M1 ~ Δ SOM, т.к. они — прямоугольные и имеют общий острый угол при вершине S, тогда имеем:
Построим M1M2┴OM; OM2=O1M1.
Пусть высота усеченной пирамиды OO1=h. Тогда из ΔМ1М2М по т. Пифагора имеем:
ВИДЕОУРОК
Усечённой пирамидой ABCDA1B1C1D1 называется часть пирамиды SABCD, заключённая между её основанием и секущей плоскостью, параллельной основанию.
Основаниями усечённой пирамиды называются параллельные грани ABCD и A1B1C1D1 (ABCD – нижнее основание, A1B1C1D1 – верхнее основание).
Высотой усечённой пирамиды называется отрезок прямой, перпендикулярный её основаниям и заключённый между их плоскостями.
Усечённая пирамида называется правильной, если её основания – правильные многоугольники и прямая, соединяющая центры оснований, перпендикулярна плоскости оснований.
Апофемою правильной усечённой пирамиды называют высоту её боковой грани.
Свойства усечённой пирамиды.
Основания – подобные многоугольники.
Боковые грани – трапеции.
Отношение высоты к высоте пирамиды, из которой она получена, равно отношению разности сторон одной грани к длине нижнего основания этой самой грани.
Поверхность усечённой пирамиды.
Площадь боковой поверхности усечённой пирамиды равна сумме площадей её боковых граней.
Полная поверхность усечённой пирамиды равна сумме площади боковой поверхности и площадей оснований.
Боковая поверхность правильной усечённой пирамиды равна произведению полусуммы периметров оснований на апофему.
где Р и Р1 – периметры оснований, m – апофема усечённой пирамиды.
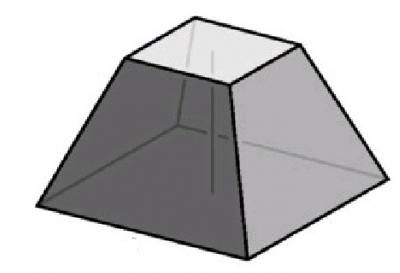
Правильная четырёхугольная усечённая пирамида.
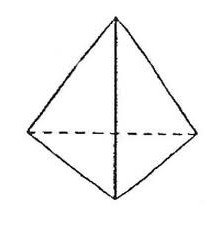
Правильная треугольная усечённая пирамида.
Правильная шестиугольная усечённая пирамида.
ЗАДАЧА:
В правильной четырёхугольной усечённой пирамиде стороны оснований равны 5 и 11 дм, а диагональ пирамиды – 12 дм. Определите боковую поверхность пирамиды.
РЕШЕНИЕ:
В усечённой пирамиде АС1 имеем
А1В1 = В1С1 = С1D1 = D1А1 = 5 дм,
АВ = ВС = СD = DА = 11 дм и
А1С = 12 дм.
Найти боковую поверхность.
Из вершины А1 проведём А1N ⊥ AB и А1M ⊥ AC, тогда А1N – апофема пирамиды.
Боковая поверхность
Sбок = 1/2 (P + P1) × A1N.
где P = 4AB = 44
дм, а
P1 = 4A1B1 = 20
дм.
В квадратах АВСD и А1В1С1D1 по иіх сторонам определяем диагонали
АС = 11√͞͞͞͞͞2 (дм),
A1С1 = 5√͞͞͞͞͞5 (дм).
Рассмотрев равнобедренную трапецию АА1С1С, находим
и соответственно
Тогда из прямоугольного ∆ А1MC находим высоту пирамиды
Из равнобедренного прямоугольного ∆ AMN (∠ ANM = 90°), гипотенуза которого AM = 3√͞͞͞͞͞2 (дм), находим сторону
Апофему данной пирамиды найдём из прямоугольного
Подставляя найденные значения P, P1 и A1N в формулу боковой поверхности пирамиды, получим:
Sбок = 1/2 (44 + 20)×5 = 160 (дм2).
ОТВЕТ:
S = 160 дм2 = 1,6 м2.
ЗАДАЧА:
Высота правильной четырёхугольной усечённой пирамиды
равна 4
см. Стороны оснований равны 2
см и
8 см. Найдите площадь диагональных сечений.
РЕШЕНИЕ:
Начертим чертёж.
Диагональные сечения
AA1C1D и BB1D1D– равные равнобедренные трапеции с высотой ОО1 = h = 4 см и с основаниями
– диагоналями оснований АС и А1С1 та ВD и В1D1 соответственно. ABCD – квадрат, а поэтому
AC2 = AD2 + CD2 =
= 82 + 82 = 128,
AC = √͞͞͞͞͞128 = 8√͞͞͞͞͞2 (cм).
A1B1C1D1 – квадрат, а поэтому
A1C12 = A1D12 + C1D12 = 22 + 22 = 8,
A1C1 = √͞͞͞͞͞8 = 2√͞͞͞͞͞2 (cм).
ОТВЕТ: 20√͞͞͞͞͞2 (cм2)
ЗАДАЧА:
В правильной четырёхугольной усечённой пирамиде высота
равна 2
см, а стороны оснований – 3 см и 5
см. Найдите диагональ этой пирамиды.
РЕШЕНИЕ:
Начертим чертёж.
Диагональным сечением данной пирамиды
является равнобедренная трапеция АА1С1С.
Так как
А1С1 и АС –
диагонали квадратов, А1В1С1D1 и ABCD, то
А1С1 = А1В1 ∙ √͞͞͞͞͞2 = 3√͞͞͞͞͞2 (см) и
АС = АВ ∙ √͞͞͞͞͞2 = 5√͞͞͞͞͞2 (см).
Проведём
А1К ⊥
АС
и С1Н ⊥ АС. Тогда А1С1НК – прямоугольник
и А1С1 =
КН. Так что, прямоугольные треугольники АА1К и СС1Н равны по гипотенузе и катету.
Тогда,
АК = СН = 1/2 (АС – А1С1) =
= 1/2 (5√͞͞͞͞͞2 – 3√͞͞͞͞͞2) = √͞͞͞͞͞2 (см).
Тогда,
СК = АС – АК = 5√͞͞͞͞͞2 – √͞͞͞͞͞2 =
4√͞͞͞͞͞2 (см),
и по
теореме Пифагора в ∆ А1СК:
ОТВЕТ: 6 см
ЗАДАЧА:
В правильной четырёхугольной пирамиде плоскость, проведённая
параллельно основанию, делит высоту пирамиды пополам. Найдите сторону основания,
если площадь сечения равна 36 см2.
РЕШЕНИЕ:
Пусть SABCD – данная правильная пирамида,
основание – квадрат
ABCD, SO – высота, O –
точка пресечения диагоналей квадрата, φ – плоскость сечения, О1 –
точка пересечения φ и SO, φ ∥ (ABC), S = 36 cм2.
Поскольку φ ∥ (ABC),
то прямые пересечения 𝜑 и боковых граней параллельны соответственно рёбрам
основания:
A1B1 ∥ AB, B1C1 ∥ BC, C1D1 ∥ CD,
A1D1 ∥ AD, 𝜑 ⊥ SO,
можно рассмотреть гомотетию с центром S и коэффициентом
которая преобразует квадрат ABCD в квадрат
А1В1С1D1, стороны которого в два раза меньше, а
SABCD = 4SА1В1С1D1 = 4 ∙ 36 (см2).
SABCD = a2 = 4 ∙
36,
a = 2 ∙ 6
= 12 (см).
ОТВЕТ: 12 см
Задания к уроку 10
- Задание 1
- Задание 2
- Задание 3
Другие уроки:
- Урок 1. Прямые и плоскости в пространстве
- Урок 2. Прямая призма
- Урок 3. Наклонная призма
- Урок 4. Правильная призма
- Урок 5. Параллелепипед
- Урок 6. Прямругольный параллелепипед
- Урок 7. Куб
- Урок 8. Пирамида
- Урок 9. Правильная пирамида
- Урок 11. Цилиндр
- Урок 12. Вписанная и описанная призмы
- Урок 13. Конус
- Урок 14. Усечённый конус
- Урок 15. Вписанная и описанная пирамиды
- Урок 16. Сфера и шар
- Урок 17. Комбинация тел
Данный сайт находится в режиме тестирования, обо всех выявленных проблемах Вы можете сообщить на почту
Формулы усеченной пирамиды
Для расчёта всех основных параметров усеченной пирамиды воспользуйтесь калькулятором.
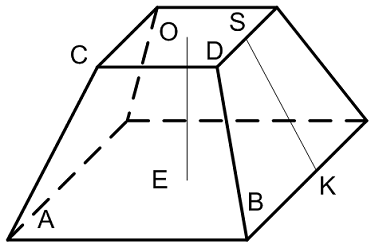
Площадь верхнего основания правильной усеченной пирамиды
$$
S_{верх.основ} = {N * CD^2 over 4 * tan(180/N)}
$$
Площадь нижнего основания правильной усеченной пирамиды
$$
S_{нижн.основ} = {N * AB^2 over 4 * tan(180/N)}
$$
Объём усеченной пирамиды
$$
V = {1 over 3} * OE * (S_{верх.основ} + sqrt{S_{верх.основ} * S_{нижн.основ}} + S_{нижн.основ})
$$
Апофема усеченной пирамиды
Так как боковая сторона усеченной пирамиды – это трапеция, то высота этой трапеции и будет апофемой усеченной пирамиды
$$
SK = sqrt{AC^2 — ({(AB — CD)^2 + AC^2 — BD^2 over 2 * (AB — CD)})^2}
$$
Площадь боковой поверхности
Площадью боковой поверхности усеченной пирамиды является сумма всех боковых сторон, каждая боковая сторона является трапецией
$$
S_{Бок.стороны} = {1 over 2} * SK * (CD + AB)
$$
Пирамида — это многогранник, в основании которого лежит многоугольник. Все грани в свою очередь образуют треугольники, которые сходятся в одной вершине. Пирамиды бывают треугольными, четырехугольными и так далее. Для того чтобы определить, какая пирамида перед вами, достаточно посчитать количество углов в ее основании. Определение «высота пирамиды» очень часто встречается в задачах по геометрии в школьной программе. В статье попробуем рассмотреть разные способы ее нахождения.
Части пирамиды
Каждая пирамида состоит из следующих элементов:
- боковые грани, которые имеют по три угла и сходятся в вершине;
- апофема представляет собой высоту, которая опускается из ее вершины;
- вершина пирамиды – это точка, которая соединяет боковые ребра, но при этом не лежит в плоскости основания;
- основание – это многоугольник, на котором не лежит вершина;
- высота пирамиды представляет собой отрезок, который пересекает вершину пирамиды и образует с ее основанием прямой угол.
Как найти высоту пирамиды, если известен ее объем
Через формулу объема пирамиды V = (S*h)/3 (в формуле V — объем, S – площадь основания, h — высота пирамиды) находим, что h = (3*V)/S. Для закрепления материала давайте сразу же решим задачу. В треугольной пирамиде площадь основания равна 50 см2, тогда как ее объем составляет 125 см3. Неизвестна высота треугольной пирамиды, которую нам и необходимо найти. Здесь все просто: вставляем данные в нашу формулу. Получаем h = (3*125)/50 = 7,5 см.
Как найти высоту пирамиды, если известна длина диагонали и ее ребра
Как мы помним, высота пирамиды образует с ее основанием прямой угол. А это значит что высота, ребро и половина диагонали вместе образуют прямоугольный треугольник. Многие, конечно же, помнят теорему Пифагора. Зная два измерения, третью величину найти будет несложно. Вспомним известную теорему a² = b² + c², где а – гипотенуза, а в нашем случае ребро пирамиды; b – первый катет или половина диагонали и с – соответственно, второй катет, или высота пирамиды. Из этой формулы c² = a² — b².
Теперь задачка: в правильной пирамиде диагональ равна 20 см, когда как длина ребра – 30 см. Необходимо найти высоту. Решаем: c² = 30² — 20² = 900-400 = 500. Отсюда с = √ 500 = около 22,4.
Как найти высоту усеченной пирамиды
Она представляет собой многоугольник, который имеет сечение параллельно ее основанию. Высота усеченной пирамиды – это отрезок, который соединяет два ее основания. Высоту можно найти у правильной пирамиды, если будут известны длины диагоналей обоих оснований, а также ребро пирамиды. Пусть диагональ большего основания равна d1, в то время как диагональ меньшего основания – d2, а ребро имеет длину – l. Чтобы найти высоту, можно с двух верхних противоположных точек диаграммы опустить высоты на ее основание. Мы видим, что у нас получились два прямоугольных треугольника, остается найти длины их катетов. Для этого из большей диагонали вычитаем меньшую и делим на 2. Так мы найдем один катет: а = (d1-d2)/2. После чего по теореме Пифагора нам остается лишь найти второй катет, который и является высотой пирамиды.
Теперь рассмотрим все это дело на практике. Перед нами задача. Усеченная пирамида имеет в основании квадрат, длина диагонали большего основания равняется 10 см, в то время как меньшего – 6 см, а ребро равняется 4 см. Требуется найти высоту. Для начала находим один катет: а = (10-6)/2 = 2 см. Один катет равен 2 см, а гипотенуза – 4 см. Получается, что второй катет или высота будет равна 16-4 = 12, то есть h = √12 = около 3,5 см.