Как найти высоту проекции пирамиды - Исправление недочетов и поиск решений вместе с Examum.ru

Определить натуральную величину высоты пирамиды

Задача определения натуральной величины высоты пирамиды соответствует задаче определения расстояния от точки до плоскости.
Решение задачи в начертательной геометрии возможно двумя методами: (1) заменой плоскостей проекций перевести плоскость
основания пирамиды в проецирующее положение и (2) опустить перпендикуляр из вершины на плоскость основания,
найти пересечение прямой перпендикуляра с плоскостью и определить натуральную величину отрезка прямой от вершины пирамиды
до точки пересечения с основанием.

Метод замены плоскостей проекций

В плоскости основания пирамиды проводится линия частного положения (в примере — горизонталь BH). Строится плоскость проекции
заменяющая одну из исходных плоскостей (в примере П₄ заменяет фронтальную проекцию). На новой проекции, плоскость
основания занимает проецирующее положение и расстояние от любой точки до этой плоскости очевидно представляется
перпендикуляром. В примере, h — высота пирамиды проведённая из вершины к основанию. Так как h параллелен плоскости проекций,
то его длинна определяет натуральную величину высоты пирамиды.

Натуральная величина перпендикуляра

В плоскости основания определены горизонталь и фронталь. Из вершины пирамиды проводится перпендикуляр к основанию.
Через перпендикуляр проведена горизонтально проецирующая плоскость-посредник пересекающая основание по 12.
На фронтальной проекции пересечение 1₂2₂ и перпендикуляра даёт общую точку для перпендикуляра и 12,
которая лежит в плоскости основания. Следовательно, эта точка пересечения N определяет точку пересечения перпендикуляра и
основания. Натуральная величина перпендикуляра AN определена
методом прямоугольного треугольника: фронтальная проекция AN использована как
катет-основание прямоугольного треугольника, второй катет определен как растояние между концами перпендикуляра измеренное
вдоль оси Y. Гипотенуза полученного треугольника определяет натуральную величину высоты пирамиды.

Натуральная величина двугранного угла при ребре.
Заменой плоскостей проекций определить натуральную величину треугольника.

Определение натуральной величины.

Решение задач по начертательной геометрии.

Источник

Построение проекций пирамиды

Построить проекции пирамиды, основанием которой является треугольник ABC, а ребро SA определяет высоту h пирамиды.

1. Строим проекции треугольника АВС.

2. Строим фронталь в плоскости треугольника АВС.

3. Строим горизонтаь в плоскости треугольника АВС.

4. Через точку А проводим перпендикуляр к плоскости АВС

5. На перпендикуляре h строим отрезок произвольной длины АК и определяем его натуральную величину.

6. Строим высоту AS.

8. Строим ребра пирамиды.

9. С помощью конкурирующих точек 3 и 4 определяем видимость ребер пирамиды на фронтальной плоскости проекций.

10. С помощью конкурирующих точек 5 и 6 определяем видимость ребер пирамиды на горизонтальной плоскости проекций.

9. Оформление задачи.

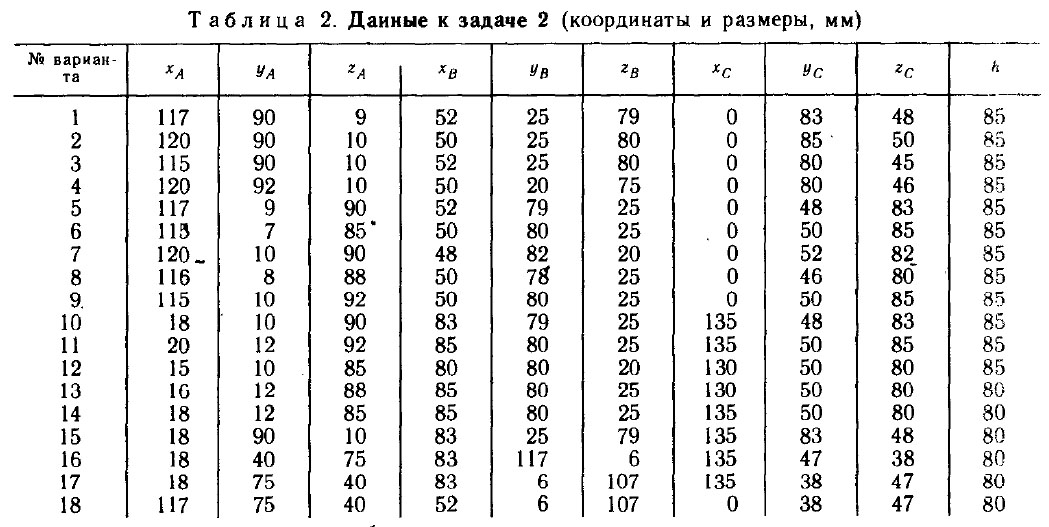
№ вар.	Х_А	Y_А	Z_А	Х_B	Y_B	Z_B	Х_C	Y_C	Z_C	h	Цена	в корзину	№ вар.
1	117	90	9	52	25	79	0	83	48	85	50 руб.	в корзину	1
2	120	90	10	50	25	80	0	85	50	85	50 руб.	в корзину	2
3	115	90	10	52	25	80	0	80	45	85	50 руб.	в корзину	3
4	120	92	10	50	20	75	0	80	46	85	50 руб.	в корзину	4
5	117	9	90	52	79	25	0	48	83	85	50 руб.	в корзину	5
6	115	7	85	50	80	25	0	50	85	85	50 руб.	в корзину	6
7	120	10	90	48	82	20	0	52	82	85	50 руб.	в корзину	7
8	116	8	88	50	78	25	0	46	80	85	50 руб.	в корзину	8
9	115	10	92	50	80	25	0	50	85	85	50 руб.	в корзину	9
10	18	10	90	83	79	25	135	48	83	85	50 руб.	в корзину	10
11	20	12	92	85	80	25	135	50	85	85	50 руб.	в корзину	11
12	15	10	85	80	80	20	130	50	80	85	50 руб.	в корзину	12
13	16	12	88	85	80	25	130	50	80	80	50 руб.	в корзину	13
14	18	12	85	85	80	25	135	50	80	80	50 руб.	в корзину	14
15	18	90	10	83	25	79	135	83	48	80	50 руб.	в корзину	15
16	18	40	75	83	117	6	135	47	38	80	50 руб.	в корзину	16
17	18	75	40	83	6	107	135	38	47	80	50 руб.	в корзину	17
18	117	75	40	52	6	107	0	38	47	80	50 руб.	в корзину	18

Начертательная геометрия решение задач

Добавить комментарий

Источник

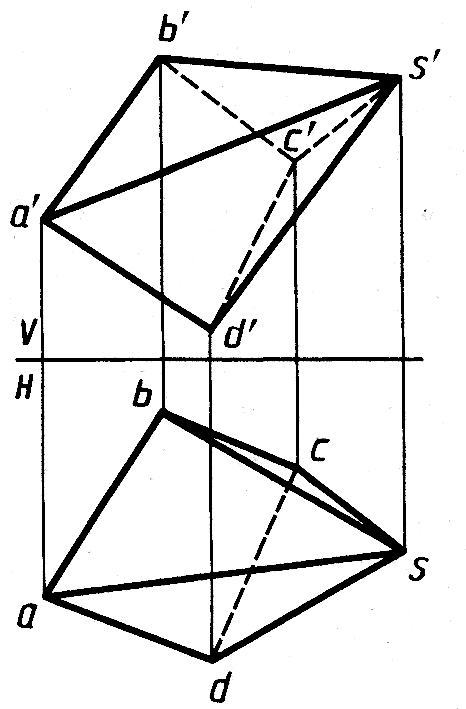
В представленной
на рисунке 8.5 пирамиде, основание и
грани которой являются плоскостями
общего положения, требуется
определить ее высоту ( расстояние от
вершины с проекциями s‘,
s до основания
с проекциями a‘b‘c‘d‘,
abcd ) и
двугранный угол между гранями с проекциями
a‘ b‘
s‘, abs
и a‘ d‘
s‘, ads.

Указанные
задачи можно решить способом перемены
плоскостей проекций.

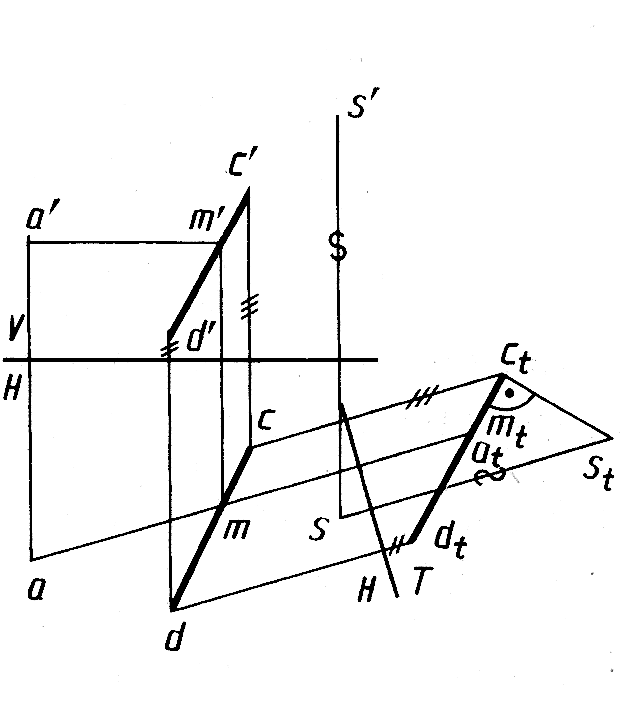
Определение
расстояния от вершины до основания
выполнено
на рисунке 8.6. При этом плоскость основания
ABCD
задана
проекциями a‘,
а точки и
d‘c‘,
dc
отрезка. Новая
плоскость проекций T(T
H)
выбрана перпендикулярной горизонтали
с проекциями a‘m‘,
am основания
(ось H/T
am)
и соответственно
плоскости основания. На плоскость
проекций T
часть основания
пирамиды проецируется в отрезок d_tc_t,
расстояние
от которого до
проекции s,
вершины и
соответствует искомой высоте
пирамиды.

Рис.8.5
Рис.8.6

Определение
угла между гранями. Двугранный
угол измеряют линейным углом,
полученным в пересечении граней
двугранного угла плоскостью,
перпендикулярной
к обеим граням двугранного
угла φ,
а следовательно,
и к линии их пересечения, т.е. к
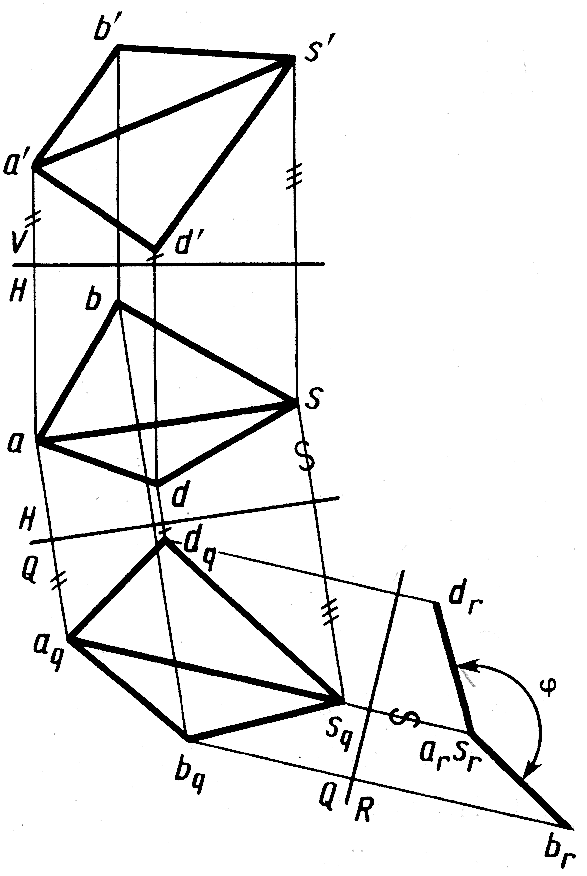
ребру двугранного угла. Определение
угла φ
между гранями пирамиды
выполнено на рисунке 8.7, где
двумя переменами плоскостей проекций
ребро с проекциями a‘s‘,
as
двугранного
угла, являющегося отрезком
общего положения, переведено
в проецирующее положение
относительно плоскости проекций
R.
Полученная
на плоскости проекций
R
проекция d_rs_r
≡
a_rb_rдвугранного
угла выражает его линейный угол.

Рис.8.7

При преобразовании
система плоскостей проекций V,
H заменена
вначале системой

H,
Q (Q

H ), в
которой плоскость Q
выбрана
параллельной ребру AS
(ось H
/Q
║ as).

Затем
система плоскостей проекций H,
Q
заменена на
систему Q, R
(R
Q
), в которой плоскость проекций R
выбрана перпендикулярной ребру
AS ( ось Q/R

a_qs_q).

8.4. Пересечение многогранников плоскостью

При
пересечении призмы или пирамиды
плоскостью в сечении получается
плоская фигура, ограниченная линиями
пересечения
секущей плоскости с гранями призмы или
пирамиды.

Простейший
пример конструирования детали
пересечением исходной заготовки в
виде прямоугольной трубы плоскостью
приведен на рисунке 8.8. В этом случае
деталь – волновод изготавливают,
отрезая часть заготовки по плоскости
R
(R_v).
Другой пример
конструирования устойчивой подставки
в виде
усеченной пирамиды показан на рисунке
8.9. Наклонная площадка
ABCD
образована
срезом верхней части пирамиды
фронтально-проецирующей
плоскостью S
(S_v).
Фронтальные
проекции a‘, b‘,
c‘, d‘
точек находятся на фронтальном следе
S_v
плоскости, а
фронтальная проекция площадки ABCD
совпадает
со следом S_v.
Профильная a«b«c«d»
и горизонтальная
abcd
проекции
площадки построены по проекциям
указанных точек на проекциях соответствующих
ребер.

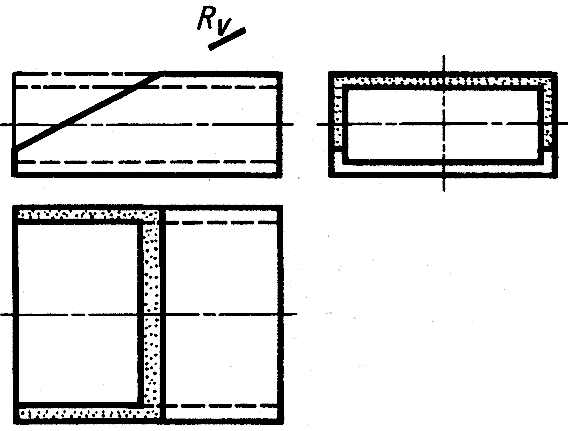
Рис.
8.8

Построение
натуральной величины
сечения пирамиды плоскостью. Во
многих случаях требуется построить
натуральный или истинный
вид сечения тела плоскостью. На
рисунке 8.9 для этой цели вверху слева
применен способ перемены плоскостей
проекций. В качестве
дополнительной плоскости принята
плоскость T,
параллельная плоскости S
и перпен-дикулярная плоскости V.
Натуральный вид
площадки – фигуры сечения a_tb_tc_td_t.
Другой
ва-риант построения натурального вида
наклонной площадки
ABCD
показан на
рисунке 8.9 справа внизу – A₀B₀C₀D₀.
Для построения использованы новые
координатные оси x₁
и у_1,
лежащие в
плоскости S.
Ось х₁ параллельна
плоскости V,
ось у₁ перпендикулярна
плоскости V.

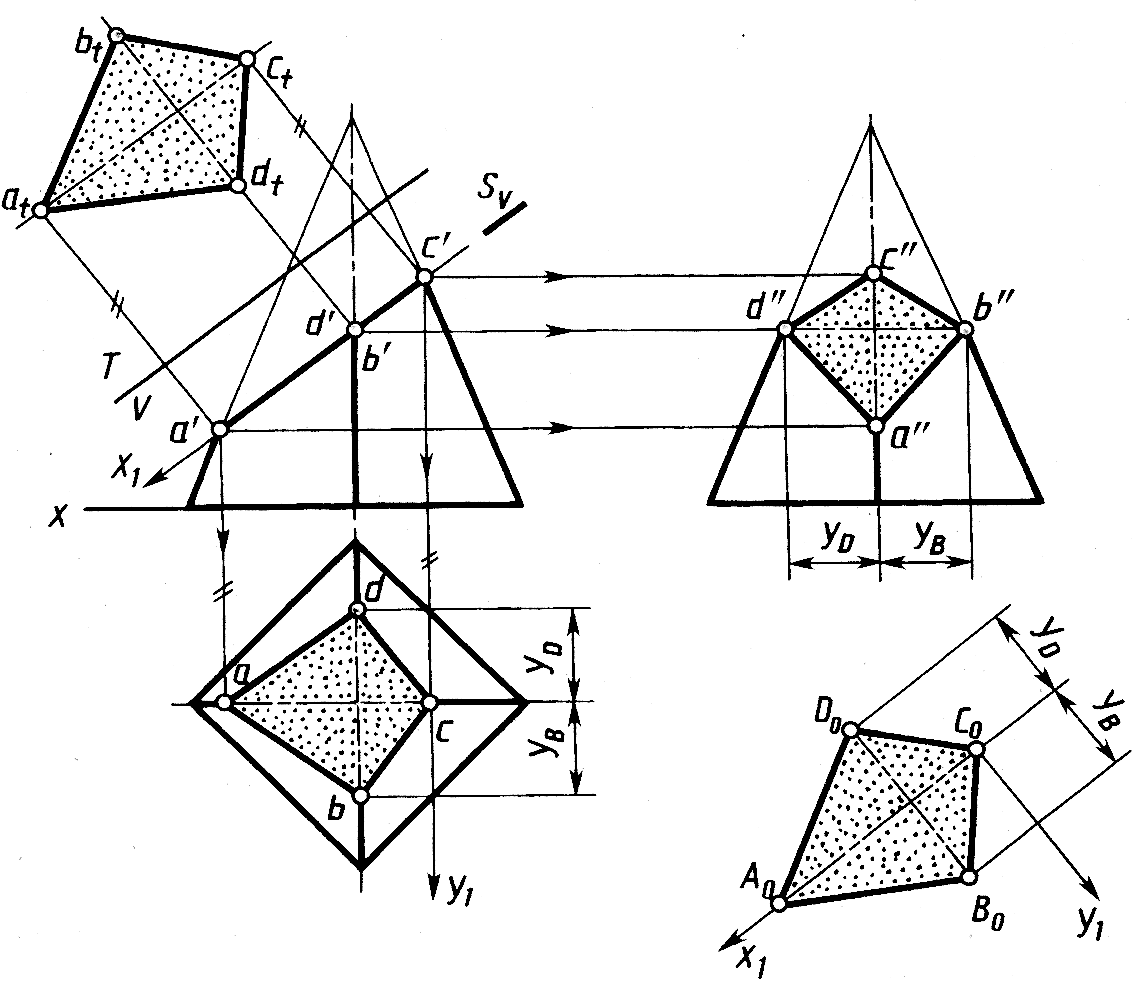
Рис.
8.9

Координаты
на оси х₁
точек A₀,
B₀,
C₀,
D₀
равны
координатам
по оси x₁
фронтальных
проекций a‘,
b‘,
c‘,
d‘
этих точек.
Координаты х₁
точек с₀,
с’ по
оси х₁
равны нулю.
Координаты y_B,
у_D
по оси у₁ точек
B₀,
D₀
равны
координатам по этой оси (параллельной
оси у)
горизонтальных
проекций b,
d.
Координаты
по оси у₁
точек А,
С равны нулю.
По указанным координатам
на осях x₁, у₁
строят
натуральную величину A₀B₀C₀D_aнаклонной площадки ABCD.

Пирамида
с вырезом. Как
пример построения сечений несколькими
плоскостями рассмотрим (рис. 8.10) построение
пирамиды с вырезом,
который образован тремя плоскостями –
горизонтальной T(T_v),
фронтально-проецирующей
R
(R_v)
и профильной
Q
(Q_v).
Горизонтальная
плоскость T
(T_v)
пересекает
боковую поверхность пирамиды по
пятиугольнику с горизонтальной
проекцией k–l–g–f–4–k,
стороны
которого параллельны
проекциям сторон основания пирамиды.
Фронтально-проецирующая
плоскость R
(R_v)
в пределах
выреза пересекает боковую
поверхность пирамиды по ломаной линии
с горизонтальной
проекцией 3–8–9–10–2
и
с профильной
проекцией 3″8″9″10″2″.
Профильная плоскость Q
(Q_v)
пересекает
в пределах
выреза боковую по-

верхность
пирамиды по ломаной с горизонтальной
проекцией в виде отрезка
прямой 5-7-6 и
с профильной
проекцией 5″7″6″.

Полученные
точки соединяют в такой
последовательности, чтобы две точки
принадлежали одной секущей плоскости
и одной грани пирамиды.

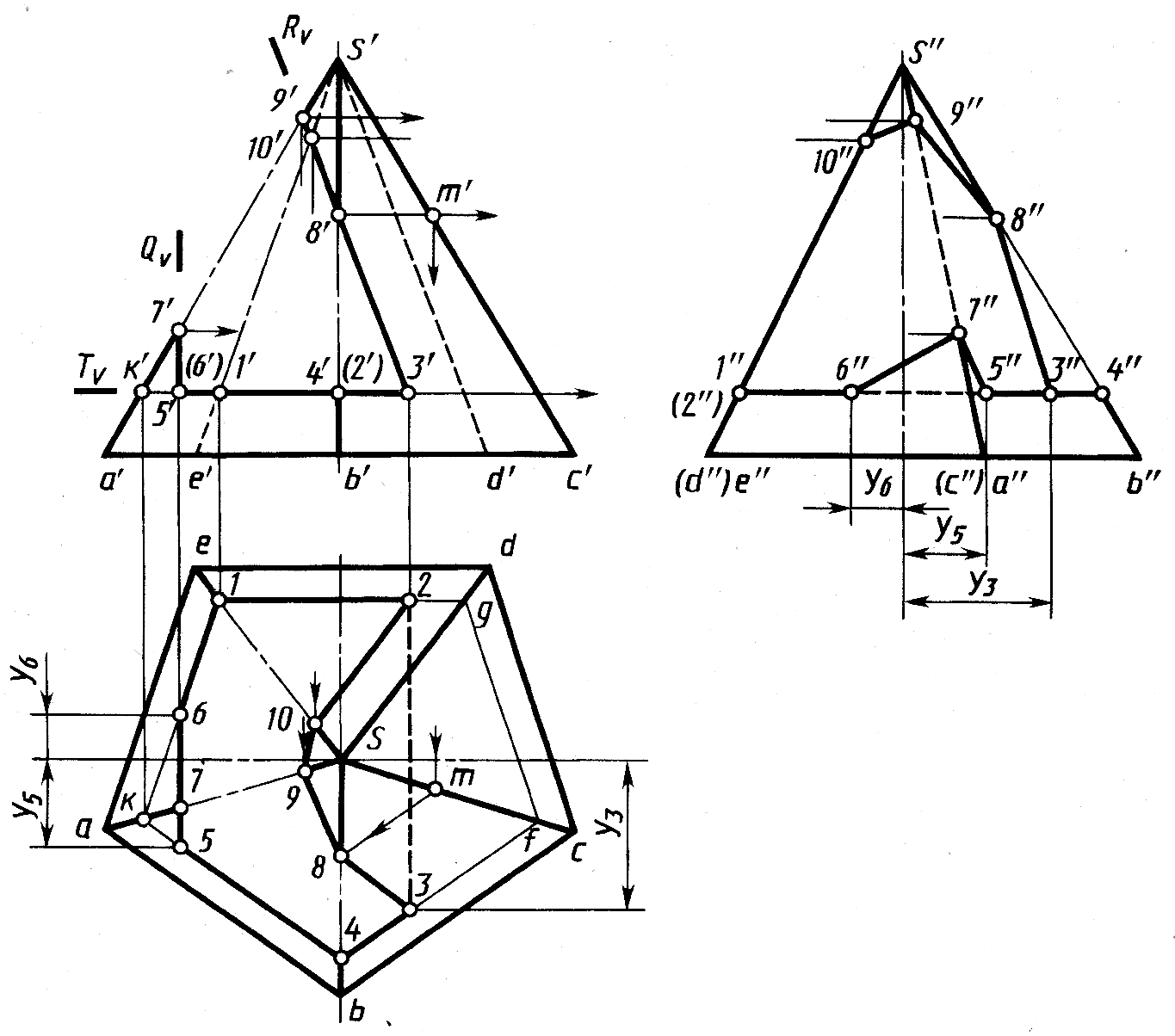
Рис.8.10

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Содержание

Определить натуральную величину высоты пирамиды
Метод замены плоскостей проекций
Натуральная величина перпендикуляра
Решение задачи способом замены плоскостей проекций.
Метод замены плоскостей проекций
Замена одной плоскости проекции
Замена двух плоскостей проекций
Использование метода замены при решении задач
Определение расстояния между параллельными плоскостями
Примеры решения метрических задач

Определить натуральную величину высоты пирамиды

Задача определения натуральной величины высоты пирамиды соответствует задаче определения расстояния от точки до плоскости. Решение задачи в начертательной геометрии возможно двумя методами: (1) заменой плоскостей проекций перевести плоскость основания пирамиды в проецирующее положение и (2) опустить перпендикуляр из вершины на плоскость основания, найти пересечение прямой перпендикуляра с плоскостью и определить натуральную величину отрезка прямой от вершины пирамиды до точки пересечения с основанием.

Метод замены плоскостей проекций

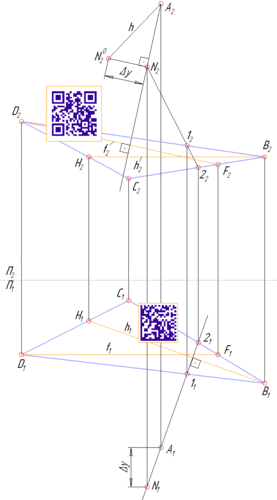
В плоскости основания пирамиды проводится линия частного положения (в примере — горизонталь BH). Строится плоскость проекции заменяющая одну из исходных плоскостей (в примере П₄ заменяет фронтальную проекцию). На новой проекции, плоскость основания занимает проецирующее положение и расстояние от любой точки до этой плоскости очевидно представляется перпендикуляром. В примере, h — высота пирамиды проведённая из вершины к основанию. Так как h параллелен плоскости проекций, то его длинна определяет натуральную величину высоты пирамиды.

Натуральная величина перпендикуляра

В плоскости основания определены горизонталь и фронталь. Из вершины пирамиды проводится перпендикуляр к основанию. Через перпендикуляр проведена горизонтально проецирующая плоскость-посредник пересекающая основание по 12. На фронтальной проекции пересечение 1₂2₂ и перпендикуляра даёт общую точку для перпендикуляра и 12, которая лежит в плоскости основания. Следовательно, эта точка пересечения N определяет точку пересечения перпендикуляра и основания. Натуральная величина перпендикуляра AN определена методом прямоугольного треугольника: фронтальная проекция AN использована как катет-основание прямоугольного треугольника, второй катет определен как растояние между концами перпендикуляра измеренное вдоль оси Y. Гипотенуза полученного треугольника определяет натуральную величину высоты пирамиды.

Источник

Решение задачи способом замены плоскостей проекций.

Как отмечалось выше, для определения расстояния от заданной точки до плоскости (высоты пирамиды) необходимо из этой точки опустить перпендикуляр на плоскость, найти основание перпендикуляра и определить истинную величину отрезка. Задача решается просто, если плоскости основания пирамиды — ΔАВС задать проецирующее положение.

1. Построим в плоскости треугольника АВС горизонталь и введем новую фронтальную плоскость π₄ перпендикулярно к данной горизонтали:

На чертеже ось х₁ перпендикулярна горизонтальной проекции горизонтали h₁ / : х₁ ^ h₁ / ; (рис.10.1)

2.Строим новую фронтальную проекцию треугольника — А₁ // В₁ // С₁ // .

[S // S_x // ] [S₁ // S_x1 // ]; [A // A_x // ] [A₁ // A_x1 // ]; [B // B_x // ] [B₁ // B_x1 // ];

[C // C_x // ] [C₁ // C_x₁ // ];

По отношению к p₄ плоскость треугольника занимает проецирующее положение(рис.10.2).

3. Из точки S₁опускаем перпендикуляр на плоскость DА₁В₁С₁, находим его основание, как точку пересечения перпендикуляра с плоскостью:

S₁K₁ 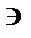S_1; S₁K₁ DА₁В₁С₁ ; S₁K₁∩DА₁В₁С₁ =K₁;

На чертеже: S₁«K₁» DA₁ // В₁ // C₁ // ;

Отрезок [S₁«K₁«]определяет натуральную величину высоты пирамиды. Измеряем его и указываем размер на чертеже.

Точку К необходимо вернуть в исходное положение, зная что S₁ / K / ¤¤ х (рис.10.3);

Задача 3. Определить натуральную величину основания пирамиды — DАВС.

Решение способом плоскопараллельного перемещения.

Для того чтобы определить натуральную величину основания пирамиды-DABC, который является плоскостью общего положения, необходимо преобразовать его в плоскость уровня.

Для решения задачи необходимо выполнить два преобразования:

1) Преобразовать плоскость треугольника – плоскость общего положения в проецирующую плоскость.

2) Преобразовать проецирующую плоскость в плоскость уровня,

переместив ΔA₁B₁C₁ плоскопараллельным движением относительно пл. p₂ в новое положение, параллельное пл. p₁, тогда на эту плоскость он спроецируется без искажения.

a₁(A₁B₁C₁) 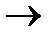a₂(A₂B₂C₂)// p₁ ;

1. Перемещаем треугольник АВС параллельно одной из плоскостей проекций так, чтобы после преобразования он занял проецирующее положение ( см. задачу №1).

2.Располагаем вырожденную фронтальную проекцию DA₂B₂C₂ –отрезок [A₂ // B₂ // C₂ // ]параллельно оси х:

При этом не изменится величина его фронтальной проекции:

[A₂ // B₂ // C₂ // ] [A₁ // B₁ // C₁ // ] (рис.11.1)

3. Горизонтальные проекции вершин А₁ / , В₁ / , . перемещаются в новое положение А₂ / ,В₂ / , . по прямым параллельным оси х. По линиям связи строим горизонтальную проекцию DA₂B₂C₂ (ΔA₂ / B₂ C₂ / ), которая конгруэнтна основанию пирамиды: [DA₂ / B₂ / C₂ / ] [DABC] (рис.11.2)

Источник

Метод замены плоскостей проекций

Для решения целого ряда задач начертательной геометрии наиболее рациональным является метод замены плоскостей проекций. Например, с его помощью можно определить натуральную величину плоской фигуры, расстояние между параллельными прямыми, опорные точки пересечения поверхностей.

Замена одной плоскости проекции

Сущность метода заключается в замене одной из плоскостей проекций на дополнительную плоскость, выбранную так, чтобы в новой системе плоскостей решение поставленной задачи значительно упрощалось. Положение фигур в пространстве при этом не меняется.

Рассмотрим на примере точек A и B, как осуществляются построения на комплексном чертеже. Изначально точка A находится в системе плоскостей П₁, П₂. Введем дополнительную горизонтальную пл. П₄. Она будет перпендикулярна фронтальной плоскости проекций П₂ и пересечет её по оси x₁. Эту ось необходимо провести на комплексном чертеже с учётом цели построения. Здесь мы расположили её произвольно.

В новой системе плоскостей положение точки A» не изменится. Чтобы найти точку A’₁, которая является проекцией т. А на плоскость П₄, проведем из A» перпендикуляр к оси x₁. На этом перпендикуляре от точки его пересечения с осью x₁ отложим отрезок A_x₁А’₁, равный отрезку A_xA’.

Данные построения основаны на равенстве ординат точек A’ и А’₁. Действительно, в системе плоскостей П₁, П₂ и в системе П₂, П₄ точка A удалена от фронтальной плоскости проекций П₂ на одно и то же расстояние.

Теперь осуществим перевод точки B в новую систему плоскостей П₁, П₄ (рис. ниже). Для этого введем произвольную фронтальную пл. П₄, которая будет перпендикулярна горизонтальной плоскости проекций П₁ и пересечет её по оси x₁.

В системе П₁, П₄ положение точки B’ останется неизменным. Чтобы найти точку B»₁, проведем из B’ перпендикуляр к оси x₁. На этом перпендикуляре от точки его пересечения с осью x₁ отложим отрезок B_x₁B»₁ равный отрезку B_xB». Описанные построения основаны на равенстве аппликат точек B» и B»₁.

Замена двух плоскостей проекций

Иногда для решения поставленной задачи требуется замена двух плоскостей проекций (рис. ниже). Пусть A’ и A» – исходные проекции точки A, находящейся в системе пл. П₁, П₂. Введем первую дополнительную плоскость П₄ и определим новую горизонтальную проекцию A’₁ точки A, как это было описано ранее.

Для осуществления второй замены плоскости проекций будем рассматривать систему пл. П₂, П₄ в качестве исходной. Введем новую фронтальную плоскость П₅ перпендикулярно горизонтальной пл. П₄. Для этого на произвольном месте чертежа проведем ось x₂ = П₄ ∩ П₅. Из точки A’₁, положение которой останется неизменным, восстановим перпендикуляр к оси x₂. На нем от точки A_x₂ отложим отрезок A_x₂A»₁ равный отрезку A»A_x₁.

Использование метода замены при решении задач

Владея методом замены применительно к одной точке, можно построить дополнительные проекции любых фигур, поскольку они представляют собой множество точек. На рисунке ниже показан перевод отрезка AB в частное положение. Новая плоскость П₄ проведена параллельно AB, поэтому отрезок проецируется на неё в натуральную величину.

На следующем рисунке показана плоскость общего положения α, заданная следами. Переведем её в новую систему плоскостей П₁, П₄ так, чтобы α занимала проецирующее положение. Для этого перпендикулярно горизонтальному следу h₀_α введем дополнительную фронтальную плоскость П₄.

Новый фронтальный след f₀_α₁ строится по двум точкам. Одна из них, X_α₁, лежит на пересечении h₀_α с осью x₁. Дополнительно возьмем точку N, принадлежащую α, и укажем её фронтальную проекцию N»₁ на плоскости П₄.

Определение расстояния между параллельными плоскостями

Параллельные плоскости α и β расположены так, как показано на рисунке. Чтобы найти расстояние между ними, необходимо из произвольной точки A, взятой на пл. α, опустить перпендикуляр AB на пл. β и определить его настоящую длину.

Для уменьшения количества геометрических построений α и β предварительно переводятся в проецирующее положение с помощью метода замены плоскостей проекций. Вспомогательная точка M используется для определения направления следов f₀_β₁ и f_0α1, параллельных друг другу.

Источник

Примеры решения метрических задач

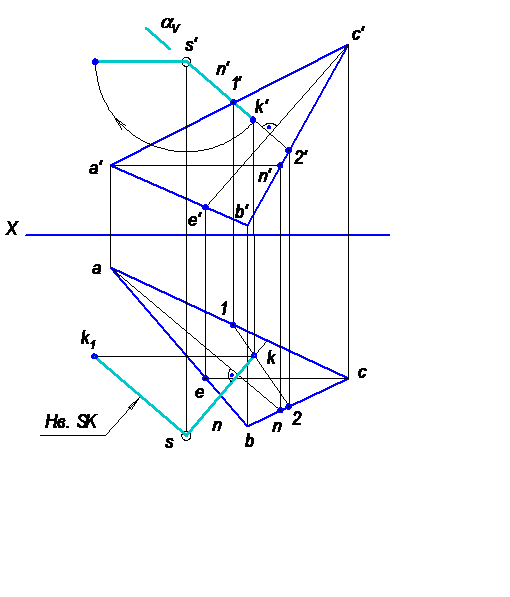
Задача 1. Определить высоту пирамиды SABC (SK).

Высота пирамиды определяется длиной перпендикуляра, опущенного из точки S на плоскость основания АВС – SK (рисунок 6.17).

Рисунок 6.17− Пример решения задачи 1

1. Опустить перпендикуляр n из точки S на основание АВС.

2. Построить основание К перпендикуляра n (точка встречи перпендикуляра с плоскостью АВС).

3. Определить натуральную величину отрезка SK, выражающего высоту пирамиды.

1. Перпендикуляр n из точки S на основание АВС пирамиды проводим без преобразования проекций. В этом случае построение проекций перпендикуляра основано на теореме о перпендикулярности прямой и плоскости, согласно которой проекции перпендикуляра к плоскости перпендикулярны к одноименным проекциям фронтали и горизонтали этой плоскости.

Поэтому на первом этапе решения задачи:

а) проводим в плоскости АВС горизонталь AN и располагаем горизонтальную проекцию перпендикуляра n перпендикулярно горизонтальной проекции горизонтали:

б) проводим в плоскости основания АВС фронталь СЕ и располагаем фронтальную проекцию перпендикуляра n перпендикулярно фронтальной проекции фронтали:

2. Основание К перпендикуляра n находим с помощью вспомогательной плоскости a:

а) заключаем перпендикуляр n во фронтально проецирующую плоскость a: nÎa; a ^V;

б) определяем линию пересечения L плоскости a и основания АВС: l = a Ç D ABC; l = 1 È 2;

в) находим точку пересечения К перпендикуляра n и основания АВС: К = n Ç D ABC.

3. Натуральную величину отрезка SK, выражающего высоту пирамиды, определяем методом вращения вокруг осей, перпендикулярных к плоскостям проекций. Для этого поворачиваем отрезок SK в положение, параллельное плоскости Н. Новая горизонтальная проекция sk₁ отрезка представляет его натуральную величину.

Задача 2.Определить угол, образованный гранью SAB и основанием АВС пирамиды (рисунок 6.18).

Угол между двумя плоскостями определяется линейным углом, полученным при сечении данных плоскостей третьей плоскостью, перпендикулярной к двум заданным. Поскольку таким путем задача решается сложно, прибегаем к одному из способов преобразования ортогональных проекций. Например, к способу замены плоскостей проекций. Решение задачи показано на рисунке 6.18.

Рисунок 6.18 − Пример решения задачи 2

1. Линию пересечения заданных плоскостей SAB и АВС – ребро АВ – из прямой общего положения преобразуем в проецирующую прямую.

2. Определить проекции плоскостей SAB и АВС в новой системе плоскостей ортогональных проекций.

3. Определить угол между гранью SAB и основанием АВС как угол между пересекающимися прямыми, в которые эти плоскости проецируются в результате преобразования.

1. Сначала заменяем плоскость V на новую V₁, располагаем ее параллельно ребру АВ (на эпюре Х₁ ½½ab) и строим новую фронтальную проекцию пирамиды. Затем заменяем плоскость Н на новую Н_1, располагая последнюю перпендикулярно ребру АВ (на эпюре Х₂ ^ a₁‘b₁‘) и строим новую горизонтальную проекцию ребра АВ.

2. Строим новую горизонтальную проекцию плоскостей SAB и АВС. Они изобразятся в виде пересекающихся прямых (рисунок 6.18).

3. Определяем угол j 0 , выражающий угол между гранью SAB и основанием АВС пирамиды.

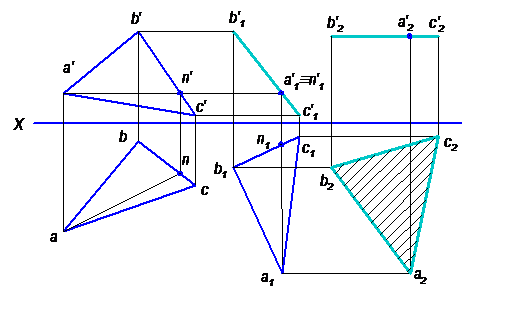
Задача № 3.Определить натуральную величину основания АВС пирамиды.

Для определения натуральной величины и формы плоской фигуры необходимо расположить ее параллельно одной из плоскостей проекций. Для этого воспользуемся способом плоскопараллельного перемещения. Решение задачи показано на рисунке 6.19.

1. Преобразовать плоскость АВС общего положения в проецирующую.

2. Преобразовать плоскость АВС в плоскость уровня и определить ее натуральную величину и форму.

1. Проводим в плоскости АВС горизонталь AN. Перемещаем горизонталь AN параллельно плоскости Н и поворачиваем ее в новом положении перпендикулярно плоскости V (на эпюре a₁n₁ ^ X). Строим новую горизонтальную проекцию a₁b₁c₁ конгруэнтную авс и новую фронтальную проекцию в виде прямой b₁‘c₁‘.

Рисунок 6.19 − Пример решения задачи 3

Перемещаем плоскость АВС параллельно плоскости V в положение, параллельное плоскости Н (на эпюре b₂‘c₂‘ || X), и находим новую горизонтальную проекцию a₂b₂c₂, представляющую натуральную величину и форму основания АВС.

Контрольные вопросы по начертательной геометрии

К теме 1. Центральные и параллельные проекции.

1.1. Какие известны вам основные методы проецирования геометрических форм на плоскости?

1.2. Сформулируйте основные свойства параллельного проецирования.

1.3. Что называют координатами точки пространства в декартовой системе координат?

К теме 2. Точка. Прямая. Плоскость на эпюре Монжа.

2.1. Постройте проекции точек, расположенных в различных углах пространства.

2.2. Что называют постоянной прямой чертежа? Как с помощью постоянной прямой чертежа построить третью проекцию точки.

2.3. Какие прямые называют линиями уровня ?

2.4. Какие прямые называют проецирующими прямыми линиями?

2.5. Приведите определение внутреннего и внешнего деления отрезка прямой.

2.6. Что называют следом прямой линии? постройте следы прямых частного положения.

2.7. Укажите правило построения следов прямой линии.

2.8. Как изображаются на чертеже пересекающиеся, параллельные и скрещивающиеся прямые линии?

2.9. Покажите способы задания плоскости общего положения и проецирующих плоскостей.

2.10 Как строят прямые линии и точки в плоскости?

2.11. Покажите способы построения горизонтали, фронтали и линии наибольшего наклона плоскостей общего положения и проецирующих плоскостей.

К теме 3. Позиционные и метрические задачи.

3.1. Покажите на примерах, как определяют точки пересечения проецирующих плоскостей прямыми линиями, линии пересечения проецирующих плоскостей плоскостями общего положения и проецирующими плоскостями.

3.2. Изобразите схему и укажите последовательность решения задачи на построение точки пересечения прямой с плоскостью общего положения.

3.3. Как определяют видимость элементов геометрических образов относите плоскостей проекций?

3.4. Изобразите схему и укажите последовательность построения линии пересечения двух плоскостей.

3.5. Изобразите схему и приведите примеры построений прямых линий, параллельных и перпендикулярных плоскостям.

3.6. Сформулируйте условие параллельности и условие перпендикулярности двух плоскостей.

3.7. Сформулируйте условие перпендикулярности двух прямых общего положения. Изобразите схему.

3.8. Как определяются на чертеже расстояния от точки до проецирующей плоскости и плоскости общего положения?

Тема № 4. Способы преобразования.

4.1. В чем состоит принцип преобразования чертежа способом замены плоскостей проекций?

4.2. Какова схема решения задачи по определению натуральной величины отсека произвольно расположенной плоскости способом замены плоскостей проекций?

4.3. В чем состоит принцип преобразования чертежа способом вращения вокруг проецирующих прямых?

4.4. Какую прямую принимают за ось вращения при переводе отсека плоскости из общего положения в горизонтально — проецирующую плоскость?

4.5. Можно ли считать плоскопараллельное перемещение вращением вокруг не выявленных осей и почему?

4.6. Укажите последовательность приемов определения натуральной величины отсека плоскости способом плоскопараллельного перемещения.

К теме 5. Пересечение поверхностей плоскостью и прямой линией.

5.1. Каковы основные способы задания поверхностей?

5.2. Укажите общую схему определения точек линии пересечения поверхностей плоскостью.

5.3. Укажите последовательность графических построений при определении точек пересечения прямой с поверхностью.

5.4. Укажите условия, при которых в сечении конуса вращения плоскостью получаются окружность, эллипс, гипербола, парабола, пересекающиеся прямые.

К теме 6. Взаимное пересечение поверхностей.

6.1. Изобразите общую схему построения линий пересечения

6.2. Назовите основные способы построения линий пересечения поверхностей.

6.3. Опишите способы секущих плоскостей и сферических посредников при определении линии пересечения поверхностей.

6.4. Какое пересечение поверхностей называют полным и неполным?

6.5. В какой последовательности соединяются точки искомой линии пересечения поверхностей и как определяется ее видимость в проекциях?

6.6. Какие точки линии пересечения поверхностей называют главными (опорными)?

К теме 7. Развертка поверхностей.

7.1. Что называют разверткой поверхностей?

7.2. Какие поверхности называют развертывающимися и какие не развертывающимися?

7.3. Укажите основные свойства разверток.

7.4. Укажите последовательность графических построений разверток поверхностей конуса и цилиндра.

К теме 8. Аксонометрические проекции.

8.1. Какие проекции называют аксонометрическими?

8.2. Что называют коэффициентом искажения?

8.3. Сформулируйте основную теорему аксонометрии – теорему Польке.

8.4. Что представляет собой треугольник следов?

8.5. Укажите коэффициенты искажений по направлениям осей в прямоугольной изометрии, в диметрии.

8.6. Укажите направления и величины осей эллипсов как изометрических и диметрических проекций окружностей, вписанных в квадрат граней куба, ребра которого параллельны координатным осям.

Источник

Источник

Необходимо построить наклонную пирамиды по известному основанию и высоте.

Для решения задачи необходимо знать теоретический материал:

— способы восстановления перпендикуляра к плоскости;

— определение натуральных величин методом вращения;

— определение видимости на чертеже с помощью конкурирующих точек (рассматривали в задаче 1).

Порядок решения задачи

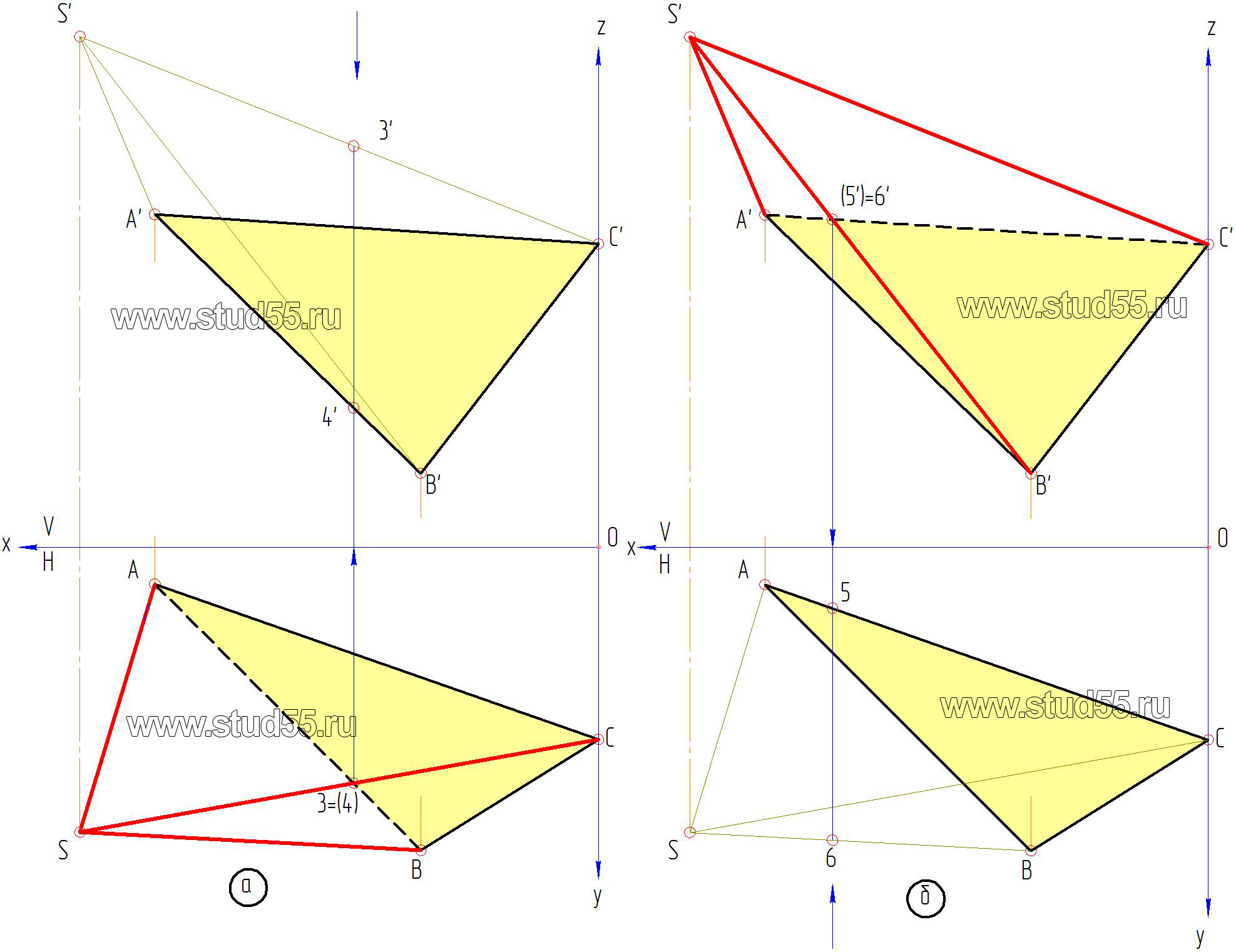
1. Согласно варианту задания наносим на комплексный чертеж координаты точек основания пирамиды, получаем плоскость в виде треугольника ABC(A’B’C’; ABC) (рис.2.1.a).

Рис. 2.1

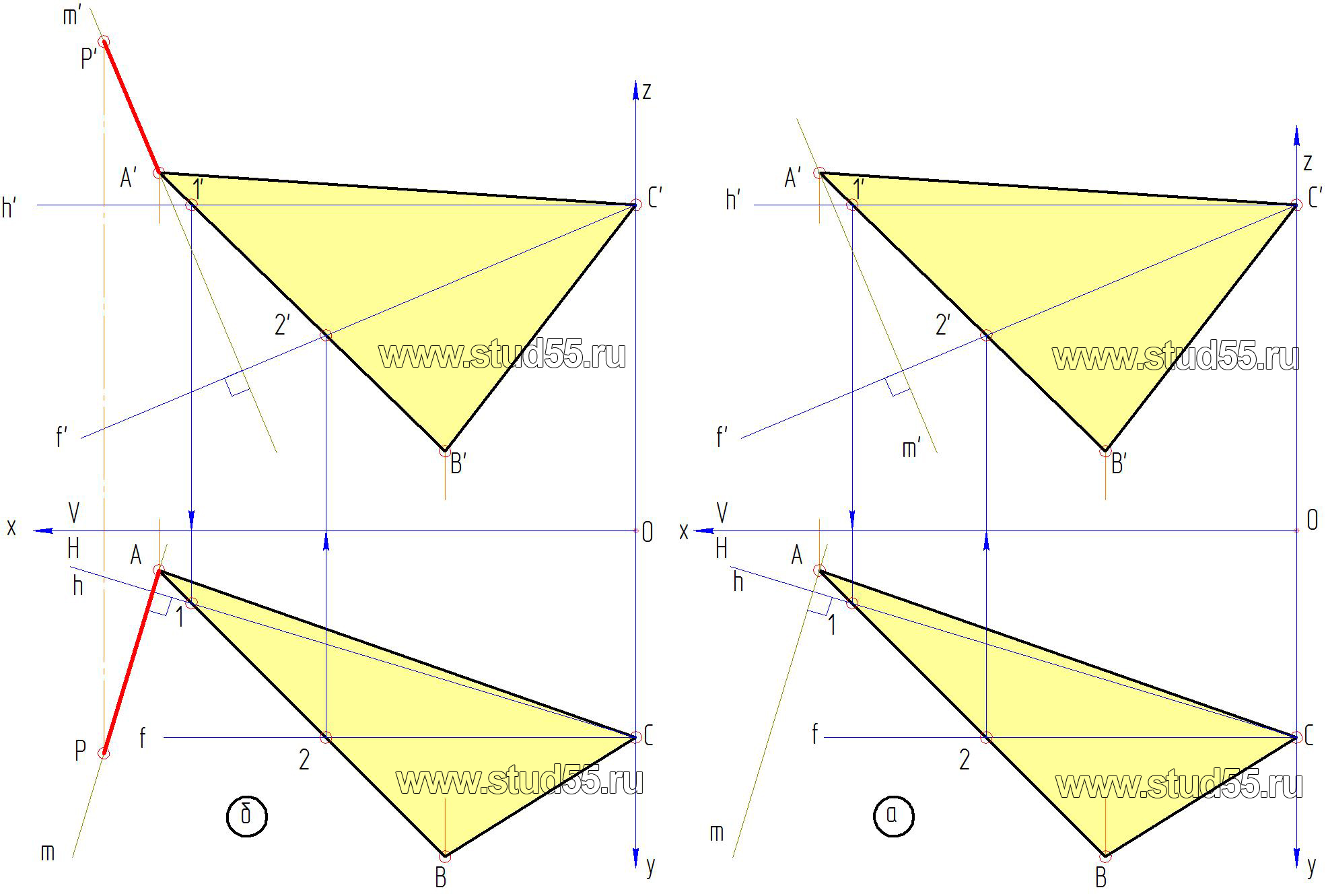
2. Для нахождения вершины пирамиды по заданной высоте необходимо к указанной плоскости провести перпендикуляр через точку А (A’; A) т.к. величина высоты задана SA, для чего:

— в заданной плоскости треугольника основания пирамиды проводим горизонталь h’и h и фронталь – f’ и f (рис.2.1.б).

— к проекциям горизонтали и фронтали, которые выражены в натуральной величине через точку А(A’; A) проводим перпендикуляр m (рис.2.2.а).

Рис.2.2

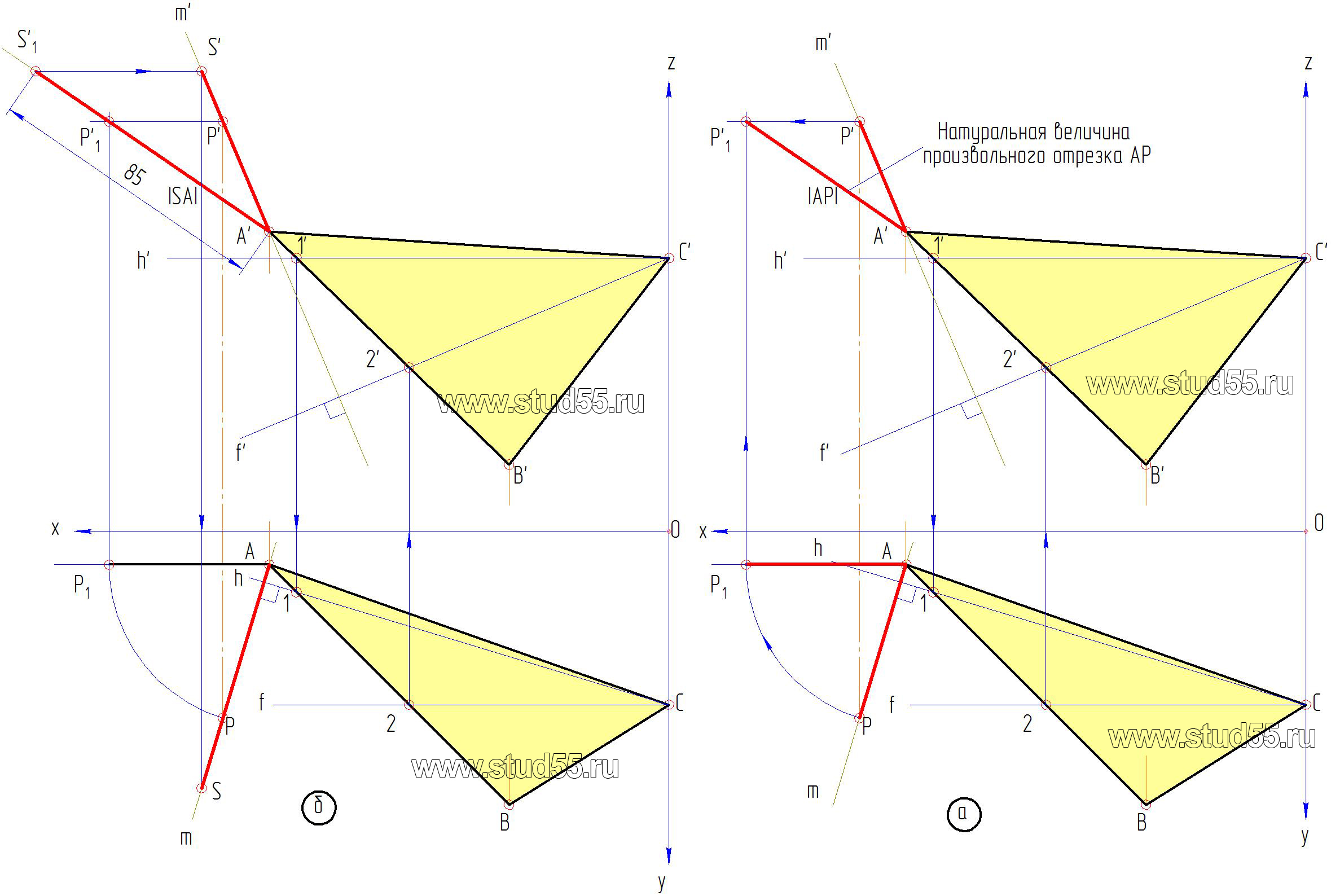
3. Так как высота пирамиды задана в натуральной величине, а проведенный перпендикуляр — в проекциях, необходимо получить линию натуральной величины произвольного отрезка на перпендикуляре. Для этого воспользуемся методом вращения:

-на проекциях перпендикуляра возьмем произвольную точку P (P’ и Р) (рис.2.2.б);

— отрезок AР в горизонтальной проекции переведем в частное положение путем разворота его вокруг точки A, до параллельности оси х, получим точку P₁ (рис.2.3.а).

— можно отметить, что при вращении точки в какой-то плоскости ее проекция на сопряженной плоскости движется по прямой параллельной оси х. Проведем ее из точки P’ и тогда по линиям связи на ней находим фронтальную проекцию точки P —P’₁

— соединив P’₁ и A’ получим линию натуральной величины отрезка перпендикуляра, на котором откладываем заданное расстояние SA (h=85мм), получая S’₁ — истинное положение вершины пирамиды.

4. Переведем истинную вершину пирамиды S’₁ на фронтальную проекцию перпендикуляра по линии параллельной оси х получаем S’ — фронтальную проекцию вершины пирамиды. По линии связи получаем ее горизонтальную проекцию – S (рис.2.3.б).

Рис.2.3

5. Таким образом, вершина пирамиды S (S’ и S) построена, соединяем ее с основанием и в заключение определяем видимость ребер пирамиды, для чего:

— возьмем на горизонтальной проекции две конкурирующие точки 3 и 4, принадлежащие соответственно линиям SC и AB спроецируем данные точки на фронтальную плоскость, получим 3’ и 4’ на линиях S’C’ и A’B’;

— по правилу определения видимости с помощью конкурирующих точек определяем, что прямая SC, в горизонтальной проекции будет видимой, т.к. ордината точки 3’, находящаяся на ней во фронтальной плоскости больше, чем ордината точки 4’, а линия AB будет невидимой (рис.2.4.а);

— аналогично определяем видимость во фронтальной плоскости, беря пару конкурирующих точек 5’ и 6’, находящихся на прямых S’B’ и A’C’. По выше изложенному правилу S’B’ на фронтальной плоскости проекций будет видимой, а A’C’–невидимой (рис.2.4.б).

Рис.2.4

Рис.2.5

У меня есть все готовые решения задач с такими координатами, купить можно >>здесь<<

Купленные чертежи по начертательной геометрии из книжки Фролова Вы легко можете скачать сразу после оплаты или я вышлю Вам на почту. Они находятся в ZIP архиве в различных форматах:
*.jpg – обычный цветной рисунок чертежа в масштабе 1 к 1 в хорошем разрешении 300 dpi;
*.cdw – формат программы Компас 12 и выше или версии LT;
*.dwg и .dxf — формат программы AUTOCAD, nanoCAD;

Раздел: Начертательная геометрия /

Рекомендуем
Комментарии
Наши товары

Источник