Ответ:
Всё в разделе «Объяснение».
Пошаговое объяснение:
- В прямоугольнике 4 стороны и все они являются высотами, так как высота — это перпендикуляр, проведённый из вершины прямоугольника к противоположной стороне этого прямоугольника.
- В прямоугольнике все углы прямые, поэтому все смежные стороны прямоугольника перпендикулярны друг к другу и являются перпендикулярами.
==============================================================
Существует множество способов нахождения высоты прямоугольника или стороны прямоугольника.
Рассмотрю 2 способа:
1) Можно найти, если известно:
Периметр прямоугольника P и одна из сторон прямоугольника a.
P = (a + b) * 2 (b — высота прямоугольника).
Тогда b = P : 2 — a.
2) Можно найти, если известно:
Площадь прямоугольника S и одна из сторон прямоугольника a.
S = ab (b — высота прямоугольника).
Тогда b = S : a.
Ответ:
Всё в разделе «Объяснение».
Пошаговое объяснение:
- В прямоугольнике 4 стороны и все они являются высотами, так как высота — это перпендикуляр, проведённый из вершины прямоугольника к противоположной стороне этого прямоугольника.
- В прямоугольнике все углы прямые, поэтому все смежные стороны прямоугольника перпендикулярны друг к другу и являются перпендикулярами.
==============================================================
Существует множество способов нахождения высоты прямоугольника или стороны прямоугольника.
Рассмотрю 2 способа:
1) Можно найти, если известно:
Периметр прямоугольника P и одна из сторон прямоугольника a.
P = (a + b) * 2 (b — высота прямоугольника).
Тогда b = P : 2 — a.
2) Можно найти, если известно:
Площадь прямоугольника S и одна из сторон прямоугольника a.
S = ab (b — высота прямоугольника).
Тогда b = S : a.
Все формулы высоты прямого угла в прямоугольном треугольнике
В прямоугольном треугольнике катеты, являются высотами. Ортоцентр — точка пересечения высот, совпадает с вершиной прямого угла.
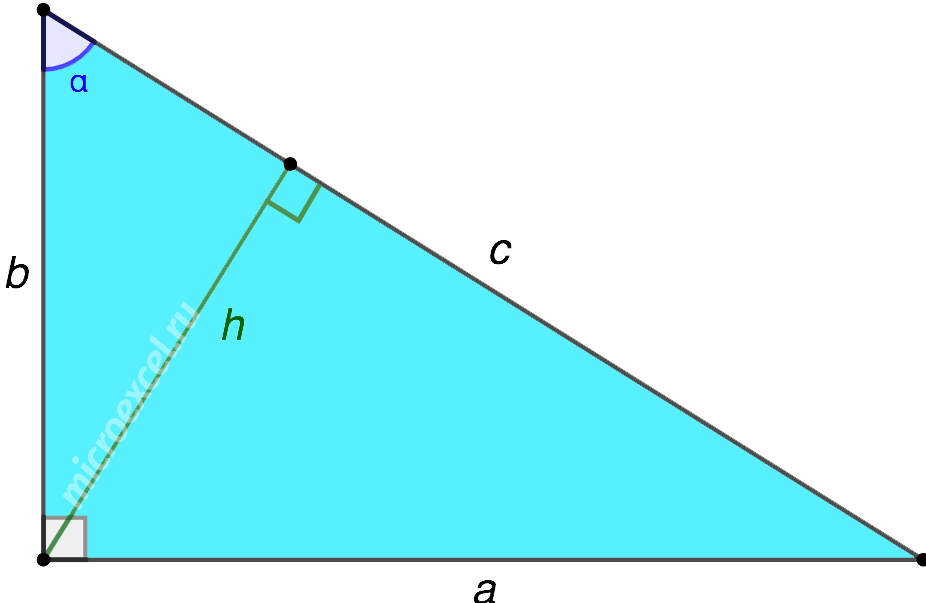
H — высота из прямого угла
a, b — катеты
с — гипотенуза
c 1 , c 2 — отрезки полученные от деления гипотенузы, высотой
α , β — углы при гипотенузе
Формула длины высоты через стороны, ( H ):
Формула длины высоты через гипотенузу и острые углы, ( H ):
Формула длины высоты через катет и угол, ( H ):
Формула длины высоты через составные отрезки гипотенузы , ( H ):
Свойства высоты прямоугольного треугольника
В данной публикации мы рассмотрим основные свойства высоты в прямоугольном треугольнике, а также разберем примеры решения задач по этой теме.
Примечание: треугольник называется прямоугольным, если один из его углов является прямым (равняется 90°), а два остальных – острые ( Содержание скрыть
Свойства высоты в прямоугольном треугольнике
Свойство 1
В прямоугольном треугольнике две высоты (h1 и h2) совпадают с его катетами.
Третья высота (h3) опускается на гипотенузу из прямого угла.
Свойство 2
Ортоцентр (точка пересечения высот) прямоугольного треугольника находится в вершине прямого угла.
Свойство 3
Высота в прямоугольном треугольнике, проведенная к гипотенузе, делит его на два подобных прямоугольных треугольника, которые также подобны исходному.
Аналогичным образом доказывается, что ∠ABD = ∠DAC.
Свойство 4
В прямоугольном треугольнике высота, проведенная к гипотенузе, вычисляется следующим образом:
1. Через отрезки на гипотенузе, образованные в результате ее деления основанием высоты:
2. Через длины сторон треугольника:
Данная формула получена из Свойства синуса острого угла в прямоугольном треугольнике (синус угла равен отношению противолежащего катета к гипотенузе) :
Примечание: к прямоугольному треугольнику, также, применимы общие свойства высоты, представленные в нашей публикации – “Высота в треугольнике abc: определение, виды, свойства”.
Пример задачи
Задача 1
Гипотенуза прямоугольного треугольника поделена высотой, проведенной к ней, на отрезки 5 и 13 см. Найдите длину этой высоты.
Решение
Воспользуемся первой формулой, представленной в Свойстве 4:
Задача 2
Катеты прямоугольного треугольника равны 9 и 12 см. Найдите длину высоты, проведенной к гипотенузе.
Решение
Для начала найдем длину гипотенузы по теореме Пифагора (пусть катеты треугольника – это “a” и “b”, а гипотенуза – “c”):
c 2 = a 2 + b 2 = 9 2 + 12 2 = 225.
Следовательно, с = 15 см.
Теперь можно применить вторую формулу из Свойства 4, рассмотренного выше:
Высота в прямоугольном треугольнике
Вспомним, что высота треугольника — это перпендикуляр, опущенный из его вершины на противоположную сторону.
В прямоугольном треугольнике катеты являются высотами друг к другу. Главный интерес представляет высота, проведённая к гипотенузе.
Один из типов экзаменационных задач банке заданий ФИПИ — такие, где в прямоугольном треугольнике высота проведена из вершины прямого угла. Посмотрим, что получается:
Высота проведена к гипотенузе . Она делит треугольник на два прямоугольных треугольника — и . Смотрим внимательно на рисунок и находим на нем равные углы. Это и есть ключ к задачам по геометрии, в которых высота опущена на гипотенузу.
Мы помним, что сумма двух острых углов прямоугольного треугольника равна . Значит, , то есть угол равен углу . Аналогично, угол равен углу .
Иными словами, каждый из трех углов треугольника равен одному из углов треугольника (и треугольника ). Треугольники и называются подобными. Давайте нарисуем их рядом друг с другом.
Они отличаются только размерами. Стороны подобных треугольников пропорциональны. Что это значит?
Возьмем треугольники и . Стороны треугольника длиннее, чем стороны треугольника в раз:
При решении задач нам пригодится равенство углов треугольников и , а также пропорциональность их сторон. Обратите также внимание, что площадь треугольника можно записать двумя разными способами: как половину произведения катетов и как половину произведения гипотенузы на проведенную к ней высоту.
Ты нашел то, что искал? Поделись с друзьями!
1. В треугольнике угол равен , — высота, , . Найдите .
Рассмотрим треугольник . В нем известны косинус угла и противолежащий катет . Зная синус угла , мы могли бы найти гипотенузу . Так давайте найдем :
(поскольку значение синуса острого угла положительно). Тогда:
Рассмотрим прямоугольный треугольник , . Поскольку
2. В треугольнике угол равен , , . Найдите высоту .
Сделайте чертеж и рассмотрите прямоугольный треугольник .
3. В треугольнике угол равен , , . К гипотенузе проведена высота . Найдите .
Это чуть более сложная задача. Ведь вам неизвестны катеты и .
Зато можно записать теорему Пифагора: .
Нам известно также, что:
Решая эту систему из двух уравнений, найдем:
Запишем площадь треугольника АВС двумя способами:
Найти высоту, проведенную из вершины прямого угла, можно было и другим способом. Мы выбрали самый короткий путь — составили и решили систему уравнений.
http://ege-study.ru/ru/ege/materialy/matematika/vysota-v-pryamougolnom-treugolnike-i-ee-svojstva/
Содержание материала
- Пример задачи
- Видео
- Окружность описанная вокруг прямоугольника
- Формулы определения радиуса окружности описанной вокруг прямоугольника
- Периметр прямоугольника
- Свойства прямоугольника:
- Диагональ прямоугольника
- Угол между диагоналями прямоугольника
- Формулы определения угла между диагоналями прямоугольника
Пример задачи
Задача 1 Гипотенуза прямоугольного треугольника поделена высотой, проведенной к ней, на отрезки 5 и 13 см. Найдите длину этой высоты.
Решение Воспользуемся первой формулой, представленной в Свойстве 4:
Задача 2 Катеты прямоугольного треугольника равны 9 и 12 см. Найдите длину высоты, проведенной к гипотенузе.
Решение Для начала найдем длину гипотенузы по теореме Пифагора (пусть катеты треугольника – это “a” и “b”, а гипотенуза – “c”):c2 = a2 + b2 = 92 + 122 = 225. Следовательно, с = 15 см.
Теперь можно применить вторую формулу из Свойства 4, рассмотренного выше:
Окружность описанная вокруг прямоугольника
Определение. Окружностью описанной вокруг прямоугольника называется круг проходящий через четыре вершины прямоугольника, центр которого лежит на пересечении диагоналей прямоугольника.
Формулы определения радиуса окружности описанной вокруг прямоугольника
1. Формула радиуса окружности описанной вокруг прямоугольника через две стороны:
2. Формула радиуса окружности описанной вокруг прямоугольника через периметр квадрата и любую сторону:
| R = | √P2 — 4Pa + 8a2 | = | √P2 — 4Pb + 8b2 |
| 4 | 4 |
3. Формула радиуса окружности описанной вокруг прямоугольника через площадь квадрата:
| R = | √S2 + a4 | = | √S2 + b4 |
| 2a | 2b |
4. Формула радиуса окружности описанной вокруг прямоугольника через диагональ квадрата:
5. Формула радиуса окружности описанной вокруг прямоугольника через диаметр описанной окружности:
6. Формула радиуса окружности описанной вокруг прямоугольника через синус угла, прилегающего к диагонали, и длину стороны противоположной этому углу:
7. Формула радиуса окружности описанной вокруг прямоугольника через косинус угла, прилегающего к диагонали, и длину стороны прилегающей к этому углу:
8. Формула радиуса окружности описанной вокруг прямоугольника через синус острого угла между диагоналями и площадью прямоугольника: R = √2S : sin β 2
Видео
Периметр прямоугольника
Определение 5. Периметр прямоугольника − это сумма всех его сторон. Обозначается периметр латинской буквой P.
Периметр прямоугольника вычисляется формулой:
 |
(5) |
где ( small a ) и ( small b ) − стороны прямоугольника.
Пример 3. Стороны прямоугольника равны 
Решение. Для нахождения периметра прямоугольника воспользуемся формулой (5). Подставляя 
Ответ:
Свойства прямоугольника:
1. Прямоугольник является параллелограммом – его противоположные стороны попарно параллельны.
Рис. 2. Прямоугольник
AB || CD, BC || AD
2. Противоположные стороны прямоугольника равны.
Рис. 3. Прямоугольник
AB = CD, BC = AD
3. Стороны прямоугольника являются его высотами.
4. Прилегающие стороны прямоугольника всегда перпендикулярны.
Рис. 4. Прямоугольник
AB ┴ BC, BC ┴ CD, CD ┴ AD, AD ┴ AB
5. Каждый угол прямоугольника прямой и равен 90 градусам. Сумма всех углов прямоугольника составляет 360 градусов.
Рис. 5. Прямоугольник
∠ABC = ∠BCD = ∠CDA = ∠DAB = 90°,
∠ABC + ∠BCD + ∠CDA + ∠DAB = 360°
6. Диагонали прямоугольника равны.
Рис. 6. Прямоугольник
AC = BD
7. Каждая диагональ прямоугольника делит его на два одинаковых прямоугольных треугольника.
Рис. 7. Прямоугольник
△ABD = △BCD, △ABC = △ACD
8. Квадрат диагонали прямоугольника равен сумме квадратов двух его смежных сторон (что вытекает из теоремы Пифагора).
Рис. 8. Прямоугольник
AC2 = AD2+ CD2
9. Диагонали прямоугольника делятся точкой пересечения пополам.
Рис. 9. Прямоугольник
AO = BO = CO = DO = АС / 2 = BD / 2
10. Около любого прямоугольника можно описать окружность. Диагональ прямоугольника является диаметром описанной окружности.
Рис. 10. Прямоугольник
АС и BD – диаметр описанной окружности и диагональ прямоугольника
11. Точка пересечения диагоналей называется центром прямоугольника и является центром описанной окружности.
12. Прямоугольник может содержать вписанную окружность и только одну, если все его стороны равны, т.е. он является квадратом.
Рис. 11. Квадрат
AВ = ВC = AD = CD
Диагональ прямоугольника
Определение 3. Диагональ прямоугольника − это отрезок, соединяющий две несмежные вершины прямоугольника.
На рисунке 2 изображен диагональ d, который является отрезком, соединяющим несмежные вершины A и C. Прямоугольник имеет две диагонали.
Для вычисления длины диагонали воспользуемся теоремой Пифагора:
или
 . . |
(1) |
Из равенства (1) найдем d:
 . . |
(2) |
Пример 1. Стороны прямоугольника равны 
Решение. Для нахождения диаметра прямоугольника воспользуемся формулой (2). Подставляя 
Ответ:
Угол между диагоналями прямоугольника
Формулы определения угла между диагоналями прямоугольника
1. Формула определения угла между диагоналями прямоугольника через угол между стороной и диагональю:
β = 2α
2. Формула определения угла между диагоналями прямоугольника через площадь и диагональ: sin β = 2Sd 2
Теги
Verified answer
Ответ:
Всё в разделе «Объяснение».
Пошаговое объяснение:
- В прямоугольнике 4 стороны и все они являются высотами, так как высота — это перпендикуляр, проведённый из вершины прямоугольника к противоположной стороне этого прямоугольника.
- В прямоугольнике все углы прямые, поэтому все смежные стороны прямоугольника перпендикулярны друг к другу и являются перпендикулярами.
==============================================================
Существует множество способов нахождения высоты прямоугольника или стороны прямоугольника.
Рассмотрю 2 способа:
1) Можно найти, если известно:
Периметр прямоугольника P и одна из сторон прямоугольника a.
P = (a + b) * 2 (b — высота прямоугольника).
Тогда b = P : 2 — a.
2) Можно найти, если известно:
Площадь прямоугольника S и одна из сторон прямоугольника a.
S = ab (b — высота прямоугольника).
Тогда b = S : a.