Как найти высоту прямоугольной трапеции 8 класс

В данной публикации мы рассмотрим различные формулы, с помощью которых можно вычислить высоту прямоугольной трапеции.

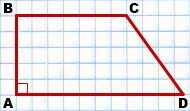
Напомним, в прямоугольной трапеции одна из боковых сторон перпендикулярна ее основаниями, и потому одновременно является высотой фигуры.

  • Нахождение высоты прямоугольной трапеции

    • Через длины сторон

    • Через основания и прилежащий угол

    • Через боковую сторону и прилежащий угол

    • Через диагонали и угол между ними

    • Через площадь и основания

Нахождение высоты прямоугольной трапеции

Через длины сторон

Высота прямоугольной трапеции abcd

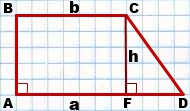
Зная длины обоих оснований и большей боковой стороны прямоугольной трапеции, можно найти ее высоту (или меньшую боковую сторону):

Формула для нахождения высоты прямоугольной трапеции через ее стороны

Данная формула следует из теоремы Пифагора. В данном случае высота h – это неизвестный катет прямоугольного треугольника, гипотенуза которого равняется d, а известный катет – разности оснований, т.е. (a-b).

Через основания и прилежащий угол

Высота прямоугольной трапеции

Если даны длины оснований и любой из прилежащих к ним острых углов, то вычислить высоту прямоугольной трапеции можно по формуле:

Формула для нахождения высоты прямоугольной трапеции через ее основания и прилежащий угол

Через боковую сторону и прилежащий угол

Высота прямоугольной трапеции с углом при основании α

Если известна длина боковой стороны прямоугольной трапеции и прилежащий к ней угол (любой), найти высоту фигуры удастся таким образом:

Формула для нахождения высоты прямоугольной трапеции через боковую сторону и прилежащий угол

Примечание: с помощью этой формулы можно, в т.ч., доказать, что меньшая боковая сторона – это и есть высота трапеции:

Расчет высоты прямоугольной трапеции через боковую сторону и прямой угол

Через диагонали и угол между ними

Диагонали прямоугольной трапеции

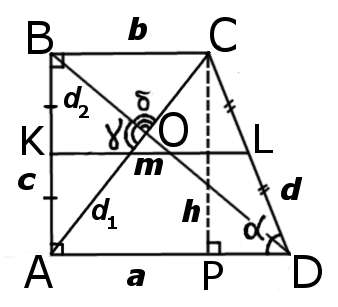
При условии, что известны длины оснований прямоугольной трапеции, диагонали и угол между ними, рассчитать высоту фигуры можно так:

Формула для нахождения высоты прямоугольной трапеции через диагонали и угол между ними

Если вместо суммы оснований известна длина средней линии, то формула примет вид:

Формула для нахождения высоты прямоугольной трапеции через диагонали и угол между ними

Элементы прямоугольной трапеции

m – средняя линия, которая равна половине суммы оснований, т.е.m = (a+b)/2.

Через площадь и основания

Высота и средняя линия прямоугольной трапеции

Если известна площадь прямоугольной трапеции и длина ее оснований (или средней линии), найти высоту можно таким образом:

Формула для нахождения высоты прямоугольной трапеции через ее площадь и основания (среднюю линию)

Источник

Прямоугольная трапеция. Формулы, признаки и свойства прямоугольной трапеции

Определение.

Прямоугольная трапеция — это трапеция у котрой одна из боковых стороны перпендикулярна основам.

Изображение прямоугольной трапеции с обозначениями
Рис.1

Признаки прямоугольной трапеции

Трапеция будет прямоугольной если выполняется одно из этих условий:

1. В тапеции есть два смежных прямых угла:

∠BAD = 90° и ∠ABC = 90°

2. Одна боковая сторона перпендикулярна основам:

AB ┴ BC, AB ┴ AD

Основные свойства прямоугольной трапеции

1. В трапеции есть два смежных прямых угла:

∠BAD = ∠ABC = 90°

2. Одна боковая сторона перпендикулярна основам:

AB ┴ BC ┴ AD

3. Высота равна меньшей боковой стороне:

h = AB

Стороны прямоугольной трапеции

Формулы длин сторон прямоугольной трапеции:

1. Формулы длины оснований через стороны и угол при нижнем основании:

a = b + d cos α = b + c ctg α = b + √d 2 — c2

b = a — d cos α = a — c ctg α = a — √d 2 — c2

2. Формулы длины оснований через стороны, диагонали и угол между ними:

a =  d1d2 · sin γ — b =  d1d2 · sin δ — b
c c
b =  d1d2 · sin γ — a =  d1d2 · sin δ — a
c c

3. Формулы длины оснований трапеции через площадь и другие стороны:

a =  2S — b      b =  2S — a
c c

4. Формула боковой стороны через другие стороны и угол при нижнем основании:

c = √d 2 — (a — b)2 = (a — b) tg α = d sin α

5. Формулы боковой стороны через основы, диагонали и угол между ними:

c =  d1d2 · sin γ =  d1d2 · sin δ
a + b a + b

6. Формулы боковой стороны через площадь, основы и угол при нижнем основании:

d =  S  =  2S
m sin α (a + b) sin α

7. Формула боковой стороны через другие стороны, высоту и угол при нижнем основании:

d =  a — b  =  c  =  h  = √c2 + (a — b)2
cos α sin α sin α

Средняя линия прямоугольной трапеции

Формулы длины средней линии прямоугольной трапеции:

1. Формулы средней линии через основание, высоту (она же равна стороне c ) и угол α при нижнем основании:

m =  a — h · ctg α  =  b + h · ctg α
2 2

2. Формулы средней линии через основания и боковые стороны сторону:

m =  a — √d 2 — c2  =  b + √d 2 — c2
2 2

Источник

Нахождение высоты прямоугольной трапеции

В данной публикации мы рассмотрим различные формулы, с помощью которых можно вычислить высоту прямоугольной трапеции.

Напомним, в прямоугольной трапеции одна из боковых сторон перпендикулярна ее основаниями, и потому одновременно является высотой фигуры.

Нахождение высоты прямоугольной трапеции

Через длины сторон

Зная длины обоих оснований и большей боковой стороны прямоугольной трапеции, можно найти ее высоту (или меньшую боковую сторону):

Данная формула следует из теоремы Пифагора. В данном случае высота h – это неизвестный катет прямоугольного треугольника, гипотенуза которого равняется d, а известный катет – разности оснований, т.е. (a-b).

Через основания и прилежащий угол

Если даны длины оснований и любой из прилежащих к ним острых углов, то вычислить высоту прямоугольной трапеции можно по формуле:

Через боковую сторону и прилежащий угол

Если известна длина боковой стороны прямоугольной трапеции и прилежащий к ней угол (любой), найти высоту фигуры удастся таким образом:

Примечание: с помощью этой формулы можно, в т.ч., доказать, что меньшая боковая сторона – это и есть высота трапеции:

Через диагонали и угол между ними

При условии, что известны длины оснований прямоугольной трапеции, диагонали и угол между ними, рассчитать высоту фигуры можно так:

Если вместо суммы оснований известна длина средней линии, то формула примет вид:

m – средняя линия, которая равна половине суммы оснований, т.е.m = (a+b) /2.

Через площадь и основания

Если известна площадь прямоугольной трапеции и длина ее оснований (или средней линии), найти высоту можно таким образом:

Свойства прямоугольной трапеции

В данной статье мы расскажем Вам о свойствах прямоугольной трапеции, как обычной, так и той, в которую вписана окружность.

Для начала напомним некоторые основные определения.

Трапеция – это четырехугольник, имеющий 2 параллельные друг другу стороны, причем 2 другие стороны параллельными не являются.

Прямоугольная трапеция — это такая трапеция, одна из боковых сторон которой перпендикулярна ее основаниям (изображена на рис.).

Средняя линия трапеции – это отрезок, который соединяет середины боковых сторон фигуры (на рис. EF).

Основные свойства прямоугольной трапеции

  1. Средняя линия EF равна половине суммы ее оснований BC и AD.
  • Средняя линия EF параллельна основаниям трапеции BC и AD.
  • На одной прямой размещаются:
    • точка пересечения (H) диагоналей прямоугольной трапеции AC и BD;
    • точка пересечения (E) продолжений боковых сторон трапеции AB и CD;
    • середины (F и G) оснований трапеции BC и AD.

    Данным свойством обладает как прямоугольная, так и равносторонняя трапеция.

    • Свойства прямоугольной трапеции, в которую вписана окружность

    SABCD = BC * AD

    Узнать подробнее о свойствах трапеции с прямым углом, в которую вписана окружность, а также ознакомиться с доказательствами этих свойств, можно на сайте uznateshe.ru.

    Понравилась статья, расскажите о ней друзьям:

    Узнать ещё

    Знание — сила. Познавательная информация

    В прямоугольную трапецию вписана окружность

    Если в условии задачи сказано, что в прямоугольную трапецию вписана окружность, можно использовать следующие свойства.

    1. Сумма оснований трапеции равна сумме боковых сторон.

    2. Расстояния от вершины трапеции до точек касания вписанной окружности равны.

    3. Высота прямоугольной трапеции равна ее меньшей боковой стороне и равна диаметру вписанной окружности.

    4. Центр вписанной окружности является точкой пересечения биссектрис углов трапеции.

    5. Если точка касания делит боковую сторону на отрезки m и n, то радиус вписанной окружности равен

    И еще два полезных свойства прямоугольной трапеции, в которую вписана окружность:

    1) Четырехугольник, образованный центром вписанной окружности, точками касания и вершиной трапеции — квадрат, сторона которого равна радиусу. (AMOE и BKOM — квадраты со стороной r).

    2) Если в прямоугольную трапецию вписана окружность, площадь трапеции равна произведению ее оснований.

    Площадь трапеции равна произведению полусуммы ее оснований на высоту:

    Обозначим CF=m, FD=n. Поскольку расстояния от вершин до точек касания равны, высота трапеции равна двум радиусам вписанной окружности, а

    источники:

    http://people-ask.ru/nauki/geometriya/svojstva-pryamougolnoj-trapecii

    В прямоугольную трапецию вписана окружность

    Источник

    Что такое прямоугольная трапеция и какими свойствами она обладает?

    Определение.

    Прямоугольная трапеция — это трапеция, у которой одна боковая сторона перпендикулярна основаниям.

    pryamougolnaya-trapeciya

    Рисунок прямоугольной трапеции

    ABCD- прямоугольная трапеция,

    AD ∥ BC — основания трапеции,

    AB и CD — ее боковые стороны,

        [AB bot AD,AB bot BC]

    Свойства прямоугольной трапеции:

    1) Высота прямоугольной трапеции равна ее меньшей боковой стороне.

    AB — высота трапеции ABCD.

    2) У прямоугольной трапеции два угла — прямые, один — острый и один — тупой.

    ∠A и ∠B — прямые, ∠D — острый, ∠C — тупой.

    3) Высота, проведенная из вершины тупого угла, делит прямоугольную трапецию на прямоугольник и прямоугольный треугольник.

    svojstva-pryamougolnoj-trapecii

        [CF bot AD]

    ABCD — прямоугольник (так как у него все углы — прямые). Следовательно, AF=BC, CF=AB.

    FCD — прямоугольный треугольник. FD=AD-AF,

    отсюда FD=AD-BC. Если AD=a, BC=b, CF=AB=h, то 

        [FD = a - b]

    и по теореме Пифагора

        [C{D^2} = C{F^2} + F{D^2},]

        [C{D^2} = {h^2} + {(a - b)^2}]

    4) Квадрат меньшей диагонали прямоугольной трапеции равен сумме квадратов ее высоты и меньшего основания.

    pryamougolnaya-trapeciya-svojstvaТреугольник ABC — прямоугольный.

    По теореме Пифагора,

        [A{C^2} = A{B^2} + B{C^2},]

        [A{C^2} = {h^2} + {b^2}]

        [AC = sqrt {{h^2} + {b^2}} ]

    5) Квадрат большей диагонали прямоугольной трапеции равен сумме квадратов ее высоты и большего основания.

    opredelenie-pryamougolnoj-trapeciiТреугольник ABD — прямоугольный.

    По теореме Пифагора,

        [B{D^2} = A{B^2} + A{D^2},]

        [B{D^2} = {a^2} + {h^2}]

        [BD = sqrt {{a^2} + {h^2}} ]

    Источник

    Прямоугольная трапеция является трапецией, у которой одна из боковых сторон перпендикулярна основаниям. Средняя линия прямоугольной трапеции равна половине суммы ее оснований. (рис.105.1)
    m=(b+d)/2

    Высота прямоугольной трапеции равна ее боковой стороне-перпендикуляру. Следовательно, площадь трапеции, которая обычно равна произведению высоты на среднюю линию, преобразуется в произведение боковой стороны на среднюю линию. (рис.105.2)
    S=hm=am=(a(b+d))/2

    Вторая боковая сторона прямоугольной трапеции, находящаяся под углом к основаниям, отличным от 90 градусов, вычисляется по теореме Пифагора в прямоугольном треугольнике с высотой.
    c=√(h^2+〖(d-b)〗^2 )=√(a^2+〖(d-b)〗^2 )

    Периметр такой трапеции вычисляется также как обычной, сложением всех ее сторон.
    P=a+b+c+d=a+b+d+√(a^2+〖(d-b)〗^2 )

    Обе диагонали прямоугольной трапеции являются гипотенузами в прямоугольных треугольниках со стороной, перпендикулярной основаниям. Поэтому вычислить их становится возможным, используя теорему Пифагора. (рис.105.3)
    d_1=√(a^2+b^2 )
    d_2=√(a^2+d^2 )

    Если боковые стороны прямоугольной трапеции в сумме дают то же, что и основания, то внутри такой трапеции можно вписать окружность. Радиусом вписанной окружности будет служить половина высоты или, в данном случае, половина квадратного корня из произведения оснований.
    r=√bc/2

    Вокруг прямоугольной трапеции нельзя описать окружность, для этого она должна стать либо равнобокой трапецией, либо прямоугольником

    Источник

    Понравилась статья? Поделить с друзьями:
  • Как в аутлук найти письмо по тексту
  • Как найти гостиницу по фотографии
  • Как составить резюме smm менеджера
  • Как найти оригинальный трек
  • Как исправить когда быстро кончаешь