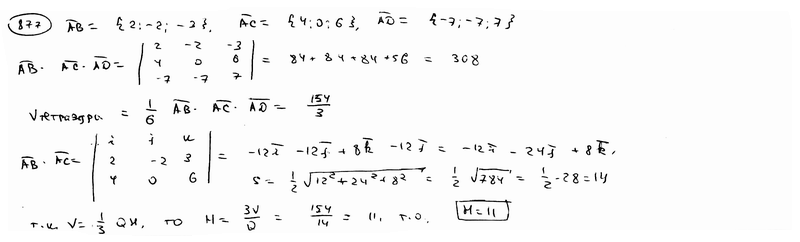Как найти высоту тетраэдра по точкам

Задача 3760 Даны вершины тетраэдра A(2; 3; 1), B(4;…

Высоту тетраэдра по векторам

Примеры

Пример 1. Проверим, лежат ли точки A (1, −1, 1) , B (2, 2, 3) , C (3, 1, 3) и D (0, 0, 1) в одной плоскости.

Решение. Вычисляем смешанное произведение векторов A B = , A C = и A D = :

( A B , A C , A D ) =

= 1 · ( −2) − 3 · 2 + 2 · 4 = 0 .

Так как смешанное произведение равно нулю, то векторы компланарны и, следовательно, точки лежат в одной плоскости.

Пример 2. Даны вершины тетраэдра A (2, 3, 1) , B (4, 1, −2) , C (6, 3, 7) и D ( −5, −4, . Найдем длину высоты, опущенной из вершины D на плоскость основания A B C (рис. 1).

Решение. Из вершины A проводим векторы A B = , A C = и A D = .

В соответствии с геометрическим смыслом смешанногопроизведения имеем:

С другой стороны,

Сравнивая эти равенства, получаем

Примечание: дробные числа записывайте
через точку, а не запятую.

Округлять до -го знака после запятой.

Как найти высоту тетраэдра формула

h = 1. Вычисляем смешанное произведение: ( A B , A C , A D ) = = 2 · 42 + 2 · 70 + ( −3) · ( −28) = 308 . Следовательно, V тетр. = 308/6 . 2. Вычисляем координаты векторного произведения: Онлайн решение Пирамиды по координатам вершин 1) чертёж пирамиды по координатам её вершин; 2) длины и уравнения рёбер, медиан, апофем, высот; 3) площади и уравнения граней; 4) система линейных неравенств, определяющих пирамиду; 5) основания и точка пересечения медиан (центроид); 6) уравнения плоскостей, проходящих через вершины параллельно противолежащим граням; 7) объём пирамиды; основания, площади и уравнения биссекторов; 9) углы между рёбрами, между рёбрами и гранями, двугранные (внутренние между гранями), телесные; 10) параметры и уравнения вписанной и описанной сфер; Внимание! Этот сервис может не работать в браузере Internet Explorer. Запишите координаты вершин пирамиды и нажмите кнопку.

A ( ; ; ), B ( ; ; ), C ( ; ; ), D ( ; ; )

Высота тетраэдра — равна корню квадратному из двух третих, помноженному на длину ребра тетраэдра

(h – высота тетраэдра, a – ребро тетраэдра)

Вывод формулы высоты тетраэдра

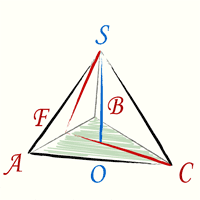
Чтобы получить формулу высоты тетраэдра необходимо произвести дополнительные геометрические построения. На рисунке красные линии CF и FS — это высоты соответствующих правильных треугольников ABC и ABS:

Теперь в треугольнике CFS известны все стороны. Высота тетраэдра, как видно из геометрических построений — это высота треугольника CFS. Подставив стороны треугольника в формулу и произведя простые сокращения (используем формулу разность квадратов) получим формулу (1).

Рассмотрим произвольный треугольник ABC и точку D , не лежащую в плоскости этого треугольника. Соединим отрезками эту точку с вершинами треугольника ABC . В результате получим треугольники ADC , CDB , ABD . Поверхность ограниченная четырьмя треугольниками ABC , ADC , CDB и ABD называется тетраэдром и обозначается DABC .
Треугольники, из которых состоит тетраэдр, называются его гранями.
Стороны данных треугольников называют ребрами тетраэдра. А их вершины – вершинами тетраэдра

Тетраэдр имеет 4 грани, 6 ребер и 4 вершины.
Два ребра, которые не имеют общей вершины, называются противоположными.
Зачастую для удобства, одну из граней тетраэдра называют основанием, а оставшиеся три грани боковыми гранями.

Но также верно и утверждение, что любая произвольная треугольная пирамида является тетраэдром. Тогда также верно, что тетраэдром называют пирамиду, в основании которой лежит треугольник.

Высотой тетраэдра называется отрезок, который соединяет вершину с точкой, расположенной на противоположной грани и перпендикулярный к ней.
Медианой тетраэдра называется отрезок, который соединяет вершину с точкой пересечения медиан противоположной грани.
Бимедианой тетраэдра называется отрезок, который соединяет середины скрещивающихся ребер тетраэдра.

Так как тетраэдр – это пирамида с треугольным основанием, то объем любого тетраэдра можно рассчитать по формуле

• S – площадь любой грани,
• H – высота, опущенная на эту грань

Правильный тетраэдр – частный вид тетраэдра

Тетраэдр, у которого все грани равносторонние треугольник называется правильным.
Свойства правильного тетраэдра:

• Все грани равны.
• Все плоские углы правильного тетраэдра равны 60°
• Так как каждая его вершина является вершиной трех правильных треугольников, то сумма плоских углов при каждой вершине равна 180°
• Любая вершина правильного тетраэдра проектируется в ортоцентр противоположной грани (в точку пересечения высот треугольника).

Пусть нам дан правильный тетраэдр ABCD с ребрами равными a . DH – его высота.
Произведем дополнительные построения BM – высоту треугольника ABC и DM – высоту треугольника ACD .
Высота BM равна BM и равна
Рассмотрим треугольник BDM , где DH , являющаяся высотой тетраэдра также и высота данного треугольника.
Высоту треугольника, опущенную на сторону MB можно найти, воспользовавшись формулой

, где
BM=, DM=, BD=a,
p=1/2 (BM+BD+DM)=
Подставим эти значения в формулу высоты. Получим

Вынесем 1/2a. Получим

Применим формулу разность квадратов

После небольших преобразований получим


Объем любого тетраэдра можно рассчитать по формуле
,
где ,

Подставив эти значения, получим

Таким образом формула объема для правильного тетраэдра

где a –ребро тетраэдра

Вычисление объема тетраэдра, если известны координаты его вершин

Пусть нам даны координаты вершин тетраэдра

Из вершины проведем векторы , , .
Для нахождения координат каждого из этих векторов вычтем из координаты конца соответствующую координату начала. Получим

Геометрических смысл смешенного произведения трех векторов заключается в следующем – смешенное произведение трех векторов равно объему параллелепипеда, построенного на этих векторах.
Так как тетраэдр есть пирамида с треугольным основанием, а объем пирамиды в шесть раз меньше объема параллелепипеда, то тогда имеет смысл следующая формула

Свойства

Зная высоту тетраэдра, можно вычислить его ребро, перевернув формулу так, чтобы ребро было равно корню из трех вторых, умноженному на высоту. a=√(3/2) h

Выразив таким образом ребро тетраэдра через его высоту, можно найти периметр тетраэдра, то есть длину всех его ребер, площадь одной грани и площадь полной поверхности тетраэдра. Периметр тетраэдра будет равен шести длинам его ребер, площадь одной грани – ребру в квадрате, умноженному на корень из трех, деленный на четыре, а площадь полной поверхности – четырем площадям одной грани. P=6a=6√(3/2) h S_1=(√3 a^2)/4=(3√3 h^2)/8 S_(п.п.)=4S_1=(3√3 h^2)/2

Через высоту, подставленную вместо ребра в определенном соотношении можно найти соответственно и радиусы вписанной и описанной окружностей в основание тетраэдра. r=h/(2√2) R=h/√2

Апофема тетраэдра проходит из вершины к противоположной стороне грани под прямым углом и рассчитать ее можно как из прямоугольного треугольника с боковым ребром по той же грани, так и из прямоугольного треугольника во внутреннем пространстве тетраэдра с высотой. l=3h/(2√2)

Чтобы вычислить объем тетраэдра, необходимо возвести в куб ребро и разделить полученное значение на шесть корней из двух, либо подставить вместо ребра корень из трех вторых, умноженный на высоту и преобразовать формулу объема для высоты. V=(√3 h^3)/8

В тетраэдр можно вписать сферу или описать сферу около него, тогда, зная высоту, чтобы вычислить радиусы вписанной и описанной сфер, необходимо воспользоваться следующими, уже готовыми формулами. (рис.60.2, 60.3) r_1=h/4 R_1=3h/4

Примеры

Пример 1. Проверим, лежат ли точки A (1, −1, 1) , B (2, 2, 3) , C (3, 1, 3) и D (0, 0, 1) в одной плоскости.

Решение. Вычисляем смешанное произведение векторов A B = <1, 3, 2>, A C = <2, 2, 2>и A D = < −1, 1, 0>:

( A B , A C , A D ) =

= 1 · ( −2) − 3 · 2 + 2 · 4 = 0 .

Так как смешанное произведение равно нулю, то векторы компланарны и, следовательно, точки лежат в одной плоскости.

Пример 2. Даны вершины тетраэдра A (2, 3, 1) , B (4, 1, −2) , C (6, 3, 7) и D ( −5, −4, . Найдем длину высоты, опущенной из вершины D на плоскость основания A B C (рис. 1).

Решение. Из вершины A проводим векторы A B = <2, −2, −3>, A C = <4, 0, 6>и A D = < −7, −7, 7>.

В соответствии с геометрическим смыслом смешанногопроизведения имеем:

С другой стороны,

Сравнивая эти равенства, получаем

1. Вычисляем смешанное произведение:

( A B , A C , A D ) =

= 2 · 42 + 2 · 70 + ( −3) · ( −28) = 308 .

Следовательно, V тетр. = 308/6 .

2. Вычисляем координаты векторного произведения:

Онлайн решение Пирамиды по координатам вершин

1) чертёж пирамиды по координатам её вершин;

2) длины и уравнения рёбер, медиан, апофем, высот;

3) площади и уравнения граней;

4) система линейных неравенств, определяющих пирамиду;

5) основания и точка пересечения медиан (центроид);

6) уравнения плоскостей, проходящих через вершины параллельно противолежащим граням;

7) объём пирамиды;

основания, площади и уравнения биссекторов;

9) углы между рёбрами, между рёбрами и гранями, двугранные (внутренние между гранями), телесные;

10) параметры и уравнения вписанной и описанной сфер;

Внимание! Этот сервис может не работать в браузере Internet Explorer.

Запишите координаты вершин пирамиды и нажмите кнопку.

Автор	Сообщение
	Заголовок сообщения: Высота тетраэдра Добавлено: 12 дек 2011, 22:00
Продвинутый Зарегистрирован: 13 ноя 2011, 10:48 Сообщений: 94 Cпасибо сказано: 7 Спасибо получено: 1 раз в 1 сообщении Очков репутации: 1	Даны координаты вершин тетраэдра ABCD найти его высоту DT. Подскажите пожалуйста порядок действий
Вернуться к началу

Alexdemath	Заголовок сообщения: Re: Высота тетраэдра Добавлено: 12 дек 2011, 22:23
	Silas Если [math]A,B,C[/math] — это вершины треугольника основания тетраэдра и [math]T(x_{{}_T},y_{{}_T},z_{{}_T})[/math] точка пересечения медиан этого треугольника, то [math]T(x_{{}_T},y_{{}_T},z_{{}_T})= T!left(frac{x_{{}_A}+x_{{}_B}+x_{{}_C}}{3},,frac{y_{{}_A}+y_{{}_B}+y_{{}_C}}{3},,frac{z_{{}_A}+z_{{}_B}+z_{{}_C}}{3},right)=ldots[/math] и длина высоты есть [math]|DT|=sqrt{(x_{{}_T}-x_{{}_D})^2+(y_{{}_T}-y_{{}_D})^2+(z_{{}_T}-z_{{}_D})^2}=ldots[/math] Напишите, что получится.
Вернуться к началу

Silas	Заголовок сообщения: Re: Высота тетраэдра Добавлено: 12 дек 2011, 22:40
	Спасибо) . Сейчас нет с собой условий задачи.Попробую позже точный ответ написать
Вернуться к началу

Silas	Заголовок сообщения: Re: Высота тетраэдра Добавлено: 13 дек 2011, 20:05
	Нашел как можно легче сделать : 1) Найти координаты векторов АВ,АС и АD. 2) Найти объём тетраэдра, умножив эти векторы (1/6)*[AB*AC]*AD. 3) Найти S основания , умножив векторно (1/2)*AB*AC. 4) Объём пирамиды V=(1/3)*S*h, отсюда h=(3*V)/S. Или ещё проще : модуль смешанного произведения AB*AC*AD поделить на модуль векторного AB*AC
Вернуться к началу

rvelikove	Заголовок сообщения: Re: Высота тетраэдра Добавлено: 25 фев 2012, 01:00
	Alexdemath писал(а): Silas Если [math]A,B,C[/math] — это вершины треугольника основания тетраэдра и [math]T(x_{{}_T},y_{{}_T},z_{{}_T})[/math] точка пересечения медиан этого треугольника, то [math]T(x_{{}_T},y_{{}_T},z_{{}_T})= T!left(frac{x_{{}_A}+x_{{}_B}+x_{{}_C}}{3},,frac{y_{{}_A}+y_{{}_B}+y_{{}_C}}{3},,frac{z_{{}_A}+z_{{}_B}+z_{{}_C}}{3},right)=ldots[/math] и длина высоты есть [math]|DT|=sqrt{(x_{{}_T}-x_{{}_D})^2+(y_{{}_T}-y_{{}_D})^2+(z_{{}_T}-z_{{}_D})^2}=ldots[/math] А почему точка пересечения медиан основания произвольного тетраэдра это «основание высоты»? Вроде это не так, тем более посчитав высоту через h=2*V/S и как расстояние от плоскости основания до точки D я получил другой (равный между собой) ответ Подскажите пожалуйста как найти эту точку «основания высоты»(знаю координаты всех вершин, надо найти вектор-высоту тетраэдра)? Пытался находить через коллинеарность нормали к основанию и вектора [math](x_{{}_D}-x_{{}_h},y_{{}_D}-y_{{}_h},z_{{}_D}-z_{{}_h}})[/math], но не получилось
Вернуться к началу

rvelikove	Заголовок сообщения: Re: Высота тетраэдра Добавлено: 25 фев 2012, 11:54
	Нашёл координаты этого «основание высоты», но для этого помимо предыдущего использовал уравнение плоскости основания, но мы ещё не проходили это Подскажите, как можно без использования плоскостей это сделать?
Вернуться к началу