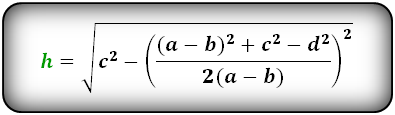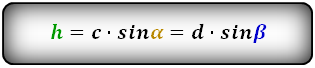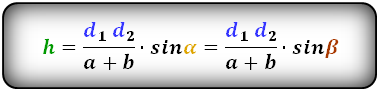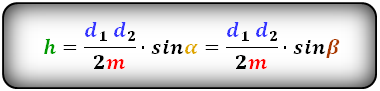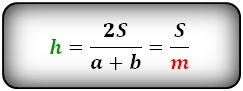Найти высоту трапеции по формулам бывает довольно сложно. Но с помощью данного онлайн-калькулятора это можно сделать в два счета. Для начала нужно в выпадающем меню выбрать известные показатели, после этого – ввести их значения в форму ниже.
В результатах появятся также значения о 17 других величинах вместе с формулами расчета. Не забудьте сохранить страницу, чтобы иметь удобную шпаргалку по геометрии всегда под рукой.
Рассчитать если известны: *
Введите данные:
Округление:
* — обязательно заполнить
В данной публикации мы рассмотрим формулы, с помощью которых можно найти высоту трапеции, а также разберем примеры решения задач для закрепления материала.
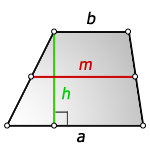
Напомним, высотой трапеции называется отрезок, соединяющий оба ее основания и перпендикулярный им.
-
Нахождение высоты трапеции
- Через длины сторон
- Через боковую сторону и прилежащий угол
- Через диагонали и угол между ними
- Через площадь
- Примеры задач
Нахождение высоты трапеции
Через длины сторон
Если известны длины всех четырех сторон трапеции, ее высота рассчитывается по формуле ниже:
Через боковую сторону и прилежащий угол
Высоту трапеции можно вычислить, если знать длину любой из ее боковых сторон и значение прилежащего к ней и основанию угла.
Через диагонали и угол между ними
Зная длину оснований трапеции, а также диагоналей и угол между ними, вычислить высоту удастся по формуле:
Если сумму оснований заменить длиной средней линии (m), то формула будет выглядеть следующим образом:
Средняя линия трапеции (m) равняется полусумме ее оснований, т.е m = (a+b)/2.
Через площадь
Высоту трапеции можно вычислить, если известны ее площадь и длины оснований (или средней линии).
Примечание: формулы для нахождения высоты равнобедренной и прямоугольной трапеций представлены на нашем сайте в отдельных публикациях.
Примеры задач
Задание 1
Найдите высоту трапеции, если ее основания равны 9 и 6 см, а боковые стороны – 4 и 5 см.
Решение
Т.к. у нас есть длины всех сторон, мы можем воспользоваться первой формулой для вычисления требуемого значения:
Кстати, т.к. высота равна одной из боковой сторон трапеции, значит она является прямоугольной.
Задание 2
Площадь трапеции равна 26 см2. Найдите ее высоту, если основания равны 10 и 3 см.
Решение
В данном случае можно применить последнюю из рассмотренных формул:
Трапеция представляет собой уникальную по своей простоте фигуру, состоящую из прямоугольника и двух присоединенных к нему прямоугольных треугольников. Стороной всех этих фигур внутри трапеции является высота, проведенная из углов при верхнем основании. Высота трапеции открывает множество вероятных решений для любых задач, и найти ее можно несколькими способами. Зная площадь трапеции и ее среднюю линию (или два основания, среднее арифметическое которых дает среднюю линию), можно вычислить высоту трапеции, разделив одно на другое:
Более изощренным является вычисление высоты трапеции через все ее стороны. В данном случае помимо высоты в трапеции нужно провести также диагональ, которая сформирует прямоугольный треугольник и даст возможность выразить высоты несколькими разными способами через разные треугольники.
Выразив все стороны треугольников через стороны трапеции и приведя подобные слагаемые, получается следующая формула:
Трапеция это фигура, которая имеет четыре стороны, две из которых параллельны, а две другие, нет. Параллельные стороны называются — верхнее основание и нижнее основание. Две другие, называются боковыми сторонами.
Высота трапеции это отрезок, длина которого, равна кратчайшему расстоянию между основаниями и следовательно расположенному перпендикулярно к этим основаниям.
1. Формула высоты трапеции через стороны и углы при основании
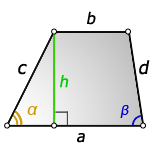
a — нижнее основание
b — верхнее основание
c , d — боковые стороны
α, β — углы трапеции
h — высота трапеции
Формулы длины высоты, (h ):
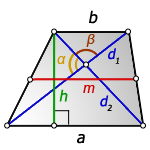
2. Формула высоты трапеции через диагонали и углы между ними
d1 , d2 — диагонали трапеции
α , β — углы между диагоналями
a , b — основания
h — высота трапеции
m — средняя линия
Формулы длины высоты, (h ):
3. Формула высоты трапеции через площадь
S — площадь трапеции
a , b — основания
h — высота трапеции
m — средняя линия
Формулы длины высоты, (h ):
Формулы площади произвольной трапеции
Формулы площади равнобедренной трапеции
Формула периметра трапеции
Все формулы по геометрии
- Подробности
-
Опубликовано: 26 сентября 2013
-
Обновлено: 13 августа 2021
Что такое трапеция
Определение
Трапеция — это геометрическая фигура, которая состоит из двух параллельных и неравных друг другу отрезков (оснований) и боковых сторон.
Все стороны трапеции могут иметь разную величину. Но если ее боковые стороны равны, значит трапеция равнобедренная.
Определение
Высота трапеции — это перпендикуляр, проведенный из любой точки одного основания фигуры до другого.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Высота трапеции
Формулы определения длины высоты трапеции:
1. Формула высоты через сторону и прилегающий угол при основании:
h = c·sin α = d·sin β
2. Формула высоты через диагонали и углы между ними:
| h = | sin γ · | d1 d2 | = | sin δ · | d1 d2 |
| a + b | a + b |
3. Формула высоты через диагонали, углы между ними и среднюю линию:
| h = | sin γ · | d1 d2 | = | sin δ · | d1 d2 |
| 2m | 2m |
4. Формула высоты трапеции через площадь и длины оснований:
5. Формула высоты трапеции через площадь и длину средней линии:
h = Sm
Видео
Площадь трапеции
Формулы определения площади трапеции:
1. Формула площади через основания и высоту:
2. Формула площади через среднюю линию и высоту:
S = m · h
3. Формула площади через диагонали и угол между ними:
| S = | d1d2 | · sin γ | = | d1d2 | · sin δ |
| 2 | 2 |
4. Формула площади через четыре стороны:
| S = | a + b | √ | c2 — | ( | (a — b)2 + c2 — d 2 | ) | 2 |
| 2 | 2(a — b) |
5. Формула Герона для трапеции S = a + b √(p — a )(p — b )(p — a — c )(p — a — d ) |a — b | где p = a + b + c + d — полупериметр трапеции.2