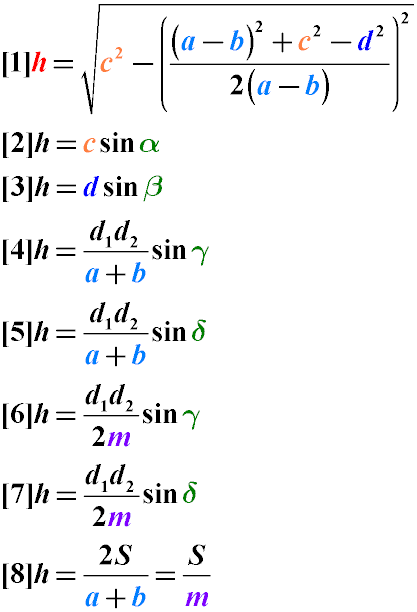Как найти высоту трапеции зная если известен косинус угла основания и боковая сторона?
На этой странице сайта размещен вопрос Как найти высоту трапеции зная если известен косинус угла основания и боковая сторона? из категории
Геометрия с правильным ответом на него. Уровень сложности вопроса
соответствует знаниям учеников 5 — 9 классов. Здесь же находятся ответы по
заданному поиску, которые вы найдете с помощью автоматической системы.
Одновременно с ответом на ваш вопрос показаны другие, похожие варианты по
заданной теме. На этой странице можно обсудить все варианты ответов с другими
пользователями сайта и получить от них наиболее полную подсказку.
Что такое трапеция
Определение
Трапеция — это геометрическая фигура, которая состоит из двух параллельных и неравных друг другу отрезков (оснований) и боковых сторон.
Все стороны трапеции могут иметь разную величину. Но если ее боковые стороны равны, значит трапеция равнобедренная.
Определение
Высота трапеции — это перпендикуляр, проведенный из любой точки одного основания фигуры до другого.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Высота трапеции
Формулы определения длины высоты трапеции:
1. Формула высоты через сторону и прилегающий угол при основании:
h = c·sin α = d·sin β
2. Формула высоты через диагонали и углы между ними:
| h = | sin γ · | d1 d2 | = | sin δ · | d1 d2 |
| a + b | a + b |
3. Формула высоты через диагонали, углы между ними и среднюю линию:
| h = | sin γ · | d1 d2 | = | sin δ · | d1 d2 |
| 2m | 2m |
4. Формула высоты трапеции через площадь и длины оснований:
5. Формула высоты трапеции через площадь и длину средней линии:
h = Sm
Видео
Площадь трапеции
Формулы определения площади трапеции:
1. Формула площади через основания и высоту:
2. Формула площади через среднюю линию и высоту:
S = m · h
3. Формула площади через диагонали и угол между ними:
| S = | d1d2 | · sin γ | = | d1d2 | · sin δ |
| 2 | 2 |
4. Формула площади через четыре стороны:
| S = | a + b | √ | c2 — | ( | (a — b)2 + c2 — d 2 | ) | 2 |
| 2 | 2(a — b) |
5. Формула Герона для трапеции S = a + b √(p — a )(p — b )(p — a — c )(p — a — d ) |a — b | где p = a + b + c + d — полупериметр трапеции.2
Теги
Высота трапеции
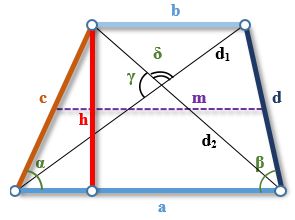
на рисунке обозначены:
a — большее основание трапеции
b — меньшее основание
c,d — боковые стороны трапеции
m — средняя линия трапеции
h — высота трапеции
d1, d2 — диагонали трапеции
α, β — углы между основанием и боковыми сторонами
γ, δ — углы между диагоналями трапеции
Формулы нахождения высоты трапеции
Высоту трапеции можно найти через длины ее сторон, диагоналей, углы между боковыми сторонами и основанием и углы между диагоналями. Также ее можно вычислить через площадь и среднюю линию трапеции:
Высота трапеции равна произведению длины боковой стороны на синус угла между этой стороной и большим основанием трапеции. (Формулы 2 и 3)
Высоту трапеции можно найти как произведение длин диагоналей и синуса угла между ними, деленное на сумму длин оснований трапеции. (Формулы 4 и 5)
Высота трапеции равна произведению длин диагоналей и синуса угла между ними, деленными на удвоенную среднюю линию трапеции (Формулы 5 и 6)
Высоту трапеции можно вычислить как площадь такой трапеции деленную на длину ее средней линии (Формула 
0
Площадь трапеции |
Описание курса
| Трапеция (задачи про основания)
как найти высоту трапеции зная если известен косинус угла основания и боковая сторона?
Зачем это… Там решается намного проще. Голову только морочите
секунду, я такую формулу просто впервые вижу, пытаюсь, косинус по условию корень из 15/4
как это впервые видите? а как же вы такие задачи решаете, если не знаете осн.триг.тождества? Посмотрите в вашем учебнике, обязательно должно быть) Если не ошибаюсь, в 8 классе проходят
ну блин, синус — прилежащий/гипотенуза, косинус — противолежащий/гипотенуза. Вот это вот знаю
Светило науки — 3 ответа — 0 раз оказано помощи
Вот. Надеюсь поймешь

Остались вопросы?
Новые вопросы по предмету Математика
Как вычислить высоту трапеции
Если в четырехугольнике только две противоположных стороны параллельны, его можно назвать трапецией. Пара непараллельных отрезков, образующих эту геометрическую фигуру, называется боковыми сторонами, а другая пара — основаниями. Расстояние между двумя основаниями определяет высоту трапеции и может быть рассчитано несколькими способами.
Инструкция
Если в условиях даны длины обоих оснований (a и b) и площадь (S) трапеции, начните вычисление высоты (h) с нахождения полусуммы длин параллельных сторон: (a+b)/2. Затем на полученное значение разделите площадь — результат и будет искомой величиной: h = S/((a+b)/2) = 2*S/(a+b).
Зная длину средней линии (m) и площадь (S) можно упростить формулу из предыдущего шага. По определению средняя линия трапеции равна полусумме ее оснований, поэтому для вычисления высоты (h) фигуры просто разделите площадь на длину средней линии: h = S/m.
Можно определить высоту (h) такого четырехугольника и в том случае, если даны только длина одной из боковых сторон (с) и угол (α), образуемый ей и длинным основанием. В этом случае следует рассмотреть треугольник, образуемый этой стороной, высотой и коротким отрезком основания, который отсекает опущенная на него высота. Этот треугольник будет прямоугольным, известная сторона будет в нем гипотенузой, а высота — катетом. Отношение длин катета и гипотенузы равно синусу противолежащего катету угла, поэтому для вычисления высоты трапеции умножьте известную длину стороны на синус известного угла: h = с*sin(α).
Такой же треугольник стоит рассмотреть и если даны длина боковой стороны (с) и величина угла (β) между ней и другим (коротким) основанием. В этом случае величина угла между боковой стороной (гипотенузой) и высотой (катетом) будет на 90° меньше известного из условий угла: β-90°. Так как отношение длин катета и гипотенузы равно косинусу угла между ними, то высоту трапеции вычислите умножением косинуса уменьшенного на 90° угла на длину боковой стороны: h = с*cos(β-90°).
Если в трапецию вписана окружность известного радиуса (r), формула вычисления высоты (h) будет очень проста и не потребует знания никаких других параметров. Такая окружность по определению должна касаться каждого из оснований только одной точкой и эти точки будут лежать на одной линии с центром круга. Это значит, что расстояние между ними будет равно диаметру (удвоенному радиусу), проведенному перпендикулярно основаниям, то есть совпадающим с высотой трапеции: h=2*r.
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.