Данный сайт находится в режиме тестирования, обо всех выявленных проблемах Вы можете сообщить на почту
Формулы усеченного конуса
Для расчёта всех основных параметров усеченного конуса воспользуйтесь калькулятором.
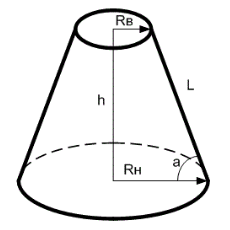
Объём усеченного конуса
$$
V = {1 over 3} * pi * h * (R_Н^2 + R_Н * R_В + R_В^2)
$$
Площадь боковой поверхности усечённого конуса
$$
S_Б = pi * (R_Н + R_В) * L
$$
Высота усеченного конуса через образующую и радиусы оснований
$$
h = sqrt{L^2 — (R_Н — R_В)^2}
$$
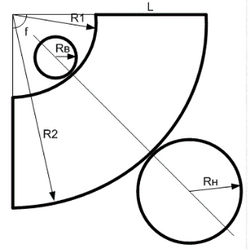
Развертка (выкройка) усеченного конуса
Длина образующей, L
$$
L = sqrt{(R_Н — R_В)^2 + h^2}
$$
$$
R_1 = {L * R_В over R_Н — R_В}
$$
$$
R_2 = L + R_1
$$
Угол ∠ f
$$
∠ f = 360° * {R_Н — R_В over L}
$$
-
Радиус и высота усеченного конуса
Радиусы оснований усеченного конуса позволяют вычислить диаметры оснований, их периметр и площадь по стандартным формулам для окружности с учетом двух различных радиусов усеченного конуса.
d=2r
D=2R
p=2πr
P=2πR
S_r=πr^2
S_R=πR^2Поскольку нам известна высота усеченного конуса, но для дальнейших вычислений нужна также и образующая, то нужно построить трапецию во внутреннем пространстве усеченного конуса таким образом, чтобы она соединяла указанные величины через радиусы. В такой трапеции, поскольку она прямоугольная, можно построить дополнительный прямоугольный треугольник и найти в нем апофему по теореме Пифагора, а также углы при основаниях и апофеме, через тригонометрические отношения
l=√(h^2+(R-r)^2 )
tanβ=h/(R-r)
α=180°-βПлощадь боковой поверхности усеченного конуса зависит от радиусов оснований конуса и от апофемы, которую можно найти, зная высоту, по формуле приведенной выше. Площадь полной поверхности состоит из площади боковой поверхности и площади двух оснований усеченного конуса.
S_(б.п.)=πl(R+r)
S_(п.п.)=S_(б.п.)+S_r+S_R=πl(R+r)+πr^2+πR^2Найти объем усеченного конуса, зная высоту и радиусы оснований, достаточно просто, поскольку стандартная формула не предполагает других элементов расчета.
V=πh/3(R^2+rR+r^2)
Как найти высоту усеченного конуса
Если вблизи вершины конуса провести сечение, можно получить идентичную, но иную по форме и размерам фигуру, называемую усеченным конусом. Она имеет не один, а два радиуса, один из которых меньше другого. Как и у обычного конуса, у этой фигуры имеется высота.
Инструкция
Перед нахождением высоты усеченного конуса ознакомьтесь с его определением. Усеченным конусом называется фигура, которая образована в результате перпендикулярного сечения плоскости обыкновенного конуса, при условии, что это сечение параллельно его основанию. Данная фигура имеет три характеристики:
— r1 — наибольший радиус;
— r2 — наименьший радиус;
— h — высота.Кроме того, как и у обычного конуса, у усеченного имеется так называемая образующая, обозначаемая буквой l. Обратите внимание на внутреннее сечение конуса: оно представляет собой равнобедренную трапецию. Если ее вращать вокруг своей оси, получится усеченный конус с теми же параметрами. В данном случае, линия, делящая равнобедренную трапецию на две других, меньшего размера, совпадает с осью симметрии и с высотой конуса. Другая боковая сторона является образующей конуса.
Зная радиусы конуса и его высоту, можно найти его объем. Он вычисляется следующим образом:V=1/3πh(r1^2+r1*r2+r2^2)Если известны два радиуса конуса, а также его объем, этого достаточно, чтобы найти и высоту фигуры:h=3V/π(r1^2+r1*r2+r2^2).В том случае, если в условии задачи даны диаметры окружностей, а не радиусы, данное выражение приобретает несколько иной вид:h=12V/π(d1^2+d1*d2+d2^2).
Зная образующую конуса и угол между ней и основанием данной фигуры, также можно найти ее высоту. Для этого нужно из другой вершины трапеции провести проекцию к большему радиусу, чтобы получился небольшой прямоугольный треугольник. Проекция будет равна высоте усеченного конуса. Если известна образующая l и угол, высота определите по следующей формуле:h=l*sinα.
Если по условию задачи известна лишь площадь сечения конуса, найти высоту невозможно, если неизвестны оба его радиуса.
Источники:
- как найти высоту конуса зная диаметр
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
Frustum of a cone is a special shape that is formed when we cut the cone with a plane parallel to its base. The cone is a three-dimensional shape having a circular base and a vertex. So the frustum of a cone is a solid volume that is formed by removing a part of the cone with a plane parallel to circular base. The frustum is not only defined for cones but can be also defined for the different types of pyramids (square pyramid, triangular pyramid, etc.).
Some of the common shapes of a frustum of cone which we discover in our daily life are buckets, lamp shade, and others. Let us learn more about the frustum of cones in this article.
What is Frustum of Cone?
Frustum is a Latin word, which means pieces, therefore frustum of cone is a solid piece of the cone. When a right circular cone is cut by a plane parallel to the base of the cone the shape so obtained is called frustum of the cone. The figure given below shows us how a plane cuts the cone parallel to its base to form the frustum of the cone.
Now, the frustum of the cone is easily defined as,
If a right circular cone is cut off by a plane parallel to it’s base, the shape of the portion between the cutting plane and the base plane is called frustum of cone.
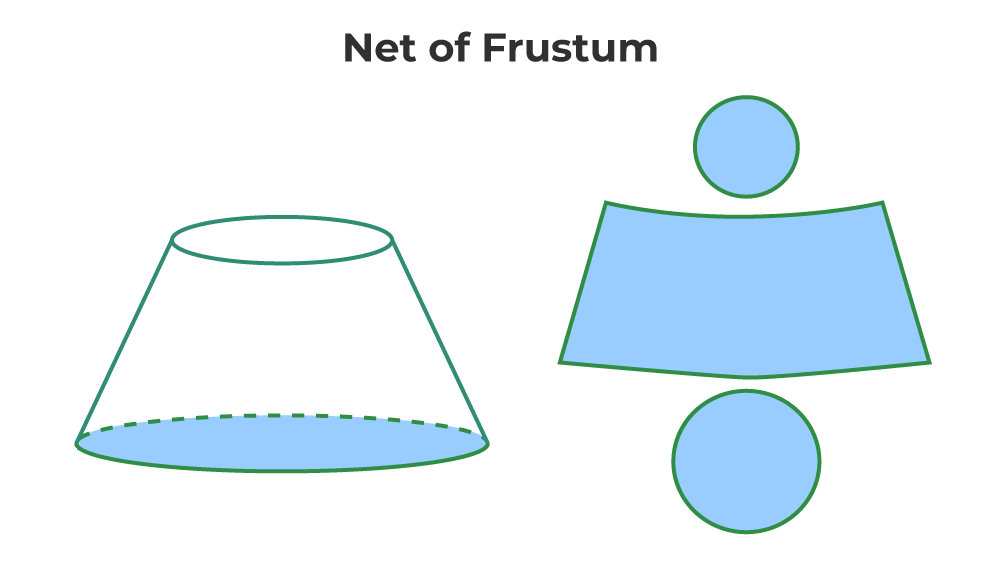
Net of Frustum of Cone
If a three-dimensional (3D) shape is cut open and made a two-dimensional shape the shape so obtained is called the net. One can assume that when the net of the figure is folded properly in a correct manner it forms the desired 3D shape. The image given below shows the net of the frustum of the cone.
Properties of Frustum of Cone
Properties of a Frustum of a cone are very similar to the cone, some of the important properties of frustum of cone are,
- Base of the cone the original cone is contained in the frustum of a cone but its vertex is not contained in the frustum.
- Formulas of frustum of a cone are dependent on its height and two radii (corresponding to the top and bottom bases).
- Height of the frustum of the cone is the perpendicular distance between the centers of its two bases.
Formulas of Frustum of Cone
Frustum of Cone is such a shape that is frequently seen in our daily life, for example, table lamps, buckets, etc. The important formulas for the frustum of a cone are,
- Volume of Frustum of Cone
- Surface Area of Frustum of Cone
Let’s learn about these formulas in detail below,
Volume of Frustum of Cone
Frustum of cone is a sliced part of a cone, where a small cone is removed from the larger cone. Therefore, to calculate the volume of the frustum of cone, one just needs to calculate the difference between the volume of the larger and smaller cone.
Let’s assume,
- Total height of the cone is to be H + h
- Total slant height to be l’ + L
- The radius of a complete cone is r
- The radius of the sliced cone is r’
Since the volume of the cone is given as V = 1/3πr2h
Volume of complete cone V1 = 1/3πr2(H+h)
Volume of smaller cone V2 =1/3πr’2(h)
Now the volume of the frustum of cone (V) can be calculated using the formula,
V = V1 – V2
V = 1/3πr2(H+h) – 1/3πr’2(h)
V= 1/3π[r2(H+h) – r’2(h)]…(1)
Using the property of similarity of the triangles of △OCD and △OAB, one can write,
r / (H + h) = r’ / h
r / r’ = (H + h) / h
H + h = hr / r’
Substitute this value of (H+h) in equation (1), and simplify,
V = 1/3π[r2(rh / r’) – r’2(h)}
= 1/3π[{hr3 – hr’3} / r’]…(2)
Using the similar triangle’s property again in △OCD and △OAB, we will find out the value of h
r / (H + h) = r’ / h
r / r’ = (H + h) / h
rh = (H + h)r’
rh = Hr’ + hr’
(r -r’)h = Hr’
h = Hr’ / (r -r’)
Substituting these values in equation (2),
V = 1/3π[{r3h – r3h} / r’]
= 1/3π[{r3 – r’3}h / r’]
= 1/3π[{r3 – r’3}{Hr’ / (r – r’)} / r’]
= 1/3πH(r2 + r’2 +rr’)
Thus,
Volume of the frustum of cone = 1/3 πH(r2 + r’2 + rr’)
Surface Area of Frustum of Cone
The surface area of frustum of cone can be calculated by the difference between the surface area of the complete cone and the smaller cone (removed from the complete cone). The surface area of the frustum of cone can be calculated using the below diagram, where one needs to sum up the surface areas of the curved surfaces, and the surface areas of the top and bottom surfaces of the frustum of cone.
Similar to the Volume of the frustum of cone, the curved surface area will be also equal to the difference between the surface areas of the bigger cone and the smaller cone.
In the figure given above, triangles OAB and OCD are similar. Therefore, using the similarity criteria, one can write,
l’ / l = r’ / r…(1)
Since, l’ = l – L, therefore, from equation (1),
(l – L) / l = r’ / r
After cross-multiplication,
lr – Lr = lr’
l(r – r’) = Lr
l = Lr / (r – r’)…(2)
The curved surface area of a complete cone = πrl
The curved surface area of the smaller cone = πr’l’
Difference between the curved surface areas of complete cone and smaller cone = π (rl – r’l’)
Thus, the curved surface area (CSA) of the frustum of cone = πl (r – r’l’/l)
Use equation (1) to substitute the value of l’/l in the above equation, and simplify,
CSA of the frustum of cone = πl (r – r’×r’/r) = πl (r2 – r’2)/r
Now, substitute the value of l from equation (2), and simplify,
CSA of the frustum of cone = πlr/(r – r’)× (r2 – r’2)/r = πl (r + r’)
Thus, one can write,
Curved surface area of frustum of cone = πl (r + r’)
Now, let’s calculate the surface area of the top and bottom bases of the frustum of the cone, such that,
The surface area of the top base of the frustum of cone having a radius r’ = πr’2
The surface area of the bottom base of the frustum of cone having a radius r = πr2
So,
Total surface area of the frustum of cone = Curved surface area of the frustum of cone + surface area of the top base + surface area of the bottom base
Therefore,
The total surface area of the frustum of cone = πl (r + r’) + πr’2 + πr2 = πl (r + r’) + π (r2 + r’2)
Thus, the total surface area of the frustum of cone is = πl (r + r’) + π (r2 + r’2)
This formula can be also written as,
The total surface area of the frustum of cone is = πl (r2 – r’2)/r + π (r2 + r’2)
So, one can write,
Total surface area of frustum of cone = πl(r + r’) + π (r2 + r’2)
or
Total surface area of frustum of cone = πl (r2 – r’2)/r + π (r2 + r’2)
Note that, l is the slant height of the smaller cone that can be given as
L = √ [H2 + (r – r’)2]
Read, More
- Volume of Cone
- Volume of Cylinder
- Volume of Sphere
Solved Examples on Frustum of Cone
Example 1: Find out the Volume of a frustum of a cone that is 15 cm high and the radii for both the bases are 5 cm and 8 cm.
Solution:
Using the formula studied above, one can write,
V = 1/3 πH(r2 + r’2 + rr’)
Given,
H = 15 cm
r’= 5 cm
r = 8 cmV = 1/3 π15(82 + 52 + 40)
V = 5π(129)
V = 645π cm3
Example 2: Find out the surface area and total surface area of a frustum of a cone which is 10 cm high and the radii for both the bases are 4 cm and 8 cm.
Solution:
We know the formula for surface area and total surface area of the frustum. We need to plug in the required values.
Curved Surface area of the frustum = πl(r+r’)
where,
L = √ [H2 + (R – r)2]Given,
H = 10 cm
r = 4 cm
R = 8 cmCalculating the value of L,
L = √ [102 + (8 – 4)2]
= √(100+16) = √(116)
Curved Surface Area of Frustum = πL(R+r)
= π√(116)×(8+4)
= 48π√(29)
Total Surface Area = Curved Surface Area of Frustum + Area of Both Bases
= 48π√(29) + π(8)2 + π(4)2
= 48π√(29) + 64π + 16π
= 48π√(29) + 80π cm2
Example 3: Let’s say we have an open metal bucket whose height is 50cm and the radii of the bases are 10cm and 20cm. Find the area of the metallic sheet used to make the bucket.
Solution:
Bucket is in the form of frustum which closed from the bottom. We need to calculate the total surface area of this frustum.
Given
H = 50 cm
r ‘= 10 cm
r = 20 cmCurved Surface Area of Frustum = πL(R+r)
L = √ [H2 + (r – r’)2]
L = √ [502 + (20 – 10)2]
= √(2500+100) = √(2600)
= √100(26) = 10√(26)
Curved Surface Area of Frustum = πL(R+r)
= π10√(26)×(20+10)
= 300π√(26)
Total Surface Area = Curved Surface Area of Frustum + Area of Both Bases
= 300π√(26) + π(20)2 + π(10)2
= 300π√(26) + 400π + 100π
= (300π√(26) + 500π) cm2
Example 4: Find out the expression of the volume for a frustum if its height is 6y, and its radii are y and 2y respectively.
Solution:
Using the formula studied above,
V = 1/3 πH(r2 + r’2 + rr’)
Given,
H = 6y
r’= y
r = 2yV = 1/3 π6[(2y)2 + (y)2 + (y)(2y)]
V = 2πy(7y2)
V = 14πy3 unit3
FAQs on Frustum of Cone
Question 1: What is the Frustum of a Cone?
Answer:
When we cut a cone in such a way that the plane of cutting is parallel to the base of the cone. The resultant figure so obtained is called the Frustum of the Cone.
Question 2: What are the Frustum of Cone Formulas?
Answer:
The formulas of the frustum of a cone are discussed below. Let’s take a frustum of base radius ‘R’ and top radius ‘r’, height ‘H’, and slant height then,
- Volume of frustum of a cone (V) = 1/3πH(r2 + rr’ + r’2)
- Total surface area of frustum of a cone = πl (r + r’) + π (r’2 + r2).
Question 3: What is the CSA of a frustum?
Answer:
The curved surface area of the frustum of a cone is calculated using the formula,
CSA = πl (r + r’)
where,
r’ is the radius of the upper circle of frustum
r is the radius base
l is the slant height
Question 4: What is the Surface Area of Frustum of Cone?
Answer:
The surface area of the frustum of a cone is calculated using the formula,
- CSA of frustum of cone = πl [ (r2 – r’2) / r’ ]
- TSA of frustum of cone = π (r2 + r’2) + πl [ (r2 – r’2) / r’]
Question 5: What is the Volume of the Frustum of Cone?
Answer:
The volume of the frustum of a cone is calculated using the formula,
- V = 1/3πh[ (r3 – r’3) / r’]
- V = 1/3πH(r2 + rr’ + r’2)
Введение
Рис. 1. Предметы из жизни, имеющие форму усеченного конуса
Как вы думаете, откуда в геометрии берутся новые фигуры? Все очень просто: человек в жизни сталкивается с похожими объектами и придумывает, как бы их назвать. Рассмотрим тумбу, на которой сидят львы в цирке, кусок морковки, который получается, когда мы нарезали только часть ее, действующий вулкан и, например, свет от фонарика (см. рис. 1).
Усеченный конус, его элементы и осевое сечение
Рис. 2. Геометрические фигуры
Мы видим, что все эти фигуры похожей формы – и снизу, и сверху они ограничены кругами, но они сужаются кверху (см. рис. 2).
Рис. 3. Отсечение верхней части конуса
Это похоже на конус. Только не хватает верхушки. Мысленно представим, что мы берем конус и отсекаем от него верхнюю часть одним взмахом острого меча (см. рис. 3).
Рис. 4. Усеченный конус
Получается как раз наша фигура, называется она усеченный конус (см. рис. 4).
Рис. 5. Сечение, параллельное основанию конуса
Пусть дан конус. Проведем плоскость, параллельную плоскости основания этого конуса и пересекающую конус (см. рис. 5).
Она разобьет конус на два тела: одно из них – конус меньшего размера, а второе и называется усеченным конусом (см. рис. 6).
Рис. 6. Полученные тела при параллельном сечении
Таким образом, усеченный конус – это часть конуса, заключенная между его основанием и параллельной основанию плоскостью. Как и в случае с конусом, усеченный конус может иметь в основании круг – в этом случае его называют круговым. Если исходный конус был прямым, то и усеченный конус называют прямым. Как и в случае с конусами, мы будем рассматривать исключительно прямые круговые усеченные конусы, если специально не указано, что речь идет о непрямом усеченном конусе или в его основаниях не круги.
Рис. 7. Вращение прямоугольной трапеции
Наша глобальная тема – тела вращения. Усеченный конус – не исключение! Вспомним, что для получения конуса мы рассматривали прямоугольный треугольник и вращали его вокруг катета? Если полученный конус пересечь плоскостью, параллельной основанию, то от треугольника останется прямоугольная трапеция. Ее вращение вокруг меньшей боковой стороны и даст нам усеченный конус. Заметим снова, что речь, разумеется, идет только о прямом круговом конусе (см. рис. 7).
Рис. 8. Основания усеченного конуса
Сделаем несколько замечаний. Основание полного конуса и круг, получающийся в сечении конуса плоскостью, называют основаниями усеченного конуса (нижним и верхним) (см. рис. 8).
Рис. 9. Образующие усеченного конуса
Отрезки образующих полного конуса, заключенные между основаниями усеченного конуса, называют образующими усеченного конуса. Так как все образующие исходного конуса равны и все образующие отсеченного конуса равны, то и образующие усеченного конуса равны (не путать отсеченный и усеченный!). Отсюда и следует равнобедренность трапеции осевого сечения (см. рис. 9).
Отрезок оси вращения, заключенный внутри усеченного конуса, называют осью усеченного конуса. Этот отрезок, разумеется, соединяет центры его оснований (см. рис. 10).
Рис. 10. Ось усеченного конуса
Высота усеченного конуса – это перпендикуляр, проведенный из точки одного из оснований к другому основанию. Чаще всего, в качестве высоты усеченного конуса рассматривают его ось.
Рис. 11. Осевое сечение усеченного конуса
Осевое сечение усеченного конуса – это сечение, проходящее через его ось. Оно имеет вид трапеции, чуть позже мы докажем ее равнобедренность (см. рис. 11).
Площади боковой и полной поверхностей усеченного конуса
Рис. 12. Конус с введенными обозначениями
Найдем площадь боковой поверхности усеченного конуса. Пусть основания усеченного конуса имеют радиусы и
, а образующая равна
(см. рис. 12).
Рис. 13. Обозначение образующей отсеченного конуса
Найдем площадь боковой поверхности усеченного конуса как разность площадей боковых поверхностей исходного конуса и отсеченного. Для этого обозначим через образующую отсеченного конуса (см. рис. 13).
Тогда искомая .
Рис. 14. Подобные треугольники
Осталось выразить .
Заметим, что из подобия треугольников , откуда
(см. рис. 14).
Можно было бы выразить , разделив на разность радиусов, но нам это не нужно, ведь в искомом выражении как раз фигурирует произведение
. Подставив вместо него
, окончательно имеем:
.
Несложно теперь получить и формулу для площади полной поверхности. Для этого достаточно добавить площади двух кругов оснований: .
Задача
Рис. 15. Иллюстрация к задаче
Пусть усеченный конус получен вращением прямоугольной трапеции вокруг ее высоты
. Средняя линия трапеции
равна
, а большая боковая стороны –
(см. рис. 15). Найти площадь боковой поверхности полученного усеченного конуса.
Решение
По формуле мы знаем, что .
Образующей конуса будет являться большая сторона исходной трапеции, то есть Радиусы конуса – это основания трапеции. Найти их мы не можем. Но нам и не надо: нужна лишь их сумма, а сумма оснований трапеции вдвое больше ее средней линии, то есть она равна
. Тогда
.
Ответ: .
Сходство усеченных конуса и пирамиды
Обратите внимание, что, когда мы говорили о конусе, мы проводили параллели между ним и пирамидой – формулы были аналогичными. Так же и здесь, ведь усеченный конус очень похож на усеченную пирамиду, так что формулы для площадей боковой и полной поверхностей усеченного конуса и пирамиды (а скоро будут и формулы для объема) аналогичны.
Задача
Рис. 1. Иллюстрация к задаче
Радиусы оснований усеченного конуса равны и
, а образующая равна
. Найти высоту усеченного конуса и площадь его осевого сечения (см. рис. 1).
Решение
Рассмотрим осевое сечение, это трапеция , основания которой – удвоенные радиусы (
и
), а боковая сторона равна образующей (
) (см. рис. 2).
Рис. 2. Иллюстрация к задаче
Проведем высоту . Отрезок
равен полуразности оснований, значит, он равен
. Тогда треугольник
подобен египетскому, а значит,
. Высоту усеченного конуса мы нашли.
А площадь осевого сечения – это просто площадь трапеции, она равна произведению полусуммы оснований () на высоту (
), то есть
.
Ответ: ,
Список рекомендованной литературы
- Геометрия. Учебник для 10-11 классов. Атанасян Л.С. и др. 18-е изд. — М.: Просвещение, 2009. — 255 с.
- Геометрия 11 класс, А.В. Погорелов, М.: Просвещение, 2002
- Рабочая тетрадь по геометрии 11 класс, В.Ф. Бутузов, Ю.А. Глазков
Рекомендованные ссылки на ресурсы сети Интернет
- 2mb.ru (Источник).
- Math24.ru (Источник).
- Igspl.na.by (Источник).
Домашнее задание
- Высота усеченного конуса равна
, а угол между образующей и плоскостью большего основания равен
. Найдите образующую усеченного конуса.
- Радиусы оснований усеченного конуса относятся как
. Найдите площадь осевого сечения усеченного конуса, если его высота равна
, а образующая –
.
- Площади оснований усеченного конуса равны
и
. Через середину его высоты проведено сечение, параллельное основаниям. Найдите площадь этого сечения.


.png)

















