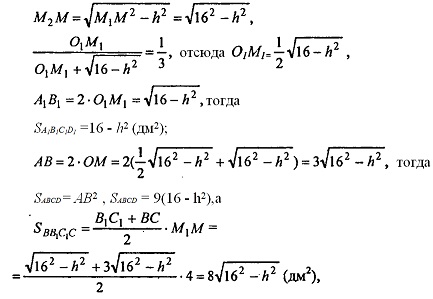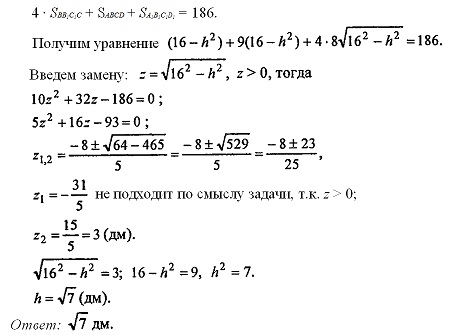Как найти высоту усеченной пирамиды через апофему

Стороны оснований правильной усеченной пирамиды дают возможность вычислить все, что связано с основаниями, используя формулы для правильных многоугольников. Среди таких параметров можно перечислить внутренний угол многоугольника, его периметр, площадь, радиус окружности, вписанной в основание, и радиус окружности, которая может быть описана около него.
γ=180°(n-2)/n
P=n(a+b+d)
S_a=(na^2)/(4 tan⁡〖(180°)/n〗 )
S_b=(nb^2)/(4 tan⁡〖(180°)/n〗 )
r_a=a/(2 tan⁡〖(180°)/n〗 )
r_b=b/(2 tan⁡〖(180°)/n〗 )
R_a=a/(2 sin⁡〖(180°)/n〗 )
R_b=a/(2 sin⁡〖(180°)/n〗 )

Зная апофему усеченной пирамиды, можно вычислить боковое ребро через прямоугольную трапецию, которая их связывает по боковой грани пирамиды. Основаниями такой трапеции являются половины сторон оснований пирамиды, поэтому по прямоугольному треугольнику боковое ребро будет равно радикалу из теоремы Пифагора. (рис. 50.2)
d=√(f^2+(b/2-a/2)^2 )=√(f^2+(b-a)^2/4)

Чтобы вычислить высоту усеченной пирамиды, необходимо найти такую же прямоугольную трапецию во внутреннем пространстве усеченной пирамиды, тогда в такой трапеции и прямоугольном треугольнике высота будет равна аналогичному радикалу через радиусы вписанных в основания окружностей и апофему (рис. 50.4)
h=√(f^2-(r_b-r_a )^2 )

Чтобы рассчитать углы при основаниях усеченной пирамиды и апофеме, можно воспользоваться в этой же трапеции/прямоугольном треугольнике тригонометрическими отношениями и принципом суммы углов трапеции.
cos⁡β=(r_b-r_a)/f
α=180°-β

Углы при основаниях и апофеме усеченной пирамиды можно вычислить в трапеции, которую боковое ребро образует с высотой пирамиды подобным образом, через радиусы вписанных в основания окружностей. (рис. 50.3)
cos⁡δ=(R_b-R_a)/d
ε=180°-δ

Площадь боковой поверхности усеченной пирамиды равна произведению количества сторон в основании на апофему и полусумму сторон оснований. Чтобы найти площадь полной поверхности через стороны усеченной пирамиды, нужно прибавить к площади боковой поверхности еще два основания.
S_(б.п.)=nf (a+b)/2
S_(п.п.)=S_(б.п.)+S_(осн.1,2)=n(f (a+b)/2+a^2/(4 tan⁡〖(180°)/n〗 )+b^2/(4 tan⁡〖(180°)/n〗 ))

Для того чтобы вычислить объем усеченной пирамиды, необходимо сначала найти высоту через теорему Пифагора, как было указано выше, а затем найти треть произведения высоты на сумму площадей оснований с квадратным корнем из их произведения.
V=1/3 h(S_осн1+S_осн2+√(S_осн1 S_осн2 ))

Усеченная пирамида, понятие, свойства

Вспомним понятие n-угольной пирамиды на примере треугольной пирамиды. Задан треугольник АВС. Вне плоскости треугольника взята точка Р, соединенная с вершинами треугольника. Полученная многогранная поверхность и называется пирамидой (рис. 1).

Рис. 1. Треугольная пирамида

Рассечем пирамиду плоскостью , параллельной плоскости основания пирамиды . Полученная между этими плоскостями фигура  и называется усеченной пирамидой (рис. 2).

Рис. 2. Усеченная пирамида

Основные элементы:

-верхнее основание ;

-нижнее основание АВС;

-боковая грань ;

-если РН – высота исходной пирамиды, то  – высота усеченной пирамиды.

Свойства усеченной пирамиды вытекают из способа ее построения, а именно из параллельности плоскостей оснований:

-все боковые грани усеченной пирамиды являются трапециями. Рассмотрим, например, грань . У нее  по свойству параллельных плоскостей (поскольку плоскости параллельны, то боковую грань исходной пирамиды АВР они рассекают по параллельным прямым), в то же время  и  не параллельны. Очевидно, что четырехугольник  является трапецией, как и все боковые грани усеченной пирамиды.

-отношение оснований одинаково для всех трапеций:

Имеем несколько пар подобных треугольников с одинаковым коэффициентом подобия. Например, треугольники  и РАВ подобны в силу параллельности плоскостей  и , коэффициент подобия:

В то же время подобны треугольники  и РВС с коэффициентом подобия:

Очевидно, что коэффициенты подобия для всех трех пар подобных треугольников равны, поэтому отношение оснований одинаково для всех трапеций.

Правильная усеченная пирамида, понятие, основные определения

Правильной усеченной пирамидой называется усеченная пирамида, полученная сечением правильной пирамиды плоскостью, параллельной основанию (рис. 3).

Рис. 3. Правильная усеченная пирамида

Определение.

Правильной называется пирамида, в основании которой лежит правильный n-угольник, а вершина проектируется в центр этого n-угольника (центр вписанной и описанной окружности).

В данном случае в основании пирамиды лежит квадрат, и вершина проектируется в точку пересечения его диагоналей. У полученной правильной четырехугольной усеченной пирамиды ABCD – нижнее основание,  – верхнее основание. Высота исходной пирамиды – РО, усеченной пирамиды –  (рис. 4).

Рис. 4. Правильная четырехугольная усеченная пирамида

Определение.

Высота усеченной пирамиды – это перпендикуляр, проведенный из любой точки одного основания к плоскости второго основания.

Апофема исходной пирамиды – РМ (М – середина АВ), апофема усеченной пирамиды –  (рис. 4).

Определение.

Апофема усеченной пирамиды – высота любой боковой грани.

Ясно, что все боковые ребра усеченной пирамиды равны между собой, то есть боковые грани – равные равнобедренные трапеции.

Теорема о площади боковой поверхности правильной усеченной пирамиды

Площадь боковой поверхности правильной усеченной пирамиды равна произведению полусуммы периметров оснований на апофему.

Доказательство (для правильной четырехугольной усеченной пирамиды – рис. 4):

Итак, необходимо доказать:

Площадь боковой поверхности здесь будет состоять из суммы площадей боковых граней – трапеций. Поскольку трапеции одинаковы, имеем:

Площадь равнобедренной трапеции – это произведение полусуммы оснований и высоты, апофема является высотой трапеции. Имеем:

Что и требовалось доказать.

Для n-угольной пирамиды:

Где n – количество боковых граней пирамиды, a и b – основания трапеции,  – апофема.

Решение задачи 1

Стороны основания правильной усеченной четырехугольной пирамиды  равны 3 см и 9 см, высота – 4 см. Найти площадь боковой поверхности.

Рис. 5. Иллюстрация к задаче 1

Решение. Проиллюстрируем условие:

Задано: , ,

Через точку О проведем прямую MN параллельно двум сторонам нижнего основания, аналогично через точку  проведем прямую  (рис. 6). Поскольку в основаниях усеченной пирамиды квадраты и построения параллельны, получим трапецию, равную боковым граням. Причем ее боковая сторона будет проходить через середины верхнего и нижнего ребра боковых граней и являться апофемой усеченной пирамиды.

Рис. 6. Дополнительные построения

Рассмотрим полученную трапецию  (рис. 6). В этой трапеции известно верхнее основание, нижнее основание и высота. Требуется найти боковую сторону, которая является апофемой заданной усеченной пирамиды. Проведем  перпендикулярно MN. Из точки  опустим перпендикуляр NQ. Получим, что большее основание разбивается на отрезки по три сантиметра (). Рассмотрим прямоугольный треугольник , катеты в нем известны, это египетский треугольник, по теореме Пифагора определяем длину гипотенузы: 5 см.

Теперь есть все элементы для определения площади боковой поверхности пирамиды:

Решение задачи 2

Пирамида пересечена плоскостью, параллельной основанию. Докажите на примере треугольной пирамиды, что боковые ребра и высота пирамиды делятся этой плоскостью на пропорциональные части.

Доказательство. Проиллюстрируем:

Рис. 7. Иллюстрация к задаче 2

Задана пирамида РАВС. РО – высота пирамиды. Пирамида рассечена плоскостью , получена усеченная пирамида , причем . Точка  – точка пересечения высоты РО с плоскостью основания усеченной пирамиды . Необходимо доказать:

Ключом к решению является свойство параллельных плоскостей. Две параллельные плоскости рассекают любую третью плоскость так, что линии пересечения параллельны. Отсюда: . Из параллельности соответствующих прямых вытекает наличие четырех пар подобных треугольников:

Из подобия треугольников вытекает пропорциональность соответствующих сторон. Важная особенность заключается в том, что коэффициенты подобия у этих треугольников одинаковы:

Отсюда:

Что и требовалось доказать.

Решение задачи 3

Правильная треугольная пирамида РАВС с высотой  и стороной основания  рассечена плоскостью , проходящей через середину  высоты РН параллельно основанию АВС. Найти площадь боковой поверхности полученной усеченной пирамиды.

Решение. Проиллюстрируем:

Рис. 8. Иллюстрация к задаче 3

АСВ – правильный треугольник, Н – центр данного треугольника (центр вписанной и описанной окружностей). РМ – апофема заданной пирамиды.  – апофема усеченной пирамиды. Согласно свойству параллельных плоскостей (две параллельные плоскости рассекают любую третью плоскость так, что линии пересечения параллельны), имеем несколько пар подобных треугольников с равным коэффициентом подобия. В частности нас интересует отношение:

Отсюда:

Найдем НМ. Это радиус окружности, вписанной в основание, соответствующая формула нам известна:

Теперь из прямоугольного треугольника РНМ по теореме Пифагора найдем РМ – апофему исходной пирамиды:

Из начального соотношения:

Теперь нам известны все элементы для нахождения площади боковой поверхности усеченной пирамиды:

Итак, мы ознакомились с понятиями усеченной пирамиды и правильной усеченной пирамиды, дали основные определения, рассмотрели свойства, доказали теорему о площади боковой поверхности. Следующий урок будет посвящен решению задач.

Список литературы

1. И. М. Смирнова, В. А. Смирнов. Геометрия. 10-11 класс: учебник для учащихся общеобразовательных учреждений (базовый и профильный уровни) / И. М. Смирнова, В. А. Смирнов. – 5-е изд., испр. и доп. – М.: Мнемозина, 2008. – 288 с.: ил.
2. Шарыгин И. Ф. Геометрия. 10-11 класс: Учебник для общеобразовательных учебных заведений / Шарыгин И. Ф. – М.: Дрофа, 1999. – 208 с.: ил.
3. Е. В. Потоскуев, Л. И. Звалич. Геометрия. 10 класс: Учебник для общеобразовательных учреждений с углубленным и профильным изучением математики /Е. В. Потоскуев, Л. И. Звалич. – 6-е изд., стереотип. – М.: Дрофа, 2008. – 233 с.: ил.

Дополнительные рекомендованные ссылки на ресурсы сети Интернет

1. Uztest.ru (Источник).
2. Fmclass.ru (Источник).
3. Webmath.exponenta.ru (Источник).

Домашнее задание

1. Задача 1: плоскость, параллельная плоскости основания правильной шестиугольной пирамиды, делит ее высоту в отношении 1:7, считая от вершины пирамиды. Высота пирамиды – 14 см, сторона основания – 2 см. найдите площадь поверхности полученной усеченной пирамиды.
2. Задача 2: площадь боковой поверхности правильной усеченной пятиугольной пирамиды – , ее высота составляет четверть высоты исходной пирамиды, апофема равна 2 см. Найдите стороны оснований и высоту усеченной пирамиды.
3. Задача 3: охарактеризуйте максимальным количеством свойств правильную усеченную четырехугольную пирамиду.

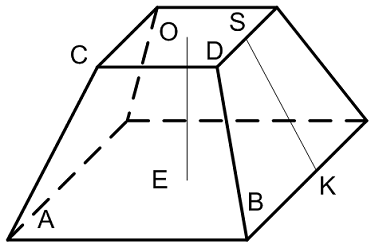
Боковые грани усеченной пирамиды — трапеции. Т.к. данная усеченная пирамида получена из правильной  4-угольной пирамиды,  то  ее боковые грани — равные равнобедренные трапеции.
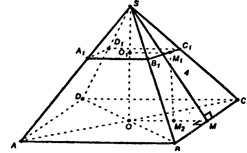
Построим OM┴BC, M₁M₁┴B₁C₁, и отрезок M1M. По теореме о 3-х перпендикулярах имеем: M₁M┴BC (M₁M┴B₁C₁), т.е. M₁M — апофема усеченной пирамиды, M₁M=4 дм.
Δ SB₁C₁  ~ Δ SBC , и Δ SO₁M₁  ~ Δ SOM, т.к. они — прямоугольные и имеют общий острый угол при вершине S, тогда имеем:


Построим M₁M₂┴OM; OM₂=O₁M₁.
Пусть высота усеченной пирамиды OO₁=h. Тогда из ΔМ₁М₂М по т. Пифагора имеем:

ВИДЕОУРОК

Задания к уроку 10

• Задание 1
• Задание 2
• Задание 3

Другие уроки: