
|
ϕ=55°45,6′ |
sin |
9,91734 |
cos |
9,75025 |
cos |
9,75025 |
sin |
9,91734 |
|
δ=10°13,4′ |
sin |
9,24916 |
cos |
9,99305 |
tg |
9,25611 |
— |
|
|
t=62°24,5′ |
– |
– |
cos |
9,66574 |
csc |
0,05244 |
ctg |
9,71818 |
|
↑ |
I |
9,16650 |
II |
9,40904 |
I |
9,05880 |
II |
9,63552 |
|
—II |
9,40904 |
β |
9,63136 |
—II |
9,63552 |
α |
0,10210 |
|
|
АГ |
0,24254 |
sin |
9,04040 |
АГ |
0,57672 |
ctg |
9,73762 |
|
h=6°18,1′; 180°—A=61°20,5′;
A=N118°39,5’W;
Aкр=241°20,5′≈241,3°
Примечание. При наличии вычислительной машины, не имеющей тригонометрических функций, пользуются табл. 6-а МТ—75 и этой же схемой. Если же у машины есть эти функции (например, в ЭВМ), то вычисления выполняются в соответствии с этой же схемой с учетом знаков.
Для вычисления высоты и азимута применяются не только формулы (4) и (5), но системы формул, в которых ставятся определенные требования к простоте и точности вычислений. Рассмотрим три системы формул, применяемых при определении места судна методом линий положения.
Система формул sin h и sin А. По данным ϕ, δ, t требуется получить простейшую систему формул для вычисления h и А. Формула (4) для h получается, как показано выше.
Формула (5) для А может быть упрощена, если найденную h ввести как известную величину. Это допустимо вследствие того, что в морских условиях азимут требуется вычислять до ±0,1°, а высота получена со значительно большей точностью, порядка ±0,1′. Теперь известными являются ϕ, δ, t и по формуле синусов из ∆PzC (см. рис. 11) получим:
sin A = sin t cosδ cosh
или
25

Следовательно, первая система формул для вычисления h и А имеет вид: sinh=sinϕ sinδ + cosϕ cosδ cost;
sin A=sint cosδ ses h
Преимущество формулы (4) в том, что она получается и исследуется по общематематическим формулам и правилам, а формулы (6) — в ее простоте. Формула sinh дает более высокую точность вычислений при небольших высотах, вследствие этого при работе с четырехзначными таблицами логарифмов применять ее можно только для высот до 30°, для пятизначных же таблиц практически допустимо вычислять высоты по sinh до 80°. Эта система формул являлась до недавнего времени наиболее распространенной на отечественном флоте, хотя трудоемкость вычислений по ним, особенно с пятью знаками, довольно велика. Наименование азимута в формуле sin А определяется не исследованием ее, а в четвертном счете по специальным правилам, приведенным на стр. 17 МТ — 75 (см. §10).
При решении по этой системе формул возможен только приближенный контроль (по сфере или глобусу) и контроль вторичными вычислениями.
Пример 5. Дано: ϕ=55°51,5’S; δ=6°22,7’N; t=49°19,3’W. Определить h и А по формулам sin h и sin A и МТ—73.
|
+ |
− |
+ |
+ |
+ |
|
|
Решение, sinh = sinϕsinδ +cosϕcosδ cost |
(—I + II); |
sin A = cos δ sin t sec h.
|
ϕ=55°51,5′ |
sin |
9,91785 |
cos |
9,74915 |
— |
9,9973 |
|
|
δ= 6°22,7′ |
sin |
9,04569 |
cos |
9,99730 |
Cos |
||
|
t=49°19,3′ |
cos |
9,81412 |
Sin |
9,8799 |
|||
|
I |
8,96354 |
II |
9,56057 |
sec h |
0,0166 |
||
|
АГ |
0,59703 |
β |
9,87337 |
sin A |
9,8938 |
||
|
Контроль |
I+ |
АГ=9,56057 |
sin h |
9,43394 |
A=NW51°32′ |
||
|
h=15045,6’; A= 308,50 |
26

Система формул sin 2 2z и sin A. При высотах, больших 30°, точность
вычислений по формуле sin h снижается, поэтому ее заменяют другой, в которой высота вычисляется по более выгодной, т.е. более точной, функции. В
данном случае более выгодной будет функция sin 2 α2 или lgsin 2 α2 . К этой
функции, путем преобразований, приведем формулу (4). Заменив в этой формуле h=900—z, получим:
cosz =sin sinδ + cosϕ cosδ cos t. (*)
Из тригонометрии на плоскости известна формула половинного угла (см. приложение 1):
или
cosz=1—2sin 2 2z
Подставив в выражение (*) вместо cosz и cost получим
(**)
выведенные значения,
|
1—2sin 2 |
z |
=sinϕ sinδ + cosϕ cosδ•1–2sin 2 |
t |
cosϕ cosδ |
|||||||||
|
2 |
|||||||||||||
|
2 |
|||||||||||||
|
но |
sinϕ sinδ + cosϕ cosδ= cos(ϕ–δ) |
||||||||||||
|
По формуле (**) |
|||||||||||||
|
cos (ϕ–δ)=1 — 2sin 2 ϕ −δ |
|||||||||||||
|
2 |
|||||||||||||
|
Следовательно, |
|||||||||||||
|
1—2sin 2 |
z |
=1—2sin 2 ϕ −δ –2cos ϕ cosδ sin 2 |
t |
||||||||||
|
2 |
2 |
2 |
|||||||||||
|
После деления этого выражения на –2 получим окончательно систему |
|||||||||||||
|
формул: |
|||||||||||||
|
sin 2 |
z |
=sin |
2 |
ϕ −δ |
+ cos ϕ cosδ sin 2 |
t |
(7) |
||||||
|
2 |
|||||||||||||
|
2 |
2 |
||||||||||||
|
sin A = sin t cosδ cosec z |
(7а) |
27

где вторая формула выведена из выражения (6) заменой sec h=cosecz. Эта система формул имеет следующие достоинства. Формула (7) дает
более точные результаты, чем формула (4), при высотах, больших 30°, и не требует исследования на знаки, так как оба ее члена всегда положительны. При вычислении с таблицами логарифмов по формуле (7) пользуются всегда таблицей для сумм α. Вместо исследования в первом члене формулы определяется знак при δ: разность ϕ–δ при ϕ и δ одноименных, причем из большего вычитается меньшее; сумма ϕ+δ при ϕ и δ разноименных. Эта система формул распространена на зарубежных флотах.
Пример 6 Дано: ϕ=48°18,7’S; δ=57°23,4′ S; t=62°53,6′ W. Определить h и
А по формулам (7) и (7а).
Решение.
|
t=62°53,6′ |
sin2 |
9,43485 |
sin |
9,9495 |
|||||
|
ϕ=48°18,7′ |
cos |
9,82287 |
— |
||||||
|
—δ=57°23,4′ |
cos |
9,73152 |
cos |
9,7315 |
|||||
|
δ—ϕ=9°04,7′ |
I=sin2 |
7,79680 |
II |
8,98924. |
|||||
|
АГ |
1,19244 |
A |
0,02702 |
csc z |
0,2146 |
||||
|
Контроль |
|||||||||
|
1+АГ |
=8,98924 |
sin2 |
9,01626 |
sin A |
9,8956 |
h=52° 24 5, z=37° 35 5′; A=51°51’SW=231,8°
Дальнейшим преобразованием (выполненным еще в XIX в) формулу (7) можно привести к виду
|
sin 2 |
z |
=sin 2 ϕ −δ |
cos2 |
t |
+sin 2 |
t |
cos2 ϕ +δ |
(8) |
|
2 |
||||||||
|
2 |
2 |
2 |
2 |
В таком виде формула удобнее для вычислений на ЭВМ, и она применена
внавигационных программах ЭВМ для вычисления расстояний и высот.
Система формул «тангенсов» (tgx, tgh, tgА). Формулы (4) и (7) состоят
из двух членов, т.е. они не логарифмические и требуют специальных таблиц для сумм α и разностей β или смешанного решения. Применение формулы (4) выгоднее при h<30°, формулы (7) — при h>30°. Можно получить систему формул, выгодных при любых углах, и, кроме того, логарифмических. Такие
28

формулы выводятся заменой переменных или, что более наглядно, разделением параллактического треугольника на два прямоугольных. Формулы, в которых все искомые получаются через наиболее выгодную функцию tgα, были выведены К.Ф.Гауссом в начале XIX в.
Выведем систему формул тангенсов из параллактического треугольника zPC (рис. 12), в котором заданы α, δ, t; требуется определить h и А светила. Из места светила С опускаем на меридиан наблюдателя сферический перпендикуляр CD=р, который всегда проходит через точки Оst и W, так как они являются полюсами меридиана наблюдателя. Расстояние ED от экватора до основания перпендикуляра обозначим через х, тогда PD=90°–х — полярное расстояние точки D, a zD=(90°–ϕ)–(90°–x)=х–ϕ – зенитное расстояние точки D.
Образовались два прямоугольных сферических треугольника PCD и DCZ. Искомые получаются путем последовательного решения этих треугольников по формуле котангенсов, чтобы получить функцию tgα, причем найденные величины вводятся в последующие вычисления как данные, чтобы формулы стали логарифмическими. Вместо формул котангенсов можно применять мнемонические правила Непера.
Рассмотрим сферический треугольник РDС, в котором известны δ, t и угол D=90°. Применяя формулу котангенсов к углу 90° в сторону стрелки, получим:
ctg 90° sin t = ctg (90° — δ)sin (90° — x) — cos (90° — x)cos t
откуда
29

|
sin x cos t = cos x tg δ |
|
|
или |
|
|
tgx=tgδsect |
(9) |
|
Определим из треугольника РОС вспомогательную величину р через |
|
|
найденное х, применяя формулу котангенсов к углу t: |
|
ctgtsin 900 |
= ctgpsin(90о − х) − cos900 cos(900 |
− x) |
|
123 |
144424443 |
|
|
1 |
0 |
|
|
откуда |
tg p — tg t cos x.
Рассмотрим второй прямоугольный сферический треугольник DZC, в
котором известны p, x —ϕ и D = 900 .
Применяя формулу котангенсов к углу А в сторону стрелки, получим
ctgp sin(x −ϕ) −cos 900 cos(x −ϕ)
14424443
0
откуда
или, подставляя вместо tg p=tgtcos x, получим
|
tgA = |
tgt cos x |
(10) |
|
|
sin(x −ϕ) |
|||
Считая полученный азимут А известным, определим h, применяя формулу котангенсов к углу 90°:
ctg 90° sin A = ctg (90°—h)sin (x-ϕ) — cos A cos (x —ϕ),
|
откуда |
||
|
tg h = cos A ctg (x — ϕ) |
. |
(11) |
В формулах (9), (10), (11) в правой части получаются различные функции, что неудобно при составлении пособий, так как увеличивается число таблиц и их объем. Поэтому для практического применения эти формулы были
приведены к двум функциям: tgα и secα = cos1α . Для этого надо произвести следующие тригонометрические преобразования:
30

|
1 |
1 |
||||||||||
|
sin(x −ϕ) = |
= |
= |
|||||||||
|
cos ec(x −ϕ) |
sec[900 −(x −ϕ)] |
||||||||||
|
= |
1 |
= |
1 |
||||||||
|
sec[90 |
0 |
+ (ϕ − x)] |
sec y |
||||||||
ctg(x-ϕ)=ctg[90°—(x-ϕ)]=tg[900+(x —ϕ)]=tgy
где у=90°+(ϕ—х) — алгебраическая формула; правило для отыскания
(ϕ—х) или в порядке записей по схеме (х~ϕ) приведено ниже.
Подставляя эти выражения в формулы (10) и (11), получим третью систему формул — «формулы тангенсов»:
tgx=tgδ sect
|
tgA = tgt sec y |
(12) |
|
sec x |
tgh = tgy sec A
y=900+(х ~ ϕ)
Правила получения величин х и у. Чтобы решать задачи по формулам (12), надо знать величину и знак х и у. Как видно из рис. 12, величина х зависит от положения точки D и, следовательно, дуга х всегда одноименна с δ (N или S).
Если t>90°, то х>90°.
В формуле для у=90°+(х~ϕ) знак «тильда» (~) означает, что при х,
одноименном с ϕ, из большего вычитается меньшее; при х и ϕ разноименных они складываются.
При применении этих правил исследовать формулы на знаки не нужно. Формулы (12) логарифмические и искомые находятся через более точную
функцию тангенсов, что и составляет достоинство этих формул. Их недостаток в том, что точное искомое h определяется через А. Решение довольно трудоемко и имеет особенности при углах около 90°.
В начале 20-х годов применительно к формулам (12) была изготовлена
31
специальная логарифмическая линейка (цилиндрическая линейка Байгрева), применявшаяся в английском и немецком флотах. У нас по этим формулам были составлены таблицы ТВА — 57.
§6. СПЕЦИАЛЬНЫЕ ТАБЛИЦЫ ДЛЯ ВЫЧИСЛЕНИЯ ВЫСОТЫ И АЗИМУТА.
УСТРОЙСТВО И ПОЛЬЗОВАНИЕ ТАБЛИЦАМИ ТВА—57
Классификация специальных таблиц. Вычисление высоты и азимута можно упростить, если применить таблицы, специально предназначенные для этой цели. С конца прошлого века вышло более 50 типов подобных таблиц. Известный советский ученый-навигатор проф. Н.Н.Матусевич (1879—1950) предложил разделить все специальные таблицы по принципу построения и работы на три типа: тригонометрические, искусственные, численные.
Тригонометрические таблицы — упрощенные таблицы логарифмов или натуральных значений нескольких тригонометрических функций. Таблицы приспособлены под определенную систему формул, полученных обычно разделением треугольника на два прямоугольных, например формулы тангенсов.
Эти таблицы, как правило, компактны и достаточно точны, но по трудоемкости близки к обычному решению по формулам и МТ. К этому типу таблиц относятся таблицы Фуса (1901 г.), Аквино, Эджетона, ТВА—57 и др.
Искусственные таблицы — таблицы видоизмененных тригонометрических функций, их логарифмов или приращений, составленные для искусственно преобразованных формул. Такие таблицы дают простейшие вычислительные операции, малы по объему, но точность их обычно недостаточна. Эти таблицы были распространены в 20-е годы, например у нас
— таблицы Ахматова «Высота и азимут в три минуты».
Численные таблицы — таблицы готовых численных значений h и А,
данных через определенный шаг аргументов ϕ, δ, t, а также поправок к ним,
32

вычисленных как приращения. По таблицам этого типа h и А вычисляются проще, надежнее и обычно с достаточной точностью, но объем таблиц большой, например американские НО-214 занимают девять томов по 250 страниц. Численные таблицы азимутов вышли у нас в 1935 г. (таблицы Ющенко), высот и азимутов выпущены в США в 1936 г., затем в Англии, Японии, а в 1958 г. и у нас — это ВАС — 58. Рассмотрим подробно наши таблицы ТВА—57 и ВАС — 58.
Устройство и пользование таблицами ТВА—57. «Таблицы для вычисления высоты и азимута» выпуска 1957 г. составлены проф. А.П.Ющенко для вычислений по формулам тангенсов (12) и представляют таблицы видоизмененных lgsecα и lgtgα; впервые опубликованы как табл. 27 в МТ—43.
Логарифмируя формулы (12), получим lgtgx=lg tgδ + lg sec t,
lgtgA=lg tgt — lg sec x + lg sec y; (*) lg tg h = lg tg у — lg sec A
С целью упрощения вычислений и повышения точности вводятся величины:
S (α) = 2•104 lg secα;
Т (α) = 2•104 lg tg α + 70725.
Здесь четырехзначные логарифмы умножены на 104, чтобы избавиться от характеристик, например вместо 0,3544 получим 3544. При умножении на 2 уточняется округление, например 2544,3•2 7089. Число 70725 введено, чтобы в таблицах не приводить отрицательных величин, так как при α<450
характеристики lg tg α отрицательны. Принимая наименьший угол α=1′, для
компенсации наибольшего отрицательного числа вводим 2•104 lg tg11′ = 70725;
после добавления этого числа все величины T от 1′ оказываются положительными (до 1′ они отрицательны).
Вводя величины S и Т в формулы (*), получим:
33
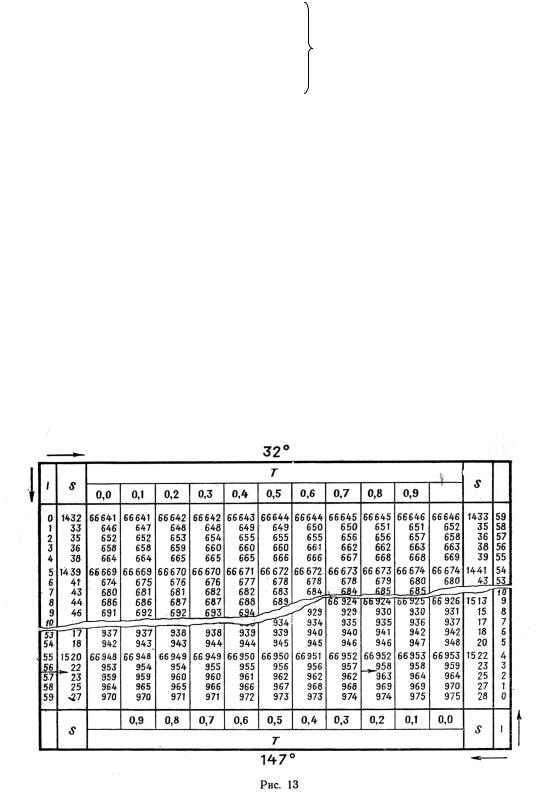
Tx=Tδ=St TA=Tt–St+Sy Th=Ty–SA
По этим рабочим формулам составлены схемы вычислений (см. пример 7), которые при решении заполняются значениями Т и S из таблиц ТВА. Выдержка из таблиц ТВА показана на рис. 13; величины S приведены через 1′, поэтому их приходится интерполировать между строк, но при углах от 75 до 104° для S выделены отдельные страницы, где они даны через 0,1′, т.е. не требуют интерполяции. Величины Т даются через 0,1′ по всей таблице. Для углов от 0 до 90° вход в таблицы производится сверху и слева (см. рис. 13), а при углах от 90 до 180° — снизу и справа (величины S и Т симметричны относительно 90°).
При работе с ТВА следует придерживаться правил, примененных при получении формул тангенсов и приведенных в §5. Эти же правила даны в самих таблицах ТВА на с.8. Из них чаще допускается промах в правиле: если t>90°, то и х>90° (выбирается снизу). Следует также помнить, что знаки в схеме
34

чередуются — в первой колонке «+», затем «—», «+» и «—». Азимут выбирается всегда сверху таблицы, т.е. в четвертном счете, причем первая буква наименования разноименна с φ, кроме случая, когда х>φ и одноименен, вторая буква одноименна с часовым углом.
Пример 7. Дано: φ=61o23.6’N; δ=6o45,7’S; t=32°56,8′ W. Определить h и
А по ТВА—57.
Решение.
Особые приемы интерполирования. При t, x или A, близких к 90° (в
пределах ±2—3°), в таблицах обязательно применяются особые приемы интерполирования величин Sx или SA. Так как Т или S меняются здесь очень быстро, а их приращения примерно одинаковы, то величины SХ и SA выбираются не на углы х или А, а по Тх или ТА (т.е. до 0,01′). Для этого к значению Sx или SA, выбранному на угол x или A, добавляются разности ДТ между полученными значениями Тх или ТA и их ближайшими значениями, приведенными в таблицах, т.е. получаем Sx=ST+∆ТХ или SA=ST+ТA с учетом знака ∆T (см.пример 8). Если этого не делать, то в высоте возможны крупные ошибки1.
Пример 8 Дано: ϕ=42°34, 5′ S; δ=47°07,4’S; t=90°20,2′ W. Определить h и
А по ТВА—57. Решение.
1 Из двух значений угла, соответствующих Т = 67444, выбирается четное 0,6′.
35
|
δ=47007,4’S |
T |
71369 |
|||||||
|
t=90020,2’W |
+S |
44618 |
T |
115344 |
|||||
|
—S |
45262 |
(45242+20) |
|||||||
|
x=90018,8’S |
Tx |
115987 |
|||||||
|
(ближ.67) |
|||||||||
|
ϕ=42034,5’S |
T |
69894 |
|||||||
|
TP |
70082 |
||||||||
|
y=137044,3’ |
+S |
2614 |
—S |
4106 |
|||||
|
A=51026,8’SW |
|||||||||
|
T |
72696 |
T |
65788 |
||||||
|
h=29031,8’ |
|||||||||
В примере ближайшим значением к Tх является T=115967, по нему и выбирается х=90°18,8′ (снизу, так как t>90°), но разность его с полученным +20.
Эта разность должна быть добавлена к ST=45242, т.е. Sx=ST+∆T=45262. Если этого не сделать, то получим h=29°29,6′ с ошибкой в 2,2′.
Таблицы ТВА—57 обладают рядом достоинств, в силу которых они применяются на нашем флоте уже около 30 лет; это: отсутствие ограничений по аргументам (можно обрабатывать любое светило в любой широте); достаточная точность при любой высоте (порядка ±0,1—0,2′); получение точного азимута, при работе почти не требуется интерполяции; компактны.
Однако таблицы имеют и недостатки: сравнительно большая трудоемкость вычислений; наличие специальных правил; разное количество цифр в Т и S (это приводит иногда к промахам); специальные правила интерполирования при t, х или А, близких к 90°; особые схемы при t, x, у, А, равных 90°; невозможность сократить вычисления способом «перемещенного места». В транспортном флоте ТВА—57 применяются как дополнительные таблицы при ВАС —58.
36
1. Теоретическая разрешающая способность телескопа:
, где λ – средняя длина световой волны (5,5·10-7 м), D – диаметр объектива телескопа, или
, где D – диаметр объектива телескопа в миллиметрах.
2. Увеличение телескопа:
, где F – фокусное расстояние объектива, f – фокусное расстояние окуляра.
3. Высота светил в кульминации:
высота светил в верхней кульминации, кульминирующих к югу от зенита ( ):
, где – широта места наблюдения, – склонение светила;
высота светил в верхней кульминации, кульминирующих к северу от зенита ( ):
, где – широта места наблюдения, – склонение светила;
высота светил в нижней кульминации:
, где – широта места наблюдения, – склонение светила.
4. Астрономическая рефракция:
приближенная формула для вычисления угла рефракции, выраженного в секундах дуги (при температуре +10°C и атмосферном давлении 760 мм. рт. ст.):
, где z – зенитное расстояние светила (для z
5. Время:
звездное время:
, где – прямое восхождение какого-либо светила, t – его часовой угол;
среднее солнечное время (местное среднее время):
Tm=T+, где T – истинное солнечное время, – уравнение времени;
всемирное время:
, где – долгота пункта с местным средним временем Tm, выраженная в часовой мере, T0 – всемирное время в этот момент;
поясное время:
, где T0 – всемирное время; n – номер часового пояса (для Гринвича n=0, для Москвы n=2, для Красноярска n=6);
декретное время:
или
6. Формулы, связывающие сидерический (звездный) период обращения планеты T с синодическим периодом ее обращения S:
для верхних планет:
;
для нижних планет:
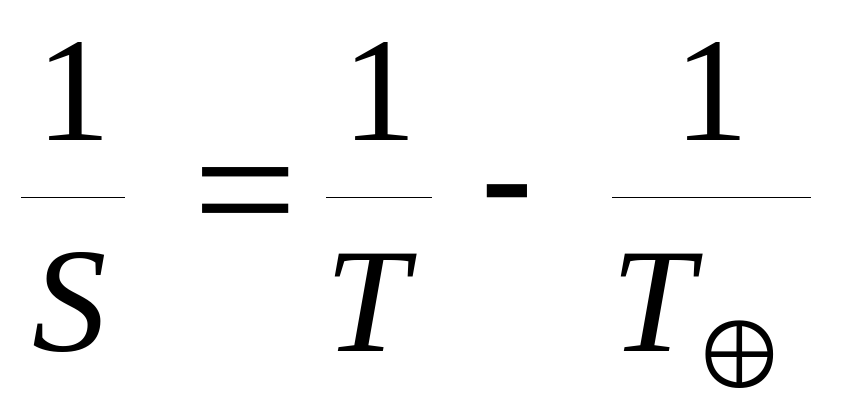
7. Третий закон Кеплера:
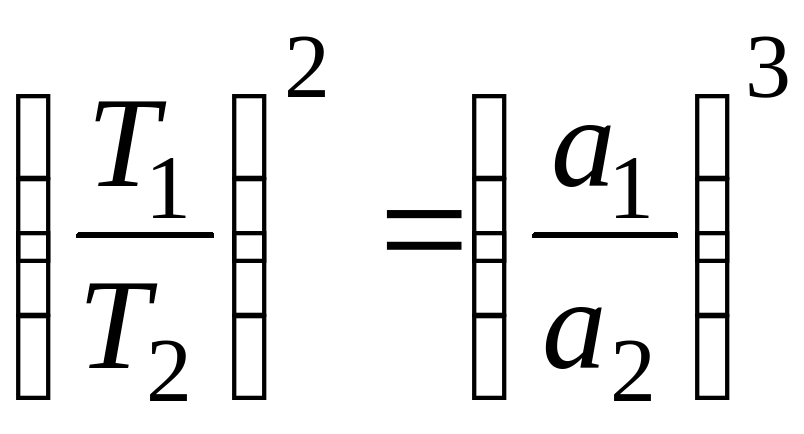
8. Закон всемирного тяготения:
, где m1 и m2 – массы притягивающихся материальных точек, r – расстояние между ними, G – гравитационная постоянная.
9. Третий обобщенный закон Кеплера:
, где m1 и m2 – массы двух взаимно притягивающихся тел, r – расстояние между их центрами, Т – период обращения этих тел вокруг общего центра масс, G – гравитационная постоянная;
для системы Солнце и две планеты:
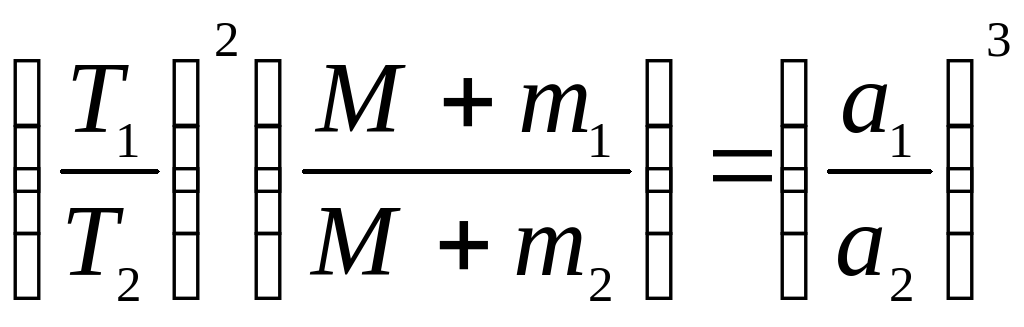
для систем Солнце и планета, планета и спутник:
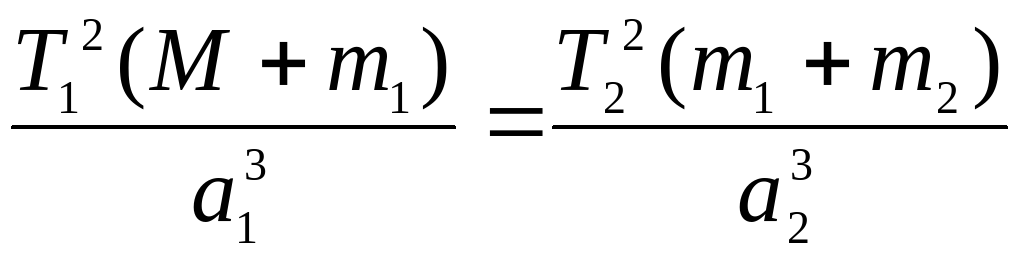
при M m1, а m1 m2,
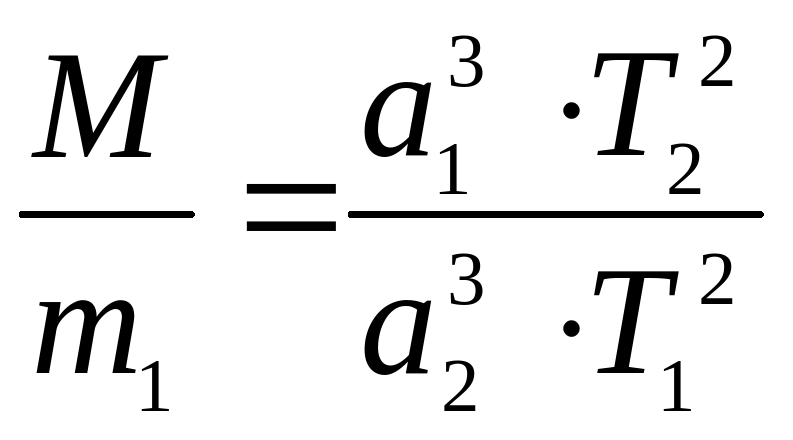
10. Линейная скорость движения тела по параболической орбите (параболическая скорость):
, где G – гравитационная постоянная, M – масса центрального тела, r – радиус-вектор избранной точки параболической орбиты.
11. Линейная скорость движения тела по эллиптической орбите в избранной точке:
, где G – гравитационная постоянная, M – масса центрального тела, r – радиус-вектор избранной точки эллиптической орбиты, a – большая полуось эллиптической орбиты.
12. Линейная скорость движения тела по круговой орбите (круговая скорость):
, где G – гравитационная постоянная, M – масса центрального тела, R – радиус орбиты, vp – параболическая скорость.
13. Эксцентриситет эллиптической орбиты, характеризующий степень отклонение эллипса от окружности:
, где c – расстояние от фокуса до центра орбиты, a – большая полуось орбиты, b – малая полуось орбиты.
14. Связь расстояний перицентра и апоцентра с большой полуосью и эксцентриситетом эллиптической орбиты:
, , , где rП – расстояния от фокуса, в котором находится центральное небесное тело, до перицентра, rА – расстояния от фокуса, в котором находится центральное небесное тело, до апоцентра, a – большая полуось орбиты, e – эксцентриситет орбиты.
15. Расстояние до светила (в пределах Солнечной системы):
, где R – экваториальный радиус Земли, ρ0– горизонтальный параллакс светила, выраженный в секундах дуги,
или , где D1 и D2 – расстояния до светил, ρ1 и ρ2 – их горизонтальные параллаксы.
16. Радиус светила:
, где ρ – угол, под которым с Земли виден радиус диска светила (угловой радиус), R – экваториальный радиус Земли, ρ0– горизонтальный параллакс светила.
17. Расстояние до звезд:
в парсеках: , где – годичный параллакс звезды, выраженный в радианах;
в астрономических единицах: , где – годичный параллакс звезды, выраженный в секундах дуги;
в километрах: , где – годичный параллакс звезды, выраженный в секундах дуги, a – средний радиус (большая полуось) земной орбиты.
18. Связь блеска звезды и ее звездной величины (формула Погсона):
, где I1 – освещенность, создаваемая звездой, звездная величина которой равна m1, и I2 – освещенность, создаваемая другой звездой, звездная величина которой равна m2.
19. Абсолютная звездная величина:
, где m – видимая звездная величина, R – расстояние до звезды в парсеках.
20. Закон Стефана–Больцмана:
ε=σT4, где ε – энергия, излучаемая в единицу времени с единицы поверхности, Т – температура (в кельвинах), а σ – постоянная Стефана–Больцмана.
21. Закон Вина:
, где λmax – длина волны, на которую приходится максимум излучения абсолютно черного тела (в сантиметрах), Т – абсолютная температура в кельвинах.
22. Закон Хаббла:
, где v – лучевая скорость удаления галактики, c – скорость света, Δλ – доплеровское смещение линий в спектре, λ – длина волны источника излучения, z – красное смещение, r – расстояние до галактики в мегапарсеках, H – постоянная Хаббла, равная 75 км / (сМпк).
4
You can use this fundamental formula in spherical astronomy[1]
$$sin a=sin phi sin delta + cos phi cos delta cos H$$
where
- $a$ is the wanted altitude,
- $phi$ is your latitude,
- $delta$ is the declination of the star, and
- $H$ is the hour angle, measured in the clockwise direction.
Pay attention to the units! (Don’t mix degrees, radians and grads. Common cause of error!)
Since I don’t know how you are familiar with the trigonometric functions (I believe pretty well), you only get $sin a$ using that formula. You need to get the $arcsin$ of that value in order to get wanted altitude $a$.
The solution above is perfectly correct in theory (on competitions, exams, and for personal use), but if you are writing a program on computer, you might find the following useful:
The factor we haven’t yet addressed is the atmospheric refraction[2] It causes the star to look higher than in reality. The effect is pretty small, on range of few arc minutes.
First you need to calculate the factor $R$ by the formula[3]
$$R=frac{16.27»cdot P}{273 + T}$$
where $P$ is the pressure in millibars and $T$ is the temperature in degrees of Celsius. You are perfectly fine using just $R=60»=1’$. Then the apparent altitude of the star is given by $a’=R+a$. Again, pay attention to the units (everything in degrees or everything in minutes …)
If you are interested in learning about positional or spherical astronomy, then I advise you to visit another Stack Exchange question about this topic. Personaly, I have had great fun with Fundamental Astronomy. But in general, the formula is derived using the spherical law of cosines.
Страница 5 из 5
2.1.5. Высота светила в кульминации
При своем суточном движении светило, вращаясь вокруг оси мира, за сутки дважды пересекает меридиан — над точками юга и севера. При этом оно один раз занимает самое высокое положение — верхняя кульминация, другой раз — самое низкое положение — нижняя кульминация.
В момент верхней кульминации над точкой юга светило достигает наибольшей высоты над горизонтом.
Кульминация — это явление прохождения светила через меридиан, момент пересечения небесного меридиана.
Светило М в течение суток описывает суточную параллель – малый круг небесной сферы, плоскость которого перпендикулярна оси мира и проходит через глаз наблюдателя.
М1 — верхняя кульминация (h max; А= 0o), М2 – нижняя кульминация (h min; A =180o), М3 – точка восхода, М4 – точка захода,
По суточному движению светила делятся на:
- невосходящие
- восходяще — заходящие (восходящие и заходящие в течении суток)
- незаходящие.
- К каким относится Солнце, Луна? (ко 2)
На рисунке 2.8 показано положение светила в момент верхней кульминации.
Как известно, высота полюса мира над горизонтом (угол PON): hP = φ. Тогда угол между горизонтом (NS) и небесным экватором (QQ1) будет равен 180° — φ — 90° = 90° — φ. Угол MOS, который выражает высоту светила М в кульминации, представляет собою сумму двух углов: Q1OS и MOQ1. Величину первого из них мы только что определили, а второй является не чем иным, как склонением светила М, равным δ.
Таким образом, мы получаем следующую формулу, связывающую высоту светила в кульминации с его склонением и географической широтой места наблюдения:
h = 90° — φ + δ.
Зная склонение светила и определив из наблюдений его высоту в кульминации, можно узнать географическую широту места наблюдения.
На рисунке изображена небесная сфера. Рассчитаем зенитное расстояние светила в данном пункте в момент верхней кульминации, если его склонение известно.
Вместо высоты h часто употребляют зенитное расстояние Z, равное 90°—h.
Зенитное расстояние — угловое расстояние точки М от зенита.
Пусть в момент верхней кульминации светило находится в точке М, тогда дуга QМ есть склонение δ светила, так как AQ — небесный экватор, перпендикулярный оси мира РР’. Дуга QZ равна дуге NP и равна географической широте местности φ. Очевидно, зенитное расстояние, изображаемое дугой ZM, равно z = φ — δ.
Если бы светило кульминировало к северу от зенита Z (т. е. точка М оказалась бы между Z и P), то z = δ— φ. По этим формулам можно рассчитать зенитное расстояние светила с известным склонением в момент верхней кульминации в пункте с известной географической широтой φ.
Высота светил в кульминации
Найдем зависимость между высотой h светила М в верхней кульминации, его склонением δ и широтой местности φ.
Рис. 20. Высота светила в верхней кульминации.
На рисунке 20 изображены отвесная линия ZZ’ ось мира РР’ и проекции небесного экватора EQ и линии горизонта NS (полуденная линия) на плоскость небесного меридиана (PZSP’N) Угол между полуденной линией NS и осью мира РР’ равен, как мы знаем, широте местности φ. Очевидно, наклон плоскости небесного экватора к горизонту, измеряемый углом EOS, равен 90° — φ (рис. 20). Звезда М со склонением δ, кульминирующая к югу от зенита, имеет в верхней кульминации высоту
h = 90° — φ + δ.
Из этой формулы видно, что географическую широту можно определить, измеряя высоту любой звезды с известным склонением δ в верхней кульминации. При этом следует учитывать, что если звезда в момент кульминации находится к югу от экватора, то ее склонение отрицательно.
- Сириус был в верхней кульминации на высоте 10°. Чему равна широта места наблюдения?
Для нижеследующих упражнений географические координаты городов можно отсчитать по географической карте.
- Каково склонение звезд, которые в вашем городе кульминируют в зените? в точке юга?
- Определите полуденную высоту Солнца в Архангельске и в Ашхабаде в дни летнего и зимнего солнцестояния.

