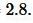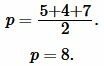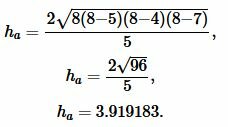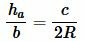Как найти высоту в треугольнике в пространстве

Уравнение высоты треугольника

Как составить уравнение высоты треугольника по координатам его вершин?

Высота треугольника — это перпендикуляр, опущенный из вершины треугольника к прямой, содержащей противолежащую сторону.

Следовательно, для составления уравнения высоты треугольника нужно:

1. Найти уравнение стороны треугольника.
2. Составить уравнение прямой, перпендикулярной этой стороне и проходящей через противолежащую вершину треугольника.

Дано: ΔABC, A(-7;2), B(5;-3), C(1;8).

Написать уравнения высот треугольника.

1) Составим уравнение стороны BC треугольника ABC.

Прямая y=kx+b проходит через точки B(5;-3), C(1;8), значит, координаты этих точек удовлетворяют уравнению прямой. Подставив координаты B и C в уравнение прямой, составляем систему уравнений и решаем её:

Таким образом, уравнение прямой BC —

Угловой коэффициент прямой, перпендикулярной BC,

Значит, уравнение высоты, проведённой к стороне BC, имеет вид

Поскольку эта прямая проходит через точку A(-7;2), подставляем координаты точки в уравнение и находим b:

Итак, уравнение высоты, проведённой к стороне BC:

2) Составим уравнение стороны AB треугольника ABC. A(-7;2), B(5;-3):

Уравнение прямой AB:

Угловой коэффициент перпендикулярной ей прямой

Значит уравнение перпендикулярной AB прямой имеет вид y=2,5x+b. Подставляем в это уравнение координаты точки C(1;8): 8=2,5·1+b, откуда b=5,5.
Получили уравнение высоты, проведённой из точки C к стороне BC: y=2,5x+5,5.
3) Составим уравнение стороны AC треугольника ABC. A(-7;2), C(1;8):

Угловой коэффициент прямой, перпендикулярной AC,

Таким образом, уравнение перпендикулярной AC прямой имеет вид

Подставив в него координаты точки B(5;-3), найдём b:

Итак, уравнение высоты треугольника ABC, опущенной из вершины B:

Высоту треугольника в пространстве

И в итоге: x+2y+z-9=0
это вы написали уравнение плоскости, проходящей через точку С перпендикулярно АВ.

Теперь нужно найти точку пересечения прямой АВ с этой плоскостью (пусть это точка Н),
тогда расстояние от С до Н и будет равно длине высоты.
Т.е.:
1) составляйте уравнение АВ (лучше параметрическое)
2) ищите точку пересечения прямой и плоскости

I. «Теперь нужно найти точку пересечения прямой АВ с этой плоскостью (пусть это точка Н),
тогда расстояние от С до Н и будет равно длине высоты.
Т.е.:
1) составляйте уравнение АВ (лучше параметрическое)
2) ищите точку пересечения прямой и плоскости»

Нужно найти не длину, а уравнение CH.

II. «Можно воспользоваться двойным векторным произведением. и найти направляющий вектор высоты. »
То есть:
AC<2,2,2>
AB

Нужно найти не длину, а уравнение CH. — Если найдёте `H`, то сможете написать уравнение по двум точкам.

Так? — Да. только вычисления не проверял. а в том, что получили, можно сократить на 36.

Высота треугольника онлайн

С помощю этого онлайн калькулятора можно найти высоту треугольника. Для нахождения высоты треугольника введите известные элементы треугольника и нажмите на кнопку «Вычислить». Теоретическую часть смотрите ниже.

Открыть онлайн калькулятор

Высота треугольника. Определение

Определение 1. Отрезок, проведенный из вершины треугольника к прямой, содержащей противоположную сторону, называется высотой треугольника.

Высота треугольника может содержаться внутри треугольника (Рис.1), совпадать со стороной треугольника (при прямоугольном треугольнике высота совпадает с катетом (Рис.2) ), проходить вне треугольника (при тупоугольном треугольнике(Рис.3)).

Теорема о пересечении высот треугольника

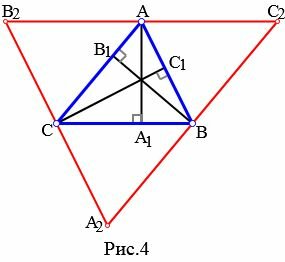
Теорема 1. Все три высоты треугольника (или их продолжения) пересекаются в одной точке.

Доказательство. Рассмотрим произвольный треугольник ABC (Рис.4). Докажем, что высоты ( small AA_1 ,) ( small BB_1 ,) ( small CC_1 ) пересекаются в одной точке. Из каждой вершины треугольника проведем прямую, параллельно противоположной стороне. Получим треугольник ( small A_2B_2C_2. ) Покажем, что точки ( small A, B, C ) являются серединами сторон треугольника ( small A_2B_2C_2. ) ( small AB=A_2C ) так как они являются противоположными сторонами параллелограмма ( small ABA_2C. ) ( small AB=CB_2 ) так как они являются противоположными сторонами параллелограмма ( small ABCB_2. ) Тогда ( small CB_2=CA_2, ) то есть точка ( small C ) является серединой стороны ( small A_2B_2 ) треугольника ( small A_2B_2C_2. ) Аналогично доказывается, что точки ( small A ) и ( small B ) являются серединами сторон ( small B_2C_2 ) и ( small A_2C_2, ) соответственно.

Далее из ( small AA_1⊥BC ) следует, что ( small AA_1⊥B_2C_2 ) поскольку ( small BC ǁ B_2C_2 ). Аналогично, ( small BB_1⊥A_2C_2, ) ( small CC_1⊥A_2B_2. ) Получили, что ( small AA_1,) ( small BB_1, ) ( small CC_1) являются серединными перпендикулярами сторон ( small B_2C_2, ) ( small A_2C_2, ) ( small A_2B_2, ) соответственно. Но серединные перпендикуляры треугольника пересекаются в одной точке (см. статью Серединные перпендикуляры к сторонам треугольника). Следовательно высоты треугольника или их продолжения пересекаются в одной точке.

Точка пересечения высот треугольника называется ортоцентром.

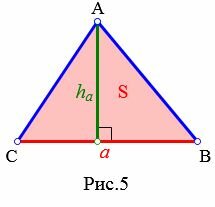
Высота треугольника по основанию и площади

Пусть известны сторона треугольника и площадь. Найти высоту треугольника, отпущенная на известную сторону (Рис.5).

Решение. Площадь треугольника по основанию и высоте вычисляется из формулы:

.

.

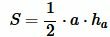
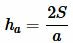(1)

Пример 1. Сторона треугольника равна ( small a=5 ) а площадь ( small S=7. ) Найти высоту треугольника.

Применим формулу (1). Подставляя значения ( small a ) и ( small S ) в (1), получим:

Ответ:

Высота треугольника по трем сторонам

Формула площади треугольника по трем сторонам имеет следующий вид (см. статью на странице Площадь треугольника онлайн):

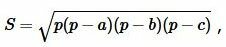(2)

где ( small a, b, c ) стороны треугольника а полупериод ( small p ) вычисляется из формулы:

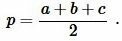(3)

Высота треугольника, отпущенная на сторону ( small a) вычисляется из формулы (1). Подставляя (2) в (1), получим формулу вычисления высоты треугольника по трем сторонам:

.

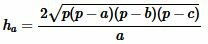(4)

Пример 2. Известны стороны треугольника: ( small a=5, ) ( small b= 4, ) ( small c=7. ) Найти высоту треугольника, отпущенная на сторону ( small a. )

Решение: Найдем, сначала полупериод ( small p ) треугольника из формулы (3):

Подставляя значения ( small a , b, c ) и ( small p ) в (4), получим:

Ответ:

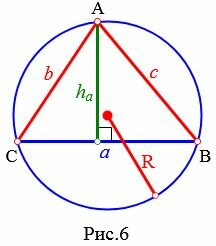
Высота треугольника по двум сторонам и радиусу описанной окружности

Рассмотрим треугольник на рисунке 6. Из теоремы синусов имеем:

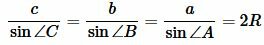(5)

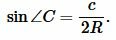(6)

Далее, из теоремы синусов имеем:

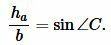(7)

Подставляя (6) в (7), получим:

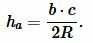(8)

Отметим, что радиус описанной окружности должен удовлетворять следующему неравенству:

(small max (b,c) ≤2R Пример 3. Известны стороны треугольника: ( small b=7, ) ( small c= 3 ) и радиус описанной окружности ( small R=4. ) Найти высоту треугольника, отпущенная на сторону ( small a. )

Решение: Проверим сначала условие (9):

(small max (7,3) ≤2 cdot 4 Ответ: ( small 2frac<5><8>. )

Высота треугольника по стороне и прилежащему к ней углу

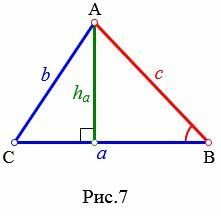
Найдем высоту ( small h_a ) треугольника на рисунке 7. Из теоремы синусов имеем:

( small frac<large h_a><large sin angle B>=frac<large c><large sin 90°>, )

( small h_a=c cdot sin angle B. )

(11)

Пример 4. Известны сторона ( small c=12 ) треугольника и прилежащий угол ( small angle B=30°. ) Найти высоту треугольника, отпущенная на сторону ( small a. )

Решение: Для нахождения высоты треугольника подставим значения ( small c=12 ) и ( small angle B=30° ) в (11). Имеем:

Параметрическое уравнение высоты треугольника в пространстве

И в итоге: x+2y+z-9=0
это вы написали уравнение плоскости, проходящей через точку С перпендикулярно АВ.

Теперь нужно найти точку пересечения прямой АВ с этой плоскостью (пусть это точка Н),
тогда расстояние от С до Н и будет равно длине высоты.
Т.е.:
1) составляйте уравнение АВ (лучше параметрическое)
2) ищите точку пересечения прямой и плоскости

I. «Теперь нужно найти точку пересечения прямой АВ с этой плоскостью (пусть это точка Н),
тогда расстояние от С до Н и будет равно длине высоты.
Т.е.:
1) составляйте уравнение АВ (лучше параметрическое)
2) ищите точку пересечения прямой и плоскости»

Нужно найти не длину, а уравнение CH.

II. «Можно воспользоваться двойным векторным произведением. и найти направляющий вектор высоты. »
То есть:
AC<2,2,2>
AB

Нужно найти не длину, а уравнение CH. — Если найдёте `H`, то сможете написать уравнение по двум точкам.

Так? — Да. только вычисления не проверял. а в том, что получили, можно сократить на 36.

Уравнение высоты треугольника

Как составить уравнение высоты треугольника по координатам его вершин?

Высота треугольника — это перпендикуляр, опущенный из вершины треугольника к прямой, содержащей противолежащую сторону.

Следовательно, для составления уравнения высоты треугольника нужно:

1. Найти уравнение стороны треугольника.
2. Составить уравнение прямой, перпендикулярной этой стороне и проходящей через противолежащую вершину треугольника.

Дано: ΔABC, A(-7;2), B(5;-3), C(1;8).

Написать уравнения высот треугольника.

1) Составим уравнение стороны BC треугольника ABC.

Прямая y=kx+b проходит через точки B(5;-3), C(1;8), значит, координаты этих точек удовлетворяют уравнению прямой. Подставив координаты B и C в уравнение прямой, составляем систему уравнений и решаем её:

Таким образом, уравнение прямой BC —

Угловой коэффициент прямой, перпендикулярной BC,

Значит, уравнение высоты, проведённой к стороне BC, имеет вид

Поскольку эта прямая проходит через точку A(-7;2), подставляем координаты точки в уравнение и находим b:

Итак, уравнение высоты, проведённой к стороне BC:

2) Составим уравнение стороны AB треугольника ABC. A(-7;2), B(5;-3):

Уравнение прямой AB:

Угловой коэффициент перпендикулярной ей прямой

Значит уравнение перпендикулярной AB прямой имеет вид y=2,5x+b. Подставляем в это уравнение координаты точки C(1;8): 8=2,5·1+b, откуда b=5,5.
Получили уравнение высоты, проведённой из точки C к стороне BC: y=2,5x+5,5.
3) Составим уравнение стороны AC треугольника ABC. A(-7;2), C(1;8):

Угловой коэффициент прямой, перпендикулярной AC,

Таким образом, уравнение перпендикулярной AC прямой имеет вид

Подставив в него координаты точки B(5;-3), найдём b:

Итак, уравнение высоты треугольника ABC, опущенной из вершины B:

Образцы выполнения некоторых заданий

Рассмотрим решения некоторых практических упражнений.

Задание 2(е)

На плоскости даны точки А(11; -5), В(6;7), С(-10; -5). Найти уравнение биссектрисы угла А.

Решение задания 2(е)

Найдем направляющий вектор биссектрисы как сумму ортов векторов и

,

или (умножая на )

.

; ;

; .

.

Таким образом, в качестве направляющего вектора биссектрисы угла А можно взять вектор 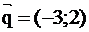и уравнение биссектрисы будет иметь вид

.

Задание 3

Дана точка (0;2) пересечения медиан треугольника и уравнения двух его сторон 5х – 4у + 15 = 0 и 4х + у – 9 = 0. Найти координаты вершин треугольника и уравнение третьей стороны.

Решение Координаты одной вершины найдем как координаты точки пересечения данных сторон, для чего решим систему уравнений

Получаем или

Точка О_ц пересечения медиан треугольника называется его центром. Отметим одно свойство центра треугольника, которое используем для нахождения координат остальных вершин:

; ,

где х_ц, у_ц – координаты центра треугольника;

х_i, y_i – координаты i-ой вершины треугольника,

Для доказательства этих формул рассмотрим треугольник А₁А₂А₃, где А_i(x_i;y_i), i = 1-3 (см.рис.2.1).

Рис.2.1. Вспомогательный чертеж к заданию 3

Пусть В середина стороны А₁А₂. Тогда А₃В – медиана треугольника А₁А₂А₃. По известному из элементарной геометрии свойству медиан треугольника .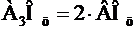

Тогда координаты точки В найдем по формулам

и ,

а координаты центра О_ц из векторного соотношения , которое в координатной форме записывается так

, .

Отсюда, выражая х_ц и у_ц через x_i, y_i, получим требуемые формулы.

Вернемся к решению задания 3. Используя доказанные формулы, полагая в них х₁ = 1 и у₁ = 5, х_ц = 0 и у_ц = 2, получим два уравнения, которым должны удовлетворять координаты остальных двух вершин

; ,

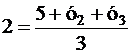
Еще два уравнения получим, если потребуем, чтобы искомые точки, вершины треугольника, принадлежали заданным сторонам, т.е. их координаты удовлетворяли уравнениям этих сторон

Итак, для определения четырех неизвестных х₂, у₂, х₃, у₃, мы имеем четыре независимых (!) условия (уравнения)

Решив эту систему, получим х₂ = -3, у₂ = 0, х₂= 2, у₃ = 1.

Наконец, уравнение третьей стороны запишем как уравнение прямой, проходящей через две заданные точки (-3;0) и (2;1)

или .

Итак, уравнение третьей стороны x – 5у + 3 = 0, а вершины треугольника имеют координаты (1;5), (-3;0), (2;1).

Задание 7

Составить уравнение линии, для каждой точки М которой, отношение расстояний до точки F( ) и до прямой
равно .

Привести уравнение линии к каноническому виду, определить тип линии и построить линию на чертеже. Показать на чертеже фокусы, директрисы, асимптоты (если они имеются у построенной линии).

Замечание. Отметим, что в заданиях этого модуля ; ; .

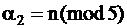
Пусть n = 101. Тогда:

, т.к. ;

, т.к. ;

, т.к. .

Итак, для n = 101 первая часть задания 7 принимает вид:

Составить уравнение линии, для каждой точки М которой, отношение расстояния до точки F(-4;1) и до прямой x = 1
равно .

Решение задания 7 (для n = 101).

Пусть М(х;у) произвольная точка искомой линии, r – расстояние от М до F и d – расстояние от точки М до прямой x = 1. Тогда

и .

По условию , т.е. d = 2r.

— уравнение искомой линии.

Упростим уравнение линии и приведем его к каноническому виду. Для этого возведем обе части уравнения в квадрат и выполним следующие преобразования уравнения

х 2 – 2х +1 = 4х 2 + 32х + 64 + 4(у – 1) 2 ,

3х 2 + 34х + 4(у – 1) 2 + 63 = 0,

,

.

Последнее уравнение – это каноническое уравнение эллипса с полуосями и ( ), центр которого находится в точке с координатами . Координаты вершин эллипса
и , т.е. (-9;1), , ,
. Построим эллипс на чертеже (см.рис.2.2).

Рис.2.2. Эллипс с уравнением

Фокусы эллипса имеют координаты , где .

.

Итак, координаты фокусов F₁(-4;1), F₂( ;1).

Директрисы эллипса имеют уравнения , где е – эксцентриситет эллипса

.

Уравнения директрис , т.е.

D₂: .

Отметим фокусы и директрисы эллипса на рис.2.2.

Обратите внимание на совпадение фокуса F₁ с точкой, данной в условии задания 7, на совпадение директрисы D₁ с прямой х = 1 из условия этого задания, и совпадение эксцентриситета е с параметром е в условии. По этому поводу см. теоретическое упражнение 18.

В пространстве даны точки А(-2; -4;1), В(3;1; -1), С(5;1;1),
S(1;-4;0). Найти координаты центра и радиус вписанной в пирамиду SABC сферы (условие сформулировано для n = 101).

Решение задания 4(м)

Пусть точка О(x₀;y₀;z₀) – центр сферы, вписанной в пирамиду SABC. Найдем точку О как точку, равноудаленную от граней пирамиды. Для этого найдем уравнения всех граней и расстояния от точки О до этих граней (уравнения некоторых граней находятся в предшествующих пункту М пунктах задания 4).

Грань АВС. Уравнение грани

или 5х – 7у – 5z – 13 = 0.

Точки О и S лежат по одну сторону от грани АВС, поэтому отклонения этих точек от грани АВС имеют одинаковые знаки. Отклонение (S) точки S от грани АВС равно

> 0.

.

Аналогично все делается для граней ABS, BCS, CAS.

Грань ABS имеет уравнение 5х + у + 15z – 1 = 0 и
.

Грань BCS имеет уравнение 5х – 3у – 5z – 17 = 0 и
.

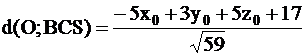
Наконец, грань CAS имеет уравнение 5х – 7у + 15z + 33 = 0 и
.

Так как О – центр сферы, вписанной в пирамиду SABC, то

d(O; ABC) = d(O; ABS) = d(O; BCS) = d(O; CAS) = r,

где r – радиус вписанной сферы.

Тогда координаты точки О должны удовлетворять системе

В отличие от других заданий этого модуля, коэффициенты и решение этой системы найдем приближенно, с помощью микрокалькулятора или ЭВМ. Получим систему

и уравнение вписанной сферы

.

1. Общее уравнение прямой на плоскости. Нормальный вектор прямой. Угол между прямыми. Условия параллельности и перпендикулярности.

2. Уравнение прямой с угловым коэффициентом. Угол между прямыми. Условия параллельности и перпендикулярности.

3. Каноническое и параметрическое уравнения прямой на плоскости. Направляющий вектор прямой. Угол между прямыми. Условия параллельности и перпендикулярности.

4. Уравнение прямой, проходящей через две заданные точки.

5. Уравнения прямых, проходящих через данную точку параллельно и перпендикулярно данной прямой (3 случая задания данной прямой: общим уравнением, каноническим уравнением, уравнением с угловым коэффициентом).

6. Общее уравнение плоскости в пространстве, нормальный вектор плоскости. Угол между плоскостями. Условие параллельности и перпендикулярности.

7. Уравнение плоскости, проходящей через три данные точки, не лежащие на одной прямой.

8. Общее, каноническое и параметрическое уравнения прямой в пространстве. Угол между прямыми. Условия параллельности и перпендикулярности.

9. Угол между прямой и плоскостью в пространстве. Условие параллельности и перпендикулярности прямой и плоскости.

10. Уравнение плоскости, проходящей через данную точку, перпендикулярно данной прямой. Уравнение прямой, проходящей через данную точку, перпендикулярно данной плоскости.

11. Расстояние от точки до: прямой на плоскости; прямой в пространстве; плоскости в пространстве.

12. Уравнение линии на плоскости. Общее уравнение кривой второго порядка.

13. Каноническое и параметрическое уравнения окружности.

14. Эллипс (фокусы и директрисы, фокальные радиусы точки, эксцентриситет). Каноническое и параметрическое уравнения эллипса.

15. Гипербола (фокусы, директрисы и асимптоты, фокальные радиусы точки, эксцентриситет). Каноническое и параметрическое уравнения гиперболы.

16. Парабола (фокус и директриса, фокальный радиус точки, эксцентриситет). Каноническое уравнение параболы.

17. Приведение общего уравнения кривой второго порядка к каноническому виду.

18. Полярные координаты на плоскости. Уравнение линии в полярных координатах.

19. Уравнение поверхности в пространстве. Общее уравнение поверхностей второго порядка.

20. Основные типы поверхностей второго порядка и их канонические уравнения.

1. Бугров Н.С., Никольский С.М. Элементы линейной алгебры и аналитической геометрии. – М.: Наука, 1980. 176 с.

2. Данко П.Е., Попов А.Г., Кожевникова Т.Я. Высшая математика в упражнениях и задачах. Ч.1: Учебное пособие для студентов втузов. – 3-е изд., перераб. и доп. – М.: Высшая школа, 1980. 320 с.

3. Ильин В.А., Позняк Э.Г. Аналитическая геометрия. – М.: Наука, 1981. 232 с.

4. Клетеник Д.В. Сборник задач по аналитической геометрии. – М.: Наука, 1980. 240 с.

5. Сборник задач по математике для втузов. Линейная алгебра и основы математического анализа/Под ред. А.В. Ефимова, Б.П. Демидович. – М.: Наука, 1981, 464 с.

6. Высшая математика. Методические указания и контрольные задания/Под ред. Ю.С. Арутюнова. – М.: Высшая школа, 1985.

7. Гусак А.А. Пособие к решению задач по высшей математике. – Изд. 3-е. – Минск: Изд-во БГУ, 1973. 532 с.

8. Кузнецов А.А. Сборник заданий по высшей математике (типовые расчеты): Учеб. пособие для втузов. – М.: Высшая школа, 1983. 175 с.

9. Погорелов А.В.Аналитическая геометрия.– М.:Наука, 1968. 176с

Автор	Сообщение
	Заголовок сообщения: Параметрическое уравнение высоты в треугольнике Добавлено: 09 авг 2017, 10:36
Начинающий Зарегистрирован: 08 авг 2017, 14:55 Сообщений: 11 Cпасибо сказано: 4 Спасибо получено: 0 раз в 0 сообщении Очков репутации: 1	Написать параметрическое уравнение высоты, проведенной из вершины А на сторону ВС в треугольнике АВС. А(2,1,-1), В(1,3,0), С(4,1,7). Что нужно почитать, что бы понять как решить эту задачу?
Вернуться к началу

dr Watson	Заголовок сообщения: Re: Параметрическое уравнение высоты в треугольнике Добавлено: 09 авг 2017, 11:37
	Знать надо почти ничего. Вариант А. 1. На прямой [math]BC[/math] берём точку [math]D[/math]. Для этого надо знать, как задать параметрически прямую, проведённую через две точки. Координаты точки [math]D[/math] будут зависеть от одного параметра. 2 Мы хотим, чтобы точка [math]D[/math] была основанием перпендикуляра, опущенного из вершины [math]A[/math], то есть чтобы векторы [math]vec{AD}[/math] и [math]vec{BC}[/math] были перпендикулярны. Для этого надо знать, что такое скалярное произведение и как с его помощью записать условие перпендикулярности. 3. Из условия перпендикулярности находим параметр, то есть получаем конкретно точку [math]D.[/math] Остаётся написать параметрическое уравнение прямой, проходящей через точки [math]A[/math] и [math]D,[/math] а это Вы уже умеете, если прошли п.1. ВАРИАНТ В. 1. Берём вектор, перпендикулярный вектору [math]vec{BC}[/math] любой ненулевой длины. Он будет направляющим вектором искомой прямой. 2. Теперь надо знать, как записать параметрическое уравнение прямой, проходящей через точку [math]A[/math] параллельно полученному направляющему вектору. PS. Чтобы в данном контексте пишется слитно. Раздельно пишется во фразах типа «что бы мне ещё поесть», «что бы я ни делал, ничего не получается»
Вернуться к началу
	За это сообщение пользователю dr Watson «Спасибо» сказали: vas999

vas999	Заголовок сообщения: Re: Параметрическое уравнение высоты в треугольнике Добавлено: 09 авг 2017, 12:40
	dr Watson писал(а): Вариант А. 1. На прямой [math]BC[/math] берём точку [math]D[/math]. Для этого надо знать, как задать параметрически прямую, проведённую через две точки. Координаты точки [math]D[/math] будут зависеть от одного параметра. А(2,1,-1), В(1,3,0), С(4,1,7). Направляющий вектор: [math]overrightarrow{BC} = left( 4-1,1-3,7-0 right)=left( 3,-2,7 right)[/math] Параметрические уравнения прямой: [math]left{!begin{aligned} & x =1+3 lambda \ & y =3-2 lambda\ & z =0+7lambda end{aligned}right.[/math] Так?
Вернуться к началу

vas999	Заголовок сообщения: Re: Параметрическое уравнение высоты в треугольнике Добавлено: 09 авг 2017, 13:58
	dr Watson писал(а): 1. Пишем уравнение плоскости через точку [math]A[/math] перпендикулярно вектору [math]BC[/math]. 2. Подставляем в неё [math]x=1=3lambda, y=ldots[/math] и находим [math]lambda[/math] — получили точку [math]D.[/math] 3. Как в варианте А. А(2,1,-1), В(1,3,0), С(4,1,7). 1. [math]overrightarrow{BC}=(3,−2,7)[/math] [math]left{!begin{aligned} & x =1+3 lambda \ & y =3-2 lambda\ & z =0+7lambda end{aligned}right.[/math] [math]3left( x-2 right) -2left( y-1 right)+7left( z+1 right) =0[/math] [math]3x-2y+7z+3= 0[/math] 2. [math]3left( 1+3 lambdaright)-2left( 3-2 lambda right)+7left( 0+7lambda right) +3 = 0[/math] [math]lambda=0[/math] [math]D= left( 1,3,0 right)[/math] Так?
Вернуться к началу

vas999	Заголовок сообщения: Re: Параметрическое уравнение высоты в треугольнике Добавлено: 09 авг 2017, 14:33
	dr Watson писал(а): 3. Из условия перпендикулярности находим параметр, то есть получаем конкретно точку [math]D.[/math] Остаётся написать параметрическое уравнение прямой, проходящей через точки [math]A[/math] и [math]D,[/math] а это Вы уже умеете, если прошли п.1. 3. [math]overrightarrow{AB}=left( 1-2,3-1,0+1 right) =left( -1,2,1 right)[/math] [math]left{!begin{aligned} & x =2- lambda \ & y =1+2 lambda \ & z =-1+ lambda end{aligned}right.[/math] Это и есть ответ?
Вернуться к началу

Как найти высоту треугольника, если даны координаты точек

Высотой в треугольнике называют отрезок прямой линии, соединяющий вершину фигуры с противолежащей стороной. Этот отрезок обязательно должен быть перпендикулярен стороне, поэтому из каждой вершины можно провести лишь одну высоту. Поскольку вершин в этой фигуре три, высот в нем столько же. Если треугольник задан координатами своих вершин, вычисление длины каждой из высот можно произвести, например, воспользовавшись формулой нахождения площади и рассчитав длины сторон.

Инструкция

Исходите в расчетах из того, что площадь треугольника равна половине произведения длины любой из его сторон на длину высоты, опущенной на эту сторону. Из этого определения вытекает, что для нахождения высоты нужно знать площадь фигуры и длину стороны.

Начните с вычисления длин сторон треугольника. Обозначьте координаты вершин фигуры так: A(X₁,Y₁,Z₁), B(X₂,Y₂,Z₂) и C(X₃,Y₃,Z₃). Тогда длину стороны AB вы сможете рассчитать по формуле AB = √((X₁-X₂)² + (Y₁-Y₂)² + (Z₁-Z₂)²). Для двух других сторон эти формулы будут выглядеть так: BC = √((X₂-X₃)² + (Y₂-Y₃)² + (Z₂-Z₃)²) и AC = √((X₁-X₃)² + (Y₁-Y₃)² + (Z₁-Z₃)²). Например, для треугольника с координатами A(3,5,7), B(16,14,19) и C(1,2,13) длина стороны AB составит √((3-16)² + (5-14)² + (7-19)²) = √(-13² + (-9²) + (-12²)) = √(169 + 81 + 144) = √394 ≈ 19,85. Длины сторон BC и AC, рассчитанные таким же способом, будут равны √(15² + 12² + 6²) = √405 ≈ 20,12 и √(2² + 3² + (-6²)) = √49 = 7.

Знания длин трех сторон, полученных на предыдущем шагу, достаточно для вычисления площади треугольника (S) по формуле Герона: S = ¼ * √((AB+BC+CA) * (BC+CA-AB) * (AB+CA-BC) * (AB+BC-CA)). Например, после подстановки в эту формулу значений, полученных из координат треугольника-образца из предыдущего шага, эта формула даст такое значение: S = ¼*√((19,85+20,12+7) * (20,12+7-19,85) * (19,85+7-20,12) * (19,85+20,12-7)) = ¼*√(46,97 * 7,27 * 6,73 * 32,97) ≈ ¼*√75768,55 ≈ ¼*275,26 = 68,815.

Исходя из площади треугольника, рассчитанной на предыдущем шаге, и длин сторон, полученных на втором шаге, вычислите высоты для каждой из сторон. Так как площадь равна половине произведения высоты на длину стороны, к которой она проведена, для нахождения высоты делите удвоенную площадь на длину нужной стороны: H = 2*S/a. Для использованного выше примера высота, опущенная на сторону AB составит 2*68,815/16,09 ≈ 8,55, высота к стороне ВС будет иметь длину 2*68,815/20,12 ≈ 6,84, а для стороны АС эта величина будет равна 2*68,815/7 ≈ 19,66.

Источники:

• даны точки найти площадь треугольника

I. «Теперь нужно найти точку пересечения прямой АВ с этой плоскостью (пусть это точка Н),
тогда расстояние от С до Н и будет равно длине высоты.
Т.е.:
1) составляйте уравнение АВ (лучше параметрическое)
2) ищите точку пересечения прямой и плоскости»

Нужно найти не длину, а уравнение CH…

II. «Можно воспользоваться двойным векторным произведением…. и найти направляющий вектор высоты…»
То есть:
AC{2,2,2}
AB{3,6,3}

[ABx[ACxAB]] итогом чего становится {-36, 36, -36) и уравнение выходит
((x-4)/(-36))=((y-1)/36)=((z-3)/(-36)
Так?

Спасибо.