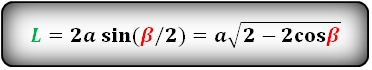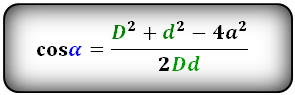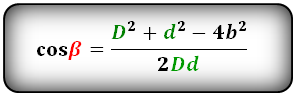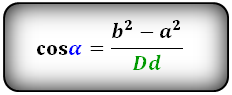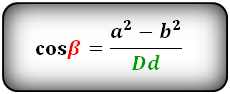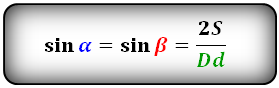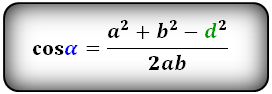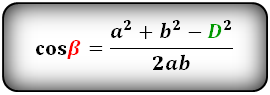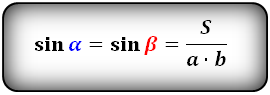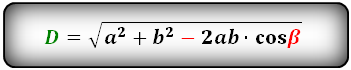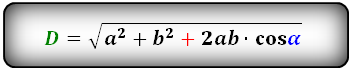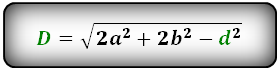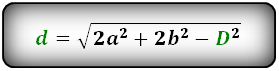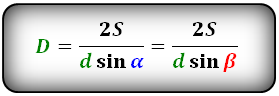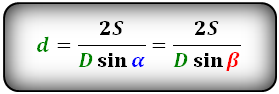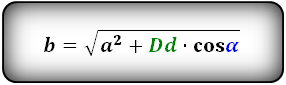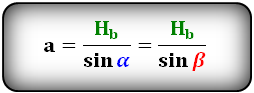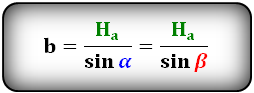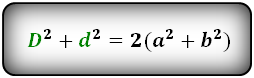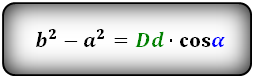Высота параллелограмма — это перпендикуляр, опущенный из любой точки одной стороны параллелограмма на прямую, содержащую противоположную сторону. Высотой параллелограмма также называют длину этого перпендикуляра. Для нахождения его высоты необходимо умножить синус угла на сторону.
.
Поделиться расчетом:
Вычислить высоту параллелограмма
зная длину стороны и угол
Основание параллелограмма a
Угол параллелограмма α°
Вычислить
Примечание. Это часть урока с задачами по геометрии (раздел параллелограмм). Если Вам необходимо решить задачу по геометрии, которой здесь нет — пишите об этом в форуме.
См. также: Свойства и площадь параллелограмма.
|
Обозначения в формулах эквивалентны обозначениям на рисунках, а именно: а — стороны, параллелограмма, параллельные друг другу b — боковые стороны параллелограмма h — высота параллелограмма d — диагональ параллелограмма S — площадь параллелограмма α — острый угол при основании параллелограмма Высота параллелограмма равна соотношению площади к основанию (Формула 1) Высота параллелограмма равна произведению боковой стороны на синус угла при основании (Формула 2) Соотношение оснований параллелограмма равно обратно пропорциональному соотношению высот, опущенных на соответствующие стороны (Формула 3) Высоты параллелограмма, опущенные из одной вершины, образуют угол, равный углу параллелограмма при соседней вершине (Рисунок 2) Высота параллелограмма равна, корню из разности квадрата боковой стороны и квадрата длины отрезка, образующего прямоугольный треугольник, другими сторонами которого являются боковая сторона и высота (Формула 4) Высота параллелограмма равна корню из разности квадрата диагонали, из которой опущена высота и квадрата длины отрезка между точкой, из которой проведена диагональ и точкой пересечения высоты и основания (Формула 5) |
Позначення у формулах еквівалентні позначенням на малюнках, а саме: а — сторони, паралелограма, паралельні один одному b — бічні сторони паралелограма h — висота паралелограма d — дiагональ паралелограма S — площа паралелограма α — гострий кут при основі паралелограма Висота паралелограма дорівнює співвідношенню площі до підстави (Формула 1) Висота паралелограма дорівнює твору бічної сторони на синус кута при його основі (Формула 2) Співвідношення підстав паралелограма дорівнює обернено пропорційному співвідношенню висот, опущених на відповідні сторони (Формула 3) Висоти паралелограма, опущені з однієї вершини, утворюють кут, рівний куту паралелограма при сусідній вершині (Малюнок 2) Висота паралелограма рівна, корню з різниці квадрата бічної сторони і квадрата довжини відрізка, створюючого прямокутний трикутник, іншими сторонами якого є бічна сторона і висота (Формула 4) Висота паралелограма дорівнює корню з різниці квадрата діагоналі, з якої опущена висота і квадрата довжини відрізка між точкою, з якої проведена діагональ і точкою пересічення висоти і основання (Формула 5) |
Решение.
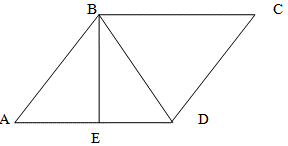
Поскольку, по условию задачи, AE=ED, то треугольники ABE и DBE равны между собой (по первому признаку равенства треугольников: равны две стороны и угол между ними, AE=ED и BE — общая сторона, а BE образует с AD угол 90 градусов). Таким образом, угол ADB равен 30 градусам. Соответственно, угол DBC также равен 30 градусам как внутренние накрест лежащие при параллельных прямых BC и AD.
Из прямоугольного треугольника ABE определим, что угол ABE равен 180 — 90 — 30 = 60 градусов. Откуда (из равенства треугольников ABE и DBE) угол EBD также равен 60 градусов. Таким образом, диагональ образует со вторым основанием угол ABD = 60 + 60 = 120 градусов. BDC = ABD = 120 градусов как внутренние накрест лежащие.
Найдем длину диагонали.
BE / BD = cos ∠EBD
BE / BD = cos 60
Подставим значение косинуса 60 градусов и получим:
BE / BD = 1/2
По условию задачи BE = 5 см, откуда
5 / BD = 1/2
BD = 10
Ответ: длина диагонали параллелограмма равна 10 см, углы, которые образует диагональ с основаниями равны 30 и 120 градусов.
|
В параллелограмме ABCD известно, что АВ=18, ВС=27, sin∠C=8/9. Найдите большую высоту параллелограмма. 1) Есть правило, что большая высота параллелограмма проведена к меньшей его стороне. Проведём высоту DH на сторону AB как меньшую (18<27). DH — искомая высота. 2) Получим прямоугольный треугольник ADH, в котором
Тогда из определения синуса как отношения противолежащего катета к гипотенузе получаем: DH/AD = 8/9 DH/27 = 8/9 DH = 8/9 * 27 DH = 8 * 3 DH = 24. Ответ: 24. автор вопроса выбрал этот ответ лучшим Знаете ответ? |
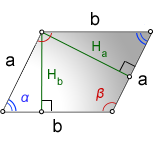
Высота — перпендикуляр исходящий из вершины угла на противоположенную сторону
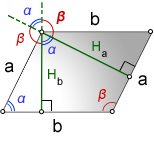
Hb — высота на сторону b
Ha — высота на сторону a
α, β — углы параллелограмма
Формулы длины высоты параллелограмма, через сторону и угол, ( Hb, Ha):
Острый угол пересечения высот, равен острому углу параллелограмма.
Тупой угол пересечения высот, равен тупому углу параллелограмма.
Формулы площади параллелограмма
Формула периметра параллелограмма
Все формулы по геометрии
Свойства биссектрисы параллелограмма
— Биссектриса по определению делит угол пополам
— Биссектриса отсекает равнобедренный треугольник (в данном случае треугольники ABF и DKC)
— Биссектрисы смежных углов, пересекаются под прямым углом (90°)
— Биссектрисы противоположных углов, равны и параллельны
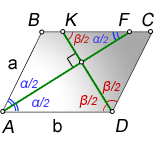
DK — биссектриса из тупого угла
α — острый угол
β — тупой угол
a — меньшая сторона
b — большая сторона
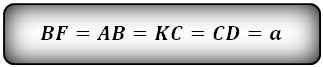
Так как треугольники ABF и DKC, равнобедренные, следовательно справедливы тождества:
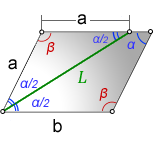
Длина биссектрисы параллелограмма
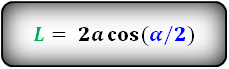
L — биссектриса параллелограмма
a, b — стороны
α, β — углы
Формулы длины биссектрисы через сторону и углы, (L):
Формулы площади параллелограмма
Формула периметра параллелограмма
Все формулы по геометрии
Свойства углов между диагоналями параллелограмма:
1. Противоположные углы равны
2. Косинус тупого угла, всегда имеет отрицательное значение: cos β <0
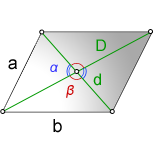
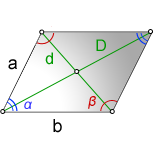
a, b — стороны параллелограмма
D — большая диагональ
d — меньшая диагональ
α — острый угол между диагоналями
β — тупой угол между диагоналями
Формулы косинуса острого и тупого углов между диагоналями, через стороны и диагонали (по теореме косинусов):
Формула синуса острого и тупого углов через площадь (S) и диагонали:
Формулы соотношения острого и тупого углов между диагоналями:
Для определения величины угла в градусах или радианах, используем функции arccos и arcsin
Формулы площади параллелограмма
Формула периметра параллелограмма
Все формулы по геометрии
Свойства углов параллелограмма:
1. Противоположные углы равны
2. Косинус тупого угла, всегда имеет отрицательное значение: cos β <0
a, b — стороны параллелограмма
D — большая диагональ
d — меньшая диагональ
α — острый угол
β — тупой угол
Формулы косинуса острого и тупого углов через стороны и диагонали (по теореме косинусов):
Формула синуса острого и тупого углов через площадь (S) и стороны:
Формулы соотношения острого и тупого углов:
Для определения величины угла в градусах или радианах, используем функции arccos или arcsin
Формулы площади параллелограмма
Формула периметра параллелограмма
Все формулы по геометрии
Свойства параллелограмма:
1. Противоположные стороны равны и параллельны
2. Противоположные углы равны
3. Точка пересечения диагоналей, делит их пополам
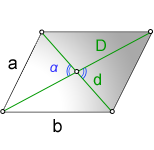
1. Длина диагонали параллелограмма через стороны, известную диагональ и угол.
a, b — стороны параллелограмма
D — большая диагональ
d — меньшая диагональ
α, β — углы параллелограмма
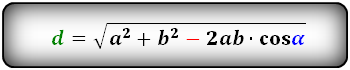
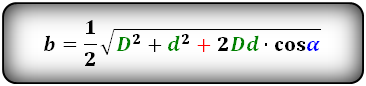
Формулы диагонали через стороны и углы параллелограмма (по теореме косинусов), (D, d):
Формулы диагонали через стороны и известную диагональ (по формуле- сумма квадратов диагоналей), (D, d):
2. Длина диагонали параллелограмма через площадь, известную диагональ и угол.
D — большая диагональ
d — меньшая диагональ
α, β — углы между диагоналями
S — площадь параллелограмма
Формулы диагонали через площадь, известную диагональ и угол между диагоналями, (D, d):
Формулы площади параллелограмма
Формула периметра параллелограмма
Все формулы по геометрии
Свойства параллелограмма:
1. Противоположные стороны равны и параллельны
2. Противоположные углы равны
3. Точка пересечения диагоналей, делит их пополам
1. Формулы длины сторон через диагонали и угол между ними.
a, b — стороны параллелограмма
D — большая диагональ
d — меньшая диагональ
α, β — углы между диагоналями
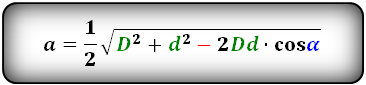
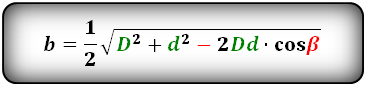
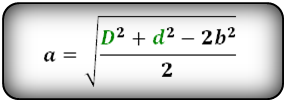
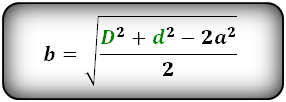
Формулы сторон параллелограмма через диагонали и угол между ними (по теореме косинусов), (a, b):
Формулы сторон параллелограмма через диагонали и сторону, (a, b):
Формулы сторон параллелограмма , (a, b):
2. Формулы длины сторон параллелограмма через высоту.
a, b — стороны параллелограмма
Hb — высота на сторону b
Ha — высота на сторону a
α, β — углы параллелограмма
Формулы сторон параллелограмма через высоту, (a, b):
3. Дополнительные, интересные формулы параллелограмма:
a, b — стороны параллелограмма
D — большая диагональ
d — меньшая диагональ
α — острый угол между диагоналями
Формула суммы квадратов диагоналей:
Формула разности квадратов сторон:
Формулы площади параллелограмма
Формула периметра параллелограмма
Все формулы по геометрии



Вычислить высоту параллелограмма зная длину стороны и угол
Вам нужно указать основание параллелограмма (a) и угол параллелограмма (α).
Формула расчёта высоты параллелограмма зная длину стороны и угол: h=a*sin(α).
Умножаем сторону на угол в градусах.

| Основание параллелограмма (a) | ||
| Угол параллелограмма (градусы) (α) |
Найти длину стороны параллелограмма зная диагональ и сторону
Периметр параллелограмма
Площадь параллелограмма
Понравилась страница? Поделитесь ссылкой в социальных сетях. Поддержите проект!
Нет комментариев.
Оставить комментарий
Заполните все поля.
Ваше имя:
| Оценка |