Как найти взаимно перпендикулярные прямые - Исправление недочетов и поиск решений вместе с Examum.ru

Взаимно перпендикулярные прямые

Взаимно перпендикулярные прямые — это прямые пересекающиеся под прямым углом. Построить взаимно перпендикулярные прямые бывает необходимо для решения той или иной задачи. Например в задаче на определение расстояния от точки до прямой.
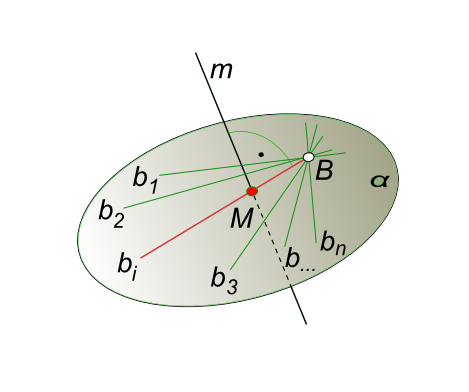
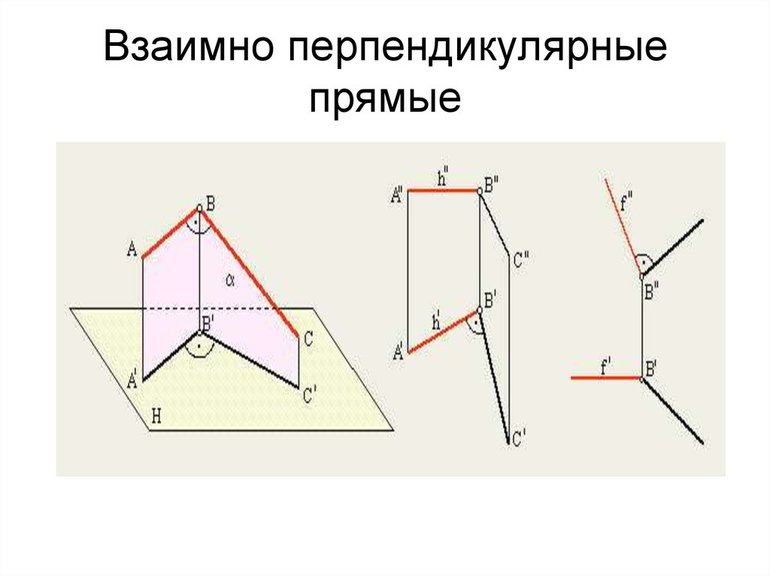
Наглядное пространственное представление графического решения задачи на построение взаимно перпендикулярных прямых дает рисунок

Взаимно перпендикулярные прямые

Через точку B можно провести множество прямых {b1, b2, …, bn}, перпендикулярных к прямой m. Это множество прямых определяет плоскость α ⊥ m.
Чтобы выделить из {b1, b2, …, bn} единственную прямую bi, пересекающую данную прямую m и следовательно взаимно перпендикулярную к ней, необходимо:
— Найти точку встречи прямой m с плоскостью α. M = m ∩ α;
— Зная положение точки M, провести через нее прямую bi и определить действительную величину отрезка [BM], выражающую искомое расстояние от точки до прямой.
На основе выше приведенного рисунка может быть решена задачи по построению перпендикулярных прямых которые не пересекаются, трех взаимно перпендикулярных прямых.

Прямой угол между двумя пересекающимися прямыми проецируется без искажения, если хотя бы одна из прямых параллельна плоскости проекций.
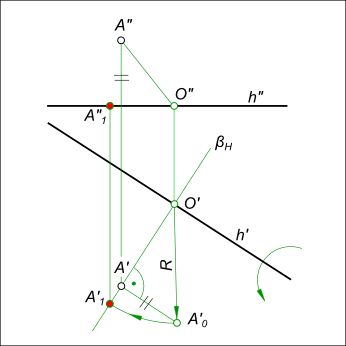
Найти расстояние от точки A до прямой h. Решение подобной задачи предполагает, что будут построены взаимно перпендикулярные прямые

Взаимно перпендикулярные прямые

Для определения натуральной величины отрезка перпендикуляра от точки A до прямой h используем способ вращения вокруг горизонтали:
— через точку A проводим горизонтально проецирующую плоскость β_H ⊥ h` и на их пересечении находим O` и по линии связи O» — проекции центра вращения;
— определяем действительную величину радиуса вращения R=[O`A`₀], применив способ прямоугольного треугольника;
— описываем дугу радиуса R до пересечения с β_H и находим точку A`₁ и расстояние от точки A до прямой h в виде отрезка [A`₁O`] ⊥ h`.
[AO] ⊥ h — это прямые пересекающиеся под прямым углом — взаимно перпендикулярные прямые.

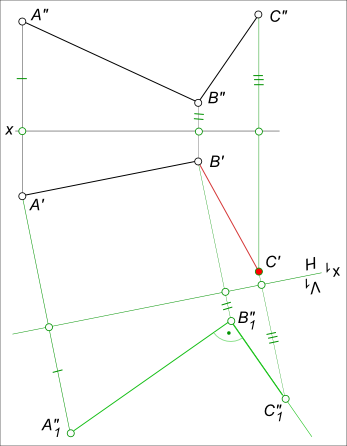
Для того чтобы построить взаимно перпендикулярные прямые, в случае когда одна из них задана прямой общего положения, необходимо перевести ее, предварительно, в положение либо горизонтали, либо фронтали

Взаимно перпендикулярные прямые

Здесь построение второй стороны прямого угла выполняется способом перемены плоскости проекции. Вводится новая фронтальная плоскость проекции V₁, для которой сторона AB прямого угла есть фронтальная прямая. И тогда прямой угол ABC проецируется на V₁ без искажения. Аппликата точки C при перемене плоскости V на V₁ остается неизменной и ее пресечение с направлением стороны BC дает положение искомой точки C₁. Искомую проекцию C` находим на пересечении линий связи точки C.

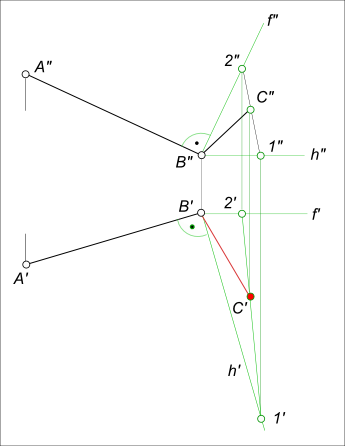
Та же задача на взаимно перпендикулярные прямые может быть решена по другим способом

Взаимно перпендикулярные прямые

Здесь сторона BC, заключается в плоскость перпендикулярную второй стороне прямого угла AB. Затем в этой плоскости проводится прямая 1 — 2 через точку C и находится горизонтальная проекция C`, как принадлежащая прямой 1` — 2`.

Источник

Основные свойства

При рассмотрении того, какие прямые называют перпендикулярными, нужно уделить внимание свойствам. Они выглядят следующим образом:

Через одну точку А можно провести только одну перпендикулярную линию основному отрезку, остальные линии будут наклонными и могут скрещиваться.
Несколько перпендикуляров никогда не будут между собой пересекаться.

Для обозначения перпендикуляра применяется знак «⊥». В подобном случае угол составляет 90°. На чертеже пересечение обозначается своеобразным квадратом, которые рисуется от двух пересекающихся линий.

Доказательство взаимного расположения

Рассматриваемый термин получил широкое распространение, он фигурирует практически в каждой геометрической задаче. В некоторых случаях о взаимном расположении известно, в других это нужно доказать. Задача доказательства заключается в определении прямого угла между двумя прямыми или плоскостями. Необходимое и достаточное условие перпендикулярности заключается в теореме:

Прямые взаимно перпендикулярны в случае, если направляющие векторы прямых перпендикулярны.
Доказательство связано с определением направления векторов, любой должен быть перпендикулярен.

Для определения расположения плоскостей или отрезков относительно друг друга следует провести геометрическое построение. Проходить отрезки должны в одной точке.

Определение перпендикулярности прямой и плоскости

Рассматривая определение перпендикулярных прямых следует учитывать, что подобное свойство применимо к плоскости. Основной признак заключается в перпендикулярности отрезка к любому другому, который находится в плоскости. Перпендикулярность прямых в пространстве указывается определенным знаком.

Доказать перпендикулярность можно проведя геометрические построения. Признаки расположения плоскости и прямой под углом 90° заключаются в следующем:

Если прямая перпендикулярна плоскости, то в ней можно отложить другую прямую, лежащую под углом 90°.
В одной точке под прямым углом может пересекаться только две линии, значит, будет лежать только одна плоскость.

Отрезки могут быть также параллельными. В этом случае нет точки, в которой будут они пересекаться.

Построение перпендикуляра

Выдержать угловой коэффициент можно различным образом. В большинстве случаев для этого нужно иметь при себе циркуль. Построить перпендикуляр можно следующим образом:

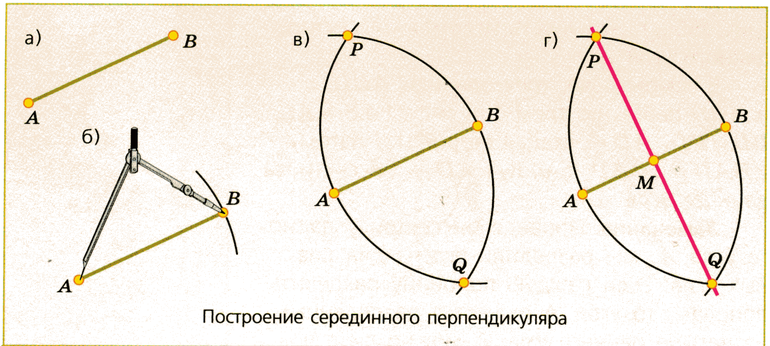
С помощью циркуля проводится построение полуокружности с центром в точке Х. На основном отрезке в результате этого получается две точки А и В. Для отображения полуокружности применяется другой цвет, полученная линия вспомогательная, поэтому не выделяется жирным.
С точки А и В проводится откладывание двух полуокружностей, пересекающихся в двух местах по касательной. Данные точки (P и Q) используются для откладывания линии, которая может пересечь их и основной отрезок с ранее отложенными точками А и В.

Существенно упростить задачу можно путем применения специального чертежного инструмента, к примеру, любого прямоугольного треугольника. Он может называться угольником, основной его признак заключается в наличии двух перпендикулярных плоскостей. Построение проводится следующим образом:

Одна из сторон, смежная с прямым углом, прикладывается к проведенному отрезку. На этом этапе главное — правильно совместить поверхность инструмента с ранее отложенной линией. Незначительное отклонение может привести к изменению угла.
Проводится откладывание вертикального отрезка.

В геометрии чаще всего применяется именно второй способ. Однако первый урок позволяет начертить два взаимно перпендикулярных отрезка с высокой точностью. Недостаток применения циркуля заключается в наличии вспомогательных линий, которые стереть сложно. Написать о взаимном расположении линий можно в описательной записке.

Трехмерное пространство

В начертательной геометрии линии всегда находятся в двухмерном пространстве. В специальных программах можно начертить отрезки в трехмерном пространстве. Подобное взаимное расположение может выглядеть следующим образом:

Два отрезка перпендикулярны относительно друг друга в случае, если они параллельны другим взаимно перпендикулярным линиям, лежащим в одной плоскости.
Показать правильное взаимное расположение можно путем обозначения угла. Для этого применяются различные способы.
Если две линии лежат в одной плоскости, то они взаимно перпендикулярны при образовании четырех прямых углов.

В жизни подобное расположение прямых встречается крайне часто. Проверить угол можно при применении специальных инструментов.

Четырехмерная система координат и лемма

Некоторые программы работают с четырехмерным пространством. Взаимное расположение плоскостей под прямым углом в этом случае имеет два смысла: они могут быть перпендикулярны в трехмерном смысле при образовании двугранного угла 90°.

Рассматриваться взаимное расположение плоскостей может и в 4-мерном смысле. Условия выглядят следующим образом:

Они должны пересекаться в точке.
Любые две линии, проведенные в плоскостях через точку пересечения также могут быть перпендикулярными.

Условия четырехмерного пространства определяют то, что через одну точку можно провести 6 взаимно перпендикулярных плоскостей. Определять их взаимное расположение можно несколькими различными способами.

Лемма, касающаяся перпендикулярности, связана с определением параллельности. Если одна из параллельных линий расположена под прямым углом относительно плоскости или отрезка, то вторая также перпендикулярна. Ответ на многие задачи связан с доказательством леммы:

Даны два параллельных отрезка а и b, а также с. Задача заключается в доказательстве b ⊥ c при условии, что a ⊥ c.
Через произвольную точку М проводится третий и четвертый отрезок, которые параллельны прямой а и с. Образующийся угол АМС равен 90°.
Параллельны b и a при условии, что третий дополнительный отрезок параллелен отрезку а. В этом случае он будет параллелен и b.

При соблюдении условий полученный угол будет являться прямым. С учетом проведенных построений можно сформулировать определение перпендикулярности параллельных отрезков.

Применение термина

Как ранее было отмечено, встречается большое количество примеров применения рассматриваемого термина. На основе теоремы и доказательства были созданы различные формулы, позволяющие определить протяженность одного из сторон геометрической фигуры.

В средних и старших классах встречается большое количество задач, связанных с определением угла и протяженности сторон построенной фигуры. В некоторых случаях проводится построение диагонали, которая делит 90° на две равные части.

В жизни взаимное перпендикулярное расположение плоскостей встречается крайне часто. Примером служат несущие элементы различных сооружений. Подобное расположение позволяет правильно распределить оказываемую нагрузку. Править наклон можно путем применения специальных измерительных инструментов.

Многие геометрические фигуры построены на основе перпендикулярного расположения отрезков. Наиболее распространен параллелограмм или квадрат, треугольник. За счет выдерживания правильного угла обеспечивается также взаимное параллельное расположение сторон.

Приведенная выше информация указывает на то, что определение угла, под которым расположены плоскости, проводится в самых различных сферах. Инженеры и строители должны с высокой точностью контролировать этот показатель.

Источник

7.2.1 Взаимно перпендикулярные прямые.

Пример:
Через точку А провести прямуюm,
перпендикулярную горизонтали h
( рис 7.4 ).

Так одна из сторон
h прямого угла, параллельна плоскости
H, то на эту плоскость спроецируется
без искажения. Поэтому через А
проводим горизонтальную проекцию
mh’.
Отмечаем точку M=
m

h.
Затем находим М(M»h
), Точки М¹¹и А
определяют m.

Если вместо
горизонтали будет задана фронталь и,
то геометрические построения по
проведению прямой mlu
аналогичны только что рассмотренному
случаю, с той лишь разницей, что построение
неискаженной проекции прямого угла
следует начинать с фронтальной проекции.

7.2.2.Взаимно перпендикулярные прямая и плоскость

Прямая
перпендикулярна к плоскости, если она
перпендикулярна к двум пересекающимся
прямым, принадлежащим данной плоскости.

Если в плоскости
взять не произвольные пересекающиеся
прямые, а горизонталь и фронталь, то
появляется возможность и в этом случае
воспользоваться известной теоремой о
проецировании прямого угла,

Пример 1. Восстановить
в вершине А перпендикуляр AD
к плоскости треугольника АВС (рис 7.5 ).

Рис.7.5. Рис.7.6

Для того, чтобы
определить направление проекций
перпендикуляра, проводим проекции
горизонтали h и фронтали 
плоскости треугольника АВС. Затем в
точке А
восставляем перпендикуляр к h,
a
в А‘
перпендикуляр к ,

Пример 2. Из точки
А опустить перпендикуляр АВ на плоскость

заданную следами (рис 7.6 ).

Для решения этой
задачи достаточно из А
провести горизонтальную проекцию
AВ_,
а из А
— ее фронтальную проекцию A»
В_v.

7.2.3. Взаимно перпендикулярные плоскости

Две плоскости
взаимно перпендикулярны, если одна из
них содержит прямую, перпендикулярную
к другой плоскости.

Поэтому построение
плоскости ,
перпендикулярной к плоскости
,
можно
осуществить двумя путями;

1. Проводим прямую
m,
перпендикулярную к плоскости 
(или ),
затем прямую m
заключаем в плоскость 
(или ).

2. Проводим прямую
n,
принадлежащую или параллельную плоскости

(или ),
затем строим плоскость 
(или),
перпендикулярно к прямой n.

Так
как через прямуюm
можно провести множество плоскостей
(первый путь решения), то задача имеет
множество решений. То же самое происходит
и при решении по второму пути ( в плоскости
или параллельно ей можно провести
множество прямых n).
Чтобы конкретизировать задачу, необходимо
указать дополнительные условия.

Пример 1. Чрез
данную прямую а провести плоскость ,
перпендикулярную к плоскости
,
заданной параллельными прямыми 1 и f
(рис.7.7.).

Рис 7.7

1. Определяем
направление проекций перпендикуляра
к плоскости .
для этого находим горизонтальную
проекцию горизонтали h’
и фронтальную проекцию фронтали ,

2. Из проекции
произвольной точки Аеа проводим проекции
перпендикуляра m’h’
и m.
Плоскость ,
т.к m

Пример
2.Через данную точку А провести
горизонтально проецирующую плоскость
,
перпендикулярную к плоскости ,
заданной следами (рис.7.8)

Искомая
плоскость рдолжна проходить перпендикулярно
к прямой, принадлежащей плоскости 
В связи с тем, что плоскость 
должна быть горизонтально проецирующей,
то прямая, перпендикулярная к ней ,
должна быть параллельна плоскости H,
т.е. являться горизонталью плоскости
а или (что тоже самое) горизонтальным
следом этой плоскости — _н.
Поэтому через горизонтальную проекцию
точки Апроводим
горизонтальный след _н_н,
фронтальный
след vоси
X.

7.3.
Определение действительной величины
угля между прямой и плоскостью. Между
двумя плоскостями

У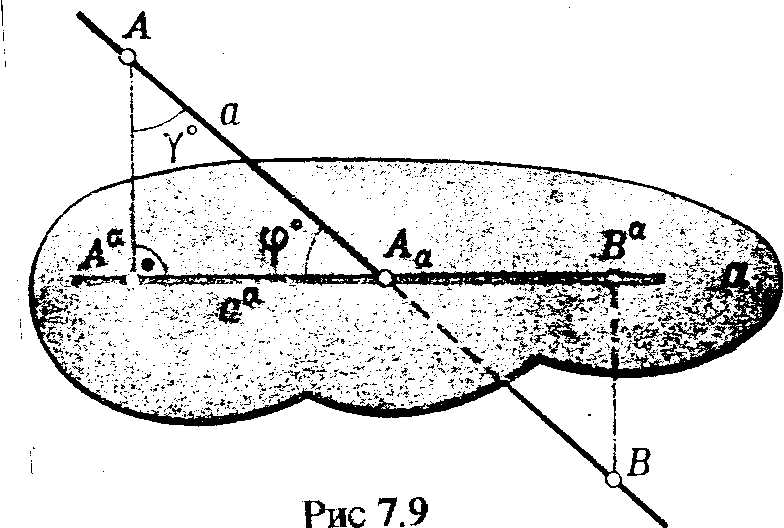глом
между прямой и плоскостью называется
угол между этой прямой и ее проекцией
на данную плоскость (прямая не
перпендикулярна плоскости).

Пространственная
геометрическая модель, иллюстрирующая
это
определение, показана на рис 7.9 .

План решения
задачи может быть, записан:

1 .Из произвольной
точки А
опускаем перпендикуляр на плоскость;

2. Определяем точку
встречи этого перпендикуляра с плоскостью
(точка
А^
ортогональная проекция точки А на
плоскость );

3.Находим точку
пересечения прямой 
с плоскостью а (точка А_—
след прямой а на плоскости );

4.Проводим (А°А_)-
проекдию прямой а на плоскость ;

5.Определяем
действительную величинуАА_А^,т.е.⁰.
Решение этой задачи может быть значительно
упрощено, если определять не ⁰между
прямой и плоскостью, а дополнительный
до 90° °
В этом случае отпадает необходимость
в определении точки А^
и

проекции а_Зная
величину у⁰
, вычисляем— ⁰=90-⁰.

Мерой угла
между двумя плоскостями служит линейный
угол, образованный двумя прямыми —
сечениями граней этого угла плоскостью,
перпендикулярной к их ребру.

Дня
построения линейного угла, являющегося
мерой двухгранного угла, необходимо
выполнить следующие графические
построения, показанные на рис 7.10 в
определенной последовательности,

1. Определяем
прямую n
— линию пересечения данных плоскостей

и 
(п=
);

2. Проводим плоскость
n
(эта плоскость будет перпендикулярна
также и к плоскостям и
;

3. Определяем
прямые a=
и b=

;

4. Находим
действительную величину °
между прямыми а и b

.
⁰—
искомый угол

7.4.Паралельность
прямых, прямой и плоскости.

Параллельность
плоскостей.

7.4.1.
Параллельные прямые.

Если
в пространстве прямые параллельны, то
их одноименные

проекции также
параллельны между собой.

аbа
b;
а
b;
а
b

Причем,
если в пространстве прямые а , b
занимают общее положение относительно
плоскостей проекций, то для выяснения
по эпюру вопроса о параллельности
прямых достаточно убедиться, будут ли
параллельны между собой их одноименные
проекции только на двух плоскостях.

Параллельность
проекции на третьей
плоскости в этом
случае автоматы чески удовлетворяется.

Если прямые
параллельны какой- либо плоскости (хотя
бы плоскости W),
то условие параллельности на третьей
плоскости может не выполняться, В этом
случае, для выяснения вопроса будут ли
прямые параллельны в пространстве,
условие параллельности их одноименных
горизонтальных и фронтальных проекций
будет необходимым, но недостаточным.
Для получения ответа следует убедиться
в параллельности их профильных проекций.

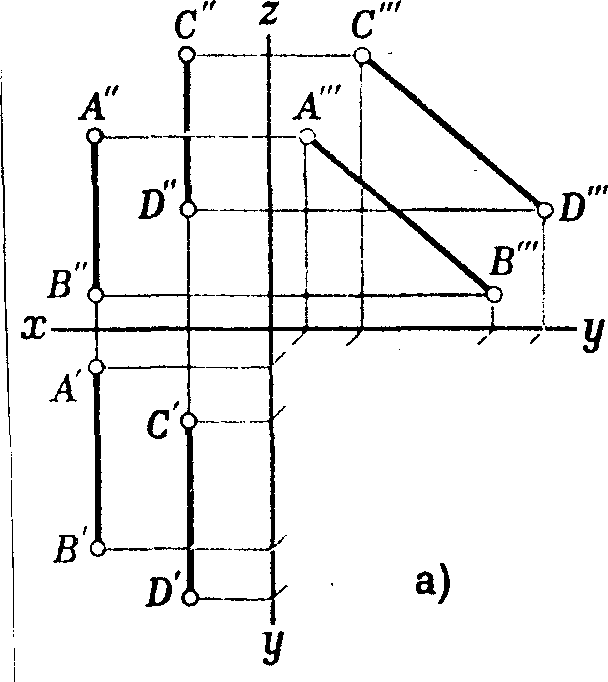
На рис 7.11 показаны
два возможных варианта взаимного
расположения прямых АВ и CD.

Рис 7.11

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Геометрия

7 класс

Урок № 7

Перпендикулярные прямые

Перечень рассматриваемых вопросов:

Перпендикулярные прямые.
Способы построения прямых углов на местности.
Экер.
Теодолит.
Свойство перпендикулярных прямых.

Тезаурус:

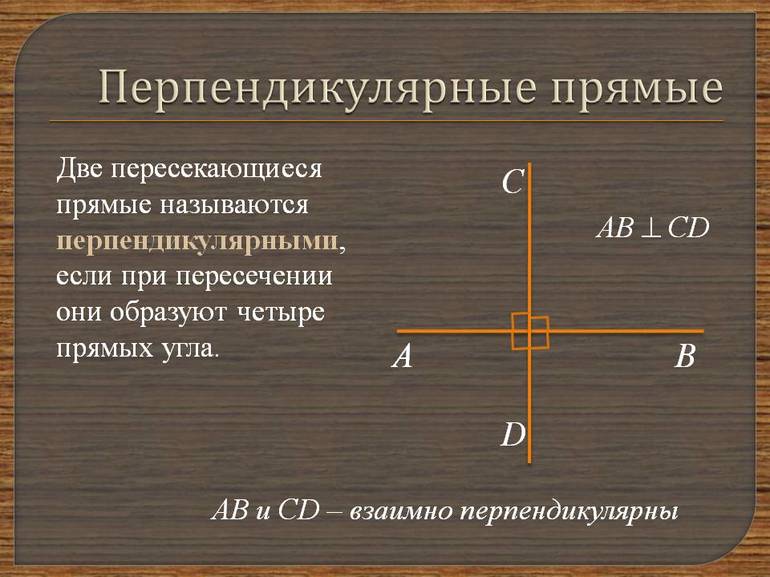
Две пересекающиеся прямые называются перпендикулярными (или взаимно перпендикулярными), если они образуют при пересечении четыре прямых угла.

Основная литература:

Атанасян Л. С. Геометрия: 7–9 класс. // Атанасян Л. С., Бутузов В. Ф., Кадомцев С. Б. – М.: Просвещение, 2017. – 384 с.

Дополнительная литература:

Атанасян Л. С. Геометрия: Методические рекомендации 7 класс. // Атанасян Л. С., Бутузов В. Ф., Глазков Ю. А. и др. – М.: Просвещение, 2019. – 95 с.
Зив Б. Г. Геометрия: Дидактические материалы 7 класс. // Зив Б. Г., Мейлер В. М. – М.: Просвещение, 2019. – 127 с.
Мищенко Т. М. Дидактические материалы и методические рекомендации для учителя по геометрии 7 класс. // Мищенко Т. М., – М.: Просвещение, 2019. – 160 с.
Атанасян Л. С. Геометрия: Рабочая тетрадь 7 класс. // Атанасян Л. С., Бутузов В. Ф., Глазков Ю. А., Юдина И. И. – М.: Просвещение, 2019. – 158 с.
Иченская М. А. Геометрия: Самостоятельные и контрольные работы 7–9классы. // Иченская М. А. – М.: Просвещение, 2019. – 144 с.

Теоретический материал для самостоятельного изучения

Ранее вы уже познакомились с прямыми и выяснили, что они могут пересекаться или не пересекаться.

Сегодня мы продолжим изучать пересекающиеся прямые, которые являются перпендикулярными.

Введём понятие «перпендикулярные прямые».

Для этого рассмотрим две пересекающиеся прямые а и b. Они образуют четыре неразвёрнутых угла. Если один из этих углов будет прямой, то остальные тоже будут прямые, т.к.

∠1 и ∠2 – смежные (по определению смежных углов),

∠1 +∠2=180°(по свойству смежных углов),

∠2=180° – 90° = 90°,

∠1 =∠ 3 = 90° – вертикальные (по свойству вертикальных углов),

∠2 =∠ 4 = 90° – вертикальные (по свойству вертикальных углов).

Обозначение перпендикулярных прямых:

а ┴ b

Построим перпендикулярные прямые.

Для этого воспользуемся чертёжным угольником и линейкой, как изображено на рисунке.

Рассмотрим свойство перпендикулярных прямых.

Две прямые, перпендикулярные к третьей, не пересекаются.

Дано:

АА₁┴РQ

ВВ₁┴РQ.

Доказать: АА₁и ВВ₁не пересекаются.

Доказательство.

Рассмотрим прямые АА₁ и ВВ₁, перпендикулярные к прямой РQ. Мысленно перегнем плоскость по прямой РQтак, чтобы верхняя часть рисунка наложилась на нижнюю. Так как прямые углы 1 и 2 равны, то луч РА наложится на луч РА₁, аналогично, луч QB наложится на луч QB₁.

Предположим, что прямые АА₁ и ВВ₁пересекаются в точке М.

Мысленно перегнем плоскость по прямой РQ, точка М накладывается на точку М₁.

Через точки М и М₁проходят две прямые АА₁ и ВВ₁, что неверно. Следовательно, предположение, что прямые АА₁и ВВ₁ пересекаются в точке М, невозможно (по аксиоме о взаимном расположении точек и прямых), следовательно, прямые АА₁и ВВ₁ один не пересекаются. Что и требовалось доказать.

Данный метод доказательства называют методом от противного. Суть этого метода заключается в том, что предполагают противоположное тому, что требуется доказать. Исходя из предположения, путём рассуждений приходят к противоречию.

Этим методом можно воспользоваться для доказательства теоремыо единственности перпендикуляра к прямой.

Из точки, не лежащей на прямой, можно провести не более одного перпендикуляра к этой прямой.

Доказательство. Пустьточка не лежит на данной прямой a. Докажем, что из точки A нельзя провести два перпендикуляра к прямой a. Предположим, что из точки A можно провести два перпендикуляра AH и AK к прямой a. Мысленно перегнем плоскость по прямойaтак, чтобы полуплоскость с границей a, содержащая точку A, наложилась на другую полуплоскость. При этом точки H и K остаются на месте, точка A накладывается на некоторую точку B. Получается, что отрезки AH и AK накладываются на отрезки BH и BK.

Углы AHB и AKB – развернутые, так как каждый из них равен сумме двух прямых углов. Поэтому точки A, H и B лежат на одной прямой, и также точки A, K и B лежат на одной прямой.

Таким образом, мы получили, что через точки A и B проходят две прямые AH и AK. Но это невозможно (по аксиоме о взаимном расположении точек и прямых). Следовательно, из точки A можно провести единственный перпендикуляр к прямой а.

Итак, сегодня получили представление о том, что такое перпендикулярные прямые, рассмотрели свойства перпендикулярных прямых, научились строить и обозначать перпендикулярные прямые, узнали о методе доказательства от противного.

Рассмотрим более сложный метод построения прямых углов на местности.

Для построения прямых углов на местности применяют специальные приборы, например, теодолит (в геодезии).

Но самый простой прибор для построения прямых углов на местности – это экер. Он состоит из двух брусков расположенных под углом 90° и укреплённых на треножнике. На концах брусков вбиты гвоздитак, что прямые, проходящие через них, перпендикулярны. Рассмотрим, как с его помощью построить прямые углы. На заданном луче, в нашем случае ОА, устанавливают экер так, что отвес находится точно над точкойО, а направление одного из брусков совпадает с лучом ОА, совмещение помогает осуществить веха, поставленная на луче ОА. Далее провешивают прямую с помощью другого бруска, получается ∠АОВ =90°.

Тренировочные задания.

1. Прямые СА и ВD взаимно перпендикулярны и пересекаются в точке О. Луч ОК – проведён из вершины прямого угла АОВ, так что∠КОВ = 52°. Найдите градусную меру ∠АОК.

Решение: нарисуем рисунок, исходя из условия задачи:

∠АОВ = 90°;

∠АОВ = ∠КОВ +∠АОК, следовательно, ∠АОК = ∠АОВ – ∠КОВ = 90° – 52° = 38°.

Ответ: ∠АОК = 38°.

2. Прямые СО и ОD взаимно перпендикулярны, найдите ∠МОВ, если ∠МОА = ∠СОА = 25°, ∠ВОD= ∠МОВ.

Решение. Т.к. прямые СО и ОD взаимно перпендикулярны, то ∠СОD = 90°

По условию задачи, ∠МОА = ∠СОА = 25°, ∠ВОD = ∠МОВ.

∠ СОD = ∠МОА + ∠СОА + ∠ВОD + ∠МОВ = 25° + 25° +2·∠МОВ = 50° + 2 · ∠МОВ = 90°

50° + 2 · ∠МОВ = 90°

∠МОВ = (90° – 50°) : 2

∠МОВ = 20°

Ответ: 20°.

Источник

Свойства перпендикулярности необходимо знать, так как большинство задач сводится к его проверке для последующего решения. Бывают случаи, когда о перпендикулярности идет речь еще в условии задания или когда необходимо пользоваться доказательством.

‍Угол с градусной мерой 90° называется прямым. Если угол меньше 90°, его называют острым, а если больше 90° — тупым. Угол, равный 180° (то есть образующий прямую линию), называют развернутым.

Два угла с одной общей стороной называются смежными.

На рисунке луч ОС делит развёрнутый ∡AOB =180° на две части, образуя тупой ∡1 и острый ∡2.

∡1 + ∡2 = 180°

Сумма смежных углов составляет 180°.

Поэтому если один из смежных углов прямой, то второй также оказывается прямым: 180° – 90° = 90°.

При пересечении двух прямых образуются четыре угла:

Обе стороны ∡1 также являются сторонами ∡3, а стороны ∡2 продолжают стороны ∡4. Такие углы называют вертикальными.

∡1 и ∡2 — смежные, как и ∡1 и ∡4. Следовательно:

∡1 + ∡2 = 180°

∡1 + ∡4 = 180°

∡2 = ∡4

То же справедливо и для ∡1 и ∡3.

Вертикальные углы равны.

Прямые, пересекающиеся под прямым углом, называются перпендикулярными.

∡1 равен 90°, остальные углы оказываются для него либо смежными, либо вертикальными, а значит, тоже равными 90°.

Перпендикулярность прямых принято обозначать так: a⟂b

Для того, чтобы доказать перпендикулярность достаточно, чтобы угол между прямыми был прямым. Для того, чтобы определить их перпендикулярность при известных уравнениях прямоугольной системы координат, необходимо применить необходимое и достаточное условие перпендикулярности прямых. Рассмотрим формулировку.

Теорема

Для того, чтобы прямые a и b были перпендикулярными, необходимо и достаточно, чтобы направляющий вектор прямой обладал перпендикулярностью относительно направляющего вектора заданной прямой b . Само доказательство основывается на определении направляющего вектора прямой и на определении перпендикулярности прямых.

Доказательство

Пусть введена прямоугольная декартова система координат Оху с заданными уравнениями прямой на плоскости, которые определяют прямые a и b. Направляющие векторы прямых a и b обозначим →a и →b. Из уравнения прямых a и b необходимым и достаточным условием является перпендикулярность векторов →a и →b. Это возможно только при скалярном произведении векторов →a=(ax, ay) и →b=(bx, by) равном нулю, а запись имеет вид (→a, →b)=ax⋅bx+ay⋅by=0. Получим, что необходимым и достаточным условием перпендикулярности прямых a и b, находящихся в прямоугольной системе координат Оху на плоскости, является (→a, →b)=ax⋅bx+ay⋅by=0, где →a=(ax, ay) и →b=(bx, by) — это направляющие векторы прямых a и b.

При рассмотрении того, какие прямые называют перпендикулярными, нужно уделить внимание свойствам. Они выглядят следующим образом:

Через одну точку А можно провести только одну перпендикулярную линию основному отрезку, остальные линии будут наклонными и могут скрещиваться.

Несколько перпендикуляров никогда не будут между собой пересекаться.

Для обозначения перпендикуляра применяется знак «⊥». В подобном случае угол составляет 90°. На чертеже пересечение обозначается своеобразным квадратом, которые рисуется от двух пересекающихся линий.

Условие перпендикулярности прямых

Условием перпендикулярности (ортогональности) двух прямых на плоскости, заданных уравнениями:

y1=k1x+b1

y2=k2x+b2

служит соотношение

k2·k2= −1

или k2= —

т.е. угловые коэффициенты k1, k2 обратны по величине и противоположны по знаку и это значит, что прямые перпендикулярны, а если произведение угловых коэффициентов не равно -1, то прямые не перпендикулярны.

Если две прямые представлены следующими уравнениями

A1x+B1y+C1 = 0

A2x+B2y+C2 = 0

то условием их перпендикулярности (уравнение перпендикулярной прямой) есть

A1A2+B1B2 = 0

Пример

Прямые 2x+3y=7 и 3x-2y=4 перпендикулярны, так как A1=2, A2=3, B1=3, B2=-2, следовательно

A1A2+B1B2 = 3*2 + 3*(-2) = 0

Доказательство взаимного расположения

Необходимое и достаточное условие перпендикулярности заключается в теореме:

Прямые взаимно перпендикулярны в случае, если направляющие векторы прямых перпендикулярны.
Доказательство связано с определением направления векторов, любой должен быть перпендикулярен.

Определение перпендикулярности прямой и плоскости

Доказать перпендикулярность можно проведя геометрические построения.

Признаки расположения плоскости и прямой под углом 90° заключаются в следующем:

Если прямая перпендикулярна плоскости, то в ней можно отложить другую прямую, лежащую под углом 90°.
В одной точке под прямым углом может пересекаться только две линии, значит, будет лежать только одна плоскость.

Отрезки могут быть также параллельными. В этом случае нет точки, в которой будут они пересекаться.

Построение перпендикуляра

Выдержать угловой коэффициент можно различным образом. В большинстве случаев для этого нужно иметь при себе циркуль.

Построить перпендикуляр можно следующим образом:

С помощью циркуля проводится построение полуокружности с центром в точке Х. На основном отрезке в результате этого получается две точки А и В. Для отображения полуокружности применяется другой цвет, полученная линия вспомогательная, поэтому не выделяется жирным.
С точки А и В проводится откладывание двух полуокружностей, пересекающихся в двух местах по касательной. Данные точки (P и Q) используются для откладывания линии, которая может пересечь их и основной отрезок с ранее отложенными точками А и В.

Построение проводится следующим образом:

Одна из сторон, смежная с прямым углом, прикладывается к проведенному отрезку. На этом этапе главное — правильно совместить поверхность инструмента с ранее отложенной линией. Незначительное отклонение может привести к изменению угла.
Проводится откладывание вертикального отрезка.

Трехмерное пространство

В начертательной геометрии линии всегда находятся в двухмерном пространстве. В специальных программах можно начертить отрезки в трехмерном пространстве.

Подобное взаимное расположение может выглядеть следующим образом:

Два отрезка перпендикулярны относительно друг друга в случае, если они параллельны другим взаимно перпендикулярным линиям, лежащим в одной плоскости. Показать правильное взаимное расположение можно путем обозначения угла. Для этого применяются различные способы. Если две линии лежат в одной плоскости, то они взаимно перпендикулярны при образовании четырех прямых углов.

В жизни подобное расположение прямых встречается крайне часто. Проверить угол можно при применении специальных инструментов.

Четырехмерная система координат и лемма

Рассматриваться взаимное расположение плоскостей может и в 4-мерном смысле.

Условия выглядят следующим образом:

Они должны пересекаться в точке.
Любые две линии, проведенные в плоскостях через точку пересечения также могут быть перпендикулярными.

Ответ на многие задачи связан с доказательством леммы:

Даны два параллельных отрезка а и b, а также с. Задача заключается в доказательстве b ⊥ c при условии, что a ⊥ c.
Через произвольную точку М проводится третий и четвертый отрезок, которые параллельны прямой а и с. Образующийся угол АМС равен 90°.
Параллельны b и a при условии, что третий дополнительный отрезок параллелен отрезку а. В этом случае он будет параллелен и b.

Если соблюдены все условия, полученный угол будет являться прямым. С учетом проведенных построений можно сформулировать определение перпендикулярности параллельных отрезков.

Как применяется термин «Взаимно перпендикулярные прямые»

Ранее мы уже упоминали о том, что встречается большое количество примеров применения рассматриваемого термина. На основе теоремы и доказательства были созданы различные формулы, позволяющие определить протяженность одного из сторон геометрической фигуры.

В жизни взаимное перпендикулярное расположение плоскостей встречается достаточно часто. Примером служат несущие элементы различных сооружений. Подобное расположение позволяет правильно распределить оказываемую нагрузку. Править наклон можно путем применения специальных измерительных инструментов.

Источник