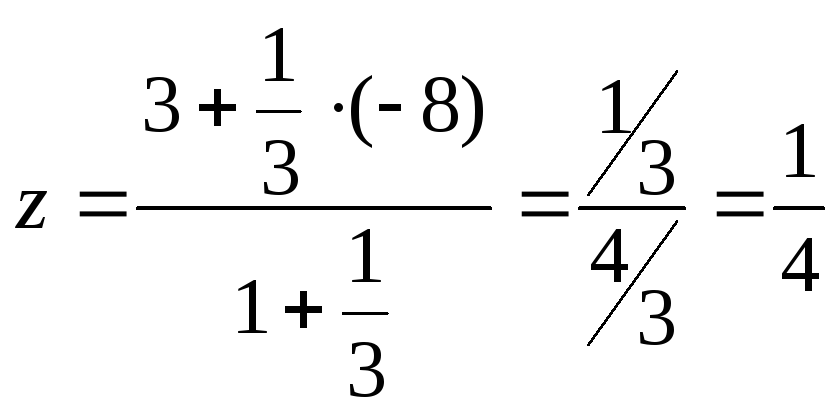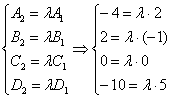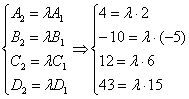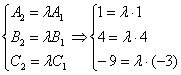Как найти взаимное расположение двух плоскостей - Исправление недочетов и поиск решений вместе с Examum.ru

Взаимное расположение плоскостей

Параллельные плоскости

Получим условия параллельности или совпадения двух плоскостей $rho_{1}$ и $rho_{2}$ заданных общими уравнениями:

$rho_{1}colon,A_{1}cdot x+B_{1}cdot y+C_{1}cdot z+D_{1}=0; quad rho_{2}colon,A_{2}cdot x+B_{2}cdot y+C_{2}cdot z+D_{2}=0,.$

(4.23)

Необходимым и достаточным условием параллельности или совпадения плоскостей (4.23) является условие коллинеарности их нормалей $vec{n}_{1}=A_{1}cdotvec{i}+B_{1}cdotvec{j}+C_{1}cdotvec{k},$ $vec{n}_{2}=A_{2}cdotvec{i}+B_{2}cdotvec{j}+C_{2}cdotvec{k}.$ Следовательно, если плоскости (4.23) параллельны или совпадают, то $vec{n}_{1}parallelvec{n}_{2}$ т.е. существует такое число lambdane0 что

$vec{n}_{1}=lambdacdotvec{n}_{2} quad Leftrightarrow quad begin{cases}A_{1}=lambdacdot A_{2},\ B_{1}=lambdacdot B_{2},\ C_{1}=lambdacdot C_{2}.end{cases}$ и наоборот.

Плоскости совпадают, если помимо этих условий справедливо $D_{1}=lambda D_{2}.$ Тогда первое уравнение в (4.23) имеет вид $lambda(A_{2}x+B_{2}y+C_{2}z+D_{2})=0$ т.е. равносильно второму, поскольку lambdane0.

Таким образом, плоскости (4.23) параллельны тогда и только тогда, когда соответствующие коэффициенты при неизвестных в их уравнениях пропорциональны, т.е. существует такое число lambdane0, что $A_{1}=lambda A_{2},$ $B_{1}=lambda B_{2},$ $C_{1}=lambda C_{2},$ но $D_{1}nelambda D_{2}.$ Плоскости (4.23) совпадают тогда и только тогда, когда все соответствующие коэффициенты в их уравнениях пропорциональны: $A_{1}=lambda A_{2},$ $B_{1}=lambda B_{2},$ $C_{1}=lambda C_{2}$ и $D_{1}=lambda D_{2}.$

Условия параллельности и совпадения плоскостей (4.23) можно записать в виде

$rho_{1}parallelrho_{2} quad Leftrightarrow quad frac{A_{1}}{A_{2}}= frac{B_{1}}{B_{2}}= frac{C_{1}}{C_{2}}nefrac{D_{1}}{D_{2}}; quad rho_{1}equivrho_{2} quad Leftrightarrow quad frac{A_{1}}{A_{2}}= frac{B_{1}}{B_{2}}= frac{C_{1}}{C_{2}}= frac{D_{1}}{D_{2}},.$

Отсюда следует критерий параллельности или совпадения двух плоскостей (4.23):

$rho_{1}parallelrho_{2}$ или $rho_{1}equivrho_{2} quad Leftrightarrow quad operatorname{rang}! begin{pmatrix}A_{1}&B_{1}&C_{1}\A_{2}&B_{2}&C_{2}end{pmatrix}=1.$

Поверхности уровня линейного четырехчлена

Семейство параллельных плоскостей

Поверхностью уровня функции f(x,y,z) трех переменных называется геометрическое место точек координатного пространства Oxyz, в которых функция принимает постоянное значение, т.е. f(x,y,z)=text{const}.

Для линейного четырехчлена p(x,y,z)=Ax+By+Cz+D уравнение поверхности уровня p(x,y,z)=text{const}. имеет вид

Acdot x+Bcdot y+Ccdot z+D=text{const}.

(4.24)

При любом фиксированном значении постоянной уравнение (4.24) описывает плоскость. Рассмотрим поведение семейства поверхностей уровня, отличающихся значением постоянной. Поскольку коэффициенты A,,B и не изменяются, то у всех плоскостей (4.24) будет одна и та же нормаль vec{n}=Avec{i}+Bvec{j}+Cvec{k}. Следовательно, поверхности уровня линейного четырехчлена P(x,y,z)=Ax+By+Cz+D D представляют собой семейство параллельных плоскостей (рис.4.19). Поскольку нормаль совпадает с градиентом (см. пункт 3 замечаний 4.2), а градиент направлен в сторону наискорейшего возрастания функции, то при увеличении постоянной поверхности уровня (4.24) переносятся параллельно в направлении нормали.

Пересекающиеся плоскости

Необходимым и достаточным условием пересечения двух плоскостей (4.22) является условие неколлинеарности их нормалей, или, что то же самое, условие непропорциональности коэффициентов при неизвестных:

$operatorname{rang}!begin{pmatrix}A_{1}&B_{1}&C_{1}\A_{2}&B_{2}&C_{2}end{pmatrix}=2.$

(4.25)

При этом условии система уравнений

$begin{cases}A_{1}cdot x+B_{1}cdot y+C_{1}cdot z+D_{1}=0,\ A_{2}cdot x+B_{2}cdot y+C_{2}cdot z+D_{2}=0end{cases}$

имеет бесконечно много решений, которые определяют прямую пересечения плоскостей, заданных уравнениями (4.23).

Угол между плоскостями

Угол между двумя плоскостями можно определить как угол между их нормальными векторами. По этому определению получаются не один угол, а два смежных угла, дополняющих друг друга до pi. В элементарной геометрии из двух смежных углов, как правило, выбирается меньший, т.е. величина varphi угла между двумя плоскостями удовлетворяет условию $0leqslantvarphileqslantfrac{pi}{2}.$

Если $vec{n}_{1}= A_{1}vec{i}+B_{1}vec{j}+C_{1}vec{k},~ vec{n}_{2}= A_{2}vec{i}+B_{2}vec{j}+C_{2}vec{k}$ — нормали к плоскостям $rho_{1}$ и $rho_{2}$ соответственно (рис.4.20,а), то величина varphi угла между этими плоскостями вычисляется по формуле:

$cosvarphi=frac{|,langle,vec{n}_{1},vec{n}_{2},rangle,|}{|vec{n}_{1}|cdot|vec{n}_{2}|}=frac{|A_{1}cdot A_{2}+B_{1}cdot B_{2}+C_{1}cdot C_{2}|}{sqrt{A_{1}^2+B_{1}^2+C_{1}^2}cdotsqrt{A_{2}^2+B_{2}^2+C_{2}^2}},.$

Необходимым и достаточным условием перпендикулярности плоскостей (4.23) является условие ортогональности их нормалей, т.е. $langle,vec{n}_{1},vec{n}_{2},rangle=0:$

$A_{1}cdot A_{2}+B_{1}cdot B_{2}+C_{1}cdot C_{2}=0,.$

При пересечении двух плоскостей образуются четыре двугранных угла (рис.4.20). Величина varphi двугранного угла удовлетворяет условию 0<varphi<pi,.

Двугранные углы, образуемые пересечением двух плоскостей

По формуле

$cosvarphi=frac{langle,vec{n}_{1},vec{n}_{2},rangle}{|vec{n}_{1}|cdot|vec{n}_{2}|}=frac{A_{1}cdot A_{2}+B_{1}cdot B_{2}+C_{1}cdot C_{2}}{sqrt{A_{1}^2+B_{1}^2+C_{1}^2}cdotsqrt{A_{2}^2+B_{2}^2+C_{2}^2}}$

(4.26)

получаем острый двугранный угол varphi , образованный плоскостями (4.23), если $A_{1}A_{2}+B_{1}B_{2}+C_{1}C_{2}>0$ (рис.4.20,а), и тупой в противном случае: $A_{1}A_{2}+B_{1}B_{2}+C_{1}C_{2}<0$ (рис.4.20,б). Другими словами, по формуле (4.26) находится тот двугранный угол, образованный плоскостями, в котором лежат точки, принадлежащие разноименным полупространствам, определяемым данными плоскостями. На рис.4.20 изображены пересекающиеся плоскости, положительные и отрицательные полупространства отмечены знаками + или – соответственно.

Пример 4.10. Найти величину того угла, образованного плоскостями $rho_{1}colon5x-3y+4z-3=0$ и $rho_{2}colon2x+y+2z+4=0,$ внутри которого лежит точка M(5;2;1).

Решение. По уравнениям плоскостей находим нормали $vec{n}_{1}=5vec{i}-3vec{j}+4vec{k},$ $vec{n}_{2}=2vec{i}+vec{j}+2vec{k},$ а также величину varphi угла между нормалями, используя (4.26):

$cosvarphi=frac{5cdot2+(-3)cdot1+4cdot2}{sqrt{5^2+(-3)^2+4^2}cdotsqrt{2^2+1^2+2^2}}=frac{15}{3sqrt{50}}=frac{1}{sqrt{2}} quad Leftrightarrow quad varphi=frac{pi}{4},.$

Подставляя координаты точки M(5;2;1) в левые части уравнений плоскостей, выясняем, каким полупространствам принадлежит эта точка. Для плоскости $rho_{1}$ имеем 5cdot5-3cdot2+4cdot1-3>0 значит, точка лежит в положительном полупространстве, определяемом плоскостью $rho_{1}.$ Для плоскости $rho_{2}$ имеем 2cdot5+2+2cdot1+4>0 значит, точка лежит также в положительном полупространстве, определяемом плоскостью $rho_{2}.$ Поскольку точка принадлежит одноименным полупространствам (положительным), то искомый угол — это угол psi, смежный найденному углу $varphi=frac{pi}{4}:$ $psi=pi-varphi=pi-frac{pi}{4}=frac{3pi}{4},.$

Пучки плоскостей

Собственные и несобственные пучки плоскостей

Собственным пучком плоскостей называется совокупность всех плоскостей, проходящих через фиксированную прямую (ось пучка).

Несобственным пучком плоскостей называется совокупность плоскостей, параллельных фиксированной плоскости (осью несобственного пучка плоскостей считается бесконечно удаленная прямая).

Любые две плоскости $rho_{1}$ и $rho_{2}$ определяют пучок плоскостей, содержащий заданные плоскости $rho_{1}$ и $rho_{2}.$ Если плоскости $rho_{1}$ и $rho_{2}$ пересекаются, то прямая пересечения является осью собственного пучка (рис.4.21,а). Если плоскости $rho_{1}$ и $rho_{2}$ параллельны, то они определяют несобственный пучок параллельных плоскостей (рис.4.21,б).

Пусть заданы уравнения двух плоскостей (4.23):

$rho_{1}colon~A_{1}cdot x+B_{1}cdot y+C_{1}cdot z+D_{1}=0; quad rho_{2}colon~A_{2}cdot x+B_{2}cdot y+C_{2}cdot z+D_{2}=0.$

Линейной комбинацией этих уравнений называется уравнение

$lambda_{1}cdot(A_{1}cdot x+B_{1}cdot y+C_{1}cdot z+D_{1})+lambda_{2}cdot(A_{2}cdot x+B_{2}cdot y+C_{2}cdot z+D_{2})=0,$

(4.27)

где числа $lambda_{1},,lambda_{2}$ — коэффициенты линейной комбинации. Его можно записать в форме

$(lambda_{1}cdot A_{1}+lambda_{2}cdot A_{2})cdot x+ (lambda_{1}cdot B_{1}+lambda_{2}cdot B_{2})cdot y+ (lambda_{1}cdot C_{1}+lambda_{2}cdot C_{2})cdot x+ lambda_{1}cdot D_{1}+lambda_{2}cdot D_{2}=0.$

Заметим, что линейная комбинация уравнений является уравнением первой степени для любых значений коэффициентов, кроме случая, когда все коэффициенты при неизвестных равны нулю, т.е. при одновременном выполнении условий

$lambda_{1}cdot A_{1}+lambda_{2}cdot A_{2}=0, quad lambda_{1}cdot B_{1}+lambda_{2}cdot B_{2}=0, quad lambda_{1}cdot C_{1}+lambda_{2}cdot C_{2}=0.$

Эти значения параметров $lambda_{1},,lambda_{2}$ считаются недопустимыми.

Уравнение (4.27) называется уравнением пучка плоскостей, содержащего плоскости

$A_{1}cdot x+B_{1}cdot y+C_{1}cdot z=0, quad A_{2}cdot x+B_{2}cdot y+C_{2}cdot z=0.$

При любых допустимых значениях параметров $lambda_{1},,lambda_{2}$ уравнение (4.27) задает плоскость, принадлежащую пучку, и наоборот, для любой плоскости пучка найдутся такие значения параметров $lambda_{1},,lambda_{2},$ что уравнение (4.27) будет задавать эту плоскость.

Доказательство утверждения аналогично доказательству свойства пучка прямых.

Пример 4.11. Составить уравнение плоскости, проходящей через прямую пересечения плоскостей 2x+2y-z+3=0, 6x-3y+2z+1=0 и через точку $M^{ast}(2;3;1).$

Решение. Искомая плоскость входит в пучок плоскостей, задаваемый уравнением (4.27)

$lambda_{1}cdot(2cdot x+2cdot y-z+3)+lambda_{2}cdot(6cdot x-3cdot y+2cdot z+1)=0.$

Подставляя координаты точки $M^{ast}(2;3;1),$ получаем:

$lambda_{1}cdot(2cdot2+2cdot3-1+3)+lambda_{2}cdot(6cdot2-3cdot3+2cdot1+1)=0 quad Leftrightarrow quad 12cdotlambda_{1}+6cdotlambda_{2}=0.$

Возьмем, например, $lambda_{1}=-1,~lambda_{2}=2$ и подставим в уравнение пучка:

-1cdot(2x+2y-z+3)+2cdot(6x-3y+2z+1)=0 quad Leftrightarrow quad 10x-8y+5z-1=0.

Итак, искомое уравнение получено.

Связки плоскостей

Собственные и несобственные связки плоскостей

Собственной связкой плоскостей называется совокупность всех плоскостей, проходящих через фиксированную точку (центр связки).

Несобственной связкой плоскостей называется совокупность плоскостей, параллельных фиксированной прямой (центром несобственной связки плоскостей считается бесконечно удаленная точка).

Уравнение собственной связки плоскостей с центром $M_{0}(x_{0},y_{0},z_{0})$ имеет вид

$Acdot(x-x_{0})+Bcdot(y-y_{0})+Ccdot(z-z_{0})=0,$

где A,,B,,C — произвольные параметры, одновременно не равные нулю.

Уравнение связки плоскостей (собственной (рис.4.22,а) или несобственной (рис.4.22,6)) можно получить в виде линейной комбинации уравнений трех плоскостей:

$lambda_{1}(A_{1}x+B_{1}y+C_{1}z+D_{1})+lambda_{2}(A_{2}x+B_{2}y+C_{2}z+D_{2})+lambda_{3}(A_{3}x+B_{3}y+C_{3}z+D_{3})=0,$

(4.28)

где $lambda_{1},,lambda_{2},,lambda_{3}$ — коэффициенты линейной комбинации. Заметим, что линейная комбинация уравнений является уравнением первой степени для любых значений коэффициентов, кроме случая, когда все коэффициенты при неизвестных равны нулю. Эти значения параметров $lambda_{1},,lambda_{2},,lambda_{3}$ считаются недопустимыми.

Уравнение (4.28) называется уравнением связки плоскостей, содержащей три плоскости

$A_{1}x+B_{1}y+C_{1}z+D_{1}=0, quad A_{2}x+B_{2}y+C_{2}z+D_{2}=0, quad A_{3}x+B_{3}y+C_{3}z+D_{3}=0.$

При любых допустимых значениях параметров $lambda_{1},,lambda_{2},,lambda_{3}$ уравнение (4.28) задает плоскость, принадлежащую связке, и наоборот, для любой плоскости связки найдутся такие значения параметров $lambda_{1},,lambda_{2},,lambda_{3},$ что уравнение (4.28) будет задавать эту плоскость.

Доказательство утверждения аналогично доказательству свойства пучка прямых.

Математический форум (помощь с решением задач, обсуждение вопросов по математике).

Кнопка "Поделиться"

Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.

Источник

Две
плоскости в пространстве могут
пересекаться, быть параллельными,
совпадать. Если
плоскости
пересекаются, то линией их пересечения
будет прямая, и плоскости образуют
двугранный угол, который измеряется
плоским углом ,
образованным
двумя
перпендикулярами,
лежащими на гранях угла и имеющими общую
вершину. Легко видеть (рис.3.6), что угол

между пересекающимися плоскостями (вид
сбоку) равен углу между нормальными
векторами этих плоскостей. Пусть даны
две плоскости

Нормальные
векторы этих плоскостей имеют координаты
соответственно
,Угол
находится по формуле

(3.5)

Отсюда
— условие перпендикулярности двух
плоскостей,

—
условие параллельности.

Пример
3.2.
Найти угол между плоскостями
,.

Решение.
Выпишем координаты нормальных векторов
плоскостей
,и
найдем угол между ними

следовательно,

,
то есть плоскости
взаимно
перпендикулярны.

Уравнение
первой степени с п
переменными
вида
называется
уравнением гиперплоскости
в
пространстве Rⁿ.
Геометрической интерпретации в Rⁿ
(n
> 3) оно не имеет.

3.3. Прямая в пространстве r3

Прямую
в пространстве можно задать несколькими
способами, например, двумя различными
точками, двумя пересекающимися
плоскостями. Зададим прямую при помощи
точкиМ₀,
через которую она пройдет, и направляющего
вектора,
который задает направление прямой.

Возьмем
на прямой (рис. 3.7)произвольную точку М
(x,y,z).
Очевидно, что векторы
иколлинеарные, то есть,
где
— некоторое число (см. формулу (2.1)). Так
как
,
то,
откуда, в силу равенства векторов,

или

Эти
три уравнения называют параметрическими
уравнениями прямой,
а число
– параметром.

Приравнивая левые
части, получим:

.
(3.6)

Эти
уравнения (их два) называются каноническими
уравнениями прямой.

Пример
3.4.
— канонические уравнения прямой,
проходящей через точкуМ₀(-4;
0; 7) в направлении, определяемом вектором
.

Если
даны уравнения двух прямых
и,
лежащих в одной или разных плоскостях,
то угол
между ними определяется углом между
направляющими векторами
и.
Таким образом,

(3.7)

Отсюда
легко получить условия перпендикулярности
и коллинеарностивекторови,
а значит и прямых.

Если
надо написать уравнение прямой, проходящей
через две данные точки
и,
то в качестве направляющего вектора
берется вектори его координаты представляются вместоm,n,p
в (3.6). А вместо
подставляются координаты одной из
данных точек, напримерМ₁.
Тогда получим уравнение

(3.8)

Пример
3.5.
найти
уравнение прямой, проходящей через
точки М₁(0;-4;5),
М₂(6;2;-7).

Решение.
Пользуясь формулой (3.8) составим уравнение
искомой прямой
или,
или.

3.4. Две важные задачи аналитической геометрии

Задача
1.
Найти длину отрезка

Пусть
отрезок
задан координатами концов:,.
Тогда длина отрезка тождественна длине
(модулю) вектора.
И потому для ее нахождения можно
пользоваться формулой (2.14).

Этой
же формулой можно пользоваться и в том
случае, когда один из концов отрезка не
фиксирован, а имеет текущие координаты
.
В этом случае.

Задача
2.
Разделить данный отрезок в заданном
отношении. Пусть в R³
дан отрезок прямой
(рис. 3.8.), координаты концов которого
известны:,.
Пусть— делящая точка с переменными координатами
изаданное отношение, в котором точкаМ
делит отрезок
.
Надо найти координаты делящей точкиМ.

Решим
задачу в векторном виде. Проведем векторы,
соединяющие начало координатО
с точками
.
Рассмотрим векторыи.
Они коллинеарны, так как лежат на одной
прямой и=по условию (2.1). Но=,=или.
Из равенства этих векторов следует
пропорциональность соответствующих
координат, то есть,,.
Из последних трех равенств находим
искомые координатых,
у, z
делящей точки М:

,
,(3.9)

В частности,
если точка Мделит отрезок
пополам, то,=1, и координаты
середины отрезка находим по формулам

,
,(3.10)

Пример
3.6.
Координаты концов отрезка прямой
даны:М₁(0;
-1; 3), М₂(5;
3; -8). Найти координаты точки М,
которая делит данный отрезок в отношении
.

Решение.
По формулам (3.9) получим

;

Итак,
координаты делящей точки
.

Соседние файлы в папке математика

Источник

Плоскость в пространстве. Взаимное расположение плоскостей

Плоскость, прямая, точка — основные понятия геометрии. Нам трудно дать им четкие определения, однако интуитивно мы понимаем, что это такое. Плоскость имеет только два измерения. У нее нет глубины. Прямая имеет лишь одно измерение, а у точки вообще нет размеров — ни длины, ни ширины, ни высоты.

Плоскость бесконечна. Поэтому в задачах мы рисуем только часть плоскости. Надо же как-то ее изобразить.

А как все это выглядит в пространстве? Очень просто. Лист плотной бумаги послужит «моделью» плоскости. Карандаши вполне могут изобразить прямые. Все аксиомы и теоремы стереометрии можно показать «на пальцах», то есть с помощью подручных материалов. Читаете — и сразу стройте такую «модель».

Две плоскости в пространстве либо параллельны, либо пересекаются. Примеры в окружающем пространстве найти легко.

Если две плоскости имеют общую точку, то они пересекаются по прямой.

Мы не рассматриваем отдельно случай «плоскости совпадают». Раз совпадают — значит, это одна плоскость, а не две.

Читаем дальше: Прямые в пространстве. Параллельность прямой и плоскости.

Спасибо за то, что пользуйтесь нашими материалами.
Информация на странице «Плоскость вu0026nbsp;пространстве. Взаимное расположение плоскостей» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.
Чтобы успешно сдать нужные и поступить в ВУЗ или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из данного раздела.

Публикация обновлена:
07.05.2023

Источник

Две различные плоскости в пространстве либо параллельны, либо пересекаются.

Параллельность двух плоскостей

Определение. Две плоскости в пространстве называются параллельными, если они не пересекаются.

Признак параллельности плоскостей. Если две пересекающиеся прямые одной плоскости соответственно параллельны двум прямым другой плоскости, то такие плоскости параллельны.

Основные свойства параллельности плоскостей.

Линии пересечения двух параллельных плоскостей третьей плоскостью параллельны.
Отрезки параллельных прямых, заключённых между двумя параллельными плоскостями, равны по длине.

Пересечение двух плоскостей

Две плоскости пересекаются по прямой. Общая прямая двух плоскостей называется ребром двугранного угла, образованного при пересечении данных плоскостей. При пересечении двух плоскостей образуются четыре двугранных угла. Если все они равны, то плоскости называются перпендикулярными.

Признак перпендикулярности плоскостей. Если одна из двух плоскостей проходит через прямую, перпендикулярную к другой плоскости, то такие плоскости перпендикулярны.

Из признака перпендикулярности плоскостей следует, что плоскость, перпендикулярная к прямой, по которой пересекаются две данные плоскости, перпендикулярна к каждой из этих плоскостей.

Угол между плоскостями — наименьший из двугранных углов, образованных при пересечении плоскостей.

Угловая величина двугранного угла — это величина линейного угла данного двугранного угла.

Чтобы найти линейный угол двугранного угла надо из произвольной точки на ребре двугранного угла провести в каждой плоскости по перпендикуляру к этому ребру. Все линейные углы двугранного угла равны друг другу.

Тренировочные задания

Дан куб $ABCDA_{1}B_{1}C_{1}D_{1}$ . Найдите угол между плоскостями $AD_{1}C_{1}$ и $A_{1}D_{1}C$ .
Дан куб $ABCDA_{1}B_{1}C_{1}D_{1}$ . Точка — середина ребра $C_{1}D_{1}$ . Найдите угол между плоскостями $KBA_{1}$ и $BCC_{1}$ .
В кубе $ABCDA_{1}B_{1}C_{1}D_{1}$ все рёбра равны . На его ребре $BB_{1}$ отмечена точка так, что . Через точки и $C_{1}$ построена плоскость , параллельная прямой $BD_{1}$ . Найдите угол наклона плоскости к плоскости грани $BB_{1}C_{1}C$ .
Дана правильная треугольная призма $ABCA_{1}B_{1}C_{1}$ , у которой сторона основания равна , а боковое ребро равно . Через точки , $C_{1}$ и середину ребра $A_{1}B_{1}$ проведена плоскость. Найдите угол между плоскостью сечения и плоскостью ABC.
Все рёбра правильной треугольной призмы $ABCA_{1}B_{1}C_{1}$ имеют длину . Точки и — середины рёбер $AA_{1}$ и $A_{1}C_{1}$ соответственно. Найдите угол между плоскостями и .
Основанием пирамиды является прямоугольник , в котором . Диагонали прямоугольника пересекаются в точке . Отрезок является высотой пирамиды . Из вершин и опущены перпендикуляры и на ребро . Найдите двугранный угол пирамиды при ребре , если .
В основании прямой призмы $ABCDA_{1}B_{1}C_{1}D_{1}$ лежит квадрат со стороной , а высота призмы равна . Точка лежит на диагонали $BD_{1}$ , причём . Найдите угол между плоскостью $A_{1}C_{1}E$ и плоскостью .

Источник

5.3.4. Взаимное расположение двух плоскостей

С параллельными плоскостями мы только что столкнулись и сейчас разовьём тему. Рассмотрим две плоскости пространства, заданные общими уравнениями:

Они могут:

1) совпадать;

2) быть параллельными: ;

3) пересекаться по некоторой прямой «эль»: .

По пунктам:

1) Совпадающие плоскости

Две плоскости совпадают, тогда и только тогда, когда их соответствующие коэффициенты пропорциональны, то есть, существует такое число «лямбда», что выполняются равенства

Рассмотрим плоскости и составим систему:

Из каждого уравнения системы следует, что . Таким образом, система совместна и плоскости совпадают.

2) Параллельные плоскости

Две плоскости параллельны тогда и только тогда, когда их коэффициенты при переменных пропорциональны: , но

На практике первые три коэффициента часто банально попарно совпадают :
(Задача 139), но могут и не совпадать, как, например, в следующей Задаче 140:

Убедимся, что эти прямые действительно параллельны. Составим пропорцию из соответствующих коэффициентов , но , что и требовалось проверить. Теперь способ академический, составим соответствующую систему:

Из первых трёх уравнений следует, что , а из четвёртого уравнения следует, что , значит, система несовместна, но коэффициенты при переменных пропорциональны, следовательно, плоскости параллельны.

3) Пересекающиеся плоскости

И третий, самый распространённый случай, когда две плоскости пересекаются по некоторой прямой :
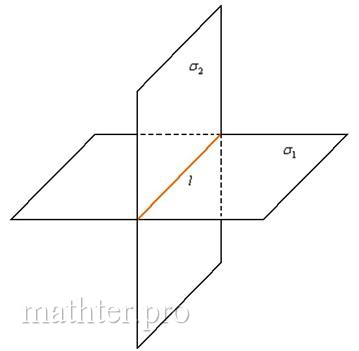
Две плоскости пересекаются тогда и только тогда, когда их коэффициенты при переменных НЕ пропорциональны, то есть НЕ существует такого значения «лямбда», чтобы выполнялись равенства

Попутно заметим важный факт: если плоскости пересекаются, то система линейных уравнений задаёт уравнение прямой в пространстве.

Но о пространственной прямой позже.

В качестве примера рассмотрим плоскости . Составим систему для соответствующих коэффициентов:

Из первых двух уравнений следует, что , но из третьего уравнения следует, что , значит, система несовместна и плоскости пересекаются.
Проверку можно выполнить и «по пижонски», одной строкой: .
И из этого случая логично вытекает следующий параграф:

5.3.5. Как найти угол между плоскостями?

5.3.3. Как найти расстояние между плоскостями?

| Оглавление |

Автор: Aлeксaндр Eмeлин

Источник