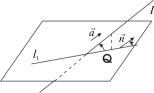
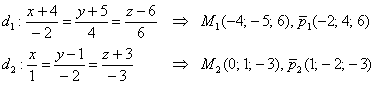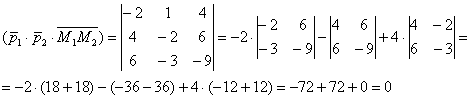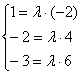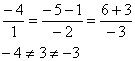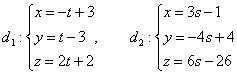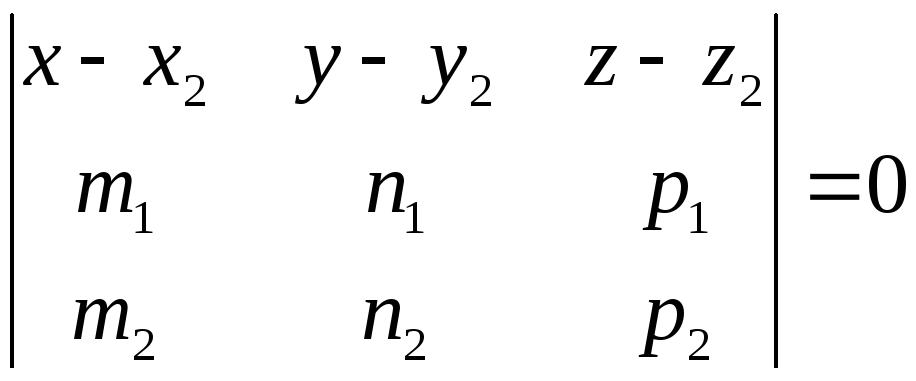Как известно из курса планиметрии, две прямые в плоскости могут пересекаться (имеют общую точку) или быть параллельными (не имеют общую точку).
В пространстве мы можем найти множество примеров ситуаций, когда две прямые не пересекаются, но они и не параллельны.
Рис. (1). Дороги на земле и на эстакадах не пересекаются.
Скрещивающиеся прямые — это прямые, которые не лежат в одной плоскости и не имеют общих точек.
Теорема «Признак скрещивающихся прямых»
Если одна из двух прямых лежит в некоторой плоскости, а другая прямая пересекает эту плоскость в точке, не лежащей на первой прямой, то эти прямые скрещивающиеся (не лежат в одной плоскости).
Доказательство
Рассмотрим прямую (AB), лежащую в плоскости, и прямую (CD), которая пересекает плоскoсть в точке (D), не лежащей на прямой (AB).
Рис. (2). Скрещивающиеся прямые.
1. Допустим, что прямые (AB) и (CD) всё-таки лежат в одной плоскости.
2. Значит, эта плоскость идёт через прямую (AB) и точку (D), то есть, она совпадает с плоскостью (α).
3. Это противоречит условиям теоремы, по которым прямая (CD) не находится в плоскости (α), а пересекает её.
Теорема доказана.
В пространстве прямые могут пересекаться, скрещиваться или быть параллельными. 
Рис. (3). Параллельные прямые.
Рис. (4). Пересекающиеся прямые.
Рис. (5). Скрещивающиеся прямые.
Теорема
Через каждую из двух скрещивающихся прямых проходит плоскость, параллельная другой прямой, и притом только одна.
Доказательство
Рассмотрим скрещивающиеся прямые (AB) и (CD).
Рис. (6). Доказательство теоремы.
1. Через точку (D) можно провести прямую (DE), параллельную (AB).
2. Через пересекающиеся прямые (CD) и (DE) можно провести плоскость (α).
3. Так как прямая (AB) не лежит в этой плоскости и параллельна прямой (DE), то она параллельна плоскости.
4. Эта плоскость единственная, так как любая другая плоскость, проходящая через (CD), будет пересекаться с (DE) и (AB), которая ей параллельна.
Теорема доказана.
1. Если прямые параллельны, то угол между ними —
0°
.
2. Углом между двумя пересекающимися прямыми называют величину меньшего из углов, образованных этими прямыми. Если все углы равны, то эти прямые перпендикулярны (образуют угол
90°
).
3. Углом между двумя скрещивающимися прямыми называют угол между двумя пересекающимися прямыми, соответственно параллельными данным скрещивающимся прямым.
Обрати внимание!
Провести соответственные прямые, параллельные данным скрещивающимся прямым, можно через любую точку. Иногда удобно выбрать эту точку на одной из данных скрещивающихся прямых и провести через эту точку прямую, параллельную другой из скрещивающихся прямых.
Пример:
Рис. (7). Куб.
Найти угол между
AB
и
B1D1
.
Выберем точку
B
на прямой
AB
и проведём через
B
прямую
BD
параллельно
B1D1
.
Рис. (8). Куб с дополнительными построениями.
Угол между
AB
и
BD
—
45°
, так как
ABCD
— квадрат.
Соотвeтственно, угол между
AB
и
B1D1
— тоже
45°
.
5.5.1. Взаимное расположение прямых
Две прямые пространства могут:
1) скрещиваться;
2) пересекаться в точке ;
3) быть параллельными ;
4) совпадать.
Случай № 1 принципиально отличается от других случаев. Две прямые скрещиваются, если они не лежат в одной плоскости. Поднимите
одну руку вверх, а другую руку вытяните вперёд – вот вам и пример скрещивающихся прямых. В пунктах же № 2-4 прямые обязательно лежат в
одной плоскости.
Как выяснить взаимное расположение прямых в пространстве?
Рассмотрим общий алгоритм и две прямые:
– прямую , заданную точкой
и направляющим вектором
;
– прямую , заданную точкой
и направляющим вектором
.
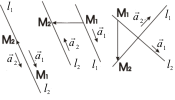
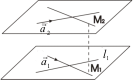
Для лучшего понимания выполним схематический чертёж, на котором в качестве примера изображены скрещивающиеся прямые
, то легко найти вектор
.
1) Если прямые скрещиваются, то векторы не компланарны, а, значит, определитель, составленный из их координат, ненулевой. Или, что
фактически то же самое, смешанное произведение векторов отлично от нуля:
Пусть . Это означает, что векторы компланарны, и вся конструкция
«схлопнулась» в одну плоскость. Следовательно, прямые либо пересекаются, либо параллельны, либо совпадают.
2) Если направляющие векторы не коллинеарны, то прямые пересекаются.
3-4) Если направляющие векторы коллинеарны, то прямые
либо параллельны, либо совпадают. Финальным гвоздём предлагаю следующий приём: берём какую-либо точку одной прямой и подставляем её координаты в
уравнение другой прямой. Если координаты «подошли», то прямые совпадают, если нет – то прямые параллельны.
…Всё ли вам понятно? Если нет, то милости прошу по ссылкам, если да, то отработаем этот незатейливый алгоритм на конкретных
практических примерах:
Задача 153
Выяснить взаимное расположение двух прямых
Решение: как и во многих задачах, решение удобно оформить по пунктам:
1) Вытаскиваем из уравнений прямых их точки и направляющие векторы:
2) Найдём вектор:
3) Вычислим смешанное произведение векторов:
Таким образом, векторы компланарны, а значит, прямые
лежат в одной плоскости и могут
пересекаться, быть параллельными или совпадать.
4) Проверим направляющие векторы на коллинеарность.
Составим систему из соответствующих координат данных векторов:
Из каждого уравнения следует, что , следовательно,
система совместна, соответствующие координаты векторов пропорциональны, и векторы коллинеарны.
Следовательно, прямые параллельны либо совпадают.
5) Выясним, есть ли у прямых общие точки. Возьмём точку ,
принадлежащую первой прямой, и подставим её координаты в уравнения прямой :
Получены неверные равенства, значит, точка «не подошла». Таким образом, общих точек у прямых нет, и им ничего не остаётся, как быть
параллельными.
Ответ:
Интересный пример для самостоятельного решения:
Задача 154
Выяснить взаимное расположение прямых
Обратите внимание, что у второй прямой в качестве параметра выступает буква . Логично. В общем случае – это две различные прямые, и у каждой прямой свой параметр.
Решение и ответ в конце книги.
Далее мы по порядку рассмотрим задачи, «посвященные» скрещивающимся прямым, затем – пересекающимся, затем – параллельным и совпадающим:


| Оглавление |
Автор: Aлeксaндр Eмeлин
Взаимное расположение прямых в пространстве
Возможны четыре различных случая расположения двух прямых в пространстве:
– прямые скрещивающиеся, т.е. не лежат в одной плоскости;
– прямые пересекаются, т.е. лежат в одной плоскости и имеют одну общую точку;
– прямые параллельные, т.е. лежат в одной плоскости и не пересекаются;
– прямые совпадают.
Получим признаки этих случаев взаимного расположения прямых, заданных каноническими уравнениями
где — точки, принадлежащие прямым
и
соответственно, a
— направляющие векторы (рис.4.34). Обозначим через
вектор, соединяющий заданные точки.
Перечисленным выше случаям взаимного расположения прямых и
соответствуют следующие признаки:
– прямые и
скрещивающиеся
векторы
не компланарны;
– прямые и
пересекаются
векторы
компланарны, а векторы
не коллинеарны;
– прямые и
параллельные
векторы
коллинеарны, а векторы
не коллинеарны;
– прямые и
совпадают
векторы
коллинеарны.
Эти условия можно записать, используя свойства смешанного и векторного произведений. Напомним, что смешанное произведение векторов в правой прямоугольной системе координат находится по формуле:
Равенство нулю смешанного произведения векторов является необходимым и достаточным условием их компланарности. Поэтому:
– прямые и
скрещивающиеся
определитель отличен от нуля;
– прямые и
пересекаются
определитель равен нулю, а вторая и третья его строки не пропорциональны, т.е.
– прямые и
параллельные
вторая и третья строки определителя пропорциональны, т.е.
а первые две строки не пропорциональны, т.е.
– прямые и
совпадают
все строки определителя пропорциональны, т.е.
Расстояние между параллельными прямыми
Найдем расстояние между параллельными прямыми, заданными каноническими уравнениями (рис.4.35)
где — произвольные точки на прямых
и
соответственно, а координаты направляющих векторов прямых пропорциональны:
Искомое расстояние равно высоте параллелограмма, построенного на векторах
и
, и может быть найдено по формуле (4.35).
Расстояние между скрещивающимися прямыми
Напомним, что расстоянием между скрещивающимися прямыми называется длина их общего перпендикуляра, т.е. кратчайшее расстояние между точками этих прямых.
Найдем расстояние между скрещивающимися прямыми, заданными каноническими уравнениями
где — произвольные точки на прямых
и
соответственно.
Искомое расстояние равно высоте параллелепипеда, построенного на векторах
(рис.4.36), т.е.
(4.38)
где
— смешанное и векторное произведения векторов. Как показано выше, прямые и
скрещивающиеся тогда и только тогда, когда векторы
некомпланарные, т.е.
Отсюда следует, что вторая и третья строки не пропорциональны. Поэтому векторы неколлинеарные, т.е.
и знаменатель в правой части (4.38) отличен от нуля.
Угол между прямыми
Угол между прямыми определяется как угол между их направляющими векторами. Поэтому величина острого угла между прямыми
вычисляется по формуле
(4.39)
Пример 4.16. Найти расстояние между прямой, проходящей через точки
, и осью абсцисс. Найти величину
острого угла между этими прямыми.
Решение. Каноническое уравнение оси абсцисс имеет вид так как ось проходит через точку
а
— ее направляющий вектор. Каноническое уравнение прямой
получено в примере 4.15,»а»:
Полагая
по формуле (4.38) получаем:
Острый угол находим по формуле (4.39):
Взаимное расположение прямой и плоскости
Возможны три случая взаимного расположения прямой и плоскости:
– прямая и плоскость пересекаются, т.е. имеют одну общую точку;
– прямая и плоскость параллельны, т.е. не имеют общих точек;
– прямая лежит в плоскости, т.е. все точки прямой принадлежат плоскости.
Получим признаки для всех этих случаев. Пусть прямая и плоскость
заданы уравнениями:
т.е. прямая проходит через точку
коллинеарно вектору
а плоскость
перпендикулярна вектору
Перечисленным выше случаям взаимного расположения прямой и плоскости
соответствуют следующие признаки:
– прямая и плоскость
пересекаются
векторы
и
не ортогональны (рис.4.37,а);
– прямая и плоскость
параллельны
векторы
и
ортогональны, а точка
не принадлежит плоскости
(рис.4.37,б);
– прямая лежит в плоскости
векторы
и
ортогональны, а точка
принадлежит плоскости
(рис.4.37,в).
Учитывая свойство скалярного произведения векторов получаем:
– прямая и плоскость
пересекаются
;
– прямая и плоскость
параллельны
– прямая лежит в плоскости
Угол между прямой и плоскостью
Угол между прямой и плоскостью
определяется как угол между прямой и ее ортогональной проекцией на плоскость (рис.4.38). Из двух смежных углов
и
, как правило, выбирают меньший. Если прямая
перпендикулярна плоскости (ее ортогональная проекция на плоскость является точкой), то угол считается равным
. Если обозначить
и
углы, образованные наклонной
с перпендикуляром к плоскости, то
Поскольку угол (или
) равен углу между направляющим вектором
прямой
и нормалью
к плоскости
, то
. Записывая скалярное произведение через координаты множителей, получаем формулу вычисления угла
между прямой и плоскостью:
(4.40)
Отсюда, например, следует полученное ранее необходимое условие параллельности прямой и плоскости.
Математический форум (помощь с решением задач, обсуждение вопросов по математике).
Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.
Щебетун Виктор
Эксперт по предмету «Математика»
Задать вопрос автору статьи
Разновидности уравнений прямой
Канонические уравнения прямой.Пусть задана точка $M_{0} left(x_{0} ,y_{0} ,z_{0} right)$, через которую проходит прямая, а также направляющий вектор $overline{R}=mcdot overline{i}+ncdot overline{j}+pcdot overline{k}$, которому она параллельна. Уравнения $frac{x-x_{0} }{m} =frac{y-y_{0} }{n} =frac{z-z_{0} }{p}$ называются каноническими уравнениями прямой.
Параметрические уравнения прямой. Введем обозначения: $frac{x-x_{0} }{m} =t$, $frac{y-y_{0} }{n} =t$, $frac{z-z_{0} }{p} =t$. Здесь $t$ — параметр. Из этих равенств получаем: $x=x_{0} +mcdot t$, $y=y_{0} +ncdot t$, $z=z_{0} +pcdot t$. Эти уравнения называются параметрическими уравнениями прямой.
Уравнение прямой, которая проходит через две заданные точки $M_{1} left(x_{1} ,y_{1} ,z_{1} right)$ и $M_{2} left(x_{2} ,y_{2} ,z_{2} right)$. Уравнения $frac{x-x_{1} }{x_{2} -x_{1} } =frac{y-y_{1} }{y_{2} -y_{1} } =frac{z-z_{1} }{z_{2} -z_{1} } $, аналогичные каноническим, называются уравнениями прямой, проходящей через две заданные точки.
Сдай на права пока
учишься в ВУЗе
Вся теория в удобном приложении. Выбери инструктора и начни заниматься!
Получить скидку 3 000 ₽
Общие уравнения прямой. Прямую линию в пространстве можно определить как линию пересечения двух не параллельных между собой плоскостей: $A_{1} cdot x+B_{1} cdot y+C_{1} cdot z+D_{1} =0$ и $A_{2} cdot x+B_{2} cdot y+C_{2} cdot z+D_{2} =0$. Решение системы уравнений, состоящей из уравнений плоскостей, называются общими уравнениями прямой.
Переход между различными видами уравнений прямой
От общих уравнений прямой можно перейти к каноническим. Для этого надо знать произвольную точку прямой и ее направляющий вектор. Выберем значение некоторой одной координаты произвольно. После этого координаты нужной точки можно найти из уравнений плоскостей, рассматривая их как систему относительно тех двух координат, которые остались. Для нахождения направляющего вектора отметим, что он должен быть перпендикулярным к нормальным векторам каждой из плоскостей. Поэтому для этого целиком подходит вектор их векторного произведения.
От канонических уравнений прямой можно перейти к общим. Для этого представим канонические уравнения как пару уравнений $frac{x-x_{0} }{m} =frac{z-z_{0} }{p} $ и $frac{y-y_{0} }{n} =frac{z-z_{0} }{p} $ и выполним преобразования.
«Взаимное расположение прямых в пространстве» 👇
Получаем: $pcdot x-mcdot z-pcdot x_{0} +mcdot z_{0} =0$ — уравнение плоскости, параллельной оси $Oy$, а $pcdot y-ncdot z-pcdot y_{0} +ncdot z_{0} =0$ — уравнение плоскости, параллельной оси $Ox$. Зная основные виды уравнений, описывающих прямые, можно более подробно рассмотреть способы расположения прямых в пространстве.
Взаимное расположение двух прямых в пространстве
Различают 3 случая взаимного расположения прямых в пространстве:
- Скрещивающиеся прямые в пространстве. Две прямых являются скрещивающимися, если они не имеют никаких общих точек и лежат в различных плоскостях. В жизни скрещивающиеся прямые — это, например, железная дорога, проходящая над автомагистралью;
- Две прямые находятся на одной плоскости и имеют одну общую точку, то есть пересекаются; Примером пересекающихся прямых в пространстве из реального мира служит обычный перекрёсток.
- Две прямые находятся на одной плоскости и не имеют общих точек, то есть параллельны друг другу. Существует частный случай параллельных прямых — это совпадающие прямые в пространстве.
Замечание 1
Вне зависимости от того, являются ли прямые пересекающимися или скрещивающимися, можно говорить об угле между ними.
Для того чтобы определить, пересекаются ли прямые в пространстве, необходимо составить систему уравнений, состоящую из уравнений этих прямых. Если эта система имеет решение, то прямые пересекаются.
Теперь рассмотрим подробнее, как определить взаимное расположение прямых в пространстве.
Пусть в пространстве заданы две прямые $L_{1} $ и $L_{2} $: $frac{x-x_{1} }{m_{1} } =frac{y-y_{1} }{n_{1} } =frac{z-z_{1} }{p_{1} } $ и $frac{x-x_{2} }{m_{2} } =frac{y-y_{2} }{n_{2} } =frac{z-z_{2} }{p_{2} } $. Выберем в пространстве произвольную точку и проведем через нее две вспомогательные прямые, параллельные данным.
Углом между прямыми $L_{1} $ и $L_{2} $ называют любой из двух сопряженных углов, образованных вспомогательными прямыми. Если величина одного из них $phi $, то величина второго $pi -phi $.
Вместо вспомогательных прямых можно взять направляющие векторы данных прямых: $overline{R_{1} }=m_{1} cdot overline{i}+n_{1} cdot overline{j}+p_{1} cdot overline{k}$ и $overline{R_{2} }=m_{2} cdot overline{i}+n_{2} cdot overline{j}+p_{2} cdot overline{k}$. Косинус одного из углов между прямыми можно найти по формуле $cos phi =frac{m_{1} cdot m_{2} +n_{1} cdot n_{2} +p_{1} cdot p_{2} }{sqrt{m_{1}^{2} +n_{1}^{2} +p_{1}^{2} } cdot sqrt{m_{2}^{2} +n_{2}^{2} +p_{2}^{2} } } $. Если значение $cos phi >0$, то получен острый угол между прямыми, если $cos phi$
Равенство $cos phi =0$ значит, что прямые перпендикулярны. Следовательно, условие перпендикулярности двух прямых в пространстве имеет вид $m_{1} cdot m_{2} +n_{1} cdot n_{2} +p_{1} cdot p_{2} =0$.
Условие параллельности двух прямых совпадает с условием коллинеарности их направляющих векторов, то есть $frac{m_{1} }{m_{2} } =frac{n_{1} }{n_{2} } =frac{p_{1} }{p_{2} }$.
Нахождение угла между прямыми частично решает также вопрос о нахождении их в одной плоскости. Имеется в виду то, что выполнение условия параллельности двух прямых одновременно означает, что они находятся в одной плоскости.
Теперь рассмотрим условие пересечения двух прямых, которое также является условием нахождения прямых в одной плоскости.
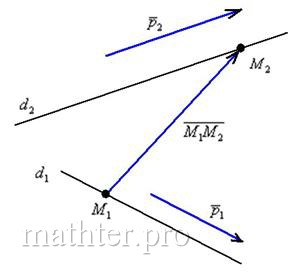
Из уравнений заданных прямых видно, что прямая $L_{1} $ проходит через точку $M_{1} left(x_{1} ,y_{1} ,z_{1} right)$, а прямая $L_{2} $ — через точку $M_{2} left(x_{2} ,y_{2} ,z_{2} right)$.
Рассмотрим вектор $overline{M_{1} M_{2} }=left(x_{2} -x_{1} right)cdot overline{i}+left(y_{2} -y_{1} right)cdot overline{j}+left(z_{2} -z_{1} right)cdot overline{k}$, который соединяет эти точки, а также направляющие векторы $overline{R_{1} }=m_{1} cdot overline{i}+n_{1} cdot overline{j}+p_{1} cdot overline{k}$ и $overline{R_{2} }=m_{2} cdot overline{i}+n_{2} cdot overline{j}+p_{2} cdot overline{k}$ прямых $L_{1} $ и $L_{2} $.
Если прямые $L_{1} $ и $L_{2} $ действительно пересекаются, то они лежат в одной плоскости $P$. В этой же плоскости $P$ лежит и вектор $overline{M_{1} M_{2} }$. Направляющий вектор $overline{R_{1} }$ коллинеарен прямой $L_{1} $, а направляющий вектор $overline{R_{2} }$ коллинеарен прямой $L_{2} $. Итак, все три вектора $overline{M_{1} M_{2} }$, $overline{R_{1} }$ и $overline{R_{2} }$ лежат в параллельных плоскостях, то есть они компланарны. Запишем условие компланарности векторов $left|begin{array}{ccc} {x_{2} -x_{1} } & {y_{2} -y_{1} } & {z_{2} -z_{1} } \ {m_{1} } & {n_{1} } & {p_{1} } \ {m_{2} } & {n_{2} } & {p_{2} } end{array}right|=0$ и получим условие пересечения двух прямых, если же это условия не выполняется, то это скрещенные прямые в пространстве.
Пример 1
Задание: Выяснить взаимное расположение прямых в пространстве:
$L_1: frac{x – 1}{1} = frac{y – 2}{3}=frac{z+1}{-2}$
$L_2: begin{cases} x-y-z+1 =0 \ x + y + 2z – 2 = 0 \ end{cases}$
Решение: Направляющий вектор первой прямой определяем по её уравнениям, он будет выглядеть как $s_1 = {1;3;-2}$.
Направляющий же вектор второй прямой определим через векторное произведение нормальных векторов, определяющих плоскости, на пересечении которых она находится:
$s_2 = n_1 × n_1 = begin{array}{|ccc|} i & j & k \ 1 & -1 & -1 \ 1 & 1 & 2 \ end{array} = — i – 3j + 2k$
В данном примере $s_1 = -s_2$, а это значит, что прямые либо параллельные, либо совпадающие.
Чтобы понять, с каким из случаев мы имеем дело, возьмём точку $M_0$с координатами $(1;2;-1)$, принадлежащую первой прямой и подставим в уравнения для второй.
В первом из них равенство не соблюдается и получается, что $1=0$. Это значит, что рассмотренная точка не лежит на второй прямой и прямые параллельны между собой.
Пример 2
Задание: провести плоскости через параллельные прямые и через прямые, которые пересекаются.
Решение каждой из этих задач начинается с того, что на нужной плоскости $P$ выбирается некоторая переменная точка $Mleft(x,y,zright)$.
Если данные прямые $L_{1} $ и $L_{2} $ — параллельны, то уравнение нужной плоскости $P$ имеет вид условия компланарности $left|begin{array}{ccc} {x-x_{1} } & {y-y_{1} } & {z-z_{1} } \ {x_{2} -x_{1} } & {y_{2} -y_{1} } & {z_{2} -z_{1} } \ {m} & {n} & {p} end{array}right|=0$ следующих трех векторов:
- $overline{M_{1} M}=left(x-x_{1} right)cdot overline{i}+left(y-y_{1} right)cdot overline{j}+left(z-z_{1} right)cdot overline{k}$ — вектор, который лежит в плоскости $P$, соединяет точку $M_{1} left(x_{1} ,y_{1} ,z_{1} right)$, принадлежещей прямой $L_{1} $, с переменной точкой $Mleft(x,y,zright)$.
- $overline{M_{1} M_{2} }=left(x_{2} -x_{1} right)cdot overline{i}+left(y_{2} -y_{1} right)cdot overline{j}+left(z_{2} -z_{1} right)cdot overline{k}$ — вектор, который лежит в плоскости $P$, соединяет точку $M_{1} left(x_{1} ,y_{1} ,z_{1} right)$, которая принадлежит прямой $L_{1} $, с точкой $M_{2} left(x_{2} ,y_{2} ,z_{2} right)$, которая принадлежит прямой $L_{2} $.
- $overline{R}=mcdot overline{i}+ncdot overline{j}+pcdot overline{k}$ — направляющий вектор одной из двух параллельных прямых, параллельный плоскости $P$.
Если данные прямые $L_{1} $ и $L_{2} $ — пересекаются, то уравнение нужной плоскости $P$ имеет вид условия компланарности $left|begin{array}{ccc} {x-x_{1} } & {y-y_{1} } & {z-z_{1} } \ {m_{1} } & {m_{2} } & {m_{3} } \ {m_{2} } & {n_{2} } & {p_{2} } end{array}right|=0$ следующих трех векторов:
- $overline{M_{1} M}=left(x-x_{1} right)cdot overline{i}+left(y-y_{1} right)cdot overline{j}+left(z-z_{1} right)cdot overline{k}$ — вектор, который лежит в плоскости $P$, соединяет точку $M_{1} left(x_{1} ,y_{1} ,z_{1} right)$, принадлежащую прямой $L_{1} $, с переменной точкой $Mleft(x,y,zright)$.
- $overline{R_{1} }=m_{1} cdot overline{i}+n_{1} cdot overline{j}+p_{1} cdot overline{k}$ — направляющий вектор прямой $L_{1} $, параллельный плоскости $P$.
- $overline{R_{2} }=m_{2} cdot overline{i}+n_{2} cdot overline{j}+p_{2} cdot overline{k}$ — направляющий вектор прямой $L_{2} $, параллельный плоскости $P$.
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме
Взаимное расположение двух прямых в пространстве
Пусть
прямые l1
и l2
заданы каноническими уравнениями
Обозначим
=
=
(х2—x1,y2—у1,z2—z1),
=(m1,n1,р),
=
(m2,n2,р2).
1)
если прямые совпадают, то все три вектора
,
,
коллинеарны.
2)
если прямые параллельны и не совпадают,
то вектора
и
коллинеарны, а вектор
им не коллинеарен.
3)
если пряже пересекаются, то никакие два
из векторов
,
,
не
коллинеарны, и все три вектора компланарны.
4)
ecли прямые скрещиваются, то векторы
,
,
некомпланарны.
Отметим,
что условия параллельности и
перпендикулярности, прямых l1
и l2
равносильны условиям коллинеарности
и ортогональности их направляющих
векторов
и
.
Следовательно,
—
необходимое
и достаточное условие параллельности
двух прямых.
m1m2
+
n1n2
+
p1p2
=
0
—
необходимое
и достаточное условие перпендикулярности
двух прямых.
Если
прямые l1
и l2
пересекаются, то величина угла φ между
ними равно либо (^,
)
либо (-^,
).
Следовательно,
Расстояние от точки до прямой в пространстве
Р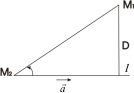
от точки M1(x1,у1,z1)
до данной прямой
,
проходящей через точкуM0(х0,у0,z0)
с направляющим вектором
= (m, n, p) определяется так
.
Уравнение
плоскости, проходящей через две заданные
прямые
Пусть
плоскость α проходят через прямые l1
и l2,
заданные соответственно уравнениями:
,
(2)
Обозначим
М2(x2,y2,z2),
=(m1,n1,р1),
=(m2,n2,p2)
и М(х,у,z)
произвольная точка плоскости α
Тогда
—
уравнение
плоскости, проходящей через две прямые.
Расстояние
между скрещивающимися прямыми
Пусть
прямые l1
и l2,
заданные уравнениями вида (2), являются
скрещивающимися. Тогда расстоянием d
между ними называется длина перпендикуляра,
проведенного из одно прямой на другую.
Заметим, что искомое расстояние равно
отрезку перпендикуляра, закаченного
между плоскостями α1
и α2,
где плоскости α1
и α2
одновременно параллельны векторам
и
,
и проходят соответственно через прямыеl1
и l2
Тогда
Взаимное
расположение прямой и плоскости
Пусть
прямая l
и плоскость α заданы соответственно
уравнениями
,
α: Ax
+
By
+
Cz
+
D
= 0.
1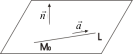
прямаяl
лежит в плоскости α, если
Am
+
Bn
+
Ср
=
0,
Аx0
+
Ву0
+
Cz0
+
D = 0.
2)
прямая l
параллельна плоскости α, если
Am
+
Bn
+
Ср = О,
Аx0
+
Ву0
+
Cz0
+
D
≠ 0.
3)
прямая l
пересекает плоскость α если
Am
+
Вn
+
Ср
0.
Угол
между прямой и плоскостью
Углом
между прямой
l
и
плоскостью
α называется угол φ, образованный прямой
l
и ее проекцией l1
на плоскость α
Тогда
и
.
КРИВЫЕ
ВТОРОГО ПОРЯДКА
Парабола
Определение:
Параболой называется геометрическое
место точек плоскости, равноудаленных
от некоторой точки, называемой фокусом
параболы и некоторой прямой, называемой
директрисой параболы.
Уравнение
параболы принятo
записывать в следующем виде:
y2
= 2px , p>0 (1)
-
каноническое
уравнение параболы.
Свойства
параболы непосредственно следуют из
свойств уравнения:
1.Абсцисса
любой точки параболы неотрицательна
2.Парабола
проходит через начало координат.
3.Парабола
симметрична относительно оси абсцисс.
4.При
неограниченном возрастании абсциссы
x
ордината у возрастает по абсолютной
величине.
Точка F(;0)
называется фокусом
параболы,
прямая
— директрисой.
Величина
р называется фокальным
параметром или
просто параметром
параболы.
Эллипс

Эллипсом
называется множество точек плоскости,
сумма расстояний от каждой из которых
до двух данных точек F1
и F2
этой плоскости, называемых фокусами
эллипса, есть величина постоянная,
равная 2а
(а>0),
большая, чем расстояние между фокусами.
Для составления
уравнение эллипса выберем прямоугольную
декартову систему координат так, чтобы
ось ОХ
проходила
через фокусы F1
и F2,
а начало координат — точка О находилась
в середине отрезка F1F2.
Обозначим
F1F2
= 2с. Тогда F1(-с,0),
F2(c,0).
Пусть М(х,у) – произвольная точка
эллипса. Тогда MF1+
MF2=
2а,
а>с.
Так
как
,
и уравнение принимает вид:
.
(2)
Пусть
координаты точки М1(х1,у1)удовлетворяют
уравнению (2).
Обозначим
r1
=
F1M1,
r2
= F2M2
— фокальные
радиусы точек М1 М2.
Тогда
,
,
значит, r1+r2=2a.
Теперь
по свойствам уравнения (2) исследуем
геометрические свойства эллипса.
1.
Оси ОХ и ОУ являются осями симметрии
эллипса. Следовательно, эллипс достаточно
исследовать только в первой координатной
четверти.
2.
Эллипс пересекает координатные оси в
точках А1(-а,0),
А2(а,0),
В1(0,b),
В2(0,-b),
называемых вершинами
эллипса.
3.
Эллипс расположен в прямоугольнике,
ограниченном прямыми х=а,
у =b.
4.
Из уравнений следует, что при возрастании
х от 0 до а
в первой координатной четверти, у
убывает от b
до 0.
По
полученным свойствам строим эллипс
Отрезок А1А2
и его длина 2а
называются большой
осью эллипса,
а отрезок B1B2
и его длина 2b
называются малой
осью эллипса.
Отрезок ОА1
с длиной а
и отрезок ОВ1
с длиной b
называются соответственно большой
и малой полуосями эллипса.
Длина отрезка F1F2=2с
называется
фокусным
расстоянием,
начало координат — центр
эллипса.
Е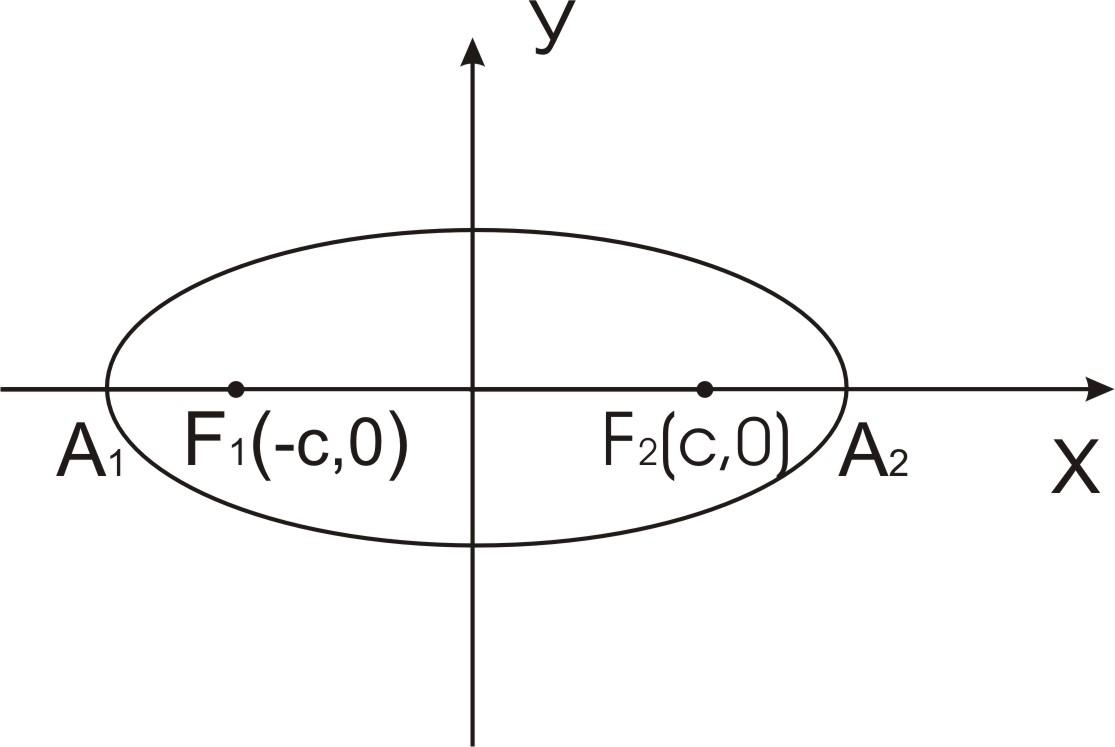
то получаем каноническое уравнение
окружности
Уравнения
х = acost,
у = bsint
—
параметрические
уравнения эллипса.
Определение.
Эксцентриситетом эллипса называется
число
Так
как с<а,
то 0<c<1.
Заметим, что у окружности оба фокуса
совпадают,
поэтому с
= 0 и ε = 0.
.
Следовательно,
эксцентриситет характеризует форму
эллипса.
Используя
понятия эксцентриситета, можно выразить
фокальные радиусы произвольной точки
M(x,у)
эллипса:
r1=а+εх,
r2=а—εх
Соседние файлы в папке Ходалевич
- #
- #