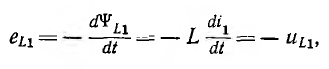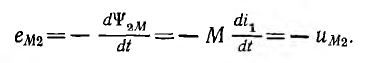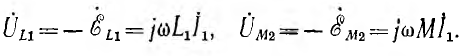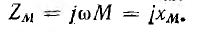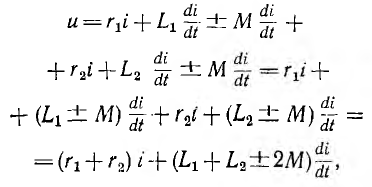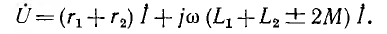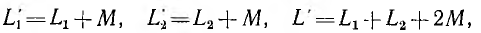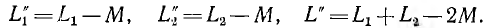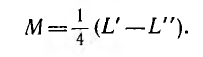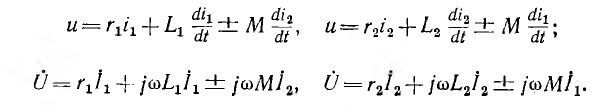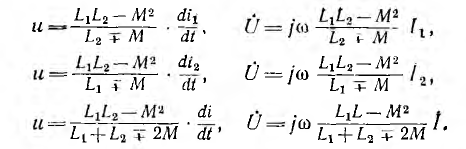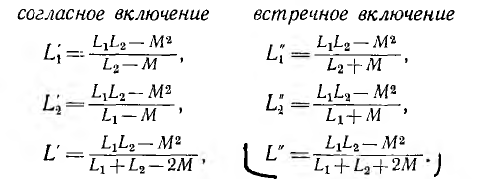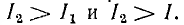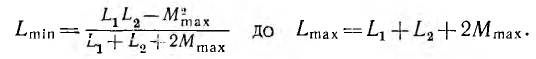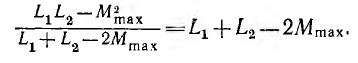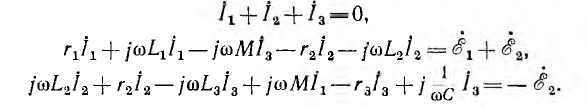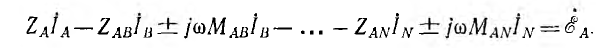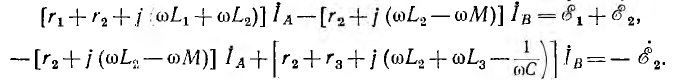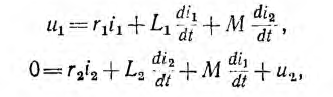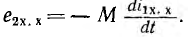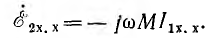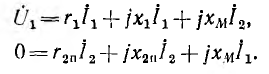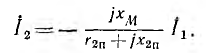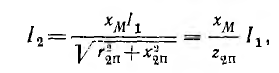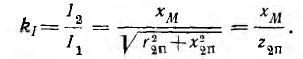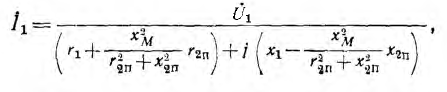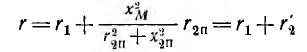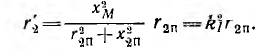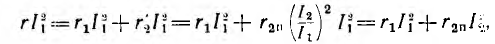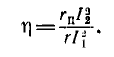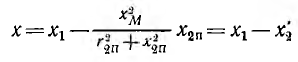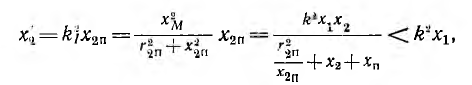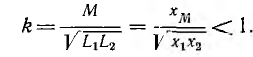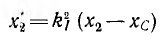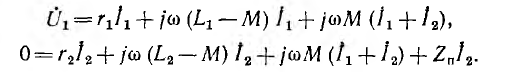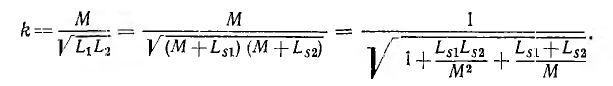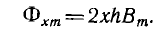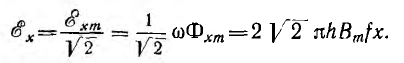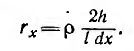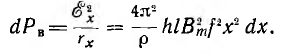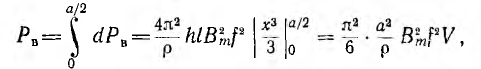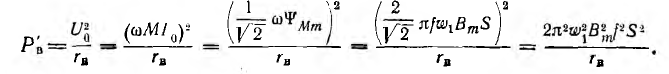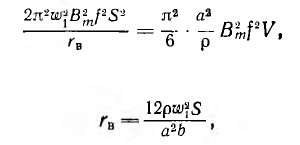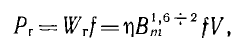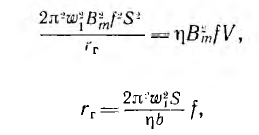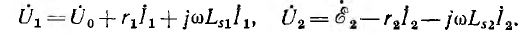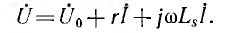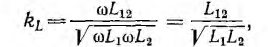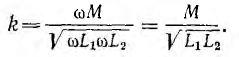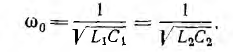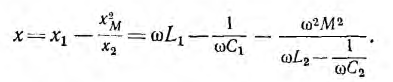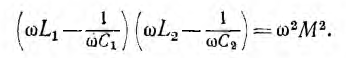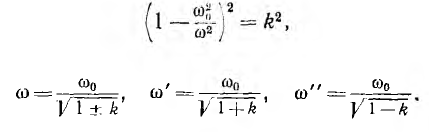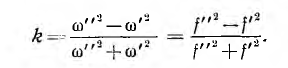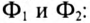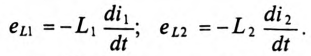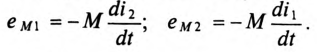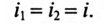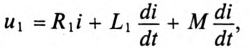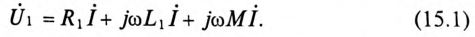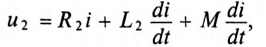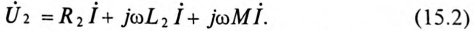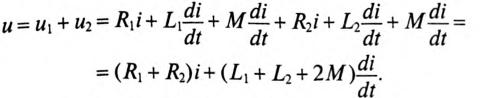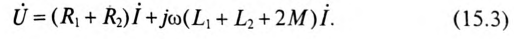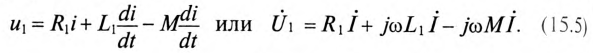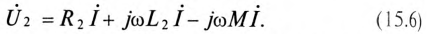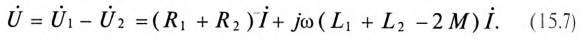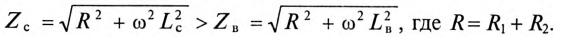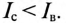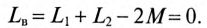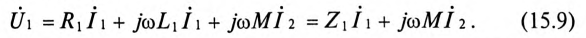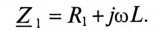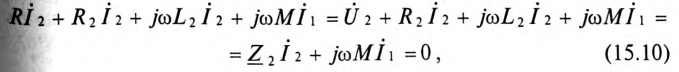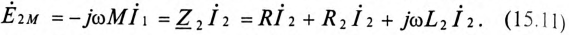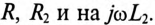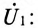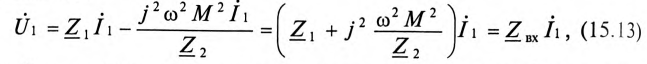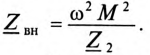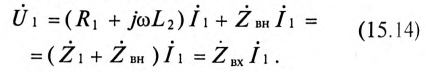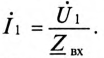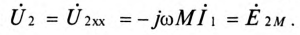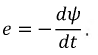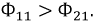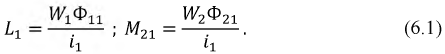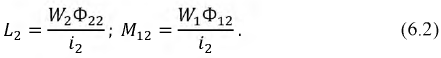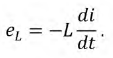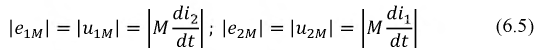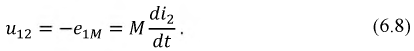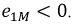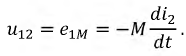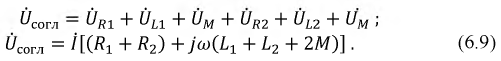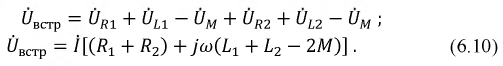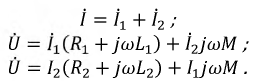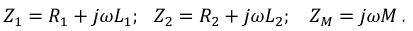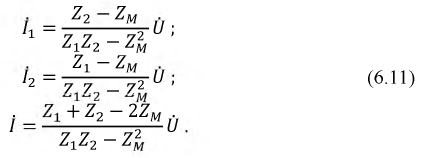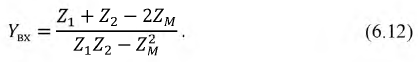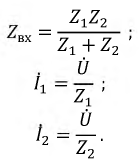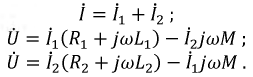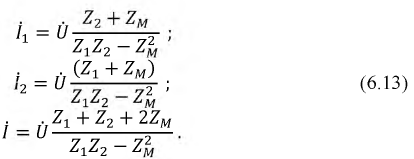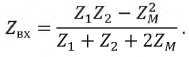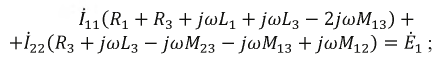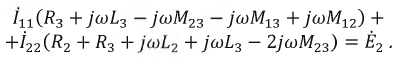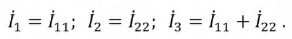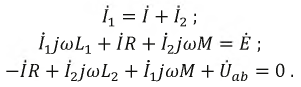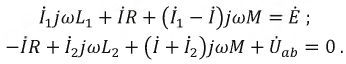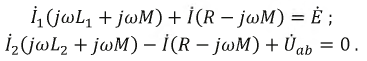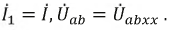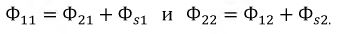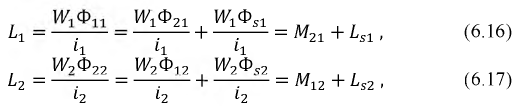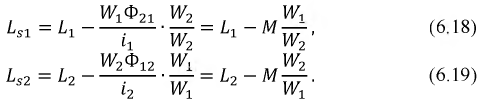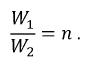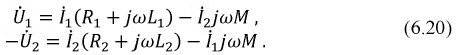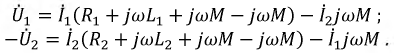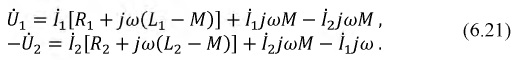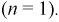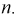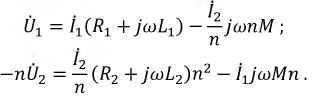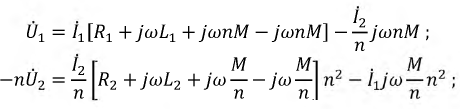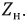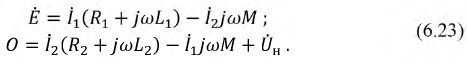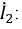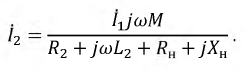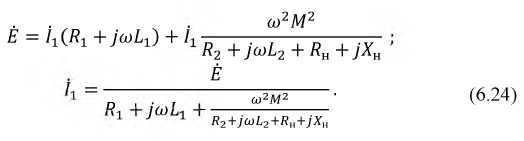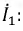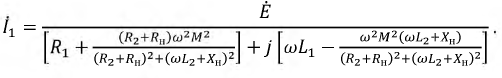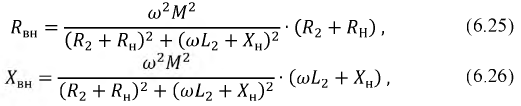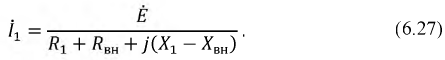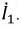Как найти взаимную индукцию катушек

Содержание:

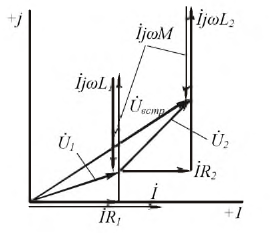
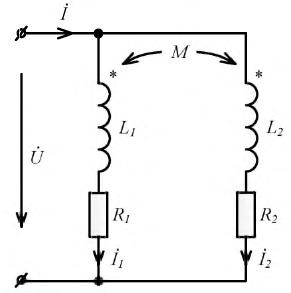
Цепи с взаимной индукцией:

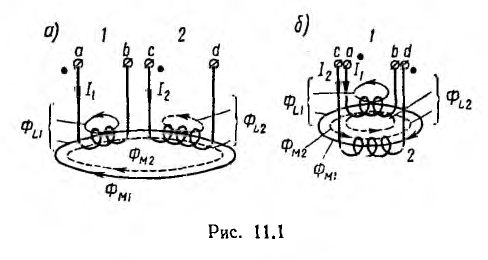
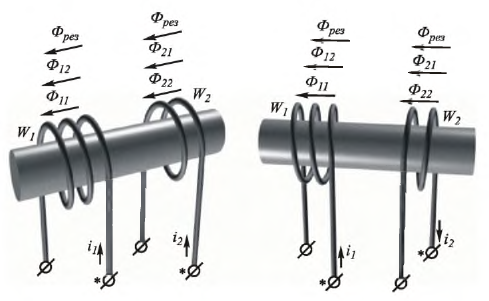
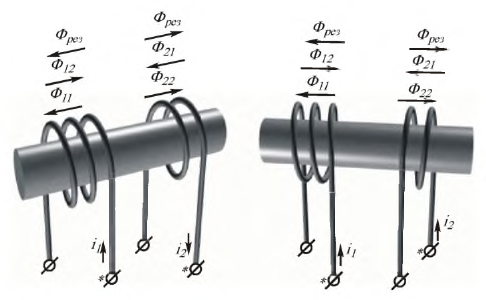
При рассмотрении цепей, отдельные ветви которых связаны между собой взаимоиндуктивкостью М , нужно ввести понятие об одноименных зажимах контуров. Зажимы двух контуров называются одноименными, если при одинаковом направлении токов относительно этих зажимов магнитные потоки самоиндукции Ф_L и взаимоиндукции Ф_M в каждом контуре совпадают по направлению. Одноименность зажимов контуров, например катушек, зависит от их взаимного расположения и направления намотки.

Из рис. 11.1, а, например, видно, что в катушках 1 и 2 с одинаковым направлением намотки одноименными являются зажимы а и b (обозначены точками), а также зажимы b и d. Если сдвинуть катушку i в положение, показанное на рис. 11.1, б, потоки взаимоиндукции Ф_м1 и Ф_м2 при том же направлении токов окажутся направленными навстречу и одноименными должны стать зажимы а и d (соответственно b и с).

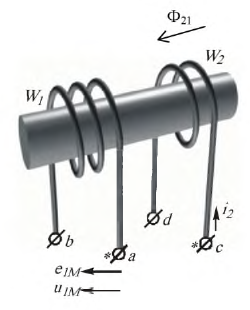
Выбирая в обеих катушках положительные направления э. д. е., напряжений и токов относительно одноименных зажимов одинаковыми, при мгновенном значении тока i₁ в первом контуре и разомкнутом втором, мгновенные значения э. д. с. самоиндукции e_Ll и напряжения u_Ll первой катушки, пренебрегая ее активным сопротивлением:

и аналогично э. д. с. взаимоиндукции е_М2 и напряжение u_м2 второй:

Здесь 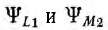— потокосцепления самоиндукции первой и взаимоиндукции второй катушек.

При синусоидальном токе для комплексных величин

Величина ωМ, имеющая размерность сопротивления, называется сопротивлением взаимоиндуктивности х_M; комплексное сопротивление взаимоиндуктивности

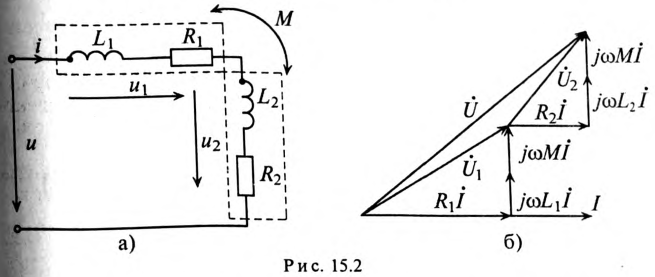
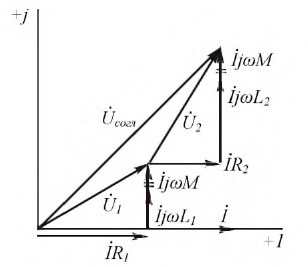
Последовательное и параллельное соединения с взаимной индукцией

При последовательном соединении катушек (рис. 11.2, а и б) ток в них один и тот же, а приложенное напряжение должно преодолеть все э. д. с. и сопротивления цепи. При согласном включении катушек (см, рис. 11.2, а), когда магнитные потоки самоиндукции и взаимоиндукции в обеих катушках направлены одинаково, э. д. с. самоиндукции и взаимоиндукции имеют одинаковые знаки.

При встречном включении катушек (см. рис. 11.2, б) магнитные потоки самоиндукции и взаимоиндукции направлены в противоположные стороны и э. д. с. взаимоиндукции имеет знак, обратный знаку э. д. с. самоиндукции.

Тогда приложенное напряжение при обходе контура по принятому положительному направлению тока

где r₁ и r₂ — активные сопротивления первой и второй катушек; L₁ и L₂ — их индуктивности, М — взаимоиндуктивность; верхний знак соответствует согласному, нижний — встречному включению. Для синусоидального напряжения и тока это же соотношение может быть записано в комплексной форме:

Следовательно, результирующие индуктивности катушек и всей цепи при согласном включении

при встречном включении

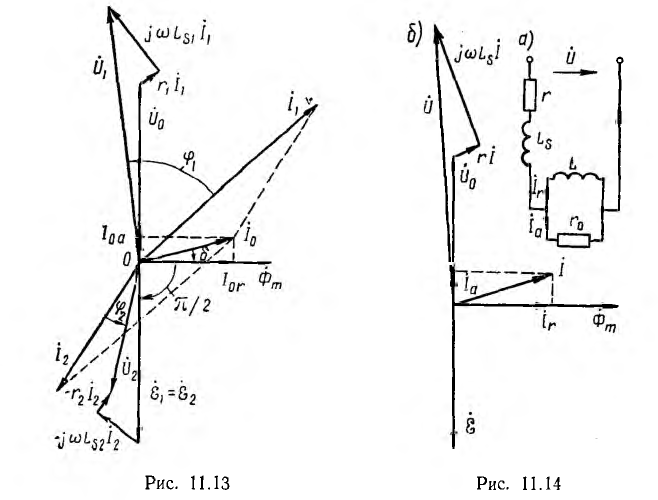
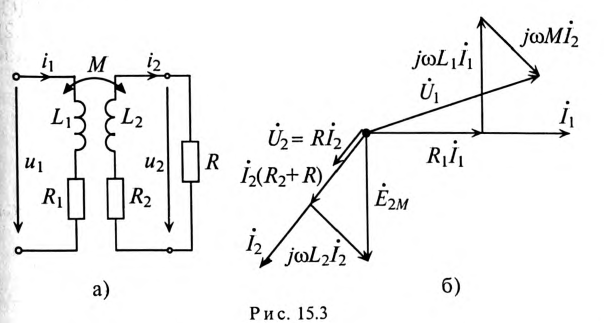
С увеличением М, например при сближении катушек, результирующие индуктивности при согласном включении увеличиваются, при встречном — уменьшаются. При М > L₂ результирующая индуктивность L₂ второй катушки при встречном включении становится отрицательной. Это значит, что вектор индуктивного напряжения U_2L этой катушки получает направление, противоположное векторам индуктивного напряжения U_lL первой катушки и U_L всей цепи; при этом, очевидно, U_lL > U_2L и U_lL > U_L (рис. 11.3). Таким образом, вектор U_2L отстает по фазе от вектора тока I на π/2, а на первом участке возникает повышенное напряжение, как будто вместо второй катушки включен конденсатор; это может быть названо случаем ложной емкости. При этом цепь в целом носит индуктивный характер.

Из выражений для результирующих индуктивностей всей цепи для согласного L’ и встречного L» включения можно вычислить взаимоиндуктивность

В других схемах включения катушек, связанных взаимоиндукцией, токи в них в общем случае сдвинуты по фазе; следовательно, часть периода потоки самоиндукции и взаимоиндукции в обеих катушках будут согласными, остальную часть — встречными. Однако принимается, что включение является согласным, если относительно одноименных зажимов совпадают выбранные положительные направления токов.

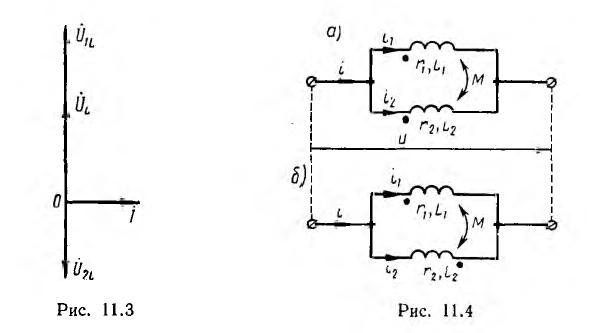
При параллельном соединении катушек (рис. 11.4) их напряжение одинаково. Тогда уравнения равновесия напряжений для первой и второй катушек, соответственно, для мгновенных значений и комплексов имеют вид:

Здесь верхний знак относится к согласному включению (рис. 11.4, а), а нижний — к встречному (рис. 11.4, б).

Если пренебречь активными сопротивлениями катушек, из этих уравнений вытекает, что

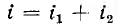
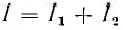
Здесь — мгновенное значение, а — комплекс тока цепи до разветвления.

Стедовательно, результирующие индуктивности первой и второй катушек и всей цепи при согласном и встречном включении будут:

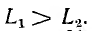
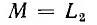
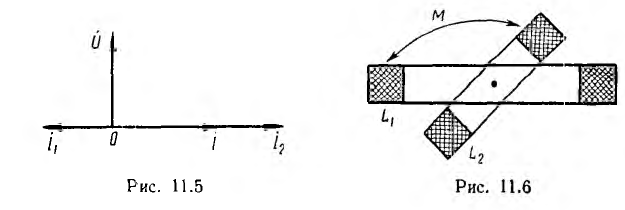
Пусть. В случае согласного включения результирующая индуктивность L₁ первой катушки при делается равной

бесконечности; это значит, что э. д. с. взаимоиндукции уравновешивает приложенное напряжение, и ток первой катушки становится равным нулю. При М > L₂ имеет место явление ложной емкости: индуктивность L₁ становится отрицательной, и вектор тока I₁ этой катушки получает направление, противоположное векторам тока I₂ второй катушки и I всей цепи (рис. 11.5); вектор ft опережает по фазе вектор напряжения U на π/2, как будто вместо первой катушки включен конденсатор, при этом, очевидно,

Для плавного изменения индуктивности применяют вариометры, состоящие из двух катушек. Меньшая катушка помещена внутри большей и может поворачиваться (рис. 11.6). При совпадении их осей взаимоиндуктивность максимальна: М = М_mах. При повороте М. уменьшается и при прямом угле между осями М= 0. Соединяя катушки параллельно и последовательно, можно получить плавное вменение результирующей индуктивности в пределах от минимального значения при параллельном встречном соединении до максимального при последовательном согласном включении, т. е. от

Если уравнять ее максимальное значение при параллельном согласном включении с минимальным значением при последовательном встречном включении, то

Расчет сложных цепей с взаимной индукцией

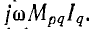
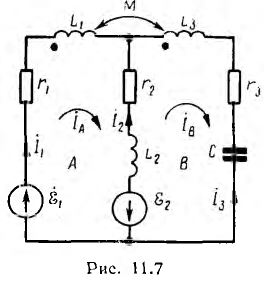
Расчет сложных цепей со взаимной индукцией можно вести символическим методом по законам Кирхгофа, так как последние справедливы для любых цепей, но в уравнениях по второму закону Кирхгофа в выражения для напряжений катушек должны быть добавлены комплексные напряжения взаимной индукции вида ± В соответствии со сказанным в  положительный знак у этого комплекса должен быть выбран при совпадении относительно одноименных зажимов ! направления обхода катушки р и направления тока в катушке q. При несовпадении указанных направлений комплекс должен получить отрицательный знак.

В качестве примера приведена система уравнений, составленных по первому и второму законам Кирхгофа для цепи рис. 11.7 в соответствии с указанными на схеме положительными направлениями э. д. с. и одноименными зажимами, а также выбранными направлениями токов ветвей и обхода контуров:

Для расчета цепей со взаимной индукцией применим также метод контурных токов, так как его вывод был основан на втором законе Кирхгофа, учитывающем э. д. с. взаимной индукции. Уравнения для контурных токов получают вид:

где М_Aв — взаимоиндуктивность катушек контуров А и В и т. п.. а знак выбирается соответственно сказанному выше. Сопротивление взаимной индукции удобно добавить к взаимным сопротивлениям контуров:

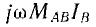
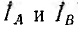
При этом правило знаков изменяется на обратное: при совпадении направлений обхода катушки контура A и тока в катушке контура В у комплекса в должен быть выбран отрицательный знак, и наоборот. Тогда, например, система уравнений для контурных токов цени рис. 11.7 получит вид:

Метод наложения, основанный на линейности уравнений, составленных по законам Кирхгофа, также применим, так как и при наличии взаимной индукции уравнения остаются линейными. Это же относится к методу эквивалентного источника энергии при условии, что ток или напряжение определяются для ветви, не связанной взаимной индукцией с остальной частью цепи.

Метод узловых напряжений для цепей со взаимной индукцией неприменим, так как его вывод основан на первом законе Кирхгофа, который не позволяет непосредственно учесть э. д. с. взаимной индукции. В общем случае цепей со взаимной индукцией неприменим и метод преобразования, так как он основан на использовании кроме второго, также и первого закона Кирхгофа.

Трансформатор без стального сердечника

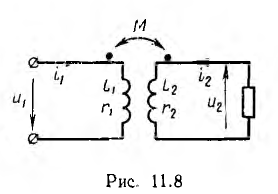
Широкое применение в электротехнике имеет трансформатор — статическое устройство, предназначенное для преобразования величины переменных напряжений и токов. В простейшем случае он не имеет ферромагнитного сердечника и представляет собой две катушки с индуктивной связью (рис. 11.8); такие трансформаторы применяются в радиотехнике.

Напряжение их источника приложено к первичной катушке трансформатора, к вторичной катушке подключена нагрузка.

Тогда уравнения по второму закону Кирхгофа для первичной и вторичной цепей при показанных на рис. 11.8 одноименных зажимах и положительных направлениях токов, при которых потоки самоиндукции и взаимоиндукции складываются, получают следующий вид:

где u₂ — напряжение на приемнике, a r_1, L₁, и r₂, L₂ — сопротивление и индуктивность, соответственно, первичной и вторичной катушек.

При холостом ходе вторичная катушка разомкнута и ток первичной цепи индуктирует во вторичной э. д. с. взаимоиндукции

При синусоидальном законе изменения величин комплекс э. д. с. холостого хода

При сопротивлении приемника 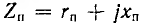уравнения трансформатора в комплексной форме имеют вид:

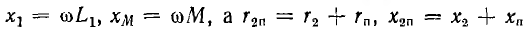
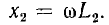
Здесь— суммарные активное и реактивное сопротивления вторичной цепи, где Из второго уравнения может быть определен комплекс вторичного тока:

Так как исходные уравнения были составлены в предположении, что потоки, пропорциональные токам, складываются, . знак минус в этом выражении, связывающем комплексы токов I₁ и I₂, указывает на то, что векторы этих токов составляют тупой угол; в пределе, при 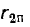=0, токи находятся в противофазе. Полученный результат соответствует правилу Ленца о направлении индуктированного тока.

Переход от комплекса вторичного тока к его действующему значению дает:

откуда может быть определен коэффициент трансформации тока

Из этих соотношений видно, что коэффициент трансформации тока не является постоянной величиной, а зависит от сопротивления приемника. Можно показать, что коэффициент трансформации напряжения 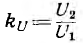также зависит от сопротивления приемника.

После подстановки значения I₂ в первое уравнение трансформатора получается выражение первичного тока:

откуда видно, как будет изменяться ток I₁ при изменении сопротивления приемника.

В знаменателе выражения для I₂ стоит результирующее полное сопротивление цепи, эквивалентной трансформатору. Результирующее активное сопротивление

состоит из суммы активного сопротивления первичной цепи и сопротивления, вносимого вторичной цепью,

Средняя (активная) мощность, потребляемая трансформатором,

т. е. равна сумме мощностей первичной и вторичной цепи, а к. п. д. трансформатора

Результирующее реактивное сопротивление

состоит из разности реактивного сопротивления первичной цепи х₁ и сопротивления x_2π вносимого вторичной цепью. При индуктивном характере нагрузки x_π > 0 и вносимое реактивное сопротивление

т. е. x₂ < х₁ так как коэффициент связи 

Следовательно, результирующее реактивное сопротивление х = х₁ — x₂ трансформатора при индуктивной нагрузке имеет также индуктивный характер и эффект ложной емкости невозможен.

При емкостной нагрузке х_π= — x_с, и вносимое реактивное сопротивление

При х_с > х₂ сопротивление х₂ <0. Следовательно, результирующее реактивное сопротивление х > x₁ и носит индуктивный характер. При x_с < х₂ и достаточно большом значении коэффициента трансформации тока k₁ сопротивление х может стать отрицательным, т. е. также получить емкостный характер.

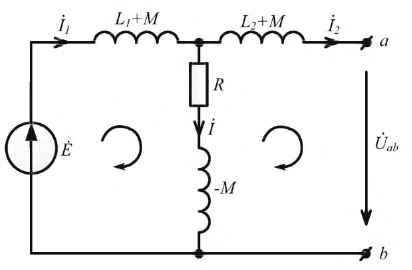
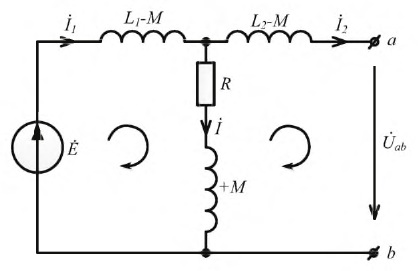
Уравнения трансформатора могут быть представлены в следующем виде:

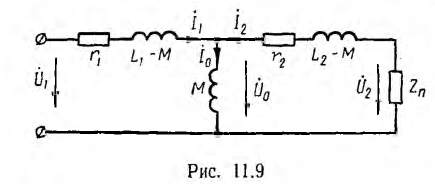
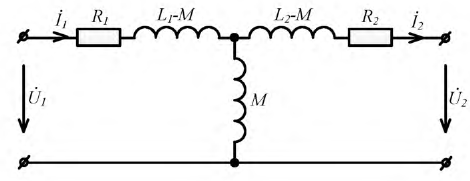
Эти же уравнения по второму закону Кирхгофа являются уравнениями для двух элементарных контуров Т-образной цепи рис. 11.9 при принятых на ней направлениях токов; следовательно, трансформатор, т. е. цепь с индуктивной связью, может быть заменен эквивалентной схемой с кондуктивной связью контуров.

Если значение М лежит между L₁ и L₂, например L₁ < М < L₂, то L₁ — М отрицательно, что эквивалентно емкости; получается схема, в которой возможно соотношение U₂ > U₁, что имеет место в трансформаторе, повышающем напряжение. При L_l> М > L₂ емкостный характер получает элемент L₂— М, что делает возможным соотношение I₁ < I₂, имеющее место в трансформаторе, понижающем напряжение.

В трансформаторе с одинаковым числом витков катушек ω₁= ω₂= ω) L₁, L₂ и М пропорциональны соответственно полным потокам и потокам взаимоиндукции, создаваемым катушками. В этом случае разности L₁ — М и L₂ — М имеют физический смысл, являясь, очевидно, индуктивностями рассеяния первичной L_sl и вторичной L_s2 катушек трансформатора . В таком трансформаторе результирующая и. с.

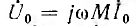
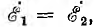
пропорциональна току и потоку намагничивающей ветви М эквивалентной схемы, а напряжение на зажимах этой ветви равно и обратно по знаку э. д. с. индуктируемых потоком взаимоиндукции в обеих катушках.

Трансформатор и катушка индуктивности со стальным сердечником

Трансформатор со стальным сердечником:

В электротехнике обычно применяют трансформаторы со стальным сердечником— магнитопроводом 3 стержневого (рис. 11.10, а) или броневого (рис. 11.10, б) типа; расположение первичной 1 и вторичной 2 обмоток (катушек) также показано на рис. 11.10.

При применении ферромагнитного магнитопровода та же взаимоиндуктивность, благодаря большому значению магнитной проницаемости µ стали по сравнению с µ₀, может быть получена при меньших числах витков ω₁ и ω₂ первичной и вторичной катушек и меньших размерах трансформатора, т. е. при малом расходе стали на магнито-провод и меди на его обмотки.

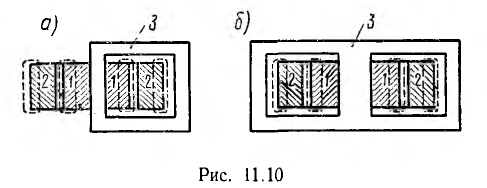
Потоки рассеяния, проходящие в основном по воздуху (пунктир на рис. 11.10), и соответствующие им индуктивности рассеяния 2L_sl и L_s2 также уменьшатся при уменьшении размеров трансформатора. Поэтому коэффициент связи возрастет, что следует из его выражения для трансформатора ω₁ = ω₂:

В трансформаторе со стальным сердечником может быть достигнут коэффициент связи, близкий к единице.

Потери в сердечнике на вихревые токи и гистерезис. Эквивалентная схема трансформатора

Периодическое перемагничивание стального сердечника вызывает потери на вихревые токи и гистерезис.

Вихревыми, или токами Фуко, называются токи, индуктируемые в магнитопроводе переменным магнитным потоком, созданным н. с. первичной и вторичной обмоток; следовательно, вихревые токи также являются следствием взаимоиндукции. Для уменьшения потерь и размагничивающего действия от вихревых токов применяют чаще всего магнитопроводы, состоящие из листов специальной стали, изолированных друг от друга; их разделение следует производить так, чтобы плоскости листов были направлены вдоль линий магнитной индукции.

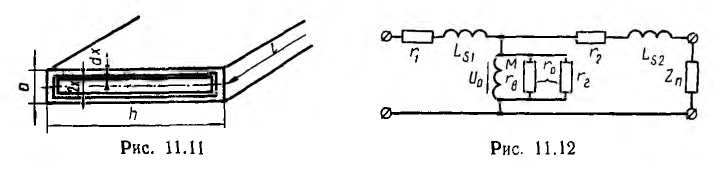
Далее произведён расчет потерь на вихревые токи в листе стали толщиной а, шириной h > а и длиной l (рис. ll.il), пронизываемом магнитным потоком, изменяющимся по синусоидальному закону. Максимальное значение индукции В_m во всех точках сечения листа принимается одинаковым и сопротивление путей вихревых токов активным, что будет иметь место при пренебрежении размагничивающим действием вихревых токов, т. е. магнитным поверхностным эффектом .

Элементарный контур вихревого тока в виде полого цилиндра высотой l с прямоугольным основанием, имеющим длину 2х, ширину, принимаемую равной h, и толщину стенки dx, пронизывается магнитным потоком, максимальное значение которого

Действующее значение э. д. е., индуктируемой в элементарном контуре,

Активное сопротивление элементарного контура

Тогда мощность, расходуемая в элементарном контуре на вихревые токи,

Мощность, расходуемая во всем листе,

где V = hla — объем листа. Отсюда видно, что потери 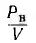в единице объема стали пропорциональны квадрату частоты и квадрату толщины листов, и, следовательно, разделение стали магнитопровода на тонкие листы приводит к уменьшению потерь на вихревые токи.

В эквивалентной схеме трансформатора необходимо учесть потери на вихревые токи добавлением ветви, потребляющей ту же мощность. Для этого дополнительное активное сопротивление r_B надо включить на напряжение U₀ намагничивающей ветви М (рис. 11.12 для трансформатора с ω₁= ω₂= ω), так как тогда потребляемая им мощность Р_B будет находиться в квадратичной зависимости от индукции и частоты, как и потери на вихревые токи:

Величина сопротивления r_в должна быть такой, чтобы потери Р’_в нем равнялись потерям Р_в в стали на вихревые токи:

Oткуда

где V, S и b — объем, сечение и средняя длина магнитопровода.

Мощность потерь на гистерезис Р_г при частоте f легко получить из формулы Штейнмеца для энергии W_r, затраченной на один цикл перемагничивания:

где коэффициент η зависит от материала, а V — объем магнитопровода. Линейная зависимость этих потерь от частоты в отличие от квадратичной зависимости потерь на вихревые токи может быть использована для разделения суммарных потерь в стали, если они известны для двух частот при одной и той же индукции В_m.

В схеме, эквивалентной трансформатору, потери Р_г на гистерезис учитываются сопротивлением 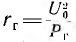включаемым также параллельно намагничивающей ветви (см. рис. 11.12).

Величина r_r определяется аналогично из равенства потерь в сопротивлении и в стали. Если принять последние пропорциональными 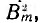, то

откуда

т. е., помимо конструктивных данных, гг зависит от частоты.

Обычно сопротивления r_в и r_r объединяются в сопротивление ветви потерь в стали 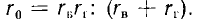Важно отметить, что при малых потерях в стали сопротивление r₀ должно быть велико, так как оно включается в схему параллельно.

Специальные электротехнические стали с малыми удельными потерями на гистерезис и вихревые токи имеют толщину от 0,5 до 0,1 мм, более тонкие листы приходится применять при повышенной частоте. В радиоэлектронике и вычислительной технике применяются также сердечники из спрессованной смеси ферромагнитного порошка с изолирующим материалом и из ферритов, получаемых спеканием окислов магнитных и немагнитных материалов.

Векторная диаграмма трансформатора

Векторная диаграмма при активно-индуктивной нагрузке для эквивалентной схемы рис. 11.12 и тем самым для трансформатора с ω₁= ω₂ и со стальным магнитопроводом показана на рис. 11.13 Нелинейность катушек со стальным сердечником при водит к тому, что при синусоидальном напряжении ток i₀ намагничивающей ветви будет несинусоидальным  Ввиду малости этого тока по сравнению с практически синусоидальными токами i₁ и i₂ при нагрузке трансформатора можно этим явлением пренебречь, считать все токи синусоидальными и изображать их векторами.

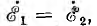
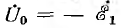
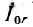
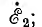
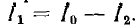
Векторная диаграмма строится в соответствии с положительными направлениями напряжений и токов, принятыми на схеме рис. 11.9. Исходным вектором удобно принять вектор потока взаимоиндукции Ф_m затем строятся векторы э. д. с. , отстающие по фазе от Ф_m на угол π/2. Напряжением определяется реактивный ток в намагничивающей ветви и активный I_оа — в ветви потерь. Эти токи в сумме дают вектор намагничивающего тока I₀, опережающий вектор потока Ф_m на угол потерь δ. Вторичный ток I₂ отстает по фазе от своей э. д. с. первичный ток находят из соотношения Первичное U₁ и вторичное U₂ напряжения определяются выражениями

Как видно из диаграммы, в трансформаторе ω₁= ω₂ напряжения и токи входа и выхода не равны друг другу 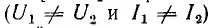и соотношения между ними определяются нагрузкой.

Линейная теория катушки индуктивности со стальным сердечником

При холостом ходе трансформатора, т. е. при разомкнутой вторичной цепи, его эквивалентная схема упрощается (рис. 11.14, а). Очевидно, что трансформатор в этом режиме аналогичен катушке со стальным сердечником, часто применяемой в электротехнике. Тогда схема рис. 11.14, а является также эквивалентной схемой катушки, если намагничивающую ветвь характеризовать не взаимоиндуктивностью М, а равной ей индуктивностью 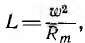где R_m — магнитное сопротивление магнитопровода; в эквивалентной схеме катушки r — активное сопротивление обмотки, L_s — ее индуктивность рассеяния, r₀—сопротивление ветви потерь.

Здесь также часто пренебрегают нелинейностью L и строят векторную диаграмму; по сравнению со случаем нагруженного трансформатора погрешность получается бoльшей.

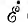
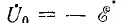
За исходный вектор векторной диаграммы (рис. 11.14, 6) удобно принять вектср потока Ф_m в магнитопроводе; вектор э. д. с. отстает на π/2 от Ф_m. Напряжение создает реактивный ток 1 г в ветви L и активный I_а в ветви г₀, которые в сумме дают вектор I тока катушки. Напряжение на зажимах катушки

Из-за наличия потерь в меди и стали сдвиг 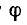по фазе между напряжением U и током I меньше π/2.

Теория катушки со стальным сердечником, учитывающая нелинейность L.

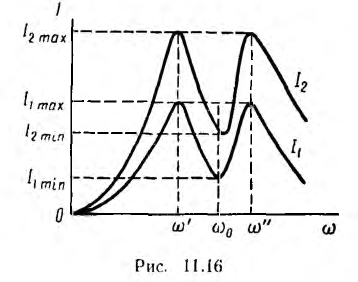
Резонанс в двух индуктивно связанных цепях

Явление резонанса в связанных цепях широко используется в технике связи, в особенности в радиотехнике — в передающих и приемных устройствах.

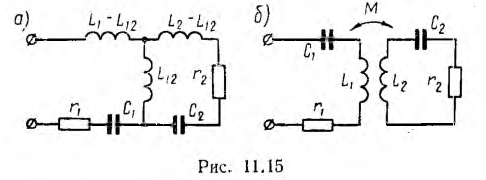
Связанными называются цепи, имеющие общую ветвь в действительной или эквивалентной схеме. Примером может служить индуктивная связь, осуществляемая при помощи общего индуктивного сопротивления (рис. 11.15, а) или путем электромагнитной индукции —трансформаторная связь (рис. 11.15, б). Оба эти вида индуктивной связи будут эквивалентны друг другу, если полные индуктивности L_l и L₂ обоих контуров соответственно равны друг другу, a L₁₂= М.

Степень связи цепей характеризуется коэффициентом связи k, который в общем случае представляет собой отношение сопротивления обшей ветви к корню квадратному из произведения одноименных с ним сопротивлений каждого из двух связанных контуров, причем в сопротивление контуров должно быть включено и сопротивление общей ветви. Тогда для простой индуктивной связи (рис. 11.15, а)

для трансформаторной связи (рис. 11.15, б) получается известное выражение

Пусть резонансная частота обеих цепей рис. 11.15, б одинакова:

Если пренебречь активным сопротивлением вторичной цепи (r₂ = 0), то из следует, что реактивное сопротивление всей цепи рис. 11.15, б, а следовательно, и эквивалентной ей цепи рис. 11.15, а равно:

При частоте т. е. в разветвленной части схемы рис. 11.15, а, эквивалентной исследуемой цепи рис. 11.15, б, имеет место резонанс токов. При наличии во вторичном контуре небольшого активного сопротивления кривая при U₁= const также проходит через минимум, но (рис. 11.16).

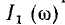
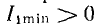
В исследуемой цепи происходит резонанс напряжений, и ток получает максимальное значение при условии х = 0, откуда

Если разделить обе части этого равенства на 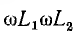и учесть выражения для резонансной частоты ω₀ обоих контуров и коэффициента связи k, условие резонанса напряжении получает вид:

откуда

Следовательно, имеются две частоты, при которых величина I₁ максимальна; резонанс напряжений имеет место между левой и разветвленной правой частью схемы рис. 11.15, а; причем для меньшей из этих частот сопротивление левой части эквивалентной схемы носит емкостный характер, а правой — индуктивный, для большей частоты — наоборот.

Решение уравнений для этой цепи относительно тока I₂ приводит к выводу, что кривая I₂ (ω) при U_l = const и малом активном сопротивлении также имеет два максимума при тех же частотах 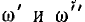в то время как минимума эта кривая достигает при частоте, несколько большей, ω₀(рис. 11.16).

Следовательно, в отличие от кривой I (ω) при U = const для уединенного контура с L и С, имеющей один максимум при последовательном соединении (см. рис. 7.6) или один минимум при параллельном соединении (см. рис. 7.10), резонансные кривые, т. е. частотные характеристики I₁(ω) и I₂(ω) цепи, состоящей из двух связанных контуров с малым активным сопротивлением, имеют два максимума и один минимум. Выражения для резонансных частот могут служить для нахождения коэффициента связи:

При больших активных сопротивлениях точки резонансов сливаются, и резонансные кривые будут иметь только по одному максимуму.

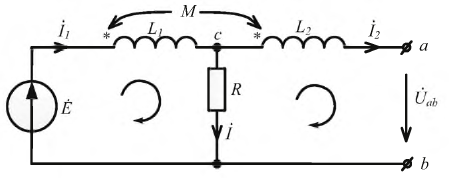
Электрические цепи с взаимной индуктивностью

Переменная магнитная связь:

Индуктивность двух взаимосвязанных катушек можно изменить, если кроме магнитной связи эти катушки соединены электрически. Индуктивность таких катушек зависит от их соединения и взаимного расположения относительно друг друга.

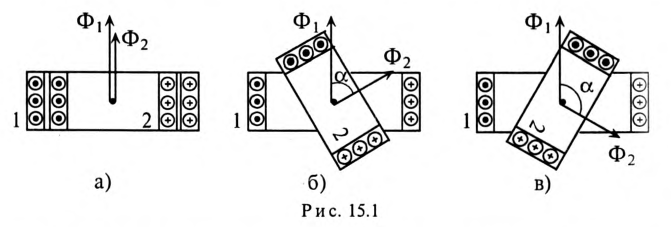
Устройство, дающее возможность изменять магнитную связь (коэффициент связи К) двух контуров или катушек, называют вариометром.

Вариометр представляет собой две катушки, одна из которых (2) может поворачиваться внутри неподвижной катушки (1), изменяя

при этом угол между магнитными потоками катушек (рис. 15.1).

В зависимости от взаимного расположения этих катушек различают их согласное и встречное включение.

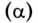
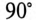
При согласном включении угол между магнитными потоками катушек не превышает и магнитные потоки катушек при этом суммируются.

При встречном включении угол между магнитными потоками катушек 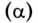превышает и магнитные потоки при этом вычитаются.

Схема замещения последовательно соединенных катушек вариометра изображена на рис. 15.2а.

При согласном включении катушек суммируются ЭДС самоиндукции, созданные магнитными потоками

Также суммируются ЭДС взаимоиндукции, созданные потоками одной катушки, пронизывающие витки другой катушки:

        

При последовательном соединении катушек (рис. 15.2а)

Составляется уравнение по второму закону Кирхгофа для первой катушки:

или

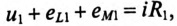
или в комплексной форме

Для второй катушки:

 или

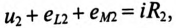
или в комплексной форме

Напряжение, приложенное к последовательно включенным катушкам (входное напряжение), определяется по формуле

Тогда 

Векторная диаграмма цепи при последовательном согласном включении двух катушек показана на рис. 15.2б.

Как следует из (15.3), общая индуктивность двух катушек вариометра при их согласном включении:

Таким образом, при согласном включении катушек ЭДС самоиндукции и взаимоиндукции складываются: (15.1) и (15.2). При встречном включении тех же катушек ЭДС самоиндукции и взаимоиндукции вычитаются:

Для второй катушки:

Тогда напряжение, приложенное к встречно включенным катушкам, определяется выражением

Из выражения (15.7) следует, что общая индуктивность двух катушек вариометра при их встречном включении:

Сравнивая (15.4) и (15.8), видим, что суммарная (эквивалентная) индуктивность двух магнитосвязанных катушек и, следовательно, их индуктивное сопротивление 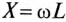при согласном включении больше, чем при встречном:

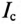
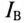
Следовательно, ток магнитосвязанных катушек при согласном включении меньше, чем ток при их встречном включении, т. е.

Если обмотку катушки выполнить двумя рядом расположенными изолированными проводами, соединенными электрически с одной стороны (концами или началами), то получится встречное включение, при котором 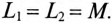При этом общая индуктивность согласно (15.8) будет равна нулю

Безындуктивные катушки, намотанные таким двойным проводом, называются бифилярными.

В ряде случаев явление взаимоиндукции бывает полезным (трансформаторы). Иногда это явление бывает нежелательным, например, если параллельно линии электропередачи расположена линия связи.
 

Воздушный трансформатор

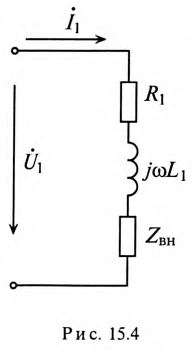
Рассмотрим в качестве примера расчета индуктивно связанных цепей воздушный трансформатор, который состоит из двух индуктивно связанных катушек (обмоток), намотанных одна на другую (рис. 15.3а).

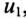
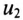
Первичная обмотка трансформатора присоединена к источнику с напряжением а к вторичной обмотке с напряжением подключается приемник, например, с активным сопротивлением R.

Положительные направления 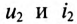выбираются так, чтобы ЭДС самоиндукции и взаимоиндукции суммировались (согласное включение):

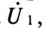
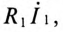
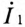
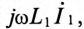
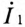
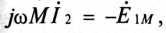
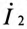
Таким образом, напряжение, приложенное к первичной обмотке трансформатора состоит из активной составляющей совпадающей по фазе с током (рис. 15.36), реактивной составляющей опережающей ток по фазе на 90°, и составляющей опережающей по фазе ток на 90°.

Сопротивление первичной обмотки трансформатора равно

Так как во вторичной цепи отсутствует источник питания, т.е. 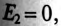то по второму закону Кирхгофа можно записать:

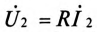
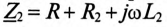
где — напряжение на приемнике R или на клеммах вторичной обмотки, a  — сопротивление вторичной цепи.

ЭДС взаимоиндукции во вторичной обмотке будет равно

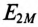
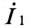
На векторной диаграмме (рис. 15.3б) показано, что отстает по фазе от тока на 90° и равна сумме падений напряжений на сопротивлениях

Из выражения (15.11) определяется ток вторичной цепи

Подставив выражение (15.12) для тока 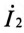в (15.9), можно определить

где 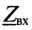— входное сопротивление нагруженного трансформатора.

Слагаемое 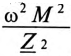 называют вносимым сопротивлением в первичную цепь, т.е.

Следовательно, для источника питания нагруженный трансформатор можно представить простой схемой замещения (рис. 15.4).

Тогда по закону Ома

Откуда

Таким образом, при заданных параметрах первичной и вторичной цепей и напряжений источника питания можно рассчитать токи 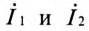и построить векторную диаграмму (рис. 15.36).

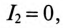
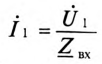
В режиме холостого хода, когда ток  и напряжение вторичной обмотки

Цепи со взаимной индуктивностью

Изменение тока в электрической цепи приводит к соответствующему изменению магнитного потока, который, в свою очередь, приводит к появлению ЭДС самоиндукции, обусловленной скоростью изменения потокосцепления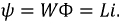  

При анализе цепей с синусоидальными токами мы познакомились с явлением самоиндукции, то есть наведением ЭДС в электрической цепи при изменении магнитного потока, обусловленного изменением тока в этой же цепи:

Кроме явления самоиндукции, в электрических цепях возможно возникновение взаимной индукции. Физически это можно объяснить так: изменение тока в одной цепи вызывает изменение величины потокосцепления взаимной индукции в другой и наоборот. В данном случае говорят, что эти цепи индуктивно связаны.

Для исследования данного явления рассмотрим две катушки (рис. 6.1).

Рис. 6.1. Индуктивно связанные катушки

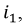
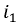
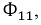
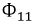
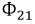
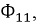
Пусть, например, в катушке 1 протекает ток  а во второй — ток отсутствует. Тогда вызывает магнитный поток который пронизывает все витки первой катушки и вызывает ЭДС самоиндукции. Поскольку катушки находятся достаточно близко друг от друга, то часть силовых линий  пронизывает витки второй катушки, где — это часть пронизывающая катушку 2. Очевидно, что

Соответственно:

 — потокосцепление первой катушки;

 — потокосцепление второй катушки.

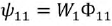
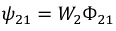
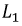
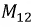
В итоге получим индуктивность первой катушки  и взаимную индуктивность обеих катушек в виде:

Аналогичная картина могла бы иметь место при протекании тока во второй катушке и отсутствии тока в первой катушке:

Т.к. магнитные свойства среды, заполняющей катушки (воздух), неизменны, то 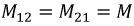— взаимная индуктивность двух катушек (индуктивная связь) — величина неизменная и зависит только от взаимного положения и чисел витков катушек. Степень индуктивной связи характеризуется коэффициентом:

ЭДС взаимоиндукции

На основании закона электромагнитной индукции изменение магнитного потока катушки вызывает ЭДС самоиндукции, которая при линейности катушки может быть определена следующим образом:

В соответствии с законом Ленца (законом электромагнитной инерции) эта ЭДС препятствует изменению потокосцепления. Приложенное к катушке напряжение уравновешивает ЭДС самоиндукции:

Для двух индуктивно связанных катушек изменение тока в одной приводит к изменению величины потокосцепления в другой и, наоборот, при этом:

Величины 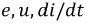в общем случае могут иметь различные знаки, которые будут определяться направлением тока в индуктивно связанных катушках. Покажем это на примере двух катушек, намотанных на общий сердечник (рис. 6.2 и 6.3).

Рис. 6.2. Варианты намотки катушек с согласно направленными магнитными потоками

Рис. 6.3. Варианты намотки катушек со встречно направленными магнитными потоками

Из анализа этих рисунков можно сделать вывод, что направление результирующего магнитного потока определяется не только направлением тока относительно зажимов, но и направлением намотки данных катушек. С целью единообразия в изображении способа соединения катушек прибегают к маркировке их зажимов (точки, звёздочки и т.д.).

Правило. Если относительно маркированных зажимов токи протекают одинаково, то магнитные потоки самоиндукции и взаимной индукции складываются, в противном случае вычитаются. При этом в первом случае говорят о согласном, а во втором — о встречном включении катушек.

Теперь перейдём к вопросу о знаке ЭДС взаимной индукции.

Пусть клеммы первой катушки разомкнуты, а во второй протекает ток указанного направления (рис. 6.4).

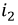
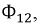
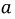
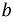
Выберем положительные направления ЭДС взаимной индукции и напряжения на её зажимах совпадающими. Ток создает поток взаимной индукции который пронизывает витки первой катушки и наводит между зажимами и ЭДС взаимной индукции.

Рис. 6.4. Схема, иллюстрирующая знак ЭДС взаимной индукции

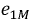
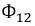
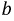
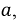
Исходя из выбранных направлений токов, напряжений и ЭДС, можно сделать вывод о том, что наводимая на зажимах первой катушки ЭДС взаимной индукции должна препятствовать изменению потока и поэтому должна быть направлена от к  т.е. встречно выбранному его положительному направлению, т.е. получится отрицательным. Исходя из этого:

Если 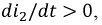то

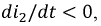
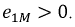
Если то  

Используя аналогичные рассуждения, можно получить выражение для случая, когда ток, ЭДС и напряжение выбраны неодинаково относительно маркированных зажимов. Например, если изменилось направление тока 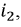то:

Расчет цепей при наличии взаимной индуктивности

Последовательное согласное включение индуктивно связанных катушек:

Рассмотрение данного вопроса начнём с простейших способов соединения двух индуктивно связанных катушек: последовательного и параллельного. При этом будем использовать комплексный метод расчета.

При согласном способе включения катушек направление тока относительно маркированных зажимов первой и второй катушек одинаковое (рис. 6.5).

Рис. 6.5. Схема последовательного согласного включения двух катушек

Составим уравнение электрического равновесия для данного участка цепи с учётом индуктивной связи по второму закону Кирхгофа:

Используя полученное выражение, построим векторную диаграмму для данного способа соединения (рис. 6.6).

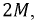
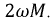
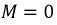
Из полученного выражения следует, что при согласном включении катушек общая индуктивность возрастает на величину а общее сопротивление — на величину  В частном случае при уравнение упрощается.

Введём параметр 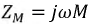 и назовём его сопротивлением взаимной индуктивности.

Рис. 6.6. Векторная диаграмма для последовательного согласного включения двух катушек

Последовательное встречное включение индуктивно связанных катушек

При встречном способе включения направление тока относительно маркированных зажимов первой и второй катушек различно (рис. 6.7).

Рис. 6.7. Схема последовательного встречного включения двух катушек

Используя полученные ранее соотношения, можно записать аналогичное уравнение для встречного включения тех же катушек:

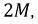
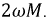
Для данного способа включения общая индуктивность уменьшится на  а входное сопротивление — на величину Аналогичным образом построена векторная диаграмма для встречного соединения катушек (рис. 6.8).

Рис. 6.8. Векторная диаграмма для последовательного встречного включения двух катушек

Параллельное согласное включение индуктивно связанных катушек

Составим систему уравнений для расчета цепи по законам Кирхгофа для схемы рис. 6.9:

Рис. 6.9. Схема параллельного согласного включения двух катушек

Обозначим:

Решим полученную систему уравнений относительно токов:

Входная проводимость цепи будет:

В случае, когда взаимная индуктивность 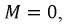получим:

Параллельное встречное включение индуктивно связанных катушек

Для схемы, представленной на рис. 6.9, при встречном включении катушек уравнения для расчета цепи по законам Кирхгофа будут иметь вид:

Решение данной системы:

Входное сопротивление цепи будет:

Соответствующие векторные диаграммы строятся аналогично случаю последовательного соединения данных катушек.

Расчет разветвлённых цепей при наличии взаимной индуктивности

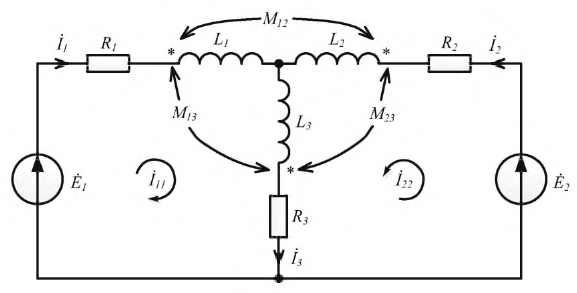
Расчёт разветвлённых цепей при наличии взаимной индуктивности представляется более сложным этапом. Он осуществляется с помощью законов Кирхгофа либо метода контурных токов. Отметим, что метод узловых потенциалов в данном случае неприменим, поскольку токи в ветвях определяются не только разностью потенциалов соседних узлов, но и токами других ветвей, с которыми они связаны индуктивно. Пусть имеются три индуктивно связанные катушки, намотанные на общий сердечник, выполненный из немагнитного материала, и подключённые к двум источникам ЭДС. Получим электрическую схему по рис. 6.10.

Рис. 6.10. Электрическая схема с индуктивно связанными катушками

Проведем расчёт методом контурных токов и составим систему уравнений относительно заданных на схеме контурных токов:

Решив систему, получим:

Эквивалентная замена индуктивных связей

Отличительной особенностью расчёта цепей с взаимной индуктивностью является то, что приходится одновременно учитывать электрические и магнитные связи. Расчёт цепей упростится, если теми или иными методами исключить магнитную связь и свести данную цепь к чисто электрической цепи. Это возможно, если прибегнуть к «развязыванию» магнитных связей, при этом в составе цепи появятся новые дополнительные элементы.

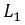
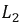
В схеме рис. 6.11 катушки и индуктивно связаны. Рассмотрим два варианта их соединения. В узле с они могут соединяться как одноименными, так и разноименными зажимами.

Рис. 6.11. Исходная схема

1. Пусть в узле с катушки соединены разноимёнными зажимами. Составим уравнения по законам Кирхгофа с учётом индуктивной связи:

Преобразуем систему уравнений к следующему виду:

Далее:

Полученная система описывает схему, представленную на рис. 6.12.

Рис. 6.12. Схема после «развязывания» магнитных связей при соединении катушек в узле разноименными зажимами

2. Если в узле с катушки соединены одноимёнными зажимами, аналогичные рассуждения позволили бы получить другую схему (рис. 6.13).

Рис. 6.13. Схема после «развязывания» магнитных связей при соединении катушек в узле одноименными зажимами

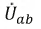
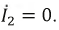
Для обоих случаев определим напряжение при условии, что  Тогда получим 

Для катушек, включенных разноименными зажимами, получим:

Для катушек, включенных одноименными зажимами, напряжение определится следующим выражением:

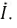
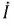
Оставаясь неизменным по модулю, в первом случае напряжение отстаёт на определённый угол, а во втором варианте — опережает ток  При этом модуль тока  не зависит от способа соединения катушек, то есть:

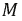
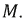
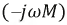
Появление параметра в процессе процедуры «развязывания» означает, что в состав цепи искусственно вводится некоторая дополнительная индуктивность Введенный элемент с сопротивлением  (см. рис. 6.12) можно формально рассматривать как емкостной элемент.

Линейный (воздушный) трансформатор

Воздушный трансформатор (рис. 6.14) является классическим примером линейной цепи, содержащей индуктивную связь.

Рис. 6.14. Схема линейного трансформатора

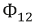
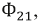
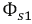
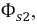
Полные магнитные потоки, создаваемые токами катушек, можно представить как сумму магнитного потока или сцепленного с витками другой катушки, и потока рассеяния или то есть

Индуктивности катушек:

где 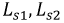— индуктивности рассеяния.

Тогда:

Введем понятие коэффициента трансформации, который представляет собой отношение числа витков первичной обмотки к числу витков вторичной обмотки:

С учетом заданных положительных направлений токов и напряжений в обмотках составим уравнения электрического равновесия для трансформатора, выбрав направление обхода в катушках по часовой стрелке:

Преобразуем данные уравнения следующим образом:

Перегруппируем слагаемые:

Полученная система уравнений позволяет построить схему замещения воздушного трансформатора, представленную на рис. 6.15.

Рис. 6.15. Схема замещения линейного трансформатора

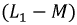
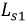
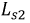
Индуктивные элементы и замещают в реальном трансформаторе индуктивности рассеяния и при условии, что количество витков катушек равны 

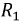
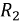
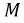
Сопротивления и замещают активное сопротивление проводов катушек. Индуктивный элемент  замещает в трансформаторе поток взаимной индукции.

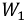
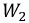
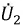
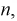
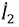
В полученной схеме отсутствует магнитная связь между катушками индуктивности, и теперь они соединены электрически. Однако в подавляющем числе случаев не равно и поэтому прибегают к составлению приведенной схемы замещения трансформатора, для которой параметры вторичной цепи приводятся к первичной. Для реализации такого приведения умножается на  а делится на

Вновь преобразуем исходные уравнения:

Проведя аналогичного рода преобразования:

и перегруппировав слагаемые:

получим систему уравнений (6.22), на основании которых составим схему замещения трансформатора (рис. 6.16).

Рис. 6.16. Схема замещения воздушного трансформатора при неравенстве количества витков в катушках

Ток во вновь образовавшейся ветви:

носит название намагничивающего тока холостого хода трансформатора. Смысловое содержание параметров схемы замещения остается тем же.

Вносимое сопротивление трансформатора

Пусть к выходным зажимам трансформатора по рис. 6.17 подключен приемник с сопротивлением

Рис. 6.17. Схема нагруженного трансформатора

Вновь составим систему уравнений для данной цепи по законам Кирхгофа с учетом выбранного направления обхода:

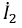
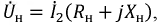
Выразим из второго уравнения ток и подставим его в первое уравнение. Так как то получим следующее выражение для тока

Подставляя его в первое уравнение, получим:

Проведя ряд алгебраических преобразований, получим следующее выражение для тока 

Обозначим:

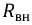
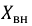
где и — соответственно активное и реактивное вносимые сопротивления трансформатора.

Тогда окончательно имеем:

Физически вносимое сопротивление представляет собой такое сопротивление, включенное последовательно с первичной обмоткой, которое позволяет учесть влияние тока нагрузки 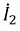на ток

Построим векторную диаграмму трансформатора под нагрузкой.

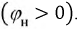
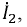
Пусть в качестве нагрузки используется активно-индуктивный потребитель Для построения диаграммы используем составленную выше систему уравнений (6.23). Построение векторной диаграммы, приведенной на рис. 6.18, целесообразно начать с тока совместив его для определённости с осью вещественных чисел.

Рис. 6.18. Векторная диаграмма линейного трансформатора под нагрузкой

Random converter

• Калькуляторы
• Электротехнические и радиотехнические калькуляторы

Калькулятор взаимной индукции

Электротехнические и радиотехнические калькуляторы

Электроника — область физики и электротехники, изучающая методы конструирования и использования электронной аппаратуры и электронных схем, содержащих активные электронные элементы (диоды, транзисторы и интегральные микросхемы) и пассивные электронные элементы (резисторы, катушки индуктивности и конденсаторы), а также соединения между ними.

Радиотехника — инженерная дисциплина, изучающая проектирование и изготовление устройств, которые передают и принимают радиоволны в радиочастотной области спектра (от 3 кГц до 300 ГГц), также обрабатывают принимаемые и передаваемые сигналы. Примерами таких устройств являются радио- и телевизионные приемники, мобильные телефоны, маршрутизаторы, радиостанции, кредитные карточки, спутниковые приемники, компьютеры и другое оборудование, которое передает и принимает радиосигналы.

В этой части Конвертера физических единиц TranslatorsCafe.com представлена группа калькуляторов, выполняющих расчеты в различных областях электротехники, радиотехники и электроники.

На этих страницах размещены конвертеры единиц измерения, позволяющие быстро и точно перевести значения из одних единиц в другие, а также из одной системы единиц в другую. Конвертеры пригодятся инженерам, переводчикам и всем, кто работает с разными единицами измерения.

Мы работаем над обеспечением точности конвертеров и калькуляторов TranslatorsCafe.com, однако мы не можем гарантировать, что они не содержат ошибок и неточностей. Вся информация предоставляется «как есть», без каких-либо гарантий. Условия.

Если вы заметили неточность в расчётах или ошибку в тексте, или вам необходим другой конвертер для перевода из одной единицы измерения в другую, которого нет на нашем сайте — напишите нам!

Канал Конвертера единиц TranslatorsCafe.com на YouTube

When the two coils are arranged in such a way that a change of current in one coil causes an emf to be induced in the other, the coils are said to have mutual inductance. The mutual inductance is denoted letter M and measured in Henry.

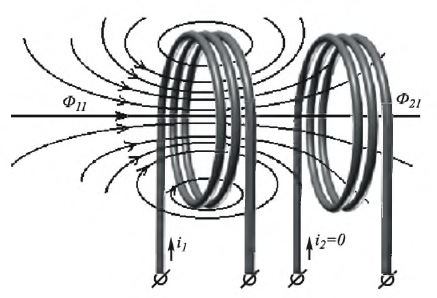
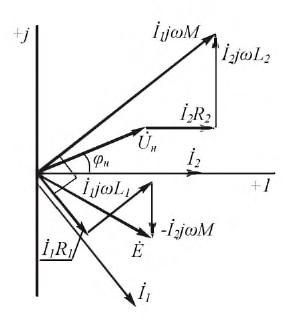
Consider two coils, coil 1 and coil 2 placed adjacent to each other. When a current I1 flows in the coil 1, a magnetic flux (Φ₁) is produced in it and some part of the Φ₁ links with the coil 2 and is known as mutual flux (Φ_m).

Now, if the current in the coil 1 changes, the mutual flux also changes, therefore an EMF is induced in the coil 2. This induced emf in the coil 2 is known as mutually induced emf (𝑒_𝑚). This mutually induced emf is responsible for the mutual inductance between the coils. The effect of mutual inductance is to either increase or decrease the total inductance of the two coils depending upon the arrangement of the coils.

Mutual Inductance Formula

The mutual inductance (M) between two coils can be determined by using any one of the following three methods depending upon the known quantities −

Method 1

If the magnitude of mutually induced emf (𝑒_𝑚) in one coil and the rate of change of current in the other coil are known, then mutual inductance (M) is given by,

$$mathrm{e_{m}=Mfrac{dl_{1}}{dt}}$$

$$mathrm{Rightarrow:M=frac{e_{m}}{(dl_{1}/dt)}:::…(1)}$$

Method 2

Consider two magnetically coupled coils, coil 1 and coil 2, having N₁ and N₂ turns respectively. If a current I₁ flowing in the coil 1, a mutual flux (Φ_m) is produced that links the coil 2. Therefore,

$$mathrm{{m}=Mfrac{dl_{1}}{dt}=frac{d}{dt}(Ml_{1})}$$

Also, the mutually induced emf is given by,

$$mathrm{e_{m}=N_{2}frac{dphi_{m}}{dt}=frac{d}{dt}(N_{2}phi_{m})}$$

Thus, by equating these two equations, we get,

$$mathrm{Ml_{1}=N_{2}phi_{m}}$$

$$mathrm{Rightarrow:M=frac{N_{2}phi_{m}}{l_{1}}:::…(2)}$$

Method 3

If the physical dimensions of the magnetic circuit are known, then the mutual inductance of it can be determined as follows −

Let, the ‘l’ and ‘a’ be the length and cross-sectional areal of the magnetic circuit. The N₁ and N₂ are number of turns in the coil 1 and coil 2 respectively.

Mutual flux,

$$mathrm{phi_{m}=frac{MMF}{Reluctance(s)}=frac{N_{1}l_{1}}{(1/mu_{0}mu_{r}a)}}$$

Where,

• μ_𝑟 = relative permeability of material of magnetic circuit,

• μ₀ = absolute permeability of vacuum or air.

$$mathrm{Rightarrow:frac{phi_{m}}{l_{1}}=frac{N_{1}}{(1/mu_{0}mu_{r}a)}}$$

$$mathrm{(because:M=frac{N_{2}phi_{m}}{l_{1}})}$$

$$mathrm{M=N_{2}(frac{N_{1}}{1/mu_{0}mu_{r}a})}$$

$$mathrm{Rightarrow:M=(frac{N_{1}N_{2}}{1/mu_{0}mu_{r}a})=frac{{N_{1}N_{2}}}{Reluctance(S)}::::…(3)}$$

Method 4

If two coils have self-inductances L1 and L2, then the mutual inductance can also be given as,

$$mathrm{M=ksqrt{L_{1}L_{2}}:::…(4)}$$

Where, k is the coefficient of coupling.

Рассмотрим
систему двух катушек с токами, когда
магнитный поток, созданный током i₁,
протекающим в катушке L₁,
полностью или частично пронизывает
витки катушки L₂,
а поток, созданный током, протекающим
по катушке L₂,
полностью или частично пронизывает
витки катушки L₁
Такие катушки
называют индуктивно- или магнитосвязанными
(рис. 2).

Рис. 2

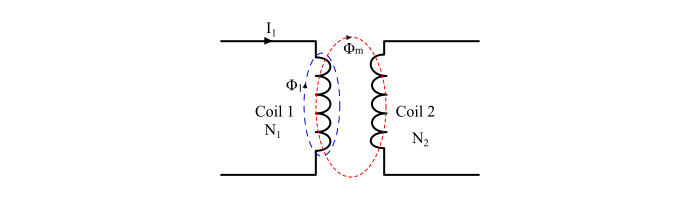
Обозначим потокосцепление второй
катушки, имеющейw₂витков, за счет пронизывающего вторую
катушку потока Ф₁₂, созданного
токомi1в первой катушке, через Ψ₁₂ = w₂∙Ф₁₂
и потокосцепление первой катушки,
имеющейw₁витков, за счет пронизывающего первую
катушку потока Ф₂₁, созданного
токомi₂
во второй катушке, черезΨ₂₁ = w₁∙Ф₂₁

Отношения
Ψ₂₁ / i₂иΨ₁₂ / i₁,
как показывают опыт и расчет, одинаковы
[1; 4], т. е.Ψ₁₂ / i₁ = Ψ₂₁ / i₂ = Mи называются взаимной индуктивностью
катушек 1 и 2 и измеряются в генри (Гн).

Часть
Ф_1Sполного потока, созданного токомi₁,
замыкается вне витков катушки 2,
аналогично, частьФ_2Sполного потока, созданного токомi₂,
замыкается вне витков катушки 1. Эти
потокиФ_1S
иФ_2Sназы­ва­ют­ся потоками рассеяния
соответст­ву­ющих катушек. Полное
потокосцепление первой катушкиΨ₁₁ = L₁ ∙ i_1.
Полное пото­ко­сцепление второй
катушкиΨ₂₂ = L₂ ∙ i₂.

Найдем
теперь отношения потока Ф₁₂к полному потокуФ₁₁,
созданному токомi₁.

.

Таким
же путем найдем отношение

.

Каждое
из отношений указывает, какая доля
потока, созданного током в одной катушке,
пронизывает соседнюю катушку. Среднее
геометрическое этих отношений называется
коэффициентом связи катушек или контуров.

.

Коэффициент
связи характеризует степень индуктивной
связи контуров или катушек и всегда
меньше единицы. Для усиления связи и
уменьшения сопротивления магнитному
потоку катушки наматывают на общий
магнитопровод из ферромагнитного
материала (электротехническая сталь,
феррит, аморфное железо). В предельном
случае сильной связи, когда нет потока
рассеивания, т. е. Ф₁₂ = Ф₁₁,Ф₂₁ = Ф₂₂,
то коэффициент связиK = 1.

Рис. 3

Если индуктивностиL₁иL₂по определению всегда положительны, то
взаимная индуктивностьМможет быть больше или меньше нуля, в
зависимости от взаимной направленности
магнитных потоков самоиндукции и
взаимной индукции. Если полное
потокосцепление контура 2 увеличивается
под влиянием тока в контуре 1, то величинаМбольше нуля и говорят,
что катушки включены согласно; если
полное потокосцепление контура 2
уменьшается под влиянием тока в контуре
1, то величинаМменьше
нуля и говорят, что катушки включены
встречно. Согласное или встречное
включение катушек на схемах отображается
специальными значками, например, точки
у соответствующих выводов. Если
протекающий в обоих катушках ток входит
в выводы помеченные знаком, то катушки
соединены согласно; если в одной катушке
ток входит в вывод, помеченный знаком,
а в другой катушке входит через вывод
не помеченный знаком, то катушки соединены
встречно.

Наличие индуктивных связей в цепи
переменного тока приводит к появлению
дополнительных ЭДС взаимной индукции,
которые должны быть учтены при составлении
уравнений по второму закону Кирхгофа.
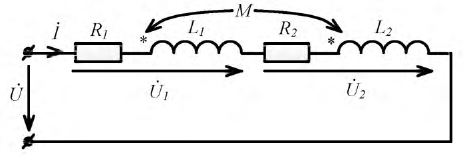
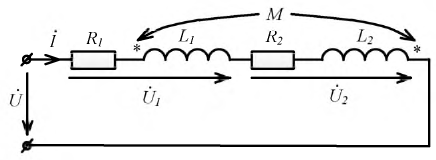
При последовательном соединении двух
магнитосвязанных катушек (рис. 3)
напряжение на зажимах всей этой ветви

u = (r₁+r₂)  i + (L₁+L₂+2  M)  di/dt.

Причем надо учитывать, что знак Мможет быть + или(на рис. 3 показан случай встречного
включения, то есть,M < 0).

Индуктивные
связи часто создают умышлено для
получения нужных свойств цепи. Например,
очень удобно регулировать собственную
индуктивность контура, плавно изменяя
взаимную индуктивность Ммежду двумя подвижными катушками.
Наиболее важные свойства индуктивно
связанных цепей проявляются в устройстве
и применении трансформаторов. Трансформатор
в простейшем случае представляет собой
два индуктивно связанных контура при
сильной связи между ними. Для усиления
связи на относительно низких частотах
контуры выполняются обычно в виде
обмоток, надетых на общий ферромагнитный
сердечник (рис. 4).

Рис. 4

На высоких частотах применяют и
воздушные трансформаторы, т. е. не
содержащие ферромагнитных сердечников.
Элек­тро­тех­ническое назначение
тако­го устройства заключается,
во-первых, в возможности трансформации
напряжения: при сильной связи между
обмотками почти одинаковый потокФ₁₂пронизывает каждый из витков, поэтому
эдс, индуцируемые в обмотках, пропорциональны
числам витков; во-вторых, в возможности
изолировать в электрическом отношении
одну цепь от другой (гальваническая
развязка), сохраняя возможность передачи
энергии и сигнала. Обмотка трансформатора,
подключенная к источнику энергии или
сигнала, называется первичной обмоткой
и обозначаетсяw₁.
Остальные обмотки называются вторичными
обмотками и обозначаютсяw₂,w₃и
так далее, где символыw₁,
w₂,w₃обозначают, кроме того, число витков
соответствующих обмоток.

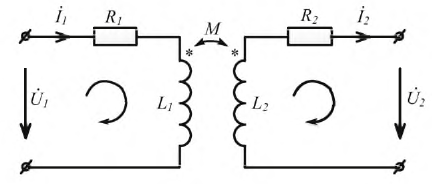
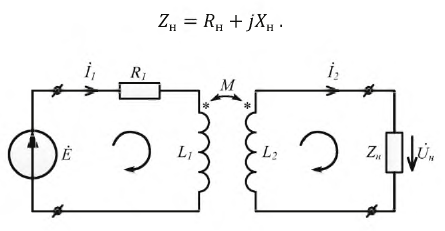
Рассмотрим
трансформатор с двумя обмотками w₁иw₂.
Сопротивления проводов, которыми
намотаны обмотки трансформатора,
обозначимr₁иr₂;
вторичная обмотка замкнута на нагрузку,
которая в общем случае представляет
собой комплексное сопротивлениеZ_н.
Тогда, при заданной полярности выводов
обмоток трансформатора на рис. 4 токи
направлены встречно. Уравнения
трансформатора при встречном направлении
токов имеют вид:

u₁ = r₁  i₁+L₁  di₁ / dt   di₂/dt,  (1a)

–u₂ = r₂  i₂+L₂  di₂ / dt   di₁/dt, (1b)

Если
напряжения и токи синусоидальны, то
уравнения трансформатора в комплексной
форме запишутся в виде:

(2)

Эти
уравнения, кроме того, являются
уравнениями, описывающими схему,
изображенную на рис. 5.

Рис. 5

Следовательно,
эта схема может рассматриваться в
качестве схемы замещения трансформатора.
Входящие в схему разности L₁–MиL₂–Mимеют физический смысл приw₁ = w₂:
они представляют собой индуктивности
рассеянияL_S1иL_S2,
связанные с соответствующими потоками
рассеянияФ_1S
иФ_2S,
которые отражают неидеальность
индуктивной связи между катушками.
(Разница между полным потоком, обусловленным
токомi₁,
и той его частью, которая пронизывает
витки второй катушки, называется потоком
рассеянияФ_1S = L₁  i₁/w₁.
Аналогично для второй катушкиФ_2S = L₂  i₂/w₂).
Из схемы замещенияL_S1 = L₁MиL_S2 = L₂M.
При неодинаковых числах витковw₁иw₂на практике пользуются так называемой
приведенной схемой замещения
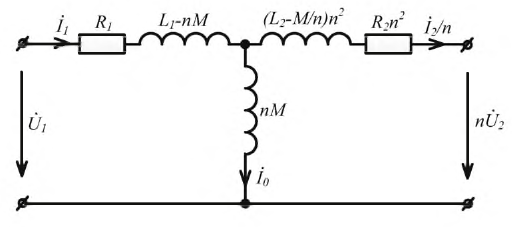
трансформатора, показанной на рис. 6.
Приведение заключается в том, что
напряжениеи
ток
заменяются величинами, приведенными
к первичной обмотке: напряжениеумножается наn,
а токделится наn.
Здесьn = w₁ / w₂– отношение чисел витков, которое
называется коэффициентом трансформации.

Придав
уравнениям (2) следующий вид:

(3)

можно преобразовать их таким образом:

(4)

Здесь
n = w₁ / w₂;
L_S1=L₁–M ∙ n;
L_S2=L₂–M / n

Рис. 6

Полученные
уравнения являются контурными уравнениями
для схемы на рис. 6 и, следовательно, эта
схема является схемой замещения
трансформатора. Эта схема содержит:
сопротивление r₁и индуктивность рассеянияL_S1первичной обмотки трансформатора;
индуктивность намагничиванияL_µ = M  nв поперечной ветви (эта ветвь называется
ветвью намагничивания); сопротивлениеr₂и индуктивность рассеянияL_S2вторичной обмотки, приведенные к
первичной обмотке трансформатора.
Индуктивные сопротивленияL_S1  иL_S2  представляют собой сопротивления
рассеяния первичной и вторичной обмоток
трансформатора, а индуктивное сопротивлениеn    Mсопротивление
ветви намагничивания.

Соседние файлы в папке Рэл

• #
• #
• #
• #
• #
• #
• #