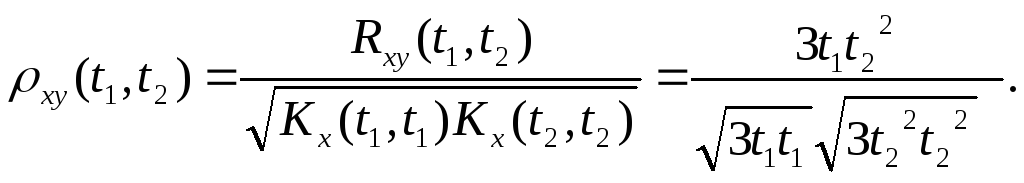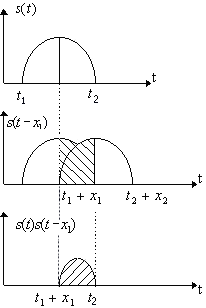Как найти взаимную корреляционную функцию

Для того чтобы
оценить степень зависимости сечений
двух случайных функций, вводят
характеристику—взаимную корреляционную
функцию.

Рассмотрим две
случайные функции X(t)
и Y{t).
При фиксированных значениях аргумента,
например t=t₁
и t=t₂,
получим два сечения—систему двух
случайных величин Х(t₁)
и Y(t₂)
с корреляционным моментом M[(t₁)
(t₂)].
Таким образом, каждая пара чисел t₁
и t₂,
определяет систему двух случайных
величин, а каждой такой системе
соответствует ее корреляционный момент.
Отсюда следует, что каждой паре
фиксированных значений t₁
и t₂
соответствует определенный корреляционный
момент; это означает, что взаимная
корреляционная функция двух случайных
функций есть функция (неслучайная) двух
независимых аргументов t₁
и t₂,
ее обозначают через R_xy(t₁,t₂).
Дадим теперь определение взаимной
корреляционной функции.

Взаимной
корреляционной функцией двух случайных
функций Х(t)
и Y(t)
называют неслучайную функцию R_xy(t₁,t₂)двух
независимых аргументов t₁
и t₂
значение которой при каждой паре
фиксированных значений аргументов
равно корреляционному моменту сечений
обеих функций, соответствующих этим же
фиксированным значениям аргументов:

R_xy(t₁,t₂)=
M[(t₁)
(t₂)].

Коррелированными
называют две случайные функции, если
их взаимная корреляционная функция не
равна тождественно нулю.

Некоррелированными
называют две случайные функции, взаимная
корреляционная функция которых
тождественно равна нулю.

Пример.
Найти взаимную корреляционную функцию
двух случайных функций Х
(t)=tU
и Y(t)=t²U,
U-случайная
величина, причем D(U)=3.

Решение.
Найдем математические ожидания;

т_x(t)=М(tU)=tm_u,
т_у(t)=М(t²U)
=t²m_u.

Найдем центрированные
функции:

(t)=X(t)—m_x(t)=
tU
—
tm_u=t(U—m_u),

(t)=Y(t)—m_y(t)=
t²U
— t²m_u=
t²(U—m_u).

Найдем
взаимную корреляционную функцию:

R_xy(t₁,t₂)=
M[(t₁)
(t₂)]=M{[
t₁(U—m_u)][
t₂²(U—m_u)]}=t₁t₂²M[(U—m_u)²]=
t₁t₂²D(U)=3t₁t₂²

Итак,
искомая взаимная корреляционная функция

R_xy(t₁,t₂)=
3t₁t₂²

§ 13. Свойства взаимной корреляционной функции

Свойство
1.
При
одновременной перестановке индексов
и аргументов взаимная корреляционная
функция не
изменяется:

R_xy(t₁,t₂)=
R_yx(t₂,t₁).

Свойство
2.
Прибавление
к случайным функциям Х(t)
и Y(t)
неслучайных слагаемых, соответственно
φ(t)
и
ψ(t),
не изменяет их взаимной корреляционной
функции:

если

X₁(t)=X(t)+φ(t)
и

Y₁(t)=Y(t)+ψ(t),

то

R_x1y2(t₁,t₂)=
R_xy(t₁,t₂).

Свойство
3.
При
умножении случайных функций Х(t)
и
У(t)
на неслучайные множители, соответственно
φ(t)
и
ψ(t),
взаимная корреляционная функция
умножается на произведение
φ(t₁)ψ(t₂):

если

X₁(t)=X(t)φ(t)
и
Y₁(t)=Y(t)+ψ(t),

то

R_x1y2(t₁,t₂)=
R_xy(t₁,t₂)
φ(t₁)ψ(t).

Свойство
4.
Абсолютная
величина взаимной корреляционной
функции двух случайных функций не
превышает среднего геометрического их
дисперсий:

Доказательства
этих свойств аналогичны доказательствам
свойств корреляционной функции.

§ 14. Нормированная взаимная корреляционная функция

Наряду с взаимной
корреляционной функцией для оценки
степени зависимости сечений двух
случайных функций пользуются
характеристикой—нормированной взаимной
корреляционной функцией.

Нормированной
взаимной корреляционной функцией двух
случайных функций Х(t)
и Y(t)
называют
неслучайную функцию двух независимых
аргументов
t₁
и t₂.

Нормированная
взаимная корреляционная функция имеет
те же свойства, что и взаимная корреляционная
функция (см. § 13), причем свойство 4
заменяется следующим свойством:
абсолютная
величина нормированной взаимной
корреляционной функции не превышает
единицы:

Пример.
Найти нормированную взаимную корреляционную
функцию двух случайных функций Х(t)=tU
и Y(t)=t²U,
где U—случайная
величина, причем D(U)=3.

Решение.
Ранее при решении примера (см. § 12), в
котором заданы те же функции, что и в
настоящем примере, были найдены функции:

R_xy(t₁,t₂)=
3t₁t₂²,
(t)=t(U—m_u),

(t)=
t²(U—m_u).

Пользуясь этим
результатами, легко найдем корреляционные
функции:

K_x(t₁,t₂)=3t₁t₂,
K_y(t₁,t₂)=3t₁²t₂²

И нормированную
функцию:

Итак, искомая
нормированная взаимная корреляционная
функция

Заметим, что функция
Y(t)
связана с X(t)
линейной функциональной зависимостью:

Y(t)=t2U=t(tU)=tX(t).

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Корреляционный анализ используется при необходимости
оценить временные свойства сигнала без применения спектрального анализа,
например, для оценки скорости изменения или длительности сигнала, временной
связи (корреляции) одного сигнала с другим.

Взаимная корреляционная функция определяет
временную связь двух сигналов во времени. Если сигналы не зависимы друг
от друга, их корреляционная функция равна нулю. Чем шире корреляционная
функция, тем большая степень связи двух сигналов друг с другом.

Взаимная корреляционная функция определяется
соотношением

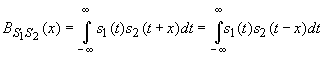
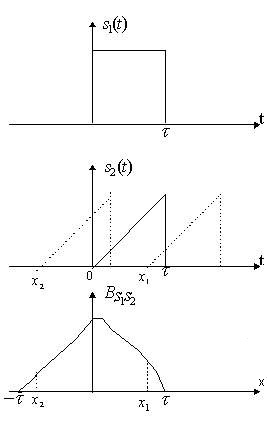
Пример получения взаимной корреляционной
функции показан на рис.1. Значение корреляционной функции в любой момент
x определяется площадью пересечения функций
и сдвинутой копии .

Рис. 1

Взаимная корреляционная функция не обязательно
симметрична и её максимум может оказаться не в точке x=0.

Автокорреляционной функцией (АКФ)
ограниченного во времени сигнала называется выражение вида

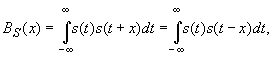
где x – временной сдвиг исходного
сигнала.

Геометрический смысл автокорреляционной функции
заключается в определении площади пересечения функции
и её копии, сдвинутой на время x (Рис.2)

Рис. 2

Изменяя время сдвига x до тех пор, пока сигнал и его копия перестанут
пересекаться (в данном случае ),
получим АКФ .
Очевидно, что при изменении знака сдвига при одинаковой его величине функция
автокорреляции одинакова, т.е. ,
что говорит о четном её характере. Ясно, что при x=0 автокорреляционная
функция имеет максимум, при этом

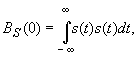
а в свою очередь полная энергия сигнала равна

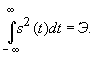
Таким образом, максимум автокорреляционной
функции определяет полную энергию сигнала. При увеличении сдвига x
АКФ убывает до нуля.

3 Корреляционный анализ сигналов

Смысл спектрального анализа сигналов заключается в изучении того, как сигнал может быть представлен в виде суммы (или интеграла) простых гармонических колебаний и как форма сигнала определяет структуру распределения по частотам амплитуд и фаз этих колебаний. В противоположность этому задачей корреляционного анализа сигналов является определение меры степени сходства и различия сигналов или сдвинутых по времени копий одного сигнала. Введение меры открывает пути к проведению количественных измерений степени схожести сигналов. Будет показано, что существует определенная взаимосвязь между спектральными и корреляционными характеристиками сигналов.

3.1 Автокорреляционная функция (АКФ)

Автокорреляционная функция сигнала с конечной энергией – это значение интеграла от произведения двух копий этого сигнала, сдвинутых относительно друг друга на время τ, рассматриваемое в функции этого временного сдвига τ:

.

Если сигнал определен на конечном интервале времени , то его АКФ находится как:

,

где  — интервал перекрытия сдвинутых копий сигнала.

Считается, что чем больше значение автокорреляционной функции  при данном значении , тем в большей степени две копии сигнала, сдвинутые на промежуток времени , похожи друг на друга. Поэтому корреляционная функция  и является мерой сходства для сдвинутых копий сигнала.

Рекомендуемые материалы

Вводимая таким образом мера сходства для сигналов, имеющих форму случайных колебаний вокруг нулевого значения, обладает следующими характерными свойствами.

Если сдвинутые копии сигнала колеблются примерно в такт друг к другу, то это является признаком их схожести и АКФ принимает большие положительные значения (большая положительная корреляция). Если копии колеблются почти в противофазе, АКФ принимает большие отрицательные значения (антисходство копий сигнала, большая отрицательная корреляция).

Максимум АКФ достигается при совпадении копий, то есть при отсутствии сдвига. Нулевые значения АКФ достигаются при сдвигах, при которых не заметно ни сходства, ни антисходства копий сигнала (нулевая корреляция,

отсутствие корреляции).

На рис.3.1 изображен фрагмент реализации некоторого сигнала на интервале времени от 0 до 1 с. Сигнал случайным образом колеблется вокруг нулевого значения. Поскольку интервал существования сигнала конечен, то конечна и его энергия. Его АКФ можно вычислить в соответствии с уравнением:

.

Автокорреляционная функция сигнала, вычисленная в MathCad в соответствии с этим уравнением, представлена на рис. 3.2. Корреляционная функция показывает не только то, что сигнал похож сам на себя (сдвиг τ=0), но и то, что некоторой схожестью обладают и копии сигнала, сдвинутые друг относительно друга приблизительно на 0.063 с (боковой максимум автокорреляционной функции). В противоположность этому копии сигнала сдвинутые на 0.032 с, должны быть антипохожи дуг на друга, то есть быть в некотором смысле противоположными друг другу.

На рис.33 показаны пары этих двух копий. По рисунку можно проследить, что понимается под похожестью и антипохожестью копий сигнала.

Корреляционная функция обладает следующими свойствами:

1. При τ = 0 автокорреляционная функция принимает наибольшее значение, равное энергии сигнала

2. Автокорреляционная функция является четной функцией временного сдвига .

3. С ростом τ автокорреляционная функция убывает до нуля

4. Если сигнал не содержит разрывов типа δ — функций, то  — непрерывная функция.

5. Если сигнал является электрическим напряжением, то корреляционная функция имеет размерность .

Для периодических сигналов в определении автокорреляционной функции тот же самый интеграл делят еще на период повторения сигнала:

.

Так введенная корреляционная функция отличается следующими свойствами:

— значение корреляционной функции в нуле равно мощности сигнала ,

— размерность корреляционной функции равна квадрату размерности сигнала, например .

Для примера вычислим корреляционную функцию гармонического колебания :

Используя ряд тригонометрических преобразований, получим окончательно:

Таким образом, автокорреляционная функция гармонического колебания является косинусоидой с тем же периодом изменения, что и сам сигнал. При сдвигах, кратных периоду колебания, гармоника преобразуется в себя и АКФ принимает наибольшие значения, равные половине квадрата амплитуды. Сдвиги по времени, кратные половине периода колебания, равносильны смещению фазы на угол , при этом меняется знак колебаний, а АКФ принимает минимальное значение, отрицательное и равное половине квадрата амплитуды. Сдвиги, кратные четверти периода, переводят, например, синусоидальное колебание в косинусоидальное и наоборот. При этом АКФ обращается в нуль. Такие сигналы, находящиеся в квадратуре друг относительно друга, с точки зрения автокорреляционной функции оказываются совершенно не похожими друг на друга.

Важным является то, что в выражение для корреляционной функции сигнала не вошла его начальная фаза. Информация о фазе потерялась. Это означает, что по корреляционной функции сигнала нельзя восстановить сам сигнал. Отображение  в противоположность отображению  не является взаимно однозначным.

Если под механизмом генерирования сигналов понимать некоего демиурга, создающего сигнал по выбранной им корреляционной функции, то он смог бы создать целую совокупность сигналов (ансамбль сигналов), имеющих действительно одну и ту же корреляционную функцию, но отличающихся друг от друга фазовыми соотношениями.

Акт выбора начальной фазы можно считать:

— актом проявления сигналом своей свободной воли, независимой от воли создателя (возникновение отдельных реализаций некоторого случайного процесса),

— результатом постороннего насилия над сигналом (введение в сигнал измерительной информации, получаемой при проведении измерений какой либо физической величины).

Аналогичным образом обстоит дело с любым периодическим сигналом. Если периодический сигнал с основным периодом Т имеет амплитудный спектр  и фазовый спектр , то корреляционная функция сигнала принимает следующий вид:

.

Уже в этих примерах проявляется некоторая связь между корреляционной функцией и спектральными свойствами сигнала. Подробнее об этих соотношениях речь пойдет в дальнейшем.

3.2 Взаимнокорреляционная функция (ВКФ).

В отличие от автокорреляционной функции взаимнокорреляционная функция определяет степень схожести копий двух различных сигналов x(t) и y(t), сдвинутых на время τ друг относительно друга:

Взаимнокорреляционная функция обладает следующими свойствами:

1. При τ = 0 взаимнокорреляционная функция принимает значение, равное взаимной энергии сигналов, то есть энергии их взаимодействия

.

2. При любом τ имеет место соотношение:

,

где  — энергии сигналов.

3. Изменение знака временного сдвига равносильно взаимной перестановке сигналов:

.

4. С ростом τ взаимнокорреляционная функция хотя и не монотонно, но убывает до нуля

5. Значение взаимнокорреляционной функции в нуле  ничем не выделяется среди других значений.

Для периодических сигналов понятие взаимнокорреляционной функции, как правило, вообще не используется.

Приборы для измерения значений автокорреляционной и взаимнокорреляционной функций называются коррелометрами или корреляторами. Коррелометры применяются, например, для решения следующих информационно-измерительных задач:

— статистический анализ электроэнцефалограмм и других результатов регистрации биопотенциалов,

— определение пространственных координат источника сигнала по величине временного сдвига, при котором достигается максимум ВКФ,

— выделение слабого сигнала на фоне сильных статических несвязанных помех,

— обнаружение и локализация каналов утечки информации путем определения корреляции между сигналами радиоэфира в помещении и за его пределами,

— автоматизированное обнаружение в ближней зоне, распознавание и поиск работающих радиоизлучающих подслушивающих устройств, включая мобильные телефоны, используемые как подслушивающие устройства,

— локализация мест утечек в трубопроводах на основании определения ВКФ двух сигналов акустического шума, вызываемого утечкой, в двух точках измерения, в которых расположены датчики на трубе.

3.3 Соотношения между корреляционными и спектральными функциями.

Как корреляционные, так и спектральные функции описывают внутреннюю структуру сигналов, их внутреннее строение. Поэтому можно ожидать, что между этими двумя способами описания сигналов существует некоторая взаимозависимость. Наличие такой связи Вы уже видели на примере периодических сигналов.

Взаимная корреляционная функция, как и любая другая функция времени, может быть подвергнута преобразованию Фурье:

.

Изменим порядок интегрирования:

Выражение в квадратных скобках можно было бы рассматривать как преобразование Фурье для сигнала y(t), но в показателе экспоненты не стоит знак минус. Это говорит о том, что внутренний интеграл дает нам выражение , комплексно сопряженное со спектральной функцией .

Но выражение  не зависит от времени, поэтому его можно вынести за знак внешнего интеграла. Тогда внешний интеграл просто даст нам определение спектральной функции  сигнала x(t). Окончательно имеем:

.

Это означает, что преобразование Фурье для взаимной корреляционной функции двух сигналов равно произведению их спектральных функций, одна из которых подвергнута комплексному сопряжению. Это произведение называется взаимным спектром сигналов:

.

Из полученного выражения следует важный вывод: если спектры сигналов x(t) и y(t) не перекрывают друг друга, то есть располагаются в различных диапазонах частот, то такие сигналы являются некоррелированными, независимыми друг от друга.

Если положить в приведенных формулах: x(t) = y(t), то получим выражение для преобразования Фурье автокорреляционной функции

.

Это означает, что автокорреляционная функция сигнала и квадрат модуля его спектральной функции связаны друг с другом посредством преобразования Фурье.

Функция  называется энергетическим спектром сигнала . Энергетический спектр показывает, как общая энергия сигнала распределяется по частотам его отдельных гармонических составляющих.

3.4 Энергетические характеристики сигналов с частотной области

Взаимная корреляционная функция двух сигналов связана преобразованием Фурье с взаимным спектром сигналов, поэтому ее можно выразить в виде обратного преобразования Фурье от взаимного спектра:

.

Теперь подставим в эту цепочку равенств значение временного сдвига . В результате получим соотношение, которое определяет смысл равенства Релея:

,

то есть интеграл от произведения двух сигналов равен интегралу от произведения спектров этих сигналов, один из которых подвергнут операции комплексного сопряжения.

Ещё посмотрите лекцию «14 Подготовка России к войне» по этой теме.

Если считать сигналы одинаковыми x(t)=y(t), получится соотношение, позволяющее фактически по одной формуле вычислять энергию сигнала, как во временной, так и в частотной области:

.

Это соотношение называется равенством Парсеваля.

Периодические сигналы обладают бесконечной энергией, но конечной мощностью. При их рассмотрении мы уже сталкивались с возможностью вычисления мощности периодического сигнала через сумму квадратов модулей коэффициентов его комплексного спектра:

.

Это соотношение обладает полной аналогией с равенством Парсеваля.