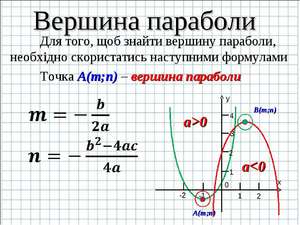
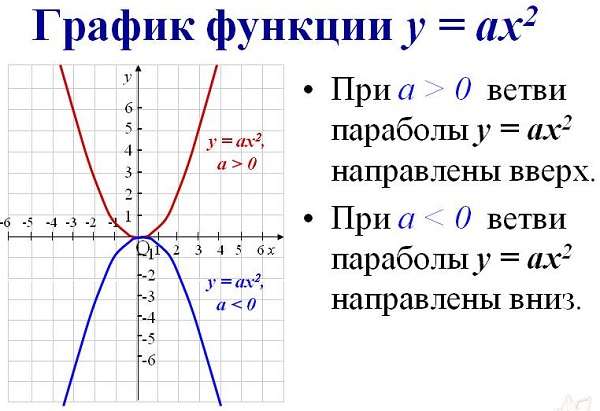
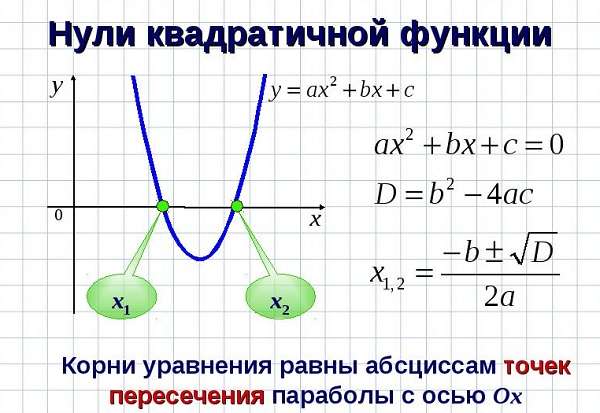
Как найти x с индексом ноль - Исправление недочетов и поиск решений вместе с Examum.ru

Как найти икс нулевое

В качестве «икс нулевое» обозначается координата вершины параболы по оси абсцисс. В этой точке функция принимает наибольшее или наименьшее значение, поэтому x0 − точка экстремума функции.

Инструкция

Если имеется аналитическое задание функции, приведите ее к стандартному виду: A*x²+B*x+C=y(x), где A − старший коэффициент при x², B − средний коэффициент при x, C − свободный член. Обратите внимание, чтобы коэффициент при x² не равнялся нулю, иначе это будет уже не квадратичная функция.

Координата вершины параболы x0 по оси абсцисс находится по формуле: x0=-B/2A. В случае приведенного квадратного уравнения, то есть, когда A=1, формула упрощается: x0=-B/2. Если в уравнении нет «икса» в первой степени, значит, коэффициент B=0, и тогда x0 тоже обращается в нуль.

Чтобы найти координату вершины параболы по оси ординат, подставьте полученное значение для x0 в уравнение. Когда вы упростите выражение, с одной стороны у вас останется «игрек», с другой − некоторое число Q. Оно и показывает ординату вершины параболы: y0=Q.

Т.к. x0 − точка экстремума функции, то ее числовое значение можно найти и при помощи дифференцирования. Найдите первую производную функции. Приравняйте ее нулю и решите полученное уравнение. Ему будет удовлетворять единственное значение x, которое и является координатой вершины параболы.

Если необходимо отметить «икс нулевое» на графике, проведите из вершины параболы пунктирной линией перпендикуляр к оси абсцисс. Точку, в которой перпендикуляр пересечет ось x, обозначьте за x0. Чтобы увидеть на графике «игрек нулевое», проведите из вершины перпендикуляр соответственно к оси ординат.

Войти на сайт

или

Забыли пароль?
Еще не зарегистрированы?

This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.

Источник

Уравнения квадратичной функции

Параболу можно описать несколькими способами. Каждый из них нужно применять в конкретных случаях для удобства вычислений. Существует три формы описания кривой:

Каноническая.
Квадратичная.
Общая.

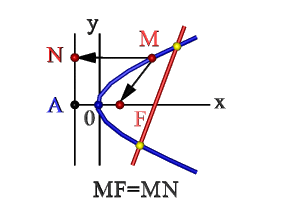
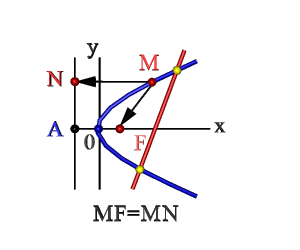
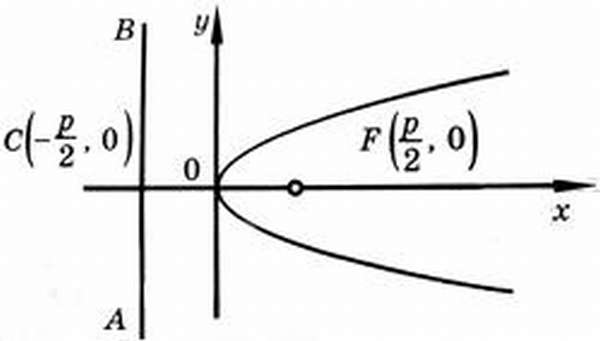
В первой форме она имеет следующий вид: y² = 2px. Если поменять местами оси декартовой системы, то получится следующий вид: x² = 2yp. Коэффициент p — фокальный параметр. Он соответствует расстоянию между фокусом и директрисой. Кроме того, его значение всегда больше нуля. Вершина лежит всегда между фокусом и директрисой кривой на расстоянии, равном p/2 (рис. 2).

Рисунок 2. Директриса и фокус.

Пусть уравнение директрисы (прямая, которая параллельна оси ОУ) имеет следующий вид: х + p/2 = 0. Координаты фокуса F — (р/2;0). Начало координат делит луч, проходящий из точки F и точки пересечения с директрисой на 2 равных отрезка. Величина FM рассчитывается таким образом: FM = [(x — p/2)^2 + y²]^0.5. Отрезок (луч) из точки М до директрисы равен p/2 + x. Если приравнять оба выражения, то равенство имеет такой вид: p/2 + x = [(x — p/2)^2 + y²]^0.5. При возведении в квадрат и приведении подобных слагаемых, получается искомое уравнение параболы (y² = 2px).

Парабола может задаваться квадратичной функцией. Она имеет такой вид: y = ax² + bx + c. Следует учитывать, что коэффициент «a» не должен быть равен 0. Если a=1, b = 0 и с = 0, функция принимает такой вид: y = ax². В этом случае формула нахождения вершины параболы выглядит таким образом:

Абсцисса вершины параболы: xa = -b / 2a.
Координата «игрек» по оси ординат: yb = — D / 2a.

В последней формуле переменная D является дискриминантом квадратного уравнения искомой функции. Он вычисляется с помощью такого соотношения: D = b² — 4ac. При а>0 фокус лежит на оси, и находится над вершиной. Ось симметрии параллельна оси ординат. Кроме того, она проходит через вершину кривой. Расстояние до нее равно ¼ величины «а». Если а<0, то ось ее симметрии параллельна оси абсцисс. Расстояние до фокуса также равно ¼а. Уравнение y = a (x — xa)^2 + ya — функция, определяющая кривую II порядка, как параболу.

Поскольку искомую функцию можно назвать кривой второго порядка, то ее уравнение может быть записано в виде квадратного многочлена в декартовой системе координат. Вид его имеет такой вид: Ax² + Bxy + Cy² + Dx + Ey + F = 0. Дискриминант равен нулю (при старших членах).

В полярной системе координат с осями p и v уравнение квадратичной функции имеет такой вид: p (1 + cos (v)) = p. Расстояние от фокуса до директрисы обозначается фокальным коэффициентом p. Кроме того, p соответствует удвоенной длине отрезка, проведенного от фокуса до вершины.

Видео

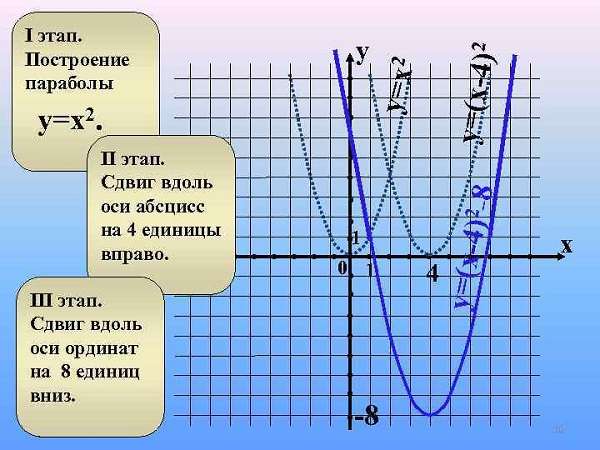
Построение параболы

Самое трудное при построении – это верно найти точки функции. Для подробного построения нужно просчитать 5–7 точек (для школьного курса хватит этого). Для этого выбираем какое-либо значение x и подставляем его в данную функцию. Итогом подсчётов будет число точки по оси ординат. После этого ставим на координатную плоскость полученные нами точки. В итоге у нас получается парабола.

Рассмотрим подробнее вопрос о нахождении точек, которые нужно отметить. Для примера возьмём функцию y =-x ²+11 x -24 с вершиной в точке (5,5;-6,25).

1) Строим таблицу

2) Заполняем таблицу

Так как парабола имеет осевую симметрию, то можно считать только значения справа или слева от вершины. Лучше считать те значения, которые ближе к 0, так удобнее. В нашем случае эти значения 4 и 5.

X	4	5	5,5	6	7
Y	-4	-6	-6,25	-6	-4

Алгоритм построения

В различных задачах нужно выполнить построение графика функции. В некоторых случаях даются координаты вершины, а в других — их следует искать, используя какой-либо метод. Чтобы построить квадратичную функцию, нужно воспользоваться таким алгоритмом:

Если вершина не задана, то нужно найти ее любым из методов.
Определить точки пересечения с осями декартовой системы координат.
Построить таблицу зависимости ординаты от абсциссы. Для этой цели нужно выделить минимум 3 значения «х». Вершина должна находиться по центру таблицы.
Выполнить построение, соединив точки.

Если необходим более точный график, то необходимо брать больше точек. Значения рассчитываются при подстановке значений «х» в функцию. Когда парабола задана функцией y = x² + c, нет смысла брать разные значения. Нужно использовать для построения искомой таблицы числа с противоположными знаками. Например, x1 = 2 и x2 = -2.

Специалисты-математики настоятельно рекомендуют не усложнять вычисления. Возможно, в школьных программах и рассматриваются различные случаи. Однако в высших учебных заведениях основной аспект изучения дисциплин с физико-математическим уклоном сводится к оптимизации процесса решения задачи.

Как найти икс нулевое
Как найти икс нулевое
x нулевое
Где можно решить любую задачу по математике, а так же x нулевое Онлайн?
Почему любое число в нулевой степени равно 1 ? Как объяснить ребенку?
Как найти икс нулевое

Как найти икс нулевое

Итак, исследование аналитически заданной функции дало вам точку на графике с координатами (x0;y0). Если старший коэффициент A > 0, то ветви параболы направлены вверх, и в вершине промежуток убывания будет сменяться промежутком возрастания. Если же A Т.к. x0 − точка экстремума функции, то ее числовое значение можно найти и при помощи дифференцирования. Найдите первую производную функции. Приравняйте ее нулю и решите полученное уравнение. Ему будет удовлетворять единственное значение x, которое и является координатой вершины параболы.
Если необходимо отметить «икс нулевое» на графике, проведите из вершины параболы пунктирной линией перпендикуляр к оси абсцисс. Точку, в которой перпендикуляр пересечет ось x, обозначьте за x0. Чтобы увидеть на графике «игрек нулевое», проведите из вершины перпендикуляр соответственно к оси ординат.

Источник

Как найти икс нулевое

Источник

x нулевое

Вы искали x нулевое? На нашем сайте вы можете получить ответ на любой математический вопрос здесь. Подробное решение с описанием и пояснениями поможет вам разобраться даже с самой сложной задачей и игрек нулевое формула, не исключение. Мы поможем вам подготовиться к домашним работам, контрольным, олимпиадам, а так же к поступлению в вуз. И какой бы пример, какой бы запрос по математике вы не ввели — у нас уже есть решение. Например, «x нулевое».

Применение различных математических задач, калькуляторов, уравнений и функций широко распространено в нашей жизни. Они используются во многих расчетах, строительстве сооружений и даже спорте. Математику человек использовал еще в древности и с тех пор их применение только возрастает. Однако сейчас наука не стоит на месте и мы можем наслаждаться плодами ее деятельности, такими, например, как онлайн-калькулятор, который может решить задачи, такие, как x нулевое,игрек нулевое формула,икс нулевое формула,как найти x нулевое,как найти y нулевое,как найти игрек нулевое,как найти икс нулевое,как найти у нулевое,как найти х нулевое,как найти х0 в физике,формула x нулевое,формула игрек нулевое,формула нулевого х,формула х нулевого,х нулевое,х нулевое как найти,х нулевое формула. На этой странице вы найдёте калькулятор, который поможет решить любой вопрос, в том числе и x нулевое. Просто введите задачу в окошко и нажмите «решить» здесь (например, икс нулевое формула).

Где можно решить любую задачу по математике, а так же x нулевое Онлайн?

Решить задачу x нулевое вы можете на нашем сайте https://pocketteacher.ru. Бесплатный онлайн решатель позволит решить онлайн задачу любой сложности за считанные секунды. Все, что вам необходимо сделать — это просто ввести свои данные в решателе. Так же вы можете посмотреть видео инструкцию и узнать, как правильно ввести вашу задачу на нашем сайте. А если у вас остались вопросы, то вы можете задать их в чате снизу слева на странице калькулятора.

Наш искусственный интеллект решает сложные математические задания за секунды.

Мы решим вам контрольные, домашние задания, олимпиадные задачи с подробными шагами. Останется только переписать в тетрадь!

Источник

Почему любое число в нулевой степени равно 1 ? Как объяснить ребенку?

Приветствую Вас, уважаемые Читатели! Сегодня хочу поговорить об очень простом утверждении, которое не вызывает у школьников проблем в применении, однако иногда может поставить в тупик каждого. Почему, собственно, любое число, будь то натуральное, рациональное, вещественное или трансцендентное, будучи возведенным в нулевую степень, становится равным единице?

Как объяснить это ребенку, только что столкнувшемуся с логическим парадоксом о том, «что значит возвести число в степень ноль раз?» Расскажу Вас про два простых ответа на этот вопрос. Поехали!

Итак, для начала необходимо вспомнить, что такое возведение в степень. Эта арифметическая операция, определяемая как результат многократного умножения числа на себя.

Здесь мы умножаем основание степени (9) столько раз, сколько указано в показателе степени (5). Вопросов не возникает, и в том случае, когда показатель степени равен 1.

А что делать с показателем степени, равным 0? Для этого нужно вспомнить свойства возведения в степень:

При умножении равных оснований показатели степени складываются, а при делении — вычитаются. Значит, чтобы получить 0 в показателе степени нам надо разделить одно число на другое:

Это только одно из объяснений. Другое также использует свойства степеней, но уже в контексте сложения:

Получается, что мы умножаем на некоторое число, которое не изменяет исходного. Таким числом, как легко догадаться, может быть только единица.

А какие способы объяснений можете предложить Вы? Пишите в комментариях!

Источник

Как найти икс нулевое

Источник

Сайт переезжает. Большинство статей уже перенесено на новую версию.
Скоро добавим автоматические переходы, но пока обновленную версию этой статьи можно найти там.

Бинарный поиск

Линейный поиск
Бинарный поиск
Бинарный поиск с вещественными числами
Поиск максимума выпуклой функции: тернарный поиск, бинарный поиск
Бинарный поиск по ответу

Линейный поиск

Мы считаем, что вы уже знаете линейный поиск, а именно умеете решать задачи такого типа:

Проверить, есть ли в массиве число X
Найти максимум в массиве
Найти сумму чисел в массиве
Найти первое четное число в массиве

Все такие задачи решаются с помощью одного прохода по массиву с помощью цикла for. Все такие алгоритмы работают за (O(n)). И даже можно понять, что быстрее, чем (O(n)) решить ни одну из этих задач не получится.

Задание

Убедитесь, что вы умеете решать эти задачи. Докажите, что быстрее, чем O(n) их решить в худшем случае нельзя.

Бинарный поиск

Однако иногда найти число X в массиве можно и быстрее! Для этого надо добавить условие на то, что массив отсортирован. Но давайте начнем не с этого.

Задание

Я загадал число X от 1 до 100. Вы можете спрашивать, больше ли мое число чем число T, я отвечаю “да” или “нет”. За сколько вопросов в худшем случае вы сможете найти число X? Как нужно действовать?

Решение и состоит в идее бинарного (двоичного) поиска — нужно первым вопросом спросить “число X больше, чем 50?”. После этого, если ответ “нет”, надо спросить “число X больше, чем 25”? И так далее, нужно уменьшать отрезок возможных значений в два раза каждый раз.

Почему нужно делить обязательно пополам? Почему бы не спросить “число X больше, чем 80?” первым же вопросом? Но если вдруг ответ “нет”, то мы останемся с 80 вариантами вместо 100. То есть деление отрезка ровно пополам гарантирует, что в худшем случае мы останемся не более чем с половиной вариантов.

Чтобы понять, как быстро это работает, введём новую математическую функцию. Логарифмом по основанию (a) от (b) будем называть число (c), такое что (a ^ c = b). Обозначается как (log_a b = c). Чаще всего мы будем работать с двоичным логарифмом, то есть в какую степень (c) нужно возвести двойку, чтобы получить (b). Поэтому договоримся, что запись (log n) означает двочный логарифм (n).

Теперь вернёмся к нашей задаче. Можно понять, что такой алгоритм работает как раз за (O(log n)) вопросов (если число 100 на заменить абстрактную переменную (n)). Несложно убедиться, что именно логарифм раз нужно поделить число на два, чтобы получилось 1.

Общий принцип

А теперь представьте такую задачу: у вас есть массив, состоящий из некоторого количества подряд идущих нулей, за которыми следует какое-то количество подряд идущих единиц.

a = [0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 1, 1, 1, 1]
n = len(a)
n

Вам дан массив, и вам нужно найти позицию первой единицы, то есть найти такое место, где заканчиваются нули, и начинаются единицы. Это можно сделать с помощью линейного поиска за один проход по массиву, но хочется сделать это быстрее.

Давайте обратимся к идее бинарного поиска. Посмотрим на элемент посередине массива. Если это нуль, то первую единицу стоит искать в правой половину массива, а если единица — то в левой.

Есть много способов писать бинарный поиск, и в его написании люди очень часто путаются. Очень удобно в данном случае воспользоваться инвариантом (это слово значит “постоянное свойство”):

Пусть переменная left всегда указывает на (0) в массиве, а переменная right всегда указывает на (1) в массиве.

Дальше мы будем переменные left и right постепенно сдвигать друг к другу, и в какой-то момент они станут соседними числами. Это и будет означать, что мы нашли место, где заканчиваются нули и начинаются единицы.

Чему равны left и right изначально, когда мы ничего про массив не знаем? Первая приходящая в голову идея — поставить их на (0) и (n-1) соответственно. Увы, в общем случае это может быть неверно, потому что a[0] может быть единицей, а a[n-1] может быть нулём. Правильнее сделать вот так:

left = -1
right = n

То есть изначально left и right указывают на несуществующие индексы. Но это нормально — например в массиве [1, 1, 1, 1] в конце алгоритма как раз должно быть left == -1, right == 0.

Осталось нам написать цикл while:

while right - left > 1:
    middle = (left + right) // 2 # именно такая формула для среднего индекса между left и right
    if a[middle] == 1:
        right = middle # right всегда должна указывать на 1
    else:
        left = middle # left всегда должна указывать на 0
print left, right
print a[left], a[right]

8 9
0 1

Мы решили задачу для ноликов и единичек, но это легко обобщается на абсолютно любую задачу, где есть какое-то свойство, которое в начале массива не выполняется, а потом выполняется.

Например, если мы хотим найти, есть ли число (X) в отсортированном массиве, то мы просто представим, что (0) — это числа, меньшие (X), а (1) — это числа, большие или равные (X). Тогда достаточно найти первую “единицу” и проверить, равно ли это число (X).

a = [1, 3, 4, 10, 10, 10, 11, 80, 80, 81] # отсортированный массив
def bin_search(a, x):
    n = len(a)
    left = -1
    right = n
    while right - left > 1:
        middle = (left + right) // 2
        if a[middle] >= x: # практически единственная строка, которая меняется от задачи к задаче
            right = middle
        else:
            left = middle
    if right != n and a[right] == x: # ответ лежит в right
        return True
    else:
        return False

print (bin_search(a, 1))
print (bin_search(a, 10))
print (bin_search(a, 20))
print (bin_search(a, 79))
print (bin_search(a, 80))
print (bin_search(a, 81)

True
True
False
False
True
True

Задание

Придумайте, как с помощью бинарного поиска решить такие задачи: * Найти первое число, равное X в отсортированном массиве, или вывести, что таких чисел нет * Найти последнее число, равное X в отсортированном массиве, или вывести, что таких чисел нет * Посчитать, сколько раз встречается число X в отсортированном массиве (в решении помогают два предыдущих пункта) * Дан массив чисел, первая часть состоит из нечетных чисел, а вторая — из четных. Найти индекс, начиная с которого все числа четные.

Все эти задачи решаются бинарным поиском за (O(log{n})). Правда нужно понимать, что в чистом виде такую задачу решать двоичным поиском бессмысленно — ведь чтобы создать массив размера (n), уже необходимо потратить (O(n)) операций.

Поэтому зачастую такие задачи сформулированы таким образом:

Дан отсортированный массив размера (n). Нужно ответить на (m) запросов вида “встречается ли число (x_i) в массиве n”?

Задание

Найдите время работы, за которое решается эта задача?

Решение: Такая задача решается за (O(n + mlog{n})) — нужно создать массив за (O(n)) и (m) раз запустить бинарный поиск.

Задание

Решите 3 первые задачи в этом контесте:

https://informatics.msk.ru/moodle/mod/statements/view.php?id=33216

Бинарный поиск с вещественными числами

У нас все еще есть функция f(x), которая сначала равна 0, а потом равна 1, и мы хотим найти это место, где она меняет значение. Но теперь аргумент функции — вещественное число. Например: * (f(x) = 1), если (x^2 > 2) * (f(x) = 0), если (x^2 leq 2)

Понятно, что при (x = sqrt 2) (f(x) = 0), а при любом даже немного большем значении (f(x) = 1). Если мы научимся решать такую задачу, то мы научимся находить корень из двух!

Увы, возникает проблема: действительные числа хранятся в компьютере неточно

# известный пример
0.1 + 0.1 + 0.1

0.30000000000000004

Тем более не сможем найти точное значение (sqrt 2), потому что это бесконечная непериодическая дробь. Так что давайте снова воспользуемся бинарным поиском, причем всегда (f(left) = 0), (f(right) = 1), и мы остановимся тогда, когда left и right будет очень-очень близко.

И тут снова возникает проблема. Помимо того, что бесконечную дробь в принципе невозможно точно хранить в компьютере, ещё и арифметические операции понижают эту точность. Поэтому, чтобы явно не использовать разность между правым и левым указателем, можно задать фиксированное число шагов, которое будет выполняться.

Так как мы знаем, что двоичный поиск работает за двоичный логарифм, можно сказать, что на угадывание десятичного разряда числа потребуется примерно три шага бинпоиска (т. к. $ $). Значит, например, если нам нужно посчитать значение функции до шести знаков после запятой, то нам нужно ещё примерно 18 шагов уже после того, как расстояние между left и right достигло одного.

Чтобы каждый раз об этом не думать, можно считать, что ста шагов бинпоиска хватит для почти любых разумных целей.

left = 0.0 # 0^2 < 2, а значит f(0) = 0
right = 10.0 # 10^2 > 2, а значит f(10) = 1
for i in range(100):
    middle = (left + right) / 2 # теперь деление не нацело, а вещественное
    if middle ** 2 > 2:
        right = middle # right всегда должна указывать на 1
    else:
        left = middle # left всегда должна указывать на 0
print left, right
print left ** 2, right ** 2

1.41421356237 1.41421356237
2.0 2.0

Вот мы и нашли корень из 2 с достаточно высокой точностью.

На самом деле, так можно искать ноль любой непрерывной функции (мы сейчас искали ноль функции (x^2 — 2)), у которой вы знаете значение меньше нуля и значение больше нуля.

Задание

Придумайте, как с помощью вещественного бинпоиска найти * (sqrt[leftroot{-2}uproot{2}17]{1000}) * какой-нибудь корень уравнения (x^4 + 3x = 5)

Поиск максимума выпуклой функции: тернарный поиск, бинарный поиск

Так мы только что научились находить корень непрерывной функции, у которой мы знаем значение меньше и больше 0. Но можно ли найти с помощью бинарного поиска локальный максимум функции? Можно!

Как известно, локальный максимум функции (f) — это просто такое (x_0), что для всех близких к нему (x) значения (f(x) < f(x_0)). Для непрерывных функций выполняется более крутая вещь: слева от максимума функция возрастает, а справа от максимума функция убывает. Так это как раз отличное условие для нашего вещественного бинарного поиска!

Если вы знаете (x_1) такое, что в его окрестности f(x) возрастает, и (x_2) такое, что в его окрестности f(x) убывает, то можно запустить между ними бинпоиск и найти точку (x_0) такую, что слева от нее возрастает значение функции, а справа — убывает. Это и есть локальный максимум.

А если функция выпуклая, то она вообще выглядит красиво: сначала возрастает, потом максимум, потом убывает.

Проблема только в одном: как по точке понять, в ее окрестности значение функции убывает или возрастает? Достаточно тыкнуть две точки очень-очень рядом с ней и сравнить их значения!

Задание

Придумайте, как с помощью вещественного бинпоиска найти * максимум функции (x — e^x) (она выпуклая, и максимум ровно один) * какой-нибудь локальный максимум функции (31x+x^3-x^4)

Тернарный поиск

Другой способ искать максимум — это тернарный поиск. Пусть известно, что максимум находится между left и right. Поделим отрезок на три равные части: * middle_left = (2 * left + right) / 3 * middle_right = (left + 2 * right) / 3

Тогда если f(middle_left) < f(middle_right), то можно спокойно заменить left на middle_left (максимум точно не левее middle_left), а если f(middle_left) > f(middle_right), то можно спокойно заменить right на middle_right. Он будет работать не за двоичный логарифм, а за логарифм по основанию полтора, что больше (но асимптотически то же самое, так как отличается в константу раз).

Оба способа работают быстро, и обобщаются на дискретный случай (то, что было в начале — когда дан массив, значения в котором сначала возрастают, а потом убывают). Но проблема есть в том, что если функция нестрого возрастает и нестрого убывает, а именно если там есть отрезки постоянства, то алгоритм не работает. В случае, когда значения функции равны, никак нельзя понять, с какой стороны искать максимум — он может быть с любой стороны.

Задание

Решите 4 и 5 задачи в этом контесте:

https://informatics.msk.ru/moodle/mod/statements/view.php?id=33216

Бинарный поиск по неотсортированному массиву

Заметьте, что в первоначальной задаче условие на то, что сначала идут нули, а потом идут единицы несущественно. Главное, чтобы мы знали индекс, который показывает на 0, и индекс, который показывает на 1. После этого бинарным поиском мы таким же способом найдем пару соседних нуля и единицы в массиве.

Поэтому бинарный поиск работает и не для возрастающих массивов / функций, если наша задача состоит именно в поиске двух соседних индексов, в которых условие выполняется и не выполняется.

Например, если мы знаем, что (f(x_0) < 0) и (f(x_1) > 0), и функция непрерывная, то бинарным поиском можно найти ноль этой функции между (x_0) и (x_1), даже если функция не монотонная!

Или, например, если нужно в массиве найти соседние четное и нечетное числа, и известно положение какого-то четного числа и какого-то нечетного числа, то это тоже можно легко сделать с помощью бинарного поиска.

Полезно иметь это в виду, это применяется в нескольких задачах контестов.

Бинарный поиск по ответу

Рассмотрим такую задачу:

Пример: “Корова в стойла”

Условие: На прямой расположены N стойл (даны их координаты на прямой), в которые необходимо расставить K коров так, чтобы минимальное расcтояние между коровами было как можно больше. Гарантируется, что (1 < K < N).

Решение:

Если решать задачу в лоб, то вообще неясно что делать. Нужно решать обратную задачу: давайте предположим, что мы знаем это расстояние X, ближе которого коров ставить нельзя. Тогда сможем ли мы расставить самих коров?

Ответ — да, можно ставить их довольно просто: самую первую ставим в самое левое стойло, это всегда выгодно. Следующие несколько стойл надо оставить пустыми, если они на расстоянии меньше X. В самое левое стойло из оставшихся надо поставить вторую корову и так далее. Даже ясно как это писать: надо идти слева направо по отсортированному массиву стойл, хранить координату последней коровы, и либо пропускать стойло, либо ставить в него новую корову.

То есть если мы знаем расстояние X, то мы можем за O(n) проверить, можно ли расставить K коров на таком расстоянии. Ну так давайте запустим бинпоиск по X, ведь при слишком маленьком X коров точно можно расставить, а при слишком большом — нельзя, и как раз эту границу и просят найти в задаче (“как можно больше”).

Осталось точно определить границы, то есть изначальные значения left и right. Нам точно хватит расстояния 0, так как гарантируется, что коров меньше, чем стойл. И точно не хватит расстояния max_coord — min_coord + 1, так как по условию есть хотя бы 2 коровы.

coords = [2, 5, 7, 11, 15, 20] # координаты стойл
k = 3 # число коров

def is_correct(x): # проверяем, можно ли поставить K коров в стойла, если между коровами расстояние хотя бы x
    cows = 1
    last_cow = coords[0]
    for c in coords:
        if c - last_cow >= x:
            cows += 1
            last_cow = c
    return cows >= k

left = 0 # расставить коров на расстоянии хотя бы 0 можно всегда
right = max(coords) - min(coords) + 1 # при таком расстоянии даже 2 коровы поставить нельзя
while right - left != 1:
    middle = (left + right) // 2
    if is_correct(middle): # проверяем, можно ли поставить K коров в стойла, если между коровами расстояние хотя бы middle
        left = middle # left всегда должна указывать на ситуацию, когда можно поставить коров
    else:
        right = middle # right всегда должна указывать на ситуацию, когда нельзя поставить коров
print left # left - максимальное расстояние, на котором можно расставить коров в стойла

Общий принцип

Такой метод и называется бинпоиск по ответу. Он очень важный и очень распространен на олимпиадах, очень рекомендую решать на него задачи.

По сути мы просто взяли задачу “найдите максимальное X, такое что какое-то свойство от X выполняется” и решили её бинпоиском. Самое сложное — увидеть такую формулировку в задаче. Поэтому рассмотрим еще один пример.

Пример: “Очень Легкая Задача”

Условие: есть два принтера, один печатает лист раз в (x) минут, другой раз в (y) минут. За сколько минут они напечатают (N) листов? (N > 0)

Решение: Здесь, в отличие от предыдущей задачи, кажется, существует прямое решение с формулой. Но вместо того, чтобы о нем думать, можно просто свести задачу к обратной. Давайте подумаем, как по числу минут (T) (ответу) понять, сколько листов напечатается за это время? Очень легко: [lfloorfrac{T}{x}rfloor + lfloorfrac{T}{y}rfloor]

Ясно, что за (0) минут (N) листов распечатать нельзя, а за (xN) минут один только первый принтер успеет напечатать (N) листов. Поэтому (0) и (xN) — это подходящие первые границы для бинарного поиска.

Примечание: заметьте, что задача в контесте немного отличается! Прочитайте внимательно условие.

Задание

Решите как можно больше задач в практическом контесте:

https://informatics.msk.ru/mod/statements/view.php?id=34097

Там могут встречаться задачи как на бинпоиск по ответу, так и на тернарный поиск по ответу.

Источник

Как найти вершину параболы: три формулы

Парабола присутствует в мире математики, физики и других наук. По траектории параболы передвигаются искусственные спутники, которые стремятся покинуть пределы Солнечной системы, мяч при игре в волейбол тоже описывает её траекторию. Нужно уметь строить параболу. А чтобы это не составляло труда, надо знать, как найти вершину параболы.

Нахождение вершины параболы: способы, примеры, советы

График функции y = ax 2 + bx + c, где a — первый коэффициент, b — второй коэффициент, c — свободный член, называется параболой. Но обратите внимание на тот факт, что a ≠0.

У каждой точки параболы есть симметричная ей, кроме одной точки, и эта точка называется вершиной. Для того чтобы найти точку, которая является вершиной, нужно определиться, что такое точка на графике. Точка на графике – это определённая координата по оси абсцисс и по оси ординат. Она обозначается как (x; y). Давайте разбираться, как найти заветные числа.

Первый способ

Если вы хотите знать, как необходимо правильно вычислять координаты вершины, то нужно только выучить формулу x0 = -b/2a. Подставляя полученное число в функцию, получим y0.

Например, y =x 2 –8 x +15;

находим первый, второй коэффициенты и свободный член;

подставляем значения a и b в формулу;

вычисляем значения y;

Значит, вершина находится в точке (4;-1).

Ветви параболы симметричны относительно оси симметрии, которая идёт через вершину параболы. Зная корни уравнения, можно без особых трудностей посчитать абсциссу вершины параболы. Предположим, что k и n — корни квадратичного уравнения. Тогда точка x0 равноудалена от точек k и n, и её можно вычислить по формуле: x0 = (k + n)/2.

Рассмотрим на примере y =x 2 –6x+5

1) Приравниваем к нулю:

2) Находим дискриминант, используя формулу: D = b 2 –4 ac:

3) Находим корни уравнения по формуле (-b±√ D)/2a:

1 — первый корень;
5 — второй корень.

Второй способ

Дополнение до полного квадрата – отличный способ узнать, где располагается вершина. Используя этот способ, вы сможете вычислить точки x и y одновременно, без нужды подставлять x в начальный пример. Рассмотрим этот метод на примере функции: y=x 2 +8 x +10.

1. Сначала нужно приравнять выражение с переменной к 0. Потом перенести c в правую сторону с противоположным знаком, то есть у нас получается выражение x 2 + 8x = -10.

2. Теперь в левой части нужно сделать полный квадрат. Для этого посчитайте (b/2) 2 и увеличьте обе части уравнения результат. В этом случае нужно подставит 8 вместо b.

У нас получается 16. Теперь прибавьте это число к обеим частям уравнения:

3. Видно, что полученное выражение – полный квадрат. Его можно представить в форме: (x + 4) 2 = 6.

4. Используйте это выражение для поиска координат вершины параболы. Чтобы посчитать x, нужно приравнять его к 0. Получаем, x =-4. Координата y равна тому, что находится в правой части, то есть y =6. Вершина параболы этого уравнения (-4, 6).

Третий способ

Если вы знаете, что такое производная, то для вас есть другая формула. Несмотря на то, куда смотрят «рога» параболы, её вершина — точка экстремума. Для этого способа надо применить следующий алгоритм:

1. Нахождение первой производной по формуле f'(x) = (ax² + bx + c)’ = 2ax + b.

2. Приравнивание производной к 0. В итоге вы получите 0 = 2ax + b, отсюда можно найти то, что нас интересует.

Рассмотрим этот способ подробнее.

Дана функция y = 4x²+16x-17;

Записываем производную и приравниваем к нулю.

f'(x) = (4x²+16x-17)’ = 8x+16 =0

Построение параболы

Рассмотрим подробнее вопрос о нахождении точек, которые нужно отметить. Для примера возьмём функцию y =-x 2 +11 x -24 с вершиной в точке (5,5;-6,25).

1) Строим таблицу

2) Заполняем таблицу

X	4	5	5,5	6	7
Y	-4	-6	-6,25	-6	-4

Советы

Правильно находите коэффициенты.

Пишите промежуточные вычисления на бумаге. Это не только облегчит нахождение вершины, но и поможет найти свои ошибки.

Делайте всё поэтапно. Следуйте алгоритму.

Обратите ваше внимание на то, что:

Нужно проверять правильно ли ваше решение.
Необходимо успокоиться. Решение любых задач по математике требует опыта. Просто нужно отработать данную тему, и тогда непременно у вас всё получится.

Видео

Это видео поможет вам научиться находить вершину параболы

Парабола, график, вершина, нули.

теория по математике 📈 функции

Функция вида y=ax 2 +bx+c, где а, b, с – некоторые числа, причем, а ≠ 0 число, х – переменная, называется квадратичной функцией.

Графиком квадратичной функции является парабола, она имеет вершину и две ветви, которые могут быть направлены либо вверх, либо вниз (рис.1). Красной точкой обозначена вершина параболы, из которой выходят ветви. Её координаты по графику – (3; –4). Направление ветвей зависит от значения коэффициента «а», то есть, если «а» – положительное число, то ветви направлены вверх; если число «а» – отрицательное, то ветви направлены вверх. На данном рисунке ветви направлены вверх, значит коэффициент «а» у формулы, которая задает эту функцию – положительное число. Коэффициент «с» показывает ординату (у) точки пересечения ветви параболы с осью у. Так, на рисунке №1 парабола пересекает ось у в точке (5;0), значит коэффициент с=5.

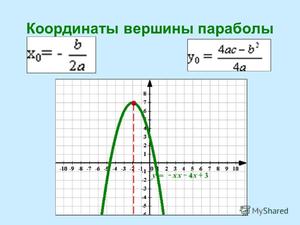
Чтобы найти координаты вершины параболы (х₀; у₀), надо воспользоваться формулой:

для нахождения у₀ можно просто подставить значение х₀ в формулу данной функции y₀=ax 2 +bx+c вместо х.

Рассмотрим это на примере конкретно заданной функции.

Пример №1

Найти вершину параболы, заданной формулой у=2х 2 – 8х + 5.

Найдем, чему равны коэффициенты: а=2; b= – 8

Подставим их в формулу и вычислим значение х₀:

х₀= − b 2 a . . = 8 2 ∙ 2 . . = 8 4 . . = 2

Теперь в заданную по условию формулу вместо х подставим найденное значение у₀=2 ∙ 2 2 – 8 ∙ 2 + 5=8 – 16 + 5= –3

Итак, мы нашли координаты вершины параболы: (2; –3).

Значения х, при которых функция принимает значения, равные нулю, называются нулями функции. Другими словами, Значения абсцисс (х) точек пересечения ветвей параболы с осью х, называются нулями функции. На рисунке №1 точки координаты точек пересечения ветвей параболы с осью х следующие: (1;0) и (5;0). Значит, нули функции – это значения х, равные 1 и 5.

Рассмотрим, как найти нули функции не по рисунку, а по заданной формуле.

Пример №2

Найти нули функции у=х 2 +4х – 5

Так как нули функции это абсциссы точек пересечения ветвей параболы с осью х, то их координаты будут (х;0), то есть у=0. Значит, вместо у подставляем нуль в нашу формулу 0=х 2 +4х – 5 и получаем квадратное уравнение, решив которое, мы и найдем значения нулей функции:

D=b 2 – 4ac=4 2 – 4 ∙ 1 ∙ ( − 5 ) = 36

Значит, нули функции равны –5 и 1

Примечание к заданию по нахождению нулей функции без графика

Если дискриминант уравнения отрицательный, значит, нулей функции нет, то есть парабола не пересекает ось х (вершина находится выше неё, если ветви направлены вверх и ниже, если ветви направлены вниз).

Рассмотрим нахождение соответствия рисунков парабол, расположенных в системе координат значениям а и с.

Пример №3

Для выполнения данного задания на соответствие необходимо сначала поработать с графиками, подписав на них, какими – отрицательными или положительными являются коэффициенты а и с.

Теперь можно выполнить соответствие:

Пример №4

Рассмотрим еще пример на соответствие

В данном задании рассмотрим коэффициенты в формулах и подчеркнем их: так, в формуле под буквой А коэффициент а=-2, т.е. отрицательный, значит, ветви направлены вниз, а это график под номером 2. В формулах под буквами Б и В первые и третьи коэффициенты одинаковые, значит, сравнить по рисунку их невозможно, следовательно, будем сравнивать по расположению вершины (справа или слева от оси у), а именно х₀.

Итак, найдем х₀ для формулы «Б»:

х₀= − b 2 a . . = − 4 2 ∙ 2 . . = − 4 4 . . = − 1

Видим, что х₀ отрицательное, значит, вершина расположена слева от оси у, а это рисунок 3. Ну и осталось привести в соответствие В и 1.

Запишем в таблицу

А) a>0, с >0 Б) а 0 В) а>0, с

На рисунках в задании изображены параболы. Вспомним, что обозначают коэффициенты а и с: а – направление ветвей (a 0 – ветви вверх); коэффициент с показывает ординату точку пересечения параболы с осью х (с >0 – пересечение в положительном направлении; с 0, с >0 – это график №1

Б) а 0 – это график №3

pазбирался: Даниил Романович | обсудить разбор | оценить

Установите соответствие между функциями и их графиками.

ФУНКЦИИ

Сразу обратим внимание на вариант В. Эта функция единственная, имеющая положительный коэффициент при х 2 (здесь а=1, т.е. а>0). При а>0 график параболы направлен ветками вверх. Такой график имеется только один – под №3. Кроме того, можно обратить внимание на коэфициент с. Она равен 3, т.е. с>0. Это указывает на то, что парабола должна пересечь ось Оу выше начала координат. Что и отображено на графике В. Получаем соответствие: В–3.

Оба других графика – 1-й и 2-й – пересекают ось Оу ниже начала координат, что соответствует значению с=–3

pазбирался: Даниил Романович | обсудить разбор | оценить

На рисунках изображены графики функций вида

Установите соответствие между знаками коэффициентов a и c и графиками функций.

Мы вспоминаем, за что отвечают коэффициенты a и b при построении графиков функции вида

Коэффициент a определяет направление ветвей параболы: если a > 0, то ветви направлены вверх, а если a 0.

Далее мы смотрим, на что влияет коэффициент c.

Коэффициент c отвечает за положение параболы относительно оси x, или же отвечает за сдвиг по оси y, а именно:

если c > 0, то вершина параболы расположена выше оси х

Из всего вышеперечисленного можно найти ответ:

pазбирался: Даниил Романович | обсудить разбор | оценить

Парабола свойства и график квадратичной функции

Что такое парабола знают, пожалуй, все. А вот как ее правильно, грамотно использовать при решении различных практических задач, разберемся ниже.

Сначала обозначим основные понятия, которые дает этому термину алгебра и геометрия. Рассмотрим все возможные виды этого графика.

Узнаем все основные характеристики этой функции. Поймем основы построения кривой (геометрия). Научимся находить вершину, другие основные величины графика данного типа.

Узнаем: как правильно строится искомая кривая по уравнению, на что надо обратить внимание. Посмотрим основное практическое применение этой уникальной величины в жизни человека.

Что такое парабола и как она выглядит

Алгебра: под этим термином понимается график квадратичной функции.

Геометрия: это кривая второго порядка, имеющая ряд определенных особенностей:

Любая прямая пересекает на плоскости искомую линию в 2-х точках – так называемые, «нули» (кроме основного экстремума графика).

Множество точек плоскости ХОY (М), расстояние FM которых до F = расстоянию MN до прямой Где F – фокус, AN – директриса. Эти понятия рассмотрим ниже.

Каноническое уравнение параболы

На рисунке изображена прямоугольная система координат (XOY), экстремум, направление ветвей чертежа функции вдоль оси абсцисс.

Каноническое уравнение имеет вид:

где коэффициент p – фокальный параметр параболы (AF).

В алгебре оно запишется иначе:

y = a x2 + b x + c (узнаваемый шаблон: y = x2).

Свойства и график квадратичной функции

Функция обладает осью симметрии и центром (экстремум). Область определения – все значения оси абсцисс.

Область значений функции – (-∞, М) или (М, +∞) зависит от направления ветвей кривой. Параметр М тут означает величину функции в вершине линии.

Как определить, куда направлены ветви параболы

Чтобы найти направление кривой такого типа из выражения, нужно определить знак перед первым параметром алгебраического выражения. Если а ˃ 0, то они направлены вверх. Если наоборот – вниз.

Как найти вершину параболы по формуле

Нахождение экстремума является основным этапом при решении множества практических задач. Конечно, можно открыть специальные онлайн калькуляторы, но лучше это уметь делать самому.

Как же ее определить? Есть специальная формула. Когда b не равно 0, надо искать координаты этой точки.

Формулы нахождения вершины:

Пример.

Имеется функция у = 4 * x2 + 16 * x – 25. Найдём вершины этой функции.

Для такой линии:

х = -16 / (2 * 4) = -2,

y = 4 * 4 — 16 * 2 — 25 = 16 — 32 — 25 = -41.

Получаем координаты вершины (-2, -41).

Смещение параболы

Классический случай, когда в квадратичной функции y = a x2 + b x + c, второй и третий параметры равны 0, а = 1 – вершина находится в точке (0, 0).

Движение по осям абсцисс или ординат обусловлено изменением параметров b и c соответственно. Сдвиг линии на плоскости будет осуществляться ровно на то количество единиц, чему равно значение параметра.

Пример.

Имеем: b = 2, c = 3.

Это означает, что классический вид кривой сдвинется на 2 единичных отрезка по оси абсцисс и на 3 по оси ординат.

Как строить параболу по квадратному уравнению

Школьникам важно усвоить, как правильно начертить параболу по заданным параметрам.

Анализируя выражения и уравнения, можно увидеть следующее:

Точка пересечения искомой линии с вектором ординат будет иметь значение, равное величине с.

Все точки графика (по оси абсцисс) будут симметричны относительно основного экстремума функции.

Кроме того, места пересечения с ОХ можно найти, зная дискриминант (D) такой функции:

Для этого нужно приравнять выражение к нулю.

Наличие корней параболы зависит от результата:

D ˃ 0, то х1, 2 = (-b ± D0,5) / (2 * a),

D = 0, то х1, 2 = -b / (2 * a),

D ˂ 0, то нет точек пересечения с вектором ОХ.

Получаем алгоритм построения параболы:

определить направление ветвей,

найти координаты вершины,

найти пересечение с осью ординат,

найти пересечение с осью абсцисс.

Пример 1.

Дана функция у = х2 5 * х + 4. Необходимо построить параболу. Действуем по алгоритму:

а = 1, следовательно, ветви направлены вверх,

координаты экстремума: х = (-5) / 2 = 5/2, y = (5/2)2 — 5 * (5/2) + 4 = -15/4,

с осью ординат пересекается в значении у = 4,

найдем дискриминант: D = 25 — 16 = 9,

ищем корни:

Х1 = (5 + 3) / 2 = 4, (4, 0),

Х2 = (5 — 3) / 2 = 1, (1, 0).

По полученным точкам можно построить параболу.

Пример 2.

Для функции у = 3 * х2 2 * х 1 нужно построить параболу. Действуем по приведенному алгоритму:

а = 3, следовательно, ветви направлены вверх,

координаты экстремума: х = (-2) / 2 * 3 = 1/3, y = 3 * (1/3)2 — 2 * (1/3) — 1 = -4/3,

с осью у будет пересекаться в значении у = -1,

найдем дискриминант: D = 4 + 12 = 16. Значит корни:

Х1 = (2 + 4) / 6 = 1, (1,0),

Х2 = (2 — 4) / 6 = -1/3, (-1/3, 0).

По полученным точкам можно построить параболу.

Директриса, эксцентриситет, фокус параболы

Исходя из канонического уравнения, фокус F имеет координаты (p/2, 0).

Прямая АВ – директриса (своего рода хорда параболы определенной длины). Ее уравнение: х = -р/2.

Эксцентриситет (константа) = 1.

Заключение

Мы рассмотрели тему, которую изучают школьники в средней школе. Теперь вы знаете, глядя на квадратичную функцию параболы, как найти её вершину, в какую сторону будут направлены ветви, есть ли смещение по осям, и, имея алгоритм построения, сможете начертить её график.

источники:

Парабола, график, вершина, нули.

http://tvercult.ru/nauka/parabola-svoystva-i-grafik-kvadratichnoy-funktsii

Источник

Как найти икс нулевое

Уравнения квадратичной функции

Видео

Построение параболы

Алгоритм построения

Теги

Как найти икс нулевое

Как найти икс нулевое

x нулевое

Где можно решить любую задачу по математике, а так же x нулевое Онлайн?

Почему любое число в нулевой степени равно 1 ? Как объяснить ребенку?

Как найти икс нулевое

Бинарный поиск

Линейный поиск

Задание

Бинарный поиск

Задание

Общий принцип

Задание

Задание

Задание

Бинарный поиск с вещественными числами

Задание

Поиск максимума выпуклой функции: тернарный поиск, бинарный поиск

Задание

Тернарный поиск

Задание

Бинарный поиск по неотсортированному массиву

Бинарный поиск по ответу

Пример: “Корова в стойла”

Общий принцип

Пример: “Очень Легкая Задача”

Задание

Как найти вершину параболы: три формулы

Нахождение вершины параболы: способы, примеры, советы

Первый способ

Второй способ

Третий способ

Построение параболы

Советы

Видео

Парабола, график, вершина, нули.

теория по математике 📈 функции

Пример №1

Пример №2

Пример №3

Пример №4

Парабола свойства и график квадратичной функции

Что такое парабола и как она выглядит

Каноническое уравнение параболы

Свойства и график квадратичной функции

Как определить, куда направлены ветви параболы

Как найти вершину параболы по формуле

Смещение параболы

Как строить параболу по квадратному уравнению

Директриса, эксцентриситет, фокус параболы

Заключение