Как найти ядро уравнения

1. Уравнения Фредгольма

1. Основные понятия

Линейным
интегральным уравнением Фредгольма
2-го рода
называется уравнение вида

где


– неизвестная функция,

– известные функции,

– действительные переменные, изменяющиеся
в интервале



– числовой множитель.

Функция


называется ядром
интегрального уравнения
(1); предполагается, что ядро
определено
в квадрате

на плоскости

и непрерывно в
,
либо его разрывы таковы, что двойной
интеграл

имеет
конечное значение.

Если

,
то уравнение (1) называется неоднородным;
если же
,
то уравнение (1) принимает вид

И
называется однородным.

Интегральное
уравнение вида

не
содержащее искомой функции

вне интеграла, называется интегральным
уравнением Фредгольма 1-го рода.

Пределы
интегрирования

в уравнениях (1), (2) и (3) могут быть как
конечными, так и бесконечными.

Решением
интегральных уравнений (1), (2) и (3)
называется любая функция

при подстановке которой в уравнения
последние обращается в тождества
относительно

1. Итерированные
   ядра. Построение резольвенты с помощью
   итерированных ядер

Пусть
имеем интегральное уравнение Фредгольма

Как
и в случае уравнений Вольтерра,
интегральное уравнение (1) можно решать
методом последовательных приближений.
Для этого полагаем

где


определяются по формулам

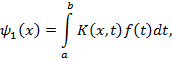
Здесь

и
вообще

, причем

Функции

определяемые по формулам (3), называются
итерированными
ядрами.
Для них справедливо соотношение

где


– любое натуральное число, меньшее

Резольвента
интегрального уравнения (1) определяется
через итерированные ядра формулой

где
ряд, стоящий в правой части, называется
рядом
Неймана ядра

.
Он сходится для

где

Решение
уравнения Фредгольма 2-го рода (1)
выражается формулой

Граница
(6) является существенной для сходимости
ряда (5). Однако решение уравнения (1)
может существовать и для значений
.

Пример
1.
Найти итерированные ядра для ядра
,
если

Решение.
Пользуясь формулами (3), найдем
последовательно:

Отсюда
следует, что итерированные ядра имеют
вид:

1. для
   n
   = 2k
   – 1

1. для
   n
   =
   2k

Где
k
= 1,2,3,…

Пример
2.
Найти итерированные ядра

и
,
если

Решение.
По определению имеем

Поэтому
данное ядро можно записать в виде

Это
ядро, как легко проверить, является
симметричным, т.е.

Имеем


Находим второе итерированное ядро:

Здесь

Так
как данное ядро

симметрично, то достаточно найти

только при

Имеем
(рис. 2)

В
интервале

имеем
,
поэтому

В
интервале

имеем
,
поэтому

В
интервале

имеем
,
поэтому

С
кладывая
найденные интегралы, получим

Выражение
для

при

мы найдем, если поменяем местами аргументы


в выражении

для
:

Итак,
второе итерированное ядро имеет вид

Замечание.
Если ядро
,
задаваемое в квадрате

разными аналитическими выражениями,
не является симметричным, то следует
отдельно рассмотреть случай
.
При

будем иметь (рис. 3)

1. Интегральные
   уравнения с вырожденным ядром

Ядро


интегрального уравнения Фредгольма
2-го рода называется вырожденным,
если оно является суммой конечного
числа произведений функций только от


на функции только от
,
т.е. если оно имеет вид

функции


будем считать непрерывными в основном
квадрате

и линейно независимыми между собой.
Интегральное уравнение с вырожденным
ядром (1)

решается
следующим образом.

Перепишем
(2) в виде

и
введем обозначения

Тогда
(3) примет вид

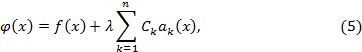
где


– неизвестная постоянная (так как
функция

неизвестна).

Таким
образом, решение интегрального уравнения
с вырожденным ядром сводится к нахождению
постоянных

Подставляя выражение (5) в интегральное
уравнение (2), после несложных выкладок
получим

В
силу линейной независимости функций


отсюда следует, что

или

Вводя
для краткости записи обозначения

получим,
что

или
в развернутом виде:

Для
нахождения неизвестных

имеем линейную систему из

алгебраических уравнений с

неизвестными. Определитель этой системы
равен

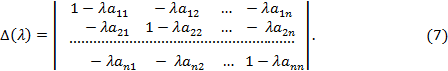
Если

,
то система (6) имеет единственное решение


получаемое по формулам Крамера

Решением
интегрального уравнения (2) будет функция

,
определенная равенством

где
коэффициенты

определяются по формулам (8).

Задача
3.
Решить интегральное уравнение

Решение.
Запишем уравнение в следующем виде:

Введем
обозначения:

где


– неизвестные постоянные. Тогда (9)
примет вид

Подставляя
выражение (11) в равенства (10), получим

Или

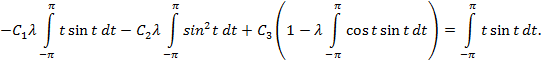
Вычисляя
входящие в эти уравнения интегралы, мы
получим систему алгебраических уравнений
для нахождения неизвестных
:

Определитель
этой системы

Система
(12) имеет единственное решение

Подставляя
найденные значения

получим решение данного интегрального
уравнения:

1. Характеристические
   числа и собственные функции

Однородное
интегральное уравнение Фредгольма 2-го
рода

всегда
имеет очевидное решение

которое называют нулевым
(тривиальным)
решением.

Значения
параметра ,
при которых это уравнение имеет ненулевые
решения

называются характеристическими
числами
уравнения (1) или ядра
,
а каждое ненулевое решение этого
уравнения называется собственной
функцией,
соответствующей характеристическому
числу .

Число


не является характеристическим числом,
так как при

из (1) следует, что

Если
ядро

непрерывно в квадрате

или суммируемо с квадратом в
,
причем числа

конечные, то каждому характеристическому
числу 
соответствует конечное число линейно
независимых собственных функций; число
таких функций называется рангом
характеристического числа. Разные
характеристические числа могут иметь
разные ранги.

Для
уравнения с вырожденным ядром

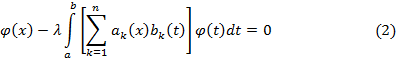
характеристические
числа являются корнями алгебраического
уравнения

степень
которого
.
Здесь

– определитель однородной линейной
системы

где
величины

имеют тот же смысл, что и в предыдущем
параграфе.

Если
уравнения (3) имеет

корней (
),
то интегральное уравнение (2) имеет

характеристических чисел; каждому
характеристическому числу

соответствует ненулевое решение

системы
(4). Соответствующие этим решениям
ненулевые решения интегрального
уравнения (2), т.е. собственные функции,
будут иметь вид

Интегральное
уравнение с вырожденным ядром имеет не
более

характеристических чисел и соответствующих
им собственных функций.

В
случае произвольного (невырожденного)
ядра характеристические числа являются
полюсами резольвенты
.
Отсюда, в частности, следует, что
интегральное уравнение Вольтерра

не имеет характеристических чисел.

Пример
1.
Найти характеристические числа и
собственные функции интегрального
уравнения

Решение.
Имеем

Вводя
обозначения

будем
иметь

Подставляя
(6) в (5), получим линейную систему однородных
уравнений

Так
как

то
система (7) примет вид

Уравнение
для нахождения характеристических
чисел:

Характеристические
числа:

При


система (8) принимает вид

откуда


произвольно. Собственная функция будет

,
или, полагая
,
получим
.

При


система (8) примет вид

откуда


произвольно, и, значит, собственная
функция будет
,
или, полагая
,
получим
.

Итак,
характеристические числа:

соответствующие
им собственные функции:

Однородное
интегральное уравнение Фредгольма
может вообще не иметь характеристических
чисел и собственных функций, либо же
может не иметь действительных
характеристических чисел и собственных
функций.

Пример
2.
Однородное интегральное уравнение

не
имеет характеристических чисел и
собственных функций.

В
самом деле, имеем

Полагая

получим

Подставляя
(10) в (9), получим

Но
так как

то
уравнение (11) дает
,
и, следовательно,
.

Итак,
данное однородное уравнение при любых

имеет только одно нулевое решение
,
а значит, оно не имеет характеристических
чисел и собственных функций.

1. Уравнения
   с симметричными ядрами

Ядро


интегрального уравнения называется
симметричным,
если выполняется условие
.

Для
интегрального уравнения Фредгольма

с
симметричным ядром

имеют место следующие теоремы.

Теорема
1.
Уравнение
(1) имеет по крайней мере одно действительное
характеристическое число.

Теорема
2.
Каждому
характеристическому числу 
соответствует конечное число

линейно независимых собственных функций
уравнения (1), причем

Число


называется рангом
или кратностью
характеристического числа.

Теорема
3.
Каждая
пара собственных функций
,
соответствующих различным характеристическим
числам
,
ортогональна, т.е.

Теорема
4.
В
каждом конечном интервале оси 
находится конечное число характеристических
чисел. Число

характеристических чисел, лежащих в
интервале
,
определяется неравенством

В
том случае, когда ядро

интегрального уравнения (1) является
функцией Грина некоторой однородной
задачи Штурма-Лиувилля, нахождение
характеристических чисел и собственных
функций сводится к решению указанной
задачи Штурма-Лиувилля.

Если
-е повторное (итерированное) ядро

ядра

есть симметричное ядро, то можно
утверждать, что

имеет по крайней мере одно характеристическое
число (действительное или комплексное)
и что
-е
степени всех характеристических чисел
– числа действительные. В частности,
для кососимметричного ядра

все характеристические числа чисто
мнимые:
,
где

– действительное.

Задача
4.
Найти характеристические числа и
собственные функции однородного
уравнения

где

Решение.
Данное уравнение представим в виде

или

Дифференцируя
обе части (15), находим

или

Повторное
дифференцирование дает

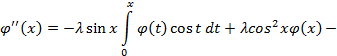
Выражение
в квадратных скобках равно
,
так что

Из
равенств (15) и (16) находим, что

Так
данное интегральное уравнение сводится
к следующей краевой задаче:

Здесь
возможны три случая.

,
или
.
Уравнение (17) принимает вид
.
Его общее решение будет
.
Используя краевые условия (18), получим
для нахождения неизвестных

систему

которая
имеет единственное решение
,

,
а следовательно, интегральное уравнение
имеет только тривиальное решение

2)

,
или
.
Общее решение уравнения (17) имеет вид

откуда

Для
нахождения значений

Система
имеет единственное решение
.
Интегральное уравнение имеет тривиальное
решение
.
Итак, при

интегральное уравнение не имеет
характеристических чисел, а значит, и
собственных функций.

3)

,
или
.
Общее решение уравнения (17) будет

Отсюда
находим, что

В
некоторых случаях неоднородное
симметричное интегральное уравнение
можно свести к неоднородной краевой
задаче. Это можно сделать тогда, когда
ядро

интегрального уравнения является
функцией Грина некоторого линейного
дифференциального оператора. Покажем
на примере, как это делается.

Пример
1.
Решить уравнение

где

Решение.
Данное уравнение перепишем в виде

Дифференцируя
дважды, найдем

или

.

Полагая
в (10) x = 0 и x
= 1, получим, что

Искомая функция

является решением неоднородной краевой
задачи

Рассмотрим
следующие случаи.

1. 
   
   Уравнение (11) имеет вид
   
   Его общее решение

Учитывая
краевые условия (12), получим для нахождения
постоянных

систему

решая
которую находим

и, следовательно,

1. 
   
   Общее решение уравнения (11)

Краевые
условия (12) дают для нахождения

систему

откуда

.

Искомая
функция приведется к виду

1. 
   
   Обозначим
   
   Общим решением уравнения (11) будет
   
   Краевые условия дают систему

Здесь,
в свою очередь, возможны два случая.

а)


не является корнем уравнения

Тогда

и,
следовательно,

б)
)

является корнем уравнения

Система (13) не совместна,а следовательно,
данное уравнение (9) не имеет решений. В
этом случае соответствующее однородное
интегральное уравнение

имеет
нетривиальные решения, т.е. числа

являются характеристическими числами,
а функции

– собственными функциями уравнения
(14).

Пример
2.
Решить уравнение

где

Решение.
Характеристические числа и соответствующие
им собственные функции имеют вид

Если

,
то решением уравнения (7) будет

Вводим
коэффициенты Фурье

правой части уравнения:

Подставляя
в (8), получим

При


уравнение (7) не имеет решений, так как

Пример
3.
Решить уравнение

где

Решение.
Характеристические числа:

Соответствующие
им собственные функции:

Если


и
,
то решение данного уравнения будет
иметь вид

и
так как

то

При


уравнение решений не имеет, так как его
правая часть, т.е. функции
,
не ортогональна к соответствующим
собственным функциям

Если
же

где

то данное уравнение имеет бесконечное
множество решений, которые даются
формулой (6):

где


– произвольная постоянная.

Список
литературы:

1. Владимиров
   В.С., Уравнения математической физики.
   М.: Наука, 2006

2. Тихонов
   А.А.. Самарский Е.И. Уравнения математической
   физики. М.: Наука, 2006

3. Краснов
   М.Л., Киселев А.И., Макаренко Г.И.,
   Интегральные уравнения, СПб.: Комкнига,
   2007

(Решено) как найти ядро линейного оператора, заданного матрицей…

Чтобы оставить комментарий, необходимо авторизоваться.

Последние вопросы

(c) ChatGPT по русски 2023. Все права защищены. При обнаружении неправомерного контента пишите на [email protected]

Ядро и образ линейного оператора

Пусть линейный оператор , действует из пространства в себя и пусть в линейном пространстве выбраны два базиса: и Разложим “новые” базисные вектора в линейные комбинации “старых” базисных векторов :

Стоящая здесь матрица м столбцом которой является координатный столбец го базисного вектора в “старом” базисе называется матрицей перехода от “старого”базиса к “новому“. Если теперь координаты вектора в “старом” базисе а координаты того же вектора в “новом” базисе то имеет место равенство

Так как разложение по базису единственно, то отсюда следует, что

Получен следующий результат.

Теорема 1.Координаты вектора в базисе и координаты того же вектора в базисе связаны соотношениями (2), где матрица перехода от “старого”базиса к “новому“ .

Посмотрим теперь, как связаны между собой матрицы и одного и того же оператора в различных базисах и пространства Матрицы и определяются равенствами Пусть Это равенство в базисе равносильно матричному равенству

а в базисе матричному равенству ( здесь приняты те же обозначения, что и в (1)). Используя теорему (1), будем иметь

так как столбец произвольный, то отсюда получаем равенство

Доказан следующий результат.

Теорема 2.Если матрица оператора в базисе а матрица того же оператора в базисе то

Замечание 1.Две произвольные матрицы и связанные соотношением где некоторая невырожденная матрица называются подобными матрицами. Таким образом, две матрицы одного и того же оператора в различных базисах подобны.

Пример 1.Матрица оператора в базисе имеет вид

Найти матрицу этого оператора в базисе Вычислить координаты вектора в базисе

Решение. Матрица перехода от старого базиса к новому и обратная к ней матрица имеют вид

поэтому по теореме 2 матрица оператора и новом базисе будет такой:

Далее, вектор имеет следующий координатный столбец в базисе По теореме 1 координатный столбец этого вектора в базисе будет иметь вид

Замечание 2. Можно обобщить этот результат на операторы, действующие из одного линейного пространства в другое. Пусть оператор действует из линейного пространства в другое линейное пространство и пусть в пространстве выбраны два базиса: и а в пространстве – два базиса и Тогда можно составить две матрицы и линейного оператора

и две матрицы и перехода от “старых” базисов к “новым”:

Нетрудно показать, что в этом случае имеет место равенство

Пусть дан линейный оператор действующий из линейного пространства в линейное пространство Следующие понятия бывают полезными при решении линейных уравнений.

Определение 1. Ядром оператора называется множество

Образом оператора называется множество

Нетрудно доказать следующее утверждение.

Теорема 3.Ядро и образ линейного оператора являются линейными подпространствами пространств и соответственно, причем имеет место равенство

Для вычисления ядра оператора надо записать уравнение в матричной форме (выбрав базисы в пространствах и соответственно) и решить соответствующую алгебраическую систему уравнений. Поясним теперь, как можно вычислить образ оператора .

Пусть матрица оператора в в базисах и Обозначим через -й столбец матрицы Принадлежность вектора образу означает, что существуют числа такие, что вектор столбец представляется в виде т.е. является элементом пространства линейных комбинаций столбцов матрицы Выбрав в этом пространстве базис (например, максимальную совокупность линейно независимых столбцов матрицы ), вычислим сначала образ оператора-матрицы : а затем построим образ оператора :

Приведем пример вычисления ядра и образа оператора, действующего из пространства в себя. В этом случае базисы и совпадают.

Пример 2.Найти матрицу, ядро и образ оператора проектирования на плоскость ( трехмерное пространство геометрических векторов).

Решение.Выберем в пространстве какой-нибудь базис (например, стандартный базис ). В этом базисе матрица оператора проектирования находится из равенства Найдем образы базисных векторов. Так как плоскость проходит через ось то

Далее (см. Р10) И аналогично

Значит, матрица оператора имеет вид

Ядро оператора-матрицы вычисляем из уравнения

Образ оператора-матрицы натянут на все линейно независимые столбцы матрицы т.е.

Ядро оператора

,

удовлетворяющее условию линейности

f(αx + βy) = αf(x) + βf(y) .

для всех 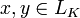и .

Содержание

Важные частные случаи

Связанные понятия

Примеры

Примеры линейных однородных операторов:

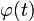
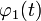
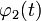
где , , — вполне определённые функции, а x(t) — преобразуемая оператором функция.

См. также

Wikimedia Foundation . 2010 .

Полезное

Смотреть что такое «Ядро оператора» в других словарях:

Ядро (значения) — Ядро нечто центральное и самое важное, часто круглое. Это слово имеет различные значения в разных областях: Содержание 1 Ядерная физика 2 Биология 3 Науки о Земле 4 Спорт … Википедия

Ядро — Содержание 1 Ядерная физика 2 Биология 3 Науки о Земле … Википедия

ЯДРО — линейного оператора линейное подпространство области определения линейного оператора, состоящее из всех векторов, к рые отображаются этим оператором в нуль. Я. линейного непрерывного оператора, определенного на нек ром топологическом векторном… … Математическая энциклопедия

Ядро интегрального уравнения — Ядром интегрального оператора называется функция двух аргументов , определяющая некий интегральный оператор равенством где   пространство с мерой , а принадлежит некоторому … Википедия

Ядро (матем.) — Интегральное уравнение функциональное уравнение, содержащее интегральное преобразование над неизвестной функцией. Если интегральное уравнение содержит также производные от неизвестной функции, то говорят об интегро дифференциальном уравнении.… … Википедия

ЯДРО — интегрального оператора функция двух аргументов К( х, у), определяющая интегральный оператор . равенством где хпробегает пространство . с мерой а принадлежит нек рому пространству функций, определенных на X. Г. Л. Литвинов … Математическая энциклопедия

ВЫРОЖДЕННОЕ ЯДРО — ядро линейного интегрального Фредгольма оператора, имеющее вид где Ри Q точки евклидовых пространств. А. Б. Бакушинский … Математическая энциклопедия

ИТЕРИРОВАННОЕ ЯДРО — функция ( х, s) К п( х, s), к рая образуется из данного ядра Кинтегрального оператора по рекуррентным соотношениям: К п наз. n й итерацией, или n м итерированным ядром, ядра K. И. я. иногда наз. повторным ядром. Если ядро Кнепрерывно или… … Математическая энциклопедия

ДЕФИНИТНОЕ ЯДРО — определенное ядро, ядро К( Р, Q )линейного интегрального Фредголъма оператора, удовлетворяющее соотношению где Р, Q точки евклидова пространства, j произвольная суммируемая с квадратом функция, j комплексно сопряженная функция. В зависимости от… … Математическая энциклопедия

ВОЛЬТЕРРА ЯДРО — функция (матрица функция) К(s, t).двух действительных переменных s, t такая, что или при или при Если такая функция является ядром линейного интегрального оператора, действующего в пространстве и сама квадратично суммируема в треугольнике, в к… … Математическая энциклопедия

Как найти базис ядра

Все права защищены 2019
Перепечатка информации возможна только при наличии
согласия администратора и активной ссылки на источник!

Дано четырехмерное пространство (как я понимаю, в нём находится базис, состоящий из четырех векторов). Нужно найти матрицу оператора в четырехмерном пространстве (получается, самим придумать и составить; как я понимаю, она будет состоять из 4 строк и 4 столбцов?), причём размерность ядра Ker равно размерности образа Im и равно 2. Далее необходимо найти исходя из составленной матрицы базис ядра и образа.

Прошу помочь разобраться в этом задании. С этими линейными операторами, ядрами, образами прям совсем туго((

задан 10 Янв 20:35

Достаточно взять любую матрицу 4×4 ранга 2. Для этого пишем первые две строки наугад, чтобы они не были пропорциональными. Скажем, 1 0 -2 3 и 0 1 4 -1. В качестве третьей строки берём любые, которые выражаются через первые две. Можно брать значения a+b, 2a-b, 3a+2b и т.п.

Базис ядра — это базис в пространстве решений однородной системы. Решаем её методом Гаусса, находя два базисных вектора. В качестве базиса образа можно взять любые два столбца, которые не пропорциональны.

Все эти абстрактные понятия на самом деле легко освоить на конкретных примерах.

@falcao вы сделали вывод о том, что ранг матрицы будет равен 2 исходя из размерности образа? Всегда такое правило действует?

@Yu_Ko: здесь оба числа равны 2, поэтому разницы нет. А общее правило такое: если матрица имеет размер nxn и ранг r, то образ имеет размерность r, а размерность ядра равна n-r. Это более или менее очевидно — особенно для образа. Ведь он состоит из столбцов матрицы и всех их линейных комбинаций. А линейно независимых столбцов, дающих базис образа, будет в точности r. Сумма же размерностей образа и ядра равна размерности всего пространства, то есть n.

@falcao как же вы выручаете! Спасибо огромное! Благодаря вам всё прояснилось, чего не добьёшься от нынешних преподавателей в вузе(

@Yu_Ko: форму для того и существует, чтобы смысл разных понятий прояснять. Преподаватели так поступают не от хорошей жизни. Дело в том, что когда в короткий по времени курс надо уложить много разных методов решения задач (включая дифференциальные уравнения, или ряды Фурье), то там поневоле приходится ограничиваться изложением типовых «рецептов». Типа, капусты вот столько, а морковки в 3 раза меньше Тут как бы уже не до кулинарных «изысков»

Построение базисов в ядре и образе линейного оператора.

Речь пойдёт о построении базисов в ядре и образе линейного оператора.

Будут рассмотрены два примера: первый пример с пояснениями; вто-

рой как образец оформления. Значок будет указывать на утверждения, требующие доказательств. Рекомендуется рассматривать эти утверждения как хорошие теоретические задачи для самостоятельного решения. Полный список теоретических задач приведён в конце.

Пусть L векторное пространство, A линейный оператор в L. Ядро (=нуль-пространство) линейного оператора полный прооб-

раз множества <0>, т. е. множество всех векторов, которые переводятся линейным оператором в 0:

Образ (=множество значений) линейного оператора множество всех векторов, у которых есть прообразы относительно A:

Ядро и образ линейного оператора являются подпространствами . Например, если L координатная плоскость (двумерное векторное

пространство с базисом e 1 , e 2 ) и оператор A проектирует радиус-векторы на ось абсцисс (=на линейную оболочку вектора e 1 ) параллельно оси ординат (=параллельно линейной оболочке вектора e 2 ), то ker A ось ординат (линейная оболочка вектора e 2 ), im A ось абсцисс (линейная оболочка вектора e 1 ):

ker A = `(e 2 ), im A = `(e 1 ).

Рассмотрим на примере, как находить базисы ядра и образа линейного оператора, заданного матрицей в некотором базисе.

Пример 1. Дана матрица линейного оператора A в базисе e = (e 1 , e 2 , e 3 , e 4 ):