-
Явно или неявно заданные функции
Если формула, связывающая аргумент x
и функциюy, имеет
вид
,
то переменнаяy называетсяявно
заданной функцией переменной x.
Например,
,
.
Если формула, связывающая аргументxи функциюу, записана в виде уравнения,
то определяемая из этого уравнения
переменнаяназываетсяфункцией,
заданной неявно.
Пример
3 (неявно
заданные функции)
1) Уравнение
задает неявно функцию
;
2) уравнение
задает неявно функцию
;
3) уравнение
задает неявно две функции
;
4) уравнение
задает неявно бесконечное множество
функций,
.
Из
примеров видно, что если уравнение
удается решить относительноу, то
осуществляется переход от неявно
заданной функции к ее явному заданию.
При этом часто получается многозначная
функция, которую всегда можно рассматривать
как совокупность однозначных функций
(совокупность однозначных ветвей
многозначной функции).
Например,

,
Однако на практике
решить уравнение
относительно переменнойуполучается
далеко не всегда или это решение
получается слишком громоздким. Например,
уравнениенельзя решить относительноy.
Поэтому в этих случаях приходится
работать с функциями, имеющими только
неявное задание.
Замечание (к неявному заданию функций)
В
уравнении
переменныеx
и
y
входят
равноправно, поэтому можно считать, что
это уравнение задает неявно функцию
или функцию
.
Например,
.
-
Параметрически заданные функции
Связь
между аргументом и функцией может быть
записана через дополнительную переменную,
называемую параметром, то есть в виде
системы, в которой прописывается
зависимость аргумента от параметра и
зависимость функции от того же параметра:

где– это параметр,
.
В этом случае функцияназываетсяфункцией,
заданной параметрически.
|
Рис. |
При |
Например, в механике
при описании движения точки по некоторой
траектории задаются абсцисса и ордината
движущейся точки как функции времени
t
(рис. 41).
От параметрически заданной функции
можно перейти к явной или неявной форме
её задания, если удаётся исключить
параметр t.
Пример
4 (параметрически
заданные функции)
1.
Таким образом,— это естьпараметрические
уравнения окружности радиуса R с центром
в начале координати, следовательно, задают две функции,
:
|
|
на верхней полуокружности
на нижней полуокружности
|
2.
Таким образом,— это естьпараметрические
уравнения эллипса с полуосями a и b и с
центром в начале координат,
они задают две функции:
|
x |
на верхней половине эллипса
на нижней половине эллипса
|
3.
|
|
уравнение той же параболы. |
Из последнего примера хорошо видно, что
для одной и той же функции можно записать
несколько вариантов параметрических
уравнений, вводя по-разному параметр.
Выполнить
исключение параметра из параметрических
уравнений не всегда возможно, поэтому
нужно уметь работать и с функциями,
имеющими только параметрические задания.
-
График функции
Графиком
функцииназывается множество точек
координатной плоскости, координаты
которых есть соответствующие друг другу
значения аргумента и функции (рис. 42).
Рис.
42
Графиком
функции может быть линия или несколько
линий или дискретное множество точек
(рис.43).
0
0
Рис.
43
График функциональной зависимости
может строиться не только в системе
декартовых прямоугольных координат
XOY, но и в других
координатных системах.
Например, в полярной системе координат
функцияy = xзаписывается в виде = и имеет графикомспираль
Архимеда(рис. 44).
|
Рис. |
Здесь |
По
умолчанию график функции
строится в системе прямоугольных
декартовых координатXOY.
Явные и неявные функции
Определение.
Функция называется явной, если она задана формулой, правая часть которой не содержит зависимой переменной.
Такая функция имеет вид: , т.е. переменная y выражается через х.
Например, ; ; .
Определение.
Неявной функцией y независимой переменной х называется функция, значения которой находятся из уравнения, связывающего х и y и, не разрешенного относительно y.
Неявная функция имеет вид: .
Например, ; .
Замечание.
Термины «явная функция» и «неявная функция» характеризуют не природу функции, а способ ее задания.
Основные характеристики функции
Изучить функцию – это значит охарактеризовать ход ее изменения (ее поведение) при изменении независимой переменной. Характеризуют функцию по следующим свойствам:
1) четность или нечетность функции;
2) периодичность функции;
4) возрастание или убывание функции (монотонность функции);
5) ограниченность функции.
Рассмотрим эти характеристики.
Четные и нечетные функции
Определение.
Функция называется четной, если она не изменяет своего значения при изменении знака аргумента, т.е. .
Например, ; ; – четные функции.
График четной функции расположен симметрично относительно оси (рис.1.4).
Определение.
Функция называется нечетной, если при изменении знака аргумента знак функции меняется на противоположный, а числовое значение её сохраняется, т.е. .
Например, ; – нечетные функции.
График нечетной функции расположен симметрично относительно начала координат (рис.1.5).
Функция может быть ни четной. ни нечетной, и в этом случае её называют функцией общего вида.
Например, ; ; .
Графики таких функций не симметричны ни относительно оси , ни относительно начала координат.
Периодические функции
Определение.
Функция называется периодической, если существует такое положительное число , что в области определения функции.
Наименьшее из положительных чисел Т, удовлетворяющих условию определения, называется периодом функции .
Например, функции , являются периодическими с периодом .
Нули функции
Определение.
Значение аргумента, при котором функция обращается в нуль, , называется нулем функции.
Например, нулями функции являются значения и .
Монотонные функции
Определение.
Функция называется возрастающей (убывающей) в некоторой области изменения аргумента, если большему значению аргумента соответствует большее (меньшее) значение функции (рис.1.6, 1.7).
Определение.
Если функция в некоторой области изменения аргумента является только возрастающей или только убывающей, то функция называется монотонной.
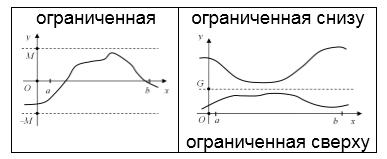
Ограниченные функции
Определение.
Функция называется ограниченной на множестве Х, если существует такое число , что для всех выполняется неравенство .
Например, функции и – ограниченные функции, т.к. и для .
График ограниченной функции лежит между прямыми и (рис.1.8).
УПРАЖНЕНИЯ
1. Найти область определения следующих функций:
1) ; Ответ: ;
2) ; Ответ: ;
3) ; Ответ: ;
4) ; Ответ: .
2. Найти множество значений функции:
1) ; Ответ: ;
2) ; Ответ: ;
3) ; Ответ: .
3. Найти , , , , если .
Ответ: ; ; ; .
4. Пусть и . Найти и .
Ответ: ; .
5. Установить чётность или нечётность функции:
1) ; Ответ: чётная;
2) ; Ответ: чётная;
3) ; Ответ: общего вида;
4) ; Ответ: нечётная.
6. Найти основные периоды функций:
1) ; Ответ: ;
2) ; Ответ: ;
3) ; Ответ: .
7. Введя промежуточные аргументы, представить данную функцию, как суперпозицию других функций:
1) ; Ответ: ; ; ;
2) ; Ответ: ; ; ; ; .
8. Для данных функций найти явные обратные:
1) ; Ответ: ;
2) ; Ответ: ;
3) ; Ответ: .
Обыкновенные дифференциальные уравнения
Содержание:
Обыкновенные дифференциальные уравнения
При решении многих задач математики, техники, экономики и других отраслей науки бывает трудно установить закон, связывающий искомые и известные переменные величины. Но удается установить связь между производными или дифференциалами этих переменных, которая выражается уравнениями или системами уравнений. Такие уравнения называют дифференциальными уравнениями. Термин «дифференциальное уравнение» введен в 1676 году В. Лейбницом.
Мы рассмотрим только уравнения с функциями одной переменной и обычными производными, которые называют обычными дифференциальными уравнениями.
Основные понятия о дифференциальных уравнениях
Определение. Дифференциальным уравнением называется уравнение, которое связывает независимую переменную x, искомую функцию y = f (x) и еепроизводные или дифференциалы разных порядков, то есть уравнение
(7.1)
Важно понять, что искомая функция в дифференциальном уравнении входит под знак дифференциала или под знак производной.
Определение. Порядком дифференциального уравнения называется наивысший порядок производной от неизвестной функции, входящей в дифференциальное уравнение.
Так, уравнение y’ – 2 xy 2 + 5 = 0 является дифференциальным уравнением первого порядка, а уравнения y» + 2 y’ – y – sin x = 0 — дифференциальным уравнением второго порядка.
Определение. Решением дифференциального уравнения (7.1) называется такая функция y = φ (x), которая при подстановке в уравнение (7.1) превращает его в тождество.
Например, для дифференциального уравнения
y’- 2 x = 0 (7.2)
решением является функция y = x 2 . Найдем производную y’= 2x и подставим в уравнение, получим: 2x – 2x = 0, 0 ≡ 0.
Следует заметить, что y = x 2 не единственное решение уравнения. Это уравнение имеет бесконечное множество решений, которые можно записать так: y = x 2 + C.
Дифференциальные уравнения первого порядка
Определение. Дифференциальным уравнением первого порядка называется уравнение, которое связывает независимую переменную x, искомую функцию y = f (x) и ее первую производную:
F (x, y, y’) = 0. (7.3)
Поскольку производную можно записать в виде отношения дифференциалов, то в уравнение производная может не входить, а будут входить дифференциалы неизвестной функции и независимой переменной.
Если уравнение (7.2) решить относительно у’, то оно будет иметь вид:
y’= f (x, y) или . (7.4)
Простые примеры показывают, что дифференциальное уравнение может иметь бесконечное множество решений. Это мы видим на примере уравнения (7.2). Легко убедиться также, что дифференциальное уравнение имеет решениями функции y = Cx, а дифференциальное уравнение — функции где C — произвольное число.
Как видим, в решение указанных дифференциальных уравнений входит произвольное число C. Предоставляя постоянной C различные значения, будем получать различные решения дифференциального уравнения.
Определение. Общим решением дифференциального уравнения (7.3) называется функция
у = φ (х, С), (7.5)
которая зависит от одной произвольной постоянной и удовлетворяет дифференциальное уравнение при произвольном значении C.
Если функция (7.5) выражается неявно, то есть в виде
Ф (х, у, С) = 0, (7.6)
то (7.6) называется общим интегралом дифференциального уравнения.
Определение. Частным решением дифференциального уравнения (7.3) называется такое решение, которое получается из общего решения (7.5) при некотором конкретном значении постоянной C.
Ф (х, у, С0) называется частным интегралом дифференциального уравнения.
На практике при решении конкретных задач часто приходится находить не все решения, а решение, которое удовлетворяет определенным начальным условиям. Одной из таких задач является задача Коши, которая для дифференциального уравнения первого порядка формулируется так: среди всех решений дифференциального уравнения (7.3) найти такое решение y, которое при заданном значении независимой переменной x = x0 равна заданному значению y0 , то есть y (x0) = y0 или (7.7)
Условие (7.7) называется начальным условием решения.
Покажем на примере, как найти частное решение дифференциального уравнения, когда известно общее решение и задано начальное условие.
Мы видим, что дифференциальное уравнение имеет общее решение y = Cx. Зададим начальное условие . Подставим эти значения в общее решение, получим 6 = 2С, откуда С = 3. Следовательно, функция y = 3x удовлетворяет и дифференциальное уравнение, и начальное условие.
Ответ на вопрос о том, при каких условиях уравнение (7.4) имеет
решение, дает теорема Коши.
ТЕОРЕМА (о существовании и единственности решения). Если функция f (x, y) и ее частная производная определены и непрерывные в области G, которая содержит точку M0 (x0; y0) , то существует единственное решение y = φ (x) уравнения (7.4), которое удовлетворяет начальному условию: y (x0) = y0.
Теорема Коши дает достаточные условия существования единого решения дифференциального уравнения (7.4). Заметим, что в условии теоремы не требуется существования частной производной .
График произвольного частного решения дифференциального уравнения называется интегральной кривой. Общему решению отвечает семья кривых. Так мы проверили, что уравнение имеет общее решение y = Cx, то ему соответствует семья прямых,
которые проходят через начало координат (рис. 1).
Уравнение имеет общее решение, ему соответствует семья равносторонних гипербол (рис. 2).
Если задано начальное условие то это означает, что задана точка M0 (x0;y0), через которую должна проходить интегральная кривая, отвечающая искомому частному решению. Таким образом, отыскание частного решения дифференциального уравнения по заданному начальному условию геометрически означает, что из семьи
интегральных кривых мы выбираем проходящую через точку M0 (x0; y0).
Надо заметить, что нахождение решения дифференциального уравнения часто называют интегрированием уравнения. При этом операцию интегрирования функций называют квадратурой.
Общего метода решения дифференциальных уравнений первого порядка не существует. Рассмотрим некоторые методы решения отдельных типов дифференциальных уравнений.
Дифференциальные уравнения с разделенными переменными
Определение. Уравнение вида
f1 (y) dy = f2 (x) dx, (7.8)
где f1 (y) и f2 (x) — заданные функции, называется дифференциальным уравнением с разделенными переменными.
В этом уравнении каждая из переменных находится только в той части уравнения, где находится ее дифференциал. Уравнение dy = f (x) dx является частным случаем уравнения (7.8). Чтобы решить уравнение (7.8), надо проинтегрировать обе его части:
.
Понятно, что произвольную постоянную С можно записывать в любой части равенства.
Пример 1. Решить дифференциальное уравнение:
, удовлетворяющее начальному условию
Решение. Проинтегрируем левую и правую части уравнения, причем для удобства потенцирования, произвольную постоянную запишем в виде ln |C| получим:
— это общее решение дифференциального уравнения.
Подставляя в общее решение начальное условие, найдем С: 2 = С.
Итак,
является частным решением данного уравнения.
Дифференциальные уравнения с разделяющимися переменными
Определение. Уравнение вида
f1 (x) f2 (y) + g1 (x) g2 (y) = 0 (7.9)
называется дифференциальным уравнением с разделяющимися переменными.
В этом уравнении переменные еще не разделены, но, поделив обе части уравнения на произведение f2 (y) g1 (x), получим уравнение с разделенными переменными:
Интегрируя это уравнение, запишем
.
Получили общий интеграл данного уравнения.
Пример 2. Решить дифференциальное уравнение
x (y + 1) dx – (x 2 + 1) ydy = 0.
Решение. Поделим обе части этого уравнения на (y + 1) (x 2 + 1), после чего получим
.
Интегрируя, получим
— общий интеграл дифференциального уравнения.
Пример 3. Найти частное решение дифференциального уравнения (1 + x 2 ) dy + ydx = 0, удовлетворяющее начальному условию y (0) = 1.
Решение. Отделим переменные, поделив уравнение на y ⋅ (1 + x 2 ), и проинтегрируем данное уравнение:
Получили общий интеграл дифференциального уравнения.
Используя начальное условие, найдем произвольную постоянную С:
ln 1 + arctg 0 = C, откуда C = 0.
Найденную постоянную подставим в общий интеграл и отыщем частное решение:
откуда
Однородные дифференциальные уравнения
Определение. Функция двух переменных f (x, y) называется однородной n- го измерения, если выполняется условие
Например, f (x, y) = x 2 + y 2 , f (tx, ty) = t 2 f (x 2 + y 2 ) — однородная функция второго измерения.
Определение. Дифференциальное уравнение
y ‘= f (x, y) (7.10)
называется однородным, если функция f (x, y) однородная нулевого измерения.
Покажем, что это уравнение можно свести к уравнению с разделенными переменными.
Рассмотрим функцию f (tx, ty). Сделаем замену будем иметь:
Тогда уравнение (7.10) запишется в виде (7.11)
В общем случае переменные в однородном уравнение не разделяются сразу. Но, если ввести вспомогательную неизвестную функцию u = u (x) по формуле
или y = xu, (7.12)
то мы сможем превратить однородное уравнение в уравнение с разделенными переменными.
Из формулы (7.12) найдем y’ = u + xu’ и уравнение примет вид: u + xu’ = φ (u),
то есть , откуда .
После интегрирования получим
Отсюда находим выражение для функции u, возвращаемся к переменной y = xu и получим решение однородного уравнения.
Чаще всего не удается найти функцию u явно выраженной, тогда, после интегрирования, в левую часть следует подставить вместо u.
В результате получим решение уравнения в неявном виде.
Пример 1. Найти решение однородного уравнения
Решение. Заменой y = xu сведем заданное уравнение к уравнению
или .
Отделяя переменные, найдем
откуда или , то есть
.
Возвращаясь к переменной y, получим общее решение: .
Линейные дифференциальные уравнения
Определение. Линейным дифференциальным уравнением первого порядка называется уравнение, которое содержит искомую функцию и ее производную в первой степени без их произведения:
y’ + P (x) y = Q (x). (7.13)
Здесь P (x), Q (x) — известные функции независимой переменной x. Например, y’ + 2 xy = x 2 .
Если Q (x) = 0, то уравнение (7.13) называется линейным однородным и является уравнением с разделяющимися переменными.
Если Q (x) ≠ 0, то уравнение (7.13) называется линейным неоднородным, которое можно решить несколькими способами.
Рассмотрим метод Бернулли, с помощью которого уравнение (7.13) можно свести к интегрированию двух дифференциальных уравнений первого порядка с разделяющимися переменными.
Решение дифференциального уравнения (7.13) ищем в виде y = u (x) v (x) или y = uv, (7.14)
где u (x), v (x) — неизвестные функции. Одну из этих функций можно взять произвольную, а другая определяется из уравнения (7.13).
Из равенства y = uv найдем производную y’:
y’= u’ ⋅ v + u⋅ v’.
Подставим y и y’ в уравнение (7.13):
u’v + uv’ + P (x) ⋅ u⋅ v = Q (x) или u’v + u (v’ + P (x) ⋅ v) = Q (x).
Выберем функцию v такой, чтобы v’ + P (x) v = 0. (7.15)
Тогда для отыскания функции u получим уравнение:
u’v = Q (x). (7.16)
Сначала найдем v из уравнения (7.15).
Отделяя переменные, имеем , откуда
Под неопределенным интегралом здесь будем понимать какую-то одну первообразную от функции P (x), то есть v будет определенной функцией от x.
Зная v, находим u из уравнения (7.16):
откуда
Здесь мы уже берем для u все первообразные.
Найденные функции u и v подставляем в (7.14) и получаем общее решение линейного дифференциального уравнения:
(7.17)
При решении конкретных примеров проще выполнять эти выкладки, чем применять громоздкую формулу (7.17).
Пример 1. Решить дифференциальное уравнение .
Решение. Решение ищем в виде y = uv, тогда y’= u’ ⋅ v + u⋅ v’.
Подставим y и y’ в уравнение: или
. (7.18)
Выражение, стоящее в скобках, приравниваем к нулю, имеем
или
Отделим переменные, домножив обе части уравнения на , тогда .
После интегрирования, получим ln |v| = ln |x| (здесь ограничимся одной первообразной), откуда v = x.
Подставим v = x в уравнение (7.18):
Общее решение запишется:
y = x (x + C) = x 2 + Cx.
Пример 2. Найти частное решение дифференциального уравнения который удовлетворяет начальному условию y (0) = 0.
Решение. Заданное уравнение — это линейное неоднородное уравнение первого порядка, решение которого ищем в виде y = u⋅v.
Тогда
Подставим v в уравнение и найдем u:
Общее решение дифференциального уравнения будет:
Подставляем начальные условия в найденное решение и находим С:
Из общего решения получаем частное решение
.
Дифференциальное уравнение Бернулли
Определение. Уравнения вида
(или )
называется дифференциальным уравнением Бернулли.
Данное уравнение отличается от уравнения (7.13) только множителем y» (или x») в правой части. Для того, чтобы права часть данного уравнения была такой, как в (7.13), разделим его левую и праву часть на y»:
Сделаем замену:
Домножим левую и правую части полученного уравнения на (n + 1) и, используя замену, получим:
Мы получили линейное дифференциальное уравнение относительно новой переменной
Пример 1. Найти общее решение дифференциального уравнения xy’ + y = y 2 ln x.
Решение. .
Сделаем замену Тогда
Данное уравнение решим, сделав замену z = u (x) ⋅ v (x).
Выбираем функцию v (x) так, чтобы выражение в скобках равнялось нулю, и эта функция была бы частным решением уравнения
Тогда .
Проинтегрировав правую часть этого уравнения по частям, получим , а при y -1 = z = uv, имеем
Обыновенное дефференциальное уравнение
Обыкновенным дифференциальным уравнением называется любое соотношение, связывающее независимую переменную искомую функцию и производные искомой функции до некоторого порядка включительно.
Обыкновенное дифференциальное уравнение может быть приведено к виду
Здесь — известная функция, заданная в некоторой области
Число т. е. наивысший из порядков производных, входящих в (1), называется порядком уравнения.
Обыкновенные дифференциальные уравнения первого порядка, разрешенные относительно производной. уравнения, интегрируемые в квадратурах
По этой ссылке вы найдёте полный курс лекций по высшей математике:
Основные понятия и определения
Понятие об уравнении первого порядка, разрешенном относительно производной. В соответствии со сказанным во введении, уравнение первого порядка имеет вид
В этой главе мы будем рассматривать уравнение, разрешенное относительно производной:
Наряду с этим уравнением мы всегда будем рассматривать перевернутое уравнение
используя последнее в окрестности тех точек, в которых обращается в бесконечность.
Во многих случаях оказывается целесообразным «место уравнении (2) и (2′) рассматривать одно равносильное им дифференциальное уравнение
Обе переменные и входят в это уравнение уже равноправно, и любую из них мы можем принять за независимую переменную.
Умножая обе части уравнения (3) на некоторую функцию получаем более симметричное уравнение:
где Обратно, всякое уравнение вида (4) можно переписать в виде уравнений (2) или (2′), разрешая его относительно или так что уравнение (4) равносильно следующим двум уравнениям:
Иногда уравнение записывают *з так называемой симметрической форме:
Возможно вам будут полезны данные страницы:
Решение уравнения. Предположим, что правая часть уравнения (2), определена на некотором подмножестве вещественной плоскости Функцию определенную в интервале мы будем называть решением уравнения (2) в этом интервале*, если:
- Существует производная для всех значений из интервала (Отсюда следует, что решение представляет собою функцию, непрерывную ею всей области определения).
- Функция обращает уравнение (2) в тождество:
справедливое для всех значений из интервала Это означает, что при любом из интервала точка принадлежит множеству и
Так как наряду с уравнением (2) рассматривается перевернутое уравнение (2′), то и решения этого перевернутого уравнения естественно присоединять к решениям уравнения (2).
В этом смысле в дальнейшем мы будем для краткости называть решения уравнения (2′) решениями уравнения (2).
Примеры с решением
Пример 1.
является решением уравнения
в интервале ибо она определена и дифференцируема в эгои интервале, и, подставляя се в уравнение (9), получаем тождество:
справедливое при всех значениях
Пример 2.
Функция есть решение равнения в интервале
Пример 3.
является решением уравнения
в интервале
Иногда функцию обращающую уравнение (2) в тождество (7), т. е. решение уравнения (2), называют интегралом этого уравнения. Мы будем употреблять термин интеграл только в смысле п. 16.
Системы обыкновенных дифференциальных уравнений
При решении многих задач нужно найти функции y1 = y1 (x), y2 = y2 (x), . yn = yn (x), которые удовлетворяют системе дифференциальных уравнений, содержащих независимую переменную x , искомые y1 , y2 , . yn и их производные.
Пример. Пусть материальная точка массы m имеет криволинейную траекторию движения в пространстве. Определить положение точки в любой момент времени t, когда на нее действует сила .
Положение точки в любой момент времени t определяется ее координатами x, y, z; следовательно, x, y, z являются функциями от t. Проекциями вектора скорости точки на оси координат будут производные x’ , y’ , z’.
Положим, что сила, а соответственно и ее проекции Fx, Fy, Fz зависят от времени t, от положения x, y, z точки и от скорости движения точки, то есть от . Искомыми неизвестными функциями в этой задаче будут три функции x = x (t), y = y (t), z = z (t). Эти
функции определяются из уравнений динамики:
Мы получили систему трех дифференциальных уравнений второго порядка. В случае движения, когда траектория является плоской кривой, лежит, например, в плоскости Оxy, получим систему двух уравнений для определения неизвестных функций x (t) и y (t):
Рассмотрим простейшие системы дифференциальных уравнений.
Системы дифференциальных уравнений первого порядка
Система n уравнений первого порядка с n неизвестными функциями имеет вид:
(7.38)
где x — независимая переменная, y1, y2, . yn — неизвестные функции.
Если в левой части уравнений системы стоят производные первого порядка, а правые части уравнений вовсе не содержат производных, то такая система уравнений называется нормальной.
Решением системы называется совокупность функций y1, y2, . yn, которые превращают каждое уравнение системы в тождество относительно x.
Задача Коши для системы (7.38) состоит в нахождении функций y1, y2, . yn , удовлетворяющих систему (7.38) и заданные начальные условия:
(7.39)
Интегрирование системы (7.38) делают следующим образом. Дифференцируем по x первое уравнение системы (7.38):
Заменим производные
их выражениями f1, f2, . fn из уравнений системы (7.38), получим уравнение
Дифференцируем полученное уравнение и, подставив в это равенство значения производных из системы (7.38), найдем
Продолжая дальше таким образом, получим
В результате получаем следующую систему уравнений:
(7.40)
Из первых (n-1) уравнений определим y2, y3, . yn:
(7.41)
и подставим их значения в последнее уравнение системы (7.40) для определения y1:
Продифференцируем это выражение (n-1) раз, определим
как функции от x, C1, C2, . Cn. Подставим эти функции в (7.41), найдем
(7.43)
Для того, чтобы полученное решение удовлетворяло заданным начальным условиям, остается только найти значение произвольных постоянных из уравнений (7.42) и (7.43) так, как мы это делали для одного дифференциального уравнения.
Пример 1. Проинтегрировать систему
когда заданы начальные условия
Решение. Дифференцируем по x первое уравнение, имеем:
. Подставляем сюда значение и из системы, получим
Из первого уравнения системы найдем и подставим в полученное нами уравнение:
или
Общим решением этого уравнения является
(*)
и тогда (**)
Подберем постоянные С1 и С2 так, чтобы выполнялись начальные условия. На основании (*) и (**) имеем:
1 = С1 – 9; 0 = С2 – 2С1 + 14, откуда С1 = 10, С2 = 6.
Таким образом, решением системы, которое удовлетворяет заданным начальным условиям, будет:
Системы линейных дифференциальных уравнений с постоянными коэффициентами
Система дифференциальных уравнений:
(7.44)
где коэффициенты aij — постоянные числа, t — независимая переменная, x1 (t), . xn (t) —
неизвестные функции, называется системой линейных дифференциальных уравнений с постоянными коэффициентами.
Эту систему можно решать путем сведения к одному уравнению n-го порядка, как это было показано выше. Но эту систему можно решить и другим способом. Покажем, как это делается.
Будем искать решение системы (7.44) в виде:
(7.45)
Надо определить постоянные α1, α2, . αn и k так, чтобы функции (7.45) удовлетворяли систему (7.44). Подставим функции (7.45) в систему (7.44):
Сократим на e kt и преобразуем систему, сведя ее к такой системе:
(7.46)
Это система линейных алгебраических уравнений относительно α1, α2, . αn. Составим определитель системы:
Мы получим нетривиальные (ненулевые) решения (7.45) только при таких k, при которых определитель превратится в ноль. Получаем уравнение n-го порядка для определения k:
Это уравнение называется характеристическим уравнением для системы (7.44).
Рассмотрим отдельные случаи на примерах:
1) Корни характеристического уравнения действительны и различны. Решение системы записывается в виде:
Пример 2. Найти общее решение системы уравнений:
Решение. Составим характеристическое уравнение:
или k 2 – 5k + 4 = 0, корни которого k1 = 1, k2 = 4.
Решение системы ищем в виде
Составим систему (7.46) для корня k1 и найдем и :
или
Откуда Положив получим
Итак, мы получили решение системы:
Далее составляем систему (7.46) для k = 4:
Откуда
Получим второй решение системы:
Общее решение системы будет:
2) Корни характеристического уравнения различны, но среди них есть комплексные:
k1 = α + iβ, k2 = α – iβ. Этим корням будут отвечать решения:
(7.47)
(7.48)
Можно доказать также, что истинные и мнимые части комплексного решения также будут решениями. Таким образом, получим два частных решения:
(7.49)
где — действительные числа, которые определяются через .
Соответствующие комбинации функций (7.49) войдут в общий решение системы.
Пример 3. Найти общее решение системы
Решение. Составляем характеристическое уравнение:
или k 2 + 12k + 37 = 0, корни которого k1 = –6 + i, k2 = –6 – i .
Подставляем поочередно k1, k2 в систему (7.46), найдем
Запишем уравнение (7.47) и (7.48) для наших данных
Перепишем эти решения в таком виде:
За частные решения можно взять отдельно действительные и отдельно мнимые части:
Общим решением системы будет
Присылайте задания в любое время дня и ночи в ➔
Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.
Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.
Сайт предназначен для облегчения образовательного путешествия студентам очникам и заочникам по вопросам обучения . Наталья Брильёнова не предлагает и не оказывает товары и услуги.
http://natalibrilenova.ru/obyiknovennyie-differentsialnyie-uravneniya/
Способы задания функций
Аналитическое задание функции
Функция %%y = f(x), x in X%% задана явным аналитическим способом, если дана формула, указывающая последовательность математических действий, которые надо выполнить с аргументом %%x%%, чтобы получить значение %%f(x)%% этой функции.
Пример
- %% y = 2 x^2 + 3x + 5, x in mathbb{R}%%;
- %% y = frac{1}{x — 5}, x neq 5%%;
- %% y = sqrt{x}, x geq 0%%.
Так, например, в физике при равноускоренном прямолинейном движении скорость тела определяется формулой %%v = v_0 + a t%%, а формула для перемещения %%s%% тела при равномерно ускоренном движении на промежутке времени от %%0%% до %%t%% записывается в виде: %% s = s_0 + v_0 t + frac{a t^2}{2} %%.
Кусочно-заданные функции
Иногда рассматриваемая функция может быть задана несколькими формулами, действующими на различных участках области ее определения, в которой изменяется аргумент функции. Например:
$$
y = begin{cases}
x ^ 2,~ если~x < 0, \
sqrt{x},~ если~x geq 0.
end{cases}
$$
Функции такого вида иногда называют составными или кусочно-заданными. Примером такой функции является %%y = |x|%%
Область определения функции
Если функция задана явным аналитическим способом с помощью формулы, но область определения функции в виде множества %%D%% не указана, то под %%D%% будем всегда подразумевать множество значений аргумента %%x%%, при которых данная формула имеет смысл. Так для функции %%y = x^2%% областью определения служит множество %%D = mathbb{R} = (-infty, +infty)%%, поскольку аргумент %%x%% может принимать любые значения на числовой прямой. А для функции %%y = frac{1}{sqrt{1 — x^2}}%% областью определения будет множество значений %%x%% удовлетворяющих неравенству %%1 — x^2 > 0%%, т.е. %%D = (-1, 1)%%.
Преимущества явного аналитического задания функции
Отметим, что явный аналитический способ задания функции достаточно компактен (формула, как правило, занимает немного места), легко воспроизводим (формулу нетрудно записать) и наиболее приспособлен к выполнению над функциями математических действий и преобразований.
Некоторые из этих действий — алгебраические (сложение, умножение и др.) — хорошо известны из школьного курса математики, другие (дифференцирование, интегрирование) будем изучать в дальнейшем. Однако этот способ не всегда нагляден, так как не всегда четок характер зависимости функции от аргумента, а для нахождения значений функции (если они необходимы) требуются иногда громоздкие вычисления.
Неявное задание функции
Функция %%y = f(x)%% задана неявным аналитическим способом, если дано соотношение $$F(x,y) = 0, ~~~~~~~~~~(1)$$ связывающее значения функции %%y%% и аргумента %%x%%. Если задавать значения аргумента, то для нахождения значения %%y%%, соответствующего конкретному значению %%x%%, необходимо решить уравнение %%(1)%% относительно %%y%% при этом конкретном значении %%x%%.
При заданном значении %%x%% уравнение %%(1)%% может не иметь решения или иметь более одного решения. В первом случае заданное значение %%x%% не принадлежит области определения неявно заданной функции, а во втором случае задает многозначную функцию, имеющую при данном значении аргумента более одного значения.
Отметим, что если уравнение %%(1)%% удается явно разрешить относительно %%y = f(x)%%, то получаем ту же функцию, но уже заданную явным аналитическим способом. Так, уравнение %%x + y^5 — 1 = 0%%
и равенство %%y = sqrt[5]{1 — x}%% определяют одну и ту же функцию.
Параметрическое задание функции
Когда зависимость %%y%% от %%x%% не задана непосредственно, а вместо этого даны зависимости обоих переменных %%x%% и %%y%% от некоторой третьей вспомогательной переменной %%t%% в виде
$$
begin{cases}
x = varphi(t),\
y = psi(t),
end{cases} ~~~t in T subseteq mathbb{R}, ~~~~~~~~~~(2)
$$то говорят о параметрическом способе задания функции;
тогда вспомогательную переменную %%t%% называют параметром.
Если из уравнений %%(2)%% удается исключить параметр %%t%%, то приходят к функции, заданной явной или неявной аналитической зависимостью %%y%% от %%x%%. Например, из соотношений
$$
begin{cases}
x = 2 t + 5, \
y = 4 t + 12,
end{cases}, ~~~t in mathbb{R},
$$ исключением параметра %%t%% получим зависимость %%y = 2 x + 2%%, которая задает в плоскости %%xOy%% прямую.
Графический способ
Пример графического задания функции
Приведенные выше примеры показывают, что аналитическому способу задания функции соответствует ее графическое изображение, которое можно рассматривать как удобную и наглядную форму описания функции. Иногда используют графический способ задания функции, когда зависимость %%y%% от %%x%% задают линией на плоскости %%xOy%%. Однако при всей наглядности он проигрывает в точности, поскольку значения аргумента и соответствующие им значения функции можно получить из графика лишь приближенно. Возникающая при этом погрешность зависит от масштаба и точности измерения абсциссы и ординаты отдельных точек графика. В дальнейшем графику функции отведем роль только иллюстрации поведения функции и поэтому будем ограничиваться построением «эскизов» графиков, отражающих основные особенности функций.
Табличный способ
Отметим табличный способ задания функции, когда некоторые значения аргумента и соответствующие им значения функции в определенном порядке размещаются в таблице. Так построены известные таблицы тригонометрических функций, таблицы логарифмов и т.п. В виде таблицы обычно представляют зависимость между величинами, измеряемыми при экспериментальных исследованиях, наблюдениях, испытаниях.
Недостаток этого способа состоит в невозможности непосредственного определения значений функции для значений аргумента, не входящих в таблицу. Если есть уверенность, что непредставленные в таблице значения аргумента принадлежат области определения рассматриваемой функции, то соответствующие им значения функции могут быть вычислены приближенно при помощи интерполяции и экстраполяции.
Пример
| x | 3 | 5.1 | 10 | 12.5 |
| y | 9 | 23 | 80 | 110 |
Алгоритмический и словесный способы задания функций
Функцию можно задать алгоритмическим (или программным) способом, который широко используют при вычислениях на ЭВМ.
Наконец, можно отметить описательный (или словесный) способ задания функции, когда правило соответствия значений функции значениям аргумента выражено словами.
Например, функцию %%[x] = m~forall {x in [m, m + 1)}, m in mathbb{Z}%%, называемую целой частью %%x%% (или «антье от %%x%%»), описывают обычно словами: «Наибольшее целое число, не превосходящее %%x%%».
Явные и неявные
В этой статье мы познакомимся с неявными функциями и техникой их дифференцирования. Вспомним для начала, как выглядят функции, заданные явно. Это “обычные” функции вида y=f(x)y=f(x), с которыми вы уже имели дело и умеете вычислять их производные. Запись y=f(x)y=f(x) обозначает, что мы функцию yy смогли выразить (явно представить) через её аргумент xx. З неявными функциями дело обстоит иначе. Здесь мы не можем “перетащить” yy в левую сторону выражения, а все что содержит xx — в правую. Такие функциональные зависимости в общем виде можно записать так:
F(x,y)=0F(x, y)=0
Эта запись означает, что величины xx и yy как-то связанны между собой, но ничего не говорится о том, как yy выражается через xx (и можно ли это вообще сделать). Одну и ту же функцию (но не каждую) можно записать как в явном так и в неявном виде. Например, неявно заданную функцию F(x,y)=3xy+5xF(x, y)=3xy+frac{5}{x} можно записать явно: y(x)=−53x2y(x)=-frac{5}{3x^2}. В этом случае нам удалось выразить yy через xx. Или, если:
F(x,y)=x2+y2−1=0F(x, y)=x^2+y^2-1=0
то
y=±1−x2y=pm sqrt{1-x^2}
Здесь функция получилась многозадачной (именно двузначной, отвечающей двум знакам), но это не страшно. Мы все-равно представили yy как выражение зависящее от xx. В правой стороне у нас присутствует только xx.
Но существуют случаи, когда этого сделать нельзя. Можно навести множество примеров таких функций. Например:
F(x,y)=ylnx+eyy2F(x, y)=yln x+e^yy^2
Ну попробуйте выразить отсюда yy через xx. То есть запишите эту функцию в виде y=f(x)y=f(x). Вот вам и пример неявной заданной функции. Ещё пример:
F(x,y)=xsinx+ysiny−12F(x, y)=xsin x+ysin y-12
Здесь, мы хотя и не можем выразить yy через xx, но мы все-равно можем считать yy функцией от аргумента xx. Так как каждому значению xx будут соответствовать какие-то значения yy.
Естественно, возникает вопрос о дифференцировании подобных функций. Вы уже понимаете, что эта операция очень важна, и было бы тяжело поверить, что математики ничего не придумали на этот счет.
Дифференцирование неявно заданных функций
Оказывается, что для того чтобы посчитать производную от yy по xx нам не обязательно решать уравнение:
F(x,y)=0F(x, y)=0
Теоретически можно доказать (пользуюсь определением производной, производя предельный переход и т. д.), что:
dydx=−∂F(x,y)∂x∂F(x,y)∂yfrac{dy}{dx}=-frac{frac{partial F(x, y)}{partial x}}{frac{partial F(x, y)}{partial y}}
Обозначение ∂partial обозначает частную производную. Мы здесь имеем дело с двумя переменными xx и yy и берем производные от функции F(x,y)F(x, y) по этим величинам. Так, выражение:
∂F(x,y)∂xfrac{partial F(x, y)}{partial x}
говорит, что берется производная от F(x,y)F(x, y) по xx, при этом величина yy считается постоянной. Следует обратить внимание на знак “минус” перед дробью, а также на то, что мы не можем сократить числитель и знаменатель на ∂F(x,y)partial F(x, y), так как производные берутся по разным величинам. Вооружившись этой главной формулой вычисления производных от неявных функций, перейдем к разбору нескольких примеров.
Примеры
F(x,y)=x2+y2−1F(x, y)=x^2+y^2-1
∂F(x,y)∂x=2x, ∂F(x,y)∂y=2yfrac{partial F(x, y)}{partial x}=2x, frac{partial F(x, y)}{partial y}=2y
dydx=−∂F(x,y)∂x∂F(x,y)∂y=−2x2y=−xyfrac{dy}{dx}=-frac{frac{partial F(x, y)}{partial x}}{frac{partial F(x, y)}{partial y}}=-frac{2x}{2y}=-frac{x}{y}
F(x,y)=xsinx+ysiny−12F(x, y)=xsin x+ysin y-12
∂F(x,y)∂x=sinx+xcosx, ∂F(x,y)∂y=siny+ycosyfrac{partial F(x, y)}{partial x}=sin x+x cos x, frac{partial F(x, y)}{partial y}=sin y+y cos y
dydx=−∂F(x,y)∂x∂F(x,y)∂y=−sinx+xcosxsiny+ycosyfrac{dy}{dx}=-frac{frac{partial F(x, y)}{partial x}}{frac{partial F(x, y)}{partial y}}=-frac{sin x+xcos x}{sin y+ycos y}
- F(x,y)=3xy+5xF(x, y)=3xy+frac{5}{x}
∂F(x,y)∂x=3y−5×2, ∂F(x,y)∂y=3xfrac{partial F(x, y)}{partial x}=3y-frac{5}{x^2}, frac{partial F(x, y)}{partial y}=3x
dydx=−∂F(x,y)∂x∂F(x,y)∂y=−3y−5x23x=−3yx2−53x3frac{dy}{dx}=-frac{frac{partial F(x, y)}{partial x}}{frac{partial F(x, y)}{partial y}}=-frac{3y-frac{5}{x^2}}{3x}=-frac{3yx^2-5}{3x^3}
Но здесь мы можем выразить yy через xx явно:
y=−53x2y=-frac{5}{3x^2}
Подставим это выражение в формулу для производной выше:
dydx=103x3frac{dy}{dx}=frac{10}{3x^3}
А теперь поступим так, как будто нам с самого начала была известна явная зависимость y=f(x)y=f(x). То есть продифференцируем функцию y(x)=−53x2y(x)=-frac{5}{3x^2} по xx:
dydx=ddx(−53×2)=−53(−2)1×3=103x3frac{dy}{dx}=frac{d}{dx}Big(-frac{5}{3x^2}Big)=-frac{5}{3}(-2)frac{1}{x^3}=frac{10}{3x^3}
Получили то же самое. Значит мы все сделали правильно.
Елена Борисовна Калюжная
Эксперт по предмету «Математика»
Задать вопрос автору статьи
Как увидеть функцию?
Известно, что функция $y=fleft(xright)$ представляет собой некоторый закон, по которому каждому числовому значению одной переменной $x$ ставится в соответствие определенное числовое значение другой переменной $y$.
В отличие от числовой оси, предназначенной для отображения отдельных чисел, именно системы координат на плоскости позволяют отображать функционально зависимые пары чисел $x$ и $y$.
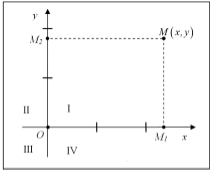
Рассмотрим систему координат на плоскости, образованную двумя взаимно перпендикулярными осями, которые называются осями координат.
Точка пересечения осей координат называется началом координат и обозначается буквой O. Горизонтальная ось направлена слева направо, называется осью абсцисс и обозначается $Ox$. Вертикальная ось направлена снизу вверх, называется осью ординат и обозначается $Oy$. С целью указания числовых значений координат на обоих осях выбирають масштабную единицу (одинаковую или разную).
При указанных условиях расположение любой точки $M$ на плоскости полностью определяется её координатами. Для определения координат нужно спроектировать точку $M$ на оси $Ox$ и $Oy$, то есть опустити перпендикуляри $MM_{1} $ и $MM_{2} $ на эти оси. Первую координату $x$ (абсциссу) точки $M$ указывает положение точки $M_{1} $ на осі $Ox$. Вторую координату $y$ (ординату) точки $M$ указывает положение точки $M_{2} $ на осі $Oy$. То, что точка $M$ имеет своими координатами числа $x$ и $y$, записывают в виде $Mleft(x,; yright)$.
Оси координат делят плоскость на четыре части, которые называются четвертями или квадрантами. Квадранти нумеруют римскими цифрами против часовой стрелки. Знаки координат в каждом из квадрантов следующие:
«Функция и её способы задания» 👇
- I квадрант — $x>0,; ; y>0$;
- II квадрант — $x0$;
- III квадрант — $x
- IV квадрант — $x>0,; ; y
Точки на оси $Oy$ имеют координату $x=0$, точки на оси $Ox$ имеют координату $y=0$. Начало координат имеет нулевые значения обеих координат.
Обратная задача — построение точки $M$ по её заданным координатам $x$ и $y$ — решается посредством предварительного построения её проекций, то есть точек $M_{1} left(x,; 0right)$ и $M_{2} left(0,; yright)$ на осях $Ox$ и $Oy$ соответственно. Далее через эти точки следует провести прямые, перпендикулярные осям, и на их пересечении будет получена точка $M$.
Описанные координаты, которые применяются для определения положения точек на плоскости, называются прямоугольными. Их также называют декартовыми в честь французского учёного XVII века Рене Декарта, которого считают основателем аналитической геометрии.
Особенности поведения функций
Использование прямоугольной системы координат для графического отображения функций позволяет видеть характерные особенности их поведения.
Монотонность функции
Рассмотрим функцию $y=fleft(xright)$ на интервале $left(a,; bright)$. Будем выбирать на нём произвольные точки $x_{1} y_{2} $), невозрастающей (если $ y_{1} ge y_{2} $) и неубывающей (если $ y_{1} le y_{2} $).
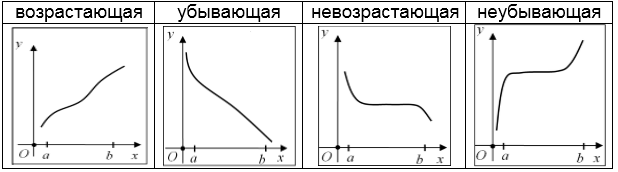
Описанное поведение называется монотонностью функции на данном интервале. При этом возрастающие и убывающие функции называют строго монотонными.
Ограниченность функции
Случай 1
Рассмотрим функцию $y=fleft(xright)$ на интервале $left(a,; bright)$. Будем выбирать на нём произвольные точки $x^{*} $ и сравнивать значения $y^{*} =fleft(x^{*} right)$ с некоторым заданным числом $M>0$. На этом интервале функция считается ограниченной, если справедливо неравенство $left|y^{*} right|le M$.
График такой функции расположен в полосе между горизонтальными прямыми, проведёнными через точки $y=M$ и $y=-M$.
Пример 1
Рассмотрим функцию $y= sin x$ и число $M=1$. Функция ограничена, так как значения $left|sin xright|le 1$ для любых $-infty
Случай 2
На интервале $left(a,; bright)$ функция считается ограниченной сверху или ограниченной снизу, если существует такое число $G$, что $y^{*} le G$ или $y^{*} ge G$ соответственно. При этом график функции располагается или под, или над горизонтальной прямой, проведённой через точку $y=G$.
Пример 2
Функция $y=frac{1}{x} $ ограничена сверху на интервале $left(-infty ,; 0right)$, и ограничена снизу на интервале $left(0,; +infty right)$, причем в обоих случаях $G=0$, то есть соответствующие графики расположены ниже и выше оси $Ox$.
Четность и нечетность функции
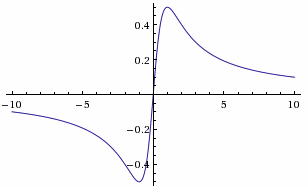
Рассмотрим функцию $y=fleft(xright)$ на интервале $left(-a,; aright)$, симметричном относительно начала координат. Данная функция будет считаться четной на этом интервале, если справедливо равенство $fleft(-xright)=fleft(xright)$, и нечетной, если $fleft(-xright)=-fleft(xright)$. Если же ни одно из указанных условий не выполняется, то функция не относится ни к четным, ни к нечетным.
График четной функции симметричен относительно оси $Oy$, нечетной — относительно начала координат.
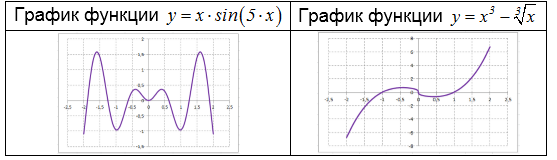
Задача 1
Проанализировать на четность (нечетность) функцию $y=xcdot sin left(5cdot xright)$.
Заменим в функции $x$ на $-x$. Получим:
[fleft(-xright)=left(-xright)cdot sin left(-5cdot xright)=left(-xright)cdot left(-sin left(5cdot xright)right)=xcdot sin left(5cdot xright)=fleft(xright). ]
Следовательно, данная функция четная. Её график симметричен относительно оси $Oy$.
Задача 2
Проанализировать на четность (нечетность) функцию $y=x^{3} -sqrt[{3}]{x} $.
Заменим в функции $x$ на $-x$. Получим:
[fleft(-xright)=left(-xright)^{3} -sqrt[{3}]{-x} =-left(x^{3} right)-left(-sqrt[{3}]{x} right)=-left(x^{3} right)+sqrt[{3}]{x} =-fleft(xright). ]
Следовательно, данная функция нечетная. Её график симметричен относительно начала координат.
Периодичность функции
Рассмотрим функцию $y=fleft(xright)$ на интервале $left(a,; bright)$. Данная функция будет считаться периодической на этом интервале, если существует некоторое постоянное число $T>0$, для которого $fleft(xpm Tright)=fleft(xright)$ при $a
Задача 3
Найти период функции $y=sin left(2cdot x+5right)$ при $ -infty
Условие периодичности имеет вид $sin left(2cdot left(x+Tright)+5right)=sin left(2cdot x+5right)$. По формуле для разности синусов получим $sin Tcdot cos left(2cdot x+5+Tright)=0$. Сомножитель $sin T$ не зависит от $x$, и поэтому уравнение $sin T=0$ дает значение основного периода $T=pi $. Из уравнения $cos left(2cdot x+5+Tright)=0$ значение периода, независимого от $x$, получить невозможно.
Способы задания функции
Кроме графического и аналитического способов задания функции, использованных выше, существует еще и табличный.
При табличном способе в определенном порядке выписываются значения аргумента $x_{1} ,; x_{2} ,; ldots ,; x_{n} $ и соответствующие значения функции $y_{1} ,; y_{2} ,; ldots ,; y_{n} $. В таком виде часто получают функции во время измерительных экспериментов. Кроме того, таблицы значений разнообразных специальных функций мы можем видеть в справочниках.
Форма аналитического способа задания функции может быть явной, неявной и параметрической.
Если функция $y$ аргумента $x$ имеет вид уравнения, разрешенного относительно $y$, то есть $y=fleft(xright)$, то такая форма аналитического задания называется явной. Примеры представлены в задачах выше.
Если аргумент $x$ и функция $y$ связаны между собой уравнением, не разрешенным относительно $y$, то есть в виде $Fleft(x,; yright)=0$, то такая форма аналитического задания называется неявной. Например, $y^{2} +cos left(x+yright)=0$.
Если соответствующие значения аргумента $x$ и функции $y$ связаны между собой через третью вспомогательную переменную (параметр) $t$, то есть $x=xleft(tright)$ и $y=yleft(tright)$, то такая форма аналитического задания называется параметрической. Например, $x=2cdot tgt$, $y=5cdot cos t$.
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме







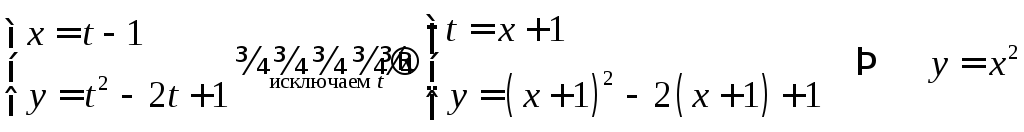 —
—