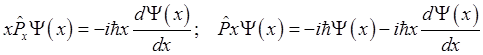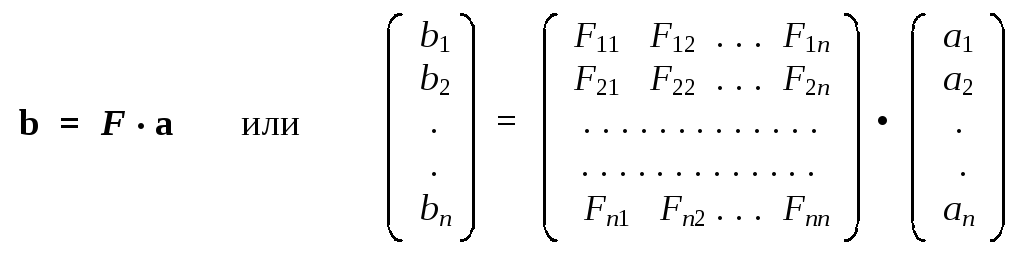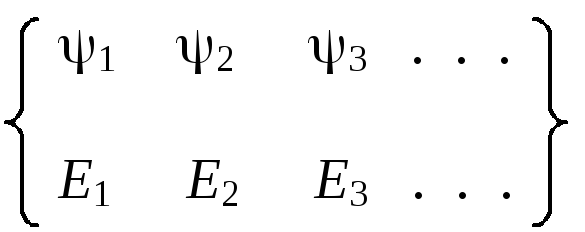Как найти явный вид оператора

Установим теперь явный вид
операторов квантовой механики. Ранее было показано, что оператор координаты
сводится к умножению на координату . Для того,
чтобы найти вид остальных операторов, помимо оператора координаты нужно задать
ещё оператор импульса.

В квантовой механике вектору импульса ставится в
соответствие дифференциальный
векторный оператор вида

                                                     (1.33).

Хотя данное определение носит
аксиоматический характер в его пользу можно высказать ряд соображений,
некоторые из которых будут рассмотрены ниже.

Найдём собственные
функции и спектр собственных значений оператора .
Уравнение для собственных функций проекции оператора  имеет вид

                                           (1.34)

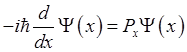
Его решением является волновая функция вида

                              (1.35), где введено обозначение .
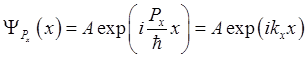
Функция удовлетворяет стандартным требованиям при любых ,  спектр значений которых, таким образом,
является непрерывным. Коэффициент A
определится из условия нормировки (1.25), которое в данном
конкретном случае имеет вид

                                  (1.36).

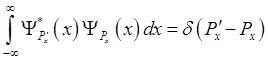
Отсюда, используя интегральное представление -функции

                                             (1.37), а также её свойство

                                                (1.38)

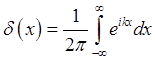
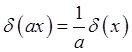
получим .  Собственную
функцию оператора  можно представить, как
произведение собственных функций его проекций

                                       (1.39), где .

После того как были определены операторы
координаты и импульса, можно найти явный вид других операторов квантовой
механики. В частности оператор
момента определяется как
векторное произведение операторов координаты и импульса

                                                   (1.40).

Оператор
Гамильтона представляет собой сумму операторов кинетической и
потенциальной энергии. В частности для одной частицы в потенциальном поле имеем

                                               (1.41).

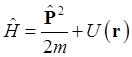
Соотношения
неопределённости.

Выше было
установлено, что условием существования  определённого значения наблюдаемой в
некотором  состоянии является требование, чтобы волновая функция этого состояния
была собственной функцией соответствующего оператора. Таким образом, для того
чтобы две наблюдаемые могли иметь одновременно точные значения необходимо,
чтобы операторы этих наблюдаемых имели общие собственные функции.  Как было
показано ранее, это возможно лишь в том случае, если операторы этих наблюдаемых
коммутируют. В противном случае наблюдаемые могут быть совместно измерены лишь
с некоторой погрешностью. Определим границы этой погрешности.

Пусть  и  операторы
динамических переменных, причём

                                         (1.42), где ,  так же как  и  является
эрмитовым оператором. Введём операторы отклонения от среднего  и .
Очевидно, что эти операторы эрмитовы, а их коммутатор равен правой части
выражения (1.42):

                                                  (1.43).

Рассмотри заведомо неотрицательное выражение

                                     (1.44), в котором — произвольное
действительное число. Используя условие эрмитовости, выражение (1.44) можно
преобразовать следующим образом

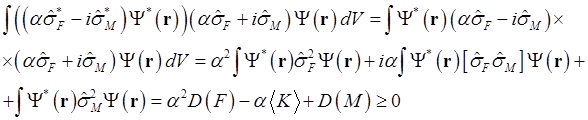
(1.45), где  и . Полученное в правой части формулы (1.45)
выражение представляет собой квадратичный трёхчлен относительно переменной  . Для того, чтобы он был неотрицательным
при любых значениях , должно выполняться
условие . Тогда окончательно получаем

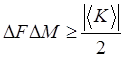
                                                (1.46), где и — среднеквадратичные флуктуации наблюдаемых
F и M:

                         (1.47).

Рассмотрим коммутационные соотношения для проекций
операторов координаты r и импульса . Очевидно, что разноимённые проекции этих
операторов коммутируют, так как они действуют на разные переменные. Для x— проекций этих операторов получим

и следовательно

                                          (1.48).

Те же правила коммутации, очевидно, имеют место и для y- и z- проекций
операторов координаты и импульса. Сравнивая выражения (1.48) и (1.42), с учётом
(1.47) получим соотношения
неопределённости для координаты и импульса

 ,                              (1.49)

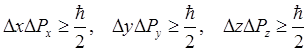
где  — среднеквадратичные
флуктуации соответствующих величин. Таким образом, координата частицы и
одноимённая проекция её импульса могут быть известны одновременно только с
некоторой неточностью, определяемой соотношением (1.49).

Уважаемый посетитель!

Чтобы распечатать файл, скачайте его (в формате Word).

Ссылка на скачивание — внизу страницы.

Квантовомеханические операторы

В формализме квантовой механики, наряду
с вектором (функцией) состояния, важную
роль играет понятие
оператора.

В математическом смысле оператор
представляет собой некоторую процедуру(операцию), выполняемую над векторами.
Например, «оператор поворота»R()
поворачивает любой вектор на заданный
угол,
«оператор проектирования»Р(х)
переводит вектор в его проекцию на осьхи т.д.

Если начальный и конечный векторы
выразить через их координаты в виде
векторов-строк или векторов-столбцов,
то оператор можно изобразить в виде
квадратной матрицы:

В тех случаях, когда оператор относится
к наблюдаемой с дискретным спектром,
его всегда можно изобразить посредством
матрицы (совокупности чисел — матричных
элементов). Если же наблюдаемая имеет
непрерывный спектр, то сопоставляемая
оператору матрица должна была бы иметь
бесконечно большой размер, так что
использовать ее для практических
вычислений было бы невозможно. В такой
ситуации вместо векторов состояния
следует использовать их функциональные
представления (волновые функции).
Соответственно, вместо матричной формы
операторов следует использовать
алгебраические или аналитические
процедуры (преобразования). Их наглядными
примерами могут служить:

оператор
дифференцирования,переводящий
некоторую функцию (первообразную) в ее
производную

оператор интегрирования,переводящий некоторую функцию
(производную) в ее первообразную

Представления операторов

Явный вид оператора, так же как и явный
(координатный) вид вектора состояния,
зависит от выбранного базиса. Другими
словами, наряду с представлениями
вектора состояния, мы имеем и соответствующие
представления операторов. Такие
представления взаимосвязаны между
собой и могут быть преобразованы друг
в друга посредством унитарных операторов.
Рассмотрим операторное уравнение вида:
b = F
• a.
В двух разных базисах, переход между
которыми осуществляется двумя взаимно
обратными унитарными операторамиU₂₁иU₁₂,
это уравнение будет выглядеть по-разному:

Связь между представлениями оператора
Fбудет выглядеть
так:

( F)₁=U₁₂
•(F)₂•U₂₁и (F )₂=U₂₁
•(F)₁•U₁₂

Спектральные свойства операторов

Каждый оператор Fимеет некоторый набор
собственных
векторов (f₁,f₂, … ,f_n)
и собственных
чисел или
собственных
значений (f₁,f₂, … ,f_n), которые удовлетворяют т.н.
«уравнению на собственные значения»:

F •
f = f
• f

Этот набор:

называется спектром
оператора.

Типы операторов в квантовой механике

В абстрактной математике операторы
могут быть бесконечно разнообразными.
Однако в формализме квантовой механике
используются лишь три типа операторов.

Операторы квантовомеханических наблюдаемых

Выберем некоторую наблюдаемую Аи
возьмем набор базисных состояний
соответствующего спектрального
анализатора (т.е. таких состояний, в
которых наблюдаемаяАимеет строго
определенные численные значения:А=А_i). Теперь
построим операторА, для которого
векторы указанных базисных состояний
будут собственными векторами, а указанные
значения наблюдаемой — собственными
значениями. Такой оператор, являющийся,
в сущности, математической моделью
спектрального анализатора (и процедуры
измерения), и будет называться
оператором
квантово-механической наблюдаемой А.

Таким образом, каждой наблюдаемой можно
сопоставить математический объект —
оператор наблюдаемой.Эти операторы
обладают рядом полезных свойств и
позволяют в компактной и удобной форме
записывать многие квантово-механические
уравнения.

Наиболее часто понятие оператора
используется для следующих целей.
Предположим, что явный вид оператора Анекоторой наблюдаемойАнам известен.
Тогда, решив «задачу на собственные
значения», мы найдем, с одной стороны,

• набор допустимых
  значений наблюдаемой А (т.е. ее
  спектрА₁,А₂,… ),

• набор собственных
  векторов (или функций), описывающих
  такие состояния, в которых наблюдаемаяАимеет строго определенное значение
  (одно из допустимых).

Собственные векторы любого оператора
обладают одним полезным свойством —
они всегда образуют один из возможных
базисных наборов, который можно
использовать для разложения (анализа)
произвольных векторов и функций
состояния.

Типичный пример представляет собой
т.н. «стационарное уравнение Шредингера»

H=E

Решив это уравнение, мы найдем набор
волновых функций, собственных для
оператора Гамильтона (Н), каждая
из которых описывает особое состояние
системы с точно известной и постоянной
энергией:

Любая волновая функция может быть
представлена в виде ЛК этих собственных
функций оператора Гамильтона:

 = С₁ ₁+С₂ ₂+С₃ ₃+ . . .

Пусть система находится в определенном
состоянии, которое описывается вектором
состояния |
или волновой функцией(х).
Построим следующую конструкцию:

 A 
= 

| A
| 

= _
^*A

dx

Если вектор | _k(или
функция) является собственным для оператораА, то выполняется соотношение
A|_k=A_k
|_k.
Следовательно,

 A 
= 
_k
| A
| _k

= 
_k
| A_k
| _k

= A_k

_k
| _k

= A_k

(Вектор | _kпредполагается нормированным, поэтому
его скалярный квадрат_k|_k= 1.)

Если вектор | (или
функция) не является собственным для оператораА, то его можно предварительно
разложить в суперпозицию собственных
векторов:

| =С₁|₁+С₂|₂
+ …

Тогда

A|
=С₁ A|₁
+С₂ A|₂
+ … = С₁ A₁
|₁
+С₂ A₂|₂
+ …

Соответственно:

 A =|A|=

= (₁|С₁* +₂|С₂* + …)•(С₁ A₁ |₁
+С₂ A₂|₂
+ …)

Раскрыв скобки, получим сумму произведений
типа:

C_j*C_i
A_i

_j
| _i


В тех случаях, когда индексы iиj различны, такие
произведения будут равны нулю, поскольку
разные собственные векторы оператораАортогональны:_j|_i= 0
приij. В итоге в сумме
останутся только произведения вида:

C_i*C_i
A_i

_i
| _i

= C_i*C_i
A_i

где P_i= C_i*C_i
представляют собой вероятности
обнаружения определенных численных
значений наблюдаемойА=А_i.
Тогда получим:

 A =|A|=Р₁А₁+Р₂А₂+ …

Комбинация, стоящая справа, представляет
собой т.н. «математическое ожидание»
или среднее значение
случайной величины. Таким образом,
рассматриваемая здесь конструкцияA =|A|при
вычислении дает
среднее значение для любой наблюдаемойА, выражаемой функцией распределения.

Соседние файлы в папке лекции (текст)

• #
• #
• #
• #
• #
• #
• #
• #
• #

Явный вид — оператор

Cтраница 1

Явный вид оператора Н зависит, разумеется, от рассматриваемой частной физической системы; как найти его вид для некоторых частных случаев, обсуждалось выше. Оператор Н является элементом алгебры наблюдаемых системы, и его свойства задаются определяющими алгебраическими соотношениями для этой конкретной системы.
 [1]

Явный вид оператора На зависит от модели, выбранной для описания активного атома.
 [3]

Явный вид операторов О, и значения коэффициентов с -, входящих в это выражение, приведены в конце гл.
 [4]

Однако явный вид оператора р ( или матрицы pmn) неизвестен и не может быть определен только из уравнения ( 2 3) без использования дополнительных сведений о свойствах подсистемы. Мы ограничимся пока случаем стационарных состояний, когда матрица плотности не изменяется во времени.
 [5]

Используя явный вид операторов С и С, нетрудно показать, что на общей области определения С С в смысле неравенства квадратичных форм.
 [6]

Итак, явный вид операторов зависит от вида представления. В § 30 будет показано, что перестановочны соотношения между операторами не меняются при переходе1 от одного представления к другому.
 [7]

Итак, явный вид операторов зависит от вида представления. В § 30 будет показано, что перестановочные соотношения между операторами не меняются при переходе от одного представления к другому.
 [8]

Для нахождения явного вида операторов ak, a рассмотрим сначала одно состояние с номером k, игнорируя все остальные.
 [9]

Здесь не рассматривается явный вид оператора Н, следует отметить только, что он является одноэлектронным оператором ( так как я з — одноэлектронная функция), который, строго говоря, определяется однозначно лишь для молекулы с одним электроном ( например, Щ): в этом случае Н есть фактический электронный гамильтониан молекулы. Отложим обсуждение этого вопроса до конца настоящей главы, ограничиваясь здесь утверждением, что Н содержит оператор кинетической энергии электрона и усредненный эффективный потенциал, действующий на выделенный электрон и создаваемый всеми ядрами и остальными электронами молекулы.
 [10]

Это и есть явный вид оператора слагающей импульса.
 [11]

Ниже мы выпишем явный вид операторов Гамильтона, но предварительно введем некоторые обозначения. Однако этих операторов недостаточно для описания лазера. Дело в том, что поле связано с зеркалами, которыми обусловлены затухание и флуктуации поля.
 [12]

Выбор связан с представлением в явном виде оператора opt в задачах, описанных в предыдущем параграфе.
 [13]

Наконец, находим матрицу D, используя явный вид операторов А, В, С, D, Е, F, приведенный в разд.
 [14]

Эти соотношения можно проверить и непосредственно, используя явный вид операторов Лиувилля, или лиувилианов.
 [15]

Страницы:  

   1

   2

Оператором, обратным к F̂ , будемназывать такой оператор F̂ −1 , для которого выполняется соотношение:defdefF̂ −1 F̂ = F̂ F̂ −1 = 1̂.В соответствии с некоммутативностью произведения укажем на некорF̂ректность записей типа . Необходимо использовать обратный операĜ−1−1тор: F̂ Ĝ либо Ĝ F̂ (при этом могут получиться различные результаты).158◦ . Целая положительная степень оператора: F̂ n .

Это nкратное перемножение оператора F̂ на себя:defF̂ n = F̂. . · F̂} .| · .{zn раз9◦ . Оператор под знаком функции: f (F̂ ). Если функция f (z)допускает разложение в ряд Тейлора в окрестности нуляf (z) =∞Xcn z n ,n=0то оператор F̂ под ее знаком определяется следующим образом:∞Xdefnf (F̂ ) =cn z .n=0z=F̂Таким образом, для внесения оператора под знак функции необходимознание коэффициентов тейлоровского разложения этой функции.Определения 1◦ –9◦ широко используются при выводе различныхоператорных тождеств.

Предлагаем читателю самостоятельно убедиться в справедливости тождеств:[Â, B̂] = −[B̂, Â];[Â, Â] = 0.(2.4)(2.5)Пример 2.2. Вывести «сочетательный закон» для операторов:ÂB̂ Ĉ = Â(B̂ Ĉ) = (ÂB̂)Ĉ.(2.6)Решение. Закон (2.6) выводится элементарно из определения произведения операторов 6◦ и операторного равенства 1◦ .В квантовой механике большая роль отводится так называемым линейным операторам, которые удовлетворяют условиюdefF̂ (αΨ + βΦ) = αF̂ Ψ + β F̂ Φ(2.7)для произвольных функций Φ, Ψ и произвольных комплексных констант α, β.16Для выполнения принципа суперпозиции состояний операторы физических величин обязаны быть линейными. В дальнейшем всюду, еслине оговорено особо, операторы предполагаются линейными.Рекомендуем самостоятельно доказать следующие свойства билинейности коммутатора:[Â, β B̂ + γ Ĉ] = β[Â, B̂] + γ[Â, Ĉ],[α + β B̂, Ĉ] = α[Â, Ĉ] + β[B̂, Ĉ].(2.8)Пример 2.3.

Вывести «распределительный закон» для операторов:Â(B̂ + Ĉ) = ÂB̂ + ÂĈ,(2.9)(Â + B̂)Ĉ = ÂĈ + B̂ Ĉ.Решение. Для произвольной функции Ψ выполняем последовательность преобразований:(6◦ )(5◦ )(2.7)Â(B̂ + Ĉ)Ψ = Â[(B̂ + Ĉ)Ψ] = Â(B̂Ψ + ĈΨ) =(6◦ )(5◦ )= Â(B̂Ψ) + Â(ĈΨ) = (ÂB̂)Ψ + (ÂĈ)Ψ = (ÂB̂ + ÂĈ)Ψ.В соответствии с определением 1◦ приходим к первому операторномуравенству (2.9). Аналогично выводится и второе тождество (2.9).Тождества (2.6) и (2.9) показывают, что при алгебраических преобразованиях с линейными операторами можно поступать как с обычными числами.

Недопустимо лишь произвольно изменять порядок сомножителей в произведениях без учета правил коммутации. В частности, за скобки можно выносить либо только крайний левый, либотолько крайний правый операторы (см. (2.9)).Если возникает необходимость изменения порядка сомножителей,то необходимо учитывать коммутационное соотношение между операторами. На основе (2.2) легко вывести следующее тождество:F̂ Ĝ = ĜF̂ + [F̂ , Ĝ].Пример 2.4. Раскрыть скобки в произведениях операторов:(F̂ − Ĝ)(F̂ + Ĝ);17(F̂ + Ĝ)2 .(2.10)Решение.

Преобразования осуществляем с использованием тождеств(2.1), (2.9):(F̂ − Ĝ)(F̂ + Ĝ) = F̂ (F̂ + Ĝ) − Ĝ(F̂ + Ĝ) == F̂ 2 − Ĝ2 + F̂− ĜF̂} = F̂ 2 − Ĝ2 + [F̂ , Ĝ];| Ĝ {z[F̂ ,Ĝ](F̂ + Ĝ)2 = (F̂ + Ĝ)(F̂ + Ĝ) = F̂ (F̂ + Ĝ) + Ĝ(F̂ + Ĝ) =(2.10)= F̂ 2 + Ĝ2 + F̂+ ĜF̂} = F̂ 2 + 2F̂ Ĝ + Ĝ2 − [F̂ , Ĝ].| Ĝ {z{F̂ ,Ĝ}Мы намеренно представили результаты в форме, наиболее близкой ксоответствующим тождествам для обычных чисел. Отличие заключается в дополнительных слагаемых — коммутаторах.

В случае обычныхчисел эти коммутаторы тождественно обращаются в нуль.Пример 2.5. Выразить оператор (F̂ Ĝ)−1 через F̂ −1 и Ĝ−1 .Решение. Легко показать, что F̂ 1̂ = 1̂F̂ = F̂ (сделайте самостоятельно!).По определению обратного оператора 7◦ ,(F̂ Ĝ)(F̂ Ĝ)−1 = 1̂.(2.11)Преобразуем левую часть (2.11) в соответствии с «сочетательным законом» (2.6) и домножим обе части (2.11) слева сначала на F̂ −1 , а затемна Ĝ−1 . В результате получим тождество:(F̂ Ĝ)−1 = Ĝ−1 F̂ −1 .(2.12)Таким образом, обращение произведения изменяет порядок следованиясомножителей на противоположный.

Тождество (2.12) лишний раздемонстрирует отличие операторов от обычных чисел. Если же операторы коммутируют, мы приходим к традиционному правилу обращенияпроизведения чисел.Пример 2.6. Выразить коммутатор [Â, B̂ Ĉ] через коммутаторы[Â, B̂] и [Â, Ĉ].Решение. Приведем вначале два вспомогательных тождества:1) F̂ + 0̂ = F̂ ; 2) F̂ − F̂ = 0̂ (доказать самостоятельно!).Дальнейшие выкладки мы осуществляем без подробных комментариев:18(2.2)[Â, B̂ Ĉ] = ÂB̂ Ĉ − B̂ Ĉ Â = ÂB̂ Ĉ + 0̂ − B̂ Ĉ Â =(2.1)(2.9)= ÂB̂ Ĉ + |B̂ ÂĈ {z− B̂ ÂĈ} −B̂ Ĉ Â = ÂB̂ Ĉ − B̂ ÂĈ + B̂ ÂĈ − B̂ Ĉ Â =0̂= (ÂB̂ − B̂ Â)Ĉ + B̂(ÂĈ − Ĉ Â) = [Â, B̂]Ĉ + B̂[Â, Ĉ].Выпишем окончательный ответ:[Â, B̂ Ĉ] = [Â, B̂]Ĉ + B̂[Â, Ĉ].(2.13)Полученное тождество чрезвычайно удобно при «упрощении» коммутаторов.Задачи для самостоятельного решения6.

Доказать тождества:[F̂ , Ĝ] = −[Ĝ, F̂ ];{F̂ , Ĝ} = {Ĝ, F̂ }.7. Доказать тождества (2.8).8. Доказать тождество Якоби:[Â, [B̂, Ĉ]] + [Ĉ, [Â, B̂]] + [B̂, [Ĉ, Â]] = 0̂.(2.14)9∗ . Разложить оператор (F̂ − λĜ)−1 по степеням малого параметра λ.∞X−1(Ответ: (F̂ − λĜ) =(λF̂ −1 Ĝ)n .)n=010∗ . Доказать тождество Бекера – Кэмпбела – Хаусдорфа:eF̂ Ĝ e−F̂ = Ĝ + [F̂ , Ĝ] +11[F̂ , [F̂ , Ĝ]] + [F̂ , [F̂ , [F̂ , Ĝ]]] + .

. .2!3!11∗ . Для операторов, удовлетворяющих условиям [F̂ , [F̂ , Ĝ]] = 0,[Ĝ, [F̂ , Ĝ]] = 0, доказать тождество Вейля:1eF̂ +Ĝ = e− 2 [F̂ ,Ĝ] eF̂ eĜ .19Таблица 2.1Операторы основных физических величин№ВеличинаОператорПримечание1координата rr̂ = r2импульс pp̂ = −iℏ∇r̂Ψ(r) = rΨ(r)X∂∂= −iℏp̂ = −iℏek∂xk∂r3орб. момент L4кин. энергия T5потенц. энергия V6полная энергия E7четность P2.3.L̂ = [r × p̂]p̂2T̂ =2mV̂ = V (r)Ĥ = T̂ + V̂Iˆ — инверсияkℏ2 2T̂ Ψ(r) = −∇ Ψ(r)2mV̂ Ψ(r) = V (r)Ψ(r)Ĥ — гамильтонианˆIΨ(r)= Ψ(−r)Операторы различных физических величинВ таблице 2.1 собраны операторы важнейших физических величин(здесь и далее m — масса частицы).

Первые шесть из них используются как в классической, так и в квантовой механике. Четность жеявляется чисто квантовой характеристикой микрообъектов. Предлагаем самостоятельно убедиться в линейности приведенных операторов.В данном параграфе мы будем вычислять коммутаторы (т.

е. находить их явный вид) операторов важнейших физических величин.Вначале рассмотрим операторы координаты и импульса. Для удобства мы будем пользоваться декартовым базисом.Пример 2.7. Вычислить коммутатор [x, p̂x ].Решение. Согласно своему определению, коммутатор является оператором. Поэтому его явный вид можно найти, подействовав им на произвольную функцию.

Из таблицы 2.1 возьмем явный вид операторапроекции импульса:∂p̂x = −iℏ.(2.15)∂xВ соответствии с (2.15) и определением произведения 6◦ , имеем:∂Ψ;∂x∂∂Ψp̂x xΨ = p̂x (xΨ) = −iℏ(xΨ) = −iℏΨ − iℏx.∂x∂xxp̂x Ψ = x(p̂x Ψ) = −iℏx20На основании 4◦ и 5◦ получаем:[x, p̂x ]Ψ = xp̂x Ψ − p̂x xΨ = iℏΨ.(2.16)Поскольку равенство (2.16) должно выполняться для произвольнойфункции Ψ, мы, согласно 1◦ , приходим к операторному равенству 2 :[x, p̂x ] = iℏ.(2.17)Операторное тождество (2.17) является одним из основных соотношений квантовой теории.Аналогичным образом можно показать, что[x, p̂x ] = [y, p̂y ] = [z, p̂z ] = iℏ,т. е. операторы декартовой координаты и одноименной проекции импульса не коммутируют.

Пары этих операторов называют также канонически сопряженными.Пример 2.8. Вычислить коммутаторы: 1) [x, p̂y ]; 2) [x, y]; 3) [p̂x , p̂y ].Решение.1. Коммутатор [x, p̂y ] вычисляем по аналогии с предыдущим примером, однако, вследствие независимости переменных x и y,∂∂(xΨ) = x −iℏΨ = xp̂y Ψ.p̂y xΨ = −iℏ∂y∂yТаким образом, [x, p̂y ] = 0 (в смысле нулевого оператора).Данное утверждение можно обобщить: разноименные декартовы координаты и проекции импульсов коммутируют.2.

Оператор координаты является обычным числовым множителем.Значение произведения чисел не зависит от порядка следования сомножителей. Поэтому [x, y] = 0. Вообще, все декартовы координатыкоммутируют друг с другом.3. Произведение p̂x p̂y , в соответствии с определением 6◦ , с точностью до постоянного множителя является смешанной производной.

Смешанные производные функций, удовлетворяющих стандартным условиям, не зависят от порядка дифференцирования. Поэтому[p̂x , p̂y ] = 0. Как и в случае с координатами, все декартовы компоненты импульса коммутируют друг с другом.2Строго говоря, в правой части (2.17) следовало бы, в соответствии с 1◦ , поставить iℏ1̂, но, как правило, единичный оператор здесь не указывается.21Обобщим теперь результаты предыдущих двух примеров, введя обозначения x1 ≡ x, x2 ≡ y, x3 ≡ z; p̂x ≡ p̂1 , . . . :[xk , p̂l ] = iℏδkl ;[xk , xl ] = 0;(2.18)[p̂k , p̂l ] = 0.Пример 2.9. Вычислить коммутатор [r, p̂2 ].Решение. Вначале запишем коммутатор в декартовых компонентах, затем воспользуемся свойством билинейности (2.8).

Упростим получившиеся коммутаторы по правилу (2.13), оставшиеся коммутаторы вычислим в соответствии с (2.18):XX(2.8) X(2.13)[r, p̂2 ] = [ek xk ,p̂l p̂l ] =ek [xk , p̂l p̂l ] =k=lXk,lk,l(2.18)ek {[xk , p̂l ]p̂l + p̂l [xk , p̂l ]} = 2iℏXek δkl p̂l = 2iℏp̂.k,lДанный пример наглядно демонстрирует использование правила«упрощения» (2.13).Пример 2.10. Вычислить коммутатор [f (x), p̂x ], где f (x) — дифференцируемая функция координат.Решение.