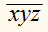Задуманное число на 84 больше, чем треть самого задуманного числа. Найдите задуманное число.
Для решения задачи потребуется составить уравнение.
Х — задуманное число; Х : 3 — третья часть от задуманного числа.
Уравнение: Х — Х : 3 = 84. Чтобы исключить выражение Х : 3, всё перемножим на 3
3Х — Х = 252;
2Х = 252; Х = 126.
Проверим уравнение: 126 — 126 : 3 = 84; 126 — 42 = 84.
Ответ: 126 задуманное число.
система выбрала этот ответ лучшим
Если внимательно прочитать задание, становится понятно, что оно не такое уж и сложное, каким может показаться на первый взгляд.
Нужно понимать, что для того, чтобы найти одну третью часть числа, необходимо данное число разделить на три.
Есть несколько вариантов решения задачи из вопроса. Из них мне больше нравится способ решения с использованием уравнения с одним неизвестным.
Пусть х — число, которое задумали, тогда третья часть этого числа будет равна х/3. Так как по условию задачи исходное число больше своей трети на 84, составим уравнение:
х — 84 = х/3.
Решаем данное уравнение.
х — х/3 = 84, 2х/3 = 84, х = (84*3)/2, х = 126.
Ответ: задуманное число 126.
Сыррожа
[172K]
4 года назад
Ну так включите голову и составьте элементарное алгебраическое уравнение типа:
X — X / 3 = 84
Или после несложных преобразований:
3X — X = 84 * 3
А чтобы еще проще было усвоить:
2X = 252
Откуда закономерно вытекает, что X = 126.
Для тех кто в танке: X — это задуманное автором вопроса искомое число.
Вот только мне интересно: зачем превращать БВ в площадку для дистанционного обучения школьных «прогульщиков»? В том смысле, что проекту от таких вопросов есть ли доход? Неужто у нас столько «шалопаев» в среде тинейджеров — не пойму я как-то это всё…
Бульбозавр
[450K]
4 года назад
Конечно такое задание подразумевает два варианта решения, ведь оно еще и выявляет логическое мышление ребенка.
С помощью уравнения решать конечно хорошо, но проще будет просто внимательно почитать условия задачи и понять, что там сказано.
А в задаче говорится о числе, и его трех третях, причем 84 это две части из этих третей.
Решение будет простым, если всего лишь 84 разделить на два и это будет равно одной трети – 42.
1/3=42
42х3=126 , а если записать проще из условия задачи , то 42+84=126.
Master-Margarita
[135K]
4 года назад
Решение:
Для решения задачи составим следующее равенство, где х обозначим за задуманное число:
х — 84 = х : 3 (задуманное число на 84 меньше, чем треть от задуманного числа)
3 * (х — 84) = х,
3х — 3 * 84 = х,
2х = 3 * 84,
х = (3 * 84) : 2,
х = 3 * 42 = 136.
Ответ: Таким образом, задуманное число составляет 126.
duselldorf
[4.3K]
4 года назад
Пусть х — задуманное число, тогда треть от задуманного числа равна х / 3, а разница между задуманным числом на 84 больше, чем треть задуманного числа.
Составим уравнение:
х — 1 / 3 * х = 84
2 / 3 * х = 84
х = 84 : (2 / 3)
х = 84 * 3 / 2
х = 126.
Ответ: 126 — задуманное число равно 126.
Валентина МД
[33.2K]
4 года назад
Задуманное число примем за х, тогда треть от него равна 1/3 х, разница между ними по условию равна 84. Составим уравнение:
х — 1/3 х = 84,
2/3 х = 84; х = 84 : 2/3; или х = 84 * 3/2, х = 126.
Ответ: 126 — задуманное число.
Проверка:
126 — 126/3 = 84.
Натишка2210
[36.3K]
4 года назад
Давайте составим уравнение, где х — задуманное число.
х = х/3 + 84
Умножим все на 3. Получим:
3х=х+252
2х=252
х=126
Проверяем:
Задуманное число 126, треть от него 42, на 84 меньше задуманного.
Ответ: 126
storus
[73.8K]
4 года назад
Обозначим задуманное число через х.
Тогда получаем уравнение с одной неизвестной х=х/3+84, которое легко решается.
Первым делом переносим все неизвестные члены уравнения в одну сторону:
х-х/3=84
Избавляемся от дроби, умножив обе части уравнения на три:
3х-х=252.
2х=252
Находим, чему равен х:
х=252/2
х=126
Правильный ответ: задуманное число равно 126.
AlexSEO
[85.9K]
4 года назад
Можно решить, составляя несложное уравнение: х = 1/3х + 84, 3х = х + 252 (умножаем обе части уравнения на 3), 2х = 252, х = 126. Это правильный ответ, поскольку: 126 / 3 = 42, 42 + 84 = 126.
Но, достаточно понять из условия, что 84 это не что иное, а 2/3 числа и решение будет еще более простым: 84 * 3 / 2 = 126.
Знаете ответ?
Методы решения задач на арифметические действия: как найти задуманное число при условии сложения с его восьмой частью?
Введение
В школьной программе математики встречаются задачи, которые требуют нахождения неизвестного числа при условии, что оно складывается с определенной дробью или частью самого числа. Один такой пример — нахождение числа при сложении его с восьмой частью.
Метод решения
Предположим, что неизвестное число записано как $x$. Тогда условие можно записать уравнением:
$x + frac{x}{8} = y$
где $y$ — задуманное число.
Для решения этого уравнения нужно привести его к виду:
$x + frac{x}{8} = frac{9x}{8} = y$
Теперь можно выразить $x$ через $y$:
$x = frac{8y}{9}$
Это и есть ответ на задачу: чтобы найти задуманное число при условии, что оно складывается с его восьмой частью, нужно умножить это число на $9/8$.
Пример
Допустим, задуманное число равно 72. Как найти число, которое при сложении с его восьмой частью дает 72?
По формуле $x = frac{8y}{9}$ получаем:
$x = frac{8 cdot 72}{9} = 64$
Ответ: число, которое при сложении с его восьмой частью дает 72, равно 64.
Заключение
Метод нахождения задуманного числа при условии сложения с его восьмой частью прост и применим во многих задачах. Он заключается в простом алгебраическом преобразовании и позволяет быстро решить такую задачу.
Предложите кому-либо задумать некоторое двузначное число. Затем попросите разделить задуманное число на 3, на 5 и на 7, и назвать вам остатки от деления. После этого вы сможете отгадать задуманное число, точнее, его вычислить. Как это сделать?
Показать решение
Ваш отзыв , 08 Сен 2012
Обозначение
десятеричной записи числа.
Запись
обозначает число, в
котором х сотен, у десятков и z единиц. Это число можно представить в виде
многочлена:
где
х – цифра указывающая
количество сотен в числе
у – цифра указывающая количество
десятков в числе
z – цифра указывающая
количество единиц в числе.
ПРИМЕР:
Четырёхзначное число с цифрами a, b, c
и d можно обозначить
Эта запись означает
1000a + 100b + 10c + d.
ПРИМЕР:
378
= 100 × 3 + 10 × 7 + 8.
ЗАДАЧА:
В двузначном числе цифра десятков на 4 больше цифры единиц. Когда это число
разделили на цифру единиц, то в частном получилось 24, а в остатке число, которое
на 2 меньше делителя. Найти задуманное число.
РЕШЕНИЕ:
Решая эту
задачу, можно использовать обозначение десятеричной записи числа. Заданное
число можно обозначить
В
соответствии с этим обозначением можно записать:
а по условию задачи имеем:
= 24
и ост (х – 4) – 2
=
24(х – 4) + х – 6.
10х + х
– 4 = 24(х – 4) + х – 6,
10х – 4 = 24х – 96 – 6,
14х
= 98, х = 7, тогда 10 × 7 + 7 – 4 = 73.
Задуманное число 73.
Алгоритм
решения задач, в которых используется формула двузначного числа.
Вводится
обозначение:
х – цифра десятков
у – цифра единиц
Искомое
двузначное число
10х + у
Составляется
система уравнений.
ЗАДАЧА:
Двузначное число в четыре раза больше суммы
его цифр. Если к этому числу прибавить произведение его цифр, то получится 32. Найдите это
двузначное число.
РЕШЕНИЕ:
х – цифра
десятков, у – цифра
единиц.
10х + у – искомое число, тогда по условию задачи:
2х2 + 12х – 32 = 0,
х2 + 6х
– 16 = 0.
х1 = –8 (посторонний корень)
х1 = 2, тогда у =
4.
ОТВЕТ: 24
Задания к уроку 37
- Учебники
- 7 класс
- Алгебра 👍
- Макарычев
- №252
авторы: Макарычев, Миндюк, Нешков, Суворова.
издательство: «Просвещение» 2013 г.
Раздел:
- ГЛАВА I. ВЫРАЖЕНИЯ, ТОЖДЕСТВА, УРАВНЕНИЯ
- Дополнительные упражнения к главе I
- К параграфу 3
Если к задуманному числу прибавить 7, полученную сумму умножить на 3 и из произведения вычесть 47, то получится задуманное число. какое число задумано?
reshalka.com
ГДЗ учебник по алгебрее 7 класс Макарычев. Номер №252
Решение
Пусть x − задуманное число, тогда:
(x + 7) * 3 − 47 = x
3x + 21 − 47 = x
3x − x = 47 − 21
2x = 26
x = 26 : 2
x = 13 − задуманное число.
Ответ: 13
- Предыдущее
- Следующее
Нашли ошибку?
Если Вы нашли ошибку, неточность или просто не согласны с ответом, пожалуйста сообщите нам об этом