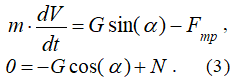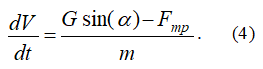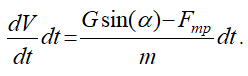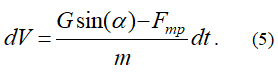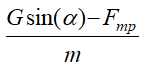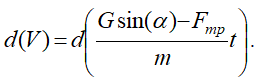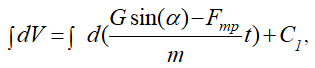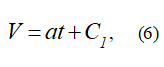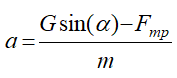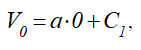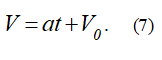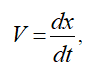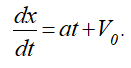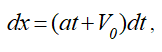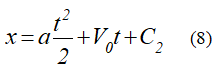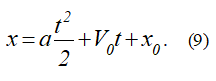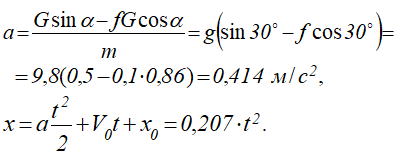Как найти закон движения тела если - Исправление недочетов и поиск решений вместе с Examum.ru

Пример решения задачи по определению закона движения точки твердого тела массой m, начинающего скользить из состояния покоя по наклонной плоскости с заданным углом и коэффициентом трения скольжения f.

Задача

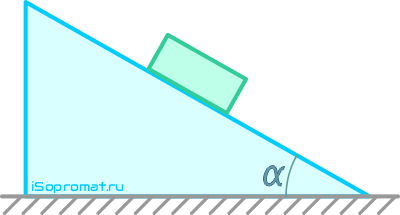
По наклонной плоскости из состояния покоя начинает скользить тело массой m = 1 кг (рисунок 5.1). Коэффициент трения скольжения f = 0,1.

Рисунок 5.1

Определить закон движения точки, если угол α = 30°.

Другие примеры решений >
Помощь с решением задач >

Решение

В данном случае тело движется поступательно, следовательно, его можно рассматривать как материальную точку. Направим ось x вдоль движения. Начало оси возьмем в начальном положении точки. Тогда x₀= 0.

Поскольку движение начинается из состояния покоя, начальная скорость V₀ тоже равна нулю.

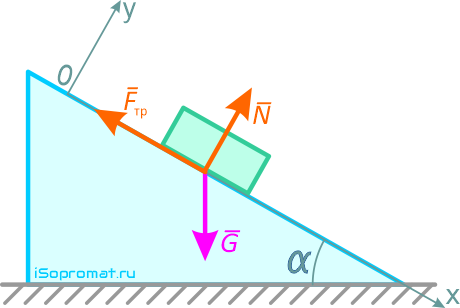
Расположим тело в произвольный момент времени и покажем все силы, действующие на него, включая реакции связей. На тело действуют сила тяжести G, сила трения F_тр и нормальная реакция наклонной плоскости N (рисунок 5.2).

Рисунок 5.2

Запишем уравнение второго закона динамики в векторном виде

и в проекциях на оси координат

Из второго уравнения системы (3) можно определить величину нормальной реакции поверхности:

Первое уравнение системы (3) разделим слева и справа на m:

С точки зрения математики полученное уравнение является простейшим дифференциальным уравнением с разделяющимися переменными. Уравнение связывает две переменные величины – скорость точки и время.

Смысл разделения переменных заключается в том, чтобы все слагаемые уравнения, куда входит скорость, были с одной стороны от знака равенства, а слагаемые, куда входит время – с другой стороны знака равенства.

Умножив уравнение (4) на dt слева и справа, получим

Сокращая слева на dt, получим:

Величина

постоянная и ее можно внести под знак дифференциала. Тогда уравнение (5) перепишется в виде равенства двух дифференциалов:

Если дифференциалы равны, то интегралы равны с точностью до постоянной величины:

или

где

это ускорение точки.

Полученный результат дает зависимость проекции скорости на ось x от времени и от постоянной интегрирования C₁.

Для определения постоянной C₁ воспользуемся начальным значением скорости. Зная значение скорости точки в начальный момент времени V₀, и подставляя его в (6), получим

или C₁ = V₀.

Таким образом, зависимость скорости от времени примет вид

Учитывая, что

снова получим дифференциальное уравнение первого порядка относительно координаты x

Снова разделим переменные

и после интегрирования получим

где C₂ – вторая постоянная интегрирования. Для определения C₂ воспользуемся значением координаты x в начальный момент. Получим C₂ = x₀.

Тогда (8) запишется в виде

Подставляя начальные значения и исходные данные, получим

Ответ: Таким образом, тело движется вниз по наклонной плоскости по закону x = 0,207∙t².

Другие примеры решения задач >

Источник

Каждый обращал внимание на все многообразие видов движения, с которыми он сталкивается в своей жизни. Однако любое механическое движение тела сводится к одному из двух типов: линейное или вращательное. Рассмотрим в статье основные законы движения тел.

О каких типах движения пойдет речь?

Как было отмечено во введении, все виды движения тела, которые рассматриваются в классической физике, связаны либо с прямолинейной траекторией, либо с круговой. Любые другие траектории можно получить благодаря комбинации этих двух. Далее в статье будут рассмотрены следующие законы движения тела:

Равномерное по прямой линии.

Равноускоренное (равнозамедленное) по прямой линии.

Равномерное по окружности.

Равноускоренное по окружности.

Движение по эллиптической траектории.

Равномерное движение, или состояние покоя

Вам будет интересно:Преподаватели СПБГУ: педагогический состав, факультеты, направления

Этим движением с научной точки зрения начал интересоваться впервые Галилей в конце XVI — начале XVII века. Изучая инерционные свойства тела, а также введя понятие о системе отсчета, он догадался, что состояние покоя и равномерного движения — это одно и то же (все зависит от выбора объекта, относительно которого рассчитывают скорость).

Вам будет интересно:Характеристика движения под углом к горизонту: формулы, решение задачи с лучником

Впоследствии Исаак Ньютон сформулировал свой первый закон движения тела, согласно которому скорость последнего является постоянной величиной всегда, когда нет внешних сил, изменяющих характеристики движения.

Равномерное прямолинейное перемещение тела в пространстве описывается следующей формулой:

s = v * t

Где s — расстояние, которое преодолеет тело за время t, двигаясь со скоростью v. Это простое выражение также записывается в следующих формах (все зависит от величин, которые известны):

v = s / t; t = s / v

Перемещение по прямой с ускорением

Согласно второму закону Ньютона, наличие внешней силы, действующей на тело, неминуемо приводит к появлению ускорения у последнего. Из определения ускорения (быстрота изменения скорости) следует выражение:

Вам будет интересно:Тюркизмы в русском языке: понятие, история появления, звучание и примеры

a = v / t или v = a * t

Если действующая на тело внешняя сила будет оставаться постоянной (не будет изменять модуля и направления), то ускорение также не изменится. Такой тип движения называется равноускоренным, где ускорение выступает коэффициентом пропорциональности между скоростью и временем (скорость растет линейно).

Для этого движения пройденный путь рассчитывается с помощью интегрирования скорости по времени. Закон движения тела для пути при равноускоренном перемещении приобретает форму:

s = a * t2 / 2

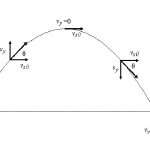
Самым распространенным примером этого движения является падение любого предмета с высоты, при котором сила тяжести сообщает ему ускорение g = 9,81 м/с2.

Прямолинейное ускоренное (замедленное) движение с наличием начальной скорости

По сути, речь идет о комбинации двух видов перемещения, рассмотренных в предыдущих пунктах. Представим простую ситуацию: автомобиль ехал с некоторой скоростью v0, затем водитель нажал на тормоза, и транспортное средство через некоторое время остановилось. Как описать движение в этом случае? Для функции скорости от времени справедливо выражение:

v = v0 — a * t

Здесь v0 — начальная скорость (до торможения авто). Знак минус говорит о том, что внешняя сила (трения скольжения) направлена против скорости v0.

Как и в предыдущем пункте, если взять интеграл по времени от v(t), то получаем формулу для пути:

s = v0 * t — a * t2 / 2

Отметим, что по этой формуле вычисляется только путь торможения. Чтобы узнать расстояние, пройденное автомобилем за все время его движения, следует найти сумму двух путей: для равномерного и для равнозамедленного движения.

В примере описанном выше, если бы водитель нажал не на педаль тормоза, а на педаль газа, тогда в представленных формулах поменялся бы знак «-» на «+».

Движение по окружности

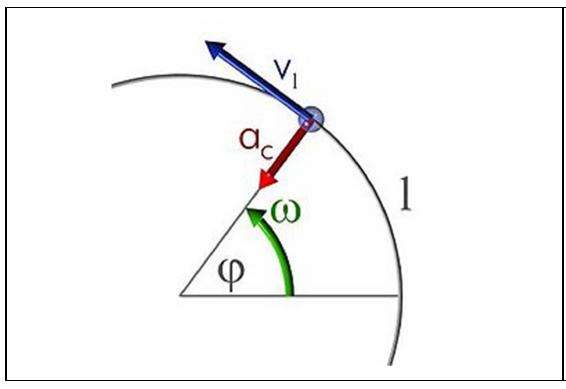
Любое движение по окружности не может происходить без ускорения, поскольку даже при сохранении модуля скорости изменяется ее направление. Ускорение, которое связано с этим изменением, называется центростремительным (именно оно искривляет траекторию тела, превращая ее в окружность). Модуль этого ускорения вычисляют так:

ac = v2 / r, r — радиус

В этом выражении скорость может зависеть от времени, как это происходит в случае равноускоренного движения по окружности. В последнем случае ac будет быстро расти (квадратичная зависимость).

Центростремительное ускорение определяет силу, которую нужно прикладывать, чтобы удерживать тело на круговой орбите. Примером являются соревнования по метанию молота, когда спортсмены прикладывают значительные усилия, чтобы раскрутить снаряд до его метания.

Вращение вокруг оси с постоянной скоростью

Этот вид движения идентичен предыдущему, только описывать его принято не с использованием линейных физических величин, а с применением угловых характеристик. Закон вращательного движения тела, когда угловая скорость не изменяется, в скалярной форме записывается так:

L =I * ω

Здесь L и I — моменты импульса и инерции, соответственно, ω — угловая скорость, которая с линейной связана равенством:

v = ω * r

Величина ω показывает, на сколько радиан повернется тело за секунду. Величины L и I имеют такой же смысл, как импульс и масса для прямолинейного движения. Соответственно, угол θ, на который повернется тело за время t, вычисляется так:

θ = ω * t

Примером этого типа движения является вращение маховика, находящегося на коленчатом вале в двигателе автомобиля. Маховик — это массивный диск, которому очень тяжело придать какое-либо ускорение. Благодаря этому он обеспечивает плавность изменения крутящего момента, который передается от двигателя к колесам.

Вращение вокруг оси с ускорением

Если к системе, которая способна вращаться, прикладывать внешнюю силу, то она начнет увеличивать свою угловую скорость. Такая ситуация описывается следующим законом движения тела вокруг оси вращения:

F * d = I * dω / dt

Здесь F — внешняя сила, которая приложена к системе на расстоянии d от оси вращения. Произведение в левой части равенства носит название момента силы.

Для равноускоренного движения по окружности получаем, что ω зависит от времени следующим образом:

ω = α * t, где α = F * d / I — угловое ускорение

В этом случае угол поворота за время t можно определить, проинтегрировав ω по времени, то есть:

θ = α * t2 / 2

Если же тело уже вращалось с некоторой скоростью ω0, а затем начал действовать внешний момент силы F*d, то по аналогии с линейным случаем можно записать такие выражения:

ω = ω0 + α * t;

θ = ω0 * t + α * t2 / 2

Таким образом, появление внешнего момента сил является причиной наличия ускорения в системе с осью вращения.

Для полноты информации отметим, что изменить скорость вращения ω можно не только с помощью внешнего момента сил, но и благодаря изменению внутренних характеристик системы, в частности ее момента инерции. Эту ситуацию видел каждый человек, который наблюдал за вращением фигуристов на льду. Группируясь, спортсмены увеличивают ω за счет уменьшения I, согласно простому закону движения тела:

I * ω = const

Движение по эллиптической траектории на примере планет Солнечной системы

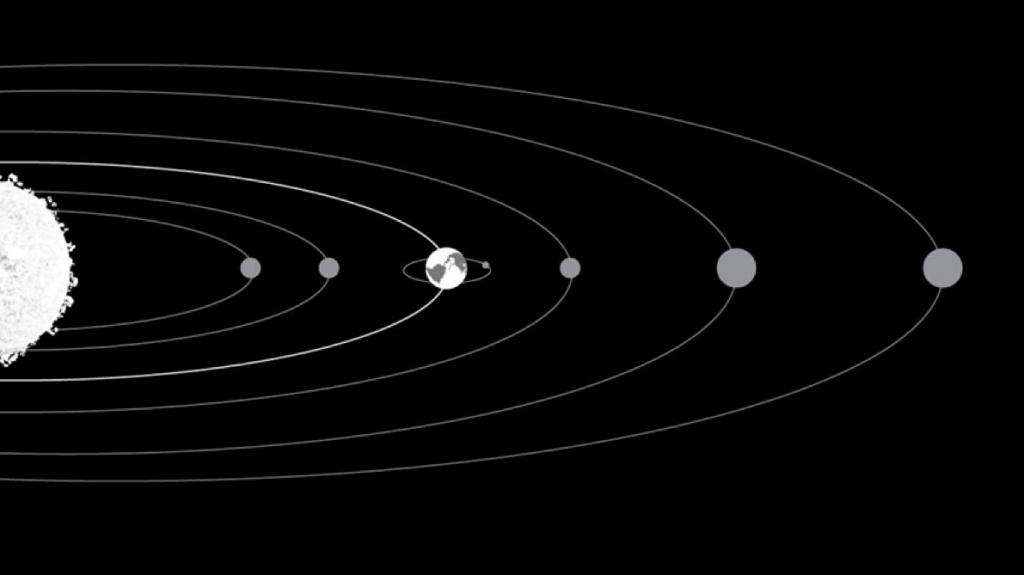
Как известно, наша Земля и другие планеты Солнечной системы вращаются вокруг своей звезды не по окружности, а по эллиптической траектории. Впервые математические законы для описания этого вращения сформулировал знаменитый немецкий ученый Иоганн Кеплер в начале XVII века. Используя результаты наблюдений своего учителя Тихо Браге за движением планет, Кеплер пришел к формулировке своих трех законов. Они формулируются следующим образом:

Планеты Солнечной системы движутся по эллиптическим орбитам, причем Солнце расположено в одном из фокусов эллипса.

Радиус-вектор, который соединяет Солнце и планету, за равные промежутки времени описывает одинаковые площади. Этот факт следует из сохранения момента импульса.

Если поделить квадрат периода обращения на куб большой полуоси эллиптической орбиты планеты, то получается некоторая константа, которая одинакова для всех планет нашей системы. Математически это записывается так:

T2 / a3 = С = const

Впоследствии Исаак Ньютон, используя эти законы движения тел (планет), сформулировал свой знаменитый закон всемирной гравитации, или тяготения. Применяя его, можно показать, что константа C в 3-м законе Кеплера равна:

C = 4 * pi2 / (G * M)

Где G — гравитационная универсальная константа, а M — масса Солнца.

Отметим, что движение по эллиптической орбите в случае действия центральной силы (тяготения) приводит к тому, что линейная скорость v постоянно меняется. Она максимальна, когда планета находится ближе всего к звезде, и минимальна вдали от нее.

Источник

В прошлой статье мы немножко разобрались с тем, что такое механика и зачем она нужна. Мы уже знаем, что такое система отсчета, относительность движения и материальная точка. Что ж, пора двигаться дальше! Здесь мы рассмотрим основные понятия кинематики, соберем вместе самые полезные формулы по основам кинематики и приведем практический пример решения задачи.

Присоединяйтесь к нам в телеграм и получайте ежедневную рассылку с полезной информацией по актуальным студенческим вопросам.

Траектория, радиус-вектор, закон движения тела

Кинематикой занимался еще Аристотель. Правда, тогда это не называлось кинематикой. Затем очень большой вклад в развитие механики, и кинематики в частности, внес Галилео Галилей, изучавший свободное падение и инерцию тел.

Итак, кинематика решает вопрос: как тело движется. Причины, по которым оно пришло в движение, ее не интересуют. Кинематике не важно, сама поехала машина, или ее толкнул гигантский динозавр. Абсолютно все равно.

Сейчас мы будем рассматривать самую простую кинематику – кинематику точки. Представим, что тело (материальная точка) движется. Не важно, что это за тело, все равно мы рассматриваем его, как материальную точку. Может быть, это НЛО в небе, а может быть, бумажный самолетик, который мы запустили из окна. А еще лучше, пусть это будет новая машина, на которой мы едем в путешествие. Перемещаясь из точки А в точку Б, наша точка описывает воображаемую линию, которая называется траекторией движения. Другое определение траектории – годограф радиус вектора, то есть линия, которую описывает конец радиус-вектора материальной точки при движении.

Радиус-вектор – вектор, задающий положение точки в пространстве.

Для того, чтобы узнать положение тела в пространстве в любой момент времени, нужно знать закон движения тела – зависимость координат (или радиус-вектора точки) от времени.

Перемещение и путь

Тело переместилось из точки А в точку Б. При этом перемещение тела – отрезок, соединяющий данные точки напрямую – векторная величина. Путь, пройденный телом – длина его траектории. Очевидно, перемещение и путь не стоит путать. Модуль вектора перемещения и длина пути совпадают лишь в случае прямолинейного движения.

В системе СИ перемещение и длина пути измеряются в метрах.

Перемещение равно разнице радиус-векторов в начальный и конечный моменты времени. Другими словами, это приращение радиус вектора.

Скорость и ускорение

Средняя скорость – векторная физическая величина, равная отношению вектора перемещения к промежутку времени, за которое оно произошло

А теперь представим, что промежуток времени уменьшается, уменьшается, и становится совсем коротким, стремится к нулю. В таком случае о средней скорости говорить на приходится, скорость становится мгновенной. Те, кто помнит основы математического анализа, тут же поймут, что в дальнейшем нам не обойтись без производной.

Мгновенная скорость – векторная физическая величина, равная производной от радиус вектора по времени. Мгновенная скорость всегда направлена по касательной к траектории.

В системе СИ скорость измеряется в метрах в секунду

Если тело движется не равномерно и прямолинейно, то у него есть не только скорость, но и ускорение.

Ускорение (или мгновенное ускорение) – векторная физическая величина, вторая производная от радиус-вектора по времени, и, соответственно, первая производная от мгновенной скорости

Ускорение показывает, как быстро изменяется скорость тела. В случае прямолинейного движения, направления векторов скорости и ускорения совпадают. В случае же криволинейного движения, вектор ускорения можно разложить на две составляющие: ускорение тангенциальное, и ускорение нормальное.

Тангенциальное ускорение показывает, как быстро изменяется скорость тела по модулю и направлено по касательной к траектории

Нормальное же ускорение характеризует быстроту изменения скорости по направлению. Векторы нормального и тангенциального ускорения взаимно перпендикулярны, а вектор нормального ускорения направлен к центру окружности, по которой движется точка.

Здесь R – радиус окружности, по которой движется тело.

Закон равноускоренного движения

Рассмотрим далее закон равноускоренного движения, то есть движения с постоянным ускорением. Будем рассматривать простейший случай, когда тело движется вдоль оси x.

Здесь — x нулевое- начальная координата. v нулевое — начальная скорость. Продифференцируем по времени, и получим скорость

Производная по скорости от времени даст значение ускорения a, которое является константой.

Пример решения задачи

Теперь, когда мы рассмотрели физические основы кинематики, пора закрепить знания на практике и решить какую-нибудь задачу. Причем, чем быстрее, тем лучше.

Кстати! Для всех наших читателей сейчас действует скидка 10% на любой вид работы.

Решим такую задачу: точка движется по окружности радиусом 4 метра. Закон ее движения выражается уравнением S=A+Bt^2. А=8м, В=-2м/с^2. В какой момент времени нормальное ускорение точки равно 9 м/с^2? Найти скорость, тангенциальное и полное ускорение точки для этого момента времени.

Решение: мы знаем, что для того, чтобы найти скорость нужно взять первую производную по времени от закона движения, а нормальное ускорение равняется частному квадрата скорости и радиуса окружности, по которой точка движется. Вооружившись этими знаниями, найдем искомые величины.

Нужна помощь в решении задач? Профессиональный студенческий сервис готов оказать ее.

Источник

Кинематика изучает простейшую форму движения – механическое движение. Кинематически определить движение тела – это значит указать его положение относительно выбранной системы отсчета в каждый момент времени.

Движение материальной точки (в дальнейшем будем говорить просто точки) задано, если известен закон движения.

Закон движения. Закон движения – это уравнение, позволяющее определить положение точки относительно выбранной системы отсчета в любой момент времени.

Основная задача кинематики точки. По известному закону движения определить траекторию движения точки, ее положение на траектории, скорость и ускорение точки в ее положении на траектории.

Способы задания движения точки

В зависимости от выбора системы отсчета существуют три способа задания движения точки – векторный, координатный и естественный. Рассмотрим эти способы задания движения в отдельности.

Векторный способ задания движения точки

Пусть точка движется вдоль некоторой линии. В качестве начала отсчета выберем произвольный центр . Положение точки на линии определяется радиус-вектором (рис.К.9).

Таким образом, вектор определяет положение движущейся точки в любой момент времени. Следовательно, уравнение является законом движения при векторном способе задания движения.

Величина $vec v = mathop {lim }limits_{Delta t to o} frac{{Delta vec r}}{{Delta t}} = frac{{dvec r}}{{dt}}$ называется вектором скорости точки. Вектор скорости точки всегда направлен по касательной к годографу (траектории движения точки) в сторону перемещения точки.

Величина $vec a = mathop {lim }limits_{Delta t to o} frac{{Delta vec v}}{{Delta t}} = frac{{dvec v}}{{dt}}$ называется вектором ускорения точки.

Определим направление вектора . Направление вектора vec a определяется направлением вектора . Пусть точка движется по некоторой траектории (рис.К.10) от точки ${A_1}$ к точке ${A_2}$ . Пусть скорость в точке ${A_1}$ равна ${vec v_1}$ , а скорость в точке ${A_2}$ равна ${vec v_2}$ . Перенесем вектор ${vec v_2}$ параллельно самому себе из точки ${A_2}$ в точку ${A_1}$ .

Тогда вектор $Delta vec v = {vec v_2} - {vec v_1}$ .

Как показано на рис.К.10, вектор направлен в сторону вогнутости траектории движения точки, следовательно и вектор ускорения vec a всегда направлен в ту же сторону, то есть в сторону вогнутости траектории движения точки.

Координатный способ задания движения точки

Пусть точка движется вдоль некоторой линии. В качестве системы отсчета выберем декартовую систему координат с началом в произвольном центре . Тогда положение точки на линии определяются текущими координатами в любой момент времени $left{ begin{array}{l} x = x(t)\ y = y(t) end{array} right.$

Следовательно, система уравнений $left{ begin{array}{l} x = x(t)\ y = y(t) end{array} right.$ определяют закон движения точки при координатном способе задания движения. Исключая из закона движения время , получим уравнение вида , являющееся уравнением траектории движения точки.

Пример. Закон движения записывается уравнениями $left{ begin{array}{l} x = 5t + 5\ y = 6t + 7 end{array} right.$ . Найти уравнение траектории движения точки.

Решение. Из первого уравнения следует, что или $(t + 1) = frac{x}{5}$ . Тогда из второго уравнения $y = 6(t + 1) + 1 = frac{6}{5}x + 1$ . Или $y = frac{6}{5}x + 1$ . Таким образом получено, что траекторией движения точки является прямая линия $y = frac{6}{5}x + 1$ .

Компоненты скорости и ускорения движущейся точки в любой момент времени определяются по формулам

${v_x} = frac{{dx(t)}}{{dt}} = dot x(t)$

${a_x} = {dot v_x} = ddot x(t)$

${v_y} = frac{{dy(t)}}{{dt}} = dot y(t)$

${a_y} = {dot v_y} = ddot y(t)$ (К.9)

Модули скорости и ускорения $v = sqrt {v_x^2 + v_y^2}$

$a = sqrt {a_x^2 + a_y^2}$ (К.10)

Векторы скорости и ускорения

$vec v = {v_x}vec i + {v_y}vec j$

$vec a = {a_x}vec i + {a_y}vec j$ .

Источник

Что такое закон движения тела?

Закон движения тела определение

Пусть тело перемещается я по некоторой траектории.

Длина пройденного пути зависит от затраченного времени.

Определение закона движения тела:

Зависимость пути от времени называется законом движения тела.

С точки зрения математики закон движения является функцией. Как всякую функцию закон движения можно представить аналитически, т.е. в виде формулы, графически, т.е. в виде графика или в табличном виде.

Найти закон движения тела

Пример. Найти закон движения тела.

Пусть тело движится по прямой линии.

В момент времени ноль оно было в нулевой точке, в момент времени 1 секунда оно прошло 2 метра, ещё через секунду тело прошло ещё 2 метра.

В табличном виде закон движения этого тела:

Теперь, глядя в эту таблицу, представим закон движения в графическом виде.

В аналитическом виде, т.е. в виде формулы, закон движения тела в нашем случае выглядит так:

S = 2t

Источник