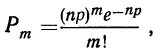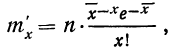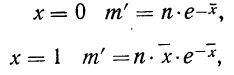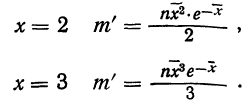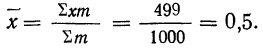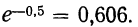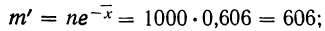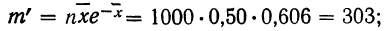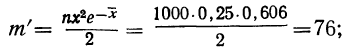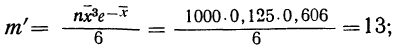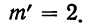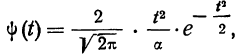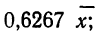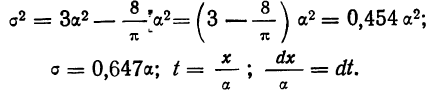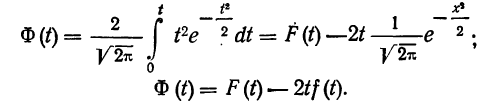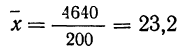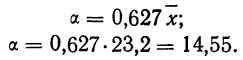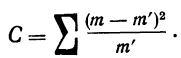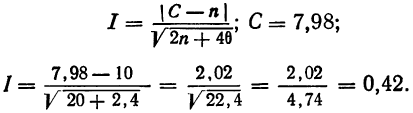Формулы: законы распределения случайных величин
В данном разделе вы найдете формулы по теории вероятностей, описывающие законы распределения дискретных и непрерывных случайных величин: биномиальный, Пуассона, экспоненциальный, равномерный, нормальный.
Каталог формул по теории вероятности онлайн
Законы распределения на этой странице
|
|
Понравилось? Добавьте в закладки
Дискретные случайные величины
Биномиальное распределение ДСВ
Пусть дискретная случайная величина $X$ — количество «успехов» в последовательности из $n$ независимых случайных экспериментов, таких что вероятность «успеха» в каждом из них равна $p$ («неуспеха» — $q=1-p$).
Закон распределения $X$ имеет вид:
| $x_k$ | 0 | 1 | … | k | … | n |
| $p_k$ | $q^n$ | $ncdot p cdot q^{n-1}$ | $C_n^k cdot p^k cdot q^{n-k}$ | $p^n$ |
Здесь вероятности находятся по формуле Бернулли:
$$
P(X=k) = C_n^k cdot p^k cdot (1-p)^{n-k} = C_n^k cdot p^k cdot q^{n-k}, k=0,1,2,…,n.
$$
Числовые характеристики биномиального распределения:
$$M(X)=np, quad D(X)=npq, sigma(X)=sqrt{npq}.$$
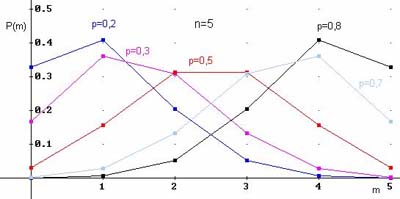
Примеры многоугольников распределения для $n=5$ и различных вероятностей:
Примеры решенных задач на биномиальный закон ДСВ
Пуассоновское распределение ДСВ
Распределение Пуассона моделирует случайную величину, представляющую собой число событий, произошедших за фиксированное время, при условии, что данные события происходят с некоторой фиксированной средней интенсивностью и независимо друг от друга.
При условии $pto 0$, $n to infty$, $np to lambda = const$ закон распределения Пуассона является предельным случаем биномиального закона. Так как при этом вероятность $p$ события $A$ в каждом испытании мала, то закон распределения Пуассона называют часто законом редких явлений.
Ряд распределения по закону Пуассона имеет вид:
| $x_k$ | 0 | 1 | … | k | … |
| $p_k$ | $e^{-lambda}$ | $lambda e^{-lambda}$ | … | $frac{lambda^k}{k!}cdot e^{-lambda}$ | … |
Вероятности вычисляются по формуле Пуассона:
$$
P(X=k)=frac{lambda^k}{k!}cdot e^{-lambda}, k=0,1,2,…
$$
Числовые характеристики для распределения Пуассона:
$$M(X)=lambda, quad D(X)=lambda, sigma(X)=sqrt{lambda}.$$
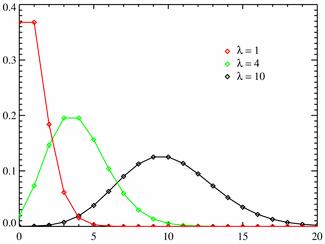
Разные многоугольники распределения при $lambda = 1; 4; 10$.
Примеры решенных задач на закон Пуассона
Геометрическое распределение ДСВ
Пусть происходит серия независимых испытаний, в каждом из которых событие может появится с одной и той же вероятностью $p$. Тогда случайная величина $X$ — количество испытаний до первого появления события, имеет геометрическое распределение вероятностей.
Формула для вероятностей:
$$
P(X=k) = q^k cdot p, k=0,1,2,…,n,…
$$
Ряд распределения геометрического закона:
| $x_k$ | 0 | 1 | 2 | … | k | … |
| $p_k$ | $p$ | $qcdot p$ | $q^2 cdot p$ | … | $q^k cdot p$ | … |
Числовые характеристики:
$$M(X)=frac{q}{p}, quad D(X)=frac{q}{p^2}.$$
Примеры решенных задач на геометрическое распределение
Гипергеометрическое распределение ДСВ
Из урны, в которой находятся $N$ шаров ($K$ белых и $N-K$ чёрных шаров), наудачу и без возвращения вынимают $n$ шаров ($n le N$). Найти закон распределения случайной величины $X$ — равной числу белых шаров среди выбранных.
Случайная величина $X$ может принимать целые значения от $0$ до $K$ (если $n lt K$, то до $n$). Вероятности вычисляются по формуле:
$$
P(X=k)=frac{C_K^k cdot C_{N-K}^{n-k}}{C_N^n}, quad 0le k le K.
$$
Числовые характеристики:
$$M(X)=frac{K}{N}cdot n, quad D(X)=frac{K}{N}cdot n cdot frac{N-n}{N} cdot frac{N-K}{N-1}.$$
Примеры задач на гипергеометрическое распределение
Решаем теорию вероятностей на отлично. Закажите сейчас!
Непрерывные случайные величины
Показательное распределение НСВ
Экспоненциальное или показательное распределение — абсолютно непрерывное распределение, моделирующее время между двумя последовательными свершениями одного и того же события.
Плотность распределения величины $X$(везде $ lambda gt 0)$:
$$
f(x)=
left{
begin{array}{l}
0, x lt 0\
lambda e^{-lambda x}, xge 0 \
end{array}
right.
$$
Функция распределения величины $X$:
$$
F(x)=
left{
begin{array}{l}
0, x lt 0\
1- e^{-lambda x}, xge 0 \
end{array}
right.
$$
Числовые характеристики можно найти по формулам:
$$M(X)=frac{1}{lambda}, quad D(X)=frac{1}{lambda^2}, quad sigma= frac{1}{lambda}.$$
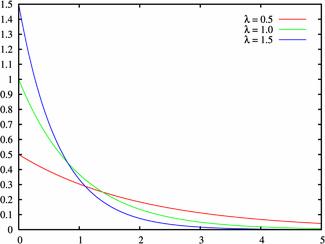
Плотность распределения при различных значениях $lambda gt 0$:
Примеры решенных задач на показательное распределение
Равномерное распределение НСВ
Равномерный закон распределения используется при анализе ошибок округления при проведении числовых расчётов (например, ошибка округления числа до целого распределена равномерно на отрезке), в ряде задач массового обслуживания, при статистическом моделировании наблюдений, подчинённых заданному распределению.
Плотность распределения на отрезке $(a;b)$:
$$
f(x)=
left{
begin{array}{l}
0, x le a\
frac {1}{b-a}, a lt x le b, \
0, x gt b, \
end{array}
right.
$$
Функция распределения:
$$
F(x)=
left{
begin{array}{l}
0, x le a\
frac {x-a}{b-a}, a lt x le b, \
1, x gt b, \
end{array}
right.
$$
Числовые характеристики равномерно распределенной случайной величины:
$$M(X)=frac{a+b}{2}, quad D(X)=frac{(b-a)^2}{12}, quad sigma=frac{b-a}{2sqrt{3}}.$$
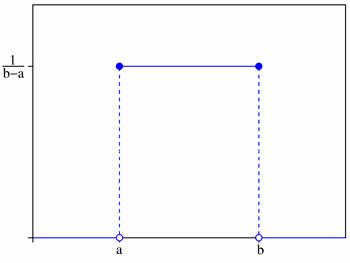
График плотности вероятностей:
Примеры решенных задач на равномерное распределение
Нормальное распределение или распределение Гаусса НСВ
Нормальное распределение, также называемое распределением Гаусса, – распределение вероятностей, которое играет важнейшую роль во многих областях знаний, особенно в физике.
Физическая величина подчиняется нормальному распределению, когда она подвержена влиянию огромного числа случайных помех. Ясно, что такая ситуация крайне распространена, поэтому можно сказать, что из всех распределений в природе чаще всего встречается именно нормальное распределение — отсюда и произошло одно из его названий.
Плотность распределения нормальной случайной величины $X$ имеет вид:
$$f(x)= frac{1}{sigmasqrt{2pi}} expleft({-frac{(x-a)^2}{2sigma^2}}right). $$
При $a=0$ и $sigma=1$ эта функция принимает вид:
$$varphi(x)= frac{1}{sqrt{2pi}} e^{-x^2/2}.$$
Скачать таблицу для функции $varphi(x)$
Числовые характеристики для нормального распределения:
$$M(X)=a, quad D(X)=sigma^2.$$
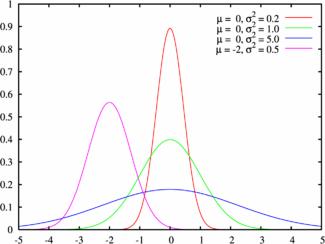
Пример графика плотности распределения для различных значений среднего и СКО:
Нормальный закон распределения случайной величины с параметрами $a=0$ и $sigma=1$ называется стандартным или нормированным, а соответствующая нормальная кривая — стандартной или нормированной.
Функция Лапласа определяется как:
$$Phi(x)= frac{1}{sqrt{2pi}}int_0^x e^{-t^2/2} dt$$
Скачать таблицу для функции Лапласа
Вероятность попадания нормально распределенной случайной величины $X$ в заданный интервал $(alpha, beta)$:
$$
P(alpha lt X lt beta) = Phileft( frac{beta-a}{sigma} right) — Phileft( frac{alpha-a}{sigma} right).
$$
Вероятность отклонения нормально распределенной случайной величины $X$ на величину $delta$ от математического ожидания (по модулю).
$$
P(|X -a|lt delta) = 2 Phileft( frac{delta}{sigma} right).
$$
Примеры решенных задач на нормальное распределение
Полезная страница? Сохрани или расскажи друзьям
Решенные задачи по теории вероятностей
Ищете готовые задачи по теории вероятностей? Посмотрите в решебнике:
Подробно решим теорию вероятностей. Закажите сейчас!
Полезные ссылки
|
|
Содержание:
Законы распределения:
Распределение случайных переменных: Каждая из случайных переменных имеет ряд возможных значений, могущих возникнуть с определенной вероятностью.
Случайные переменные величины могут носить прерывный (дискретный) и непрерывный характер. Возможные значения прерывной случайной переменной отделены друг от друга конечными интервалами. Возможные значения непрерывной случайной переменной не могут быть заранее перечислены и непрерывно заполняют некоторый промежуток.
Примерами прерывных случайных переменных могут служить:
- число попаданий при п выстрелах, если известна вероятность попадания при 1 выстреле. Число попаданий может быть 0, 1, 2….. n;
- число появлений герба при n бросаниях монеты.
Примеры непрерывных случайных переменных:
- ошибка измерения;
- дальность полета снаряда.
Если перечислить все возможные значения случайной переменной и указать вероятности этих значений, то получится распределение случайной переменной. Распределение случайной переменной указывает на соотношение между отдельными значениями случайной величины и их вероятностями.
Распределение случайной переменной будет задано законом распределения, если точно указать, какой вероятностью обладает каждое значение случайной переменной.
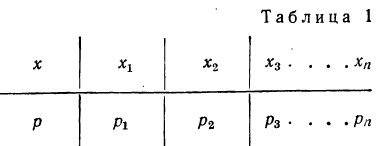
Закон распределения имеет чаще всего табличную -форму изложения. В этом случае перечисляются все возможные значения случайной переменной и соответствующие им вероятности:
Такая таблица называется также рядом распределения случайной переменной.
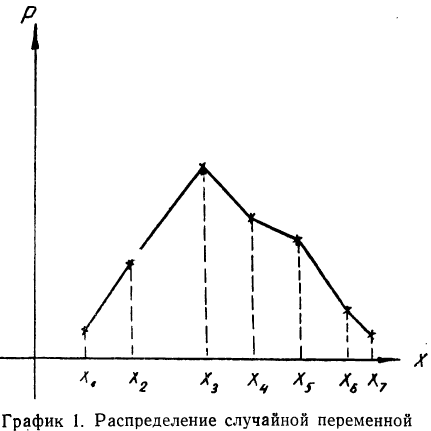
Для наглядности ряд распределения изображают графически, откладывая на прямоугольной системе координат по оси абсцисс возможные значения случайной переменной, а по оси ординат — их вероятности. В результате графического изображения получается многоугольник или полигон распределения (график 1). Многоугольник распределения является одной из форм закона распределения.
Функция распределения
Ряд распределения является исчерпывающей характеристикой прерывной случайной перемен-
Вероятность того, что Х<х, зависит от текущей переменной х и является функцией от х. Эта функция носит название функции распределения случайной переменной X.
F(x) = P(X
Функция распределения является одной из форм выражения закона распределения. Она является универсальной характеристикой случайной переменной и может существовать для прерывных и непрерывных случайных переменных.
Функция распределения F(x) называется также интегральной функцией распределения, или интегральным законом распределения.
Основные свойства функции распределения могут быть сформулированы так:
- F(x) всегда неотрицательная функция, т. е.
- Так как вероятность не может быть больше единицы, то
- Ввиду того что F(x) является неубывающей функцией, то при
- Предельное значение функции распределения при х=
равно нулю, а при х=
равно единице.
Если случайная переменная X дискретна и задана рядом распределения, то для нахождения F(x) для каждого х необходимо найти сумму вероятностей значений X, которые лежат до точки х.
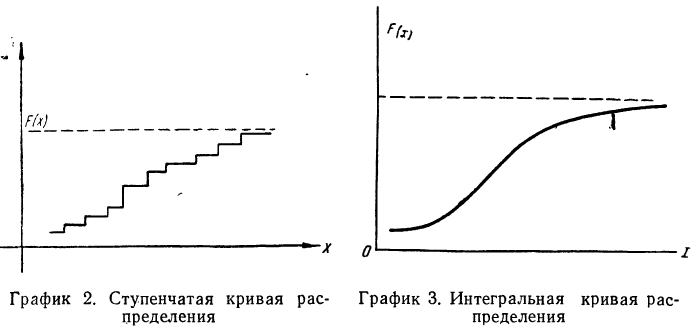
Графическое изображение функции распределения представляет собой некоторую неубывающую кривую, значения которой начинаются с 0 и доходят до 1.
В случае дискретной случайной переменной величины вероятность F(x) увеличивается скачками всякий раз, когда х при своем изменении проходит через одно из возможных значений 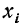
В случае непрерывной случайной переменной величины функция F(x) при графическом изображении дает плавную, монотонно возрастающую кривую следующего вида (см. график 3).
Обычно функция распределения непрерывной случайной переменной представляет собой функцию, непрерывную во всех точках. Эта функция является также дифференцируемой функцией. График функции распределения такой случайной переменной является плавной кривой и имеет касательную в любой ее точке.
Плотность распределения
Если для непрерывной случайной переменной X с функцией распределения F(x) вычислять вероятность попадания ее на участок от х до х+ 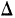
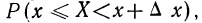
Если величину 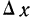
т. е. производной от функции распределения, которая характеризует плотность, с которой распределяются значения случайной переменной в данной точке. Эта функция называется плотностью распределения и часто обозначается f(x). Ее называют также дифференциальной функцией распределения, или дифференциальным законом распределения.
Таким образом, функция плотности распределения f(x) является производной интегральной функции распределения F(x).
Вероятность того, что случайная переменная X примет значение, лежащее в границах от а до 6, равна определенному интегралу в тех же пределах от плотности вероятности, или:
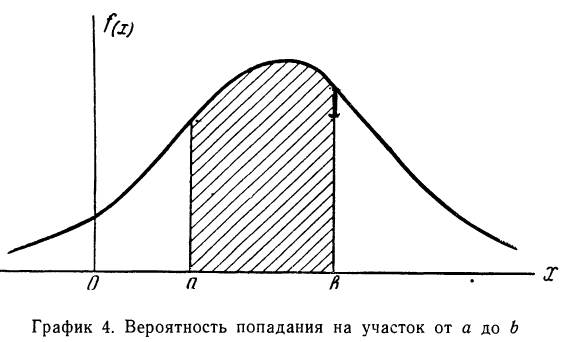
Кривая, изображающая плотность распределения случайной переменной, называется кривой распределения (дифференциальной).
Построим кривую некоторой заданной функции плотности вероятности и найдем участок, ограниченный абсциссами а и b. Площадь, ограниченная соответствующими ординатами кривой распределения самой кривой и осью абсцисс, и отобразит вероятность того, что случайная переменная будет находиться в данных пределах (см. график 4).
Плотность распределения является одной из форм закона распределения, но существует только для непрерывных случайных величин.
Основные свойства плотности распределения могут быть сформулированы так:
1. Плотность распределения есть функция, не могущая принимать отрицательных значений, т. е.
Отсюда в геометрическом изображении плотности распределения (в кривой распределения) не может быть точек, лежащих ниже оси абсцисс.
2.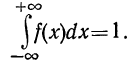
Среди законов распределения большое значение имеют биномиальное распределение, распределение Пуассона и нормальное распределение.
Биномиальное распределение
Если производится n независимых испытаний, в каждом из которых вероятность появления данного события А есть величина постоянная, равная р, и, следовательно, вероятность непоявления события А также постоянна и равна q=1—р, то число появлений события А во всех n испытаниях представляет собой случайную переменную. Вероятность того, что событие А появится в n испытаниях m раз, равна:
т. е. m+1, члену разложения бинома 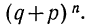
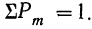
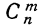
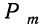
Ввиду того что вероятности 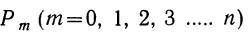
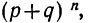
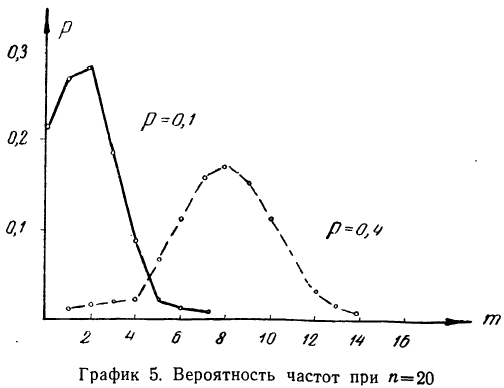
График биномиального распределения, на котором по оси абсцисс откладываются числа наступлений события, а по оси ординат — вероятности этих чисел, представляет собой ломаную линию. Форма графика зависит от значений р, q и n.
Если р и q одинаковы, то график распределения симметричен. Если же р и q неодинаковы, то график распределения будет скошенным.
Одна из частот на графике имеет максимальное значение. Это наиболее вероятная частота. Ее значение можно определить приближенно, аналитически как произведение nр.
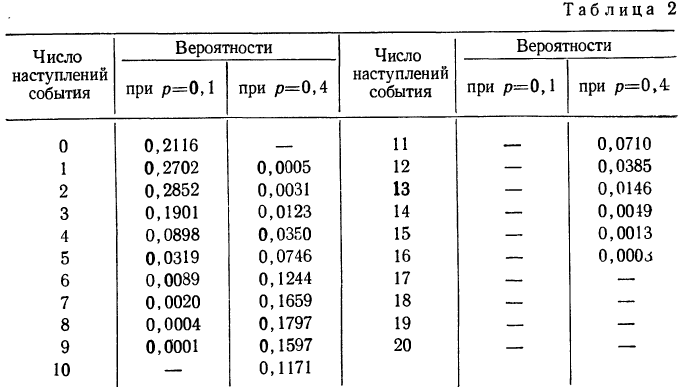
Найдем вероятности числа наступления события А при 20 испытаниях при p = 0,1 и р = 0,4 и построим график их распределений (см. график 5). Найдем вероятности частот при n = 20 для p = 0,1 и р=0,4.
График показывает, что приближение р к 0,5 вносит в распределение большую симметрию. Оказывается также, что при увеличении n распределение становится симметричным и для
Биномиальное распределение имеет широкое распространение в практической деятельности людей. Например, продолжительное наблюдение за качеством выпускаемой заводом продукции показало, что p-я часть ее является браком. Иначе говоря, мы выражаем через р вероятность для любого изделия оказаться бракованным. Биномиальное распределение показывает вероятность того, что в партии, содержащей n изделий, окажется m бракованных, где m = 0, 1, 2, 3 … n.
Предположим, имеется 100 изделий из партии изделий, в ко торой доля брака равна 0,05. Вероятность того, что из этих из делий окажется 10 бракованных, равна:
Закон биномиального распределения называется также схемой Бернулли. .
Нормальное распределение
Расчет вероятностей по формуле биномиального распределения при больших n очень громоздок. При этом значении m прерывны, и нет возможности аналитически отыскать их сумму в некоторых границах. Лаплас нашел закон распределения, являющийся предельным законом при неограниченном возрастании числа испытаний n и называемый законом нормального распределения.
Плотность вероятности нормального распределения выражается при этом формулой:
где t представляет собой нормированное отклонение частоты т от наиболее вероятной частоты nр, т. е. 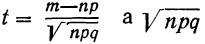
Максимальная ордината кривой соответствует точке m=nр, т. е. математическому ожиданию случайной переменной m; величина этой ординаты равна 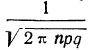
Для практического нахождения вероятностей используют таблицу значений f(t).
Эмпирические и теоретические распределения
В примерах распределений, приведенных в разделе I, мы пользовались данными, почерпнутыми из наблюдений.
Поэтому всякий наблюденный ряд распределения назовем эмпирическим, а график, изображающий распределение
частот этого ряда, — эмпирической кривой распределения. Эмпирические кривые распределения могут быть представлены полигоном и гистограммой. При этом изображение в виде полигона применяется для рядов с прерывными значениями признака, а гистограмма— для рядов с непрерывными значениями признака.
Наблюдая многочисленные ряды распределения, математики стремятся описать эти распределения путем анализа образования величины признака, пытаются построить теоретическое распределение, исходя из данных об эмпирическом распределении.
Мы уже видели на примере распределения случайной переменной, что распределение ее задается законом распределения. Закон распределения, заданный в виде функции распределения, позволяет математически описать ряды распределения некоторых совокупностей.
Теоретическим законом распределения многих совокупностей, наблюдаемых на практике, является нормальное распределение. Иначе говоря, многие эмпирические подчинены закону нормального распределения, функция плотности вероятности которого приведена в предыдущем параграфе.
Чтобы эту формулу применять для нахождения теоретических данных по некоторому эмпирическому ряду, необходимо вероятностные характеристики заменить данными эмпирического ряда. При этой замене величина стандартизованного отклонения t будет представлять собой 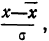
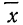
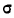
Следовательно, нормальное распределение ряда распределения зависит от величин средней арифметической и его среднего квадратического отклонения.
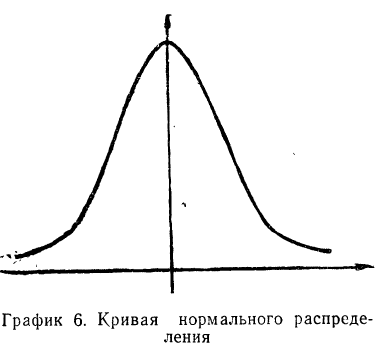
Свойства кривой нормального распределения
Дифференциальный закон нормального распределения, заданный функцией:
имеет ряд свойств. Полагая 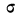
Рассмотрим ее свойства.
- Кривая нормального распределения имеет ветви, удаленные в бесконечность, причем кривая асимптотически приближается к оси Ot.
- Функция является четной: t(—t) = f(t). Следовательно, кривая нормального распределения симметрична относительно оси Оу.
- Функция имеет максимум при t = 0. Величина этого максимума равна
Следовательно, модального значения кривая
достигает при t = 0, а так как 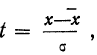
Наибольшую частоту кривая будет иметь при значении х, равном среднему арифметическому из отдельных вариантов. Средняя арифметическая является центром группирования частот ряда.
4. При t=±1 функция имеет точки перегиба. Это означает, что кривая имеет точки перегиба при отклонениях от центра
группирования 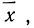
5. Сумма частостей, лежащих в пределах от а до b, равна определенному интегралу в тех же пределах от функции f(t), т. е.
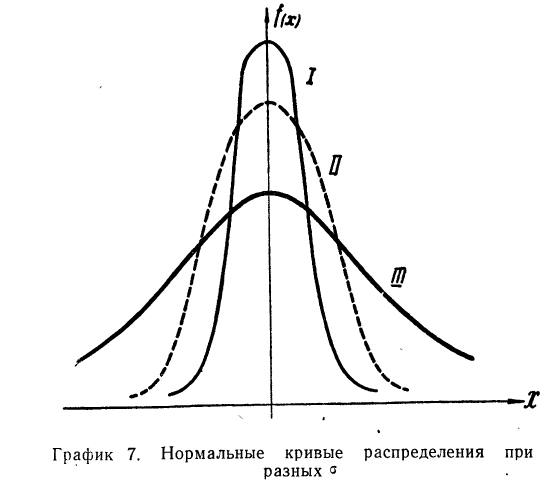
Если учесть действительную величину среднего квадратического отклонения, то окажется, что при больших величинах о значение f(t) мало, при малых, наоборот, велико. Отсюда изменяется и форма кривой распределения. При больших 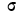
На графике 7 показаны 3 кривые нормального распределения (I, II, III) при 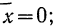
Зная общие свойства кривой нормального распределения, рассмотрим те условия, которые приводят к образованию кривых данного типа.
Формирование нормального распределения
Закон нормального распределения является наиболее распространенным законом не только потому, что он наиболее часто встречается, но и потому, что он является предельным законом распределения, к которому приближается ряд других законов распределения.
Нормальное распределение образуется в том случае, когда действует большое число независимых (или слабо зависимых), случайных причин. Подчиненность закону нормального распределения проявляется тем точнее, чем больше случайных величин действует вместе. Основное условие формирования нормального распределения состоит в том, чтобы все случайные величины, действующие вместе, играли в общей сумме примерно одинаковую роль. Если одна из случайных ошибок окажется по своему влиянию резко превалирующей над другими, то закон распределения будет обусловлен действием этой величины.
Если есть основания рассматривать изучаемую величину как сумму многих независимых слагаемых, то при соблюдении указанного выше условия ее распределение будет нормальным, независимо от характера распределения слагаемых.
Нормальное распределение встречается часто в биологических явлениях, отклонениях размеров изделий от их среднего размера, погрешностях измерения и т. д.
Если взять распределение людей по номеру носимой ими обуви, то это распределение будет нормальным. Но это правило применимо только в том случае, когда численность совокупности велика и сама совокупность однородна.
Из того факта, что нормальное распределение встречается нередко в разных областях, не следует, что всякий признак распределяется нормально. Наряду с нормальным распределением существуют другие различные распределения.
Но все же умение выявить нормальное распределение в некоторой эмпирической совокупности является важным условием для ряда практических расчетов и действий. Зная, что эмпирическое распределение является нормальным, можно определить оптимальные размеры предприятий, размеры резервов и т. д.
Важным условием определения характера данной эмпирической кривой является построение на основе эмпирических данных теоретического нормального распределения.
Построение кривой нормального распределения
Первый способ. Для того чтобы построить кривую нормального распределения, пользуются следующей егo формулой:
где N — число проведенных испытаний, равное сумме частот эмпирического распределения
k — величина интервала дробления эмпирического ряда распределения;
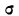
t—нормированное отклонение, т. е.
Величина 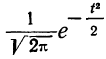
Для нахождения значений теоретических частот (см. пример 1) сначала необходимо найти среднюю арифметическую эмпирического ряда распределения, т. е. 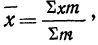
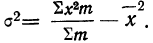
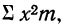
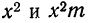
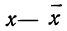
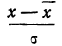
Найденная при умножении величина и составляет теоретическую частоту каждого варианта, записанного в строке (графа 9). Ввиду того что частоты могут быть только целыми числами, округляем их до целых и получим теоретические частоты, которые будем обозначать 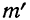
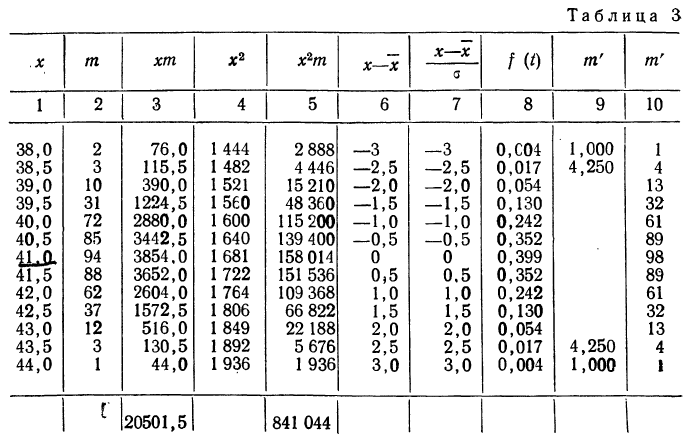
Пример 1.
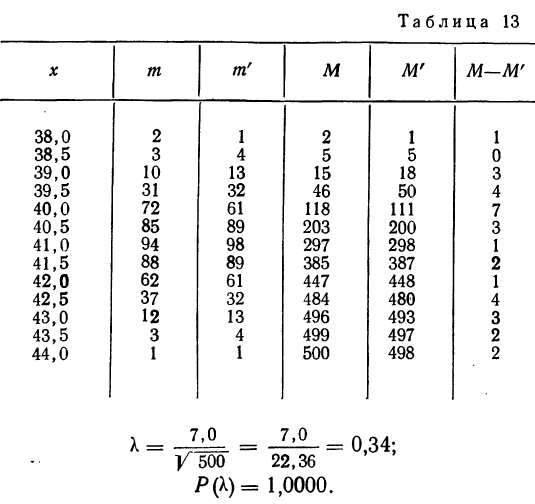
В таблице 3 приведено эмпирическое распределение веса 500 спиралей и расчет частот нормального распределения. (Вес спиралей х дан в миллиграммах.)
Из таблицы находим:
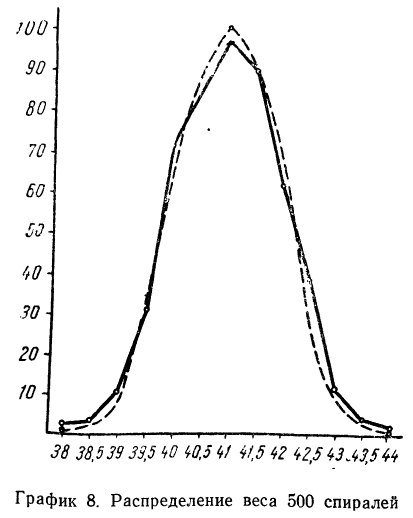
Строим график эмпирических и теоретических данных. На графике 8 сплошной линией дано изображение эмпирического распределения, а пунктирной — построенного на его основе теоретического распределения.
Пример 2.
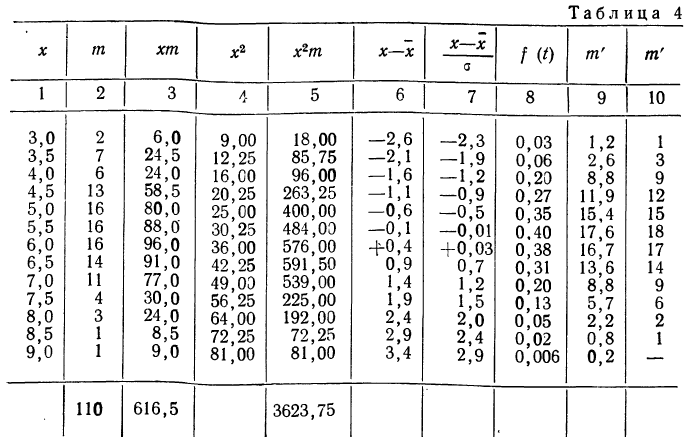
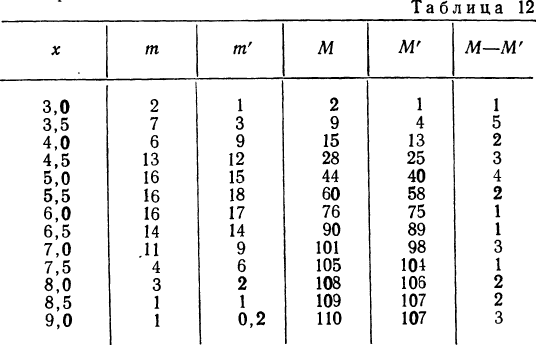
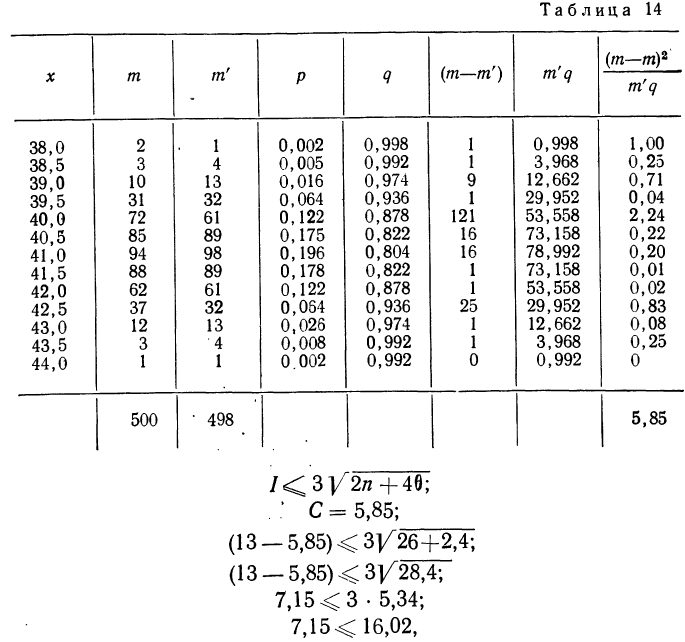
В таблице 4 дается эмпирическое распределение ПО замеров межцентрового расстояния при шевинговании зубцов динамомашины 110412 и расчет теоретических частот.
Исчислим:
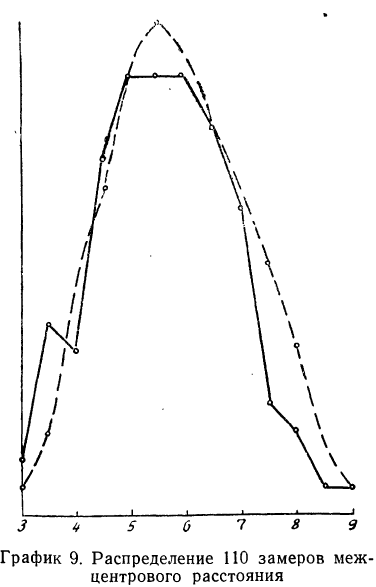
Построим графики эмпирического и теоретического распределений (см. график 9).
Оба эмпирических распределения хорошо воспроизводятся теоретическим нормальным распределением.
Второй способ построения кривой нормального распределения основан на применении функции стандартизованного нормального распределения, в котором 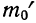
За начало отсчета признака при этом способе построения берется его средняя арифметическая. Ей соответствует наибольшая ордината.
Вычисление ординат производится по формуле:
где N — число наблюдений;
k — величина интервала эмпирического распределения.
Так как значение наибольшей ординаты получается при
t = 0, когда 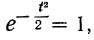
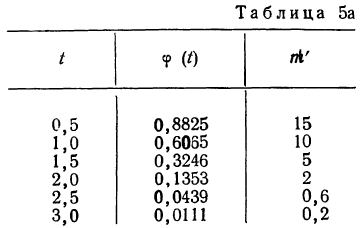
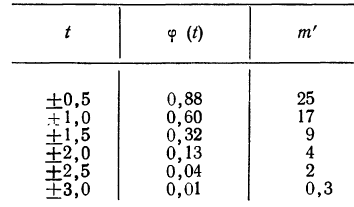
Придавая t последовательно значения 0,5; 1,0; 1,5; 2,0, т. е. сначала меньшие, а потом увеличивающиеся, находим в таблице стандартизованного нормального распределения для данных t соответствующие 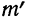
Например, при t = 0,5 величина стандартизованного нормального распределения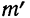
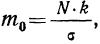
Пример 3.
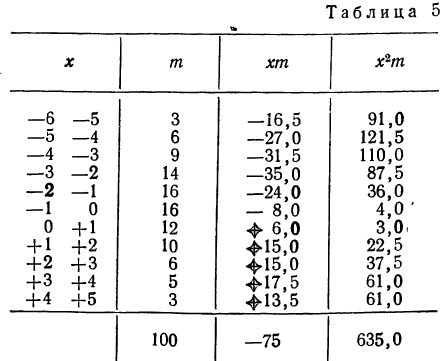
Взяты результаты измерения 100 отклонений шага резьбы х от всей длины резьбы. Получен следующий ряд распределения, для которого по общим правилам производится расчет средней и дисперсии.
Отсюда;
Рассчитаем наибольшую ординату:
так как величина 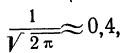
Взяв значение t = 0,5 по таблице стандартизованного нормального распределения, находим 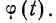
Для данного примера будем иметь:
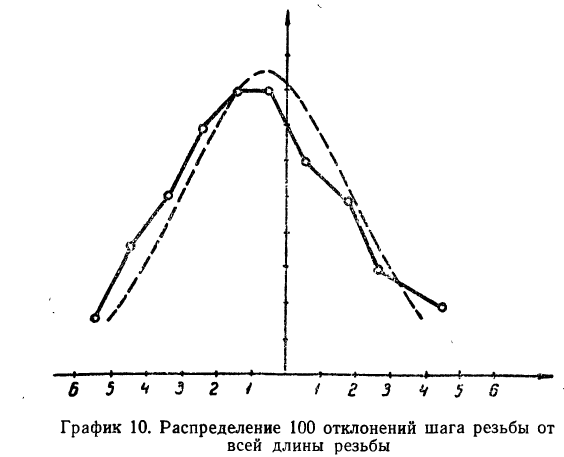
Полученный результат наносим на график, а для сравнения наносим на график и результаты непосредственных измерений отклонений (см. график 10).
Как видно из графика, теоретическая кривая довольно близко воспроизводит полигон эмпирического распределения.
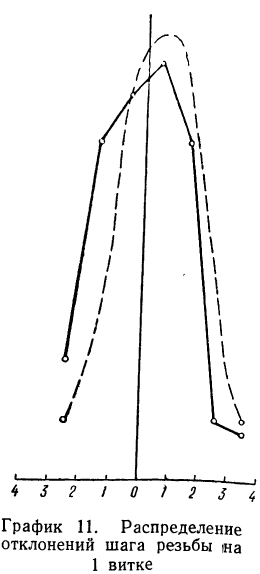
Пример 4.
Даны результаты измерений отклонений шага резьбы (х) в микронах на 1 витке от среднего значения. Приводятся эти данные с соответствующими расчетами:
Теоретические частоты (ординаты) рассчитываются так же, как и в предыдущем примере. Сначала находится величина наибольшей частоты:
затем другие частоты:
Эмпирические и теоретические частоты наносим на график (см. график 11) и убеждаемся, что эмпирическое распределение довольно близко воспроизводится теоретическим распределением.
Третий способ построения кривой нормального распределения (или вычисления теоретических частот) по имеющимся эмпирическим данным основан на применении функции:
которая дает площадь нормальной кривой, заключенной между —t и +t.
Вообще говоря, можно находить площадь нормальной кривой, заключенную между любыми точками 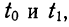
применяя функцию F(t). Искомая площадь будет представлять собой 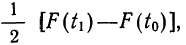
Пример 5.
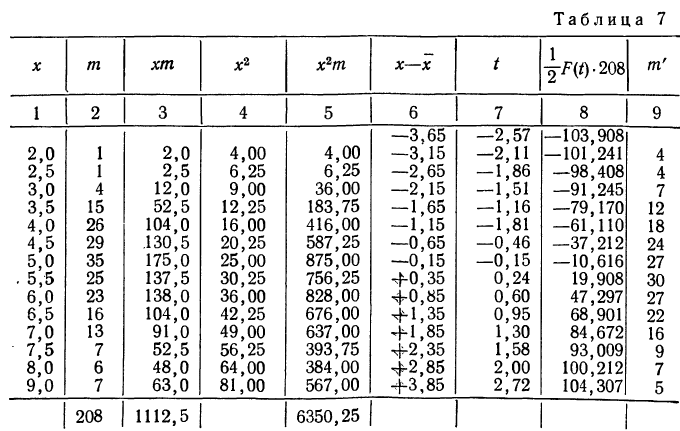
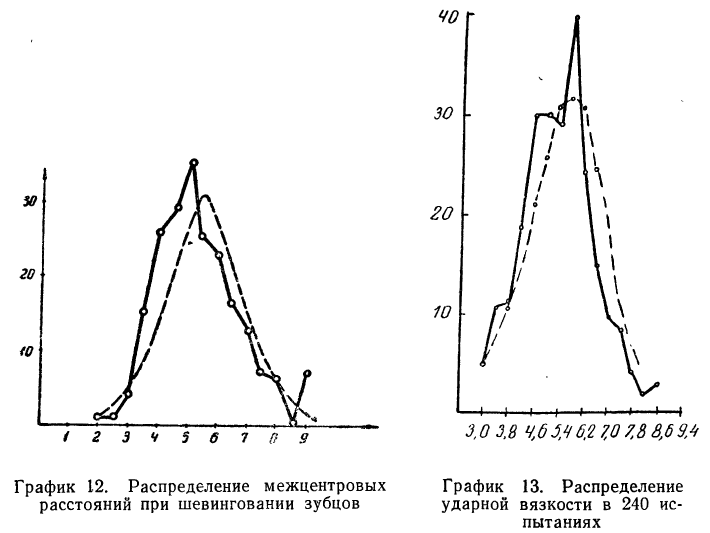
Получены результаты 208 измерений межцентровых расстояний при шевинговании зубцов шестерни динамо-машины (см. табл. 7). Вычислим нужные параметры и теоретические частоты и построим графики эмпирического и теоретического распределений.
Колонки 1, 2, 3, 4 и 5 необходимы для расчетов 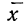
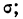
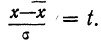
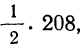
Чтобы получить теоретическую частоту для каждого интервала, достаточно из верхней строки (в 8-й колонке) вычесть число той же колонки, стоящее строкой ниже.
На графике 12 показано, что теоретическое распределение достаточно точно отражает эмпирически полученный материал, только наблюдается некоторое смещение теоретической кривой вправо, что, очевидно, вызвано большим удельным весом правого конца эмпирического распределения.
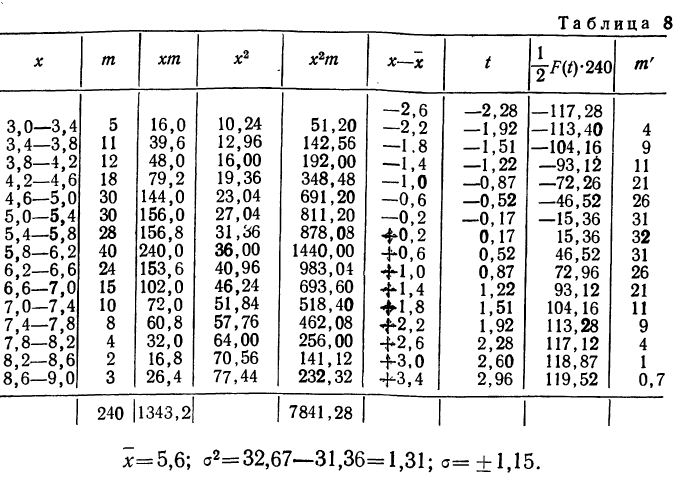
Пример 6.
Дается ряд распределения ударной вязкости в 240 испытаниях. Приведем этот ряд распределения и построим для него теоретическое распределение (см. график 13).
Критерии согласия
Определение близости эмпирических распределений к теоретическому нормальному распределению по графику может быть недостаточно точным, субъективным и по-разному оценивать расхождения между ними. Поэтому математики выработали ряд объективных оценок для того, чтобы определить, является ли данное эмпирическое распределение нормальным. Такие оценки называются критериями согласия. Критерии согласия были предложены разными учеными, занимавшимися этим вопросом. Рассмотрим критерии согласия Пирсона, Романовского, Колмогорова и Ястремского.
Критерий согласия Пирсона основан на определении величины 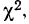
где m — эмпирические частоты;
m’ — теоретические частоты.
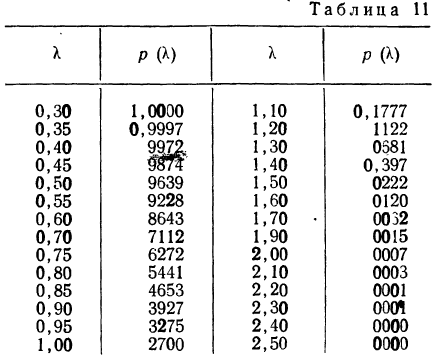
Для оценки того, насколько данное эмпирическое распределение воспроизводится нормальным распределением, исчисляют по распределению Пирсона вероятности достижения 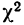
Значения 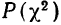
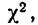
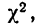
Пересечение данного столбца с соответствующей строкой дает искомую вероятность
При вероятностях, значительно отличающихся от нуля, расхождение между теоретическими и эмпирическими частотами можно считать случайным.
Проф. В. И. Романовский предложил более простой метод оценки близости эмпирического распределения к нормальному, используя величину
Он предложил вычислять отношение:
где k — число степеней свободы.
Если указанное отношение имеет абсолютное значение, меньшее трех, то предлагается расхождение между теоретическим и эмпирическим распределениями считать несущественным; если же это отношение больше трех, то расхождение существенно. Несущественность расхождения (когда величина отношения Романовского меньше трех) говорит о возможности принять за закон данного эмпирического распределения нормальное распределение.
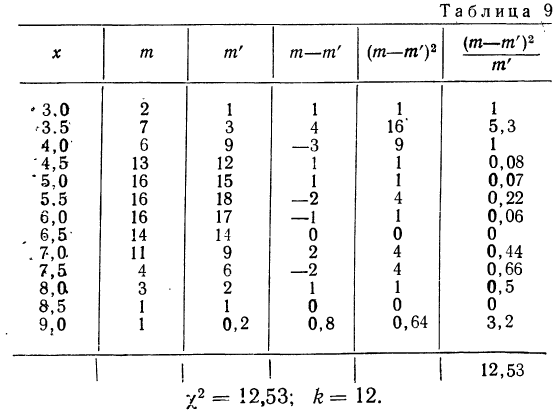
По данным примера 2 рассчитаем величину
Пример 7.
Вычисление 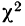
Из таблицы 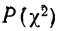
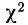
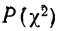
Находим отношение Романовского:
Это отношение значительно меньше трех, поэтому расхождение между теоретическими и эмпирическими частотами можно считать несущественными, и, таким образом, теоретическое распределение достаточно хорошо воспроизводит эмпирическое.
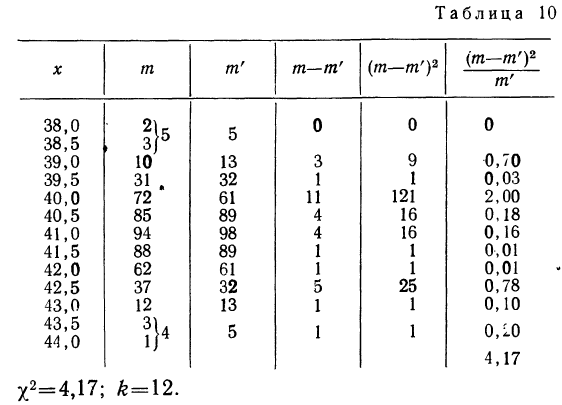
Пример 8.
Вычислим критерий 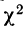
По таблице находим вероятность 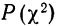
Отношение Романовского
также значительно меньше трех, поэтому теоретическое воспро* изведение эмпирического ряда достаточно удовлетворительное.
Критерий 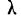
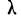
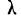
где D — максимальная граница разности: 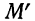
Приведем таблицу значений 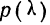
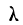
Если найденному значению 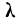
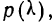
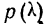
Рассмотрим применение этого критерия на двух примерах.
Пример 9.
В таблице вероятностей 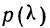
Эта большая вероятность указывает на то, что расхождение между наблюдением и теоретическим распределением вполне могло быть случайным.
Пример 10.
Величина вероятности 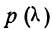
Критерий Б. С. Ястремского. В общем виде критерий Ястремского можно записать следующим неравенством:
где
Для числа групп, меньших 20, 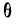
Значение I, меньшее 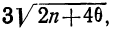
При значениях I, больших 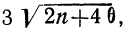
Пример 11.
Определим величину I и оценим эмпирическое распределение 500 спиралей (m) по сравнению с соответствующим нормальным (m’).
что говорит о нормальном распределении исследуемой совокупности.
Элементарные приемы определения «нормальности» распределения. Для определения элементарными способами близости данного опытного распределения к нормальному прибегают к числам Вестергарда и к сравнению средней арифметической, моды и медианы.
Числами Вестергарда являются: 0,3; 0,7; 1,1; 3. Для пользования ими определяют сначала основные характеристики — среднюю арифметическую 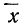
Для того чтобы данное эмпирическое распределение было подчинено закону нормального распределения, необходимо, чтобы распределение удовлетворяло следующим условиям:
- в промежутке от
была расположена
часть всей совокупности;
- в промежутке от
была расположена
часть всей совокупности;
- в промежутке от
было расположено
всей совокупности;
- в промежутках от —3 до +3 было расположено 0,998 всей совокупности.
Для приводимого распределения 500 спиралей по весу (пример 1) все эти условия соблюдаются, что говорит о подчинении данного распределения закону нормального распределения.
К элементарным приемам определения «нормальности» следует отнести применение графического метода, особенно удобное с помощью полулогарифмической сетки Турбина. На сетке накопленные эмпирические частоты при нормальном их распределении дают прямую линию. Всякое отклонение от прямой свидетельствует об отклонении эмпирического распределения от «нормального».
Распределение Пуассона
Вероятности частот событий, редко встречающихся при некотором числе испытаний, находят по формуле:
где m — частота данного события;
n — число испытаний;
р — вероятность события при одном испытании;
е= 2,71828.
Это выражение носит название закона распределения Пуассона.
Подставим вместо nр среднее число фактически наблюдавшихся случаев в эмпирическом материале. Теоретические ординаты кривой распределения по закону Пуассона m’ найдем по формуле:
где х — переменное значение числа раз;
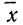
n — число наблюдений.
При
Пример 12.
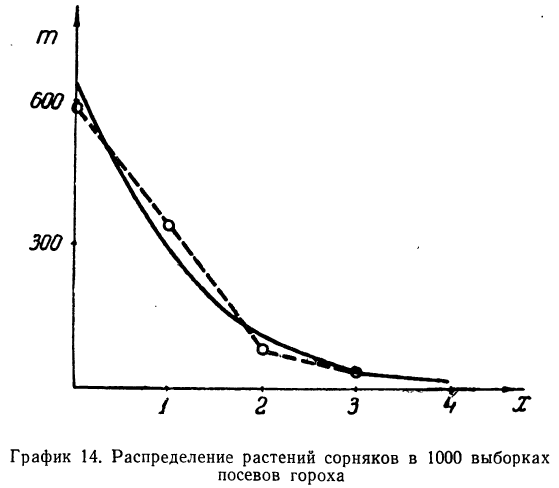
Наблюдалось следующее распределение растений сорняков в 1000 выборках посевов гороха. Результаты эксперимента записаны в следующей таблице:
Определим по закону Пуассона теоретические частоты разного числа растений сорняков. Для этого предварительно исчислим среднее число растений сорняков в одной выборке:
Из таблицы находим
Определим теоретическое число выборок, в которых число растений сорняков будет равно 0:
то же:
для числа растений сорняков, равного 1:
для числа растений сорняков, равного 2:
для числа растений сорняков, равного 3:
для числа растений сорняков более 3:
Графическое сопоставление обоих распределений говорит о соответствии между эмпирическим и теоретическим распределениями.
Распределение Максвелла
В технике часто встречается распределение по закону Максвелла. Это — распределение существенно положительных величин. Например, эмпирическое распределение эксцентриситетов биений теоретически воспроизводится распределением Максвелла.
Дифференциальный закон распределения Максвелла выражается следующей формулой:
где 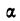
Интегральный закон распределения выразится тогда:
Пример 13.
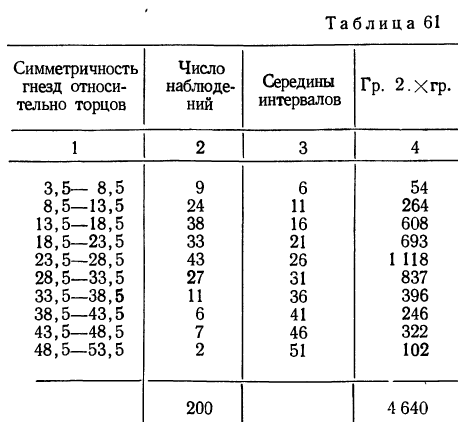
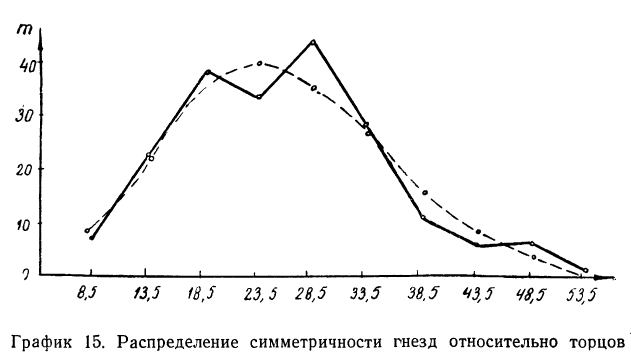
Заимствуем из книги А. М. Длина таблицу распределения симметричности гнезд относительно торцов в круглых плашках (в 0,01 мм) и проведем дополнительные расчеты.
Из этой таблицы легко определим среднюю симметричность:
и параметр рассеяния:
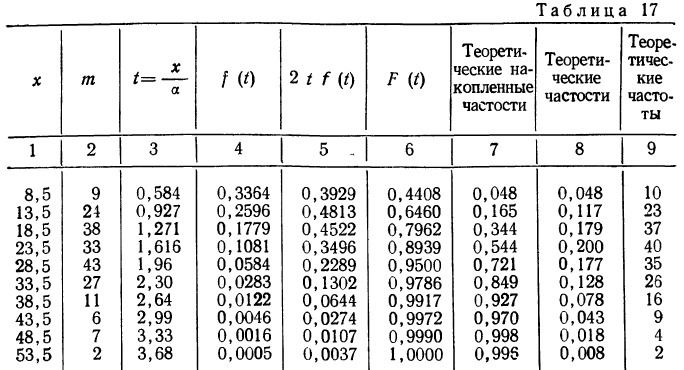
Формула интегрального распределения по закону Максвелла позволяет найти накопленные, а затем теоретические частости и частоты.
Изобразим на графике 15 данные эмпирического и теоретического рядов распределения.
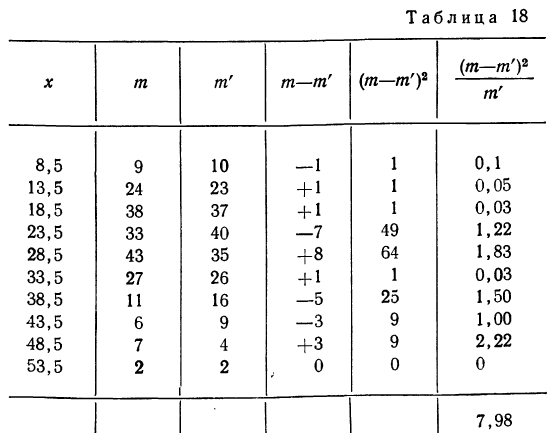
Определим близость их по критерию согласия Ястремского. Для этого приведем в табл. 18 расчет величины С:
По критерию Ястремского находим
Величина I значительно меньше 3. Следовательно, данное эм лирическое распределение хорошо согласуется с законом распределения Максвелла.
- Дисперсионный анализ
- Математическая обработка динамических рядов
- Корреляция — определение и вычисление
- Элементы теории ошибок
- Статистические оценки
- Теория статистической проверки гипотез
- Линейный регрессионный анализ
- Вариационный ряд
Случайной
называется величина, которая в результате
испытаний может принять то или иное
значение, причем заранее неизвестно,
какое именно.
Случайные
величины могут быть дискретными и
непрерывными. Непрерывными
случайными величинами являются: время
безотказной работы элементов, устройств,
агрегатов, систем; время вынужденного
простоя оборудования из-за отказов;
уровень того или иного технического
параметра и т.д. Дискретными
случайными величинами являются: число
неисправных элементов, устройств,
агрегатов из общего числа находящихся
в эксплуатации; число дефектных изделий
в какой-либо партии продукции; количество
повреждений элементов какого-либо
оборудования в единицу времени и т.д.
Из-за
невозможности указать, какое конкретное
значение примет случайная величина в
данном эксперименте, для ее характеристики
применяются вероятности того, что она
будет равна заданному значению или
окажется в указанных пределах возможного
значения. При этом используются понятия
числовых
характеристик
распределений случайных величин.
Основные
числовые
характеристики
случайных величин – математическое
ожидание
(среднее
значение),
дисперсия,
среднее
квадратическое отклонение,
мода,
медиана,
коэффициент
вариации.
Если
задан ряд распределений вероятностей
для значений
случайной величиныX,
то математическое ожидание определяется
по формуле
.
Показателями,
характеризующими степень рассеяния
случайной величины около своего
математического ожидания, являются
дисперсия и среднее квадратическое
отклонение:
,
,
Для
более полного описания случайных величин
вводятся понятия функции распределения
F(x)
и плотности распределения f(x).
Функция
распределения
определяет для каждого значения х
вероятность того, что случайная величина
X
примет значение, меньшее х:
.
Плотность
распределения
непрерывной случайной величины – первая
производная от функции распределения:
,
.
Тогда
математическое ожидание и дисперсия
непрерывной случайной величины
определятся как
,
,
.
Пример.
Энергосистема ограничивает промышленное
предприятие в потреблении электрической
мощности. При этом в течение года возможны
дефициты в 5, 10 и 15 МВт с вероятностями
соответственно 0,001, 0,0004 и 0,0002. Определить
математическое ожидание недоотпуска
электроэнергии промышленному предприятию
за год.
Решение.
.
В
году 8760 часов.
Биномиальное
распределение
Если производится серия N
независимых опытов, причём вероятность
появления изучаемого события в каждом
опыте постоянна и равна р,
а вероятность его непоявления равна
,
то вероятностьпоявления данного события точноi
раз равна
где
Пример.
На электростанции работает четыре
однотипных генератора. Вероятность
аварийного повреждения каждого из них
.
Составить закон распределения вероятного
числа повреждённых генераторов.
Решение.
Число повреждённых генераторов является
дискретной случайной величиной. Пользуясь
формулой биномиального распределения,
находим:
|
Число |
0 |
1 |
2 |
3 |
4 |
|
Вероятность |
0,922 |
0,075 |
0,023 |
0,00003 |
0,0000001 |
Распределение
Пуассона.
Этот закон позволяет определить
вероятность
наступления ровноk
событий за промежуток времени t:
,
,
,
где
– параметр закона распределения –
математическое ожидание числа событий
за времяt;
– интенсивность случайного события.
Закон
распределения Пуассона может быть
получен из биномиального распределения
при достаточно больших N
и малых р
тогда
.
Пример
1.
Выпущена партия резисторов 100000 штук.
Вероятность того, что резистор имеет
брак,
.
Найти вероятность того, что в партии
ровно пять бракованных резисторов.
Решение.
.
Пример
2.
Определить вероятность того, что за 500
ч работы произойдет два отказа в сложном
изделии, если известно, что интенсивность
отказов
Решение.
Экспоненциальное
распределение.
Интегральная функция экспоненциального
распределения выражает вероятность
отказа изделия или элемента за данный
интервал времени:
.
Функция
надежности R(t)
используется в качестве модели вероятности
безотказной работы за то же время:
,
где
– интенсивность отказов, которая для
экспоненциального распределения
постоянна.
Плотность
вероятности отказов
Среднее
время до возникновения отказа или
среднее время безотказной работы
является математическим ожиданием
экспоненциального распределения, т.е.
величиной, обратной интенсивности
отказов
.
Заменяя
в функции надёжности R(t)
величину
,
обратной ейполучим
,
Таким
образом, зная среднее время безотказной
работы
или постоянную интенсивность отказов
,
можно в случае экспоненциального
распределения найти вероятность
безотказной работы для интервала времени
от момента включения элемента, устройства
или агрегата до любого заданного моментаt.
Вероятность
безотказной работы на интервале,
превышающем среднее время
,
равна
.
Дисперсия
времени безотказной работы
.
Среднее
квадратическое отклонение
Равенство
среднеквадратического отклонения
среднему времени работы – характерный
признак экспоненциального распределения.
Пример.
Время безотказной работы силового
трансформатора при перегрузке распределено
по экспоненциальному закону
,
гдеt
– время, ч. Найти вероятность того, что
трансформатор в перегрузочном режиме
проработает безотказно в течение 100 ч.
Решение.
.
Среднее
время безотказной работы
Вероятность
безотказной работы при
равна
.
Зависимость
интенсивности отказов от времени
представлена на рис. 1.7.
Рис
1.7. Кривая жизни изделия
Гамма-распределение.
Гамма-распределение в теории надёжности
применяется для описания характера
изменения параметров надёжности в
первый период эксплуатации и в период
износа. Если отказ устройства или системы
возникает тогда, когда происходит не
менее k
отказов его элементов, а отказы элементов,
подчинены экспоненциальному закону с
параметром
плотность вероятности отказа определяется
как
,
где
– исходная интенсивность отказов
элементов устройства, отказ которого
вызывается отказомk
элементов;
Этому
распределению подчиняется время работы
резервированных устройств, отказ которых
вызывается отказом k
их элементов.
При
k=1
гамма-распределение совпадает с
экспоненциальным распределением. При
увеличении k
гамма-распределение приближается к
симметричному распределению, что и
показывает рис. 1.7.
Распределение
Вейбулла.
В теории надежности распределение
Вейбулла применяется в следующей форме:
где
– приведённое значение среднего времени
безотказной работы;– параметр формы распределения.
Вероятность
отсутствия отказов за время t
Интенсивность
отказов
α=2
,
Рис.
1.8. Изменение формы гамма-распределения
в зависимости от k
Рис.
1.9. Изменение формы распределения
Вейбулла в зависимости от а
При
интенсивность отказов – убывающая
функция; при– возрастающая, что соответствует
периодам начальных отказов и старения
(рис. 1.7).
Нормальное
(гауссовское) распределение.
Плотность вероятности нормального
распределения характеризует время
возникновения отказа:

где
T
– математическое ожидание времени
между отказами;
– среднее квадратическое отклонение.
Функция
распределения соответствует вероятности
отказа за время t:
Главная
особенность этого закона состоит в
том, что он является предельным;
к нему при определенных условиях
приближаются другие законы распределения;
в теории надёжности применяется для
оценки постепенных отказов.
Распределение
.
Оно играет большую роль при решении
задач, связанных с оценкой параметров
надежности, определяемых при испытаниях
или эксплуатации оборудования.
Рассмотрим
k
независимых случайных величин
каждая из которых распределена по
нормальному закону с параметрами
,
,
т.е.
.
Сумма
квадратов этих величин обозначается
,
.
Параметр
k
называется числом
степеней свободы.
Плотность
распределения
имеет вид

.
Соседние файлы в папке УПЭЭС
- #
- #
- #
- #
- #
- #
Основные законы распределения непрерывных случайных величин
Определение характеристической функции и её использование в теории вероятностей. Нормальный закон распределения и его значение в теории вероятностей. Логарифмически нормальный закон. Гамма-распределение. Экспоненциальный закон и его использование в теории надёжности, теории очередей. Равномерный закон. Распределения хи-квадрат, Вейбула, Стьюдента, Фишера.
Характеристическая функция
Во многих задачах полезной характеристикой случайной величины является её характеристическая функция. Характеристической функцией случайной величины называется математическое ожидание комплексной случайной величины
, рассматриваемое как функции параметра
(здесь и далее в этой части
– мнимая единица). Таким образом, характеристическая функция непрерывной случайной величины
задаётся формулой
, где
– плотность вероятности.
Отметим следующие свойства характеристической функции:
1) при любом действительном значении характеристическая функция по модулю не превосходит единицы, то есть
2) характеристическая функция равна единицы при , то есть
.
Плотность вероятности случайной величины можно выразить через её характеристическую функцию:
Таким образом, характеристическая функция случайной величины является её полной вероятностной характеристикой. Зная характеристическую функцию случайной величины, можно найти её плотность вероятности, а следовательно, и функцию распределения, то есть полностью определить закон распределения случайной величины. Через характеристическую функцию можно выразить также числовые характеристики случайной величины, в частности её математическое ожидание и дисперсию:
Нормальный закон распределения (закон Гаусса)
Плотность вероятности нормально распределённой случайной величины выражается формулой
(8.1)
Кривая распределения изображена на рис. 16. Она симметрична относительно точки (точка максимума). При уменьшении
ордината точки максимума неограниченно возрастает, при этом кривая пропорционально сплющивается вдоль оси абсцисс, так что площадь под её графиком остаётся равной единицы (рис. 17).
Нормальный закон распределения широко применяется в задачах практики. Объяснить причины этого впервые удалось Ляпунову. Он показал, что если случайная величина может рассматриваться как сумма большого числа малых слагаемых, то при достаточно общих условиях закон распределения этой случайной величины близок к нормальному независимо от того, каковы законы распределения отдельных слагаемых. А так как практически случайные величины в большинстве случаев бывают результатом действия множества причин, то нормальный закон оказывается наиболее распространённым законом распределения (подробнее об этом [url]см. часть 9[/url]). Укажем числовые характеристики нормально распределённой случайной величины (математическое ожидание и дисперсия):
Таким образом, параметры и
в выражении (8.1) нормального закона распределения представляют собой математическое ожидание и среднее квадратическое отклонение случайной величины. Принимая это во внимание, формулу (8.1) можно представить следующим образом:
Эта формула показывает, что нормальный закон распределения полностью определяется математическим ожидание и дисперсией случайной величины. Таким образом, математическое ожидание и дисперсия полностью характеризуют нормально распределённую случайную величину. Разумеется, что в общем случае, когда характер закона распределения неизвестен, знание математического ожидания и дисперсии недостаточно для определения этого закона распределения.
Характеристическая функция нормального распределения случайной величины задаётся формулой
Пример 1. Найти вероятность того, что нормально распределённая случайная величина удовлетворяет неравенству
.
Решение. Используя свойство 3 плотности вероятности (см. раздел 4, часть 4), получаем
Положим , тогда
где — функция Лапласа.
Выполним некоторые числовые расчёты. Если положить в условии примера 1, то
Последний результат означает, что с вероятностью, близкой к единице (0,9973), случайная величина, подчиняющаяся нормальному закону распределения, не выходит за пределы интервала . Это утверждение называют правилом трёх сигм.
Наконец, если , то случайная величина, распределённая по нормальному закону с такими параметрами, называется стандартизированной нормальной величиной. На рис. 18 изображён график плотности вероятности этой величины
Примеры с использованием нормального закона распределения приведены также в части 9.
Логарифмически нормальное распределение
Говорят, что случайная величина имеет логарифмически нормальное распределение (сокращённо логнормальное распределение), если её логарифм
распределён нормально, то есть если
, где величина
имеет нормальное распределение с параметрами
.
Плотность логнормального распределения задаётся формулой
Математическое ожидание и дисперсию логнормального распределения определяют по формулам
Кривая этого распределения изображена на рис. 19.
Логарифмически нормальное распределение встречается в ряде технических задач. Оно даёт распределение размеров частиц при дроблении, содержаний элементов в минералах в извержённых горных пародах, численности рыб в море и т.д. Встречается такое распределение во всех задачах, где логарифм рассматриваемой величины можно представить в виде суммы большого количества независимых равномерно малых величин:
то есть
, где
независимы.
Гамма-распределение
Говорят, что случайная величина имеет гамма-распределение с параметрами
и
, если её плотность распределения вероятностей имеет вид
где
— гамма-функция Эйлера.
На рис. 20 показаны кривые распределения вероятностей при значениях параметра и
(при
получаем экспоненциальное распределение).
Математическое ожидание и дисперсия, подчинённые гамма-распределению, задаются формулами
Отметим, что при гамма-распределение имеет моду
(графически это означает, что кривая распределения имеет точку максимума , рис. 20).
Экспоненциальный закон распределения
Экспоненциальным распределением называется частный случай гамма-распределения с параметрами , то есть то есть плотность вероятности в этом случае
Используя свойства два плотности распределения ([url]см.[/url]), можно найти функцию распределения экспоненциального закона:
Основные характеристики (математическое ожидание и дисперсия) случайной величины , распределённой по экспоненциальному, имеют вид
Характеристическая функция экспоненциального распределения задаётся формулой
Кривая экспоненциального распределения вероятностей показана на рис. 21,а, а график функции распределения — на рис. 21,б.
Статистический смысл параметра состоит в следующем:
есть среднее число событий на единицу времени, то есть
есть средний промежуток времени между двумя последовательными событиями.
Экспоненциальное (показательное) распределение часто встречается в теории массового обслуживания (например, — время ожидания при техническом обслуживании или
— продолжительность телефонных разговоров, ежедневно регистрируемых на телефонной станции) и теории надёжности (например,
— срок службы радиоэлектронной аппаратуры).
Пример 2. Случайная величина — время работы радиолампы — имеет показательное распределение. Определить вероятность того, что время работы лампы будет не меньше 600 ч, если среднее время работы радиолампы 400 ч.
Решение. По условию задачи математическое ожидание случайной величины равно 400 ч, следовательно,
. Искомая вероятность есть
Распределение Вейбула
Случайная величина подчиняется закону распределения Вейбула с параметрами
, если её плотность распределения вероятностей записывается в виде
Математическое ожидание и мода случайной величины, распределённые по закону Вейбула, имеют следующий вид:
Кривая распределения Вейбула изображена на рис. 22.
Распределение Вейбула в ряде случаев характеризует срок службы радиоэлектронной аппаратуры и, кроме того, применяется для аппроксимации различных несимметричных распределений в математической статистике.
Равномерный закон распределения
Случайная величина называется распределённой равномерно на отрезке
, если её плотность распределения вероятностей постоянна на данном отрезке:
Все возможные значения равномерно распределённой случайной величины лежат в пределах некоторого интервала; кроме того. в пределах этого интервала все значения случайной величины одинаково вероятны (обладаю одной и той же плотностью вероятности). Равномерно распределение реализуется в экспериментах, где наудачу ставиться точка на отрезке (
— абсцисса поставленной точки). Равномерно распределённая случайная величина встречается также в измерительной практике при округлении отчётов измерительных приборов до целых делений шкал. Ошибка при округлении отчёте до ближайшего целого деления является случайной величиной
, которая может принимать с постоянной плотностью вероятности любое значение между двумя соседними целыми делениями.
Математическое ожидание и дисперсия равномерно распределённой случайной величины
Характеристическая функция равномерного распределения задаётся формулой
График плотности равномерного распределения изображён на рис. 23.
Пример 3. Найти вероятность попадания случайной величины, имеющей равномерное распределение на отрезке , на участок
, представляющий собой часть отрезка
.
Решение. Используя свойство 3 плотности вероятности, получаем
Графически вероятность представляется в виде площади заштрихованного прямоугольника на рис. 24.
Распределение хи-квадрат ![chi^2]()
Частный случай гамма-распределения с параметрами и
называется распределением хи-квадрат с
степенями свободы (пишут
). Если случайная величина
подчиняется закону
, то её плотность распределения вероятностей есть
Основные характеристики распределение хи квадрат (математическое ожидание и дисперсия):
Кривые распределения (для различных значений ) изображены на рис. 25.
Случайная величина , подчиняющаяся хи-квадрат распределению, равна сумме квадратов
независимых случайных величин
, каждая из которых имеет стандартизированное нормальное распределение, то есть
Пусть и
— независимые случайные величины, имеющие хи-квадрат распределение со степенью свободы соответственно
и
. Сумма этих случайных величин имеет также хи-квадрат распределение с
степенями свободы:
Заметим, что распределение при больших значениях
с достаточной для практических расчётов точностью аппроксимируется нормальным распределением с математическим ожиданием
и дисперсией
. Поэтому при больших значениях
вероятности рассчитываются по нормальному закону.
Распределение играет большую роль в математической статистике. Подробнее об этом [url]см. часть 11[/url].
Распределение Стьюдента
Распределение хи-квадрат Случайная величина есть отношение двух независимых случайных величин
и
, то есть
Распределение случайной величины называется распределением Стьюдента с
степенями свободы. Его плотность задаётся формулой
Математическое ожидание и дисперсия случайной величины, подчинённой распределению Стьюдента , есть
Кривые распределения Стьюдента (для различных значений ) изображены на рис. 26.
Как и в случае и хи-квадрат распределением, при увеличении распределение Стьюдента стремиться к нормальному, более того, стандартизованному нормальному (то есть с нулевым математическим ожиданием и единичной дисперсией). Распределение Стьюдента, как хи-квадрат распределение, широко применяется в задачах математической обработки измерений.
Распределение Фишера
Пусть случайная величина равна отношению двух независимых случайных величин
и
, то есть
Распределение случайной величины называется распределением Фишера с
и
степенями свободы. Оно имеет следующую плотность вероятности
Математическое ожидание случайной величины, подчинённой распределению Фишера, определяется по формуле
Графики плотностей вероятностей распределения Фишера (для различных значений ) изображены на рис. 27.
Между случайными величинами, имеющими нормальное распределение: хи-квадрат, Стьюдента и Фишера, имеют место соотношения
Математический форум (помощь с решением задач, обсуждение вопросов по математике).
Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.

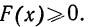
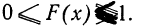
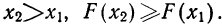
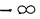 равно нулю, а при х=
равно нулю, а при х=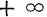 равно единице.
равно единице.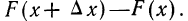
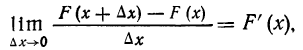
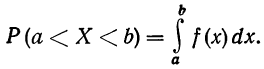
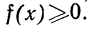
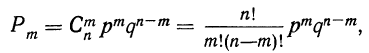
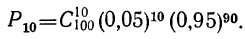
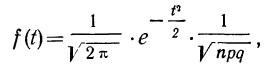
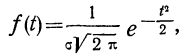
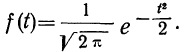
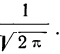
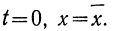
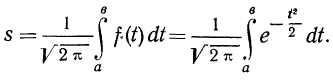
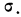
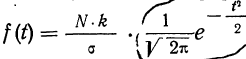
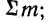
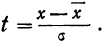
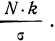
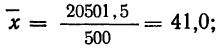
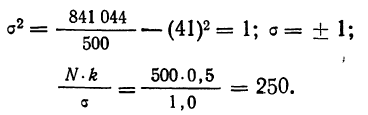
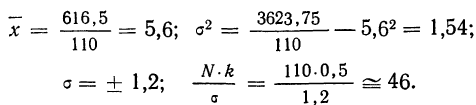
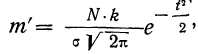
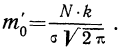
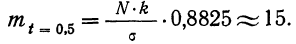
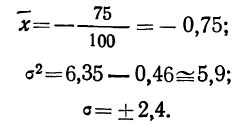
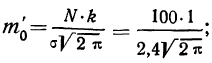
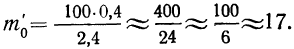

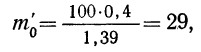
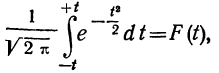
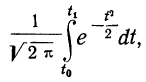
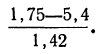
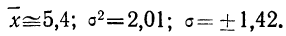
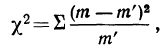
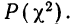
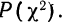
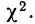
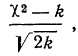
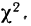
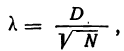
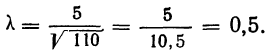
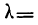
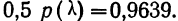
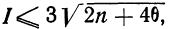
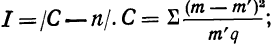
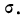
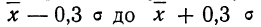 была расположена
была расположена 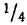 часть всей совокупности;
часть всей совокупности;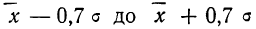 была расположена
была расположена 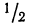 часть всей совокупности;
часть всей совокупности;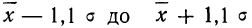 было расположено
было расположено  всей совокупности;
всей совокупности;