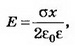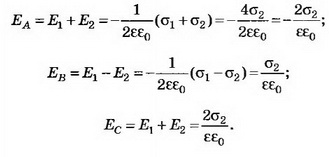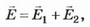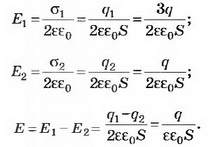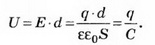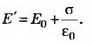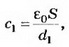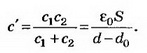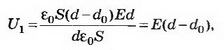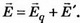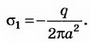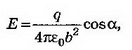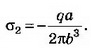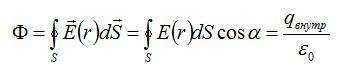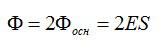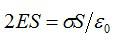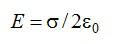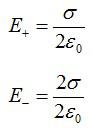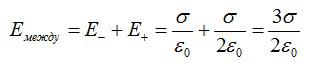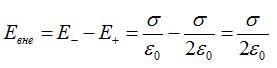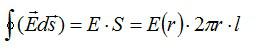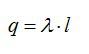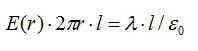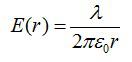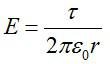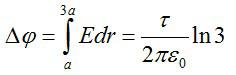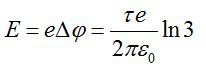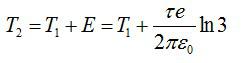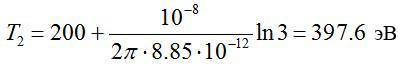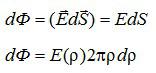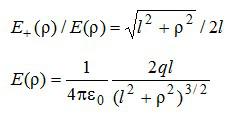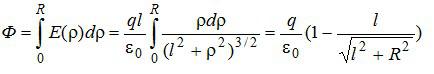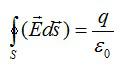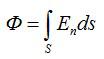Жидкевич В. И. Электрическое поле плоскости // Фізіка: праблемы выкладання. — 2009. — № 6. — С. 19—23.
Задачи по электростатике можно разделить на две группы: задачи о точечных зарядах и задачи о заряженных телах, размеры которых нельзя не учитывать [1—5].
Решение задач по расчёту электрических полей и взаимодействий точечных зарядов основано на применении закона Кулона и не вызывает особых затруднений. Более сложным является определение напряжённости поля и взаимодействия заряженных тел конечных размеров: сферы, цилиндра, плоскости. При вычислении напряжённости электростатических полей различной конфигурации следует подчеркнуть важность принципа суперпозиции и использовать его при рассмотрении полей, созданных не только точечными зарядами, но и зарядами, распределёнными по поверхности и объёму. При рассмотрении действия поля на заряд формула F=qE в общем случае справедлива для точечных заряженных тел и только в однородном поле применима для тел любых размеров и формы, несущих заряд q.
Электрическое поле конденсатора получается в результате наложения двух полей, созданных каждой пластиной.
В плоском конденсаторе можно рассматривать одну пластину как тело с зарядом q1 помещённое в электрическое поле напряжённостью Е2, созданное другой пластиной.
Рассмотрим несколько задач.
1. Бесконечная плоскость заряжена с поверхностной плотностью σ>0. Найдите напряжённость поля Е и потенциал ϕ по обе стороны плоскости, считая потенциал плоскости равным нулю. Постройте графики зависимостей Е(х), ϕ(х). Ось х перпендикулярна плоскости, точка х=0 лежит на плоскости.
Решение. Электрическое поле бесконечной плоскости является однородным и симметричным относительно плоскости. Его напряжённость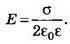
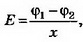
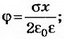
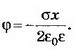
2. Две плоскопараллельные тонкие пластины, расположенные на малом расстоянии d друг от друга, равномерно заряжены зарядом поверхностной плотностью σ1 и σ2. Найдите напряжённости поля в точках, лежащих между пластинами и с внешней стороны. Постройте график зависимости напряжённости Е(х) и потенциала ϕ(х), считая ϕ(0)=0. Рассмотрите случаи, когда: a) σ1=-σ2; б) σ1= σ2; в) σ1=3σ2—
Решение. Так как расстояние между пластинами мало, то их можно рассматривать как бесконечные плоскости.
Напряжённость поля положительно заряженной плоскости равна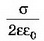
Согласно принципу суперпозиции поле в любой рассматриваемой точке будет создаваться каждым из зарядов в отдельности.
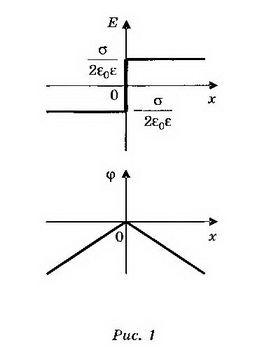
а) Поля двух плоскостей, заряженных равными и противоположными по знаку зарядами (плоский конденсатор), складываются в области между плоскостями и взаимно уничтожаются во внешних областях (рис. 2, а).
При х<0 Е=0, ϕ=0; при 0<x<d 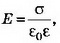
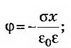
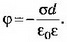
Если плоскости конечных размеров, то поле между плоскостями не будет строго однородным, а поле вне плоскостей не будет точно равно нулю.
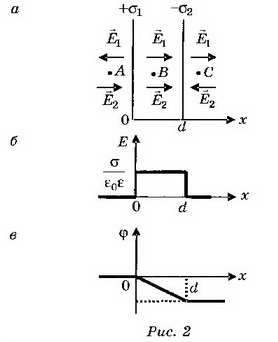
б) Поля плоскостей, заряженных равными по величине и знаку зарядами (σ1=σ2), компенсируют друг друга в пространстве между плоскостями и складываются во внешних областях (рис. 3, а). При х<0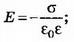
Воспользовавшись графиком Е(х) (рис. 3, б), построим качественно график зависимости ϕ(х) (рис. 3, в).
в) Если σ1= σ2, то, учитывая направления полей и выбирая направление направо за положительное, находим:
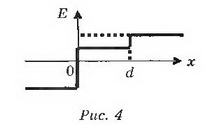
Зависимость напряжённости Е от расстояния показана на рисунке 4.
3. На одной из пластин плоского конденсатора ёмкостью С находится заряд q1=+3q, а на другой q2=+q. Определите разность потенциалов между пластинами конденсатора.
Решение. 1-й способ. Пусть площадь пластины конденсатора S, а расстояние между ними d. Поле внутри конденсатора однородное, поэтому разность потенциалов (напряжение) на конденсаторе можно определить по формуле U=E*d, где Е — напряжённость поля внутри конденсатора.
где Е1, Е2 — напряжённости поля, создаваемого пластинами конденсатора.
Тогда
2-й способ. Добавим на каждую пластину заряд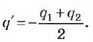
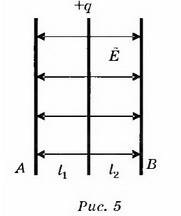
4. В пространство между обкладками незаряженного плоского конденсатора вносят тонкую металлическую пластину, имеющую заряд +q. Определите разность потенциалов между обкладками конденсатора.
Решение. Так как конденсатор не заряжен, то электрическое поле создаётся только пластиной, имеющей заряд q (рис. 5). Это поле однородное, симметричное относительно пластины, и его напряжённость 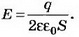
Разность потенциалов между обкладками конденсатора 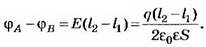
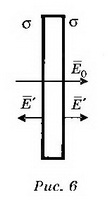
5. В однородное электрическое поле напряжённостью Е0 перпендикулярно силовым линиям помещают заряженную металлическую пластину с плотностью заряда на поверхности каждой стороны пластины σ (рис. 6). Определите напряжённость поля Е’ внутри и снаружи пластины и поверхностную плотность зарядов σ1и σ2, которая возникнет на левой и правой сторонах пластины.
Решение. Поле внутри пластины равно нулю и является суперпозицией трёх полей: внешнего поля Е0, поля, создаваемого зарядами левой стороны пластины, и поля, создаваемого зарядами правой стороны пластины. Следовательно,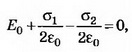
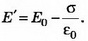
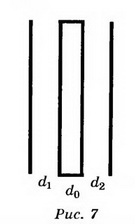
6. В плоском воздушном конденсаторе напряжённость поля Е= 104 В/м. Расстояние между обкладками d=2 см. Чему будет равна разность потенциалов, если между пластинами параллельно им поместить металлический лист толщиной d0=0,5 см (рис. 7)?
Решение. Поскольку электрическое поле между пластинами однородное, то U=Ed, U=200 В.
Если между пластинами пометить металлический лист, то получается система из двух последовательно соединённых конденсаторов с расстоянием между пластинами d1 и d2. Ёмкости этих конденсаторов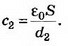
Так как конденсатор отключён от источника тока, то заряд конденсатора при внесении металлического листа не меняется: q’=CU=С’U1;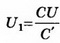
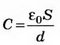
U1=150 В.
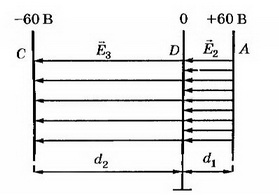
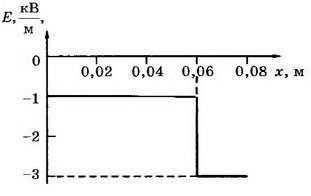
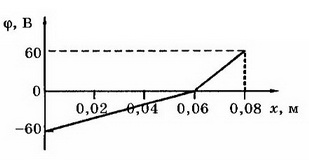
7. На пластинах А и С, расположенных параллельно на расстоянии d=8 см друг от друга, поддерживаются потенциалы ϕ1= 60 В и ϕ2=-60 В соответственно. Между ними поместили заземлённую пластину D на расстоянии d1=2 см от пластины А. На сколько изменилась напряжённость поля на участках AD и CD? Постройте графики зависимостей ϕ(x) и Е(х).
Решение. Первоначальная напряжённость поля между пластинами А и С:
E1=1,5 кВ/м.
Напряжённость поля на участке AD: Е2= ϕ1/d1, Е2=3 кВ/м, т. е. увеличилась на 1,5 кВ/м. Напряжённость поля на участке CD Е3= ϕ2/d2, т.е. уменьшилась на Е3=0,5 кВ/м. Поскольку векторы 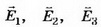
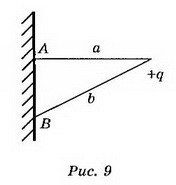
8. Точечный заряд q=5*10-9 Кл находится на расстоянии 3 см от проводящей заземлённой стенки. Найдите поверхностную плотность заряда, индуцированного на стенке в точке А, ближайшей к заряду, и в точке В, находящейся на расстоянии 5 см от заряда.
Решение. В точках А, В, расположенных в непосредственной близости к поверхности проводника (рис. 9), поле создаётся точечным зарядом q и зарядом q’, индуцированным на стенке:
В точке А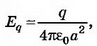
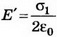
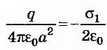
В точке В величина нормальной составляющей напряжённости поля точечного заряда
где b — расстояние от заряда до точки, cosα=a/b,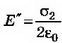
Следовательно,
Список использованной литературы
1. Балаш, В. А. Задачи по физике и методы их решения / В. А. Балаш. — 4-е изд. — М. : Просвещение, 1983. — 432 с.
2. Бутиков, Е. И. Физика в примерах и задачах / Е. И. Бутиков, А. А. Быков, А. С. Кондратьев. — 3-е изд. — М. : Наука, 1989. — 462 с.
3. Зилъберман, Г. Е. Электричество и магнетизм / Г. Е. Зильберман. — М. : Наука, 1990. — 384 с.
4. Меледин, Г. В. Физика в задачах / Г. В. Меледин. — 2-е изд. — М. : Наука, 1990. — 270 с.
5. Сборник задач по физике / Л. П. Баканина [и др.]; под ред. С. М. Козела. — М. : Наука, 1990. — 347 с.
Поле равномерно заряженной плоскости
Пусть бесконечная плоскость (рис.3.5)
заряжена равномерно с поверхностной
плотностью заряда
(=dQ/dS–заряд, приходящийся на единицу площади
поверхности).
Рис.3.5
Выделим на плоскости площадку Sи окружим ее цилиндрической замкнутой
поверхностью с основанием, параллельным
плоскости. Так как линии вектора Е
перпендикулярны плоскости и параллельны
образующим цилиндра, то полный поток
через цилиндрическую замкнутую
поверхность равен сумме потоков лишь
через два ее основания:
NЕ=2ES
Согласно теореме Остроградского-Гаусса
,
Приравняв правые части для N,
получим
(3.11)
Из (3.11) следует, что напряженность поля
бесконечной заряженной плоскости в
точках не зависит от расстояния до них.
Следовательно, поле плоскости является
однородным.
Поле двух бесконечных параллельных
разноименно заряженных плоскостей(рис.3.6)
Рис.3.6
Пусть поверхностные плотности заряда
плоскостей +и -равны по величине. Как видно из рис.3.6,
линии полей слева и справа от плоскостей
направлены навстречу друг другу. Поэтому
суммарная напряженность поля вне
плоскостей Е=0. В области между плоскостями,
с учетом (3.11).
(3.12)
Таким образом, поле между плоскостями
однородно. Однородным можно считать и
поле внутри конечных параллельных
плоскостей (плоский конденсатор).
Работа сил электростатического поля при перемещении заряда. Потенциал
О
работу по перемещению зарядаQ0из точки 1 в точку 2, совершаемую полем
зарядаQ(рис. 3.7).
Рис.3.7
Так как при движении заряда Q0сила взаимодействия его с зарядомQ,
создающим поле, по закону Кулона зависит
от расстоянияr:
,
то сначала
определим элементарную работу dAна бесконечно малом участкеdℓ:
dA=Fdℓcosα,
здесь α –
угол между векторами Fиdℓ. Учитывая, чтоdℓcosα=dr,
найдем полную работу как интеграл:

Отсюда следует, что работа электрического
поля не зависит от формы пути, а
определяется начальным и конечным
положениями заряда Q0.
Это означает, чтоэлектростатическое
поле является потенциальным, а его силы
– консервативными.
Из (3.13) следует, что работа, совершаемая
при перемещении заряда в электростатическом
поле вдоль любого замкнутого контура,
равна нулю, то есть:
Последнее равенство можно записать,
учитывая, что
,
Тогда для
электростатического поля имеем:
,
где Еℓ=Е
сosα– проекция вектора
Е на перемещениеdℓ.
Этот интеграл называется циркуляциейвектора напряженности.Для
электростатического поля циркуляция
вдоль любого замкнутого контура равна
нулю.
Из раздела “механика” известно, что
работа консервативных сил равна убыли
потенциальной энергии:
А12=Wn1
–Wn2.
Сравнивая это равенство с (3.13), получим
формулу потенциальной энергии заряда
Q0, находящегося
в поле зарядаQ:
По мере удаления от заряда Qпотенциальная энергия убывает и можно
принять, что в бесконечностиWп=0,
тогда постоянная интегрирования
С = 0
(3.14)
Отношение Wп/Q0не зависит от заряда и может служитьэнергетической характеристикой поля,
называемойпотенциалом поля в данной
точке, созданным зарядом Q:
(3.15)
Из формул (3.14) и (3.15) следует, что потенциал
поля точечного заряда (шара) Q:
(3.16)
Работа, совершаемая электрическими
силами по перемещении заряда Q0из точки 1 в точку 2, может быть вычислена
через разность потенциалов:
А12 =Wп1–Wп2=Q0(φ1– φ2)
(3.17)
Если точка 2 находится в бесконечности,
то φ2= 0 и следовательно,
А12 =
φ1Q0,
откуда
,
(3.18)
где Q0-величина
перемещаемого в поле заряда.
Таким образом, потенциал данной точки
поля определяется работой, совершаемой
силами поля при перемещении единичного
заряда из этой точки в бесконечность.
За единицу потенциала принятВольт:
Знак потенциала
определяется знаком заряда, создающего
поле. Если поле образовано системой
зарядов, то его потенциал равен
алгебраической сумме потенциалов полей
всех зарядов (принцип суперпозиции):
Точки пространства с равными потенциалами
образуют поверхность, называемую
эквипотенциальной. Такой поверхностью,
например, является поверхность равномерно
заряженной проводящей сферы.
Работа при переменном заряде Qвдоль эквипотенциальной поверхностиA=QΔφ=0.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
§ 4. Поле бесконечной равномерно заряженной плоскости
Пусть поверхностная плотность заряда (заряд единицы поверхности) равна σsigma. Силовые линии перпендикулярны плоскости, густота их везде одинакова.
Это следует из соображений симметрии. На рис. 4.1 показано поле для σ>0.sigma>0.
Напряжённость поля по каждую сторону плоскости одна и та же, независимо от расстояния до плоскости (поле однородно). Приведём без доказательства выражение для модуля напряжённости электрического поля по любую сторону плоскости:
| E=k2πσ=σ2ε0E=k2pileft|sigmaright|=dfrac{left|sigmaright|}{2varepsilon_0}. | (4.1) |
Эту формулу можно обобщить. Пусть σsigma произвольного знака. Направим ось `x` перпендикулярно плоскости (рис. 4.2). Можно убедиться непосредственной проверкой, что при x>0 Ex=σ2ε0x>0;E_x=dfracsigma{2varepsilon_0}, при x<0 Ex=-σ2ε0x<0;E_x=dfrac{-sigma}{2varepsilon_0} при любом знаке σsigma. Здесь ExE_x проекция напряжённости на ось `x`. Для запоминания обобщённых формул можно формально считать σ>0sigma>0 и писать выражение для ExE_x при x>0x>0 и x<0x<0. Полученные формулы окажутся справедливыми и при σ<0sigma<0. Обобщение полезно тем, что нет знака модуля.
Равномерно заряженные пластины параллельны и находятся на расстоянии друг от друга много меньшем их размеров. Найти плотности зарядов σ1sigma_1 и σ2sigma_2 на пластинах, зная, что напряжённость поля в точках `A` и `B` вблизи пластин EA= 6000E_A = 6000 Н/Кл, EB=2000E_B = 2000 Н/Кл (рис. 4.3).
Направим ось `x` на рис. 4.3 перпендикулярно пластинам, от первой ко второй. В любой точке по принципу суперпозиции полей напряжённость E→=E1→+E2→overrightarrow E=overrightarrow{E_1}+overrightarrow{E_2}, где E1→, E2→overrightarrow{E_1},;overrightarrow{E_2} — напряжённости полей, созданных первой и второй пластинами. Запишем последнее равенство в проекциях на ось `x`:
Ex=E1x+E2xE_x=E_{1x}+E_{2x}.
Это равенство справедливо для любой точки. Для точек `A` и `B` оно имеет более конкретный вид:
Для т. A: EA=σ12ε0-σ22ε0A:;E_A=dfrac{sigma_1}{2varepsilon_0}-dfrac{sigma_2}{2varepsilon_0},
Для т. B: EB=σ12ε0+σ22ε0B:;E_B=dfrac{sigma_1}{2varepsilon_0}+dfrac{sigma_2}{2varepsilon_0}.
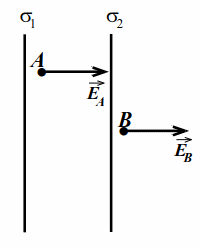 |
| Рис. 4.3 |
Решая систему из последних двух уравнений, находим:
σ1=ε0(EA+EB)=7.08·10-8Кл/м2, σ2=ε0(EA-EB)=-3.54·10-8Кл/м2.begin{array}{l}sigma_1=varepsilon_0(E_A+E_B)=7.08cdot10^{-8}mathrm{Кл}/mathrm м^2,;\sigma_2=varepsilon_0(E_A-E_B)=-3.54cdot10^{-8}mathrm{Кл}/mathrm м^2.end{array}
Заметим, что для решения задачи с использованием для напряжённости формулы с модулем пришлось бы перебрать возможные случаи для знаков зарядов пластин, поскольку знаки заранее неизвестны. Это усложнило бы решение. Попробуйте решить задачу вторым способом и сравните его с первым.
Теорема Гаусса выражает связь между потоком вектора напряженности электрического поля через замкнутую поверхность и алгебраической суммой зарядов, заключенных в объеме, ограниченном этой поверхностью. О примерах использования теоремы Гаусса на практике поговорим в этой статье.
Присоединяйтесь к нам в телеграме, чтобы не только решать задачи, но и быть в курсе актуальных новостей для студентов всех специальностей.
Задачи на теорему Гаусса с решением
Если вам нужно сначала освежить теоретические знания, читайте подробную теорию по теореме Гаусса в нашем справочнике. Ну а перед решением задач не забудьте повторить памятку и на всякий случай держите под рукой полезные формулы.
Кстати, при решении задач на теорему Гаусса придется довольно часто брать интегралы. Хотите научиться делать это по-быстрому? У нас уже есть отдельная статья и видео на эту тему.
Задача на теорему Гаусса №1: напряженность поля плоскости
Условие
Определите напряженность поля бесконечной заряженной плоскости. Поверхностная плотность заряда сигма.
Решение
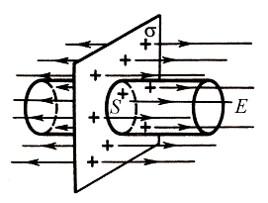
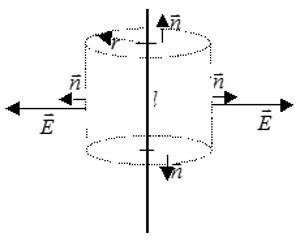
Линии напряженности перпендикулярны рассматриваемой плоскости и направлены в обе стороны от неё. Выберем в качестве гауссовой поверхности цилиндр с основанием, параллельным плоскости:
По теореме Гаусса:
Поток сквозь цилиндр равен сумме потоков сквозь боковую поверхность цилиндра и потокам сквозь оба его основания. Поток сквозь боковую поверхность равен нулю, так как линии напряженности параллельны ей:
Согласно теореме Гаусса:
Отсюда:
Ответ: см. выше.
Задача на теорему Гаусса №2: напряженность поля двух пластин
Условие
Электрическое поле создано двумя параллельными заряженными тонкими пластинами с поверхностными плотностями заряда + сигма и -2 сигма. Площадь каждой пластины S, расстояние между пластинами d можно считать значительно меньшим их продольных размеров. Какова напряженность электрического поля, созданного этими пластинами?
Решение
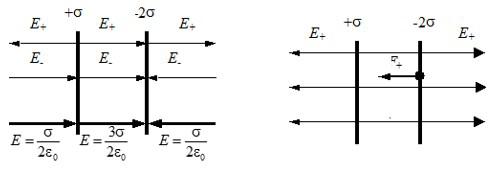
Для электрического поля действует принцип суперпозиции: результирующее поле равно векторной сумме отдельных полей каждой пластины. Из предыдущей задачи мы знаем формулу, по которой вычисляется напряженность поля тонкой заряженной пластины, запишем для каждой из них:
Векторы напряженности между пластинами совпадают по направлению, результирующая напряженность равна:
Справа и слева от пластин, во внешней области, векторы направлены в разные стороны:
Для наглядности приведем рисунок:
Ответ: см. выше.
Задача на теорему Гаусса №3: напряженность электрического поля бесконечной нити
Условие
Определить напряженность электрического поля, создаваемую бесконечной тонкой нитью, равномерно заряженной с линейной плотностью заряда лямбда.
Решение
Напряженность будем искать при помощи теоремы Гаусса. Наша задача – определить зависимость напряженности от расстояния от нити. В качестве поверхности выберем цилиндр с боковыми стенками, параллельными нити. Будем учитывать только поток вектора напряженности через боковую поверхность, так как поток через основания цилиндра равен нулю:
Заряд нити внутри рассматриваемой поверхности равен заряду отрезка нити длиной l:
По теореме Гаусса:
Отсюда:
Ответ: см. выше.
Задача с применением теоремы Гаусса №4
Условие
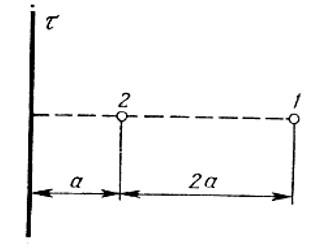
Электрическое поле создано бесконечной заряженной прямой линией с равномерно распределённым зарядом (τ = 10 нКл/м). Определить кинетическую энергию Т2 электрона в точке 2, если в точке 1 его кинетическая энергия Т1 = 200 эВ. Расстояние точки 2 от линии равно а = 0,5 см, точки 1 – b=1,5 см.
Решение
Ранее рассмотренные задачи были примерами вычисления полей с помощью теоремы Гаусса. Теперь рассмотрим задачу, которая решается сиспользованием этой информации. Из предыдущей задачи возьмем выражение для напряженности поля заряженной нити:
Разность потенциалов поля в двух точках будет равна:
При прохождении этой разницы потенциалов электрон приобретёт кинетическую энергию:
Конечная энергия частицы будет равна:
Получим:
Ответ: 397.6 эВ.
Задача на теорему Гаусса №5: поток электрического поля
Условие
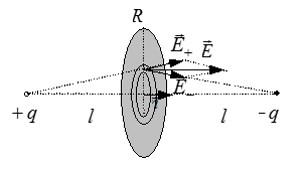
Два точечных заряда q и –q расположены на расстоянии 2l друг от друга. Найти поток вектора напряженности через круг радиуса R. Плоскость круга проходит через его середину и перпендикулярна отрезку прямой, соединяющей заряды.
Решение
Рассмотрим элементарный поток результирующего электрического поля через бесконечно малую кольцевую зону круга:
В записи потока учтено, что вектор напряженности перпендикулярен поверхности круга. Выразим напряженность электрического поля через «ро», используя подобие треугольников, показанных на рисунке:
Вычисление потока сводится к взятию интеграла:
Ответ: см. выше.
Примеры применения теоремы Гаусса можно найти не только в электростатике, но и в других областях физики.
Вопросы на теорему Гаусса
Вопрос 1. Сформулируйте теорему Гаусса.
Ответ. Теорема Гаусса гласит:
Поток вектора напряженности электростатического поля через замкнутую поверхность равен алгебраической сумме зарядов внутри поверхности, деленной на эпсилон нулевое (электрическую постоянную).
Вопрос 2. Что такое поток вектора напряженности?
Ответ. Поток вектора напряженности – скалярная физическая величина, определяемая как число линий вектора напряженности, пронизывающих некоторую поверхность S. Поток напряженности электрического поля через поверхность S конечного размера определяется как алгебраическая сумма элементарных потоков:
Вопрос 3. Что такое силовые линии напряженности?
Ответ. Это линии, с помощью которых используются для графического представления поля:
- касательная к силовой линии в каждой точке пространства направлена вдоль вектора поля;
- густота силовых линий пропорциональна напряженности поля в данной точке;
- поток вектора напряженности пропорционален числу силовых линий, пронизывающих поверхность.
Вопрос 4. Где начинаются и где заканчиваются силовые линии?
Ответ. Силовые линии начинаются и заканчиваются на зарядах, оставаясь непрерывными в пустом пространстве.
Вопрос 5. Верно ли утвержление: теорема Гаусса справедлива только для неподвижных зарядов.
Ответ. Нет, так как заряд частицы не зависит от ее скорости.
Нужна помощь в решении задач и других студенческих заданий? Обратитесь в профессиональный студенческий сервис за качественным решением проблем.