Как найти заряд через линейную плотность - Исправление недочетов и поиск решений вместе с Examum.ru

Сосредоточенные и распределенные заряды

Заряды можно распределять по какой-либо области тел, тогда их называют распределенными. Когда же заряд целиком собран в одну точку, его называют точечным. Большинство школьных задач физики связано с точечными зарядами.

Сосредоточенный заряд

Электрический заряд, сосредоточенный в какой-либо точке пространства, называют точечным.

Рис. 1. Точечный заряд

Силу взаимодействия точечных зарядов можно вычислить, используя закон Кулона.

Распределенные заряды

Электрический заряд, так же, можно распределять по объему, площади, или длине. Такие заряды называют распределенными. Чтобы описать эти заряды, используют понятие плотности заряда.

Если заряд распределен по:
— объему, говорят о объемной плотности заряда;
— площади, употребляют поверхностную плотность;
— длине, используют линейную плотность.

Примечание: Плотности отрицательных зарядов записывают со знаком «минус».

Формула линейной плотности заряда

Рис. 2. Заряд распределен по длинному тонкому телу

[ large boxed {tau = frac{q}{L} } ]

( large q left(text{Кл} right) ) – заряд;

( large L left(text{м} right) ) – длина, по которой распределен заряд;

( large tau left(frac{text{Кл}}{text{м}} right) ) – линейная плотность заряда;

Формула поверхностной плотности заряда

Любая поверхность обладает площадью, распределяя по ней заряд, получим поверхностную его плотность.

Этот термин используют, например, для вычисления электрического поля заряженной плоскости, или плоского конденсатора (двух параллельных плоскостей).

Рис. 3. Заряд распределен по плоской поверхности

[ large boxed {sigma = frac{q}{S} } ]

( large S left(text{м}^{2} right) ) – площадь, по которой распределен заряд;

( large sigma left(frac{text{Кл}}{text{м}^{2}} right) ) – поверхностная плотность заряда;

Формула объемной плотности заряда

Функция, описывающая плотность распределения заряда в трехмерном пространстве, входит в одно из уравнений Максвелла.

Рис. 4. Заряд распределен по объему тела

[ large boxed {rho = frac{q}{V} } ]

( large V left(text{м}^{3} right) ) – объем, по которому распределен заряд;

( large rho left(frac{text{Кл}}{text{м}^{3}} right) ) – объемная плотность заряда;

Примечание:

Джеймс Клерк Максвелл (1831 — 1879) – талантливый шотландский математик и физик. Популяризатор науки, экспериментатор и конструктор научных приборов.

Описал электромагнитное взаимодействие с помощью своих уравнений (уравнения Максвелла). Система этих уравнений лежит в основе современной электродинамики.

Предсказал электромагнитные волны, обнаружил, что свет имеет электромагнитную природу и может создавать давление.

Занимался исследованиями в области молекулярной физики и термодинамики. Использовал математический аппарат статистики, получил температурное распределение скоростей молекул.

Проводил исследования в области астрономии и оптики, для планеты Сатурн провел анализ устойчивости колец.

Именно Максвелл заложил трехцветный принцип, который используется в цветной фотографии и телевидении.

Оценка статьи:

Загрузка…

Источник

Для упрощения
математических расчетов электростатических
полей часто пренебрегают дискретной
структурой зарядов. Считают, что заряд
распределен непрерывно и вводят понятие
о плотности заряда.

Рассмотрим различные
случаи распределения зарядов.

1.Заряд
распределен вдоль линии.
Пусть на бесконечно малом участке
находится заряд.
Введем величину

.
(1.5)

Величина
называется линейной плотностью заряда.
Ее физический смысл – заряд, приходящийся
на единицу длины.

2.Заряд
распределен по поверхности.
Введем поверхностную плотность заряда:

.
(1.6)

Её физический
смысл – заряд, приходящийся на единицу
площади.

3.Заряд
распределен по объёму.
Введем объёмную плотность заряда:

.
(1.7)

Её физический
смысл – заряд, сосредоточенный в единице
объёма.

Заряд,
сосредоточенный на бесконечно малом
участке линии, поверхности или в
бесконечно малом объёме можно считать
точечным. Напряжённость поля, создаваемого
им, определится формулой:

.
(1.8)

Для нахождения
напряжённости поля, создаваемого всем
заряженным телом, нужно применить
принцип суперпозиции полей:

.
(1.9)

В этом случае, как
правило, задача сводится к вычислению
интеграла.

1.3.Применение принципа суперпозиции к расчету электростатических полей. Электростатическое поле на оси заряженного кольца

Постановка
задачи.
Пусть имеется тонкое кольцо радиуса R,
заряженное с линейной плотностью заряда
τ.
Необходимо рассчитать напряжённость
электрического поля в произвольной
точке А,
расположенной на оси заряженного кольца
на расстоянии x
от плоскости кольца (рис. ).

Выберем
бесконечно малый элемент длины кольца
dl;
заряд dq,
находящийся на этом элементе равен dq=
τ·dl.
Этот заряд создает в точке А
электрическое поле напряжённостью
.
Модуль вектора напряжённости равен:

.
(1.10)

По
принципу суперпозиции полей напряжённость
электрического поля, создаваемого всем
заряженным телом, равна векторной сумме
всех векторов
:

.
(1.11)

Разложим
вектора
на составляющие: перпендикулярные оси
кольца ()
и параллельные оси кольца ().

.
(1.12)

Векторная
сумма перпендикулярных составляющих
равна нулю:
,
тогда.
Заменяя сумму интегралом, получим:

.
(1.13)

Из
треугольника (рис.1.2) следует:

=.
(1.14)

Подставим выражение (1.14) в формулу (1.13) и вынесем за знак интеграла постоянные величины, получим:

.
(1.15)

Так
как
,
то

.
(1.16)

С
учетом того, что
,
формулу (1.16) можно представить в виде:

.
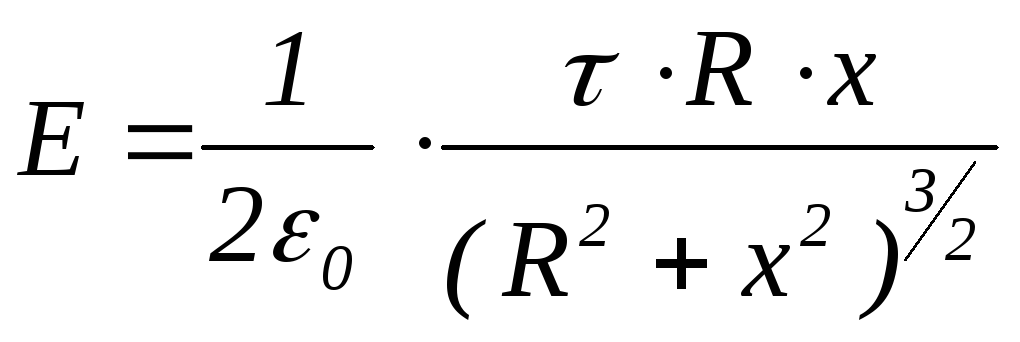
(1.17)

1.4.Геометрическое описание электрического поля. Поток вектора напряжённости

Для
математического описания электрического
поля нужно указать в каждой точке
величину и направление вектора

,
то есть задать векторную функцию.

Существует
наглядный (геометрический) способ
описания поля с помощью линий вектора
(силовых линий) (рис.13.).

Линии напряжённости
проводят следующим образом:

касательная
к линии в каждой точке должна совпадать
с направлением поля;
число
линий пересекающих единичную площадку,
перпендикулярную к ним, должно быть
равно численному значению вектора
.

Существует
правило:
линии вектора напряжённости электрических
полей, создаваемых системой неподвижных
зарядов, могут начинаться или заканчиваться
лишь на зарядах либо уходить в
бесконечность.

На
рисунке 1.4 показано изображение
электростатического поля точечного
заряда с помощью линий вектора
,
а на рисунке 1.5 — изображение
электростатического поля диполя^{^}.

1.5.
Поток
вектора напряжённости электростатического
поля

П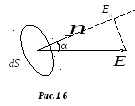оместим
в электрическое поле бесконечно малую
площадку dS (рис.1,6).
Здесь

— единичный вектор нормали к площадке.
Вектор напряжённости электрического
поля

образует с нормалью

некоторый угол α.
Проекция вектора

на направление нормали равна E_n=E·cos
α .

Потоком вектора
через бесконечно малую площадку
называется скалярное произведение

,
(1.18)

или

.
(1.19)

Поток вектора
напряжённости электрического поля
является алгебраической величиной; его
знак зависит то взаимной ориентации
векторов
и
.

Поток
вектора
через произвольную поверхностьSконечной величины определится интегралом:

.
(1.20)

Если
поверхность замкнутая, интеграл отмечают
кружочком:

.
(1.21)

Для замкнутых
поверхностей нормаль берется наружу
(рис.1.7).

Поток
вектора напряжённости имеет наглядный
геометрический смысл: он численно равен
числу линий вектора
,
проходящих через поверхностьS.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Естественные науки / Физика. Электричество и магнетизм, колебания и волны / 1.1.11. ПЛОТНОСТЬ ЗАРЯДА

Линейная плотность заряда вычисляется по формуле:

где t – линейная плотность заряда; Q – заряд; l – длина.

Поверхностная плотность заряда:

где s – поверхностная плотность заряда; Q – электрический заряд; S – площадь поверхности.

Объемная плотность заряда:

где r – объемная плотность заряда; Q – электрический заряд; V – объем.

Источник

When measuring electric fields from various continuous charge distributions such as linear, surface, and volume, we come across electric charge density. When understanding current electricity, we must also consider the concept of charge density. To understand charge density, we must first understand this concept of density. The density of an object is defined as its mass per unit volume. Similarly, depending on the type of continuous charge arrangement, we can think of charge density as charge per unit length, surface, or volume.

What is Charge density?

Charge density is defined as the amount of electric charge that can be accumulated over a unit length or unit area or unit volume of a conductor. In other words, it indicates how much charge is stored in a specific field. It calculates the distribution of the charge and can be positive or negative.

The charge may be scattered over a one-dimensional or two-dimensional or three-dimensional surface. The charge density is categorized into three types:

Linear charge density
Surface charge density, and
Volume charge density.

Its value is directly proportional to the amount of charge but changes inversely with the surface dimensions.

Linear charge density

The linear charge density is defined as the amount of charge present over a unit length of the conductor. It is denoted by the symbol lambda (λ). Its standard unit of measurement is Coulombs per meter (Cm^-1) and the dimensional formula is given by [M⁰L^-1T¹I¹].

Its formula equals the ratio of charge value to the length of the conducting surface.

λ = q/l

where,

λ is the linear charge density,

q is the charge,

l is the length of surface.

Surface charge density

The surface charge density is defined as the amount of charge present over a unit area of the conductor. It is denoted by the symbol sigma (σ). Its standard unit of measurement is coulombs per square meter (Cm^-2) and the dimensional formula is given by [M⁰L^-2T¹I¹].

Its formula equals the ratio of charge value to the area of the conducting surface.

σ = q/A

where,

σ is the surface charge density,

q is the charge,

A is the area of surface.

Volume charge density

The volume charge density is defined as the amount of charge present over a unit volume of the conductor. It is denoted by the symbol rho (ρ). Its standard unit of measurement is coulombs per cubic meter (Cm^-3) and the dimensional formula is given by [M⁰L^-3T¹I¹].

Its formula equals the ratio of charge value to the volume of the conducting surface.

ρ = q/V

where,

σ is the surface charge density,

q is the charge,

V is the volume of surface.

Sample Problems

Problem 1: Calculate the linear charge density of a surface if the charge is 2 C and length is 4 m.

Solution:

We have,

q = 2

l = 4

Using the formula we have,

λ = q/l

= 2/4

= 0.5 Cm^-1

Problem 2: Calculate the linear charge density of a surface if the charge is 5 C and the length is 3 m.

Solution:

We have,

q = 5

l = 3

Using the formula we have,

λ = q/l

= 5/3

= 1.67 Cm^-1

Problem 3: Calculate the charge if the linear charge density of a surface is 3 Cm^-1 and the length is 5 m.

Solution:

We have,

λ = 3

l = 5

Using the formula we have,

λ = q/l

=> q = λl

= 3 (5)

= 15 C

Problem 4: Calculate the surface charge density of a surface if the charge is 20 C and the area is 10 m².

Solution:

We have,

q = 20

A = 10

Using the formula we have,

σ = q/A

= 20/10

= 2 Cm^-2

Problem 5: Calculate the charge if surface charge density of a surface is 5 Cm^-2 and the area is 20 m².

Solution:

We have,

σ = 5

A = 20

Using the formula we have,

σ = q/A

=> q = σA

= 5 (20)

= 100 C

Problem 6: Calculate the volume charge density of a surface if charge is 50 C and the volume is 80 m³.

Solution:

We have,

q = 50

V = 80

Using the formula we have,

ρ = q/V

= 50/80

= 0.625 Cm^-3

Problem 7: Calculate the charge if the volume charge density of a surface is 1 Cm^-3 and volume is 25 m³.

Solution:

We have,

ρ = 1

V = 25

Using the formula we have,

ρ = q/V

=> q = ρV

= 1 (25)

= 25 C

Last Updated :
24 May, 2022

Like Article

Save Article

Источник