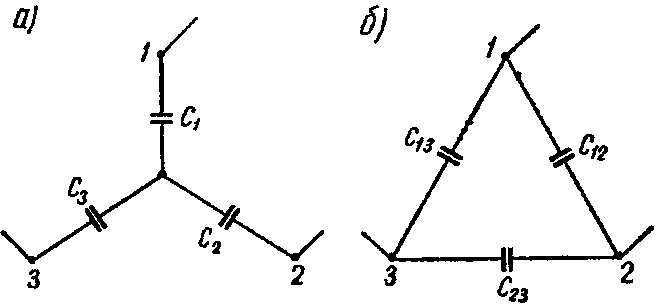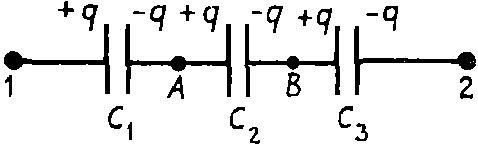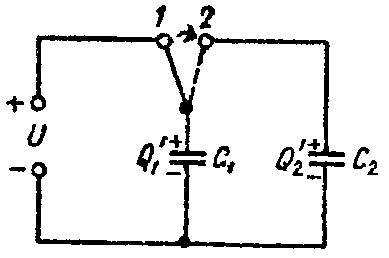Как найти заряд конденсатора по схеме - Исправление недочетов и поиск решений вместе с Examum.ru

Главная
→
Примеры решения задач ТОЭ
→
Расчет электрической цепи постоянного тока с конденсаторами

Расчет электрической цепи постоянного тока с конденсаторами

Основные положения и соотношения

1. Общее выражение емкости конденсатора

C= Q U .

2. Емкость плоского конденсатора

C= ε a ⋅S d = ε r ⋅ ε 0 ⋅S d ,

здесь

S — поверхность каждой пластины конденсатора;

d — расстояние между ними;

ε_a = ε_r·ε₀ — абсолютная диэлектрическая проницаемость среды;

ε_r — диэлектрическая проницаемость среды (относительная диэлектрическая проницаемость);

ε 0 = 1 4π⋅ с 2 ⋅ 10 −7 ≈8,85418782⋅ 10 −12 Ф м – электрическая постоянная.

3. При параллельном соединении конденсаторов С₁, С₂, …, С_n эквивалентная емкость равна

C= C 1 + C 2 +…+ C n = ∑ k=1 n C k .

4. При последовательном соединении конденсаторов эквивалентная емкость определяется из формулы

1 C = 1 C 1 + 1 C 2 +…+ 1 C n = ∑ k=1 n 1 C k .

Для двух последовательно соединенных конденсаторов эквивалентная емкость составляет:

C= C 1 ⋅ C 2 C 1 + C 2 ,

а напряжения между отдельными конденсаторами распределяются обратно пропорционально их емкостям:

U 1 =U⋅ C 2 C 1 + C 2 ; U 2 =U⋅ C 1 C 1 + C 2 .

5. Преобразование звезды емкостей в эквивалентный треугольник емкостей или обратно (рис. а и б)

Рис. 0

осуществляется по формулам:

Y→Δ { C 12 = C 1 ⋅ C 2 ΣC ; C 13 = C 1 ⋅ C 3 ΣC ; C 23 = C 2 ⋅ C 3 ΣC , где ΣC= C 1 + C 2 + C 3 , Δ→Y { C 1 = C 12 + C 13 + C 12 ⋅ C 13 C 23 ; C 2 = C 12 + C 23 + C 12 ⋅ C 23 C 13 ; C 3 = C 13 + C 23 + C 13 ⋅ C 23 C 12 .

6. Энергия электростатического поля конденсатора:

W= C⋅ U 2 2 = Q⋅U 2 = Q 2 2C .

7. Расчет распределения зарядов в сложных цепях, содержащих источники э.д.с. и конденсаторы, производится путем составления уравнений по двум законам:

1) По закону сохранения электричества (закон сохранения электрического заряда): алгебраическая сумма зарядов на обкладках конденсаторов, соединенных в узел и не подключенных к источнику энергии, равна алгебраической сумме зарядов, имевшихся на этих обкладках до их соединения:

ΣQ=Σ Q ′ .

2) По второму закону Кирхгофа: алгебраическая сумма э. д. с. в замкнутом контуре равна алгебраической сумме напряжений на участках контура, в том числе на входящих в него конденсаторах:

∑ k=1 n E k = ∑ k=1 n U C k = ∑ k=1 n Q k C k .

Приступая к решению задачи, надо задаться полярностью зарядов на обкладках конденсаторов.

Решение задач на расчет электрической цепи постоянного тока с конденсаторами

Задача. Доказать формулу эквивалентной емкости при последовательном соединении конденсаторов (рис. 1).

Рис. 1

Решение

На рис. 1 представлено последовательное соединение трех конденсаторов. Если батарею конденсаторов подключить к источнику напряжения U₁₂, то на левую пластину конденсатора С₁ перейдет заряд +q, на правую пластину конденсатора С₃ заряд –q.

Вследствие электризации через влияние правая пластина конденсатора С₁ будет иметь заряд –q, а так как пластины конденсаторов С₁ и С₂ соединены и были электронейтральны, то вследствие закона сохранения заряда заряд левой пластины конденсатора C₂ будет равен +q, и т. д. На всех пластинах конденсаторов при таком соединении будет одинаковый по величине заряд.

Найти эквивалентную емкость — это значит найти конденсатор такой емкости, который при той же разности потенциалов будет накапливать тот же заряд q, что и батарея конденсаторов.

Разность потенциалов U₁₂ = φ₁ — φ₂ складывается из суммы разностей потенциалов между пластинами каждого из конденсаторов

U 12 = φ 1 − φ 2 =( φ 1 − φ A )+( φ A − φ B )+( φ B − φ 2 )= U 1A + U AB + U B2 .

Воспользовавшись формулой напряжения на конденсаторе

U= q C ,

запишем

q C = q C 1 + q C 2 + q C 3 .

Откуда эквивалентная емкость батареи из трех последовательно включенных конденсаторов

1 C = 1 C 1 + 1 C 2 + 1 C 3 .

В общем случае эквивалентная емкость при последовательном соединении конденсаторов

1 C = 1 C 1 + 1 C 2 +…+ 1 C n = ∑ k=1 n 1 C k .

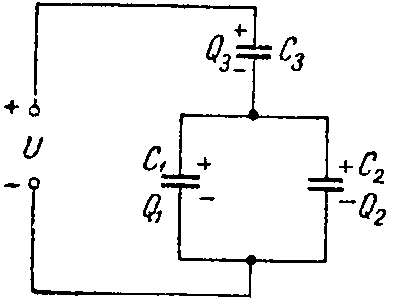
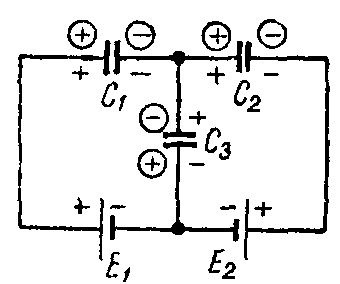
Задача 1. Определить заряд и энергию каждого конденсатора на рис. 2, если система подключена в сеть с напряжением U = 240 В.

Рис. 2

Емкости конденсаторов: C₁ =50 мкФ; C₂ =150 мкФ; C₃ =300 мкФ.

Решение

Эквивалентная емкость конденсаторов C₁ и C₂, соединенных параллельно

C₁₂ = C₁ + C₂ = 200 мкФ,

эквивалентная емкость всей цепи равна

C= C 12 ⋅ C 3 C 12 + C 3 = 200⋅300 500 =120 мкФ.

Заряд на эквивалентной емкости

Q = C·U = 120·10^–6·240 = 288·10^–4 Кл.

Той же величине равен заряд Q₃ на конденсаторе C₃, т.е. Q₃ = Q = 288·10^–4 Кл; напряжение на этом конденсаторе

U 3 = Q 3 C 3 = 288⋅ 10 −4 300⋅ 10 −6 =96 В.

Напряжение на конденсаторах C₁ и C₂ равно

U₁ = U₂ = U — U₃ = 240 — 96 = 144 В.

их заряды имеют следующие значения

Q₁ = C₁·U₁ = 50·10^–6·144 = 72·10^–4 Кл;

Q₂ = C₂·U₂ = 150·10^–6·144 = 216·10^–4 Кл.

Энергии электростатического поля конденсаторов равны

W 1 = Q 1 ⋅ U 1 2 = 72⋅ 10 −4 ⋅144 2 ≈0,52 Дж; W 2 = Q 2 ⋅ U 2 2 = 216⋅ 10 −4 ⋅144 2 ≈1,56 Дж; W 3 = Q 3 ⋅ U 3 2 = 288⋅ 10 −4 ⋅96 2 ≈1,38 Дж.

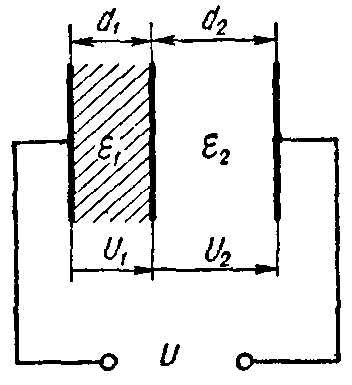
Задача 2. Плоский слоистый конденсатор (рис. 3), поверхность каждой пластины которого S = 12 см², имеет диэлектрик, состоящий из слюды (ε_r₁ = 6) толщиною d₁ = 0,3 мм и стекла (ε_r₂ = 7) толщиною d₂ =0,4 мм.

Пробивные напряженности слюды и стекла соответственно равны E₁ = 77 кВ/мм, E₂ = 36 кВ/мм.

Рис. 3

Вычислить емкость конденсатора и предельное напряжение, на которое его можно включать, принимая для более слабого слоя двойной запас электрической прочности.

Решение

Эквивалентная емкость слоистого конденсатора определится как емкость двух последовательно соединенных конденсаторов

C= C 1 ⋅ C 2 C 1 + C 2 = ε a1 ⋅S d 1 ⋅ ε a2 ⋅S d 2 ε a1 ⋅S d 1 + ε a2 ⋅S d 2 = ε a1 ⋅ ε a2 ⋅S ε a1 ⋅ d 2 + ε a2 ⋅ d 1 .

Подставляя сюда числовые значения, предварительно заменив ε_a₁ = ε_r₁·ε₀ и ε_a₂ = ε_r₂·ε₀, получим

C= ε 0 ⋅ ε r1 ⋅ ε r2 ⋅S ε r1 ⋅ d 2 + ε r2 ⋅ d 1 =8,85⋅ 10 −12 ⋅ 6⋅7⋅12⋅ 10 −4 6⋅0,4⋅ 10 −3 +7⋅0,3⋅ 10 −3 =99⋅ 10 −12 Ф.

Обозначим общее напряжение, подключаемое к слоистому конденсатору, через U_пр, при этом заряд конденсатора будет равен

Q = C·U_пр.

Напряжения на каждом слое будут равны

U 1 = Q C 1 = C⋅ U пр ε a1 ⋅S d 1 = ε a2 ⋅ d 1 ε a1 ⋅ d 2 + ε a2 ⋅ d 1 ⋅ U пр ; U 2 = Q C 2 = C⋅ U пр ε a2 ⋅S d 2 = ε a1 ⋅ d 2 ε a1 ⋅ d 2 + ε a2 ⋅ d 1 ⋅ U пр .

Напряженности электростатического поля в каждом слое

E 1 = U 1 d 1 = ε a2 ε a1 ⋅ d 2 + ε a2 ⋅ d 1 ⋅ U ′ пр ; E 2 = U 2 d 2 = ε a1 ε a1 ⋅ d 2 + ε a2 ⋅ d 1 ⋅ U ″ пр .

Здесь U’_np — общее напряжение, подключаемое к конденсатору, при котором пробивается первый слой, a U»_np — общее напряжение, при котором происходит пробой второго слоя.

Из последнего выражения находим

U ′ пр = E 1 ⋅ ε a1 ⋅ d 2 + ε a2 ⋅ d 1 ε a2 =49,5 кВ; U ″ пр = E 2 ⋅ ε a1 ⋅ d 2 + ε a2 ⋅ d 1 ε a1 =27,0 кВ.

Таким образом, более слабым слоем является второй; согласно условию, принимая для него двойной запас прочности, находим, что конденсатор может быть включен на напряжение, равное

27,0 кВ / 2 = 13,5 кВ.

Задача 3. Обкладки плоского конденсатора с воздушным диэлектриком расположены на расстоянии d₁ = 1 см друг от друга. Площадь обкладок S = 50 см². Конденсатор заряжается до напряжения U = 120 В и затем отсоединяется от источника электрической энергии.

Определить, какую надо совершить работу, если увеличить расстояние между пластинами до d₂ = 10 см. Краевым эффектом можно пренебречь; другими словами, емкость конденсатора можно считать обратно пропорциональной расстоянию между обкладками.

Решение

Энергия заряженного плоского конденсатора равна

W 1 = C 1 ⋅ U 2 2 = ε 0 ⋅S d 1 ⋅ U 2 2 ,

где С₁ — емкость до раздвижения обкладок.

Так как конденсатор отключен от источника, то при изменении расстояния между обкладками его заряд остается постоянным. Поэтому из~ соотношения

Q = C₂·U₂,

где C₂ — емкость конденсатора после раздвижения обкладок, следует, что, так как C₂ = ε₀·S/d₂ стало меньше в 10 раз (d₂ увеличилось в 10 раз), то напряжение на конденсаторе U₂ увеличилось в 10 раз, т. е. U₂ = 10U.

Таким образом, энергия конденсатора после отключения и раздвижения обкладок на расстояние d₂ будет больше первоначальной

W 2 = ε 0 ⋅S d 2 ⋅ U 2 2 2 = ε 0 ⋅S 10 d 1 ⋅ ( 10U ) 2 2 =10⋅ ε 0 ⋅S d 1 ⋅ U 2 2 =10⋅ W 1 .

Увеличение энергии произошло за счет работы внешних сил, затраченной на раздвижение обкладок.

Таким образом, надо совершить работу, равную

W 2 − W 1 =9⋅ W 1 =9⋅ ε 0 ⋅S d 1 ⋅ U 2 2 =2,86⋅ 10 −7 Дж.

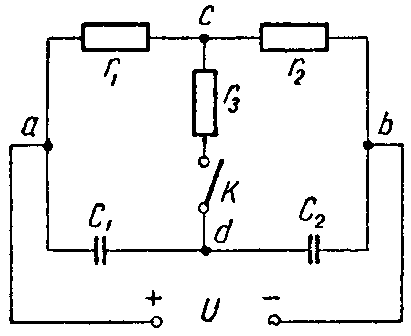
Задача 4. Для схемы (рис. 4) определить напряжение каждого конденсатора в двух случаях: при замкнутом и разомкнутом ключе К.

Даны: C₁ = 30 мкФ; C₂ = 20 мкФ; r₁ = 100 Ом. r₂ = 400 Ом. r₃ = 600 Ом, U = 20 В.

Решение

Ключ К разомкнут. Конденсаторы соединены между собой последовательно; их ветвь находится под полным напряжением источника; напряжение распределяется между ними обратно пропорционально емкостям

U 1 = C 2 C 1 + C 2 ⋅U= 20⋅ 10 −6 30⋅ 10 −6 +20⋅ 10 −6 ⋅20=8 В; U 2 =U− U 1 =20−8=12 В.

Рис. 4

Ключ К замкнут. Через сопротивления r₁ и r₂ протекает ток

I= U r 1 + r 2 = 20 500 =0,04 А,

а через сопротивление r₃ ток не протекает.

Поэтому точки c и d равнопотенциальны (φ_c = φ_d). Следовательно, напряжение между точками a и c (U_ac = φ_a — φ_c) равно напряжению между точками a и d (U_ad = φ_a — φ_d).

Таким образом, напряжение на первом конденсаторе равно падению напряжения на сопротивлении r₁

U_C₁ = I·r₁ = 0,04·100 = 4 В.

Аналогично напряжение на втором конденсаторе равно

U_C₂ = I·r₂ = 0,04·400 = 16 В.

Задача 5. Определить напряжение на зажимах конденсаторов и их энергию после перевода рубильника из положения 1 в положение 2, показанное пунктиром на рис. 5, если U = 25 В; C₁ = 5 мкФ; C₂ = 120 мкФ. Конденсатор C₂ предварительно не был заряжен.

Рис. 5

Решение

Когда рубильник находится в положении 1, то конденсатор C₁ заряжен до напряжения U и его заряд равен

Q = C₁·U = 5·10^–6·25 = 125·10^–6 Кл.

После перевода рубильника в положение 2, заряд Q распределяется между конденсаторами C₁ и C₂ (рис. 5). Обозначим эти заряды через Q’₁ и Q’₂.

На основании закона сохранения электричества имеем

Q = Q’₁ + Q’₂ = 125 10^–6 Кл. (1)

По второму закону Кирхгофа имеем

0= U C1 − U C2 = Q ′ 1 C 1 − Q ′ 2 C 2 ,

или

Q ′ 1 5⋅ 10 −6 − Q ′ 2 120⋅ 10 −6 =0. (2)

Решая уравнения (1) и (2), найдем

Q’₁ = 5 10^–6 Кл; Q’₂ = 120 10^–6 Кл.

Доставка свежих и аппетитных японских суши в Новороссийске — ям ям..

Напряжение на зажимах конденсаторов станет равным

U C1 = Q ′ 1 C 1 = U C2 = Q ′ 2 C 2 = 5⋅ 10 −6 5⋅ 10 −6 =1 В.

Энергия обоих конденсаторов будет равна

W= C 1 ⋅ U C1 2 2 + C 2 ⋅ U C2 2 2 =62,5⋅ 10 −6 Дж.

Подсчитаем энергию, которая была запасена в конденсаторе С₁, при его подключении к источнику электрической энергии

W нач = C 1 ⋅U 2 = 5⋅ 10 −6 ⋅ 25 2 2 =1562,5⋅ 10 −6 Дж.

Как видим, имеет место большая разница в запасе энергии до и после переключения. Энергия, равная 1562,5·10^–6 — 62,5·10^–6 = 1500·10^–6 Дж, израсходовалась на искру при переключении рубильника из положения 1 в положение 2 и на нагревание соединительных проводов при перетекании зарядов из конденсатора C₁ в конденсатор C₂ после перевода рубильника в положение 2.

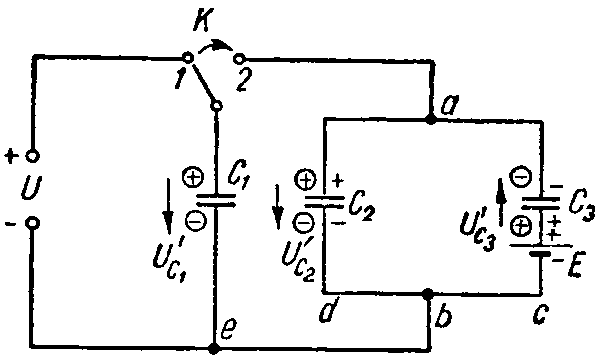
Задача 6. Вычислить напряжение, которое окажется на каждом из конденсаторов схемы (рис. 6) после перевода рубильника К из положения 1 в положение 2.

Емкости конденсаторов равны: C₁ = 10 мкФ; C₂ = 30 мкФ; C₃ = 60 мкФ; напряжение U = 30 В, а э. д. с. E = 50 В.

Рис. 6

Решение

Рубильник находится в положении 1. Заряд конденсатора C₁ равен

Q₁ = C₁·U = 10·10^–6·30 = 0,3·10^–3 Кл.

В указанном положении рубильника конденсаторы C₂ и C₃ соединены последовательно друг с другом, поэтому их заряды равны: Q₂ = Q₃. Знаки зарядов показаны на рис. 6 отметками без кружков. По второму закону Кирхгофа имеем

E= U C2 + U C3 = Q 2 C 2 + Q 3 C 3 = Q 2 ⋅ C 2 + C 3 C 2 ⋅ C 3 ,

откуда

Q 2 = Q 3 = C 2 ⋅ C 3 C 2 + C 3 ⋅E= 30⋅ 10 −6 ⋅60⋅ 10 −6 90⋅ 10 −6 ⋅50=1⋅ 10 −3 Кл.

При переводе рубильника в положение 2 произойдет перераспределение зарядов. Произвольно задаемся новой полярностью зарядов на электродах (показана в кружках; предположена совпадающей с ранее имевшей место полярностью); соответствующие положительные направления напряжений на конденсаторах обозначены стрелками. Обозначим эти заряды через Q’₁, Q’₂ и Q’₃. Для их определения составим уравнения на основании закона сохранения электрических зарядов и второго закона Кирхгофа.

Для узла a

Q’₁ + Q’₂ — Q’₃ = Q₁ + Q₂ — Q₃. (1)

Для контура 2ebda2

0= U ′ C1 − U ′ C2 = Q ′ 1 C 1 − Q ′ 2 C 1 .

Для контура bcadb

E= U ′ C2 − U ′ C3 = Q ′ 2 C 2 + Q ′ 3 C 3 .

Уравнения (1) — (3), после подстановки числовых значений величин, примут вид

Q’₁ + Q’₂ — Q’₃ = 0,3·10^–3; (4)

3Q’₁ — Q’₂ = 0; (5)

2Q’₂ + Q’₃ = 3·10^–3. (6)

Решая совместно уравнения (4) — (6), получим

Q’₁ = 0,33·10^–3 Кл; Q’₂ = 0,99·10^–3 Кл; Q’₃ = 1,02·10^–3 Кл.

Так как знаки всех зарядов оказались положительными, то фактическая полярность обкладок соответствует предварительно выбранной.

Напряжения на конденсаторах после перевода рубильника будут равны

U C1 = Q ′ 1 C 1 = 0,33⋅ 10 −3 10⋅ 10 6 =33 В; U C2 = Q ′ 2 C 2 = 0,99⋅ 10 −3 30⋅ 10 6 =33 В; U C3 = Q ′ 3 C 3 = 1,02⋅ 10 −3 60⋅ 10 6 =17 В.

Задача 7. Определить заряд и напряжение конденсаторов, соединенных по схеме рис. 7, если C₁ = 5 мкФ; C₂ = 4 мкФ; C₃ = 3 мкФ; э. д. с. источников E₁ = 20 В и E₂ = 5 В.

Рис. 7

Решение

Составим систему уравнений на основании закона сохранения электричества и второго закона Кирхгофа, предварительно задавшись полярностью обкладок конденсаторов, показанной в кружках

− Q 1 + Q 2 − Q 3 =0; E 1 = U C1 − U C3 = Q 1 C 1 − Q 3 C 3 ; E 2 =− U C2 − U C3 =− Q 2 C 2 − Q 3 C 3 .

Подставляя сюда числовые значения и решая эту систему уравнений, получим, что Q₁ = 50 мкКл; Q₂ = 20 мкКл; Q₃ = –30 мкКл.

Таким образом, истинная полярность зарядов на обкладках конденсаторов C₁ и C₂ соответствует выбранной, а у конденсатора C₃ — противоположна выбранной.

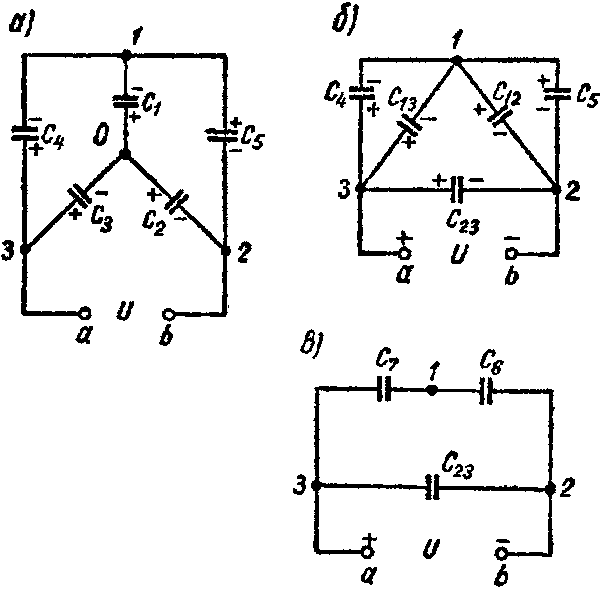
Задача 8. Пять конденсаторов соединены по схеме рис. 3-22, а, емкости которых C₁ = 2 мкФ; C₂ = 3 мкФ; C₃ = 5 мкФ; C₄ = 1 мкФ; C₅ = 2,4 мкФ.

Рис. 8

Индивидуалка Дана (34 лет) т.8 926 650-82-63 Москва, метро Сокол.

Определить эквивалентную емкость системы и напряжение на каждом из конденсаторов, если приложенное напряжение U = 10 В.

Решение

1-й способ. Звезду емкостей C₁, C₂ и C₃ (рис. 8, а) преобразуем в эквивалентный треугольник емкостей (рис. 8, б)

C 12 = C 1 ⋅ C 2 C 1 + C 2 + C 3 =0,6 мкФ; C 13 = C 1 ⋅ C 3 C 1 + C 2 + C 3 =1,0 мкФ; C 23 = C 2 ⋅ C 3 C 1 + C 2 + C 3 =1,5 мкФ.

Емкости C₁₂ и C₅ оказываются соединенными параллельно друг другу и подключенными к точкам 1 и 2; их эквивалентная емкость

C₆ = C₁₂ + C₅ = 3 мкФ.

Аналогично

C₇ = C₁₃ + C₄ = 2 мкФ.

Схема принимает вид изображенный на рис. 8, в. Емкость схемы между точками а и b равняется

C ab = C 23 + C 6 ⋅ C 7 C 6 + C 7 =2,7 мкФ.

Вычислим напряжение на каждом из конденсаторов.

На конденсаторе C₇ напряжение равно

U 7 = C 6 C 6 + C 7 ⋅U=6 В.

Таково же напряжение и на конденсаторах C₄ и C₁₃

U₄ = U₃₁ = 6 В.

Напряжение на конденсаторе C₆ равно

U₆ = U — U₇ = 4 В;

U₅ = U₁₂ = 4 В.

Вычислим заряды

Q₄ = C₄·U₄ = 6·10^–6 Кл;

Q₅ = C₅·U₅ = 9,6·10^–6 Кл;

Q₁₂ = C₁₂·U₁₂ = 6·10^–6 Кл;

Q₁₃ = C₁₃·U₃₁ = 2,4·10^–6 Кл.

По закону сохранения электричества для узла 1 схем 8, а и б имеем

–Q₄ — Q₁ + Q₅ = –Q₄ — Q₁₃ + Q₁₂ + Q₅,

отсюда

Q₁ = Q₁₃ — Q₁₂ = 3,6·10^–6 Кл,

а напряжение на конденсаторе, емкостью C₁ составляет

U 1 = Q 1 C 1 =1,8 В.

Далее находим напряжения и заряды на остальных конденсаторах

U₃₁ = U₁ + U₃,

отсюда

U₃ = U₃₁ — U₁ = 4,2 В;

Q₃ = C₃·U₃ = 21·10^–6 Кл,

также

U₁₂ = U₂ — U₁ = 4,2 В,

откуда

U₂ = U₁₂ + U₁ = 5,8 В;

Q₂ = C₂·U₂ = 17,4·10^–6 Кл.

Так как знаки всех зарядов оказались положительными, то фактическая полярность зарядов на обкладках совпадает с предварительно выбранной.

2-й способ. Выбрав положительные направления напряжений на конденсаторах (а тем самым и знаки зарядов на каждом из них) по формуле закона сохранения электричества (закона сохранения заряда) составляем два уравнения и по второму закону Кирхгофа три уравнения (рис. 8, а)

для узла 1

Q₅ — Q₁ — Q₄ = 0; (1)

для узла О

Q₁ + Q₂ — Q₃ = 0; (2)

для контура О13О

Q 1 C 1 − Q 4 C 4 + Q 3 C 3 =0; (3)

для контура О12О

Q 1 C 1 + Q 5 C 5 − Q 2 C 2 =0; (4)

для контура a3О2b

Q 3 C 3 + Q 2 C 2 =U. (5)

Система уравнений (1) — (5) — содержит пять неизвестных: Q₁, Q₂, Q₃, Q₄ и Q₅. Решив уравнения, найдем искомые заряды, а затем и напряжения на конденсаторах. При втором способе решения эквивалентную емкость схемы С_ab можно найти из отношения

C ab = Q U ,

где Q = Q₃ + Q₄, или Q = Q₂ + Q₅.

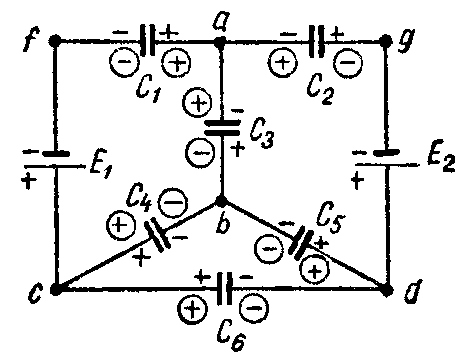
Задача 9. В схеме рис. 9 найти распределение зарядов, если E₁ = 20 В; E₂ = 7 В; C₁ = 7 мкФ; C₂ = 1 мкФ; C₃ = 3 мкФ; C₄ = 4 мкФ; C₅ = C₆ = 5 мкФ.

Рис. 9

Решение

При выбранном распределении зарядов (в кружках), как показано на схеме, система уравнений будет иметь вид:

для узла а

Q₁ + Q₂ + Q₃ = 0;

для узла b

–Q₃ — Q₄ — Q₅ = 0;

для узла c

–Q₁ + Q₄ + Q₆ = 0;

для контура afcba

E 1 = U C1 + U C4 − U C3 = Q 1 C 1 + Q 4 C 4 − Q 3 C 3 ;

ля контура gdbag

E 2 = U C5 − U C3 + U C2 = Q 5 C 5 − Q 3 C 3 + Q 2 C 2 ;

для контура cbdc

0= U C4 − U C5 − U C6 = Q 4 C 4 − Q 5 C 5 − Q 6 C 6 .

Подставляя сюда числовые значения и решая полученную систему шести уравнений, найдем искомые заряды

Q₁ = 35 мкКл; Q₂ = –5 мкКл; Q₃ = –30 мкКл;

Q₄ = 20 мкКл; Q₅ = 10 мкКл; Q₆ = 15 мкКл.

Таким образом, истинные знаки зарядов Q₁, Q₄, Q₅ и Q₆ соответствуют выбранным, а знаки Q₂ и Q₃ противоположны выбранным.

Фактическое расположение знаков зарядов на конденсаторах дано не в кружках.

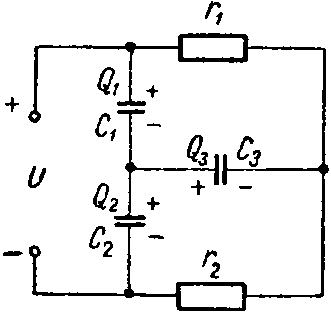
Задача 10. Определить заряд и энергию каждого конденсатора в схеме (рис. 10). Данные схемы: C₁ = 6 мкФ; C₂ = 2 мкФ; C₃ = 3 мкФ; r₁ = 500 Ом; r₂ = 400 Ом; U = 45 В.

Рис. 10

Решение

Через сопротивления протекает ток

I= U r 1 + r 2 =0,05 А.

Задавшись полярностью зарядов на обкладках конденсаторов, составим систему уравнений:

− Q 1 + Q 2 + Q 3 =0; U= U C1 + U C2 = Q 1 C 1 + Q 2 C 2 ; I⋅ r 1 = U C1 + U C3 = Q 1 C 1 + Q 3 C 3 ,

или

Q 1 = Q 2 + Q 3 ; 45= Q 1 6⋅ 10 −6 + Q 2 2⋅ 10 −6 ; 25= Q 1 6⋅ 10 −6 + Q 3 3⋅ 10 −6 .

Решив эту систему уравнений, найдем, что

Q₁ = 90 мкКл; Q₂ = 60 мкКл; Q₃ = 30 мкКл.

последовательное соединение конденсаторов,
параллельное соединение конденсаторов,
Расчет цепи конденсаторов,
Конденсатор в цепи постоянного тока,
Цепи с конденсаторами

Комментарии

Источник

Конденсатором называется система, состоящая из двух проводников, расположенных достаточно близко друг от друга. Проводники называют обкладками конденсатора. Если на обкладки конденсатора поместить равные по модулю и противоположные по знаку заряды, то разность потенциалов (напряжение) между обкладками будет пропорциональна заряду обкладок, т. е. отношение заряда к напряжению не будет зависеть от заряда. На основании этого утверждения, которое приводим без доказательства, вводится понятие электроёмкости (ёмкости конденсатора).

Ёмкостью конденсатора называется отношение заряда $$ Q$$ одной из обкладок к разности потенциалов $$ U$$ между этой обкладкой и соседней:

$$ C={displaystyle frac{Q}{U}}$$.

(10.1)

Если взят заряд на положительно заряженной обкладке, то $$ Q>0, U>0$$ и получится $$ C>0$$. Если заряд взят на отрицательной обкладке, то Q<0, U<0Q<0,;U<0 и опять будет $$ C>0$$. Итак, из определения ёмкости следует, что ёмкость величина положительная. В системе СИ ёмкость измеряется в фарадах: `1″Ф»=1` Кл/В.

Требование близости обкладок друг к другу связано с тем, что для независимости $$ C$$ от $$ Q$$ в (10.1) нужно, чтобы поле от зарядов на обкладках было сосредоточено практически полностью между обкладками, т. е. все силовые линии, начинающиеся на одной обкладке, заканчивались только на другой и не уходили на окружающие тела. В этом случае окружающие тела не будут влиять на ёмкость конденсатора.
Можно вывести, что ёмкость плоского конденсатора

$$ C={displaystyle frac{varepsilon {varepsilon }_{0}S}{d}}$$.

(10.2)

Здесь $$ S$$ — площадь обкладок, $$ d$$ — расстояние между ними, $$ varepsilon $$ — диэлектрическая проницаемость диэлектрика между обкладками.
При последовательном соединении изначально не заряженных конденсаторов с ёмкостями $$ {C}_{1}, {C}_{2}, …$$, общий заряд равен заряду каждого конденсатора, общее напряжение равно сумме напряжений на отдельных конденсаторах, общая ёмкость определяется из формулы: $$ {displaystyle frac{1}{C}}={displaystyle frac{1}{{C}_{1}}}+{displaystyle frac{1}{{C}_{2}}}+…$$

Полезно помнить формулу для частного случая последовательного соединения двух конденсаторов: $$ C={displaystyle frac{{C}_{1}{C}_{2}}{{C}_{1}+{C}_{2}}}$$.

Для последовательно соединённых n одинаковых конденсаторов ёмкостью $$ {C}_{1}$$ каждый $$ C={C}_{1}/n.$$

Если последовательно соединены предварительно заряженные конденсаторы, то применение перечисленных выше свойств и формул может привести к неправильному результату!
При параллельном соединении конденсаторов с емкостями $$ {C}_{1,} {C}_{2}, …$$ общий заряд равен сумме зарядов отдельных конденсаторов, общее напряжение равно напряжению на каждом, общая ёмкость равна сумме ёмкостей:

$$ C={C}_{1}+{C}_{2}+…$$

Рис. 10.1

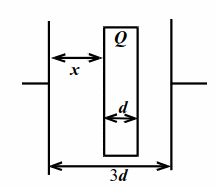
В плоский конденсатор параллельно его обкладкам вставлена пластина из диэлектрика с диэлектрической проницаемостью $$ varepsilon $$ (рис. 10.1). Площадь обкладок конденсатора и пластины $$ S$$, толщина пластины $$ d$$, расстояние между обкладками $$ 3d$$. Найти ёмкость такого конденсатора.

Пусть расстояние от пластины до левой обкладки конденсатора $$ x$$. Наклеим мысленно на обе стороны пластины тонкую проводящую и незаряженную фольгу. От этого ничего не изменится. Обе фольги можно рассматривать как своеобразные провода, соединяющие три последовательно соединённых конденсатора с расстояниями $$ x$$, $$ d$$ и $$ 2d-x$$. Для общей ёмкости $$ C$$:

$$ {displaystyle frac{1}{C}}={displaystyle frac{x}{{varepsilon }_{0}S}}+{displaystyle frac{d}{varepsilon {varepsilon }_{0}S}}+{displaystyle frac{2d-x}{{varepsilon }_{0}S}}$$.

Окончательно $$ C={displaystyle frac{varepsilon {varepsilon }_{0}S}{d(2varepsilon +1)}}.$$ Заметим, что не заданная в условии величина $$ x$$ «исчезла» в процессе решения.

Рис. 10.2

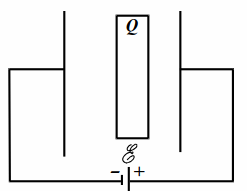
В плоский конденсатор ёмкостью $$ C$$ вставлена параллельно обкладкам плоская проводящая пластина с зарядом $$ Q$$ (рис. 10.2). Конденсатор подсоединён к источнику с ЭДС $$ mathcal{E}$$. Площади пластины и обкладок конденсатора равны. Толщина пластины равна расстоянию от неё до правой обкладки и составляет четверть от расстояния между обкладками. Найти заряд конденсатора.

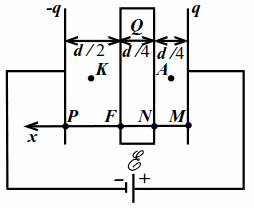
Пусть $$ d$$ – расстояние между обкладками, $$ S$$ – их площадь. Пусть $$ q$$ заряд правой обкладки. Тогда заряд левой будет $$ -q$$, т. к. заряд в значительных количествах не может накапливаться на соединительных проводах и в источнике. Направим ось $$ x$$ влево (рис. 10.3).

Рис. 10.3

Заметим, что поле внутри пластины отсутствует и разность потенциалов $$ {varphi }_{N}-{varphi }_{F}$$ между точками $$ N$$ и $$ F$$ равна нулю. Кроме того, заряды на поверхностях пластины создают вне пластины такое же поле, как и заряд $$ Q$$, если бы его расположить на любой из двух поверхностей пластины. Это легко показать отдельно.

Разность потенциалов $$ {varphi }_{M}-{varphi }_{P}$$ между точками $$ M$$ и $$ P$$ равна $$ mathcal{E}$$. Поэтому

$$ ({varphi }_{M}-{varphi }_{N})+({varphi }_{N}-{varphi }_{F})+({varphi }_{F}-{varphi }_{P})=mathcal{E}$$.

У нас $$ {varphi }_{M}-{varphi }_{N}={E}_{A}{displaystyle frac{d}{4}}, {varphi }_{N}-{varphi }_{F}=0, {varphi }_{F}-{varphi }_{P}={E}_{K}{displaystyle frac{d}{2}}$$.

Здесь — $$ {E}_{A}$$ и $$ {E}_{K}$$ — проекции напряжённости результирующего поля на ось `x`. По принципу суперпозиции полей

$$ {E}_{A}={displaystyle frac{q}{2{varepsilon }_{0}S}}-{displaystyle frac{Q}{2{varepsilon }_{0}S}}-{displaystyle frac{-q}{2{varepsilon }_{0}S}}={displaystyle frac{1}{2{varepsilon }_{0}S}}left(2q-Qright)$$,

$$ {E}_{K}={displaystyle frac{q}{2{varepsilon }_{0}S}}+{displaystyle frac{Q}{2{varepsilon }_{0}S}}-{displaystyle frac{-q}{2{varepsilon }_{0}S}}={displaystyle frac{1}{2{varepsilon }_{0}S}}left(2q+Qright)$$.

Подставляя выражения для $$ {E}_{A}$$, $$ {E}_{K}$$ и разностей потенциалов в первое
уравнение, получим после упрощений $$ 6q+Q=8mathcal{E}{displaystyle frac{{varepsilon }_{0}S}{d}}$$.

Так как $$ {displaystyle frac{{varepsilon }_{0}S}{d}}=C$$, то $$ q=(8Cmathcal{E}-Q)/6$$.

Следует заметить, что знак найденного заряда правой обкладки зависит от соотношения заданных в условии задачи величин.

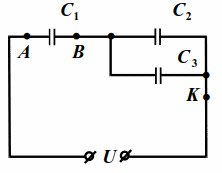Рис. 10.4

На схему (рис. 10.4) подано напряжение `U=24` В. Ёмкости конденсаторов `C_1=1` мкФ, $$ {C}_{2}=2$$ мкФ, $$ {C}_{3}=3$$ мкФ. Найти напряжения на конденсаторах.

В задачах, где есть схемы с конденсаторами, обычно предполагается, что схемы собраны из первоначально незаряженных конденсаторов.

Ёмкость между точками $$ B$$ и $$ K$$:

$$ {C}_{BK}={C}_{2}+{C}_{3}=5$$ мкФ.

Общая емкость: $$ {C}_{AK}={displaystyle frac{{C}_{1}{C}_{BK}}{{C}_{1}+{C}_{BK}}}={displaystyle frac{5}{6}}$$ мкФ.

Общий заряд всей батареи конденсаторов $$ {q}_{AK}={C}_{AK}U=20·{10}^{-6 }mathrm{Кл}.$$

Так как заряд $$ {q}_{1}$$ конденсатора $$ {C}_{1}$$ равен заряду батареи, то напряжение на этом конденсаторе $$ {U}_{1}={q}_{1}/{C}_{1}={q}_{AK}/{C}_{1}=20$$ В. Напряжения на конденсаторах $$ {C}_{2}$$ и $$ {C}_{3}$$ равны напряжению между точками $$ B$$ и $$ K$$ и в сумме с $$ {U}_{1}$$ дают $$ U$$.
Поэтому $$ {U}_{2}={U}_{3}={U}_{BK}=U-{U}_{1}=4$$ В.

Приведённая в задаче схема негромоздкая, и ответ легко получить в общем виде:

$$ {U}_{1}={displaystyle frac{{C}_{2}+{C}_{3}}{{C}_{1}+{C}_{2}+{C}_{3}}}U=20$$ B,

$$ U2=U3={displaystyle frac{{C}_{1}}{{C}_{1}+{C}_{2}+{C}_{3}}}U=4$$ B.

Источник

Емкость конденсатора определяется как способность конденсатора накапливать максимальный электрический заряд (Q) в своем теле. Заряд хранится в виде электростатической энергии. Емкость конденсаторов измеряется в единицах СИ- фарадах. Эти единицы могут быть обозначены в микрофарадах, нанофарадах, пикофарадах или фарадах. Формула для определения емкости конденсатора следующая:

C = Q/V = εA/d = ε0 εr A/d

Где,

C — емкость,

Q — заряд,

V — разность потенциалов между пластинами,

А — площадь между пластинами,

d — расстояние между пластинами.

ε — диэлектрическая проницаемость диэлектрика

ε0 — диэлектрическая проницаемость свободного пространства

εr — относительная диэлектрическая проницаемость свободного пространства

Собственная емкость

Свойство собственной емкости относится к конденсаторам с изолированным проводником. Как видно из названия, емкость — это свойство изолированного проводника повышать разность потенциалов до одного В. Обычно нормальные проводники имеют взаимную емкость. Это также измеряется в единицах СИ, то есть в фарадах.

Собственная емкость проводящей сферы радиусом R определяется выражением:

C = 4 π ɛ _o R

Ниже приведены некоторые примеры значения собственной емкости:

Для верхней пластины генератора Ван де Графа, имеющей радиус 20 см, собственная емкость составляет 22,24 пФ.
Для планеты Земля собственная емкость составляет 710 мкФ.

Паразитная емкость

Паразитная емкость — это нежелательная емкость, т.е. шум. Даже такие компоненты, как резисторы, катушки индуктивности и провод, имеют свою некоторую емкость. Обычно на высоких частотах это приводит к появлению шума в цепи.

Паразитную емкость нельзя полностью устранить, но ее можно уменьшить. Разработчики схем должны позаботиться о паразитной емкости при проектировании схемы. Разделение и расстояние между компонентами и дорожками платы должно строго соблюдаться для уменьшения нежелательной емкости.

Она также измеряется в единицах СИ, то есть в фарадах.

Примерами являются: емкость между витками катушки, емкость между двумя соседними проводниками.

Емкость простых схем

Расчет емкости не что иное , как решение теоремы Лапласа ∇ 2 φ = 0 с постоянным потенциалом на поверхности конденсатора. Ниже приведены значения емкости для некоторых простых схем:

Заряд конденсатора

Способность конденсатора накапливать максимальный заряд (Q) на своих металлических пластинах называется его значением емкости (C). Полярность накопленного заряда может быть отрицательной или положительной, например, положительный заряд (+ ve) на одной пластине и отрицательный заряд (-ve) на другой пластине конденсатора. Выражения для заряда, емкости и напряжения приведены ниже.

C = Q/V, Q = CV, V = Q/C

Таким образом, заряд конденсатора прямо пропорционален его емкости и разности потенциалов между пластинами конденсатора. Заряд измеряется в кулонах. Один кулон заряда конденсатора можно определить как емкость в одну фараду между двумя проводниками, которые работают с напряжением в один вольт.

Заряд Q, накопленный в конденсаторе, имеющем емкость C, разность потенциалов V и воздух в качестве его диэлектрика, определяется выражением:

Q = CV = (ε × (A × V))/d

Где,

ε0 — диэлектрическая проницаемость свободного пространства,

εr — относительная диэлектрическая проницаемость диэлектрического материала,

ε — диэлектрическая проницаемость диэлектрического материала.

Из двух вышеупомянутых случаев мы можем наблюдать:

Заряд конденсатора прямо пропорционален площади пластин, диэлектрической проницаемости диэлектрического материала между пластинами и обратно пропорционален расстоянию между пластинами. Таким образом, чем больше площадь пластин, тем больше заряд конденсатора, а чем больше расстояние между пластинами, тем меньше заряд конденсатора.

Параллельный пластинчатый конденсатор

На приведенном выше рисунке показана схема конденсатора с параллельными пластинами. Как мы знаем, емкость прямо пропорциональна площади пластин (A) и обратно пропорциональна расстоянию (d) между двумя металлическими пластинами. Значение емкости конденсатора с параллельными пластинами определяется выражением:

C = k ε0A/d

Где, k — диэлектрическая проницаемость, а ε0 — диэлектрическая проницаемость свободного пространства, равная 8,854 · 10 -12 Ф/м. Диэлектрическая постоянная (k) — это параметр, связанный с диэлектрическим материалом, который увеличивает емкость по сравнению с воздухом. Чем больше площадь поверхности пластин, тем больше значение емкости, и наоборот. Еще один пример схемы конденсатора с параллельными пластинами показан на рисунке ниже.

Пример емкости №1

Теперь мы рассчитаем емкость конденсатора с параллельными пластинами в пикофарадах, у которого площадь поверхности пластин составляет 200 см2, и они разделены воздухом в качестве его диэлектрического материала с расстоянием 0,4 см.

Уравнение емкости конденсатора с параллельными пластинами выглядит следующим образом:

C = A/d

ε = 8,854 X 10-12Ф / м.

A = 200 см2 = 0,02 м2

D = 0,4 см = 0,004 м

Теперь мы подставляем эти значения в приведенное выше уравнение:

C = 8,854 X 10-12 * (0,02 м2 / 0,004 м) = 44,27 пФ

И получаем, емкость конденсатора с параллельными пластинами составляет 44,27 пФ.

Зарядка и разрядка конденсатора

Схема ниже используется для объяснения заряда и разряда конденсатора. Предположим, что конденсатор, который показан на схеме, полностью разряжен. В этой схеме емкость конденсатора составляет 100 мкФ, а напряжение питания, подаваемое на эту схему, составляет 12 В.

Теперь переключатель, который подключен к конденсатору в цепи, перемещается в точку A. Затем конденсатор начинает заряжаться зарядным током (i). Напряжение зарядки на конденсаторе равно напряжению питания, когда конденсатор полностью заряжен, то есть VS = VC = 12 В. Когда конденсатор полностью заряжен, это означает, что конденсатор поддерживает заряд с постоянным напряжением, даже если напряжение питания отключено от цепи.

В случае идеальных конденсаторов, заряд на конденсаторе остается постоянным, но в случае обычных конденсаторов полностью заряженный конденсатор медленно разряжается из-за его тока утечки.

Когда переключатель перемещается в положение B, конденсатор медленно разряжается за счет включения лампы, которая помещена в цепь. Наконец-то он полностью разряжен до нуля. Сначала лампа ярко светится, когда конденсатор полностью заряжен, но яркость лампы уменьшается по мере уменьшения заряда конденсатора.

Пример заряда конденсатора №2

Теперь давайте вычислим заряд конденсатора в приведенной выше схеме. Уравнение заряда конденсатора имеет следующий вид:

Q = CV

C = 100 мкФ

V = 12V

Теперь мы подставляем эти значения в приведенное выше уравнение:

Q = 100 мкФ * 12 В = 1,2 мкФ

Следовательно, заряд конденсатора в приведенной выше схеме составляет 1,2 мКл.

Ток протекающий через конденсатор

Ток (i), протекающий через любую электрическую цепь, — это скорость заряда (Q), протекающего через нее, относительно времени. Но заряд конденсатора прямо пропорционален приложенному через него напряжению. Соотношение между зарядом, током и напряжением конденсатора приведено в уравнении ниже:

I (t) = d Q (t) / dt = C dV (t) / dt

Мы знаем, что:

Q = CV

V = Q / C

V (t) = Q (t) / C

Q (t) = CV (t)

Отношение тока к напряжению определяется выражением:

I (t) = C dV (t) / dt

Из этого соотношения мы можем заметить, что ток, протекающий через конденсатор в цепи, является произведением емкости и скорости изменения напряжения, приложенного к цепи. Ток, протекающий через конденсатор, прямо пропорционален емкости конденсатора и величине напряжения.

Чем больше ток, тем выше емкость цепи и чем выше приложенное напряжение, тем больше ток, протекающий по цепи. Если напряжение постоянное, то и заряд постоянен, поэтому заряд не протекает. Следовательно, ток, протекающий по цепи, станет нулевым.

Единица емкости (Фарад)

Джозия Латимер Кларк в 1861 году впервые использовал термин Фарад. Фарад — стандартная единица измерения емкости. Это очень большая единица измерения емкости.

Емкость одна фарада определяется как емкость с одним кулоном заряда, работающая при напряжении в один вольт.

C = Q / V

1Фарад = 1Кулон / 1В

Сейчас доступны конденсаторы с большой емкостью в сотни фарад. Эти конденсаторы с высокими значениями емкости называются «суперконденсаторами». В этих конденсаторах используется большая площадь поверхности для передачи высокой энергии, поскольку они имеют высокие значения емкости.

При низком напряжении суперконденсаторы обладают способностью накапливать большую энергию с высокими значениями емкости. Эти высокоэнергетические суперконденсаторы используются в переносных портативных устройствах для замены больших, тяжелых и дорогих конденсаторов литиевого типа, поскольку они хранят большую энергию, как батареи. Эти конденсаторы также используются в аудио- и видеосистемах в транспортных средствах для замены высоковольтных батарей.

Разделение Фарада

Стандартная единица измерения емкости — фарады. Но это очень большая единица измерения емкости. В этом фараде есть несколько дополнительных единиц; это микрофарады (мкФ), нанофарады (нФ) и пикофарады (пФ).

1 мкФ (мкФ) = (1/1000000) Ф = 10-6 Ф

1нано-Фарад (мкФ) = (1/1000000000) Ф = 10-9 Ф

1 пико-Фарад (мкФ) = (1/1000000000000) Ф = 10-12 Ф

Теперь мы увидим некоторые преобразования между единицами измерения емкости,

(i) преобразование 33 пФ в нФ => 33 пФ = 0,033 нФ

(ii) преобразование 22 нФ в мкФ => 22 нФ = 0,022 мкФ

(iii) преобразование 11 мкФ в Ф => 11 мкФ = 0,11 Ф

Энергия в конденсаторе

Энергия — это количество некоторой работы против электростатического поля для полной зарядки конденсатора. В конденсаторе на начальной стадии зарядки заряд Q передается между пластинами с одной пластины на другую. Этот заряд либо + Q, либо –Q меняется местами между двумя пластинами конденсатора. После преобразования некоторого заряда между пластинами образуется электрическое поле, в этом случае нам потребуется дополнительная работа, чтобы зарядить конденсатор полностью. Эта дополнительная работа называется энергией, запасенной в конденсаторе. Энергия измеряется в джоулях (Дж). Теперь мы приведем уравнения для этой энергии и работы:

dW = V dQ

dW = (Q / C) dQ

После интегрирования приведенного выше уравнения:

W = Q 2 / 2C

W = (CV) 2 / 2C

W = CV 2 /2 Джоулей

Наконец, мы получаем, что энергия, хранящаяся в конденсаторе, равна:

Энергия (W) = CV 2 /2 Джоулей

Теперь посчитаем энергию, запасенную в конденсаторе емкостью 200 мкФ, работающего с напряжением 12 В.

W = CV 2 /2

W = (200 × 10-6 × 12 2 ) / 2 = 14,4 м Дж

Вот и все, что вам нужно было знать о емкости и заряде конденсатора. Если вам нравятся наши статьи, то оставляйте свои комментарии.

С Уважением, МониторБанк

Источник

Конденсатор .

Конденсатор это устройство, способное накапливать электрический заряд.

Конденсатор также называют электрической емкостью.

Конденсатор имеет два электрических контакта.

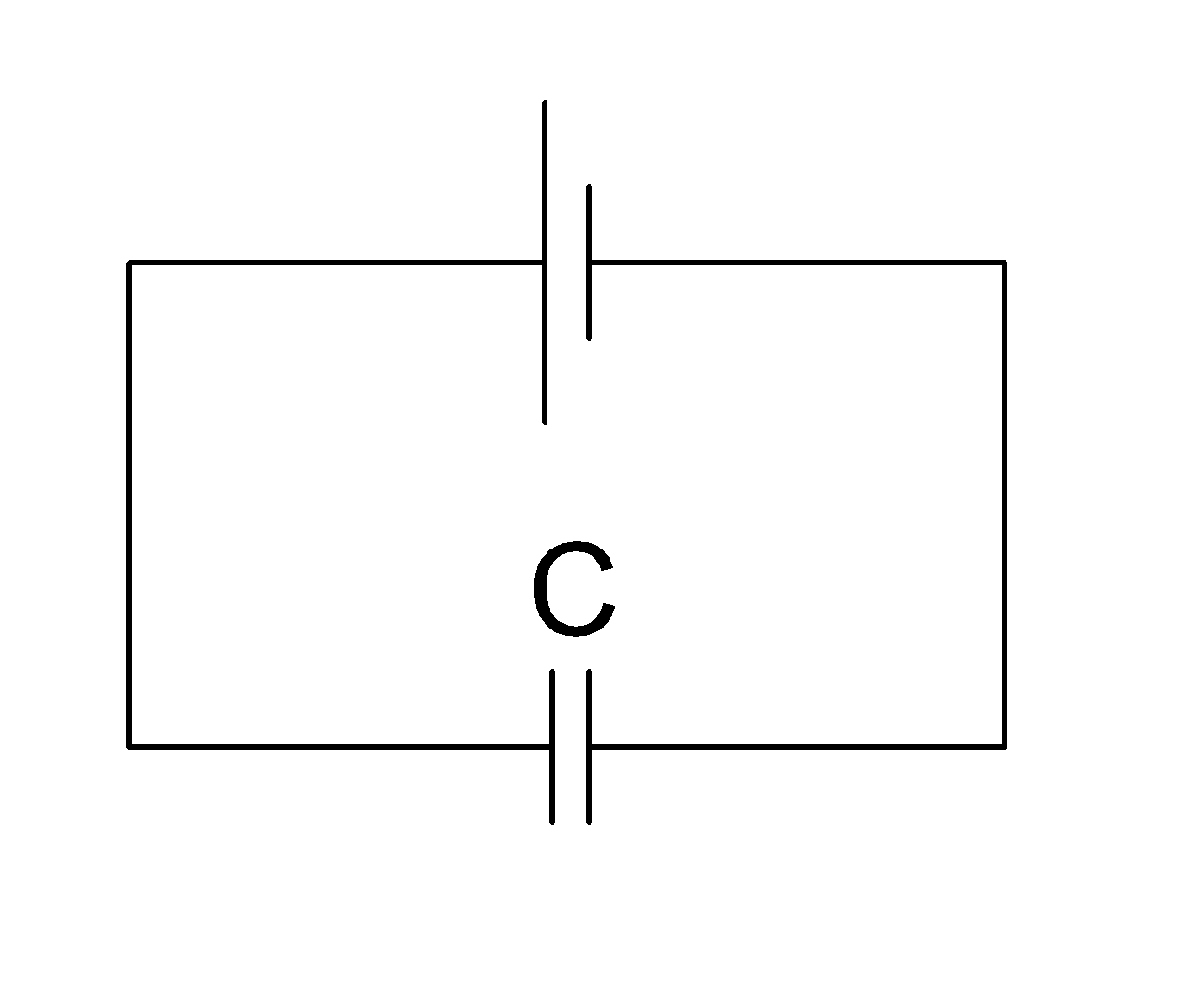
На этой схеме конденсатор подключен к источнику питания(батарейке):

Сверху источник питания, снизу конденсатор.

Конденсатор на схеме обозначается буквой (C )

Любой конденсатор обладает емкостью ( C )

Емкость конденсатора измеряется в фарадах [Ф]

1 фарад это довольно большая величина, обычно емкость конденсаторов намного меньше
одного фарада.

Обычно емкости конденсаторов даны в:

Микрофарадах ( ( 1 мкФ= 10^{-6} Ф ) )

Нанофарадах ( ( 1 нФ =10^{-9} Ф ) )

Пикофарадах ( (1 пФ= 10^{-12} Ф ) )

Чем больше емкость конденсатора , тем больший заряд он может накопить.

( q=CU )

(q)- заряд конденсатора

(U) — напряжение на конденсаторе

Задача 1.

Найти заряд

конденсатора, если напряжение на нем составляет (U=100 Вольт ), а его

емкость (C=0,0001 Ф . )