Конденсаторы часто применяются в электрических схемах, помогая трансформировать электросигнал под определенные характеристики. Используя их основное свойство — накапливать электрический заряд, можно регулировать прохождение тока по цепи, убирать нежелательные пульсации напряжения или повысить энергоэффективность сети. При решении подобных задач в расчет берутся конкретные параметры того или иного электронакопителя, а также общие процессы, связанные с зарядом и разрядом конденсаторов.
- Заряд конденсатора
- Процессы зарядки и разрядки конденсаторов
- Емкость и энергия конденсатора
- Как зарядить конденсатор
- Время, необходимое для зарядки конденсатора
- Заряд конденсатора: формула
- Время разряда конденсатора
Заряд конденсатора
Устройство обычного конденсатора состоит из двух пластин (обкладок), подключаемых к выходам цепи, и диэлектрика между ними. При этом величина заряда, накаливаемого конденсатором, зависит от его емкостной характеристики основных параметров: площади обкладок, толщины и диэлектрических свойств прокладочного материала.
Емкость конденсатора определяется по формуле:
C = S • ε • ε0 / d,
где S – площадь обкладок, ε — диэлектрическая проницаемость прокладки, ε0 — диэлектрическая постоянная (8,85•10-12 Ф/м), d – расстояние между пластинами.
Конденсируемый же заряд равняется произведению емкости конденсатора на напряжение в цепи: q = С × U.
Процессы зарядки и разрядки конденсаторов
При включении конденсатора в цепь через него начинает проходить ток. С движением электронов по проводнику на одной обкладке устройства скапливается отрицательный заряд, а на другой (при недостатке электронов) — положительный. Между пластинами образуется индуктивное поле, создающее разность потенциалов определенного значения. В проводниках постоянного тока накопление заряда идет до тех пор, пока уровень напряжения на обкладках не сравняется с номинальным напряжением элемента питания, после чего течение электротока останавливается.
Когда цепь размыкается и на конденсатор не подается напряжение, он может сохранять заряд на протяжение определенного времени, а затем с исчезновением электрического поля между пластинами заряд начнет перетекать в проводник. Процесс разряда конденсатора характеризуется переходом электронов с одной обкладки на другую. Конденсатор разряжается полностью, когда количество свободных электронов на обеих пластинах сравнивается. При этом все электродинамические процессы в цепи прекращаются.
Емкость и энергия конденсатора
Конденсатор, как и всякий объект, получающий электрический заряд, обладает энергией. Для его зарядки требуется определенная работа, которая идет на разделение заряженных частиц — именно она считается энергией конденсаторного устройства. Ее можно увидеть, если заряженный конденсатор присоединить, например, к светодиоду. Накопитель отдаст заряд лампочке, и она на некоторое время загорится, тем самым энергия перейдет в свет и тепло.
Для определения энергии конденсатора в расчет берут количество заряда, толщину диэлектрика и напряженность электрического поля. Последняя является векторной величиной и представляет собой силу, действующую на точечный заряд.
Поскольку заряды на обкладках равны между собой по модулю, во внимание принимается только значение напряженности одной из них, а значит, эта величина делится пополам — Е/2. Общая же энергия определяется по формуле:
Wp = qEd/2.
Произведение напряженности на расстояние между пластинами само себе представляет разность потенциалов или напряжение — U = E × d. Таким образом, энергию можно выразить через заряд и напряжение на конденсаторе. Формула будет иметь следующий вид:
Wp = qU/2.
Учитывая, что заряд и напряжение находятся в зависимости от емкости конденсатора, можно вывести еще пару формул энергии:
Wp = q2/2C
Wp = CU2/2
Как зарядить конденсатор
Для зарядки конденсатора требуется генератор электротока. Возникающие при этом процессы удобнее разобрать на примере простой цепи, включающей в себя конденсатор (С) и резистор (R).
Зарядка конденсатора от источника постоянной ЭДС
В соответствии с законом Ома разность потенциалов, возникающая на резисторе и конденсаторе, суммарно равна электродвижущей силе генератора тока. Математически это можно представить следующими формулами:
UC = q/C – напряжение конденсатора;
UR = IR – напряжение резистора;
ε = UC + UR – ЭДС источника.
Для пояснения зарядного процесса определим равенство
IR = ε – q / C.
Эта формула представляет динамические изменения заряда силы тока. Более конкретно это может быть выражено уравнением:
I = dq / dt.
Изменение заряда во времени можно подставить к сопротивлению. Соответственно, получаем
R • dq / dt = ε – q / C.
В строгом смысле это уравнение предписывает бесконечное время зарядки конденсаторного устройства. Однако этим можно пренебречь, если учесть, что заряд фактически дискретен и может быть подвержен случайным изменением и флуктуациям. Таким образом, в данном выражении имеются в виду усредненная динамика зарядного процесса. На его основании можно записать изменение ЭДС и составляющих напряжений обоих элементов цепи:
dε = d(IR) + d(q/C).
Фактически ЭДС генератора не меняется во времени, а значит, dε = 0, а емкость конденсатора и сопротивление обладают постоянными значениями, поэтому их можно обозначить без d:
R • dI = — 1/C • dq.
Поделив данное уравнение на временной период, за который заряжается конденсатор, можно вывести выражение, учитывающее корреляцию между динамикой заряда и силой тока:
dI / dt = –I/RC.
Это уравнение означает отношение скорости, с которой уменьшается сила тока к ее фактическому значению.
В начале процесса заряда конденсатора значение q равняется нулю. В этот момент при наибольшей разнице напряжений источника питания и электронакопителя сила тока имеет максимальное значение. По мере увеличения заряда значение I постепенно падает. Когда конденсатор заряжается полностью, его напряжение сравнивается с ЭДС генератора, а сила тока принимает значение 0. Соответственно, электродинамический процесс прекращается.
Дополнительно можно рассмотреть, как в процессе зарядки трансформируется энергия. Вполне очевидно, что генератор тока является причиной возникновения электротока в цепи и, следовательно, заряда электронакопителя.
В этом усматривается некое противоречие: когда конденсатор получает от генератора тока заряд q, это значит, что ЭДС выполнила работу равную заряду (А = qe), однако энергия самого накопителя определяется по формуле W = q2 / 2C = qε / 2, что составляет только половину от работы, произведенной источником питания. Этот парадокс объясняется самим фактом прохождения тока по электроцепи, которое сопровождается выделением тепловой энергии на резисторе, то есть определенное количество энергопотери приходится на тепло.
Дифференциальные расчеты для малых отрезков времени процесса зарядки показывают, что энергия от генератора, действительно, разделяется на электрическую, идущую на заряд конденсаторного устройства, и тепловую. При этом сопротивление цепи само по себе никак не влияет на количество выделяемой теплоты, которое равняется энергии конденсатора.
Заряд конденсатора, ток
При подключении конденсатора к источнику тока в начале зарядки заряд на пластинах практически отсутствует. Максимальное значение I в этой ситуации объясняется минимальным сопротивлением. С увеличением заряженных частиц, возрастает сопротивление индуктивного поля, которое препятствует прохождению тока по проводнику.
Период времени, за начальную точку которого берут момент наибольшей силы тока, а за конечную полное прекращение движения заряженных частиц, носит название переходного периода зарядки конденсатора.
Начальный момент зарядки конденсатора характеризуется нулевым напряжением между его пластинами. Показатель U начинает возрастать с появлением на обкладках разноименно заряженных частиц. Большая сила тока в начале процесса обусловливает большую скорость увеличения напряжения. По мере ее падения рост напряжения замедляется, достигнув максимального значения при полной зарядке электронакопителя.
График увеличения напряжения имеет вид параболы, будучи противоположным графику снижения силы тока.
Математически динамическую взаимозависимость тока, напряжения и емкости конденсатора можно выразить следующим образом:
I = С • dV / dt.
Время, необходимое для зарядки конденсатора
Время зарядки конденсатора определяется его емкостью, электродвижущей силой генератора тока, напряжением и сопротивлением в цепи.
Заряд конденсатора описывается как экспоненциальный процесс. Чтобы оценить его время, принимается, что значение заряда увеличивается равномерно, при этом скорость заряда приравнивается к силе тока в начале процесса. Отсюда следует уравнение постоянной времени:
τ = q / I0 = RC.
Зависимость динамики напряжения от длительности зарядки определяется по следующей формуле:
U(t) = UC • (1 – e-t/τ).
Значение высчитывается с привлечением основания натурального логарифма (е), которое относится к функции экспоненты и равняется приблизительно 2,718. При этом UC обозначает напряжение ЭДС источника.
Процент заряда по постоянной времени τ определяется в соответствии с формулой:
(1 — 1/еτ) • 100%.
Таким образом, конденсатор достигает почти полной зарядки за 5 τ.
• 1 τ — 63,2%;
• 2 τ — 86,5%
• 3 τ — 95,1%
• 4 τ — 98,2%
• 5 τ — 99,3%
Учитывая экспоненциальный характер увеличения напряжения конденсатора, можно сказать, что время его зарядки до уровня ЭДС генератора длится бесконечно долго.
Заряд конденсатора: формула
Конденсатор заряжается довольно быстро. Обычно для этого достаточно нескольких миллисекунд. Равенство напряжения электродвижущей силы источника питания и электронакопителя определяет максимальный заряд конденсатора. Формула заряда может быть определена с учетом общих параметров конденсатора:
q = Uεε0S/d.
Также можно принять во внимание конструкционные особенности конденсатора. Так, для цилиндрического накопителя заряд равняется:
q = U2πεε0l/ln(r2/r1),
где l – высота цилиндров, r2 – радиус наружной пластины, r1 — радиус внутренней пластины.
Время разряда конденсатора
Если конденсатор переключить на нагрузку резистора, он сам станет источником питания и будет отдавать заряд в цепь. Движение тока при этом начинается от пластины с отрицательным зарядом на положительно заряженную пластину и далее по контуру. Напряжение в начальный момент будет такое же как и после полной зарядки накопителя. В соответствии с законом Ома можно определить и первоначальную силу тока:
IC = UC / R.
Отдавая заряд, конденсатор будет терять напряжение. Соответственно будет уменьшаться и сила тока. Снижение обоих показателей идет по экспоненциальной кривой с замедлением скорости падения. Это значит, что динамику разрядки конденсатора можно описать, как и в случае зарядки, при помощи постоянной времени τ.
Изменение основных электрических показателей при заряде и разряде конденсатора играют ключевую роль в электротехнике и радиоэлектронике. Эта функциональность в полной мере проявляется в цепях переменного тока, где оба процесса сменяют друг друга с определенной периодичностью. На частотно-зависимых качествах электронакопителей основан принцип действия таких электроустановок, как колебательные контуры, реле времени, цепи обратной связи, частотные фильтры и другие.
Понравилась статья? Расскажите друзьям:
Оцените статью, для нас это очень важно:
Проголосовавших: 3 чел.
Средний рейтинг: 5 из 5.
Закон сохранения энергии для колебательного контура и анализ графика колебаний
Вадим Муранов, победитель всероссийского конкурса «Учитель года», преподаватель физики с 24-летним опытом работы.
Всем добрый день! Рад приветствовать вас на нашем очередном уже 26-ом воскресном мастер-классе!
Тема нашего сегодняшнего мастер-класса «Колебания»
«Сила тока в идеальном колебательном контуре меняется со временем так, как показано на рисунке. Определите заряд конденсатора в момент времени 7 мкс.
Вместо таблицы в этой задаче график колебаний. Что можно определить по данному графику? Прежде всего, любой график колебаний – это зависимость некой величины (не важно какой) от времени. В данном случае, если мы внимательно посмотрим, увидим, что здесь синусоида
Первое, что определяется по графику – это промежуток по времени между двумя пиками или впадинами этого графика. И этот промежуток является периодом колебаний
Второе, что можно определить, – это максимальное значение величины, чей график изображен на рисунке. В данном случае это сила тока, поэтому по максимальной точке можно определить максимальное или амплитудное значение силы тока. Иными словами, верхняя точка графика – это амплитуда той величины, чей это график
Необходимо найти заряд на конденсаторе в момент времени t=7 мкс. Но моменту времени 7 мкс соответствует некое значение силы тока, которое мы можем легко определить по графику. Находим 7 мкс, опускаемся вниз, видим, что это соответствует силе тока
Сразу должен сказать, что этот минус нам ни о чем не говорит, это просто обозначает, что ток течет в другом направлении, поэтому минус для нас неважен. И сам заряд мы так же определим, это будет положительный ответ.
Можно по-разному находить этот заряд: можно составить уравнение заряда в зависимости заряда от времени, и с помощью него определить величину этого заряда, но мы поступим по-другому.
Вспомним, что в нашей задаче написано, что контур идеальный, а, на самом деле, все задачи, с которыми вы будете встречаться в школе, будут связаны с идеальными маятниками и идеальными колебательными контурами.
Для идеального колебательного контура выполняется следующая вещь: в любой момент времени суммарная энергия, сосредоточенная в этом контуре (в конденсаторе и в катушке), будет равна любой из максимальных, то есть максимальной энергии электрического поля или максимальной энергии магнитного поля
Wэ + Wм = Wэм = WМм
Вот это равенство является законом сохранения энергии для идеального колебательного контура. Запомните это равенство, оно вам пригодится в грядущих событиях. Сейчас мы тоже это равенство применим, и даже не один раз.
Еще раз: суммарная энергия, запасенная в контуре, равна максимальным значениям энергии электрического поля конденсатора или максимальному значению энергии магнитного поля. В данном случае нам удобнее приравнять это к максимальной энергии магнитного поля, т. к. нам известна максимальная сила тока.
Запишем
и домножим это равенство на 2С, чтобы полностью убрать все знаменатели.
В итоге получаем
Замечаем, что произведение LC присутствует в формуле периода , знаменитая формула Томсона.
Отсюда выражаем произведение LC и получаем
Заменим LC на , но сначала выразим заряд в квадрате
А теперь вместо LC подставляем и получаем
Далее убираем квадрат у заряда
Теперь подставляем все известные значения и вычисляем по инженерному калькулятору
Получаем приблизительный ответ Кл. Теперь переводим это в микрокулоны 0,57 мкКл. Вот таким должен быть ответ!
Все видео по физике
Спасибо за то, что пользуйтесь нашими материалами.
Информация на странице «Закон сохранения энергии для колебательного контура и анализ графика колебаний» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать нужные и поступить в ВУЗ или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими статьями из данного раздела.
Публикация обновлена:
08.05.2023
Что такое конденсатор
Конденсатор или как в народе говорят — «кондер», образуются от латинского «condensatus», что означает как «уплотненный, сгущенный». Он представляет из себя пассивный радиоэлемент, который обладает таким свойством, как сохранение электрического заряда на своих обкладках, если, конечно, перед этим его зарядить каким-нибудь источником питания.
Грубо говоря, конденсатор можно рассматривать как батарейку или аккумулятор электрической энергии. Но вся разница в том, что аккумулятор или батарейка имеют в своем составе источник ЭДС, тогда как конденсатор лишен этого внутреннего источника.
Из чего состоит конденсатор
Любой конденсатор состоит из двух или более металлических обкладок, которые не соприкасаются друг с другом. Для более полного понимания, как все это устроено в конденсаторе, давайте представим себе блин.
намажем его сгущенкой
и сверху положим точно такой же блин
Должно выполняться условие: эти два блина не должны прикасаться друг с другом. То есть верхний блин должен лежать на сгущенке и не прикасаться с нижним блином. Тут, думаю, все понятно. Перед вами типичный «блинный конденсатор» :-). Вот таким образом устроены все конденсаторы, только вместо блинов используются тонкие металлические пластины, а вместо сгущенки различный диэлектрик. В качестве диэлектрика может быть воздух, бумага, электролит, слюда, керамика, и так далее. К каждой металлической пластине подсоединены проводки — это выводы конденсатора.
Схематически все это выглядит примерно вот так.


Как вы могли заметить, из-за диэлектрика конденсатор не может проводить ток. Но это относиться только к постоянному току. Переменный ток конденсатор пропускает через себя без проблем с небольшим сопротивлением, номинал которого зависит от частоты тока и емкости самого конденсатора.
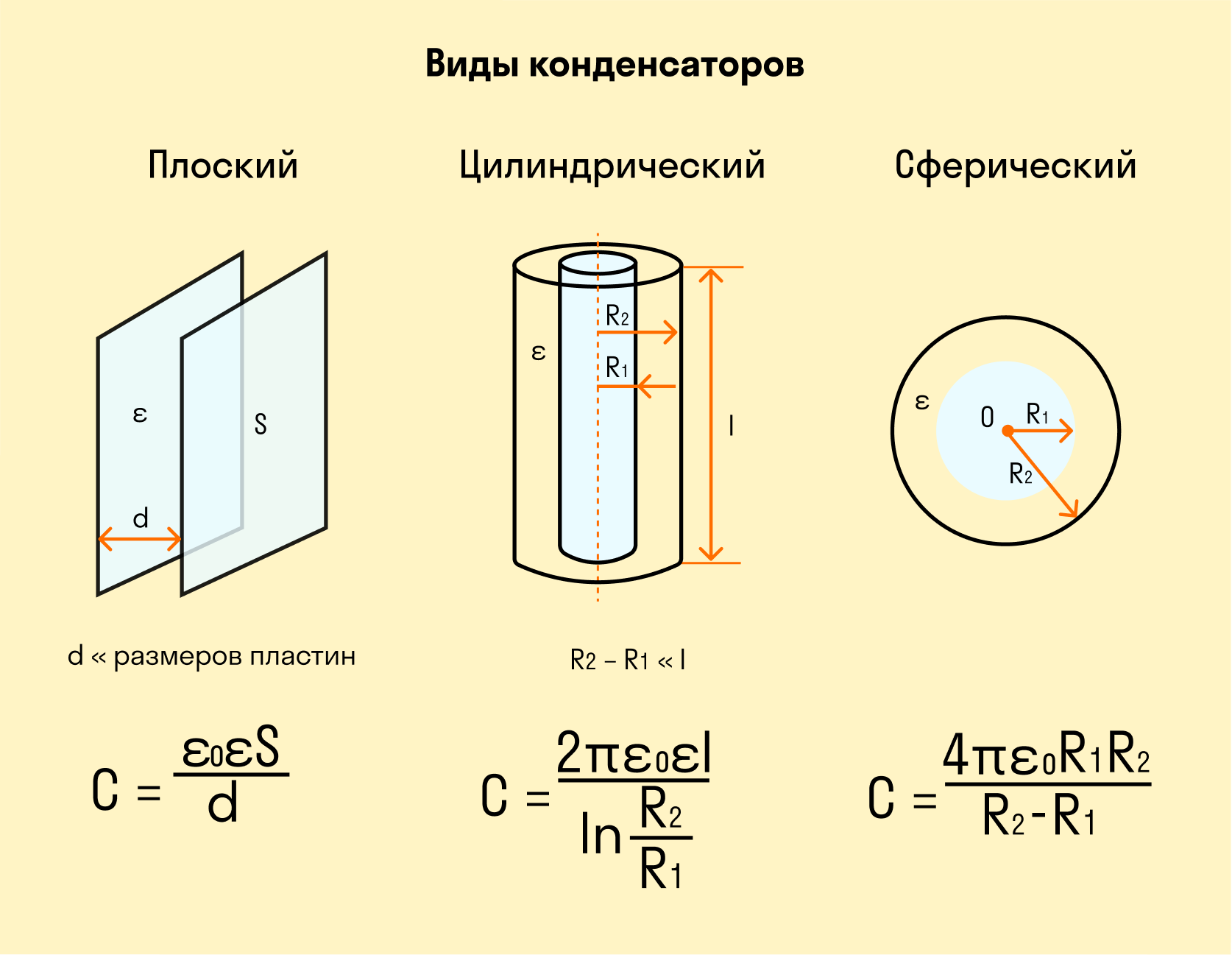
Виды конденсаторов
Где и для чего используются
Как уже говорили, сложно найти схему без конденсаторов. Их применяют для решения самых разных задач:
- Для сглаживания скачков сетевого напряжения. В таком случае их ставят на входе устройств, перед микросхемами, которые требовательны к параметрам питания.
- Для стабилизации выходного напряжения блоков питания. В таком случае надо искать их перед выходом.
Часто можно увидеть электролитические цилиндрические конденсаторы - Датчик прикосновения (тач-пады). В таких устройствах оной из «пластин» конденсаторов является человек. Вернее, его палец. Наше тело обладает определённой проводимостью. Это и используется в датчиках прикосновения.
- Для задания необходимого ритма работы. Время заряда конденсаторов разной ёмкости отличается. При этом цикл заряд/разряд конденсатора остаётся величиной постоянной. Это и используется в цепях, где надо задавать определённый ритм работы.
- Ячейки памяти. Память компьютеров, телефонов и других устройств — это огромное количество маленьких конденсаторов. Если он заряжен — это единица, разряжен — ноль.
- Есть стартовые конденсаторы, которые помогают «разогнать» двигатель. Они накапливают заряд, потом резко его отдают, создавая требуемый «толчок» для разгона мотора.
- В фотовспышках. Принцип тот же. Сначала накапливается заряд, затем выдаётся, но преобразуется в свет.
Конденсаторы встречаются часто и область их применения широка. Но надо знать как правильно их подключить.
Процессы зарядки и разрядки конденсаторов.
С устройством мы разобрались, теперь разберемся, что произойдет, если подключить к конденсатору источник постоянного тока. На принципиальных электрических схемах конденсатор обозначают следующим образом:
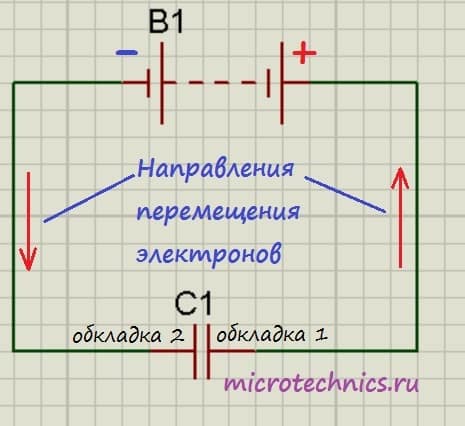
Итак, мы подключили обкладки конденсатора к полюсам источника постоянного тока. Что же будет происходить?
Свободные электроны с первой обкладки конденсатора устремятся к положительному полюсу источника. Из-за этого на обкладке возникнет недостаток отрицательно заряженных частиц, и она станет положительно заряженной. В то же время электроны с отрицательного полюса источника тока переместятся ко второй обкладке конденсатора. В результате чего на ней возникнет избыток электронов, соответственно, обкладка станет отрицательно заряженной. Таким образом, на обкладках конденсатора образуются заряды разного знака (как раз этот случай мы и рассматривали в первой части статьи), что приводит к появлению электрического поля, которое создаст между пластинами конденсатора определенную разность потенциалов. Процесс зарядки будет продолжаться до тех пор, пока эта разность потенциалов не станет равна напряжению источника тока. После этого процесс зарядки закончится, и перемещение электронов по цепи прекратится.
При отключении от источника конденсатор может на протяжении длительного времени сохранять накопленные заряды. Соответственно, заряженный конденсатор является источником электрической энергии, это означает, что он может отдавать энергию во внешнюю цепь. Давайте создадим простейшую цепь, просто соединив обкладки конденсатора друг с другом:
В данном случае по цепи начнет протекать ток разряда конденсатора, а электроны начнут перемещаться с отрицательно заряженной обкладки к положительной. В результате напряжение на конденсаторе (разность потенциалов между обкладками) начнет уменьшаться. Этот процесс завершится в тот момент, когда заряды пластин конденсаторов станут равны друг другу, соответственно электрическое поле между обкладками пропадет и по цепи перестанет протекать ток. Вот так и происходит разряд конденсатора, в результате которого он отдает во внешнюю цепь всю накопленную энергию.
Емкость и энергия конденсатора.
Важнейшей характеристикой является электрическая емкость конденсатора. Это физическая величина, которая определяется как отношение заряда конденсатора q одного из проводников к разности потенциалов между проводниками:
C = frac{q}{Deltavarphi} = frac{q}{U}
Емкость конденсатора изменяется в Фарадах, но величина 1 Ф является довольно большой, поэтому чаще всего емкость измерятся в микрофарадах (мкФ), нанофарадах (нФ) и пикофарадах (пФ). А поскольку мы уже вывели формулу для расчета напряженности, то давайте выразим напряжение на конденсаторе следующим образом:
U = Ed = frac{qd}{varepsilon_0thinspacevarepsilon S}
Здесь у нас d — это расстояние между пластинами конденсатора, а q — заряд конденсатора. Подставим эту формулу в выражение для емкости:
C = frac{qvarepsilon_0thinspacevarepsilon S}{qd} = frac{varepsilon_0thinspacevarepsilon S}{d}
Если в качестве диэлектрика у нас выступает воздух, то во всех формулах можно подставить varepsilon = 1.
Для запасенной энергии конденсатора справедливы следующие выражения:
W = frac{CU^2}{2} = frac{qU}{2} = frac{q^2}{2C}
Помимо емкости конденсаторы характеризуются еще одним параметром, а именно величиной напряжения, которое может выдержать его диэлектрик. При слишком больших значениях напряжения электроны диэлектрика отрываются от атомов, и диэлектрик начинает проводить ток. Это явление называется пробоем конденсатора, и в результате обкладки оказываются замкнутыми друг с другом. Собственно, характеристикой, которая часто используется при работе с конденсаторами является не напряжение пробоя, а рабочее напряжение. Это такая величина напряжения, при которой конденсатор может работать неограниченно долгое время, и пробоя не произойдет.
Итак, мы сегодня рассмотрели основные свойства конденсаторов, их устройство и характеристики! Так что на этом заканчиваем статью, а в следующей мы будем обсуждать различные варианты соединений и маркировку. Не пропустите!
Устройство конденсатора. От чего зависит емкость?
Емкость плоского конденсатора зависит от трех основных факторов:
- Площадь пластин — A
- Расстояние между пластинами – d
- Относительная диэлектрическая проницаемость вещества между пластинами — ɛ
Расстояние между пластинами
Емкость конденсатора обратно пропорциональна расстоянию между пластинами. Для того чтобы объяснить природу влияния этого фактора, необходимо вспомнить механику взаимодействия зарядов в пространстве (электростатику).
Если конденсатор не находится в электрической цепи, то на заряженные частицы, расположенные на его пластинах влияют две силы. Первая — это сила отталкивания между одноименными зарядами соседних частиц на одной пластине. Вторая – это сила притяжения разноименных зарядов между частицами, находящимися на противоположных пластинах. Получается, что чем ближе друг к другу находятся пластины, тем больше суммарная сила притяжения зарядов с противоположным знаком, и тем больше заряда может разместится на одной пластине.
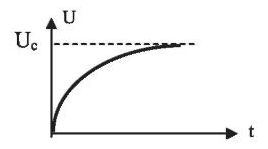
Время, необходимое для зарядки конденсатора
В идеальных условиях, когда источник напряжения мощный, нет препятствий потоку электричества, конденсатор безупречен, время зарядки конденсатора будет равно 0.
На практике же на каждом участке цепи существует явное (резисторы) или неявное (провода, источник напряжения и т.п.) сопротивление. В этом случае время заряда конденсатора будет зависеть от сопротивления во всей цепи и его емкости.
В самом начале заряда на обкладках накопителя много свободного места, напряжение равно нулю. Начальный ток в этот момент максимален. По мере заполнения конденсатора заряженными частицами их поток постепенно снижается, U растет все медленнее. Когда не останется свободного места на обкладках, ток прекратится, напряжение станет максимальным и равным таковому источника.
Экспонента увеличения энергии в конденсаторе изображена на рисунке. Сама формула зависимости нарастания напряжения от времени заряда имеет следующий вид:
U=Uc*[1-e(-t/τ)]
где Uс – электродвижущая сила источника, t – время заряда, τ – постоянная времени, равная R*C (R – сопротивление).
За время τ зарядка конденсатора дойдет до (1 – 1/e)*100% ≈ 63% от U.
За 3τ – до (1 – 1/e3)*100% ≈ 95% от U.
За 5τ – до (1 – 1/e5)*100% ≈ 99% от U.
Время заряда конденсатора точно до уровня напряжения источника длится бесконечно долго.
Из вышеприведенной формулы вычисления напряжения можно вывести расчет времени зарядки накопителя до определенных показателей:
t = – ln (1 – U/Uc) * RC
Зарядка конденсатора от источника постоянной ЭДС
Рассмотренный в предыдущем разделе процесс зарядки конденсатора посредством перенесения заряда с одной обкладки на другую имеет исключительно теоретический интерес, как метод расчета энергии конденсатора. Реально конденсаторы заряжают, подключая их к источнику ЭДС, например, к гальванической батарее.
Пусть конденсатор емкостью C подключен к источнику, ЭДС которого равна ε
(Рис. 145). Полное электрическое соединение цепи (включающее и внутренне сопротивление источника) обозначим
R
. При замыкании ключа в цепи пойдет электрический ток, благодаря которому на зарядках конденсатора будет накапливаться электрический заряд. По закону Ома сумма напряжений на конденсаторе (~U_C = frac{q}{C}) и резисторе (U_R = IR) равна ЭДС источника (varepsilon = U_C + U_R), что приводит к уравнению
(~IR = varepsilon — frac{q}{C}) . (1)
В этом уравнении заряд конденсатора и сила тока зависят от времени. Скорость изменения заряда конденсатора по определению равна силе тока в цепи (~I = frac{Delta q}{Delta t}), что позволяет получить уравнение, описывающее изменение заряда конденсатора с течением времени
(~R frac{Delta q}{Delta t} = varepsilon — frac{q}{C}) . (2)
Можно также получить уравнение, непосредственно описывающее изменение силы тока в цепи с течением времени. Для этого на основании уравнения (1) запишем уравнения для малых изменений входящих величин
(~Delta varepsilon = Delta (IR) + Delta left (frac{q}{C} right )) .
Формально эту операцию можно описать следующим образом: уравнение (1) следует записать для двух моментов времени t
и (
t
+ Δ
t
), а затем из второго уравнения вычесть первое. Так как ЭДС источника постоянна, то ее изменение равно нулю Δ
ε
= 0, сопротивление цепи и емкость конденсатора постоянны, поэтому их можно вынести из под знака изменения Δ , поэтому полученное уравнение приобретает вид
(~R Delta I = — frac{1}{C} Delta q) .
Наконец разделим его на промежуток времени, в течение которого произошли эти изменения, в результате получаем искомое уравнение (с учетом связи между силой тока и изменения заряда)
(~frac{Delta I}{Delta t} = -frac{1}{RC} I) . (3)
Математическая смысл этого уравнения указывает, что скорость уменьшения тока пропорциональна самой силе тока. Для однозначного решения этого уравнения необходимо задать начальное условие – значение силы тока в начальный момент времени I
0 = I(0).
С уравнениями такого типа мы познакомились в «математическом отступлении», поэтому здесь его анализ проведем кратко.
В начальный момент времени, когда заряд конденсатора равен нулю, скорость возрастания заряда (то есть сила тока) максимальна и равна (~I_0 = Delta left (frac{Delta q}{Delta t} right )_0 = frac{varepsilon}{R}).
Затем по мере накопления заряда сила тока будет уменьшаться, когда напряжение на конденсаторе станет равным ЭДС источника, заряд конденсатора достигнет максимального стационарного значения (~overline{q} = Cvarepsilon) и ток в цепи прекратится.
Схематически зависимости заряда конденсатора и силы тока в цепи от времени показаны на рис. 146. Для оценки времени зарядки конденсатора можно принять, что заряд возрастает до максимального значения с постоянной скоростью, равной силе тока в начальный момент времени. В этом случае
(~tau = frac{overline{q}}{I_0} = RC) . (4)
Аналогичная оценка исчезновения тока, полученная на основании уравнения (3) приводит к этому же результату.
Строго говоря, время зарядки конденсатора, описываемой уравнением (2) равно бесконечности. Это парадокс можно исключить, если принять во внимание дискретность электрического заряда.
Кроме того, заряд конденсатора, подключенного к батарее с течением времени случайным образом изменяется, флуктуирует, поэтому рассматриваемое уравнение описывает некоторые усредненные характеристики процесса.
Тем не менее, полученная оценка времени RC широко применяется в приближенных расчетах, часто ее называют просто временем зарядки конденсатора
Рассмотрим теперь превращения различных форм энергии в данном процессе. Понятно, что причиной тока в цепи и как следствие зарядки конденсатора являются сторонние силы источника.
На первый взгляд, энергетический баланс включает определенное противоречие: если источник сообщил конденсатору заряд q
, то сторонние силы совершили при этом работу
A
0 =
qε
, при этом энергия конденсатора стала равной (~W = frac{q2}{2C} = frac{q varepsilon}{2}) , что в два раза меньше работы совершенной источником.
Противоречие исчезает, если принять во внимание, что в процессе зарядки по цепи течет электрический ток, поэтому на резисторе выделяется некоторое количество теплоты, то есть часть энергии источника переходит в тепловую. Мысленно разобьем время зарядки на малые промежутки Δt
i (
i
= 1,2,3…). Перепишем уравнение (1) в виде
(~varepsilon = IR + frac{q}{C}) , (5)
и умножим его на величину малой порции заряда, переносимого за малый промежуток времени Δt
i, Δ
q
i =
I
iΔ
t
i . В результате получим
(~varepsilon Delta q_i = I_i R Delta q_i + frac{q_i}{C} Delta q_i) . (6)
Здесь обозначено q
i — заряд конденсатора перед перенесением рассматриваемой порции заряда. Каждый член полученного уравнения имеет явный физический смысл:[~varepsilon Delta q_i = delta A] — работа сторонних сил по перемещению порции заряда Δ
q<br>i;[~frac{q_i}{C} Delta q_i = Delta W_C] — увеличение энергии конденсатора при увеличении его заряда на Δ
q<br>i;[~I_i R Delta q_i = I2_i R Delta t_i = delta Q] — количество теплоты, выделившееся на резисторе, при протеканиипорции заряда Δ
q
i.
Таким образом, закон сохранения энергии, выражаемый уравнением баланса (6) для малого промежутка времени оказывается выполненным, следовательно, он будет выполнен и для всего процесса зарядки.
Просуммируем выражение (5) по всем промежуткам времени зарядки, в результате чего получим:[~sum_i varepsilon Delta q_i = varepsilon overline{q} = A] — полная работа сторонних сил по перенесению электрического заряда, равного стационарному заряду конденсатора;[~sum_i frac{q_i}{C} Delta q_i = frac{overline{q2}}{2C} = frac{varepsilon overline{q}}{2} = frac{C varepsilon2}{2}] — энергия заряженного конденсатора;
наконец, (~sum_i I_i R Delta q_i = sum_i I2_i R Delta t_i) — количество выделившейся на резисторе теплоты.
Принимая во внимание уравнение (3) и формулы из «математического отступления», последнюю сумму можно выразить в виде
(~Q = R sum_i I2_i Delta t_i = R frac{1}{2} I2_0 tau = R frac{1}{2} left ( frac{varepsilon}{R} right )2 RC = frac{C varepsilon2}{2}) . (6)
Эта сумма же может быть вычислена графически. Формула (1) задает зависимость напряжения на резисторе (U_R = IR) от заряда конденсатора. Эта зависимость линейна, ее график (Рис. 147) является отрезком прямой линии.
За малый промежуток времени через резистор протечет малый заряд Δq
i, при этом выделится количество теплоты (~delta Q_i = I_i R Delta q_i), которое численно равно площади узкой полоски, выделенной на рисунке.
Полное количество теплоты, выделившейся при прохождении всего заряда численно равно площади треугольника под графиком зависимости U
R(
q
), то есть
Заряд конденсатора. Ток
По своему предназначению конденсатор напоминает батарейку, однако все же он сильно отличается по принципу работы, максимальной емкости, а также скорости зарядки/разрядки.
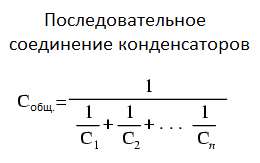
Последовательное соединение конденсаторов
Если же соединение конденсаторов в батарею производится в виде цепочки и к точкам включения в цепь непосредственно присоединены пластины только первого и последнего конденсаторов, то такое соединение конденсаторов называется последовательным. При последовательном соединении все конденсаторы заряжаются одинаковым количеством электричества, так как непосредственно от источника тока заряжаются только крайние пластины, а остальные пластины заряжаются через влияние. При этом заряд пластины будет равен по величине и противоположен по знаку заряду пластины 1, заряд пластины 3 будет равен по величине и противоположен по знаку заряду пластины 2 и т. д.
Напряжения на различных конденсаторах будут, вообще говоря, различными, так как для заряда одним и тем же количеством электричества конденсаторов различной емкости всегда требуются различные напряжения.
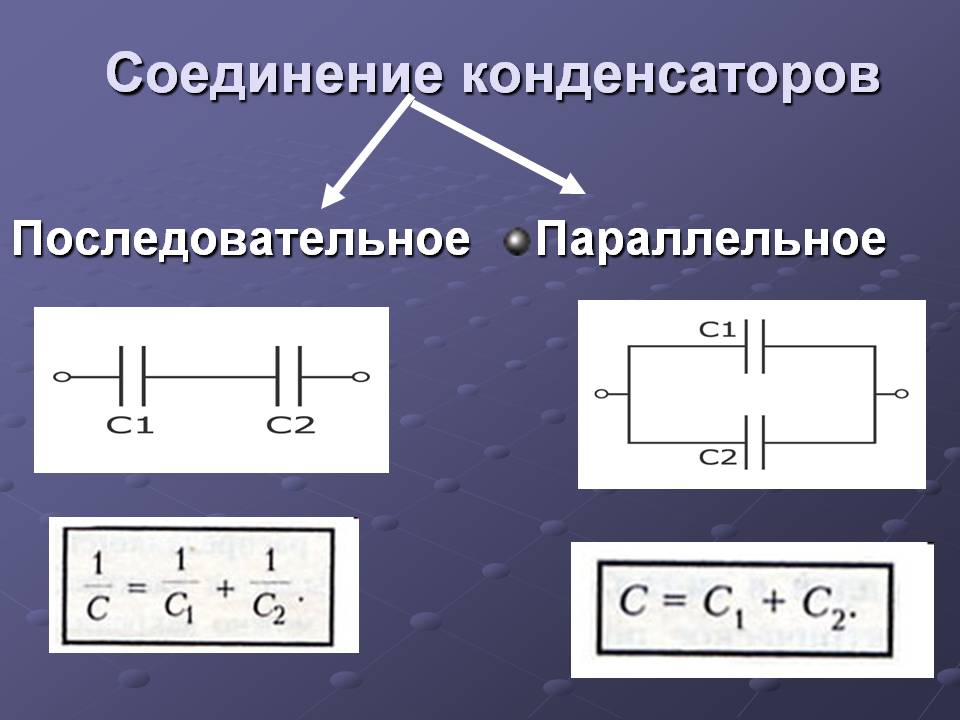
Типы соединений конденсаторов.
Чем меньше емкость конденсатора, тем большее напряжение необходимо для того, чтобы зарядить этот конденсатор требуемым количеством электричества, и наоборот.
Таким образом, при заряде группы конденсаторов, соединенных последовательно, на конденсаторах малой емкости напряжения будут больше, а на конденсаторах большой емкости — меньше.
Аналогично предыдущему случаю можно рассматривать всю группу конденсаторов, соединенных последовательно, как один эквивалентный конденсатор, между пластинами которого существует напряжение, равное сумме напряжений на всех конденсаторах группы, а заряд которого равен заряду любого из конденсаторов группы. Возьмем самый маленький конденсатор в группе. На нем должно быть самое большое напряжение. Но напряжение на этом конденсаторе составляет только часть общего напряжения, существующего на всей группе конденсаторов. Напряжение на всей группе больше напряжения на конденсаторе, имеющем самую малую емкость. А отсюда непосредственно следует, что общая емкость группы конденсаторов, соединенных последовательно, меньше емкости самого малого конденсатора в группе.
Последовательное соединение конденсаторов – это соединение двух или более конденсаторов в форме цепи, в которой каждый отдельный конденсатор соединяется с другим отдельным конденсатором только в одной точке. Ток (iC), заряжающий последовательную цепь конденсаторов, будет одинаковым для всех конденсаторов, поскольку у него есть только один возможный путь прохождения.
Вследствие того что через все последовательно соединенные конденсаторы течет одинаковый ток, количество накопленого электрического заряда для каждого конденсатора будет одинаковым, независимо от его емкости. Так происходит, потому что электрический заряд, накапливаемый на обкладке любого конденсатора, должен прийти с обкладки примыкающего конденсатора. Таким образом, последовательно соединенные конденсаторы имеют одинаковый электрический заряд.
Стоит почитать: все об электолитических конденсаторах.
Правая обкладка первого конденсатора С1 соединяется с левой второго конденсатора С2, у которого правая обкладка соединяется с левой третьего конденсатора С3. Это означает, что в режиме постоянного тока конденсатор С2 электрически изолирован от общей цепи. В итогое эффективная площадь обкладок уменьшается до площади обкладок самого маленького конденсатора. Это объясняется тем, что как только обкладки наименшей площади заполнятся электрическим зарядом, данный конденсатор перестанет пропускать ток. В результате ток прекратиться во всей цепи, и процесс зарядки остальных конденсаторов также прекратится. При последовательном соединении общее расстояние между обкладками увеличивается до суммы расстояний между обкладками всех конденсаторов.
Таким образом, последовательная цепь формирует один большой конденсатор с площадью обкладок элемента с наименьшей емкостью, и расстоянием между обкладками, равному сумме всех расстояний в цепи. На каждый отдельный конденсатор в последовательной цепи падает разное напряжение. Поскольку емкость обратно пропрциональна напряжению (С = Q/V), то чем меньше емкость конденсатора, тем большее напряжение на него упадет. Применим закон Кирхгофа для напряжения в последовательной цепи из трех конденсаторов.
Емкость конденсатора прямо пропорциональна его заряду и обратно пропорциональна его напряжению — C = Q/V. Как уже упоминалось выше, последовательно соединенные конденсаторы имеют одинаковый электрический заряд — Qобщ = Q1 = Q2 = Q3. Из данного уравнения можно легко вывести формулу общей емкости для любого частного случая последовательного соединения.
Если в цепи есть и последовательное и параллельное соединение, то такую цепь называют смешанной или последовательно-параллельной. Тем не менее, смешанное соединение может иметь как последовательный, так и параллельный характер.
Типы соединений конденсаторов.
Законы последовательного и параллельного соединения проводников
Для детального понимания на практике обоих типов соединений, приведем формулы, объясняющие законы данных типов соединений. Расчет мощности при параллельном и последовательном типе соединения отличается.
При последовательной схеме имеется одинаковая сила тока во всех проводниках:
I = I1 = I2.
Согласно закону Ома, данные типы соединений проводников в разных случаях объясняются иначе. Так, в случае последовательной схемы, напряжения равны друг другу:
U1 = IR1, U2 = IR2.
Помимо этого, общее напряжение равно сумме напряжений отдельно взятых проводников:
U = U1 + U2 = I(R1 + R2) = IR.
Полное сопротивление электроцепи рассчитывается как сумма активных сопротивлений всех проводников, вне зависимости от их числа.
В случае параллельной схемы совокупное напряжение цепи аналогично напряжению отдельных элементов:
U1 = U2 = U.
А совокупная сила электротока рассчитывается как сумма токов, которые имеются по всем проводникам, расположенным параллельно:
I = I1 + I2.
Чтобы обеспечить максимальную эффективность электрических сетей, необходимо понимать суть обоих типов соединений и применять их целесообразно, используя законы и рассчитывая рациональность практической реализации.
Как правильно соединять конденсаторы?
У многих начинающих любителей электроники в процессе сборки самодельного устройства возникает вопрос: “Как правильно соединять конденсаторы?”
Казалось бы, зачем это надо, ведь если на принципиальной схеме указано, что в данном месте схемы должен быть установлен конденсатор на 47 микрофарад, значит, берём и ставим. Но, согласитесь, что в мастерской даже заядлого электронщика может не оказаться конденсатора с необходимым номиналом!
Похожая ситуация может возникнуть и при ремонте какого-либо прибора. Например, необходим электролитический конденсатор ёмкостью 1000 микрофарад, а под рукой лишь два-три на 470 микрофарад. Ставить 470 микрофарад, вместо положенных 1000? Нет, это допустимо не всегда. Так как же быть? Ехать на радиорынок за несколько десятков километров и покупать недостающую деталь?
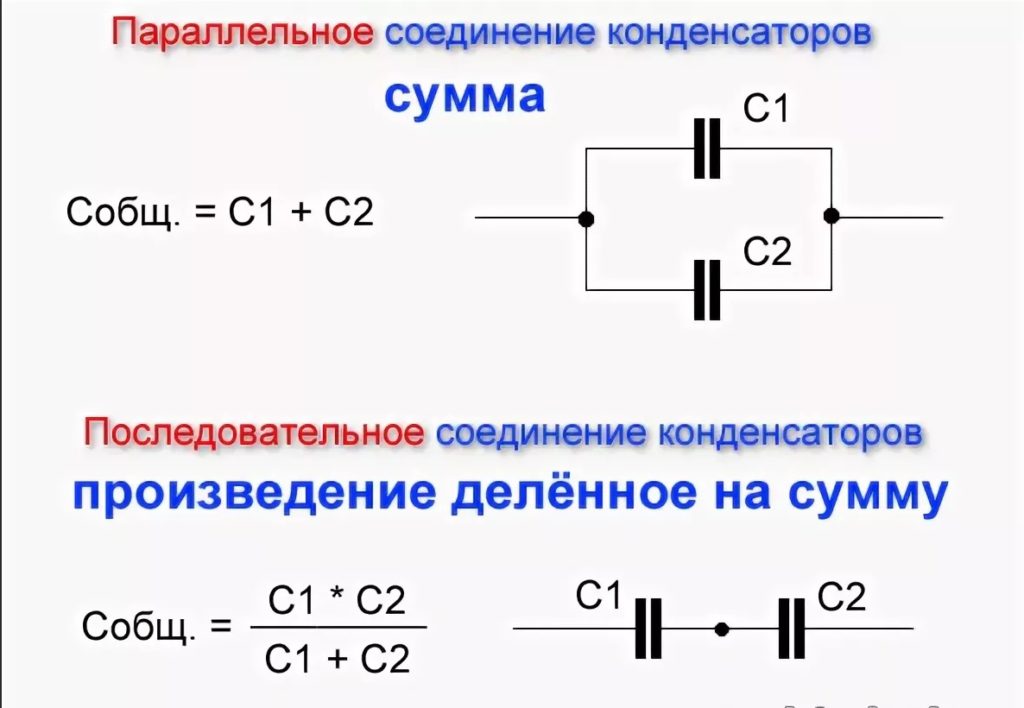
Как выйти из сложившейся ситуации? Можно соединить несколько конденсаторов и в результате получить необходимую нам ёмкость. В электронике существует два способа соединения конденсаторов: параллельное и последовательное.
В реальности это выглядит так:
Параллельное соединение Принципиальная схема параллельного соединения Последовательное соединение Принципиальная схема последовательного соединения
Также можно комбинировать параллельное и последовательное соединение. Но на практике вам вряд ли это пригодиться.
Как рассчитать общую ёмкость соединённых конденсаторов?
Помогут нам в этом несколько простых формул. Не сомневайтесь, если вы будете заниматься электроникой, то эти простые формулы рано или поздно вас выручат.
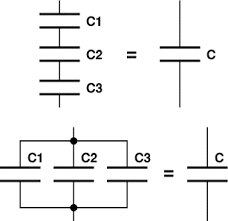
Общая ёмкость параллельно соединённых конденсаторов:
С1 – ёмкость первого;
С2 – ёмкость второго;
С3 – ёмкость третьего;
СN – ёмкость N-ого конденсатора;
Cобщ – суммарная ёмкость составного конденсатора.
Следующая
РазноеЧто такое активная мощность?
Как найти заряд конденсатора в тот момент, когда энергия электрического поля конденсатора и энергия магнитного опля катушки становятся одинаковыми?
Колебательный
контур содержит конденсатор емкостью 40 мкФ и катушку индуктивностью 18 мГн.
Максимальная сила тока в катушке 1,2 A. Определите заряд
конденсатора в тот момент, когда энергия электрического поля конденсатора и
энергия магнитного опля катушки становятся одинаковыми.
Решение.
Согласно
закону сохранения энергии, полная энергия колебательного контура равна
максимальной энергии магнитного поля катушки.
(а
также максимальной энергии электрического поля конденсатора).
Поскольку
по условию задачи в рассматриваемый момент времени энергия электрического поля
конденсатора равна энергии магнитного поля катушки: Wэ = Wм , то Wэ = ½Wм.max
. С другой стороны, энергия электрического поля конденсатора при искомой
величине заряда q выражается следующей формулой.
Приравниваем
два выражения для Wэ , находим q.
Ответ:
q
= 7,2•10-4 Кл.
Источник: Подготовка к тестированию по физике. Шепелевич. В. Г.
Содержание
- 1 формулы для конденсаторов
- 1.1 В чем измеряется емкость конденсатора
- 1.2 Формула энергии конденсатора
- 1.3 Формула заряда конденсатора
- 1.4 Формула тока утечки конденсатора
- 2 Конденсатор
- 2.1 Плоский конденсатор
- 2.2 Заряд конденсатора. Ток
- 2.3 Заряд конденсатора. Напряжение
- 2.4 Разряд конденсатора
- 2.5 Устройство конденсатора. От чего зависит емкость?
- 2.6 Площадь пластин
- 2.7 Расстояние между пластинами
- 2.8 Относительная диэлектрическая проницаемость
- 2.9 Номинальное напряжение
- 2.10 Ток утечки
- 2.11 Напряжение между обкладками
- 2.12 Устройство конденсатора. От чего зависит емкость
- 3 Слободянюк А.И. Физика 10/16.4
- 3.1 16.4 Зарядка конденсатора от источника постоянной ЭДС
- 3.2 Примечания
- 4 Конвертер величин
- 4.1 Применение
- 4.2 Резистивно-емкостные фильтры нижних частот
формулы для конденсаторов
Одним из важных элементов электрической цепи является конденсатор, формулы для которого позволяют рассчитать и подобрать наиболее подходящий вариант. Основная функция данного устройства заключается в накоплении определенного количества электроэнергии. Простейшая система включает в себя два электрода или обкладки, разделенные между собой диэлектриком.
В чем измеряется емкость конденсатора
Одной из важнейших характеристик конденсатора является его емкость. Данный параметр определяется количеством электроэнергии, накапливаемой этим прибором. Накопление происходит в виде электронов. Их количество, помещающееся в конденсаторе, определяет величину емкости конкретного устройства.
Для измерения емкости применяется единица – фарада. Емкость конденсатора в 1 фараду соответствует электрическому заряду в 1 кулон, а на обкладках разность потенциалов равна 1 вольту. Эта классическая формулировка не подходит для практических расчетов, поскольку в конденсаторе собираются не заряды, а электроны.
Емкость любого конденсатора находится в прямой зависимости от объема электронов, способных накапливаться при нормальном рабочем режиме. Для обозначения емкости все равно используется фарада, а количественные параметры определяются по формуле: С = Q / U, где С означает емкость, Q – заряд в кулонах, а U является напряжением.
Таким образом, просматривается взаимная связь заряда и напряжения, оказывающих влияние на способность конденсатора к накоплению и удержанию определенного количества электричества.
Для расчетов емкости плоского конденсатора используется формула:
в которой ε0 = 8,854187817 х 10-12 ф/м представляет собой постоянную величину. Прочие величины: ε – является диэлектрической проницаемостью диэлектрика, находящегося между обкладками, S – означает площадь обкладки, а d – зазор между обкладками.
Формула энергии конденсатора
С емкостью самым тесным образом связана другая величина, известная как энергия заряженного конденсатора. После зарядки любого конденсатора, в нем образуется определенное количество энергии, которое в дальнейшем выделяется в процессе разрядки. С этой потенциальной энергией вступают во взаимодействие обкладки конденсатора. В них образуются разноименные заряды, притягивающиеся друг к другу.
В процессе зарядки происходит расходование энергии внешнего источника для разделения зарядов с положительным и отрицательным значением, которые, затем располагаются на обкладках конденсатора. Поэтому в соответствии с законом сохранения энергии, она не исчезает бесследно, а остается внутри конденсатора в виде электрического поля, сосредоточенного между пластинами. Разноименные заряды образуют взаимодействие и последующее притяжение обкладок между собой.
Каждая пластина конденсатора под действием заряда создает напряженность электрического поля, равную Е/2. Общее поле будет складываться из обоих полей, возникающих в каждой обкладке с одинаковыми зарядами, имеющими противоположные значения.
Таким образом, энергия конденсатора выражается формулой: W=q(E/2)d. В свою очередь, напряжение выражается с помощью понятий напряженности и расстояния и представляется в виде формулы U=Ed. Это значение, подставленное в первую формулу, отображает энергию конденсатора в таком виде:W=qU/2. Для получения окончательного результата необходимо использовать определение емкости: C=q/U, и в конце концов энергия заряженного конденсатора будет выглядеть следующим образом: Wэл = CU2/2.
Формула заряда конденсатора
Для выполнения зарядки, конденсатор должен быть подключен к цепи постоянного тока. С этой целью может использоваться генератор. У каждого генератора имеется внутреннее сопротивление. При замыкании цепи происходит зарядка конденсатора. Между его обкладками появляется напряжение, равное электродвижущей силе генератора: Uc = E.
Обкладка, подключенная к положительному полюсу генератора, заряжается положительно (+q), а другая обкладка получает равнозначный заряд с отрицательной величиной (- q). Величина заряда q находится в прямой пропорциональной зависимости с емкостью конденсатора С и напряжением на обкладках Uc. Эта зависимость выражается формулой: q = C x Uc.
В процессе зарядки одна из обкладок конденсатора приобретает, а другая теряет определенное количество электронов. Они переносятся по внешней цепи под влиянием электродвижущей силы генератора. Такое перемещение является электрическим током, известным еще как зарядный емкостной ток (Iзар).
Течение зарядного тока в цепи происходит практически за тысячные доли секунды, до того момента, пока напряжение конденсатора не станет равным электродвижущей силе генератора. Напряжение увеличивается плавно, а потом постепенно замедляется.
Далее значение напряжения конденсатора будет постоянным. Во время зарядки по цепи течет зарядный ток. В самом начале он достигает максимальной величины, так как напряжение конденсатора имеет нулевое значение.
Согласно закона Ома Iзар = Е/Ri, поскольку к сопротивлению Ri приложена вся ЭДС генератора.
Формула тока утечки конденсатора
Ток утечки конденсатора вполне можно сравнить с воздействием подключенного к нему резистора с каким-либо сопротивлением R. Ток утечки тесно связан с типом конденсатора и качеством используемого диэлектрика. Кроме того, важным фактором становится конструкция корпуса и степень его загрязненности.
Некоторые конденсаторы имеют негерметичный корпус, что приводит к проникновению влаги из воздуха и возрастанию тока утечки. В первую очередь это касается устройств, где в качестве диэлектрика использована промасленная бумага. Значительные токи утечки возникают из-за снижения электрического сопротивления изоляции. В результате нарушается основная функция конденсатора – способность получать и сохранять заряд электрического тока.
Основная формула для расчета выглядит следующим образом: Iут = U/Rd, где Iут, – это ток утечки, U – напряжение, прилагаемое к конденсатору, а Rd – сопротивление изоляции.
Источник: https://electric-220.ru/news/kondensator_formuly/2016-09-22-1067
Конденсатор
Конденсатор – электронный компонент, предназначенный для накопления электрического заряда. Способность конденсатора накапливать электрический заряд зависит от его главной характеристики – емкости. Емкость конденсатора (С) определяется как соотношение количества электрического заряда (Q) к напряжению (U).
Емкость конденсатора измеряется в фарадах (F) – единицах, названых в честь британского ученого физика Майкла Фарадея. Емкость в один фарад (1F) равняется количеству заряда в один кулон (1C), создающему напряжение на конденсаторе в один вольт (1V). Вспомним, что один кулон (1С) равняется величине заряда, прошедшего через проводник за одну секунду (1sec) при силе тока в один ампер (1A).
Однако кулон, это очень большое количество заряда относительно того, сколько способно хранить большинство конденсаторов. По этой причине, для измерения емкости обычно используют микрофарады (µF или uF), нанофарады (nF) и пикофарады (pF).
- 1nF = 0.000000001 = 10-9 F
- 1pF = 0.000000000001 = 10-12 F
Плоский конденсатор
Существует множество типов конденсаторов различной формы и внутреннего устройства. Рассмотрим самый простой и принципиальный — плоский конденсатор. Плоский конденсатор состоит из двух параллельных пластин проводника (обкладок), электрически изолированных друг от друга воздухом, или специальным диэлектрическим материалом (например бумага, стекло или слюда).
Заряд конденсатора. Ток
По своему предназначению конденсатор напоминает батарейку, однако все же он сильно отличается по принципу работы, максимальной емкости, а также скорости зарядки/разрядки.
Рассмотрим принцип работы плоского конденсатора. Если подключить к нему источник питания, на одной пластине проводника начнут собираться отрицательно заряженные частицы в виде электронов, на другой – положительно заряженные частицы в виде ионов. Поскольку между обкладками находиться диэлектрик, заряженные частицы не могут «перескочить» на противоположную сторону конденсатора. Тем не менее, электроны передвигаются от источника питания — до пластины конденсатора. Поэтому в цепи идет электрический ток.
В самом начале включения конденсатора в цепь, на его обкладках больше всего свободного места. Следовательно, начальный ток в этот момент встречает меньше всего сопротивления и является максимальным. По мере заполнения конденсатора заряженными частицами ток постепенно падает, пока не закончится свободное место на обкладках и ток совсем не прекратится.
Время между состояниями «пустого» конденсатора с максимальным значением тока, и «полного» конденсатора с минимальным значением тока (т.е. его отсутствием), называют переходным периодом заряда конденсатора.
Заряд конденсатора. Напряжение
В самом начале переходного периода зарядки, напряжение между обкладками конденсатора равняется нулю. Как только на обкладках начинают появляться заряженные частицы, между разноименными зарядами возникает напряжение. Причиной этому является диэлектрик между пластинами, который «мешает» стремящимся друг к другу зарядам с противоположным знаком перейти на другую сторону конденсатора.
На начальном этапе зарядки, напряжение быстро растет, потому что большой ток очень быстро увеличивает количество заряженных частиц на обкладках. Чем больше заряжается конденсатор, тем меньше ток, и тeм медленнее растет напряжение. В конце переходного периода, напряжение на конденсаторе полностью прекратит рост, и будет равняться напряжению на источнике питания.
Как видно на графике, сила тока конденсатора напрямую зависит от изменения напряжения.
Формула для нахождения тока конденсатора во время переходного периода:
- ΔVc/Δt – Изменение напряжения на конденсаторе за отрезок времени
Разряд конденсатора
После того как конденсатор зарядился, отключим источник питания и подключим нагрузку R. Так как конденсатор уже заряжен, он сам превратился в источник питания. Нагрузка R образовала проход между пластинами. Отрицательно заряженные электроны, накопленные на одной пластине, согласно силе притяжения между разноименными зарядами, двинутся в сторону положительно заряженных ионов на другой пластине.
В момент подключения R, напряжение на конденсаторе то же, что и после окончания переходного периода зарядки. Начальный ток по закону Ома будет равняться напряжению на обкладках, разделенном на сопротивление нагрузки.
Как только в цепи пойдет ток, конденсатор начнет разряжаться. По мере потери заряда, напряжение начнет падать. Следовательно, ток тоже упадет. По мере понижения значений напряжения и тока, будет снижаться их скорость падения.
Время зарядки и разрядки конденсатора зависит от двух параметров – емкости конденсатора C и общего сопротивления в цепи R. Чем больше емкость конденсатора, тем большее количество заряда должно пройти по цепи, и тем больше времени потребует процесс зарядки/разрядки ( ток определяется как количество заряда, прошедшего по проводнику за единицу времени). Чем больше сопротивление R, тем меньше ток. Соответственно, больше времени потребуется на зарядку.
Продукт RC (сопротивление, умноженное на емкость) формирует временную константу τ (тау). За один τ конденсатор заряжается или разряжается на 63%. За пять τ конденсатор заряжается или разряжается полностью.
Для наглядности подставим значения: конденсатор емкостью в 20 микрофарад, сопротивление в 1 килоом и источник питания в 10В. Процесс заряда будет выглядеть следующим образом:
Устройство конденсатора. От чего зависит емкость?
Емкость плоского конденсатора зависит от трех основных факторов:
- Расстояние между пластинами – d
- Относительная диэлектрическая проницаемость вещества между пластинами — ɛ
Площадь пластин
Чем больше площадь пластин конденсатора, тем больше заряженых частиц могут на них разместится, и тем больше емкость.
Расстояние между пластинами
Емкость конденсатора обратно пропорциональна расстоянию между пластинами. Для того чтобы объяснить природу влияния этого фактора, необходимо вспомнить механику взаимодействия зарядов в пространстве (электростатику).
Если конденсатор не находится в электрической цепи, то на заряженные частицы, расположенные на его пластинах влияют две силы. Первая — это сила отталкивания между одноименными зарядами соседних частиц на одной пластине. Вторая – это сила притяжения разноименных зарядов между частицами, находящимися на противоположных пластинах. Получается, что чем ближе друг к другу находятся пластины, тем больше суммарная сила притяжения зарядов с противоположным знаком, и тем больше заряда может разместится на одной пластине.
Относительная диэлектрическая проницаемость
Не менее значимым фактором, влияющим на емкость конденсатора, является такое свойство материала между обкладками как относительная диэлектрическая проницаемость ɛ. Это безразмерная физическая величина, которая показывает во сколько раз сила взаимодействия двух свободных зарядов в диэлектрике меньше, чем в вакууме.
Материалы с более высокой диэлектрической проницаемостью позволяют обеспечить большую емкость. Объясняется это эффектом поляризации – смещением электронов атомов диэлектрика в сторону положительно заряженной пластины конденсатора.
Поляризация создает внутренне электрическое поле диэлектрика, которое ослабляет общую разность потенциала (напряжения) конденсатора. Напряжение U препятствует притоку заряда Q на конденсатор. Следовательно, понижение напряжения способствует размещению на конденсаторе большего количества электрического заряда.
Ниже приведены примеры значений диэлектрической проницаемости для некоторых изоляционных материалов, используемых в конденсаторах.
- Порошки оксидов металлов – от 6 до 20
Номинальное напряжение
Второй по значимости характеристикой после емкости является максимальное номинальное напряжение конденсатора. Данный параметр обозначает максимальное напряжение, которое может выдержать конденсатор. Превышение этого значения приводит к «пробиванию» изолятора между пластинами и короткому замыканию. Номинальное напряжение зависит от материала изолятора и его толщины (расстояния между обкладками).
Следует отметить, что при работе с переменным напряжением нужно учитывать именно пиковое значение (наибольшее мгновенное значение напряжения за период). Например, если эффективное напряжение источника питания будет 50В, то его пиковое значение будет свыше 70В.
Соответственно необходимо использовать конденсатор с номинальным напряжением более 70В.
Однако на практике, рекомендуется использовать конденсатор с номинальным напряжением не менее в два раза превышающим максимально возможное напряжение, которое будет к нему приложено.
Ток утечки
Также при работе конденсатора учитывается такой параметр как ток утечки. Поскольку в реальной жизни диэлектрик между пластинами все же пропускает маленький ток, это приводит к потере со временем начального заряда конденсатора.
Источник: http://hightolow.ru/capacitor1.php
Напряжение между обкладками
В самом начале переходного периода зарядки, напряжение между обкладками конденсатора равняется нулю. Как только на обкладках начинают появляться заряженные частицы, между разноименными зарядами возникает напряжение. Причиной этому является диэлектрик между пластинами, который «мешает» стремящимся друг к другу зарядам с противоположным знаком перейти на другую сторону конденсатора.
На начальном этапе зарядки, напряжение быстро растет, потому что большой ток очень быстро увеличивает количество заряженных частиц на обкладках. Чем больше заряжается конденсатор, тем меньше ток, и тeм медленнее растет напряжение. В конце переходного периода, напряжение на конденсаторе полностью прекратит рост, и будет равняться напряжению на источнике питания.
Как видно на графике, сила тока конденсатора напрямую зависит от изменения напряжения.
Формула для нахождения тока конденсатора во время переходного периода:
- Vc/t – Изменение напряжения на конденсаторе за отрезок времени
Устройство конденсатора. От чего зависит емкость
Емкость плоского конденсатора зависит от трех основных факторов:
- Расстояние между пластинами – d
- Относительная диэлектрическая проницаемость вещества между пластинами — ?
Слободянюк А.И. Физика 10/16.4
книги
Предыдующая страница
16.4 Зарядка конденсатора от источника постоянной ЭДС
Рассмотренный в предыдущем разделе процесс зарядки конденсатора посредством перенесения заряда с одной обкладки на другую имеет исключительно теоретический интерес, как метод расчета энергии конденсатора. Реально конденсаторы заряжают, подключая их к источнику ЭДС, например, к гальванической батарее.
Пусть конденсатор емкостью C подключен к источнику, ЭДС которого равна ε (Рис. 145). Полное электрическое соединение цепи (включающее и внутренне сопротивление источника) обозначим R. При замыкании ключа в цепи пойдет электрический ток, благодаря которому на зарядках конденсатора будет накапливаться электрический заряд. По закону Ома сумма напряжений на конденсаторе (~U_C = frac{q}{C}) и резисторе (U_R = IR) равна ЭДС источника (varepsilon = U_C + U_R), что приводит к уравнению
(~IR = varepsilon — frac{q}{C}) . (1)
В этом уравнении заряд конденсатора и сила тока зависят от времени. Скорость изменения заряда конденсатора по определению равна силе тока в цепи (~I = frac{Delta q}{Delta t}), что позволяет получить уравнение, описывающее изменение заряда конденсатора с течением времени
(~R frac{Delta q}{Delta t} = varepsilon — frac{q}{C}) . (2)
Можно также получить уравнение, непосредственно описывающее изменение силы тока в цепи с течением времени. Для этого на основании уравнения (1) запишем уравнения для малых изменений входящих величин
(~Delta varepsilon = Delta (IR) + Delta left (frac{q}{C} right )) .
Формально эту операцию можно описать следующим образом: уравнение (1) следует записать для двух моментов времени t и (t + Δt), а затем из второго уравнения вычесть первое. Так как ЭДС источника постоянна, то ее изменение равно нулю Δε = 0, сопротивление цепи и емкость конденсатора постоянны, поэтому их можно вынести из под знака изменения Δ , поэтому полученное уравнение приобретает вид
(~R Delta I = — frac{1}{C} Delta q) .
Наконец разделим его на промежуток времени, в течение которого произошли эти изменения, в результате получаем искомое уравнение (с учетом связи между силой тока и изменения заряда)
(~frac{Delta I}{Delta t} = -frac{1}{RC} I) . (3)
Математическая смысл этого уравнения указывает, что скорость уменьшения тока пропорциональна самой силе тока. Для однозначного решения этого уравнения необходимо задать начальное условие – значение силы тока в начальный момент времени I0 = I(0).
С уравнениями такого типа мы познакомились в «математическом отступлении», поэтому здесь его анализ проведем кратко.
В начальный момент времени, когда заряд конденсатора равен нулю, скорость возрастания заряда (то есть сила тока) максимальна и равна (~I_0 = Delta left (frac{Delta q}{Delta t} right )_0 = frac{varepsilon}{R}).
Затем по мере накопления заряда сила тока будет уменьшаться, когда напряжение на конденсаторе станет равным ЭДС источника, заряд конденсатора достигнет максимального стационарного значения (~overline{q} = Cvarepsilon) и ток в цепи прекратится.
Схематически зависимости заряда конденсатора и силы тока в цепи от времени показаны на рис. 146. Для оценки времени зарядки конденсатора можно принять, что заряд возрастает до максимального значения с постоянной скоростью, равной силе тока в начальный момент времени. В этом случае
(~tau = frac{overline{q}}{I_0} = RC) . (4)
Аналогичная оценка исчезновения тока, полученная на основании уравнения (3) приводит к этому же результату.
Строго говоря, время зарядки конденсатора, описываемой уравнением (2) равно бесконечности. Это парадокс можно исключить, если принять во внимание дискретность электрического заряда.
Кроме того, заряд конденсатора, подключенного к батарее с течением времени случайным образом изменяется, флуктуирует, поэтому рассматриваемое уравнение описывает некоторые усредненные характеристики процесса.
Тем не менее, полученная оценка времени RC широко применяется в приближенных расчетах, часто ее называют просто временем зарядки конденсатора.
Рассмотрим теперь превращения различных форм энергии в данном процессе. Понятно, что причиной тока в цепи и как следствие зарядки конденсатора являются сторонние силы источника.
На первый взгляд, энергетический баланс включает определенное противоречие: если источник сообщил конденсатору заряд q, то сторонние силы совершили при этом работу A0 = qε , при этом энергия конденсатора стала равной (~W = frac{q2}{2C} = frac{q varepsilon}{2}) , что в два раза меньше работы совершенной источником.
Противоречие исчезает, если принять во внимание, что в процессе зарядки по цепи течет электрический ток, поэтому на резисторе выделяется некоторое количество теплоты, то есть часть энергии источника переходит в тепловую. Мысленно разобьем время зарядки на малые промежутки Δti (i = 1,2,3…). Перепишем уравнение (1) в виде
(~varepsilon = IR + frac{q}{C}) , (5)
и умножим его на величину малой порции заряда, переносимого за малый промежуток времени Δti, Δqi = IiΔti . В результате получим
(~varepsilon Delta q_i = I_i R Delta q_i + frac{q_i}{C} Delta q_i) . (6)
Здесь обозначено qi — заряд конденсатора перед перенесением рассматриваемой порции заряда. Каждый член полученного уравнения имеет явный физический смысл:[~varepsilon Delta q_i = delta A] — работа сторонних сил по перемещению порции заряда Δqi;[~frac{q_i}{C} Delta q_i = Delta W_C] — увеличение энергии конденсатора при увеличении его заряда на Δqi;[~I_i R Delta q_i = I2_i R Delta t_i = delta Q] — количество теплоты, выделившееся на резисторе, при протеканиипорции заряда Δqi.
Таким образом, закон сохранения энергии, выражаемый уравнением баланса (6) для малого промежутка времени оказывается выполненным, следовательно, он будет выполнен и для всего процесса зарядки.
Просуммируем выражение (5) по всем промежуткам времени зарядки, в результате чего получим:[~sum_i varepsilon Delta q_i = varepsilon overline{q} = A] — полная работа сторонних сил по перенесению электрического заряда, равного стационарному заряду конденсатора;[~sum_i frac{q_i}{C} Delta q_i = frac{overline{q2}}{2C} = frac{varepsilon overline{q}}{2} = frac{C varepsilon2}{2}] — энергия заряженного конденсатора;
наконец, (~sum_i I_i R Delta q_i = sum_i I2_i R Delta t_i) — количество выделившейся на резисторе теплоты.
Принимая во внимание уравнение (3) и формулы из «математического отступления», последнюю сумму можно выразить в виде
(~Q = R sum_i I2_i Delta t_i = R frac{1}{2} I2_0 tau = R frac{1}{2} left ( frac{varepsilon}{R} right )2 RC = frac{C varepsilon2}{2}) . (6)
Эта сумма же может быть вычислена графически. Формула (1) задает зависимость напряжения на резисторе (U_R = IR) от заряда конденсатора. Эта зависимость линейна, ее график (Рис. 147) является отрезком прямой линии.
За малый промежуток времени через резистор протечет малый заряд Δqi, при этом выделится количество теплоты (~delta Q_i = I_i R Delta q_i), которое численно равно площади узкой полоски, выделенной на рисунке.
Полное количество теплоты, выделившейся при прохождении всего заряда численно равно площади треугольника под графиком зависимости UR(q), то есть
(~Q = frac{1}{2} C varepsilon cdot varepsilon = frac{C varepsilon2}{2} = frac{q2_0}{2 C}) . (7)
Таким образом, энергетический баланс полностью сходится и для всего процесса целиком: работа, совершенная источником равна сумме энергии конденсатора и количества выделившейся теплоты (A = W_C + Q). Схематически преобразование энергии в этом процессе показано на рис. 148.
Интересно заметить, что количество теплоты, выделяющееся при зарядке, не зависит о сопротивления цепи и в точности равно энергии конденсатора. То есть, половина энергии источника переходит в энергию электрического поля, а вторая в тепловую энергию, выделяющуюся в цепи: природа требует своеобразный пятидесятипроцентный налог в виде тепловых потерь, не зависимо от сопротивления цепи и емкости конденсатора[1].
Примечания
- ↑ Но эти параметры цепи определяют время процесса.
Следующая страница
Источник: http://www.physbook.ru/index.php/%D0%A1%D0%BB%D0%BE%D0%B1%D0%BE%D0%B4%D1%8F%D0%BD%D1%8E%D0%BA_%D0%90.%D0%98._%D0%A4%D0%B8%D0%B7%D0%B8%D0%BA%D0%B0_10/16.4
Конвертер величин
Постоянная времени определяется по формуле
где τ — постоянная времени в секундах, R — сопротивление в омах и C — емкость в фарадах. Постоянная времени RC-цепи определяется как время, которое требуется, чтобы конденсатор зарядился до 63,2% его максимально возможного заряда при условии, что начальный заряд нулевой. Отметим, что конденсатор зарядится до 63,2% за время τ и почти полностью (до 99,3%) зарядится за время 5τ.
Энергия E, которую хранит полностью заряженный до напряжения V конденсатор, при условии, что время заряда T ≫ τ, определяется формулой
где C — емкость в фарадах и V — напряжение в вольтах.
Максимальный ток I определяется по закону Ома:
Максимальный заряд Q определяется по формуле
где C — емкость в фарадах и V — напряжение в вольтах.
Фильтрующие электролитические конденсаторы на системной плате компьютера
Применение
Частотный разделитель ADSL — это фильтр нижних частот и три соединителя в корпусе
Конденсаторы часто используются в различных электрических и электронных устройствах и системах. Вероятно, вы не найдете ни одно электронное устройство, в котором не содержится хотя бы один конденсатор.
Конденсаторы используются для хранения энергии, обеспечения импульсов энергии, для фильтрации питающего напряжения, для коррекции коэффициента мощности, для развязки по постоянному току, в электронных частотных фильтрах, для фильтрации шумов, для запуска электродвигателей, для хранения информации, для настройки колебательных контуров, в различных датчиках, в емкостных экранах мобильных телефонов… Этот список можно продолжать до бесконечности.
Резистивно-емкостные (RC) цепи обычно используются в качестве простых фильтров нижних и верхних частот, а также простейших интегрирующих и дифференцирующих цепей.
Резистивно-емкостные фильтры нижних частот
Пример двухкаскадного RC-фильтра нижних частот с неинвертирующим операционным усилителем с единичным коэффициентом передачи, который используется в качестве буфера между двумя каскадами фильтра
Фильтры нижних частот пропускают только низкочастотные сигналы и подавляют высокочастотные сигналы. Частота среза определяется компонентами фильтра.
Такие фильтры широко используются в электронике. Например, их используют в сабвуферах для того, чтобы не подавать на них звуки высоких частот, которые они не могут воспроизводить. Фильтры нижних частот используются также в радиопередатчиках для блокировки нежелательных высокочастотных составляющих в передаваемом сигнале.
У тех, кто пользуется ADSL подключением к Интернету, всегда установлены частотные разделители с такими фильтрами нижних частот, которые предотвращают возникновение помех в аналоговых устройствах (телефонах) от сигналов DSL и воздействия помех от аналоговых устройств на оборудование DSL, подключенное к обычной телефонной линии.
Фильтры нижних частот используются для обработки сигналов перед их аналого-цифровым преобразованием. Такие фильтры улучшают качество аналоговых сигналов при их дискретизации и необходимы для подавления высокочастотных компонентов сигнала выше частоты Найквиста таким образом, чтобы он удовлетворял требованиям теоремы Котельникова для данной частоты дискретизации, то есть максимальная частота не должна быть выше половины частоты выборки.
На верхнем рисунке показан простой фильтр нижних частот. В нем используются только пассивные компоненты, поэтому он называется пассивным фильтром нижних частот (ФНЧ). В более сложных пассивных ФНЧ используются также катушки индуктивности.
В отличие от пассивных фильтров нижних частот, в активных фильтрах используются усилительные устройства, например, транзисторы или операционные усилители. В пассивные фильтрах также часто имеются операционные усилители, применяемые для развязки.
В зависимости от количества конденсаторов и катушек индуктивности, влияющих на крутизну частотной характеристики фильтра, они обычно называются «фильтрами первого порядка», «второго порядка» и так далее.
Фильтр, состоящий только из одного резистора и одного конденсатора, называется фильтром первого порядка.
Простой пассивный RC-фильтр верхних частот
Фильтры верхних частот пропускают только высокочастотные составляющие сигналов и ослабляют низкочастотные составляющие. Фильтры верхних частот используются, например, в разделительных фильтрах звуковых частот (кроссоверах) для подавления низкочастотных составляющих в сигналах, подаваемых на высокочастотные динамики («пищалки»), которые не могут воспроизводить такие сигналы и к тому же обладают малой мощностью по сравнению с мощностью низкочастотных сигналов.
Активный фильтр верхних частот с операционным усилителем
Фильтры верхних частот часто используются для блокировки постоянной составляющей сигналов в тех случаях, когда она нежелательна.
Например, в профессиональных микрофонах очень часто используется «фантомное» питание постоянным напряжением, которое подается по микрофонному кабелю. В то же время микрофон записывает переменные сигналы, такие как человеческий голос или музыка.
Постоянное напряжение не должно появляться на выходе микрофона и не должно поступать на вход микрофонного усилителя, поэтому для его блокировки используется фильтр верхних частот.
Простой полосовой фильтр, собранный из двух каскадов — фильтра нижних частот (C2, R2) и фильтра высоких частот (C1, R1)
Если фильтр нижних частот и фильтр верхних частот стоят друг за другом, они образуют полосовой фильтр, который пропускает частоты только в определенной полосе частот и не пропускает частоты за пределами этой полосы. Такие фильтры широко используются в радиоприемниках и радиопередатчиках.
В приемниках полосовые фильтры используются только для селективного пропускания и усиления сигналов радиостанции в требуемой узкой полосе частот. При этом сигналы других радиостанций за пределами этой полосы подавляются. Передатчики могут передавать радиосигналы только в определенном разрешенном для них диапазоне частот.
Поэтому в них используются полосовые фильтры для ограничения полосы передаваемого сигнала таким образом, что он вписывался в допустимые пределы.
Постоянная времени определяется по формуле
где τ — постоянная времени в секундах, R — сопротивление в омах и C — емкость в фарадах. Постоянная времени RC-цепи определяется как время, которое требуется, чтобы конденсатор зарядился до 63,2% его максимально возможного заряда при условии, что начальный заряд нулевой. Отметим, что конденсатор зарядится до 63,2% за время τ и почти полностью (до 99,3%) зарядится за время 5τ.
Энергия E, которую хранит полностью заряженный до напряжения V конденсатор, при условии, что время заряда T ≫ τ, определяется формулой
где C — емкость в фарадах и V — напряжение в вольтах.
Максимальный ток I определяется по закону Ома:
Максимальный заряд Q определяется по формуле
где C — емкость в фарадах и V — напряжение в вольтах.
Фильтрующие электролитические конденсаторы на системной плате компьютера