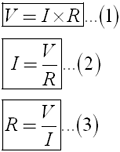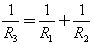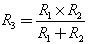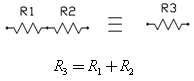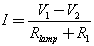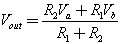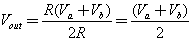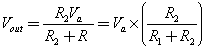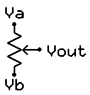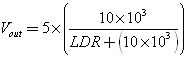Один из способов определения силы тока в резисторе – это ее прямое измерение мультиметром. Измерения следует проводить в разрыве цепи после резистора следующим образом:
– выставить на тестере максимально допустимый диапазон,
– присоединить щупы прибора к месту разрыва цепи.
Применив закон Ома, искомую величину можно также определить расчетным путем:
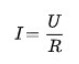
где I – сила тока, U – напряжение, R – сопротивление (единицы измерения ампер (А), вольт (В), ом (Ом) соответственно).
В приборостроении и электротехнике применяются различные типы соединения и подключения резисторов, что обеспечивает разнообразие электротехнических свойств электрических схем.
Типы соединений резисторов
Соединение элементов в одну цепь осуществляется следующими способами:
-
последовательно;
-
параллельно;
-
смешанно.
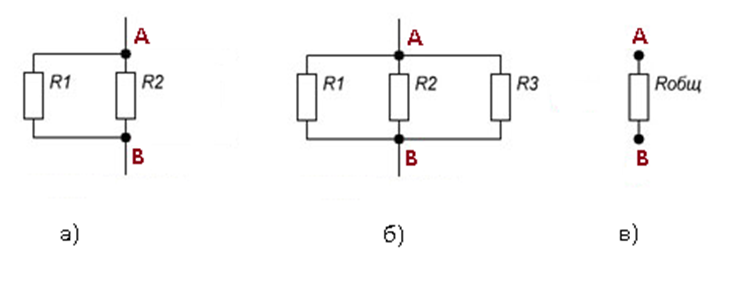
Общие схемы типов соединений представлены на рисунке 1.
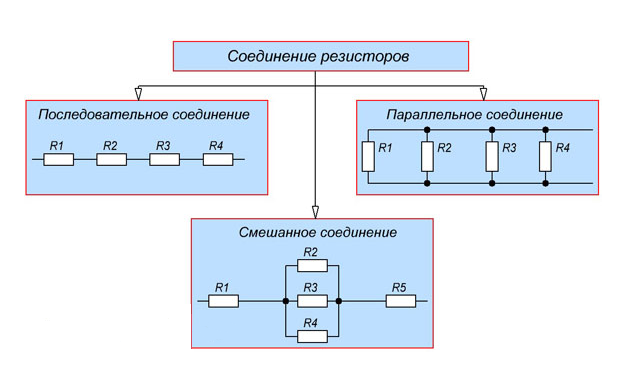
Рисунок 1. Типы соединений резисторов
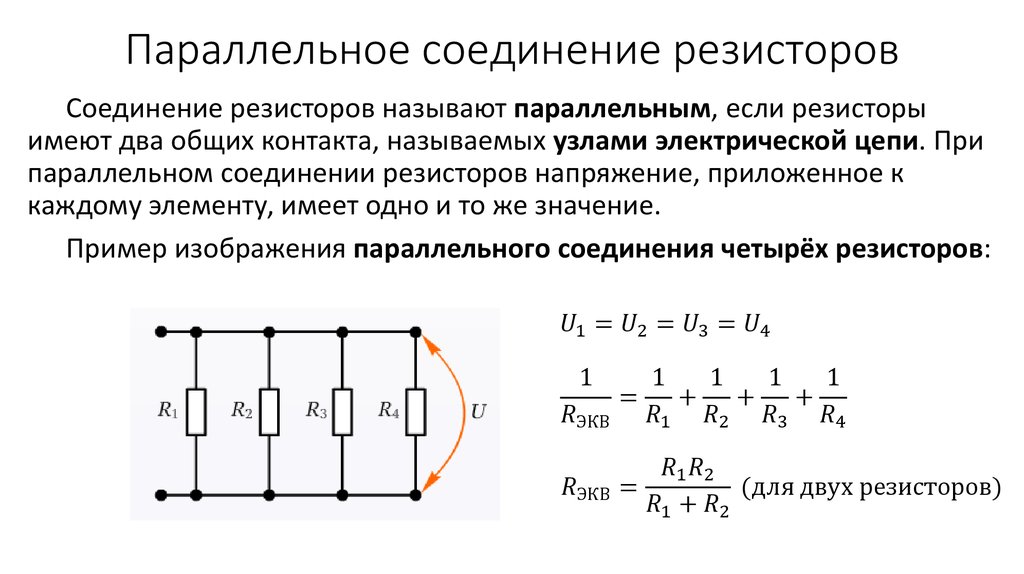
Параллельным соединением принято считать соединение, при котором элементы цепи соединены так, что их начала могут соединиться в одной точке, а концы – в другой (см.рис.2)
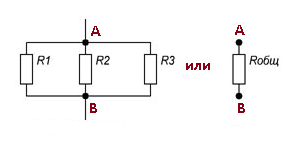
Рисунок 2. Параллельное соединение резисторов
Потоку заряженных частиц при прохождении участка АВ предоставлено несколько вариантов пути, поэтому на каждом участке с резистором будет протекать ток, величиной, обратно пропорциональной сопротивлению резистора.
При увеличении нагрузки параллельного соединения, в случае подключения большого числа резисторов способом параллельного соединения в электрическую цепь, общее сопротивление цепи значительно уменьшится, за счет увеличения числа путей, предоставленных потоку заряженных частиц. Увеличение количества возможных вариантов движения влечет за собой уменьшение противодействия движению тока.
Как найти сопротивление параллельно соединенных резисторов?
Общее сопротивление резисторов в случае параллельного соединения определено по закону Ома в следующем соотношении:
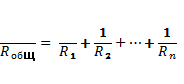
и рассчитывается по формуле:
Для примера произведем расчет общего сопротивления для цепи из двух резисторов, обладающих сопротивлением R1= R2=7Ом (см. рис.3а)
R12= 7*7/ (7+7) = 3,5Ом
Сопротивление на участке АВ
(1– 2) в 2 раза меньше R каждого из резисторов.
При параллельном подсоединении к рассматриваемой цепи еще одного резистора, также обладающего аналогичным сопротивлением R3=7Ом (см. рис.3б) общее сопротивление цепи рассчитывается с учетом предыдущих вычислений, где R12= 3,5Ом
Rобщ= 3,5*7/ (3,5+7) = 2,33 Ом
R123< R3
Рисунок 3. Увеличение цепи параллельного соединения резисторов
Из расчетов следует, что общее сопротивление (см. рис.3в) всегда будет меньше сопротивления любого параллельно включенного резистора. Такое условие обеспечивается равенством токов на входе и выходе узлов или групп параллельных резисторов и постоянством напряжения в сети.
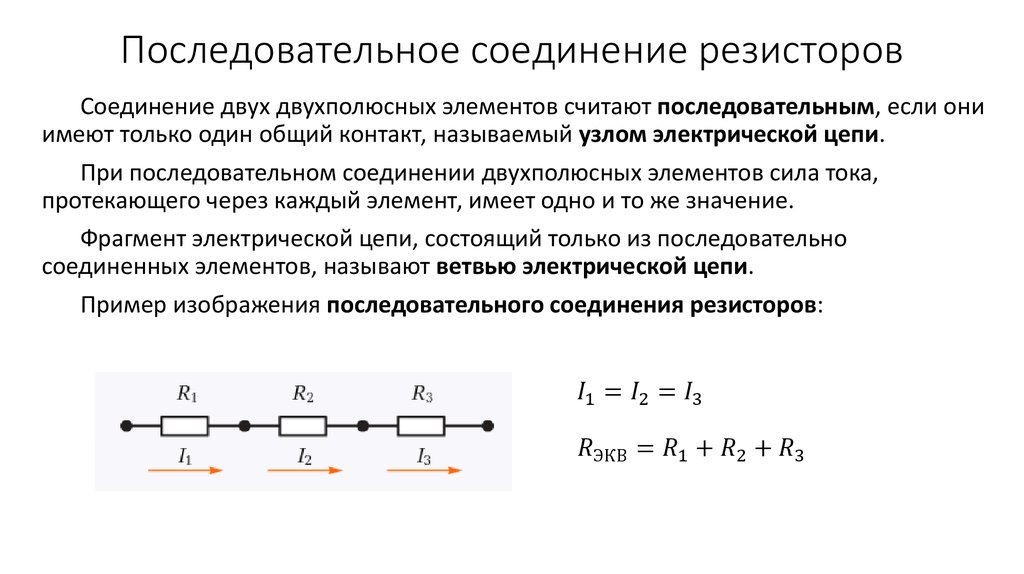
Что такое последовательное соединение резисторов?
При последовательном соединении резисторы подсоединяются друг за другом, при этом конец предыдущего резистора соединен с началом последующего резистора (рисунок 4).
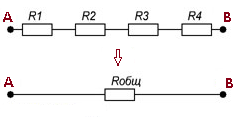
Рисунок 3. Последовательное соединение резисторов.
Потоку заряженных частиц при прохождении участка АВ предоставлен один путь, поэтому, чем больше резисторов подсоединено, тем большее сопротивление движущимся заряженным частицам они оказывают, то есть общее сопротивление участка цепи Rобщ возрастает.
Формула для расчета общего сопротивления при последовательном соединении имеет вид:
Как рассчитать напряжения на последовательно соединенных резисторах?
Последовательное соединение резисторов увеличивает общее сопротивление. Ток во всех частях схемы будет одинаковым, при этом будет определяться падение напряжения на каждом резисторе.
Общее напряжение питания на резисторах, соединенных последовательно, равно сумме разностей потенциалов на каждом резисторе:
URобщ =UR1+ UR2 + UR3+ UR4
Применив закон Ома, можно вычислить напряжение на каждом резисторе:
UR1=I*R1, UR2=I*R2, UR3=I*R3, UR4=I*R4
Напряжение на участке АВ рассчитывается по формуле:
UАВ=I* (R1
+ R2+R3+R4)
А ток в цепи:
Резисторы, соединенные последовательно, применяются в электротехнике в качестве делителя напряжения.
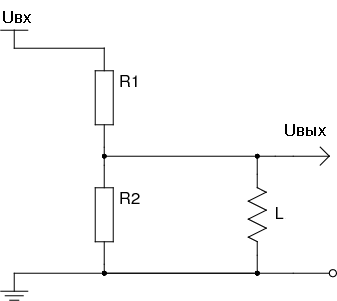
Рисунок 5. Схема простейшего делителя напряжения
Регулируя сопротивление обоих резисторов можно выделить требуемую часть входящего напряжения. При необходимости деления напряжения на несколько частей к источнику напряжения подключается несколько последовательно соединенных резисторов.
Смешанное соединение резисторов
В электротехнике наиболее распространено использование различных комбинаций параллельного и последовательного подключения. Силу тока при смешанном соединении резисторов определяют путем разделения цепи на последовательно соединенные части. Однако для определения общего сопротивления в случае параллельного сопротивления различных частей следует применять соответствующую формулу.
Алгоритм расчета смешанного подключения аналогичен правилу расчета базовой схемы последовательного и параллельного подключения резисторов. В этом нет ничего нового: нужно правильно разложить предложенное решение на пригодные для расчета части. Участки с элементами подключаются поочередно или параллельно. Гибридное резистивное соединение представляет собой комбинацию последовательного и параллельного. Эту комбинацию иногда называют последовательно-параллельным соединением.
На рисунке 6 представлена схема смешанного соединения резисторов.
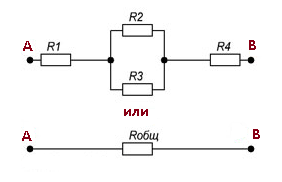
Рисунок 6. Смешанное соединение резисторов.
На рисунке показано, что резисторы R2 и R3
соединены параллельно, а R1, R23
и R4 последовательно.
Чтобы рассчитать сопротивление этого соединения, вся схема делится на простейшие части, начиная с параллельного или последовательного сопротивления. Тогда следующий алгоритм выглядит следующим образом:
1. Определите эквивалентное сопротивление части резистора, подключенной параллельно.
2. Если эти части содержат резисторы, включенные последовательно, сначала рассчитайте их сопротивление.
3. Вычислив эквивалентное сопротивление резистора, перерисовываем схему. Обычно схема получается из последовательного эквивалентного сопротивления.
4. Рассчитайте сопротивление цепи.
Другие способы подключения хорошо видны на примере, показанном на рисунке. Без специальных расчетов очевидно, что параллельное соединение резисторов создает несколько путей для тока. Следовательно, в одиночном контуре его сила будет меньше по сравнению с контрольными точками на входе и выходе. При этом напряжение на отметке остается неизменным.
Пример участка цепи для расчета сопротивления смешанного соединения показан на рисунке 5.
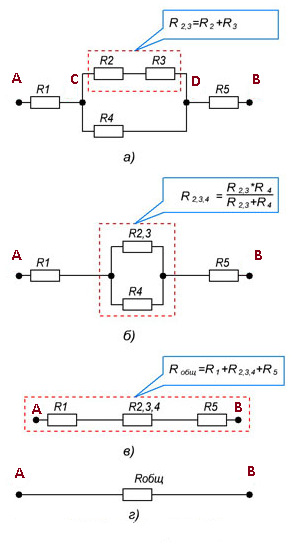
Рисунок 7. Общее сопротивление участка цепи со смешанным соединением резисторов.
В этой статье мы рассмотрим резистор и его взаимодействие с напряжением и током, проходящим через него. Вы узнаете, как рассчитать резистор с помощью специальных формул. В статье также показано, как специальные резисторы могут быть использованы в качестве датчика света и температуры.
Представление об электричестве
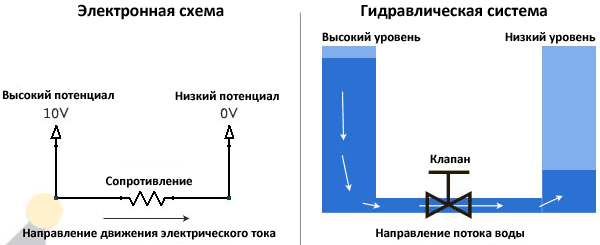
Новичок должен быть в состоянии представить себе электрический ток. Даже если вы поняли, что электричество состоит из электронов, движущихся по проводнику, это все еще очень трудно четко представить себе. Вот почему я предлагаю эту простую аналогию с водной системой, которую любой желающий может легко представить себе и понять, не вникая в законы.
Обратите внимание, как электрический ток похож на поток воды из полного резервуара (высокого напряжения) в пустой(низкое напряжение). В этой простой аналогии воды с электрическим током, клапан аналогичен токоограничительному резистору.
Из этой аналогии можно вывести некоторые правила, которые вы должны запомнить навсегда:
— Сколько тока втекает в узел, столько из него и вытекает
— Для того чтобы протекал ток, на концах проводника должны быть разные потенциалы.
— Количество воды в двух сосудах можно сравнить с зарядом батареи. Когда уровень воды в разных сосудах станет одинаковым, она перестанет течь, и при разряде аккумулятора, разницы между электродами не будет и ток перестанет течь.
— Электрический ток будет увеличиваться при уменьшении сопротивления, как и скорость потока воды будет увеличиваться с уменьшением сопротивления клапана.
Я мог бы написать гораздо больше умозаключений на основе этой простой аналогии, но они описаны в законе Ома ниже.
Резистор
Резисторы могут быть использованы для контроля и ограничения тока, следовательно, основным параметром резистора является его сопротивление, которое измеряется в Омах. Не следует забывать о мощности резистора, которая измеряется в ваттах (Вт), и показывает, какое количество энергии резистор может рассеять без перегрева и выгорания. Важно также отметить, что резисторы используются не только для ограничения тока, они также могут быть использованы в качестве делителя напряжения для получения низкого напряжения из большего. Некоторые датчики основаны на том, что сопротивление варьируется в зависимости от освещённости, температуры или механического воздействия, об этом подробно написано в конце статьи.
Закон Ома
Понятно, что эти 3 формулы выведены из основной формулы закона Ома, но их надо выучить для понимания более сложных формул и схем. Вы должны быть в состоянии понять и представить себе смысл любой из этих формул. Например, во второй формуле показано, что увеличение напряжения без изменения сопротивления приведет к росту тока. Тем не менее, увеличение тока не увеличит напряжение (хотя это математически верно), потому что напряжение — это разность потенциалов, которая будет создавать электрический ток, а не наоборот (см. аналогию с 2 емкостями для воды). Формула 3 может использоваться для вычисления сопротивления токоограничивающего резистора при известном напряжении и токе. Это лишь примеры, показывающие важность этого правила. Вы сами узнаете, как использовать их после прочтения статьи.
Последовательное и параллельное соединение резисторов
Понимание последствий параллельного или последовательного подключения резисторов очень важно и поможет вам понять и упростить схемы с помощью этих простых формул для последовательного и параллельного сопротивления:
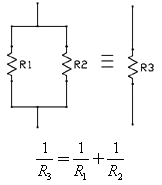
В этом примере схемы, R1 и R2 соединены параллельно, и могут быть заменены одним резистором R3 в соответствии с формулой:
В случае с 2-мя параллельно соединёнными резисторами, формулу можно записать так:
Кроме того, что эту формулу можно использовать для упрощения схем, она может быть использована для создания номиналов резисторов, которых у вас нет.
Отметим также, что значение R3 будет всегда меньше, чем у 2 других эквивалентных резисторов, так как добавление параллельных резисторов обеспечивает дополнительные пути
электрическому току, снижая общее сопротивление цепи.
Последовательно соединённые резисторы могут быть заменены одним резистором, значение которого будет равно сумме этих двух, в связи с тем, что это соединение обеспечивает дополнительное сопротивление тока. Таким образом, эквивалентное сопротивление R3 очень просто вычисляется: R3=R1+R2
В интернете есть удобные он-лайн калькуляторы для расчета последовательного и параллельного соединения резисторов.
Токоограничивающий резистор
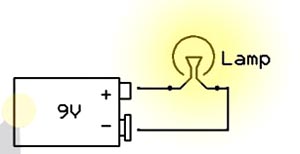
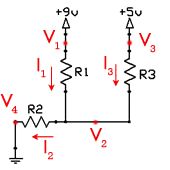
Самая основная роль токоограничивающих резисторов — это контроль тока, который будет протекать через устройство или проводник. Для понимания их работы, давайте сначала разберём простую схему, где лампа непосредственно подключена к 9В батареи. Лампа, как и любое другое устройство, которое потребляет электроэнергию для выполнения определенной задачи (например, светоизлучение) имеет внутреннее сопротивление, которое определяет его текущее потребление. Таким образом, отныне, любое устройство может быть заменено на эквивалентное сопротивление.
Теперь, когда лампа будет рассматриваться как резистор, мы можем использовать закон Ома для расчета тока, проходящего через него. Закон Ома гласит, что ток, проходящий через резистор равен разности напряжений на нем, поделенное на сопротивление резистора: I=V/R или точнее так:
I=(V1-V2)/R
где (V1-V2) является разностью напряжений до и после резистора.
Теперь обратите внимание на рисунок выше, где добавлен токоограничительный резистор. Он будет ограничивать ток идущий к лампе, как это следует из названия. Вы можете контролировать, количество тока протекающего через лампу, просто выбрав правильное значение R1. Большой резистор будет сильно снижать ток, а небольшой резистор менее сильно (так же, как в нашей аналогии с водой).
Математически это запишется так:
Из формулы следует, что ток уменьшится, если значение R1 увеличится. Таким образом, дополнительное сопротивление может быть использовано для ограничения тока. Однако важно отметить, что это приводит к нагреву резистора, и вы должны правильно рассчитать его мощность, о чем будет написано дальше.
Вы можете воспользоваться он-лайн калькулятором для расчета токоограничительного резистора светодиода.
Резисторы как делитель напряжения
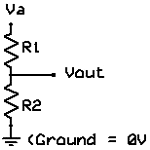
Как следует из названия, резисторы могут быть использованы в качестве делителя напряжения, другими словами, они могут быть использованы для уменьшения напряжения путем деления его. Формула:
Если оба резистора имеют одинаковое значение (R1=R2=R), то формулу можно записать так:
Другой распространенный тип делителя, когда один резистор подключен к земле (0В), как показано на рисунке 6B.
Заменив Vb на 0 в формуле 6А, получаем:
Узловой анализ
Теперь, когда вы начинаете работать с электронными схемами, важно уметь их анализировать и рассчитывать все необходимые напряжения, токи и сопротивления. Есть много способов для изучения электронных схем, и одним из наиболее распространенных методов является узловой, где вы просто применяете набор правил, и рассчитываете шаг за шагом все необходимые переменные.
Упрощенные правила узлового анализа
Определение узла
Узел – это любая точка соединения в цепи. Точки, которые связаны друг с другом, без других компонентов между ними рассматриваются как единый узел. Таким образом, бесконечное число проводников в одну точку считаются одним узлом. Все точки, которые сгруппированы в один узел, имеют одинаковые напряжения.
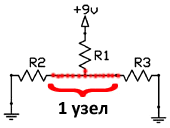
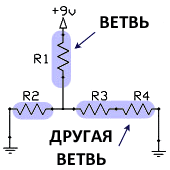
Определение ветви
Ветвь представляет собой набор из 1 и более компонентов, соединенных последовательно, и все компоненты, которые подсоединены последовательно к этой цепи, рассматриваются как одна ветвь.
Все напряжения обычно измеряются относительно земли 
Ток всегда течет от узла с более высоким напряжением на узел с более низким.
Напряжение на узле может быть высчитано из напряжения около узла, с помощью формулы:
V1-V2=I1*(R1)
Перенесем:
V2=V1-(I1*R1)
Где V2 является искомым напряжением, V1 является опорным напряжением, которое известно, I1 ток, протекающий от узла 1 к узлу 2 и R1 представляет собой сопротивление между 2 узлами.
Точно так же, как и в законе Ома, ток ответвления можно определить, если напряжение 2х соседних узлах и сопротивление известно:
I 1=(V1-V2)/R1
Текущий входящий ток узла равен текущему выходящему току, таким образом, это можно записать так: I 1+ I3=I2
Важно, чтобы вы были в состоянии понимать смысл этих простых формул. Например, на рисунке выше, ток протекает от V1 до V2, и, следовательно, напряжение V2 должно быть меньше, чем V1.
Используя соответствующие правила в нужный момент, вы сможете быстро и легко проанализировать схему и понять её. Это умение достигается практикой и опытом.
Расчет необходимой мощности резистора
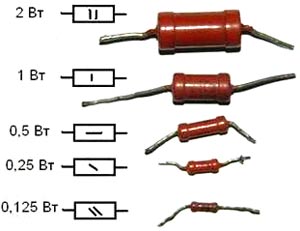
При покупке резистора вам могут задать вопрос: «Резисторы какой мощности вы хотите?» или могут просто дать 0.25Вт резисторы, поскольку они являются наиболее популярными.
Пока вы работаете с сопротивлением больше 220 Ом, и ваш блок питания обеспечивает 9В или меньше, можно работать с 0.125Вт или 0.25Вт резисторами. Но если напряжение более 10В или значение сопротивления менее 220 Ом, вы должны рассчитать мощность резистора, или он может сгореть и испортить прибор. Чтобы вычислить необходимую мощность резистора, вы должны знать напряжение через резистор (V) и ток, протекающий через него (I):
P=I*V
где ток измеряется в амперах (А), напряжение в вольтах (В) и Р — рассеиваемая мощность в ваттах (Вт)
На фото предоставлены резисторы различной мощности, в основном они отличаются размером.
Разновидности резисторов
Резисторы могут быть разными, начиная от простых переменных резисторов (потенциометров) до реагирующих на температуру, свет и давление. Некоторые из них будут обсуждаться в этом разделе.
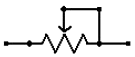
Переменный резистор (потенциометр)
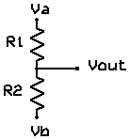
На рисунке выше показано схематическое изображение переменного резистора. Он часто упоминается как потенциометр, потому что он может быть использован в качестве делителя напряжения.
Они различаются по размеру и форме, но все работают одинаково. Выводы справа и слева эквивалентны фиксированной точке (например, Va и Vb на рисунке выше слева), а средний вывод является подвижной частью потенциометра, а также используется для изменения соотношения сопротивления на левом и правом выводах. Следовательно, потенциометр относится к делителям напряжения, которым можно выставить любое напряжение от Va к Vb.
Кроме того, переменный резистор может быть использован как тока ограничивающий путем соединения выводов Vout и Vb, как на рисунке выше (справа). Представьте себе, как ток будет течь через сопротивление от левого вывода к правому, пока не достигнет подвижной части, и пойдет по ней, при этом, на вторую часть пойдет очень мало тока. Таким образом, вы можете использовать потенциометр для регулировки тока любых электронных компонентов, например лампы.
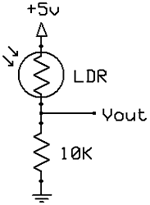
LDR (светочувствительные резисторы) и термисторы
Есть много датчиков основанных на резисторах, которые реагируют на свет, температуру или давление. Большинство из них включаются как часть делителя напряжения, которое изменяется в зависимости от сопротивления резисторов, изменяющегося под воздействием внешних факторов.
Терморезисторы
Фоторезистор (LDR)
Как вы можете видеть на рисунке 11A, фоторезисторы различаются по размеру, но все они являются резисторами, сопротивление которых уменьшается под воздействием света и увеличивается в темноте. К сожалению, фоторезисторы достаточно медленно реагируют на изменение уровня освещённости, имеют достаточно низкую точность, но очень просты в использовании и популярны. Как правило, сопротивление фоторезисторов может варьироваться от 50 Ом при солнце, до более чем 10МОм в абсолютной темноте.
Как мы уже говорили, изменение сопротивления изменяет напряжение с делителя. Выходное напряжение можно рассчитать по формуле:
Если предположить, что сопротивление LDR изменяется от 10 МОм до 50 Ом, то Vout будет соответственно от 0.005В до 4.975В.
Термистор похож на фоторезистор, тем не менее, термисторы имею гораздо больше типов, чем фоторезисторы, например, термистор может быть либо с отрицательным температурным коэффициентом (NTC), сопротивление которого уменьшается с повышением температуры, или положительным температурным коэффициентом (PTC), сопротивление которого будет увеличиваться с повышением температуры. Сейчас термисторы реагируют на изменение параметров среды очень быстро и точно.
Схемотехническое обозначение резисторов
Про определение номинала резистора используя цветовую маркировку можно почитать здесь.
Оригинал статьи
Теги:
2016-12-18
Какой заряд протечет через резистор после замыкания ключа? Активным сопротивлением катушки пренебречь. Параметры $mathcal{E}, r, L$ и $R$ заданы.
Решение:
Напряжение на катушке равно напряжению на сопротивлении:
$Li_{L}^{ prime} = i_{R}R$. (1)
Через достаточно большое время ток в цепи определяется законом Ома:
$I = frac{ mathcal{E}}{r}$ (2)
(ток через сопротивление Я равен нулю, поскольку активное (омическое) сопротивление катушки равно нулю).
Проинтегрируем обе части (1) по времени в пределах от нуля до бесконечности:
$int_{0}^{ infty} Li_{L}^{ prime} dt = int_{0}^{ infty} i_{R} Rdt$ (3)
или
$L int_{0}^{ infty} i_{L}^{ prime} dt = R int_{0}^{ infty} i_{R}dt$,
где $i_{L}$ и $i_{R}$ — токи через катушку и сопротивление соответственно. Учитывая, что $i_{L}(0) = 0$ и $i_{L}( infty) = I$, $q = int_{0}^{ infty} i_{R} dt$ — заряд, прошедший через сопротивление, из (2,3) находим:
$q = frac{LI}{R} = frac{L mathcal{E}}{Rr}$.
Задача может быть решена без применения интегрирования. Перепишем (1) в виде:
$L frac{ Delta i}{ Delta t} = frac{ Delta q}{ Delta t} R$
или
$L Delta i = Delta q R$. (5)
Суммируя (5) по всем промежуткам времени с учетом (2), приходим к полученному выше ответу.
Резистор (от латинского «resisto», что означает «сопротивляюсь») – это пассивный элемент электрической цепи, обладающий определённым или переменным значением электрического сопротивления. В отличие от активных элементов, пассивные не имеют возможности управлять потоком электронов.
В народе резисторы называют «резюками» или просто «сопротивление». Резисторы отвечают за линейное преобразование силы тока в напряжение и наоборот, а также для ограничения тока и поглощения электрической энергии.
Резистор является одним из самых популярных компонентов и используется в большинстве электронных устройств.
Содержание статьи
- Для чего нужен резистор в электрической цепи
- Основные характеристики резисторов
- Способ монтажа
- Выводные резисторы
- SMD-резисторы
- Виды резисторов по характеру изменения сопротивления
- Типы резисторов по характеру вольтамперной характеристики
- Виды резисторов по назначению
- Шумы резисторов и способы их уменьшения
- Обозначение резисторов на схеме
- Цветовая маркировка резисторов с проволочными выводами
- Виды соединения резисторов в электроцепи
- Последовательное соединение
- Параллельное соединение
- Смешанное соединение
- Соединение нескольких резисторов в одной схеме
- Видео: что такое резистор простым языком
Для чего нужен резистор в электрической цепи
Наглядный пример работы резистора
С помощью резистора в электроцепи ограничивают ток, получая нужную его величину. В соответствии с законом Ома, чем больше сопротивление при стабильном напряжении, тем меньше сила тока.
Закон Ома выражается формулой U = I*R, в которой:
- U – напряжение, В;
- I – сила тока, А;
- R – сопротивление, Ом.
Также резисторы работают как:
- преобразователи тока в напряжение и наоборот;
- делители напряжения, это свойство применяется в измерительных аппаратах;
- элементы для снижения или полного удаления радиопомех.
Основные характеристики резисторов
Параметры, которые нужно учитывать при выборе резистора, зависят от характера схемы, в которой он будет использован. К основным характеристикам относятся:
- Номинальное сопротивление. Эта величина измеряется в Ом, 1 кОм (1000 Ом), 1 МОм (1000 кОм), 1 ГОм (1000 МОм).
- Максимальная рассеиваемая мощность — предельная мощность, которую способен рассеивать элемент при долговременном использовании. На схемах номинальную мощность рассеивания указывают только для мощных резюков. Чем выше мощность, тем больше размеры детали.
- Класс точности. Определяет, на сколько фактическая величина сопротивления может отличаться от заявленной.
При необходимости принимают во внимание предельное рабочее напряжение, избыточный шум, устойчивость к температуре и влаге, коэффициент напряжения. Если деталь планируется установить в аппарат, работающий на высоких и сверхвысоких частотах, учитывают паразитную емкость и паразитную индуктивность. Эти величины должны быть минимальными.
Способ монтажа
По технологии монтажа резисторы разделяют на выводные и SMD.
Выводные резисторы
Радиальный выводной резистор Аксиальный выводной резистор
Предназначены для монтажа сквозь печатную плату. Выводы могут располагаться аксиально и радиально. Такие детали использовались в старой аудио- и видеоаппаратуре. Сейчас они применяются в простых аппаратах и в тех случаях, когда использование SMD-резисторов по каким-либо причинам невозможно.
Выводные резисторы по конструкции бывают проволочными, металлопленочными и композитными.
Из чего состоит резистор проволочного типа
В проволочных резисторах резистивным компонентом является проволока, намотанная на сердечник. Бифилярная намотка (двумя параллельными проводами, изолированными друг от друга, или обычным двужильным проводом) снижает паразитную индуктивность. К концам обмотки присоединяют выводы из многожильной меди или латунных пластин. Для защиты от влаги, механических повреждений и загрязнений, проволочные резюки покрывают неорганической эмалью, устойчивой к повышенным температурам.
Чем отличается металлопленочный резистор от проволочного
У металлопленочного резистора резистивным элементом является не проволока, а пленка из металлосплава. Резистивные компоненты (проволока или пленка) в резисторе изготавливаются из сплавов с высоким удельным сопротивлением: манганина, константана, нихрома, никелина.
SMD-резисторы
SMD-резисторы (или чип-резисторы) рассчитаны на поверхностный монтаж и выводов не имеют. Эти миниатюрные детали малой толщины изготавливаются прямоугольной или овальной формы. Имеют небольшие контакты, впаянные в поверхность. Их преимущества – экономия места на плате, упрощение и ускорение процесса сборки платы, возможность использования для автоматизированного монтажа.
SMD-резисторы изготавливают по пленочной технологии. Они могут быть тонко- и толстопленочными. Резистивную толстую или тонкую пленку наносят на изоляционную подложку. Подложка выполняет две функции: основания и теплоотводящего компонента.
Из чего делают чип-резисторы
Тонкопленочные элементы, к которым предъявляются особые требования по влагостойкости, изготавливаются из нихрома. При производстве толстопленочных моделей используются диоксид рутения, рутениты свинца и висмута.
Виды резисторов по характеру изменения сопротивления
Резисторы бывают постоянными и переменными. Постоянные имеют два вывода и стабильное сопротивление, отображенное в маркировке. В переменных (регулировочных и подстроечных) резисторах этот параметр меняется в допустимых пределах, в зависимости от рабочего режима.
В переменных резюках три вывода. На схеме указывается номинал между крайними выводами. Значение сопротивления между средним выводом и крайними регулируется путем перемещения скользящего контакта (бегунка) по резистивному слою. При этом сопротивление между средним и одним из крайних выводов возрастает, а между средним и другим крайним выводами – падает. При движении «бегунка» в другую сторону эффект обратный.
Что делают подстроечные резисторы
Они созданы для периодической подстройки, поэтому подвижная система рассчитана на небольшое количество циклов перемещения – до 1000.
Регулировочные резисторы рассчитаны на многократное использование – более 5 тысяч циклов.
Типы резисторов по характеру вольтамперной характеристики
По ВАХ резисторы разделяются на линейные и нелинейные. Сопротивление линейных резюков не зависит от напряжения и тока, а сопротивление нелинейных элементов меняется, в зависимости от этих (или других) величин. Малогабаритные линейные детали типа МЛТ (металлизированные лакированные термостойкие) используются в аппаратуре связи – магнитофонах и радиоприемниках.
Примером нелинейных резисторов может служить обычная осветительная лампочка, чье сопротивление в выключенном состоянии намного меньше, чем в режиме освещения. В фоторезисторах сопротивление меняется под действием света, в терморезисторах – температуры, тензорезисторах – деформации резисторного слоя, магниторезисторах – магнитного поля.
Виды резисторов по назначению
Резисторы по назначению разделяются на два основных типа – общего назначения и специальные. В свою очередь, специальные сопротивления делятся следующим образом:
- Высокочастотные. Для чего нужны такие резисторы в электроцепях: благодаря низким собственным емкостям и индуктивностям, высокочастотные резисторы могут применяться в схемах, в которых частота достигает сотни мегагерц, они выполняют в них функции балластных или оконечных нагрузок.
- Высокоомные. Величина сопротивления находится в диапазоне от нескольких десятков МОм до ТОм, величина напряжения небольшая – до 400 В. Высокоомные элементы работают в ненагруженном состоянии, поэтому большая мощность им не нужна. Их мощность рассеивания не превышает 0,5 Вт. Высокоомные резисторы служат для ограничения тока в дозиметрах, приборах ночного видения и других приборах с малыми токами.
- Прецизионные и сверхпрецизионные. Эти устройства имеют высокий класс точности: допустимое значение сопротивления составляет 1% от номинального и менее. Для сравнения: у обычных резисторов допустимый диапазон составляет 5% и более. Прецизионные устройства используются в основном в приборах измерения высокой точности.
Шумы резисторов и способы их уменьшения
Собственные шумы резистивных элементов состоят из тепловых и токовых шумов. Тепловые шумы, спровоцированные движением электронов в токопроводящем слое, усиливаются при повышении температуры нагрева детали и температуры окружающей среды. При протекании тока генерируются токовые шумы. Токовые шумы, значение которых существенно выше тепловых, в основном характерны для непроволочных резисторов.
Способы борьбы с шумами:
- Применение в схеме типов резисторов, в которых шумы невелики, благодаря технологии изготовления.
- Переменные резисторы шумят больше постоянных, поэтому в схеме стараются использовать элементы с переменным сопротивлением минимального номинала или не применять их вообще.
- Использование резюков с бОльшей мощностью, чем требуется по технологии.
- Принудительное охлаждение элемента путем установки поблизости вентилятора.
Обозначение резисторов на схеме
| Обозначение по ГОСТ 2.728-74 | Описание |
|
|
Постоянный резистор без указания номинальной мощности рассеивания |
|
|
Постоянный резистор номинальной мощностью рассеивания 0,05 Вт |
|
|
Постоянный резистор номинальной мощностью рассеивания 0,125 Вт |
|
|
Постоянный резистор номинальной мощностью рассеивания 0,25 Вт |
|
|
Постоянный резистор номинальной мощностью рассеивания 0,5 Вт |
|
|
Постоянный резистор номинальной мощностью рассеивания 1 Вт |
|
|
Постоянный резистор номинальной мощностью рассеивания 2 Вт |
|
|
Постоянный резистор номинальной мощностью рассеивания 5 Вт |
Обозначение переменных, подстроечных и нелинейных резисторов на схемах:
| Обозначение по ГОСТ 2.728-74 | Описание |
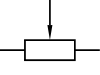
|
Переменный резистор (реостат). |
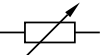
|
Переменный резистор, включенный как реостат (ползунок соединён с одним из крайних выводов). |

|
Подстроечный резистор. |
|
|
Подстроечный резистор, включенный как реостат (ползунок соединён с одним из крайних выводов). |
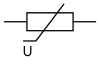
|
Варистор (сопротивление зависит от приложенного напряжения). |

|
Термистор (сопротивление зависит от температуры). |
|
|
Фоторезистор (сопротивление зависит от освещённости). |
Условное обозначение резистора на схеме – прямоугольник размерами 4х10 мм. На схемах значение сопротивления постоянного резюка менее кОма проставляется рядом с его условным обозначением числом без единицы измерения. При номинале от одного кОм до 999 кОм рядом с числом ставят букву «К», от одного МОм – букву «М». Характеристики резисторов указывают на их поверхности, для чего применяют буквенно-цифровой код или группу цветных полосок.
Примеры буквенно-цифрового обозначения для сопротивления, выраженного целым числом:
- 25 Ом – 25 R;
- 25 кОм – 25 K;
- 25 МОм – 25 M.
Если для выражения величины сопротивления используется десятичная дробь, то порядок расположения цифр и букв будет иным, например:
- 0,25 Ом – R 25;
- 0,25 кОм – K 25;
- 0,25 МОм – M 25.
Если сопротивление выражается числом, отличным от нуля и с десятичной дробью, то буква в обозначении играет роль запятой, например:
- 2,5 Ом – 2R5;
- 2,5 кОм – 2K5;
- 2,5 МОм – 2M5.
Производители в силу несовершенства производственной технологии не в состоянии на 100% гарантировать соответствие заявленного значения сопротивления фактическому. Допустимая погрешность обозначается в % и проставляется после номинального значения, например ±5%, ±10%, ±20%. Класс точности может определяться буквой, в зависимости от производителя, – русской или латинской.
|
Допустимая погрешность, ±% |
20 |
10 |
5 |
2 |
1 |
0,5 |
0,2 |
0,1 |
|
Буква |
||||||||
|
Русская |
В |
С |
И |
Л |
Р |
Д |
У |
Ж |
|
Латинская |
M |
K |
J |
G |
F |
D |
C |
B |
Цветовая маркировка резисторов с проволочными выводами
Для резисторов применяют цветовую кодировку, которая наносится 3, 4, 5, 6 цветовыми кольцами. Если кольца смещены к одному из выводов, то первым (с него и начинается расшифровка кода) считается кольцо, находящееся к выводу ближе всего. Если кольца расположены приблизительно равномерно, то следует помнить, что первое кольцо не делают серебристым или золотистым. В некоторых моделях чтение кода начинают с той стороны, где находятся парные кольца, отдельно стоящее кольцо обычно находится в конце шифра.
Таблица расшифровки цветовых колец
|
Цвет |
Число |
Десятичный множитель |
Класс точности, % |
Температурный коэффициент сопротивления |
% отказов |
|
Черный |
0 |
1*100 |
— |
— |
— |
|
Коричневый |
1 |
1*101 |
1 |
100 |
1 |
|
Красный |
2 |
1*102 |
2 |
50 |
0,1 |
|
Оранжевый |
3 |
1*103 |
— |
15 |
0,01 |
|
Желтый |
4 |
1*104 |
— |
25 |
0,001 |
|
Зеленый |
5 |
1*105 |
0,5 |
— |
— |
|
Синий |
6 |
1*106 |
0,25 |
10 |
— |
|
Фиолетовый |
7 |
1*107 |
0,1 |
5 |
— |
|
Серый |
8 |
1*108 |
0,05 |
— |
— |
|
Белый |
9 |
1*109 |
— |
1 |
— |
|
Серебристый |
— |
1*10-2 |
10 |
— |
— |
|
Золотой |
— |
1*10-1 |
5 |
— |
— |
В четырехполосном коде первые две полосы означают два знака номинала, третья полоска – это десятичный множитель, то есть это степень, в которую нужно возвести число, обозначающее номинал. Четвертая полоска указывает класс точности элемента. В пятиполосном шифре третья полоса обозначает знак номинала, четвертая – десятичный множитель, а пятая – класс точности. Если присутствует шестая полоса, то она обозначает температурный коэффициент. Если же это кольцо шире остальных в полтора раза, то оно характеризует процент отказов.
В расшифровке кодов проволочных резисторов помогут удобные онлайн-программы. Тем более имеет смысл к ним обратиться при расшифровке кода SMD-резистора, поскольку существует несколько вариантов маркировок, с которыми самостоятельно разобраться будет очень непросто.
Виды соединения резисторов в электроцепи
Эффективная работа элементов электроцепи с резистором зависит от правильного выбора не только самого сопротивления, но и способа его соединения в цепи, который может быть последовательным, параллельным или смешанным.
Последовательное соединение
Последовательное соединение резисторов
В такой схеме каждый последующий резистор подсоединяется к предыдущему, образуя неразветвленную цепь. Ток в последовательно соединенных «резюках» одинаковый, напряжение разное. Общее сопротивление нескольких последовательно расположенных «резюков» определяется очень просто – суммированием их номиналов.
Формула: Rобщ. = R1 + R2 +…+ Rn
Чем больше элементов в последовательной схеме, тем больше суммарное сопротивление.
Параллельное соединение
Параллельное соединение резисторов
При параллельном соединении резисторы соединяются между собой вводами и выводами. Напряжение на этих элементах одинаково, а ток между ними распределяется. Чем больше ветвей образуется, тем больше вариантов протекания тока и тем меньше общее сопротивление.
Формула: Rобщ. = 1/R1 + 1/R2 +…+ 1/Rn
Смешанное соединение
Смешанное соединение резисторов
При таком способе варианты соединения элементов комбинируют. Сопротивление каждого участка с определенным типом соединения рассчитывается по указанным выше правилам.
Соединение нескольких резисторов в одной схеме
Если у вас под рукой не оказалось сопротивления нужного номинала, то можно его получить при помощи правильного соединения нескольких резюков. Так, если вам нужно сопротивление 100 кОм, а есть две резистивные детали по 50 кОм, то их можно соединить последовательно и получить нужный результат. Сопротивление в 100 кОм можно получить параллельным соединением элементов по 200 кОм.
Видео: что такое резистор и как он работает
Была ли статья полезна?
Да
Нет
Оцените статью
| (0) |
Что вам не понравилось?
Другие материалы по теме
19.04.2018
Как подобрать резистор по назначению и принципу работы
Характеристики самых распространенных видов резисторов по типу, материалу, назначению, принципу работы. Какие параметры необходимо учитывать при работе. Номинальное и реальное сопротивление.
31.10.2017
Калькулятор цветовой маркировки резисторов
Резисторы – это элементы для построения электрических схем, предназначенные для контроля и регулирования величины силы тока. Разделяют на постоянные, переменные, подстроечные. Для идентификации постоянных резисторов SMD – устройств, монтируемых на поверхность, – все производители разработали буквенно-цифровые обозначения для крупных элементов и цветовой код для деталей очень маленьких размеров.
21.06.2018
Графическое обозначение радиодеталей на схемах
Радиодетали – электронные компоненты, собираемые в аналоговые и цифровые устройства: телевизоры, измерительные приборы, смартфоны, компьютеры, ноутбуки, планшеты. Если ранее детали изображались приближенно к их натуральному виду, то сегодня используются условные графические обозначения радиодеталей на схеме, разработанные и утвержденные Международной электротехнической комиссией.

Специалист в области радиоэлектроники и электронных компонентов. Консультант по подбору деталей в компании РадиоЭлемент.
Калькулятор Закона Ома для участка цепи
Немецкий физик Гео́рг Си́мон Ом в 1826 году подтвердил на опыте закон, выражающий связь между силой тока в цепи, напряжением и сопротивлением. Закон Ома для участка цепи применяют для расчетов сопротивления резистора на участке схемы ,а так же для определения тока через резистор при известном напряжении и сопротивлении.
Закон Ома для участка цепи
I сила тока (А)
U напряжение (В)
R сопротивление (Ом)



Расчет значения для участка цепи
Для расчета введите любые ДВА параметра из трех
Поиск резистора на сайте
Внимание! Производители объединяют резисторы в серии или ряды: E6, E12, E24…
Для подбора компонента будет использована серия E24.
Обнаружили ошибку или неточность в работе калькулятора? Сообщите нам об этом.
Соблюдайте технику безопасности во время работы с электронными компонентами!