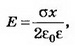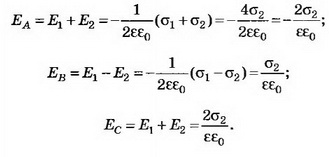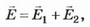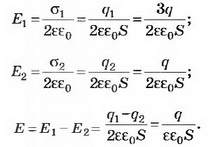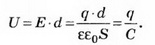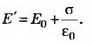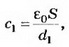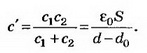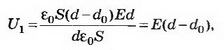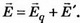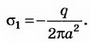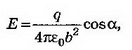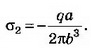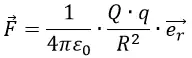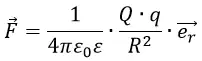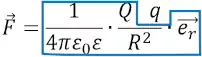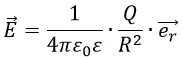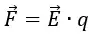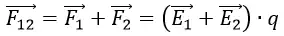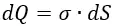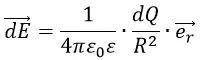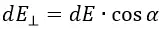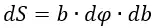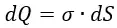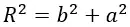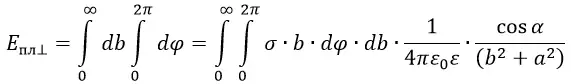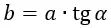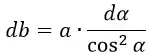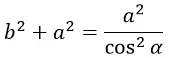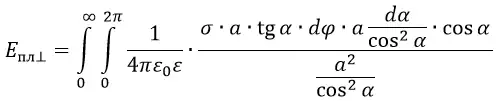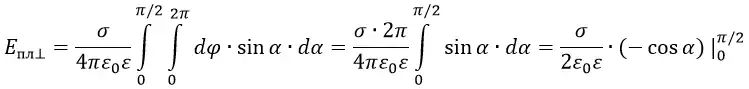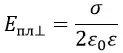Как найти заряд одной пластины

Пластины
плоского конденсатора площадью S
= 100 см²

каждая притягиваются друг к другу
с силой F
=4,910^-3Н.
Пространство
между пластинами
заполнено слюдой. Найти: 1) величину
заряда, находящегося на каждой пластин
q;
2) напряженность поля между пластинами
Е;
3) энергию в единице объема поля
конденсатора ,
диэлектрическая проницаемость слюды
_сл
= 6.

Дано:

S
= 0,01 м² Анализ:
Пластины конденсатора заряжены F
= 4,910^-3
Н
разноименными зарядами
и поэтому

_ел
= 6
притягиваются друг к
другу. Взаимодействие пластин можно
рассматривать следующим образом: заряд
одной

_______________
пластины создает поле с напряженностью
и это поле действует на заряд другой
пластины с силой F
= qE₁.

E
— ? q
— ? 
— ? , где E₁
— напряженность поля одной пластины, а
q
– заряд
другой пластины.

Решение:
Для
нахождения заряда одной из пластин
вспомним формулу для нахождения
напряженности поля бесконечно протяженной
заряженной пластины

где

— поверхностная плотность заряда
пластины.

Подставив
формулу для напряженности поля одной
пластины в формулу для силы взаимодействия
пластин равна, получим

Отсюда найдем
заряд одной пластины

Подставим
численные данные

Зная заряд, определим
напряженность поля конденсатора

Получим
численный ответ

Объемная плотность
энергии равна

Подставим
выражение для q
в формулу
для определения объемной плотности
энергии, получим

Вычислим численные
значения заряда одной пластины,
напряженность поля конденсатора и
объемную плотность энергии поля
конденсатора:

Ответ:
а) на одной пластине находится заряд
равный 10^-7
Кл, напряженность поля равна 1,910⁵
В/м, объемная плотность энергии равна
1,910⁷
Дж/м³
.

3.4.4. Основные формулы и соотношения

Электроёмкость
уединённого проводника:

Электроёмкость
системы проводников:

Ёмкость плоского
конденсатора:

Ёмкость уединённой
сферы:

Энергия уединённого
заряженного проводника:

3.4.4. Задачи для самостоятельного решения

Задача
3.13. Плоский
конденсатор заполнен диэлектриком и
на его пластины подана некоторая разность
потенциалов. Его энергия при этом
W
= 20 мкДж. После того как конденсатор
отключили от источника напряжения,
диэлектрик вынули из конденсатора.
Работа, которую надо было совершить
против сил электрического поля, чтобы
вынуть диэлектрик,
А
= 70 мкДж. Найти диэлектрическую
проницаемость 
диэлектрика.

Ответ:

= 4,5.

Задача
3.14. Конденсатор
с парафиновым диэлектриком (ε
= 2.0) ёмкостью С
= 44.2 пФ заряжен до разности потенциалов
U
= 150В и отключен
от источника. Напряженность поля внутри
конденсатора Е
= 600В/м.

Определите
поверхностную плотность заряда пластин
конденсатора и

как
изменится энергия конденсатора при
увеличении расстояния между пластинами
в два раза
d₂
=2
d₁?

Ответ:

Задача
3.15.Два
металлических шарика, первый с зарядом

q₁
= 10 нКл и радиусом R₁
= 3 см и второй с потенциалом ₂
= 3 кВ и радиусом R₂
=2 см, соединены проволочкой, емкостью
которой можно пренебречь.

Найдите:
а) потенциал ₁
первого шарика до разряда;

б)
энгергии W₁
и W₂
каждого шарика до разряда;

в)
заряд q₂

и потенциал ₂
второго шарика после разряда;

г)
работу разряда.

Ответ:
а) ₁
= 3 кВ; б) W₁
= 15 мкДж, W₂
= 90 мкДж;

в)
q₂
= 12 нКл, ₂
= 5,4 кВ; г) А
= 24 мкДж.

Задача
3.16.Два
металлических шарика, первый с зарядом

q₁
= 10 нКл и радиусом R₁
= 3 см и второй с потенциалом ₂
= 3 кВ и радиусом R₂
=2 см, соединены проволочкой, емкостью
которой можно пренебречь.

Найдите:
а) заряд q₂
второго шарика до разряда;

б)
заряд q₁
и потенциал ₁
первого шарика после разряда;

в)
энергию W
соединенных проводником шариков;

г) тепло, выделевшееся
при соединении шариков проволочкой.

Ответ:
б) q₂
= 20 нКл;

г)
q₁
= 18 нКл, ₁
= 5,4 кВ; е) W
= 81 мк Дж;
ж)
А
= 24 мкДж.

Задача
3.17. Площадь
пластин плоского воздушного конденсатора
S
= 0,01 м²,
расстояние между ними d
= 5 мм. Какая разность потенциалов U
была приложена к пластинам конденсатора,
если известно, что при разряде конденсатора
выделилось Q
= 4,19 мДж тепла?

Ответ:
U
= 21,7 кВ.

Задача
3.18. Конденсатор
ёмкостью C₁
= 3 мкФ зарядили до разности потенциалов
U₁
=300 В, а конденсатор ёмкостью C₂
= 2мкФ — до
U₂
= 200В. После зарядки и отсоединения от
источника питания конденсаторы соединили
параллельно.

Найдите
разность потенциалов на обкладках
конденсаторов после соединения. Как
изменится энергия этой системы
конденсаторов после их соединения?

Задача
3.119 Два
металлических шарика радиусами R₁=
5см и R₂=
10см имеют заряды q₁=
40 нКл и q₂=
40 нКл соответственно.

Найдите
потенциалы этих шаров. Найдите энергию,
которая выделится при разряде, если
шары соединить проводником, емкость
которого пренебрежимо мала.

Ответ:

Задача
3.20. 177. К
батарее с э.д.с. Е = 300 В подключены два
плоских конденсатора емкостями С₁
= 2 пФ и С₂
= 3 пФ.

Определите
заряд Q
и U
на пластинах конденсаторов при их
последовательном соединении.

Определите
заряд Q
и U
на пластинах конденсаторов при их
параллельном соединении.

Ответ:

Задача
3.21. Плоский
конденсатор, заполненный диэлектриком,
заряжен до некоторой разности потенциалов.
Его энергия при этом W
= 20 мкДж. После того как конденсатор
отключили от источника, диэлектрик
вынули из конденсатора, при этом была
совершена работа равная А = 70 мкДж.

Определите
диэлектрическую проницаемость диэлектрика
ε.

До
какого напряжения был первоначально
заряжен конденсатор, если расстояние
между пластинами d
= 0,02м., а
площадь каждой из них равна S
= 100см²?

Ответ:

80

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Наряду с резисторами одними из наиболее часто используемых электронных компонентов являются конденсаторы. И в этой статье мы разберемся, из чего они состоят, как работают и для чего применяются 👍 В первую очередь, рассмотрим устройство и принцип работы, а затем плавно перейдем к основным свойствам и характеристикам — заряду, энергии и, конечно же, емкости конденсатора.

Плоский конденсатор.

Итак, простейший конденсатор представляет из себя две плоские проводящие пластины, расположенные параллельно друг другу и разделенные слоем диэлектрика. Причем расстояние между пластинами должно быть намного меньше, чем, собственно, размеры пластин:

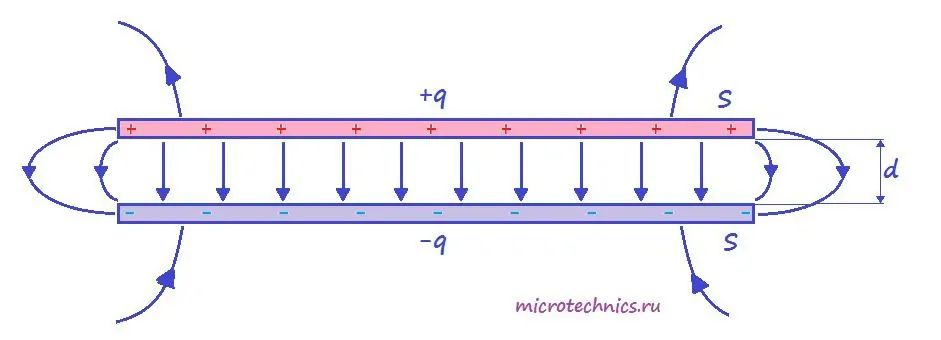
Такое устройство называется плоским конденсатором, а пластины — обкладками конденсатора. Стоит уточнить, что здесь мы рассматриваем уже заряженный конденсатор (сам процесс зарядки мы изучим чуть позже), то есть на обкладках сосредоточен определенный заряд. Причем наибольший интерес представляет тот случай, когда заряды пластин конденсатора одинаковы по модулю и противоположны по знаку (как на рисунке).

А поскольку на обкладках сосредоточен заряд, между ними возникает электрическое поле. Поле плоского конденсатора, в основном, сосредоточено между пластинами, однако, в окружающем пространстве также возникает электрическое поле, которое называют полем рассеяния. Очень часто его влиянием в задачах пренебрегают, но забывать о нем не стоит.

Для определения величины этого поля рассмотрим еще одно схематическое изображение плоского конденсатора:

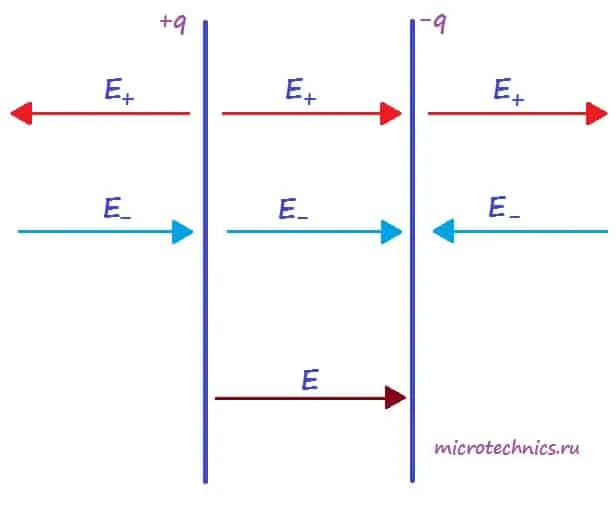
Каждая из обкладок конденсатора в отдельности создает электрическое поле:

• положительно заряженная пластина (+q) создает поле, напряженность которого равна E_{+}
• отрицательно заряженная пластина (-q) создает поле, напряженность которого равна E_{-}

Выражение для напряженности поля равномерно заряженной пластины выглядит следующим образом:

E_{пл} = frac{sigma}{2varepsilon_0thinspacevarepsilon}

Здесь sigma— это поверхностная плотность заряда: sigma = frac{q}{S}, а varepsilon — диэлектрическая проницаемость диэлектрика, расположенного между обкладками конденсатора. Поскольку площадь пластин конденсатора у нас одинаковая, как и величина заряда, то и модули напряженности электрического поля, равны между собой:

E_+ = E_- = frac{q}{2varepsilon_0thinspacevarepsilon S}

Но направления векторов разные — внутри конденсатора вектора направлены в одну сторону, а вне — в противоположные. Таким образом, внутри обкладок результирующее поле определяется следующим образом:

E = E_+ + E_- = frac{q}{2varepsilon_0thinspacevarepsilon S} + frac{q}{2varepsilon_0thinspacevarepsilon S} = frac{q}{varepsilon_0thinspacevarepsilon S}

Соответственно, вне конденсатора (слева и справа от обкладок) поля пластин компенсируют друг друга и результирующая напряженность равна 0.

Процессы зарядки и разрядки конденсаторов.

С устройством мы разобрались, теперь разберемся, что произойдет, если подключить к конденсатору источник постоянного тока. На принципиальных электрических схемах конденсатор обозначают следующим образом:

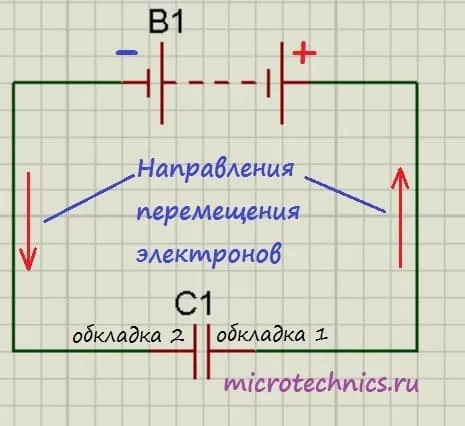
Итак, мы подключили обкладки конденсатора к полюсам источника постоянного тока. Что будет происходить?

Свободные электроны с первой обкладки конденсатора устремятся к положительному полюсу источника. Из-за этого на обкладке возникнет недостаток отрицательно заряженных частиц, и она станет положительно заряженной. В то же время электроны с отрицательного полюса источника тока переместятся ко второй обкладке конденсатора. В результате чего на ней возникнет избыток электронов, соответственно, обкладка станет отрицательно заряженной.

Таким образом, на обкладках конденсатора образуются заряды разного знака (как раз этот случай мы и рассматривали в первой части статьи), что приводит к появлению электрического поля, которое создаст между пластинами конденсатора определенную разность потенциалов. Процесс зарядки будет продолжаться до тех пор, пока эта разность потенциалов не станет равна напряжению источника тока. После этого процесс зарядки закончится, и перемещение электронов по цепи прекратится.

При отключении от источника конденсатор может на протяжении длительного времени сохранять накопленные заряды. Соответственно, заряженный конденсатор является источником электрической энергии, это означает, что он может отдавать энергию во внешнюю цепь. Давайте создадим простейшую цепь, просто соединив обкладки конденсатора друг с другом:

В данном случае по цепи начнет протекать ток разряда конденсатора, а электроны начнут перемещаться с отрицательно заряженной обкладки к положительной. В результате напряжение на конденсаторе (разность потенциалов между обкладками) начнет уменьшаться. Этот процесс завершится в тот момент, когда заряды пластин конденсаторов станут равны друг другу, соответственно электрическое поле между обкладками пропадет и по цепи перестанет протекать ток. Именно так происходит разряд конденсатора, в результате которого он отдает во внешнюю цепь всю накопленную энергию. Как видите, здесь нет ничего сложного.

Емкость и энергия конденсатора.

Важнейшей характеристикой является электрическая емкость конденсатора. Это физическая величина, которая определяется как отношение заряда q одного из проводников к разности потенциалов между проводниками:

C = frac{q}{Deltavarphi} = frac{q}{U}

Емкость конденсатора изменяется в Фарадах, но величина 1 Ф является неимоверно большой, поэтому чаще всего используются микрофарады (мкФ), нанофарады (нФ) и пикофарады (пФ). А поскольку мы уже вывели формулу для расчета напряженности, то давайте выразим напряжение на конденсаторе следующим образом:

U = Ed = frac{qd}{varepsilon_0thinspacevarepsilon S}

Здесь у нас d — это расстояние между пластинами конденсатора, а q — заряд конденсатора. Подставим эту формулу в выражение для емкости:

C = frac{qvarepsilon_0thinspacevarepsilon S}{qd} = frac{varepsilon_0thinspacevarepsilon S}{d}

Если в качестве диэлектрика выступает воздух, то во всех формулах можно подставить varepsilon = 1. Для запасенной же энергии конденсатора справедливы следующие выражения:

W = frac{CU^2}{2} = frac{qU}{2} = frac{q^2}{2C}

Помимо емкости конденсаторы характеризуются еще одним параметром, а именно величиной напряжения, которое может выдержать его диэлектрик. При слишком больших значениях напряжения электроны диэлектрика отрываются от атомов, и диэлектрик начинает проводить ток. Это явление называется пробоем конденсатора, и в результате обкладки оказываются замкнутыми друг с другом. Собственно, характеристикой, которая часто используется при работе с конденсаторами является не напряжение пробоя, а рабочее напряжение. Это такая величина напряжения, при которой конденсатор может работать неограниченно долгое время, и пробоя не произойдет.

Итак, резюмируем — сегодня рассмотрели основные свойства конденсаторов, их устройство и характеристики, так что на этом заканчиваем статью, а в следующей мы будем обсуждать различные варианты соединений и маркировку.

Задачи по электростатике можно разделить на две группы: задачи о точечных зарядах и задачи о заряженных телах, размеры которых нельзя не учитывать [1—5].

Решение задач по расчёту электрических полей и взаимодействий точечных зарядов основано на применении закона Кулона и не вызывает особых затруднений. Более сложным является определение напряжённости поля и взаимодействия заряженных тел конечных размеров: сферы, цилиндра, плоскости. При вычислении напряжённости электростатических полей различной конфигурации следует подчеркнуть важность принципа суперпозиции и использовать его при рассмотрении полей, созданных не только точечными зарядами, но и зарядами, распределёнными по поверхности и объёму. При рассмотрении действия поля на заряд формула F=qE в общем случае справедлива для точечных заряженных тел и только в однородном поле применима для тел любых размеров и формы, несущих заряд q.

Электрическое поле конденсатора получается в результате наложения двух полей, созданных каждой пластиной.

В плоском конденсаторе можно рассматривать одну пластину как тело с зарядом q₁ помещённое в электрическое поле напряжённостью Е₂, созданное другой пластиной.

Рассмотрим несколько задач.

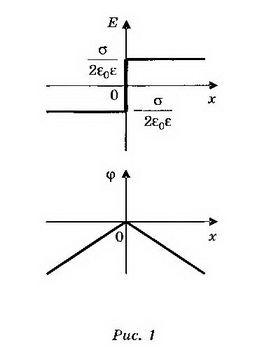
1. Бесконечная плоскость заряжена с поверхностной плотностью σ>0. Найдите напряжённость поля Е и потенциал ϕ по обе стороны плоскости, считая потенциал плоскости равным нулю. Постройте графики зависимостей Е(х), ϕ(х). Ось х перпендикулярна плоскости, точка х=0 лежит на плоскости.

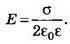
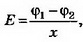
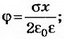
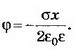
Решение. Электрическое поле бесконечной плоскости является однородным и симметричным относительно плоскости. Его напряжённостьСвязь между напряжённостью и разностью потенциалов между двумя точками однородного электростатического поля выражается формулойгде х — расстояние между точками, измеренное вдоль силовой линии. Тогда  ϕ₂=ϕ₁-Eх. При х<0 при х>0  Зависимости Е(х) и ϕ(х) представлены на рисунке 1.

2. Две плоскопараллельные тонкие пластины, расположенные на малом расстоянии d друг от друга, равномерно заряжены зарядом поверхностной плотностью σ₁ и σ₂. Найдите напряжённости поля в точках, лежащих между пластинами и с внешней стороны. Постройте график зависимости напряжённости Е(х) и потенциала ϕ(х), считая ϕ(0)=0. Рассмотрите случаи, когда: a) σ₁=-σ₂; б) σ₁= σ₂; в) σ₁=3σ₂—

Решение. Так как расстояние между пластинами мало, то их можно рассматривать как бесконечные плоскости.

Напряжённость поля положительно заряженной плоскости равна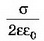и направлена от неё; напряжённость поля отрицательно заряженной плоскости направлена к ней.

Согласно принципу суперпозиции поле в любой рассматриваемой точке будет создаваться каждым из зарядов в отдельности.

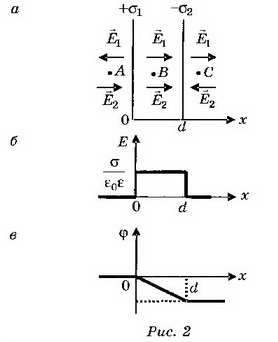
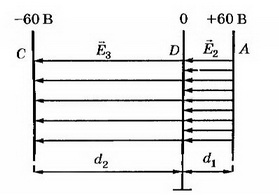
а) Поля двух плоскостей, заряженных равными и противоположными по знаку зарядами (плоский конденсатор), складываются в области между плоскостями и взаимно уничтожаются во внешних областях (рис. 2, а).

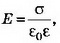
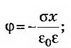
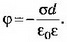
При х<0 Е=0, ϕ=0; при 0<x<d при x>d Е=0,Графики зависимости напряжённости и потенциала от расстояния х приведены на рисунке 2, б, в.

Если плоскости конечных размеров, то поле между плоскостями не будет строго однородным, а поле вне плоскостей не будет точно равно нулю.

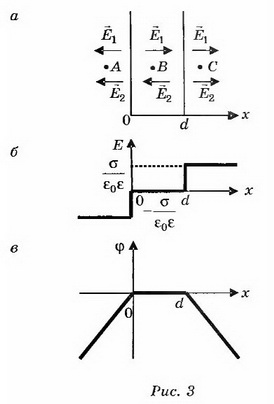
б) Поля плоскостей, заряженных равными по величине и знаку зарядами (σ₁=σ₂), компенсируют друг друга в пространстве между плоскостями и складываются во внешних областях (рис. 3, а). При х<0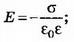при 0<x<d E=0; при х>d 

Воспользовавшись графиком Е(х) (рис. 3, б), построим качественно график зависимости ϕ(х) (рис. 3, в).

в) Если σ₁= σ₂, то, учитывая направления полей и выбирая направление направо за положительное, находим:

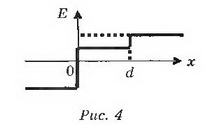
Зависимость напряжённости Е от расстояния показана на рисунке 4.

3. На одной из пластин плоского конденсатора ёмкостью С находится заряд q₁=+3q, а на другой q₂=+q. Определите разность потенциалов между пластинами конденсатора.

Решение. 1-й способ. Пусть площадь пластины конденсатора S, а расстояние между ними d. Поле внутри конденсатора однородное, поэтому разность потенциалов (напряжение) на конденсаторе можно определить по формуле U=E*d, где Е — напряжённость поля внутри конденсатора.

где Е₁, Е₂ — напряжённости поля, создаваемого пластинами конденсатора.

Тогда

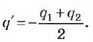
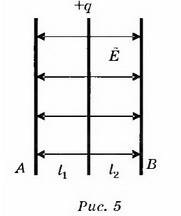
2-й способ. Добавим на каждую пластину зарядТогда пластины конденсатора будут иметь заряды +q и -q. Поля одинаковых зарядов пластин внутри конденсатора компенсируют друг друга. Добавленные заряды не изменили поле между пластинами, а значит, и разность потенциалов на конденсаторе. U=q/C.

4. В пространство между обкладками незаряженного плоского конденсатора вносят тонкую металлическую пластину, имеющую заряд +q. Определите разность потенциалов между обкладками конденсатора.

Решение. Так как конденсатор не заряжен, то электрическое поле создаётся только пластиной, имеющей заряд q (рис. 5). Это поле однородное, симметричное относительно пластины, и его напряжённость 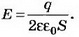Пусть потенциал металлической пластины равен  ϕ. Тогда потенциалы обкладок А и В конденсатора будут равны ϕ-ϕ_А=ϕEl₁; ϕ_А=ϕ-El₁; ϕ-ϕ_B=ϕ-El₂; ϕ_B=ϕ-El₂.

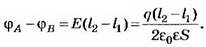
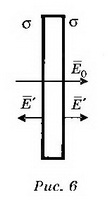
Разность потенциалов между обкладками конденсатора Если пластина находится на одинаковом расстоянии от обкладок конденсатора, то разность потенциалов между обкладками равна нулю.

5. В однородное электрическое поле напряжённостью Е₀ перпендикулярно силовым линиям помещают заряженную металлическую пластину с плотностью заряда на поверхности каждой стороны пластины σ (рис. 6). Определите напряжённость поля Е’ внутри и снаружи пластины и поверхностную плотность зарядов σ₁и σ₂, которая возникнет на левой и правой сторонах пластины.

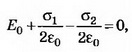
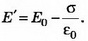
Решение. Поле внутри пластины равно нулю и является суперпозицией трёх полей: внешнего поля Е₀, поля, создаваемого зарядами левой стороны пластины, и поля, создаваемого зарядами правой стороны пластины. Следовательно,где σ₁ и σ₂ — поверхностная плотность заряда на левой и правой сторонах пластины, которая возникает после внесения пластины в поле Е₀. Суммарный заряд пластины не изменится, поэтому σ₁+σ₂=2σ, откуда σ₁=σ-ε₀E₀, σ₂=σ+ε₀E₀. Поле снаружи пластины является суперпозицией поля Е₀ и поля заряженной пластины Е. Слева от пластиныСправа от пластины 

6. В плоском воздушном конденсаторе напряжённость поля Е= 10⁴ В/м. Расстояние между обкладками d=2 см. Чему будет равна разность потенциалов, если между пластинами параллельно им поместить металлический лист толщиной d₀=0,5 см (рис. 7)?

Решение. Поскольку электрическое поле между пластинами однородное, то U=Ed, U=200 В.

Если между пластинами пометить металлический лист, то получается система из двух последовательно соединённых конденсаторов с расстоянием между пластинами d₁ и d₂. Ёмкости этих конденсаторов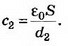Их общая ёмкость

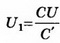
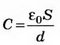
Так как конденсатор отключён от источника тока, то заряд конденсатора при внесении металлического листа не меняется: q’=CU=С’U₁;где  емкость конденсатора до внесения в него металлического листа. Получаем:

U₁=150 В.

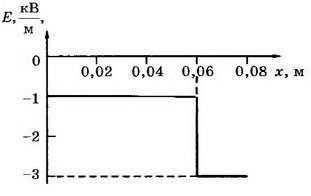
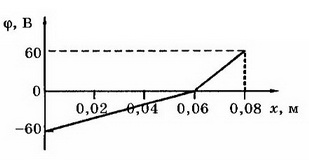
7. На пластинах А и С, расположенных параллельно на расстоянии d=8 см друг от друга, поддерживаются потенциалы ϕ₁= 60 В и ϕ₂=-60 В соответственно. Между ними поместили заземлённую пластину D на расстоянии d₁=2 см от пластины А. На сколько изменилась напряжённость поля на участках AD и CD? Постройте графики зависимостей ϕ(x) и Е(х).

Решение. Первоначальная напряжённость поля между пластинами А и С:

E₁=1,5 кВ/м.

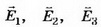
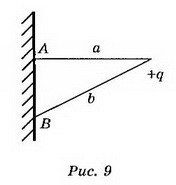
Напряжённость поля на участке AD: Е₂= ϕ₁/d₁, Е₂=3 кВ/м, т. е. увеличилась на 1,5 кВ/м. Напряжённость поля на участке CD  Е₃= ϕ₂/d₂, т.е. уменьшилась на Е₃=0,5 кВ/м.  Поскольку векторы направлены противоположно положительному направлению оси Ох, то Е_г, Е₂, Е₃<0 (рис. 8).

8. Точечный заряд q=5*10^-9 Кл находится на расстоянии 3 см от проводящей заземлённой стенки. Найдите поверхностную плотность заряда, индуцированного на стенке в точке А, ближайшей к заряду, и в точке В, находящейся на расстоянии 5 см от заряда.

Решение. В точках А, В, расположенных в непосредственной близости к поверхности проводника (рис. 9), поле создаётся точечным зарядом q и зарядом q’, индуцированным на стенке:

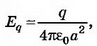
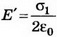
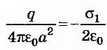
В точке Агде а — расстояние от заряда до стенки,. Но поле внутри проводника равно нулю; следовательно,. Отсюда  

В точке В величина нормальной составляющей напряжённости поля точечного заряда

где b — расстояние от заряда до точки, cosα=a/b,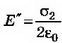— напряжённость поля плоскости.

Следовательно,

Список использованной литературы

1. Балаш, В. А. Задачи по физике и методы их решения / В. А. Балаш. — 4-е изд. — М. : Просвещение, 1983. — 432 с.

2. Бутиков, Е. И. Физика в примерах и задачах / Е. И. Бутиков, А. А. Быков, А. С. Кондратьев. — 3-е изд. — М. : Наука, 1989. — 462 с.

3. Зилъберман, Г. Е. Электричество и магнетизм / Г. Е. Зильберман. — М. : Наука, 1990. — 384 с.

4. Меледин, Г. В. Физика в задачах / Г. В. Меледин. — 2-е изд. — М. : Наука, 1990. — 270 с.

5. Сборник задач по физике / Л. П. Баканина [и др.]; под ред. С. М. Козела. — М. : Наука, 1990. — 347 с.

Конденсатором называется система, состоящая из двух проводников, расположенных достаточно близко друг от друга. Проводники называют обкладками конденсатора. Если на обкладки конденсатора поместить равные по модулю и противоположные по знаку заряды, то разность потенциалов (напряжение) между обкладками будет пропорциональна заряду обкладок, т. е. отношение заряда к напряжению не будет зависеть от заряда. На основании этого утверждения, которое приводим без доказательства, вводится понятие электроёмкости (ёмкости конденсатора).

Ёмкостью конденсатора называется отношение заряда $$ Q$$ одной из обкладок к разности потенциалов $$ U$$ между этой обкладкой и соседней:

Если взят заряд на положительно заряженной обкладке, то $$ Q>0, U>0$$ и получится $$ C>0$$. Если заряд взят на отрицательной обкладке, то Q<0, U<0Q<0,;U<0 и опять будет $$ C>0$$. Итак, из определения ёмкости следует, что ёмкость величина положительная. В системе СИ ёмкость измеряется в фарадах: `1″Ф»=1` Кл/В.

Требование близости обкладок друг к другу связано с тем, что для независимости $$ C$$ от $$ Q$$ в (10.1) нужно, чтобы поле от зарядов на обкладках было сосредоточено практически полностью между обкладками, т. е. все силовые линии, начинающиеся на одной обкладке, заканчивались только на другой и не уходили на окружающие тела. В этом случае окружающие тела не будут влиять на ёмкость конденсатора.
Можно вывести, что ёмкость плоского конденсатора

Здесь $$ S$$ — площадь обкладок, $$ d$$ — расстояние между ними, $$ varepsilon $$ — диэлектрическая проницаемость диэлектрика между обкладками.
При последовательном соединении изначально не заряженных конденсаторов с ёмкостями $$ {C}_{1}, {C}_{2}, …$$, общий заряд равен заряду каждого конденсатора, общее напряжение равно сумме напряжений на отдельных конденсаторах, общая ёмкость определяется из формулы: $$ {displaystyle frac{1}{C}}={displaystyle frac{1}{{C}_{1}}}+{displaystyle frac{1}{{C}_{2}}}+…$$

Полезно помнить формулу для частного случая последовательного соединения двух конденсаторов: $$ C={displaystyle frac{{C}_{1}{C}_{2}}{{C}_{1}+{C}_{2}}}$$.

Для последовательно соединённых n одинаковых конденсаторов ёмкостью $$ {C}_{1}$$ каждый $$ C={C}_{1}/n.$$

Если последовательно соединены предварительно заряженные конденсаторы, то применение перечисленных выше свойств и формул может привести к неправильному результату!
При параллельном соединении конденсаторов с емкостями $$ {C}_{1,} {C}_{2}, …$$ общий заряд равен сумме зарядов отдельных конденсаторов, общее напряжение равно напряжению на каждом, общая ёмкость равна сумме ёмкостей:

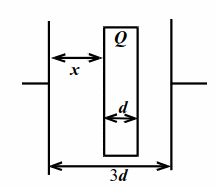Рис. 10.1

В плоский конденсатор параллельно его обкладкам вставлена пластина из диэлектрика с диэлектрической проницаемостью $$ varepsilon $$ (рис. 10.1). Площадь обкладок конденсатора и пластины $$ S$$, толщина пластины $$ d$$, расстояние между обкладками $$ 3d$$. Найти ёмкость такого конденсатора.

Пусть расстояние от пластины до левой обкладки конденсатора $$ x$$. Наклеим мысленно на обе стороны пластины тонкую проводящую и незаряженную фольгу. От этого ничего не изменится. Обе фольги можно рассматривать как своеобразные провода, соединяющие три последовательно соединённых конденсатора с расстояниями $$ x$$, $$ d$$ и $$ 2d-x$$. Для общей ёмкости $$ C$$:

$$ {displaystyle frac{1}{C}}={displaystyle frac{x}{{varepsilon }_{0}S}}+{displaystyle frac{d}{varepsilon {varepsilon }_{0}S}}+{displaystyle frac{2d-x}{{varepsilon }_{0}S}}$$.

Окончательно $$ C={displaystyle frac{varepsilon {varepsilon }_{0}S}{d(2varepsilon +1)}}.$$ Заметим, что не заданная в условии величина $$ x$$ «исчезла» в процессе решения.

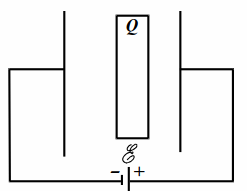Рис. 10.2

В плоский конденсатор ёмкостью $$ C$$ вставлена параллельно обкладкам плоская проводящая пластина с зарядом $$ Q$$ (рис. 10.2). Конденсатор подсоединён к источнику с ЭДС $$ mathcal{E}$$. Площади пластины и обкладок конденсатора равны. Толщина пластины равна расстоянию от неё до правой обкладки и составляет четверть от расстояния между обкладками. Найти заряд конденсатора.

Пусть $$ d$$ – расстояние между обкладками, $$ S$$ – их площадь. Пусть $$ q$$ заряд правой обкладки. Тогда заряд левой будет $$ -q$$, т. к. заряд в значительных количествах не может накапливаться на соединительных проводах и в источнике. Направим ось $$ x$$ влево (рис. 10.3).

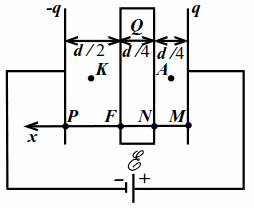Рис. 10.3

Заметим, что поле внутри пластины отсутствует и разность потенциалов $$ {varphi }_{N}-{varphi }_{F}$$ между точками $$ N$$ и $$ F$$ равна нулю. Кроме того, заряды на поверхностях пластины создают вне пластины такое же поле, как и заряд $$ Q$$, если бы его расположить на любой из двух поверхностей пластины. Это легко показать отдельно.

Разность потенциалов $$ {varphi }_{M}-{varphi }_{P}$$ между точками $$ M$$ и $$ P$$ равна $$ mathcal{E}$$. Поэтому

$$ ({varphi }_{M}-{varphi }_{N})+({varphi }_{N}-{varphi }_{F})+({varphi }_{F}-{varphi }_{P})=mathcal{E}$$.

У нас $$ {varphi }_{M}-{varphi }_{N}={E}_{A}{displaystyle frac{d}{4}}, {varphi }_{N}-{varphi }_{F}=0, {varphi }_{F}-{varphi }_{P}={E}_{K}{displaystyle frac{d}{2}}$$.

Здесь — $$ {E}_{A}$$ и $$ {E}_{K}$$ — проекции напряжённости результирующего поля на ось `x`. По принципу суперпозиции полей

$$ {E}_{A}={displaystyle frac{q}{2{varepsilon }_{0}S}}-{displaystyle frac{Q}{2{varepsilon }_{0}S}}-{displaystyle frac{-q}{2{varepsilon }_{0}S}}={displaystyle frac{1}{2{varepsilon }_{0}S}}left(2q-Qright)$$,

$$ {E}_{K}={displaystyle frac{q}{2{varepsilon }_{0}S}}+{displaystyle frac{Q}{2{varepsilon }_{0}S}}-{displaystyle frac{-q}{2{varepsilon }_{0}S}}={displaystyle frac{1}{2{varepsilon }_{0}S}}left(2q+Qright)$$.

Подставляя выражения для $$ {E}_{A}$$, $$ {E}_{K}$$ и разностей потенциалов в первое
уравнение, получим после упрощений $$ 6q+Q=8mathcal{E}{displaystyle frac{{varepsilon }_{0}S}{d}}$$.

Так как $$ {displaystyle frac{{varepsilon }_{0}S}{d}}=C$$, то $$ q=(8Cmathcal{E}-Q)/6$$.

Следует заметить, что знак найденного заряда правой обкладки зависит от соотношения заданных в условии задачи величин.

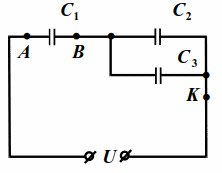Рис. 10.4

На схему (рис. 10.4) подано напряжение `U=24` В. Ёмкости конденсаторов `C_1=1` мкФ, $$ {C}_{2}=2$$ мкФ, $$ {C}_{3}=3$$ мкФ. Найти напряжения на конденсаторах.

В задачах, где есть схемы с конденсаторами, обычно предполагается, что схемы собраны из первоначально незаряженных конденсаторов.

Ёмкость между точками $$ B$$ и $$ K$$: 

$$ {C}_{BK}={C}_{2}+{C}_{3}=5$$ мкФ.

Общая емкость: $$ {C}_{AK}={displaystyle frac{{C}_{1}{C}_{BK}}{{C}_{1}+{C}_{BK}}}={displaystyle frac{5}{6}}$$ мкФ.

Общий заряд всей батареи конденсаторов $$ {q}_{AK}={C}_{AK}U=20·{10}^{-6 }mathrm{Кл}.$$

Так как заряд $$ {q}_{1}$$ конденсатора $$ {C}_{1}$$ равен заряду батареи, то напряжение на этом конденсаторе $$ {U}_{1}={q}_{1}/{C}_{1}={q}_{AK}/{C}_{1}=20$$ В. Напряжения на конденсаторах $$ {C}_{2}$$ и $$ {C}_{3}$$ равны напряжению между точками $$ B$$ и $$ K$$ и в сумме с $$ {U}_{1}$$ дают $$ U$$.
Поэтому $$ {U}_{2}={U}_{3}={U}_{BK}=U-{U}_{1}=4$$ В.

Приведённая в задаче схема негромоздкая, и ответ легко получить в общем виде:

$$ {U}_{1}={displaystyle frac{{C}_{2}+{C}_{3}}{{C}_{1}+{C}_{2}+{C}_{3}}}U=20$$ B,

$$ U2=U3={displaystyle frac{{C}_{1}}{{C}_{1}+{C}_{2}+{C}_{3}}}U=4$$ B.

Выполним расчёт электрического поля плоской пластины бесконечных размеров, которая заряжена с постоянной плотностью. В основу положим закон Кулона для взаимодействия 2-х точечных электрических зарядов в вакууме. Если в какой-то точке пространства находится заряд Q, а на удалении R от него расположен некий пробный заряд q, то на данный пробный заряд в соответствии с формулой действует сила F.

Где ε₀ – диэлектрическая проницаемость вакуума;
R – расстояние между двумя зарядами Q и q;
Q и q – величины электрических зарядов;
e_r – единичный вектор, направленный по линии зарядов.

Если два электрических заряда Q и q помещены не в вакуум, в пространство с веществом, то к формуле добавляется относительная диэлектрическая проницаемость ε, которая отличает проводящие свойства какого-либо вещества от вакуума. ε является безразмерной константой.

В данной формуле можно выделить часть, которая не зависит от пробного заряда q:

Обозначим её буквой E:

Она носит название «напряжённость электрического поля». Из определения следует, что напряжённость поля не зависит от величины пробного заряда q, помещённого в точку. Напряжённость электрического поля определяется однозначно исходным зарядом Q, а также расстоянием R до точки, то есть геометрией пространства.

В таком случае сила кулона F будет равна:

Эта формула применима для любого точечного заряда.

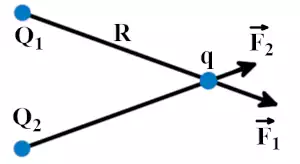
Электрическое поле обладает свойством суперпозиции. Если есть несколько электрических зарядов Q₁ и Q₂, то каждый заряд взаимодействует с точечными силами F₁ и F₂, и общая сила складывается по правилу сложения векторов.

В такой ситуации можно написать:

F₁₂ – суммарная сила.

Из формулы можно увидеть, что напряжённость электрического поля складывается. Этот факт называется принципом суперпозиции электрического поля, и он будет использован для расчёта сложной системы электрических зарядов, то есть зарядов, распределённых по плоскости.

Расчёт напряжённости электрического поля плоской пластины

Постановка задачи: имеется бесконечная плоская пластина с определённой плотностью заряда σ. Выделим на ней площадку dS. Заряд dQ площадки dS будет равен:

Будем считать, что плоская пластина равномерно заряжена и σ не зависит от координат.

Посчитаем напряжённость электрического поля всей плоской пластины в точке A, находящейся на удалении a от этой пластины: E(A)=?

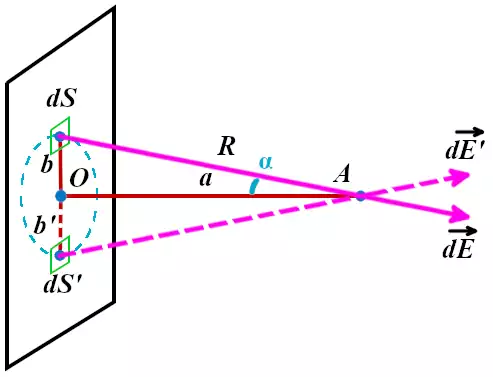
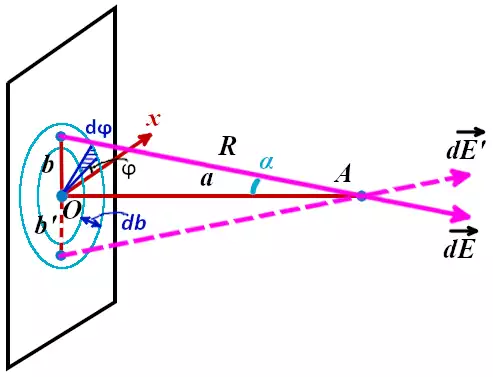
Для примера возьмём на плоской пластине небольшую площадку площадью dS на удалении b от центра. Обладая электрическим зарядом dQ, эта площадка создаёт электрическое поле с напряжённостью dE в точке A по закону Кулона.

На расстоянии b‘, равному расстоянию b, будет находится площадка dS‘, которая будет создавать электрическое поле с напряжённостью dE‘, равное по величине напряжённости поля dE, но направленное под другим углом. При сложении двух этих полей сумма расположенных параллельно пластине составляющих их векторов будет равны нулю. В связи с этим нам нужно учитывать только составляющую, расположенную перпендикулярно поверхности плоской пластины.

Обозначим угол между напряжённостью поля dE и перпендикуляром к пластине через α. Тогда интересующая нас составляющая dE_⊥ будет равна:

Точно такую же составляющую будут создавать все точки на плоской пластине, находящиеся на удалении b от точки O. Это связано с тем, что расстояния от них до точки A, а также углы между перпендикуляром и напряжённостями электрического поля будут такими же.

Выделим окружность радиусом b и толщиной db на плоской пластине. В полученном кольце рассмотрим элемент, расположенный под углом ϕ к оси x. Элемент вырезается из кольца в виде сегмента с размером dϕ. При малости dϕ и при малости db этот участок плоской пластины можно считать квадратом. В таком случае площадь dS будет равна:

Заряд dQ равен:

Полную напряжённость электрического поля кольца можно посчитать путём интегрирования по ϕ. А полное поле всей пластины можно посчитать путём интегрирования всех колец по b от 0 до ∞.

Для вычисления интеграла сделаем замену переменных и выразим всё через угол α. В этом случае получим:

В данной формуле сокращаем cos²α и a. Интеграл от 0 до ∞ выразится в интеграл от 0 до π/2.

Физический смысл этой формулы состоит в том, что напряжённость электрического поля около равномерно заряженной плоской пластины не зависит от расстояния до этой пластины.