Как найти заряд заземленного шара - Исправление недочетов и поиск решений вместе с Examum.ru

2019-11-22

Найдите, чему равен заряд заземленного металлического шара радиуса $r$, если на расстоянии $R$ от его центра находится точечный заряд $q$.

Решение:

Потенциал шара должен быть равен нулю. Потенциал поля в центре шара, равный, конечно, потенциалу шара, складывается из потенциала поля точечного заряда $q$ и поля, создаваемого зарядом $Q$ шара. Заряд $Q$ распределён по шару не равне лерно, но если шар разбить на маленькие участки с зарядами $Delta q$, то потенциал поля, создаваемого зарядом шара в центре, можно выразить как суммарный потенциал полей точечных зарядов $Delta q$. Таким образом, можно записать для центра, шара:

$Delta phi = sum frac{ Delta q}{r} = frac{1}{r} sum Delta q = frac{Q}{r}$, причем $frac{Q}{r} + frac{q}{R} = 0$.

Отсюда $Q = — frac{r}{R}q$.

Многие читатели использовали формулу для емкости конденсатора $C = frac{ Delta Q}{ Delta phi}$, полагая емкость шара равной $r$. Но это справедливо лишь для изолированного шара с равномерно распределенным зарядом.

Источник

Пусть имеется
заряд q₁,
расположенный на расстоянии x₁
от центра заземлённой проводящей сферы
радиуса a
(рис.8). Для того, чтобы найти поле,
созданное вокруг сферы зарядом q₁
и поверхностными зарядами, индуцированными
на сфере, применим метод электрических
изображений.

Введём в рассмотрение
заряд q₂,
расположенный на расстоянии x₂
от центра сферы. Оба заряда совместно
должны обеспечить нулевое значение
потенциала на поверхности сферы.
Определим величину и положение заряда
q₂.

Рис.8. Изображение
заряда относительно сферы

Потенциал,
создаваемый в произвольной точке С на
сфере зарядами q₁
и q₂
равен

,
(25)

где

,

.

Для выполнения
условия

необходимо,
чтобы

(26)

или

.
(27)

С учётом

выражение (27) примет вид:

(28)

При перемещении
точки С по сфере отношение (28) должно
быть величиной постоянной, значит

(29)

Дифференцируя
(28) по x_c,
находим

(30)

Из (30) получаем

,
(31)

а после подстановки
(31) в (28)

имеем

.
(32)

При этих положении
и величине заряда q₂
система двух зарядов в свободном
пространстве вне сферы и поле заряда у
металлической сферы совпадают.

При расположении
у металлической заземлённой сферы
нескольких зарядов используется принцип
суперпозиции. Необходимо лишь для
каждого из заданных зарядов найти
положение и величину его электрического
изображения.

Программа POLE32
и работа с ней

Для
расчётов полей скалярного электрического
потенциала в рассмотренных выше задачах
предназначена программа POLE32.EXE.
Программа работает в среде Windows.
Для установки в системах Windows
ME, 2000, XP
просто скопируйте указанный файл в
рабочую папку. В системе Windows
9x может
потребоваться дополнительный файл
MSVBVM32.DLL.
Предполагается,
что поля рассчитываются в вакууме.

На
экране монитора появляется меню выбора
варианта задачи:

1
— Отдельные заряды; 2 — Заряды над
плоскостью;

3
— Заряды и сфера; 4 — Заряды в угле.

Введите
номер варианта:

Затем
последовательно запрашиваются и вводятся
параметры конкретной задачи: число
зарядов, их величины и координаты,
положение центра и радиус сферы или
угол между плоскостями (45, 60, 90 градусов).
Также задаются координаты левого нижнего
угла экрана монитора и его длина по
горизонтальной оси х. При вводе последних
надо следить, чтобы на экране отображалась
интересующая вас область поля.

По
завершении ввода на тёмном экране
отобразиться геометрия задачи. В верхней
строке экрана отображаются координаты
текущего положения курсора мыши и
значение потенциала в этой точке.

При
щелчке левой кнопкой мыши в любой точке
экрана программа вычерчивает линию
постоянного потенциала, проходящую
через эту точку. По завершении построения
линии на экране отображается эта линия,
значение её потенциала и снова появляется
курсор мыши. Число и местоположение
линий постоянного потенциала не
ограничено и определяется пользователем.

Программа
позволяет корректировать картину поля
на экране. Работа производится с каждой
линией отдельно. Для этого необходимо
выделить нужную линию: подводим к ней
курсор (при этом курсор меняет вид с
крестового на стрелку), фиксируем свой
выбор нажатием левой кнопки мыши и
клавишами работаем с изображением:

A
(или левая кнопка мыши) — вставить/удалить
линию;

S
(или средняя кнопка мыши, колесо) —
увеличить толщину линии;

D
(или правая кнопка мыши) — уменьшить
толщину линии;

1…6
— изменение толщины линии (1 — малое, 6 —
большое);

F1
— справка;

Пробел
— фильтрация изображения;

Esc
— выход из программы.

Кроме
того, в обновленную версию были добавлены
следующие функции:

*
возможность отключения звука (так как
звук более не нужен для работы);

*
подсказки;

*
сохранение данных в файл и дальнейшая
загрузка для повторной работы с ними;

*
сохранение изображения в графический
файл (меню «Экспорт»), а также возможность
сохранения инвертированного (негативного)
изображения (сделано для удобства
просмотра, поставить флажок «Инвертировать
изображение при экспорте»);

*
кнопочное меню.

Для
построения эквипотенциальных линий
необходимо выполнить следующие действия:

1)
Вставить нужные линии;

2)
Отрегулировать их толщину так, чтобы
они были непрерывными (меню «Толщина»
для задания степени изменения толщины,
средняя и правая кнопки мыши для
увеличения/уменьшения толщины
соответственно);

3)
Запустить алгоритм фильтрации (кнопка
«Начать фильтрацию»), который уберет
излишнюю толщину линий;

4)
Сохранить изображение (кнопка «Экспорт»).

Рассмотрим
примеры работы с программой.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Спрятать решение

Решение.

Поскольку шар заземлён, потенциал любой его точки равен нулю. В том числе, и потенциал в центре шара

Здесь используется формула для потенциала точечного заряда. В проводниках заряд может находиться только на их поверхности, а расстояние от любой точки поверхности шара до его центра одинаково. Окончательно

Спрятать критерии

Критерии проверки:

Правильное решение оценивается в 5 баллов независимо от выбранного участником метода.

Критерий	Баллы
Указано, что потенциал шара равен нулю	1
Указано, что в шаре заряд находится только на поверхности	1
Записано выражение для потенциала в центре шара, создаваемого зарядом q	1
Записано выражение для потенциала в центре шара, создаваемого зарядами шара	1
Получен ответ	1

Классификатор: Электродинамика. Потенциал электрического поля

Источник

Сообщить заряд телу можно, либо трением о другое тело, либо, прикоснувшись этим телом к заряженному телу. То есть, электризация происходит либо при трении тел, либо, когда незаряженное тело прикасается к заряженному.

Сравним электризацию при трении и соприкосновении

Потрем кусочек эбонита о шерсть. Во время трения эбонит получает электроны, поэтому, заряжается отрицательно.

А шерсть электроны отдает, поэтому, заряжается положительно. Сколько электронов отдала шерсть, столько же получил эбонит.

Поэтому, заряды эбонита и шерсти равны по модулю, но имеют противоположные знаки.

После электризации трением одно тело содержит положительный заряд, другое – отрицательный. Заряды всегда численно равны.

После электризации соприкосновением заряды тел равны не всегда. Чем больше размеры тела, тем большую часть заряда оно получит.

Как распределяются заряды при соприкосновении

Возьмем два шара, имеющие одинаковые размеры. Один из шаров наэлектризуем, а второй оставим незаряженным. Если шары соприкоснутся, то заряд распределится поровну между двумя шарами (рис. 1).

Рис. 1. Если размеры совпадают, то при контакте тел между телами заряд распределяется на две равные части

Заменим теперь шар незаряженный шаром, имеющим большие размеры. При соприкосновении на большой шар перейдет большая часть заряда (рис. 2). То есть, заряд теперь распределяется не поровну.

Рис. 2. Когда размеры различаются, при контакте тел заряд между телами распределяется на неравные части

Заряд, полученный телом при соприкосновении, зависит от размеров тела. Чем больше размеры тела, тем большая часть заряда перейдет на него при соприкосновении.

Это свойство используется при заземлении. Земной шар имеет значительно большие размеры, по сравнению с телами, которые на нем находятся.

Передавая заряд земле, тело становится электрически нейтральным, потому, что на землю стекает почти весь заряд тела (рис. 3).

Рис. 3. Заземляя тело, мы передаем весь его заряд на земной шар

В левой части рисунка 3 изображено тело до заземления. Оно имеет заряд «+q». А в правой — после заземления, тело заряда не имеет.

Примечание: Заземление – это передача избыточного заряда от тела к земле. Тела заземляют, соединяя с землей отрезком толстой проволоки, или кабеля. Заземление металлических корпусов электроприборов применяют для защиты людей от удара электрическим током.

Несколько случаев для контакта двух одинаковых тел удобно объяснить на примере решения задач.

Три задачи о распределении заряда между двумя одинаковыми шарами

Распределение зарядов между двумя телами, имеющими одинаковые размеры, но различные заряды, просто показать на примерах решения задач.

Задача 1

Даны два одинаковых шара. Один шар имеет положительный заряд величиной 0,8 Кулона, а второй – отрицательный заряд 0,2 Кулона. Каким окажется заряд каждого шара после их соприкосновения?

Решение:

Шар, имеющий положительный заряд, обладает недостатком электронов.

При соприкосновении с ним отрицательно заряженного шара, избыток электронов с него полностью переходит на положительный шар, так, что компенсирует часть положительного заряда.

Общий заряд шаров имеет положительный знак и равен ( 0,8 Кл — 0,2 Кл ) = 0,6 Кл. Этот заряд перераспределится между шарами поровну, потому, что в условии сказано, что шары имеют одинаковые размеры.

Ответ:

После соприкосновения заряд каждого шара положительный и равен 0,3 Кл.

Задача 2

Даны два одинаковых шара. Один шар имеет положительный заряд величиной 0,3 Кулона, а второй – отрицательный заряд 0,7 Кулона. Каким окажется заряд каждого шара после их соприкосновения?

Решение:

Шар, имеющий положительный заряд, имеет недостаток электронов.

Часть электронов при соприкосновении переходит с отрицательного на положительный шар и компенсирует положительный заряд.

Общий заряд шаров имеет отрицательный знак и равен ( 0,7 Кл — 0,3 Кл ) = 0,4 Кл. Этот заряд перераспределится между шарами поровну, так как в условии сказано, что шары имеют одинаковые размеры.

Ответ:

После соприкосновения заряд каждого шара отрицательный и равен 0,2 Кл.

Задача 3

Даны два одинаковых шара. Один шар имеет положительный заряд величиной 0,3 Кулона, а второй – положительный заряд 0,7 Кулона. Каким окажется заряд каждого шара после их соприкосновения?

Решение:

Недостаток электронов больше у шара, имеющего больший положительный заряд. Поэтому при соприкосновении часть электронов с шара, имеющего меньший положительный заряд, перейдет на шар с большим положительным зарядом.

Общий заряд шаров имеет положительный знак и равен ( 0,7 Кл + 0,3 Кл ) = 1,0 Кл. Этот заряд перераспределится между шарами поровну, так как в условии сказано, что шары имеют одинаковые размеры.

Ответ:

После соприкосновения заряд каждого шара положительный и равен 0,5 Кл.

При контактировании тел выполняется закон сохранения заряда. Несколько случаев для двух тел одинаковых размеров записаны в виде таблицы 1.

Таблица 1. Распределение заряда при контакте двух тел, имеющих одинаковые размеры

Выводы

Возьмем два одинаковых тела. Каждое тело имеет свой заряд. Будем прикасаться одним телом к другому.

Если заряды тел численно не равны и имеют различные знаки, то часть заряда компенсируется, а оставшаяся часть распределится между телами поровну. Когда же заряды имеют одинаковые знаки, то сумма зарядов распределятся поровну между телами.
В случае, если заряды тел численно равны и имеют различные знаки, то заряд компенсируется, после соприкосновения тела не будут иметь зарядов. А когда заряды имеют одинаковые знаки, то после контакта заряд каждого тела не изменится.

Источник

Примеры решения задач по физике — концентрические проводящие сферы

Суббота, 25 февраля, 2012

Среди школьных задач по физике особняком стоят те, которые связаны с концентрическими проводящими сферами. Эти сферы могут быть заряжены, заземлены, могут находиться в поле внешних зарядов и т. д., вариаций много. В школьном курсе физики эти задачи являются одними из самых сложных. Не в последнюю очередь, конечно, непонимание данного материала связано с неспособностью учителей объяснить его грамотно и доступно. Итак, попробуем разобраться, что это за проводящие сферы и с чем их едят.

Тексты заданий я взял из сборника задач по физике для подготовительных отделений вузов.

Задача 1. Сфера радиуса r, которой сообщен заряд q, окружена концентрической тонкостенной проводящей сферической оболочкой радиуса R, заряд которой равен Q. Определите потенциалы сфер φ_in (внутренней) и φ_ex (внешней).

Решение. Потенциал на поверхности внутренней сферы φ_exскладывается из двух потенциалов: внешней сферы φ₁ и собственно внутренней сферы φ₂.

Потенциал внешней сферы φ₁ в каждой точке ее внутреннего объема одинаков и равен потенциалу на ее поверхности (подробнее о решении задач на тему «Потенциал» читайте в этой статье):

$[ varphi_1 = frac{Q}{4pivarepsilon_0 R}. ]$

Потенциал внутренней сферы φ₂ определяется известным соотношением:

$[ varphi_2 = frac{q}{4pivarepsilon_0 r}. ]$

Тогда общий потенциал φ_inна поверхности внутренней сферы равен:

$[ varphi_{in} = varphi_1 + varphi_2 = frac{1}{4pivarepsilon_0}left(frac{Q}{R}+frac{q}{r}right). ]$

Потенциал на поверхности внешней сферы также складывается из двух потенциалов: внутренней сферы φ’₁ и собственно внешней сферы φ’₂.

Потенциал внутренней сферы φ’₁ на расстоянии R от ее центра определяется известным соотношением:

$[ varphi'_1 = frac{q}{4pivarepsilon_0 R}. ]$

Формула, определяющая потенциал внешней сферы φ’₂ на ее поверхности, также хорошо известна:

$[ varphi'_2 = frac{Q}{4pivarepsilon_0 R}. ]$

Тогда общий потенциал на поверхности внешней сферы равен:

$[ varphi_{ex} = varphi'_1 + varphi'_2 = frac{q+Q}{4piepsilon_0 R}. ]$

Задача 2. Металлический шар радиуса R₁, заряженный до потенциала φ, окружают тонкой сферической проводящей оболочкой радиуса R₂. Определите потенциал шара φ₁ после того, как он будет соединен проводником с оболочкой. Первоначальный заряд оболочки равен нулю, центры оболочки и шара совпадают.

Решение. До соединения сфер проводником заряд первой был равен:

$[ q=frac{varphi R_1}{k}. ]$

После соединения часть заряда с внутренней сферы перетекло на внешнюю. Ток прекратился в тот момент, когда потенциал шара стал равен потенциалу внешней оболочки. Удобнее поэтому искать не потенциал шара, а равный ему потенциал внешней оболочки. В соответствии с результатами, полученными в предыдущей задаче, этот потенциал определяется выражением:

$[ varphi_1 = kfrac{q_1+q_2}{R_2}, ]$

где q₁ и q₂ — заряды шара и внешней оболочки после соединения их проводником соответственно. По закону сохранения заряда q = q₁ + q₂. После несложных преобразований получаем:

$[ varphi_1 = kfrac{q}{R_2} = varphifrac{R_1}{R_2}. ]$

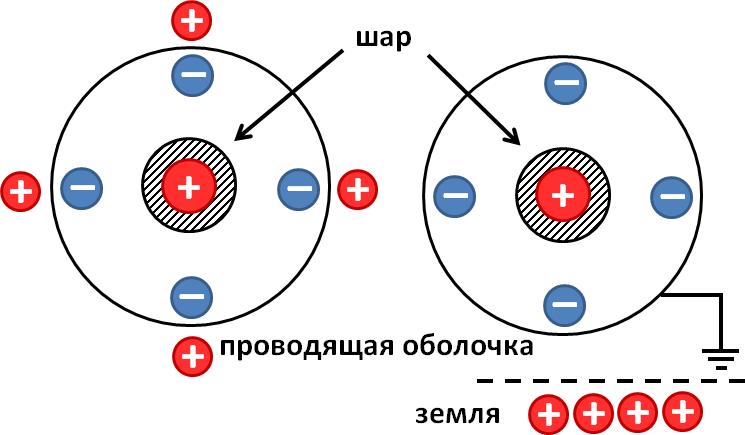
Задача 3. Металлический шар радиуса R₁, заряженный до потенциала φ, окружают концентрической сферической проводящей оболочкой радиуса R₂. Чему станет равен потенциал шара φ‘, если заземлить оболочку?

Начнем с рисунка к решению задачи:

После заземления проводящей оболочки весь положительный заряд, образовавшийся на ней вследствие явления электростатической индукции, стекает на землю. На ней остается только отрицательный заряд, поскольку он притягивается к положительному заряду внутренней сферы

Решение. Зная потенциал шара в начальный момент времени и его радиус, можно найти заряд на нем:

$[ q = frac{varphi R_1}{k}. ]$

Вследствие явления электростатической индукции на внешней оболочке должно произойти разделение заряда. Отрицательный заряд перетечет на внутреннюю поверхность оболочки, положительный — на внешнюю (см. рисунок). Это же явление возникало и в предыдущих задачах, но мы не принимали его во внимание. Почему? В условии задач было указано, что оболочка тонкая, и такое «разбегание» зарядов не приводило к сколько-нибудь существенному изменению конфигурации электростатического поля.

В этой задаче учет данного явления важен, поскольку оболочку заземляют. После заземления положительный заряд с оболочки стечет на землю, останется лишь отрицательный q₂, поскольку он притягивается к положительному заряду q₁ внутренней сферы. Потенциал заземленной оболочки станет равен потенциалу земли, то есть нулю. В этой связи и в соответствии с результатом, полученным при решении первой задачи, получаем равенство:

$[ kfrac{q_1+q_2}{R_2} = 0Leftrightarrow q_1 = q = - q_2. ]$

Используя выражение для расчета потенциала внутренней сферы подобной системы, полученное в первой задаче, находим окончательно требуемый потенциал шара:

$[ varphi' = kleft(frac{q_1}{R_1}+frac{q_2}{R_2}right) = ]$

$[ = kleft(frac{q}{R_1}-frac{q}{R_2}right) =varphileft(1-frac{R_1}{R_2}right). ]$

Опыт показывает, что редко кто понимает решение этих задач во всех деталях с первого раза. Обычно приходится долго и настойчиво разъяснять ученикам все те мелочи, без осознания которых решение сводится к пустым преобразованиям буквенных выражений с целью получения приведенного в конце учебника ответа. Понять физическую сущность этих задач и научиться применять полученные знания в будущем не просто. Однако в этом и состоит основная методическая ценность данной темы в школьном курсе физики. Лучшим помощником в ее изучении непременно станет профессиональный репетитор, грамотный наставник, который сможет придумать понятное именно вам объяснение и ответит на все возникшие вопросы. Кстати, если таковые имеются, вы можете задать их ниже в комментариях.

Репетитор по физике и математике
Сергей Валерьевич

Источник