Как найти зависимость одной функции от другой

Рассмотрим:

(7)

Пусть функции (7) определены и дифференцируемы в некоторой области .

Опр.: Некоторая функция называется зависимой в области От остальных функций из совокупности (7), если ее можно представить в виде

, (8)

Где дифференцируемая функция своих аргументов.

Если никакая из функций системы (7) не может быть выражена через остальные функции, то функции данной системы, выраженные формулой (8), по функции (7) называются независимой.

Примеры:

1)

открытый круг радиуса .

— зависима

2)

Докажем, что — независимы от противного.

Предположим

то

Рассмотрим изменение переменных по оси , т. е. .

(противоречие)

(по прямым)

— независимые, что и требовалось доказать.

, (1)

Где Определены и дифференцируемы в некоторой области .

Теорема 1

Пусть функции (1) дифференцируемы в некоторой окрестности точки (n<m). Пусть якобиан указанных функций по какой либо выборке переменных не равен 0.

Тогда функции (1) являются независимыми в окрестности .

Из m имеющихся переменных для участия в вычисления якобиана выбираются n. Если хотя бы один из указанных якобианов не равен 0, то функции независимы.

Следствие

Если функции (1) являются зависимыми, то все якобианы вида: равны нулю. В знаменателе якобиана рассматриваются всевозможные выборки переменных.

Док-во теоремы 1:

Допустим, что .

Проведем доказательство методом от противного, т. е. допустим, что одна из функций системы (1) является зависимой от остальных функций:

Где функция F дифференцируема в окрестности .

Вычислим частичную производную , по некоторой переменной .

,

где .

Подчеркнуты представители якобиана.

В идеале надо расписать по всем индексам.

Рассмотрим последнее равенство в точке . При этом множители при подчеркнутых слагаемых превращаются в коэффициенты. Поэтому получаем, что k-я строка якобиана является зависимой от остальных строк. Следовательно, якобиан равен 0, что противоречит начальному предположению.

ч. т. д.

< Предыдущая		Следующая >

Что такое функция

Понятие функции – одно из основных в математике.

На уроках математики вы часто слышите это слово. Вы строите графики функций, занимаетесь исследованием функции, находите наибольшее или наименьшее значение функции. Но для понимания всех этих действий давайте определим, что такое функция.

Определение функции можно дать несколькими способами. Все они будут дополнять друг друга.

1. Функция – это зависимость одной переменной величины от другой. Другими словами, взаимосвязь между величинами.

Любой физический закон, любая формула отражает такую взаимосвязь величин. Например, формула – это зависимость давления жидкости от глубины .

Чем больше глубина, тем больше давление жидкости. Можно сказать, что давление жидкости является функцией от глубины, на которой его измеряют.

Знакомое вам обозначение как раз и выражает идею такой зависимости одной величины от другой. Величина зависит от величины по определенному закону, или правилу, обозначаемому .

Другими словами: меняем (независимую переменную, или аргумент) – и по определенному правилу меняется .

Совсем необязательно обозначать переменные и . Например, – зависимость длины от температуры , то есть закон теплового расширения. Сама запись означает, что величина зависит от .

2. Можно дать и другое определение.

Функция – это определенное действие над переменной.

Это означает, что мы берем величину , делаем с ней определенное действие (например, возводим в квадрат или вычисляем ее логарифм) – и получаем величину .

В технической литературе встречается определение функции как устройства, на вход которого подается , а на выходе получается .

Итак, функция – это действие над переменной. В этом значении слово «функция» применяется и в областях, далеких от математики. Например, можно говорить о функциях мобильного телефона, о функциях головного мозга или функциях депутата. Во всех этих случаях речь идет именно о совершаемых действиях.

3. Дадим еще одно определение функции – то, что чаще всего встречается в учебниках.

Функция – это соответствие между двумя множествами, причем каждому элементу первого множества соответствует один и только один элемент второго множества.

Например, функция каждому действительному числу ставит в соответствие число в два раза большее, чем .

Повторим еще раз: каждому элементу множества по определенному правилу мы ставим в соответствие элемент множества . Множество называется областью определения функции. Множество – областью значений.

Но зачем здесь такое длинное уточнение: «каждому элементу первого множества соответствует один и только один элемент второго»? Оказывается, что соответствия между множествами тоже бывают разные.

Рассмотрим в качестве примера соответствие между двумя множествами – гражданами России, у которых есть паспорта, и номерами их паспортов. Ясно, что это соответствие взаимно-однозначное – у каждого гражданина только один российский паспорт. И наоборот – по номеру паспорта можно найти человека.

В математике тоже есть такие взаимно-однозначные функции. Например, линейная функция . Каждому значению соответствует одно и только одно значение . И наоборот – зная , можно однозначно найти .

Могут быть и другие типы соответствий между множествами. Возьмем для примера компанию друзей и месяцы, в которые они родились:

Каждый человек родился в какой-то определенный месяц. Но данное соответствие не является взаимно-однозначным. Например, в июне родились Сергей и Олег.

Пример такого соответствия в математике – функция . Один и тот же элемент второго множества соответствует двум разным элементам первого множества: и .

А каким должно быть соответствие между двумя множествами, чтобы оно не являлось функцией? Очень просто! Возьмем ту же компанию друзей и их хобби:

Мы видим, что в первом множестве есть элементы, которым соответствует два или три элемента из второго множества.

Очень сложно было бы описать такое соответствие математически, не правда ли?

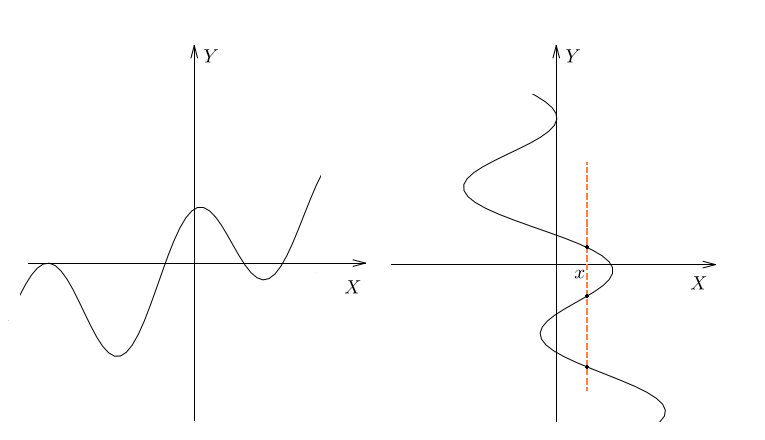
Вот другой пример. На рисунках изображены кривые. Как вы думаете, какая из них является графиком функции, а какая – нет?

Ответ очевиден. Первая кривая – это график некоторой функции, а вторая – нет. Ведь на ней есть точки, где каждому значению соответствует не одно, а целых три значения .

Перечислим способы задания функции.

1. С помощью формулы. Это удобный и привычный для нас способ. Например:

Это примеры функций, заданных формулами.

2. Графический способ. Он является самым наглядным. На графике сразу видно все – возрастание и убывание функции, наибольшие и наименьшие значения, точки максимума и минимума. В следующей статье будет рассказано об исследовании функции с помощью графика.

К тому же не всегда легко вывести точную формулу функции. Например, курс доллара (то есть зависимость стоимости доллара от времени) можно показать только на графике.

3. С помощью таблицы. С этого способа вы когда-то начинали изучение темы «Функция» — строили таблицу и только после этого – график. А при экспериментальном исследовании какой-либо новой закономерности, когда еще неизвестны ни формула, ни график, этот способ будет единственно возможным.

4. С помощью описания. Бывает, что на разных участках функция задается разными формулами. Известная вам функция задается описанием:

Даже в первой части ЕГЭ по математике есть задачи на понимание определения функции.

Задание 1. Найдите если при

Что такое ? Это функция, каждому числу x ставящая в соответствие число Например,

Тогда

Заметим, что

Значит, при

Задание 2. Найдите если при

функция, каждому числу b ставящая в соответствии число

Тогда и значение

Задание 3, подготовительная задача. Найдите область определения функции

Очевидно, что оба подкоренных выражения должны быть неотрицательны. Получим систему:

Решая ее, найдем область определения функции:

Понятие функции – одно из основных в программе математики 10-11 класса. Более того – именно с функций и графиков начинается настоящая, «взрослая» математика. Ведь сложение и вычитание, умножение и деление, дроби и пропорции – это все-таки арифметика. Математика – наука не только о числах, но и о взаимосвязях величин. Функции и графики – универсальный язык, понятный физику и биохимику, астроному, инженеру и экономисту.
В настоящее время в вариантах ЕГЭ появилась задача по теме: Функции и графики. Есть также задачи на темы: точки максимума и минимума, поведение функции.

Тема Функции и графики есть также в вариантах ОГЭ по математике. Разберем реальные задачи ОГЭ и ЕГЭ по этим темам.

Необходимая теория в этом статье, а на других страницах нашего сайта:

Чтение графика функции

Элементарные функции и их графики

Четные и нечетные функции

Периодические функции

Обратная функция

Преобразование графиков функций

Построение графиков функций

Задачи ЕГЭ по теме: Функции и графики

Задача 1. На рисунке изображены графики двух линейных функций. Найдите абсциссу точки пересечения графиков.

Решение:

Линейная функция задается формулой

Найдем формулу первой функции, возрастающей. На ее графике выделены точки и
Угол наклона этой прямой к ось абсцисс острый, значит

Формула функции: Найдем и для этого подставим координаты любой из выделенных точек, например, точки с координатами

это формула возрастающей функции.

2. Найдем уравнение второй линейной функции, убывающей. На ее графике выделены точки и

Угол наклона этой прямой к ось абсцисс тупой, значит, для нее

Уравнение этой прямой имеет вид: Найдем и для этого подставим координаты любой из выделенных точек, например, точки с координатами

это формула второй функции, убывающей.

3) Найдем абсциссу точки пересечения графиков функций. Для этого решим уравнение:

Ответ: -1,3

Задача 2. На рисунке изображен график функции , определенной на отрезке Найдите количество точек максимума функции на данном отрезке.

Решение:

Точка максимума – такая внутренняя точка области определения функции, значение функции в которой больше, чем во всех достаточно близких к ней точках (локальная «горка» на графике). Таких точек мы видим три.

Ответ: 3

Задача 3. Графики функций и пересекаются в точках С и Е, причем абсцисса точки С положительна. Найдите абсциссу точки Е.

Решение:

Найдем сначала значения параметров а и b.

График функции проходит через точку с координатами Подставим и в формулу функции Получим:

Значит, эта функция задается уравнением

График функции проходит через точку значит, линейная функция задается уравнением

Для точек пересечения графиков этих функций выполняется равенство:

Отсюда Решим это квадратное уравнение.

Так как абсцисса точки С положительна, она равна 0,5. Эта точка пересечения графиков показана на рисунке.
Абсцисса точки E (находится за пределами рисунка) равна -3.

Ответ: -3

Задача 4. Графики функций и пересекаются в точках А и В. По данным рисунка найдите абсциссу точки В.

Решение:
Запишем формулу функции

Ее график – квадратичная парабола

то есть

Вычитаем из первого уравнения второе:
то есть

Так как абсцисса вершины параболы,

Получим:

Подставив в уравнение получаем:


Значит,

Найдем точки пересечения графиков и
Для этих точек:

или
Абсцисса точки A равна -2 (как и показано на рисунке). Тогда абсцисса точки B равно 12.

Ответ: 12.

Задача 5. На рисунке изображён график функции Найдите k.

Решение:

На рисунке изображена гипербола. Ее график получен из графика функции смещением на 2 единицы влево и на одну единицу вниз

Подробно об этом в теме: Преобразования графиков функций

Чтобы найти , подставим координаты точки в формулу функции. На графике эта точка выделена жирным.

Формула функции:

Чтобы проверить правильность решения, можно подставить в формулу функции координаты второй точки, которая выделена на графике,

получили верное равенство.

Ответ:

Задача 6. На рисунке изображены графики функций и которые пересекаются в точках A и B. Найдите ординату точки B.

Решение:

На рисунке изображены прямая и парабола.

Найдем уравнение параболы. Обратим внимание на выделенные точки на графике.
и Также парабола пересекает ось ординат в точке значит,
Подставим значение с и координаты точек в формулу квадратичной функции и получим систему двух уравнений с двумя переменными:

;
.

Формула квадратичной функции:

Найдем точки пересечения параболы и прямой. Для этого решим уравнение:
корни этого уравнения:

Абсцисса точки В равна -8. Найдем ее ординату:

Ответ: 41.

Задача 7. На рисунке изображены графики функции и которые пересекаются в точках А и B. Найдите абсциссу точки B.

Решение:

На рисунке изображены гипербола и прямая.

Найдем уравнение прямой:

Формула прямой:
На прямой выделены две точки: и Подставим по очереди их координаты в уравнение прямой и получим систему двух уравнений с двумя переменными:

; вычтем из первого уравнения второе и получим

– уравнение прямой.

Найдем уравнение гиперболы. Ее график симметричен относительно начала координат, значит, ее формула .

Если то Тогда уравнение гиперболы:

Найдем точки пересечения графиков функций. Для этого решим уравнение:
Это дробно-рациональное уравнение.

Перенесем все в левую часть и приведем к общему знаменателю:

Решим увадратное уравнение:

его корни и

— абсцисса точки А, она показана на графике.
— абсцисса точки В, которую нужно было найти.

Ответ: -0,25

Задача 8. На рисунке изображены графики функции и которые пересекаются в точке А. Найдите ординату точки А.

Решение:

1) Найдем уравнение линейной функции. На ее графике выделены точки и

Линейная функция на рисунке — убывающая, значит,

Формула линейной функции: Чтобы найти b, подставим координаты любой из выделенных точек. Возьмем, например, точку

— формула линейной функции.

2) Найдем коэффициент а в формуле второй функции . На ее графике выделена точка

Подставим координаты этой точки в уравнение:

3) Найдем точки пересечения графиков функций. Для этого решим систему уравнений:

Решив это уравнение, найдем, что

Это абсцисса точки пересечения графиков. Найдем ординату этой точки.

Ответ: — 9

Задача 9. На рисунке изображён график функции вида где числа a, b, c и d — целые. Найдите d при условии, что

Решение:

Расшифруем график.

Мы складываем график линейной функции и график модуля который сдвинут вправо (так как ) и сжат или растянут. Мы складываем линейную и кусочно-линейную функции. При сложении графиков линейных функций угловой коэффициент суммы равен сумме угловых коэффициентов слагаемых.

– точка излома графика

До точки угловой коэффициент по модулю меньше, чем после точки
Значит, левее точки коэффициент равен а правее точки равен и

Находим по графику, что Получим систему

Сложив уравнения системы, получим

Подставим во второе уравнение системы, получим откуда

В точке излома графика выполняется условие тогда а так как то

Если , то . По графику

Получим уравнение откуда

Мы получили: значит, график на рисунке – это

Ответ: 4

Задачи ОГЭ по теме: Функции и графики.

Задача 10. На рисунке изображен график квадратичной функции
Какие из следующих утверждений о данной функции являются верными? Запишите их номера.

1) при
2) Функция убывает на промежутке
3)

Решение:
Неверно, при
Верно, так как – вершина параболы.
Неверно,

Ответ: 2

Задача 11. Найдите значение k по графику функции изображенному на рисунке.

Решение:

На рисунке изображена гипербола. Так как , то

Возьмем точку на графике с целыми координатами Подставим ее абсциссу и ординату в уравнение:

Ответ: 3

Задание 12. Найдите значение b по графику функции изображенному на рисунке.

Решение:

На рисунке изображен график квадратичной функции, то есть парабола.
Абсцисса вершины параболы равна значит,

Возьмем точки графика и

Подставим их координаты в уравнение функции.

.

Также подставим

.

Вычтем из первого уравнения второе и получим:

Ответ: 17,5

Определение и применение функции

Математика создает инструменты, которые используются в различных сферах жизни. Одним из таких инструментов является функция. Вспомним, что функцией называется соответствие между двумя множествами, при котором каждому элементу одного множества ставится в соответствие единственный элемент другого множества (). Так, каждому человеку можно поставить в соответствие размер обуви, каждому дню в данной местности – среднесуточную температуру, стороне квадрата – его площадь и т. д. (см. рис. 1). Все это примеры функций.

Рис. 1. Пример функции

В курсе математики мы в основном будем говорить о числовых функциях – функциях, в которых одному числу мы ставим в соответствие другое:

где ,  – числовые множества

Первое из них называют аргументом функции, а число, которое ставится ему в соответствие, – значением функции:

где  – аргумент,  – значение функции.

Другое название функции – функциональная зависимость (мы находим зависимость одной величины от другой: значения функции от ее аргумента).

С помощью числовых функций можно построить модели множества физических процессов, например:

1. Для равномерного движения можно записать зависимость пути от времени движения:

2. Для тока, протекающего на участке цепи, можно записать зависимость силы тока от напряжения:

3. Для количества теплоты, которое требуется для нагревания, можно записать зависимость от разности температур:

В экономике, биологии, логистике – везде найдется применение функциям: ими можно описать и зависимость прибыли компании от цены на товар, и рост популяции организмов с течением времени, и распределение транспортных потоков в зависимости от спроса на товар, и т. д. (см. рис. 2).

Рис. 2. Зависимость прибыли компании от цены на товар

Стоит отметить, что в определении функции мы указали, что одному аргументу ставится в соответствие некоторое значение (см. рис. 3).

Рис. 3. Одному аргументу ставится в соответствие некоторое значение

В реальных же ситуациях чаще всего целому набору переменных ставится в соответствие значение функции (см. рис. 4). Такие функции называют функциями нескольких переменных.

Рис. 4. Целому набору переменных ставится в соответствие значение функции

Но каждую функцию с несколькими переменными можно рассматривать как набор функций с одной переменной (фиксируя поочередно все остальные). Поэтому мы потренируемся работать именно с функциями одной переменной. С краткой информацией о функциях нескольких переменных вы можете ознакомиться ниже.

---

Функции нескольких переменных

Ситуации, когда мы можем сделать такое приближение и выбрать модель так, чтобы величина зависела только от одного параметра, встречаются крайне редко.

В идеальных математических объектах такое возможно, например: площадь квадрата  зависит только от стороны квадрата . Но уже площадь прямоугольника  зависит от двух переменных – двух сторон, площадь параллелограмма  – от трех (двух сторон и угла между ними).

В описании реальных процессах функцию одной переменной найти еще сложнее. Посмотрите на следующие формулы:

Везде мы видим зависимость от двух и более величин. Пройденный путь зависит не только от времени, но и от скорости движения. Сила тока определяется не только приложенным напряжением, но и сопротивлением участка цепи.

В экономике налог тоже, по сути, функция многих переменных. Например, НДС (налог на добавленную стоимость) составляет обычно  от цены, но для некоторых групп товаров он может быть  и даже . Т. е. для расчета НДС нужно знать два аргумента: цену товара и тип товара. Другие налоги учитывают еще большее количество факторов и могут являться функциями  и даже более переменных.

Так зачем же мы изучаем функцию одной переменной, если в реальных задачах она практически не встречается? Во-первых, это удобный объект для тренировки и отработки навыков работы с функциями вообще. Во-вторых, изучение функции нескольких переменных можно свести к анализу набора функций одной переменной (фиксируя по очереди значения всех переменных, кроме одной). Соответственно, изучив поведение каждой такой «проекции» функции, можно получить данные о поведении функции нескольких переменных в целом.

Рассмотрим закон Ома для участка цепи:

Берем участок цепи с определенным значением сопротивления – фиксируем . Получаем зависимость силы тока от напряжения. Сила тока будет прямо пропорциональна приложенному напряжению (см. рис. 5). Если вы забыли, что такое прямая пропорциональность, посмотрите следующий урок: Что такое функция?.

Рис. 5. Сила тока прямо пропорциональна приложенному напряжению

Можно сделать и по-другому: зафиксировать значение  (подключаем к источнику постоянного напряжения) и меняем  (например, при помощи реостата). Получим зависимость силы тока от сопротивления (см. рис. 6.) Снова функция одной переменной.

Рис. 6. Зависимость силы тока от сопротивления

Переходя от функции нескольких переменных к функции одной переменной, нужно не упустить следующий важный момент: остальные переменные должны быть неизменными. Например, доход от товара – это функция двух переменных: цены товара и количества проданного товара (см. рис. 7):

Рис. 7. Функция двух переменных

Но нельзя сделать из этого вывод, что доход прямо пропорционален цене. Ведь мы не можем зафиксировать количество проданного товара и изменять только цену: в рыночных условиях количество проданного товара зависит от цены. Т. е., вообще говоря, если мы рассматриваем в качестве переменной цену товара , то эту формулу правильнее записать так:

где  – это еще одна функция, которая показывает зависимость количества проданного товара от цены. Эту зависимость нужно учесть, и только тогда при прочих неизменных условиях можно будет рассматривать доход от продаж товара как функцию одного аргумента – его цены.

---

Аналитический способ задания функции

Аргумент функции чаще всего обозначают , но можно использовать и любую другую букву. Каждому значению аргумента ставится в соответствие значение функции. Записывают это обычно так:

Чтобы указать, как именно ставится это соответствие, записывают формулу для вычисления, например:

Если хотят показать, что каждому значению  ставится в соответствие число , то это записывают так:

Или так:

Такой способ задания функции, как мы уже знаем, называется аналитическим.

Задание 1. Зависимость перемещения тела от времени движения имеет вид:

,

где  задано в секундах,  – в метрах. Определить перемещение тела через 2 секунды.

Решение

По сути, нам нужно вычислить значение функции  при . Записывают это так:

Т. е. мы просто подставляем в формулу конкретное числовое значение аргумента  и вычисляем значение функции при этом значении аргумента.

Ответ:  м.

Области определения и значения функции

Функция – это соответствие между двумя множествами. Поэтому, чтобы задать функцию, нужно определить не только само соответствие, но и множества, между которыми оно устанавливается. Множество аргументов – это область определения функции, а множество значений функции – область значений (см. рис. 8).

Рис. 8. Области определения и значений функции

Но чаще всего область определения и область значений числовых функции не задают, предполагая, что они естественные. Естественная область определения при аналитическом задании – это область допустимых значений выражения, которое записано в формуле. Соответственно, естественная область значений – это множество всех значений, которые может принимать функция.

Почему вообще могут появляться недопустимые значения аргумента? Функции – это инструмент, и, как любой инструмент, они имеют свои ограничения при использовании: ножницами для бумаги разрежешь бумагу, но не металл.

Мы говорим о числовых функциях, поэтому и работают они с числами, а конкретнее – с действительными числами. Мы уже знаем, что некоторые операции с действительными числами не определены, а именно:

1. деление на ноль;
2. извлечение квадратного корня из отрицательного числа.

Таким образом, в некоторых случаях мы не всем значениям аргумента сможем поставить в соответствие значение функции. Значения аргумента, для которых мы не можем это сделать, называются недопустимыми значениями аргумента. А множество всех допустимых значений аргумента мы и будем подразумевать под областью определения функции (если отдельно не оговорено иное).

Рассмотрим примеры:

1.

Деления на переменную нет, недопустимых значений нет. Область определения функции – все действительные числа: .

2.

Поскольку деление на ноль не определено, то значения , при которых , являются недопустимыми. Решая уравнение, находим: . Эти значения являются недопустимыми, значит, область определения:  и .

3.

Подкоренное выражение должно быть неотрицательным, значит, . Это верно для всех значений , значит, область определения функции: .

В рассмотренных выше примерах говорится о естественной области определения. Но она может быть задана искусственно, как дополнительное условие. Например, у функции  естественной областью определения являются все числа. Но если таким образом мы задаем зависимость площади квадрата от его стороны, то нужно дополнительно указать, что  – и это будет областью определения данной функции.

Итак, область определения – это множество всех значений, которые может принимать аргумент , а область значений функции – множество значений, которые может принимать функция .

При использовании любого инструмента результат зависит от того, что это за инструмент и к чему его применили: перекрутив мясо в мясорубке, мы получим фарш. Для функций это значит, что область их значения зависит от области определения и от того, что это за функция.

Например, рассмотрим кубики с ребром  от 1 до 3. Объемы  этих кубиков будут принимать значения от 1 (для самого маленького кубика) до 27 (самого большого). На это можно посмотреть как на функцию зависимости объемов этих кубиков от длины ребра:  при  (см. рис. 9).

Рис. 9. График функции

Тогда область значений этой функции от  до : .При этом максимальное значение функции равно 27, минимальное равно 1.

На практическом занятии мы еще потренируемся искать области значений различных функций.

Базовые функции

В математике различных арифметических операций не так много. Вы уже знаете о сложении, вычитании, умножении, делении, возведении в целую степень и извлечении квадратного корня. В старших классах вы еще познакомитесь с возведением в рациональную степень и логарифмированием.

Это базовые кирпичики, из которых строится любое алгебраическое выражение, именно с помощью операций мы можем задавать различные функции. Рассмотрим простейшие функции, которые можно задать с помощью этих операций. Это тоже будут своего рода кирпичики, с помощью которых можно будет изучать свойства более сложных функций. Для каждой из них определим область определения и область значений, а также построим их графики.

1. Линейная функция сочетает в себе операции умножения на число, сложение/вычитание. Общий вид (см. рис. 10):

Рис. 10. График линейной функции

Область определения – все действительные числа, ведь нет деления на переменную или извлечения корня. В случае когда , область значений – все действительные числа.

Если же , то получаем функцию:

Т. е. любому числу  мы ставим в соответствие фиксированное число . Областью значений будет одно число . График линейной функции – прямая линия (см. рис. 11).

Рис. 11. График линейной функции

2. Обратная пропорциональность:

Операция – деление на переменную. Область определения: . Область значений:, ведь дробь может быть равна нулю только в случае, если числитель равен нулю.

График функции можно построить по точкам:

Получим следующий вид графика (см. рис. 12), который называется гиперболой.

Рис. 12. Гипербола

Обратите внимание, что гипербола состоит из двух веток, которые расположены в  и  четвертях и которые стремятся к осям координат, но не пересекают их.

Оси координат для гиперболы являются асимптотами (от греческого «несовпадающий»), т. е. прямыми, к которым график функции на бесконечности подходит все ближе и ближе (расстояние от прямой до графика функции стремится к нулю).

3.Квадратичная функция:

Область определения – все действительные числа: . Область значений: , поскольку квадрат числа – неотрицательная величина.

График строим по точкам:

Полученная кривая называется квадратичная парабола или просто парабола (см. рис. 13).

Рис. 13. Парабола

Обратите внимание, что парабола симметрична относительно оси ординат (чуть позже мы поговорим, с чем связано это свойство) и что у нее тоже есть две ветви (левая и правая).

4. Кубическая функция:

Область определения и область значений – все действительные числа: . Построив по точкам график, получим кубическую параболу (см. рис. 14):

Рис. 14. Кубическая парабола

5. Функция квадратного корня:

Область определения: , область значений: , ведь по определению арифметический квадратный корень – это неотрицательная величина.

Построив по точкам график, получим следующую кривую (см. рис. 15):

Рис. 15. График функции квадратного корня

Она имеет ту же форму, что и часть параболы. Ее так и называют – ветвь параболы. То, что графики похожи, – это не совпадение, об этом мы поговорим в последней части нашего урока.

6. Функция модуля:

Вспомним еще одну математическую конструкцию – модуль числа:

Область определения – все действительные числа: ; область значений: , поскольку модуль – это неотрицательная величина.

График можно построить, раскрыв модуль. Для неотрицательных значений  получим график функции . Для отрицательных будет график функции: . Полученная кривая – и есть график функции  («галочка») (см. рис. 16).

Рис. 16. График функции модуля

Мы разобрали простейшие функции с использованием различных операций. Для линейной функции мы рассмотрели ее общий вид, для остальных функций лишь их частные случаи. Рассматривать общий вид параболы, обратной пропорциональности и модуля мы будем в следующем уроке.

Стоит отметить, что рассмотренных функций достаточно для описания множества процессов. В природе в основном встречаются процессы, которые достаточно точно можно описать с помощью линейных, квадратичных и обратных зависимостей. Если зависимость более сложная то можно аппроксимировать ее, т. е. приблизительно описать, с помощью этих более простых функций.

---

Интерполяция и аппроксимация

При проведении различных исследований возникает такая задача: по некоторым известным значениям функции попытаться восстановить саму функцию (график или формулу) (см. рис. 17). Если мы знаем, что функция линейная, то достаточно двух значений (прямая однозначно задается двумя точками).

Рис. 17. Восстановление функции по некоторым известным значениям функции

Например, сила растяжения пружины зависит от растяжения пружины по закону Гука (см. рис. 18):

Достаточно измерить силу для двух различных значений растяжения пружины, чтобы найти жесткость пружины (коэффициент ) и восстановить функцию (см. рис. 19).

Рис. 18. Закон Гука

Рис. 19. Восстановление функции при помощи закона Гука

Но можно ли попытаться восстановить функцию, не зная, какой вид она имеет (см. рис. 20)?

Рис. 20. Восстановление функции без информации о виде функции

Такая задача называется аппроксимацией – на основании экспериментального набора значений функции в нескольких точках построить функцию, на которую с высокой точностью попадут получаемые в ходе эксперимента значения (как те, что у нас уже есть, так и остальные, которые можно получить).

Если мы хотим, чтобы построенной функции точно принадлежали все имеющиеся значения функции, то этот частный случай аппроксимации называется интерполяцией.

Существует также близкая к интерполяции задача, которая заключается в аппроксимации (т. е. приближении) какой-либо сложной функции другой, более простой функцией.

Разумеется, использование упрощенной функции не позволяет получить такие же точные результаты, какие давала бы первоначальная функция. Но для некоторых задач достигнутый выигрыш в простоте и скорости вычислений может перевесить получаемую погрешность в результатах.

Подробнее почитать об интерполяции и аппроксимации можно в интернете.

---

Нули функции

Мы уже выяснили, с чем работает такой инструмент, как функции, разобрали свойства простейших составляющих этого инструмента. Теперь выделим некоторые характерные моменты, которые помогут при исследовании функций и их графиков.

Часто при оценке значения функции мы сравниваем ее с нулем. Например, это график температуры на улице, графики зависимости скорости, силы в физике, график прибыли в экономике и прочие (см. рис. 21).

Рис. 21. Сравнение функции с нулем

Аргументы, при которых значение функции равно нулю, называют нулями функции. Исходя из определения понятно, что для нахождения нулей функции нужно найти решения уравнения:

Про нули базовых функций можно сказать следующее (см. рис. 22):

1. нулем линейной функции  является:

(при : решение уравнения );

2. функция  не имеет нулей;

3. функции , , ,  имеют нуль в точке:

Рис. 22. Нули базовых функций

Нули функции разбивают ось  на промежутки, на которых функция принимает значения только одного знака: либо только положительные, либо только отрицательные. Их так и называют – промежутки знакопостоянства.

Кроме нулей, эти промежутки еще могут определяться недопустимыми значениями аргумента. Так, например, происходит у функции . Функция не имеет нулей, но есть недопустимое значение аргумента: . Это значение разбивает ось на два промежутка: при  функция принимает положительные значения, при – отрицательные.

---

Непрерывные функции. Теорема Больцано-Коши

Рассмотренные нами графики функций выглядят по-разному. Так, график прямой, модуля, параболы можно нарисовать, не отрывая карандаш от бумаги. А вот с графиком гиперболы так не получится.

На самом деле, можно выделить два больших класса функций – непрерывные и разрывные (см. рис. 23). На бытовом уровне определение непрерывной функции мы только что сформулировали – их график можно нарисовать, не отрывая карандаш от бумаги. Есть более строгое математическое определение, но мы не будем его сейчас приводить – интуитивного понимания нам вполне достаточно.

Рис. 23. Непрерывная и разрывная функции

Непрерывные функции обладают важным свойством: пусть на отрезке  она принимает значения , , для определенности:  (см. рис. 24). В этом случае для любого  существует такое , что . Это утверждение называется теоремой Больцано-Коши.

Рис. 24. На отрезке  функция: , ,

Это свойство вполне понятно – если не «прыгать», то пройти со ступеньки  на ступеньку  можно только пройдя все промежуточные ступеньки. Из этого следует, что для смены знака «плюс» на «минус» или наоборот функция обязательно должна пройти через . Именно поэтому непрерывную функцию на промежутки знакопостоянства разбивают только ее нули.

А вот если у функции есть разрывы, то смена знака может произойти еще и в точках разрыва (как это происходит в случае гиперболы).

---

Возрастание и убывание функции

Кроме непосредственно значений функции важно понимать, как изменяется ее значение с изменением аргумента, т. е. уметь анализировать поведение функции. Так, говорят, что функция возрастает, если при увеличении аргумента значение функции увеличивается. Соответственно, функция убывает, если при увеличении аргумента значение функции уменьшается. Или более строго:

1. Функция называется монотонно возрастающей (см. рис. 25), если для любых  верно, что .

2. Функция называется монотонно убывающей (см. рис. 26), если для любых  верно, что .

Рис. 25. Монотонно возрастающая функция

Рис. 26. Монотонно убывающая функция

Для базовых функций:

1. Линейная функция  является возрастающей для  и убывающей для .

Рис. 27. Возрастающая линейная функция

Рис. 28. Убывающая линейная функция

2. Функция  является возрастающей.

Если функция не является монотонной на всей области определения, то говорят о монотонности на отдельных промежутках:

1. Функция  убывает на двух промежутках:

2. Функции  убывают при  и возрастают при :

Гораздо легче определить возрастание и убывание функции в тех случаях, когда функция задана графически: если при движении слева направо график функции идет вверх, то функция возрастает. Если вниз, то убывает.

Четность функции

Для упрощения анализа функции в ней можно выделить похожие или повторяющиеся части. Заметим, что функции  и  состоят из двух частей, которые являются зеркальным отражением друг друга (см. рис. 29).

Рис. 29. Графики функций  и

В математике говорят, что такие фигуры симметричны относительно оси, в данном случае относительно оси . Для функции это значит, что противоположным значениям аргумента  соответствуют одинаковые значения функции:

Функции, для которых выполняется это соотношение, называются четными функциями. Они получили такое название, поскольку функции всех степеней с четным показателем обладают этим свойством (, ,  и т. д.).

Аналогично посмотрим на функцию с нечетным показателем:  (см. рис. 30).

Рис. 30. Кубическая парабола

Если отразить часть ее графика относительно одной, а затем относительно второй оси – получим вторую часть графика. Или еще говорят, что эти две части графика симметричны относительно центра координат. При этом противоположным значениям аргумента  соответствуют противоположные значения функции:

Функции, для которых выполняется это соотношение, по аналогии называются нечетными функциями.

Если же для функции не выполняется ни одно из равенств:  или , то она называется функцией общего вида (см. рис. 31).

Рис. 31. Функции общего вида

Периодичность функции

Кроме того, значения функции могут повторяться через некоторый промежуток аргумента. Такие функции называются периодическими (см. рис. 32).

Рис. 32. Периодические функции

Они описывают любые повторяющиеся процессы, например колебания в физике. Примером повторяющейся функции может быть зависимость угла поворота стрелки часов от времени . С другими примерами периодических функций вы познакомитесь в старших классах, а пока что мы ограничимся определением.

Функция называется периодической с периодом T, если для каждого значения аргумента выполняется соотношение:

На графике это будет выглядеть как одинаковые повторяющиеся участки шириной T.

Исследование функции по графику

Задание 2. Исследовать функцию по ее графику (см. рис. 33).

Рис. 33. Иллюстрация к заданию 2

Решение

1. Значения аргумента изменяются от  до . Это область определения функции:

2. По графику видим, что максимальное значение функции равно , минимальное . Таким образом, область значений:

3. Значение функции равно нулю там, где она пересекает ось , т. е. нули функции:

4. Функция принимает положительные значения  на интервалах:

Функция принимает отрицательные значения  на интервалах:

5. Функция возрастает на промежутках:

Функция убывает на промежутках:

6. Функция не является симметричной ни относительно оси , ни относительно центра координат. Значит, функция общего вида. Также она не является периодической.

Обратная функция

Вернемся к определению функции: это такое соответствие между множествами, когда каждому элементу из первого множества  ставится в соответствие единственный элемент из другого множества . То есть по значению аргумента мы находим значение функции.

А можно ли выполнить обратную операцию: по значению функции определить значение аргумента? Да, для этого нам нужно поставить в соответствие элементу из множества  элемент из множества . Но не всегда это можно сделать однозначно. Например, у параболы почти каждому значению функции (кроме ) будут соответствовать два значения аргумента.

В тех случаях, когда такое обратное соответствие можно сделать однозначно, мы получим в результате новую функцию, которая называется обратной функцией к исходной.

Тот факт, что не к любой функции можно однозначно восстановить исходную, не должен нас удивлять. Если вы увидели на часах , то, не имея дополнительной информации (например, в комнате без окон), не сможете определить, сейчас  часов дня или ночи.

Рассмотрим линейную функцию:

Здесь мы значению аргумента  ставим в соответствие значение . Чтобы получить обратную функцию, нужно сделать наоборот: поставить значению  в соответствие значение . Для этого просто выразим из формулы  через y:

Или (см. рис. 34):

Рис. 34. Графики функций  и

Получили однозначное соответствие. Т. е. это функция, причем теперь  – аргумент, а  – значение функции. Но обычно переходят к привычным обозначениям:  – аргумент, а  – значение функции. Просто заменив буквы, получим:

Итак, функция, обратная линейной функции, также является линейной, только с угловым коэффициентом  и свободным коэффициентом . Функция  является обратной самой себе, ведь, если мы выразим из нее , получим:

Вернувшись к привычным обозначениям, получим ту же функцию:

А вот с функцией  получается более интересная ситуация. Попробуем выразить . Получим:  или . Это уже не функция, т. к. нет однозначного соответствия. Это видно и по графику: одному значению y соответствует два значения . Правая ветвь соответствует: , левая:  (см. рис. 35).

Рис. 35. Графики функций , ,

Чтобы записать обратную функцию, выбирают одно из значений, обычно положительное, т. е. . Или, после замены обозначений: . Т. е. функция является обратной к функции . Поэтому неудивительно, что графики этих функций имеют похожую форму.

Обратите внимание: графики обратных функций зеркально симметричны исходным графикам или их частям относительно прямой  (см. рис. 36).

Рис. 36. Графики обратных функций зеркально симметричны исходным графикам или их частям относительно прямой

И это не случайно: если точка  принадлежит графику прямой функции, то точка с координатами  будет принадлежать графику обратной (если у нее вообще есть прообраз). А такие точки симметричны друг другу относительно прямой .

Список литературы

1. Никольский С.М., Решетников Н.Н., Потапов М.К., Шевкин А.В. Алгебра, 8 класс. Учебник. – М.: ФГОС, издательство «Просвещение», 2018.
2. Дорофеев Г.В., Суворова С.Б., Бунимович Е.А. Алгебра, 8 класс. Учебник – М.: издательство «Просвещение», 2018.
3. Макарычев Ю.Н., Миндюк Н.Г., Нешков К.И., Суворова С.Б./Под ред. Теляковского С.А. Алгебра, 8 класс. Учебник. – М.: издательство «Просвещение», 2018.

Дополнительные рекомендованные ссылки на ресурсы сети Интернет

1. Интернет-портал math-prosto.ru
2. Интернет-портал yaklass.ru
3. Интернет-портал cleverstudents.ru

Домашнее задание

1. Какие из перечисленных точек принадлежат графику функции :

2. Найти нули квадратичной функции .

3. Пересекают ли график функции  прямые  и ? Если да, то найти точку пересечения.

Что такое функция — человеческим языком

Так вот, функция отражает зависимость величин друг от друга: то есть при изменении одного числа ( displaystyle x), по некоторому закону ( displaystyle fleft( x right)) изменяется ( displaystyle y). 

Зависимость, или взаимосвязь – вот ключевые слова при определении понятия функции.

Попробуй самостоятельно придумать несколько примеров из жизни, где четко проявляется зависимость одного от другого.

И?… Не можешь придумать ни один пример? Как так! Смотри:

Допустим автомобиль движется со средней скоростью ( displaystyle 110) км/ч, как тогда выразить зависимость пути ( displaystyle S) от времени ( displaystyle t)?

Что в этом случае будет ( displaystyle y), что ( displaystyle x), и как будет выражено в итоге ( displaystyle fleft( x right))?

Проведем параллели между физической формулой и привычной нам записью функции ( displaystyle y=fleft( x right)):

• ( displaystyle y=S), то есть путь, который проедет автомобилист;
• ( displaystyle x=t), время, которое он проведет в пути;
• ( displaystyle fleft( x right)=110cdot x) зависимость пути от времени, учитывая, что скорость на всем пути постоянна.

Разобрался что к чему? Теперь перейдем на математический язык.

Что такое функция — на языке математики

Она может зависеть от множества критериев. Например, как в нашем случае, зависимость пути от времени, проведенном в дороге при движении с постоянной скоростью.

Справа у нас стоит ( displaystyle x). Эта величина переменная, или, как говорят математики, «аргумент».

Логично, что чем больше времени проведет автомобилист в дороге, тем большее расстояние он проедет (конечно, если скорость будет постоянна, и он не встрянет намертво в пробках).

Справа у нас также есть ( displaystyle f), за этим скрываются все действия, совершаемые над ( displaystyle x).

В нашем случае мы говорим, что ( displaystyle S=nu cdot t), а так как ( displaystyle nu =110)км/ч, то под ( displaystyle f) скрывается умножение на ( displaystyle 110), вот мы и получаем – ( displaystyle fleft( x right)=110cdot x).

Теперь, думаю, тебе все понятно?

Подведем итог:

• ( displaystyle y=fleft( x right)) – это формула, обозначающая функцию, то есть зависимость одной переменной от другой;
• ( displaystyle x) – переменная величина, или, аргумент;
• ( displaystyle y) – зависимая величина – изменяется при изменении аргумента, то есть ( displaystyle x) согласно какой-либо определенной формуле ( displaystyle f), отражающей зависимость одной величины от другой.

Теперь, когда ты понял суть понятия «функция» и знаешь, что такое переменная величина, а что постоянная, посмотрим на определение функции, каким его дают математики.

Область определения функции

Вернемся к нашему примеру.

Автомобилист едет с постоянной скоростью и проезжает расстояние, которое зависит от того, сколько времени он провел в пути. Все верно?

Разбираемся дальше. Мы говорили, что ( displaystyle x=t), это как раз и есть время, проведенное в пути.

Каким оно может быть? Ты сейчас можешь быть крайней удивлен такой постановкой вопроса, но все же, каким может быть это время?

Правильно, чисто теоретически от ( displaystyle 0) до ( displaystyle +infty ).

Вот ты сам и определил для нашего конкретного случая множество ( displaystyle X), а иначе говоря, допустимые значения аргумента или область определения функции ( displaystyle Dleft( y right)).

Запомнить очень легко: что определяет нашу функцию? От чего зависит игрек, и что мы меняем?

Функцию определяет икс! Соответственно, область определения – это возможные значения ( displaystyle x).

Теперь давай рассматривать, что такое множество ( displaystyle Y).

Еще один важный момент

Еще раз повторю определение и сделаю на нем акцент:

Функцией называется правило ( displaystyle f), по которому каждому элементу ( displaystyle x) множества ( displaystyle X) ставится в соответствие единственный элемент ( displaystyle y) множества ( displaystyle Y).

Заметил? Слово «единственный» – это очень-очень важный элемент нашего определения. Постараюсь объяснить тебе на пальцах.

Допустим, у нас есть функция, заданная прямой. ( displaystyle y=5x+3). При ( displaystyle x=0), мы подставляем данное значение в наше «правило» и получаем, что ( displaystyle y=3).

Одному значению ( displaystyle x) соответствует одно значение ( displaystyle y). Мы даже можем составить таблицу различных значений и построить график данной функции, чтобы убедится в этом.

( displaystyle x)	( displaystyle 0)	( displaystyle 1)	( displaystyle -1)	( displaystyle 2)	( displaystyle -2)
( displaystyle y)	( displaystyle 3)	( displaystyle	( displaystyle -2)	( displaystyle 13)	( displaystyle -7)

А вот и график с нашими отмеченными точками:

Как ты убедился – графиком является прямая, в которой одному значению ( displaystyle x) соответствует одно значение ( displaystyle y) (данный факт показан красными линиями).

Соответственно, данная зависимость подходит под определение функции.

А что ты скажешь о такой зависимости: ( displaystyle y=2{{x}^{2}}-4{x}-1), то есть параболы? Является ли она функцией? Давай составим также табличку значений:

( displaystyle x)	( displaystyle 0)	( displaystyle 1)	( displaystyle -1)	( displaystyle 2)	( displaystyle -2)
( displaystyle y)	( displaystyle -1)	( displaystyle -3)	( displaystyle 5)	( displaystyle -1)	( displaystyle 15)

«Смотри! – скажешь ты, – « ( displaystyle -mathbf{1})» встречается два раза!» Так быть может парабола не является функцией? Нет, является!

То, что «( displaystyle -1)» встречается два раза далеко не повод обвинять параболу в неоднозначности!

Дело в том, что, при расчёте для ( displaystyle x=0), мы получили один игрек. И при расчёте с ( displaystyle x=2) мы получили один игрек. Так что все верно, парабола является функцией.

Посмотри на график:

Разобрался? Если нет, вот тебе жизненный пример сооовсем далекий от математики!

Допустим, у нас есть группа абитуриентов, познакомившихся при подаче документов, каждый из которых в разговоре рассказал, где он живет:

Согласись, вполне реально, что несколько ребят живут в одном городе, но невозможно, чтобы один человек жил в нескольких городах одновременно. Это как бы логичное представление нашей «параболы» – нескольким разным икс соответствует один и тот же игрек.

Теперь придумаем пример, когда зависимость не будет функцией. Допустим, эти же ребята рассказывали, на какие специальности они подали документы:

Здесь у нас совершенно другая ситуация: один человек может спокойно подать документы как на одно, так и на несколько направлений. То есть одному элементу ( displaystyle x) множества ( displaystyle X) ставится в соответствие несколько элементов ( displaystyle y) множества ( displaystyle Y). Соответственно, это не функция.

Проверим твои знания на практике. Определи по рисункам, что является функцией, а что нет:

Разобрался? А вот и ответы:

• Функцией является – В, Е.
• Функцией не является – А, Б, Г, Д.

Почему? Да вот почему:

На всех рисунках кроме В) и Е) на один ( displaystyle x) приходится несколько ( displaystyle y)!

Уверена, теперь ты с легкостью отличишь функцию от «НЕ функции», скажешь, что такое аргумент и что такое зависимая переменная, а так же определишь область допустимых значений аргумента и область определения функции.

Приступаем к следующему разделу – как задать функцию?

Аналитический способ заданий функции

Аналитический способ – это и есть задание функции с помощью формулы. Это самый универсальный и исчерпывающий и однозначный способ. 

Если у тебя есть формула, то ты знаешь о функции абсолютно все – ты можешь составить по ней табличку значений, можешь построить график, определить, где функция возрастает, а где убывает, в общем, исследовать ее по полной программе.

Рассмотрим функцию ( displaystyle fleft( x right)={{x}^{3}}-3{{x}^{2}}+{x}-2). Чему равно ( displaystyle fleft( 2 right))?

«Что это значит?» – спросишь ты. Сейчас объясню.

Напомню, что в записи ( displaystyle f(x)) выражение в скобках называется аргументом.

И этот аргумент может быть любым выражением, не обязательно просто ( displaystyle x). Соответственно, каким бы ни был аргумент (выражение в скобках), мы его запишем вместо ( displaystyle x) в выражении ( displaystyle f(x)).

В нашем примере получится так:

( displaystyle fleft( 2 right)={{2}^{3}}-3cdot {{2}^{2}}+2-2=8-12+2-2=-4).

Пример из ЕГЭ

Найдите значение выражения ( displaystyle frac{fleft( x-15 right)}{fleft( x-18 right)}), при ( displaystyle fleft( x right)={{5}^{x}}).

Уверена, что сначала ты испугался, увидев такое выражение, но в нем нет абсолютно ничего страшного!

Давай решим.

Все как и в прошлом примере: каким бы ни был аргумент (выражение в скобках), мы его запишем вместо ( displaystyle x) в выражении ( displaystyle f(x)). Например, для функции ( displaystyle fleft( x right)={{5}^{x}}:fleft( x+1 right)={{5}^{left( x+1 right)}}) .

Что же нужно сделать в нашем примере? Вместо ( displaystyle fleft( x-15 right)) надо написать ( displaystyle {{5}^{x-15}}), а вместо – ( displaystyle fleft( x-18 right)-{{5}^{x-18}}):

( displaystyle frac{{{a}^{x}}}{{{a}^{y}}}={{a}^{x-y}}) и ( displaystyle {{a}^{x+y}}={{a}^{x}}cdot {{a}^{y}})

сократить получившееся выражение:

Теперь попробуй самостоятельно найти значение следующих выражений:

• ( displaystyle fleft( x-9 right)+fleft( 16-x right)), если ( displaystyle fleft( x right)=3x+2)
• ( displaystyle 3fleft( x-4 right)-fleft( 3x right)), если ( displaystyle fleft( x right)=x-5)

Справился? Сравним наши ответы: 

• ( displaystyle 25)
• ( displaystyle -22)

Мы привыкли, что функция имеет вид ( displaystyle y=fleft( x right)), даже в наших примерах мы задаем функцию именно таким образом, однако аналитически можно задать функцию в неявном виде, например ( displaystyle 5x+2y-3=0). Попробуй построить эту функцию самостоятельно.

Справился?

Вот как строила ее я.

Какое уравнение мы в итоге вывели? Правильно! Линейное, а это значит, что графиком будет прямая линия. Сделаем табличку, чтобы определить, какие точки принадлежат нашей прямой:

( displaystyle x)	( displaystyle 0)	( displaystyle 1)	( displaystyle -1)	( displaystyle 2)	( displaystyle -2)
( displaystyle y)	( displaystyle 1.5)	( displaystyle -1)	( displaystyle 4)	( displaystyle -3.5)	( displaystyle 6.5)

А теперь строим по данным точкам график:

Вот так из неявной формулы получилась линейная функция.

А теперь посмотри следующую формулу: ( displaystyle {{y}^{2}}=x). Является ли она функцией? Согласись, вызывает затруднение…

Попробуй подставить различные значения ( displaystyle x) и посмотреть, какой ( displaystyle y) им соответствует.

( displaystyle x)	( displaystyle 0)	( displaystyle 1)	( displaystyle 4)
( displaystyle y)	( displaystyle 0)	( displaystyle -1;1)	( displaystyle -2;2)

Вот как раз то, о чем мы говорили… Одному ( displaystyle x) соответствует несколько ( displaystyle y). Попробуем нарисовать то, что получилось:

Является ли то, что у нас получилось функцией? Правильно, нет! Почему? Попробуй ответить на этот вопрос с помощью рисунка. Что у тебя вышло?

«Потому что одному значению ( displaystyle x) соответствует несколько значений ( displaystyle y)!»

Какой вывод мы можем из этого сделать?

Правильно,  функция не всегда может быть выражена явно, и не всегда то, что «замаскировано» под функцию является функцией!

Табличный способ задания функции

Как следует из названия, этот способ представляет собой простую табличку. Да, да. Наподобие той, которой мы с тобой уже составляли. Например:

( displaystyle x)	( displaystyle 0)	( displaystyle 1)	( displaystyle -1)	( displaystyle 2)	( displaystyle -2)
( displaystyle y)	( displaystyle 4)	( displaystyle -6)	( displaystyle 3)	( displaystyle -4)	( displaystyle 15)

Как ты уже знаешь, в первой строчке мы ставим значение аргумента, а во второй строчке – соответствующие ему значение функции. Таким образом, в таблице каждому иксу соответствует одно значение игрека.

Заметь, в последней приведенной табличке невозможно четко определить правило, по которому игрек зависит от икс. Так тоже бывает и в этом нет ничего страшного, просто мы не можем вот так сразу взять и определить правило.

Если тебя это смущает, приведу в пример другую таблицу:

( displaystyle x)	( displaystyle 0)	( displaystyle 1)	( displaystyle -1)	( displaystyle 2)	( displaystyle -2)
( displaystyle y)	( displaystyle 0)	( displaystyle 3)	( displaystyle -3)	( displaystyle 6)	( displaystyle -6)

Здесь ты сразу подметил закономерность – игрек в три раза больше чем икс.

А теперь задание на «очень хорошо подумать»: как ты считаешь, равносильная ли функция, заданная в виде таблицы, функции ( displaystyle y=3x)?

Не будем долго рассуждать, а будем рисовать!

Итак. Рисуем функцию, заданную обоими способами:

Видишь разницу? Дело совсем не в отмеченных точках! Присмотрись внимательнее:

Теперь увидел? Когда мы задаем функцию табличным способом, мы на графике отражаем только те точки, которые есть у нас в таблице и линия (как в нашем случае) проходит только через них.

Когда мы задаем функцию аналитическим способом, мы можем взять любые точки, и наша функция ими не ограничивается. Вот такая вот особенность. Запоминай!

Словесный способ задания функции

Как же описать функцию словесно? 

Возьмем наш недавний пример – ( displaystyle y=3x).

Данную функцию можно описать «каждому действительному значению икс соответствует его утроенное значение». Вот и все. Ничего сложного.

Ты, конечно, возразишь: «Есть настолько сложные функции, которые словесно задать просто невозможно!» Да, есть и такие, но есть функции, которые описать словесно легче, чем задать формулой.

Например: «каждому натуральному значению икс соответствует разница между цифрами, из которых он состоит, при этом за уменьшаемое берется наибольшее цифра, содержащиеся в записи числа».

Теперь рассмотрим, как наше словесное описание функции реализуется на практике:

Пусть ( displaystyle x=256)

Наибольшая цифра в данном числе – ( displaystyle 6), соответственно, ( displaystyle 6) – уменьшаемое, тогда:

( displaystyle y=6-5-2=-1).

Что такое функция

Как часто в своей жизни вы встречали слово «функция»? Скорее всего, хотя бы раз вы его слышали. В математике тоже есть своя функция, которая отражает зависимость, связь нескольких величин. Например, расстояние зависит от скорости движения и времени, площадь круга зависит от его радиуса, масса воды в бассейне зависит от его объема. 

В данной статье будет рассматриваться зависимость между двумя величинами. 

К примеру, давайте вспомним, как находится объем куба V. Он зависит от длины его ребра a. 

Для каждого значения переменной a можно найти соответствующее ему значение V. Давайте попробуем:

если a=2, то V=a3=23=8;

если a=3, то V=a3=33=27;

если a=0,1, то V=a3=0,13=0,001.

Зависимость переменной V от значения переменной a можно записать формулой: 

V=a3

Переменную a, значения которой выбираются произвольно, называют
независимой
переменной, а переменную V, значения которой определяются в зависимости от выбранного значения переменной a, называют
зависимой
переменной.

---

Одна сторона прямоугольника равна 5 см, другая x см. Выразите зависимость площади прямоугольника от его стороны. Найдите значение площади прямоугольника при x=3; 2,4; 5 см.

---

Решение

Площадь прямоугольника находится как произведение его длины a на ширину b. Запишем это формулой: 

S=ab.

Одна из сторон равна 5 см, другая x см. Подставим их в формулу:

S=5x. 

Найдем значение площади прямоугольника при различных значениях переменной x.

При x=3 см,  S=5·x=5·3=15 см2

При x=2,4 см, S=5·x=5·2,4=12 см2

При x=5 см, S=5·x=5·5=25 см2

Ответ: S=5x; 15 см2, 12 см2, 25 см2.

---

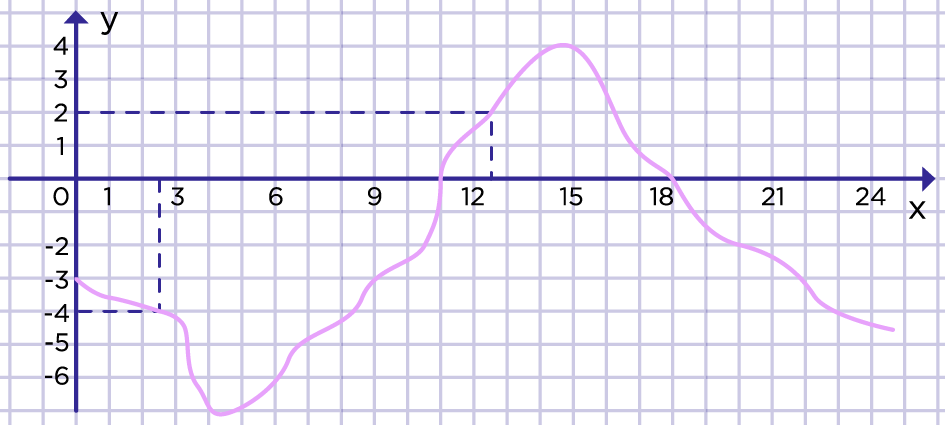
На рисунке 1 представлен график зависимости температуры y (в градусах Цельсия) от времени x (в часах). Определите, чему равна температура при x=2,5 ч, x=12,5 ч.

---

Решение

---

---

При этом, независимую переменную называют
аргументом
, а о зависимой переменной говорят, что она является
функцией
от этого аргумента. Значения зависимой переменной называют
значениями функции
, а все значения, которые принимает независимая переменная, образуют
область определения функции
. 

---

1. Маша спешила к Кате на день рождения со скоростью 7 км/ч. Выразите формулой зависимость расстояния S, пройденного Катей, от времени t в пути. 

2. Велосипедист, ехал к месту отдыха со скоростью 12 км/ч. Задайте формулой зависимость расстояния S от времени t. Вычислите, какое расстояние велосипедист проехал за 3,5 ч, за 1,5 ч, за 30 минут. 

---

Вычисление значений функции по формуле

Наиболее распространенный способ задания функции – с помощью формулы, т.к. она позволяет для любого значения аргумента находить соответствующее значение функции путем вычислений.

---

Найдите все значения функции fx=6x-42 при целых значениях аргумента, если -2≤x<4.

---

Решение

1. Найдем все целые значения аргумента на указанном промежутке: -2, -1, 0, 1, 2, 3.

2. Найдем значения функции при указанных значениях аргумента: 

если x=-2, то fx=6x-42=6·(-2)-42=-12-42=-162=-8;

если x=-1, то fx=6x-42=6·(-1)-42=-6-42=-102=-5;

если x=0, то fx=6x-42=6·0-42=-42=-2;

если x=1, то fx=6x-42=6·1-42=6-42=22=1;

если x=2, то fx=6x-42=6·2-42=12-42=82=4;

если x=3, то fx=6x-42=6·3-42=18-42=142=7.

Ответ: -8, -5, -2, 1, 4, 7.

---

Результаты вычислений в предыдущем примере удобно записать в виде таблицы значений функции (таблица 1). Поскольку мы вычисляли целочисленные значения функции, то выбирали значения с шагом 1. 

Таблица 1. Таблица значений функции fx=6x-42

x	-2	-1	0	1	2	3
f(x)	-8	-5	-2	1	4	7

В рассмотренном примере был указан промежуток, где функция определена (область определения функции), однако, если она не указана, то считают, что область определения состоит из всех значений независимых переменных, при которых формула имеет смысл.

Например, область определения функции y=x2+4 состоит из всех чисел. А вот область определения функции y=5x-7 состоит из всех чисел, кроме числа 7, т.к. при подстановке числа 7 в формулу, задающую функцию, получим в знаменателе нуль, чего быть не должно, т.к. на нуль делить нельзя. 

---

Найдите значение аргумента, при котором значение функции y=3,5x-12 равно 16.

---

Решение

1. Подставим значение функции в формулу. 

y=3,5x-12

16=3,5x-12

2. Найдем значение аргумента, решив получившееся уравнение.

3,5x-12=16

3,5x=16+12

3,5x=28

x=28∶3,5

x=8

Ответ: 8.

---

1. Функция задана формулой y=16x. В таблице 2 указаны некоторые значения аргумента. Заполните таблицу, вычислив соответствующие значения функции.

Таблица 2. Таблица значений функции y=16x

x	-8	-4	-2	1	4	16
y

2. Катер, двигаясь со скоростью v км/ч в течение 8 часов, прошел путь s км. Задайте формулой зависимость s от v. Пользуясь полученной формулой, найдите: а) s, если v=45 км/ч км/ч; б) v, если s=96 км.

---

---