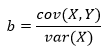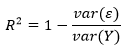Линейная регрессия применяется для анализа данных и в машинном обучении. Постройте свою модель на Python и получите первые результаты!
Что такое регрессия?
Регрессия ищет отношения между переменными.
Для примера можно взять сотрудников какой-нибудь компании и понять, как значение зарплаты зависит от других данных, таких как опыт работы, уровень образования, роль, город, в котором они работают, и так далее.
Регрессия решает проблему единого представления данных анализа для каждого работника. Причём опыт, образование, роль и город – это независимые переменные при зависимой от них зарплате.
Таким же способом можно установить математическую зависимость между ценами домов в определённой области, количеством комнат, расстоянием от центра и т. д.
Регрессия рассматривает некоторое явление и ряд наблюдений. Каждое наблюдение имеет две и более переменных. Предполагая, что одна переменная зависит от других, вы пытаетесь построить отношения между ними.
Другими словами, вам нужно найти функцию, которая отображает зависимость одних переменных или данных от других.
Зависимые данные называются зависимыми переменными, выходами или ответами.
Независимые данные называются независимыми переменными, входами или предсказателями.
Обычно в регрессии присутствует одна непрерывная и неограниченная зависимая переменная. Входные переменные могут быть неограниченными, дискретными или категорическими данными, такими как пол, национальность, бренд, etc.
Общей практикой является обозначение данных на выходе – ?, входных данных – ?. В случае с двумя или более независимыми переменными, их можно представить в виде вектора ? = (?₁, …, ?ᵣ), где ? – количество входных переменных.
Когда вам нужна регрессия?
Регрессия полезна для прогнозирования ответа на новые условия. Можно угадать потребление электроэнергии в жилом доме из данных температуры, времени суток и количества жильцов.
Где она вообще нужна?
Регрессия используется во многих отраслях: экономика, компьютерные и социальные науки, прочее. Её важность растёт с доступностью больших данных.
Линейная регрессия
Линейная регрессия – одна из важнейших и широко используемых техник регрессии. Эта самый простой метод регрессии. Одним из его достоинств является лёгкость интерпретации результатов.
Постановка проблемы
Линейная регрессия некоторой зависимой переменной y на набор независимых переменных x = (x₁, …, xᵣ), где r – это число предсказателей, предполагает, что линейное отношение между y и x: y = 𝛽₀ + 𝛽₁x₁ + ⋯ + 𝛽ᵣxᵣ + 𝜀. Это уравнение регрессии. 𝛽₀, 𝛽₁, …, 𝛽ᵣ – коэффициенты регрессии, и 𝜀 – случайная ошибка.
Линейная регрессия вычисляет оценочные функции коэффициентов регрессии или просто прогнозируемые весы измерения, обозначаемые как b₀, b₁, …, bᵣ. Они определяют оценочную функцию регрессии f(x) = b₀ + b₁x₁ + ⋯ + bᵣxᵣ. Эта функция захватывает зависимости между входами и выходом достаточно хорошо.
Для каждого результата наблюдения i = 1, …, n, оценочный или предсказанный ответ f(xᵢ) должен быть как можно ближе к соответствующему фактическому ответу yᵢ. Разницы yᵢ − f(xᵢ) для всех результатов наблюдений называются остатками. Регрессия определяет лучшие прогнозируемые весы измерения, которые соответствуют наименьшим остаткам.
Для получения лучших весов, вам нужно минимизировать сумму остаточных квадратов (SSR) для всех результатов наблюдений: SSR = Σᵢ(yᵢ − f(xᵢ))². Этот подход называется методом наименьших квадратов.
Простая линейная регрессия
Простая или одномерная линейная регрессия – случай линейной регрессии с единственной независимой переменной x.
А вот и она:
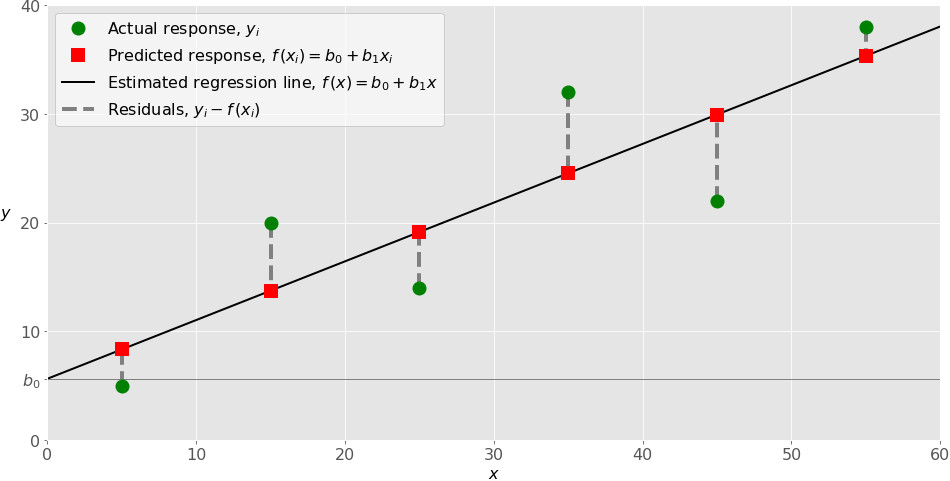
Реализация простой линейной регрессии начинается с заданным набором пар (зелёные круги) входов-выходов (x-y). Эти пары – результаты наблюдений. Наблюдение, крайнее слева (зелёный круг) имеет на входе x = 5 и соответствующий выход (ответ) y = 5. Следующее наблюдение имеет x = 15 и y = 20, и так далее.
Оценочная функция регрессии (чёрная линия) выражается уравнением f(x) = b₀ + b₁x. Нужно рассчитать оптимальные значения спрогнозированных весов b₀ и b₁ для минимизации SSR и определить оценочную функцию регрессии. Величина b₀, также называемая отрезком, показывает точку, где расчётная линия регрессии пересекает ось y. Это значение расчётного ответа f(x) для x = 0. Величина b₁ определяет наклон расчетной линии регрессии.
Предсказанные ответы (красные квадраты) – точки линии регрессии, соответствующие входным значениям. Для входа x = 5 предсказанный ответ равен f(5) = 8.33 (представленный крайним левыми квадратом).
Остатки (вертикальные пунктирные серые линии) могут быть вычислены как yᵢ − f(xᵢ) = yᵢ − b₀ − b₁xᵢ для i = 1, …, n. Они представляют собой расстояния между зелёными и красными пунктами. При реализации линейной регрессии вы минимизируете эти расстояния и делаете красные квадраты как можно ближе к предопределённым зелёным кругам.
Пришло время реализовать линейную регрессию в Python. Всё, что вам нужно, – подходящие пакеты, функции и классы.
Пакеты Python для линейной регрессии
NumPy – фундаментальный научный пакет для быстрых операций над одномерными и многомерными массивами. Он облегчает математическую рутину и, конечно, находится в open-source.
Незнакомы с NumPy? Начните с официального гайда.
Пакет scikit-learn – это библиотека, широко используемая в машинном обучении. Она предоставляет значения для данных предварительной обработки, уменьшает размерность, реализует регрессию, классификацию, кластеризацию и т. д. Находится в open-source, как и NumPy.
Начните знакомство с линейными моделями и работой пакета на сайте scikit-learn.
Простая линейная регрессия со scikit-learn
Начнём с простейшего случая линейной регрессии.
Следуйте пяти шагам реализации линейной регрессии:
- Импортируйте необходимые пакеты и классы.
- Предоставьте данные для работы и преобразования.
- Создайте модель регрессии и приспособьте к существующим данным.
- Проверьте результаты совмещения и удовлетворительность модели.
- Примените модель для прогнозов.
Это общие шаги для большинства подходов и реализаций регрессии.
Шаг 1: Импортируйте пакеты и классы
Первым шагом импортируем пакет NumPy и класс LinearRegressionиз sklearn.linear_model:
import numpy as np from sklearn.linear_model import LinearRegression
Теперь у вас есть весь функционал для реализации линейной регрессии.
Фундаментальный тип данных NumPy – это тип массива numpy.ndarray. Далее под массивом подразумеваются все экземпляры типа numpy.ndarray.
Класс sklearn.linear_model.LinearRegression используем для линейной регрессии и прогнозов.
Шаг 2 : Предоставьте данные
Вторым шагом определите данные, с которыми предстоит работать. Входы (регрессоры, x) и выход (предиктор, y) должны быть массивами (экземпляры класса numpy.ndarray) или похожими объектами. Вот простейший способ предоставления данных регрессии:
x = np.array([5, 15, 25, 35, 45, 55]).reshape((-1, 1)) y = np.array([5, 20, 14, 32, 22, 38])
Теперь у вас два массива: вход x и выход y. Вам нужно вызвать .reshape()на x, потому что этот массив должен быть двумерным или более точным – иметь одну колонку и необходимое количество рядов. Это как раз то, что определяет аргумент (-1, 1).
Вот как x и y выглядят теперь:
>>> print(x) [[ 5] [15] [25] [35] [45] [55]] >>> print(y) [ 5 20 14 32 22 38]
Шаг 3: Создайте модель
На этом шаге создайте и приспособьте модель линейной регрессии к существующим данным.
Давайте сделаем экземпляр класса LinearRegression, который представит модель регрессии:
model = LinearRegression()
Эта операция создаёт переменную model в качестве экземпляра LinearRegression. Вы можете предоставить несколько опциональных параметров классу LinearRegression:
- fit_intercept – логический (
Trueпо умолчанию) параметр, который решает, вычислять отрезок b₀ (True) или рассматривать его как равный нулю (False). - normalize – логический (
Falseпо умолчанию) параметр, который решает, нормализовать входные переменные (True) или нет (False). - copy_X – логический (
Trueпо умолчанию) параметр, который решает, копировать (True) или перезаписывать входные переменные (False). - n_jobs – целое или
None(по умолчанию), представляющее количество процессов, задействованных в параллельных вычислениях.Noneозначает отсутствие процессов, при -1 используются все доступные процессоры.
Наш пример использует состояния параметров по умолчанию.
Пришло время задействовать model. Сначала вызовите .fit() на model:
model.fit(x, y)
С помощью .fit() вычисляются оптимальные значение весов b₀ и b₁, используя существующие вход и выход (x и y) в качестве аргументов. Другими словами, .fit() совмещает модель. Она возвращает self — переменную model. Поэтому можно заменить две последние операции на:
model = LinearRegression().fit(x, y)
Эта операция короче и делает то же, что и две предыдущие.
Шаг 4: Получите результаты
После совмещения модели нужно убедиться в удовлетворительности результатов для интерпретации.
Вы можете получить определения (R²) с помощью .score(), вызванной на model:
>>> r_sq = model.score(x, y)
>>> print('coefficient of determination:', r_sq)
coefficient of determination: 0.715875613747954
.score() принимает в качестве аргументов предсказатель x и регрессор y, и возвращает значение R².
model содержит атрибуты .intercept_, который представляет собой коэффициент, и b₀ с .coef_, которые представляют b₁:
>>> print('intercept:', model.intercept_)
intercept: 5.633333333333329
>>> print('slope:', model.coef_)
slope: [0.54]
Код выше показывает, как получить b₀ и b₁. Заметьте, что .intercept_ – это скаляр, в то время как .coef_ – массив.
Примерное значение b₀ = 5.63 показывает, что ваша модель предсказывает ответ 5.63 при x, равном нулю. Равенство b₁ = 0.54 означает, что предсказанный ответ возрастает до 0.54 при x, увеличенным на единицу.
Заметьте, что вы можете предоставить y как двумерный массив. Тогда результаты не будут отличаться:
>>> new_model = LinearRegression().fit(x, y.reshape((-1, 1)))
>>> print('intercept:', new_model.intercept_)
intercept: [5.63333333]
>>> print('slope:', new_model.coef_)
slope: [[0.54]]
Как вы видите, пример похож на предыдущий, но в данном случае .intercept_ – одномерный массив с единственным элементом b₀, и .coef_ – двумерный массив с единственным элементом b₁.
Шаг 5: Предскажите ответ
Когда вас устроит ваша модель, вы можете использовать её для прогнозов с текущими или другими данными.
Получите предсказанный ответ, используя .predict():
>>> y_pred = model.predict(x)
>>> print('predicted response:', y_pred, sep='n')
predicted response:
[ 8.33333333 13.73333333 19.13333333 24.53333333 29.93333333 35.33333333]
Применяя .predict(), вы передаёте регрессор в качестве аргумента и получаете соответствующий предсказанный ответ.
Вот почти идентичный способ предсказать ответ:
>>> y_pred = model.intercept_ + model.coef_ * x
>>> print('predicted response:', y_pred, sep='n')
predicted response:
[[ 8.33333333]
[13.73333333]
[19.13333333]
[24.53333333]
[29.93333333]
[35.33333333]]
В этом случае вы умножаете каждый элемент массива x с помощью model.coef_ и добавляете model.intercept_ в ваш продукт.
Вывод отличается от предыдущего примера количеством измерений. Теперь предсказанный ответ – это двумерный массив, в отличии от предыдущего случая, в котором он одномерный.
Измените количество измерений x до одного, и увидите одинаковый результат. Для этого замените x на x.reshape(-1), x.flatten() или x.ravel() при умножении с помощью model.coef_.
На практике модель регрессии часто используется для прогнозов. Это значит, что вы можете использовать приспособленные модели для вычисления выходов на базе других, новых входов:
>>> x_new = np.arange(5).reshape((-1, 1)) >>> print(x_new) [[0] [1] [2] [3] [4]] >>> y_new = model.predict(x_new) >>> print(y_new) [5.63333333 6.17333333 6.71333333 7.25333333 7.79333333]
Здесь .predict() применяется на новом регрессоре x_new и приводит к ответу y_new. Этот пример удобно использует arange() из NumPy для генерации массива с элементами от 0 (включительно) до 5 (исключительно) – 0, 1, 2, 3, и 4.
О LinearRegression вы узнаете больше из официальной документации.
Теперь у вас есть своя модель линейной регрессии!
Источник
Нравится Data Science? Другие материалы по теме:
- 6 советов, которые спасут специалиста Data Science
- Как изучать Data Science в 2019: ответы на частые вопросы
- Схема успешного развития data-scientist специалиста в 2019 году
Предыдущий пост см. здесь.
Регрессия
Хотя, возможно, и полезно знать, что две переменные коррелируют, мы не можем использовать лишь одну эту информацию для предсказания веса олимпийских пловцов при наличии данных об их росте или наоборот. При установлении корреляции мы измерили силу и знак связи, но не наклон, т.е. угловой коэффициент. Для генерирования предсказания необходимо знать ожидаемый темп изменения одной переменной при заданном единичном изменении в другой.
Мы хотели бы вывести уравнение, связывающее конкретную величину одной переменной, так называемой независимой переменной, с ожидаемым значением другой, зависимой переменной. Например, если наше линейное уравнение предсказывает вес при заданном росте, то рост является нашей независимой переменной, а вес — зависимой.
Описываемые этими уравнениями линии называются линиями регрессии. Этот Термин был введен британским эрудитом 19-ого века сэром Фрэнсисом Гэлтоном. Он и его студент Карл Пирсон, который вывел коэффициент корреляции, в 19-ом веке разработали большое количество методов, применяемых для изучения линейных связей, которые коллективно стали известны как методы регрессионного анализа.
Вспомним, что из корреляции не следует причинная обусловленность, причем термины «зависимый» и «независимый» не означают никакой неявной причинной обусловленности. Они представляют собой всего лишь имена для входных и выходных математических значений. Классическим примером является крайне положительная корреляция между числом отправленных на тушение пожара пожарных машин и нанесенным пожаром ущербом. Безусловно, отправка пожарных машин на тушение пожара сама по себе не наносит ущерб. Никто не будет советовать сократить число машин, отправляемых на тушение пожара, как способ уменьшения ущерба. В подобных ситуациях мы должны искать дополнительную переменную, которая была бы связана с другими переменными причинной связью и объясняла корреляцию между ними. В данном примере это может быть размер пожара. Такие скрытые причины называются спутывающими переменными, потому что они искажают нашу возможность определять связь между зависимыми переменными.
Линейные уравнения
Две переменные, которые мы можем обозначить как x и y, могут быть связаны друг с другом строго или нестрого. Самая простая связь между независимой переменной x и зависимой переменной y является прямолинейной, которая выражается следующей формулой:
Здесь значения параметров a и b определяют соответственно точную высоту и крутизну прямой. Параметр a называется пересечением с вертикальной осью или константой, а b — градиентом, наклоном линии или угловым коэффициентом. Например, в соотнесенности между температурными шкалами по Цельсию и по Фаренгейту a = 32 и b = 1.8. Подставив в наше уравнение значения a и b, получим:
Для вычисления 10°С по Фаренгейту мы вместо x подставляем 10:
Таким образом, наше уравнение сообщает, что 10°С равно 50°F, и это действительно так. Используя Python и возможности визуализации pandas, мы можем легко написать функцию, которая переводит градусы из Цельсия в градусы Фаренгейта и выводит результат на график:
'''Функция перевода из градусов Цельсия в градусы Фаренгейта'''
celsius_to_fahrenheit = lambda x: 32 + (x * 1.8)
def ex_3_11():
'''График линейной зависимости температурных шкал'''
s = pd.Series(range(-10,40))
df = pd.DataFrame({'C':s, 'F':s.map(celsius_to_fahrenheit)})
df.plot('C', 'F', legend=False, grid=True)
plt.xlabel('Градусы Цельсия')
plt.ylabel('Градусы Фаренгейта')
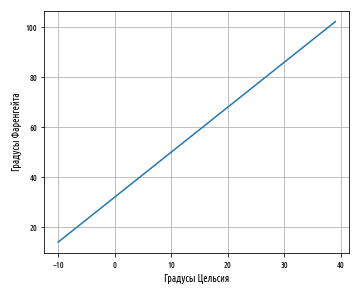
plt.show()Этот пример сгенерирует следующий ниже линейный график:
Обратите внимание, как синяя линия пересекает 0 на шкале Цельсия при величине 32 на шкале Фаренгейта. Пересечение a — это значение y, при котором значение x равно 0.
Наклон линии с неким угловым коэффициентом определяется параметром b; в этом уравнении его значение близко к 2. Как видно, диапазон шкалы Фаренгейта почти вдвое шире диапазона шкалы Цельсия. Другими словами, прямая устремляется вверх по вертикали почти вдвое быстрее, чем по горизонтали.
Остатки
К сожалению, немногие связи столь же чистые, как перевод между градусами Цельсия и Фаренгейта. Прямолинейное уравнение редко позволяет нам определять y строго в терминах x. Как правило, будет иметься ошибка, и, таким образом, уравнение примет следующий вид:
Здесь, ε — это ошибка или остаточный член, обозначающий расхождение между значением, вычисленным параметрами a и b для данного значения x и фактическим значением y. Если предсказанное значение y — это ŷ, то ошибка — это разность между обоими:
Такая ошибка называется остатком. Остаток может возникать из-за случайных факторов, таких как погрешность измерения, либо неслучайных факторов, которые неизвестны. Например, если мы пытаемся предсказать вес как функцию роста, то неизвестные факторы могут состоять из диеты, уровня физической подготовки и типа телосложения (либо просто эффекта округления до самого близкого килограмма).
Если для a и b мы выберем неидеальные параметры, то остаток для каждого x будет больше, чем нужно. Из этого следует, что параметры, которые мы бы хотели найти, должны минимизировать остатки во всех значениях x и y.
Обычные наименьшие квадраты
Для того, чтобы оптимизировать параметры линейной модели, мы бы хотели создать функцию стоимости, так называемую функцией потери, которая количественно выражает то, насколько близко наши предсказания укладывается в данные. Мы не можем просто взять и просуммировать положительные и отрицательные остатки, потому что даже самые большие остатки обнулят друг друга, если их знаки противоположны.
Прежде, чем вычислить сумму, мы можем возвести значения в квадрат, чтобы положительные и отрицательные остатки учитывались в стоимости. Возведение в квадрат также создает эффект наложения большего штрафа на большие ошибки, чем на меньшие ошибки, но не настолько много, чтобы самый большой остаток всегда доминировал.
Выражаясь в терминах задачи оптимизации, мы стремимся выявить коэффициенты, которые минимизируют сумму квадратов остатков. Этот метод называется обычными наименьшими квадратами, от англ. Ordinary Least Squares (OLS), и формула для вычисления наклона линии регрессии по указанному методу выглядит так:
Хотя она выглядит сложнее предыдущих уравнений, на самом деле, эта формула представляет собой всего лишь сумму квадратов остатков, деленную на сумму квадратов отклонений от среднего значения. В данном уравнении используется несколько членов из других уравнений, которые уже рассматривались, и мы можем его упростить, приведя к следующему виду:
Пересечение (a) — это член, позволяющий прямой с заданным наклоном проходить через среднее значение X и Y:
Значения a и b — это коэффициенты, получаемые в результате оценки методом обычных наименьших квадратов.
Наклон и пересечение
Мы уже рассматривали функции covariance, variance и mean, которые нужны для вычисления наклона прямой и точки пересечения для данных роста и веса пловцов. Поэтому вычисление наклона и пересечения имеют тривиальный вид:
def slope(xs, ys):
'''Вычисление наклона линии (углового коэффициента)'''
return xs.cov(ys) / xs.var()
def intercept(xs, ys):
'''Вычисление точки пересечения (с осью Y)'''
return ys.mean() - (xs.mean() * slope(xs, ys))
def ex_3_12():
'''Вычисление пересечения и наклона (углового коэффициента)
на примере данных роста и веса'''
df = swimmer_data()
X = df['Рост, см']
y = df['Вес'].apply(np.log)
a = intercept(X, y)
b = slope(X, y)
print('Пересечение: %f, наклон: %f' % (a,b))Пересечение: 1.691033, наклон: 0.014296В результате будет получен наклон приблизительно 0.0143 и пересечение приблизительно 1.6910.
Интерпретация
Величина пересечения — это значение зависимой переменной (логарифмический вес), когда независимая переменная (рост) равна нулю. Для получения этого значения в килограммах мы можем воспользоваться функцией np.exp, обратной для функции np.log. Наша модель дает основания предполагать, что вероятнее всего вес олимпийского пловца с нулевым ростом будет 5.42 кг. Разумеется, такое предположение лишено всякого смысла, к тому же экстраполяция за пределы границ тренировочных данных является не самым разумным решением.
Величина наклона показывает, насколько y изменяется для каждой единицы изменения в x. Модель исходит из того, что каждый дополнительный сантиметр роста прибавляет в среднем 1.014 кг. веса олимпийских пловцов. Поскольку наша модель основывается на данных о всех олимпийских пловцах, она представляет собой усредненный эффект от увеличения в росте на единицу без учета любого другого фактора, такого как возраст, пол или тип телосложения.
Визуализация
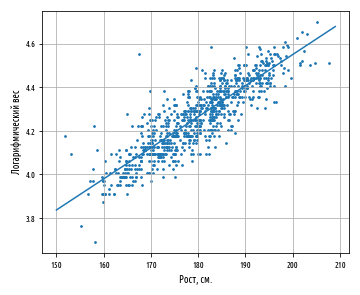
Результат линейного уравнения можно визуализировать при помощи имплементированной ранее функции regression_line и простой функции от x, которая вычисляет ŷ на основе коэффициентов a и b.
'''Функция линии регрессии'''
regression_line = lambda a, b: lambda x: a + (b * x) # вызовы fn(a,b)(x)
def ex_3_13():
'''Визуализация линейного уравнения
на примере данных роста и веса'''
df = swimmer_data()
X = df['Рост, см'].apply( jitter(0.5) )
y = df['Вес'].apply(np.log)
a, b = intercept(X, y), slope(X, y)
ax = pd.DataFrame(np.array([X, y]).T).plot.scatter(0, 1, s=7)
s = pd.Series(range(150,210))
df = pd.DataFrame( {0:s, 1:s.map(regression_line(a, b))} )
df.plot(0, 1, legend=False, grid=True, ax=ax)
plt.xlabel('Рост, см.')
plt.ylabel('Логарифмический вес')
plt.show()Функция regression_line возвращает функцию от x, которая вычисляет a + bx.
Указанная функция может также использоваться для вычисления каждого остатка, показывая степень, с которой наша оценка ŷ отклоняется от каждого измеренного значения y.
def residuals(a, b, xs, ys):
'''Вычисление остатков'''
estimate = regression_line(a, b) # частичное применение
return pd.Series( map(lambda x, y: y - estimate(x), xs, ys) )
constantly = lambda x: 0
def ex_3_14():
'''Построение графика остатков на примере данных роста и веса'''
df = swimmer_data()
X = df['Рост, см'].apply( jitter(0.5) )
y = df['Вес'].apply(np.log)
a, b = intercept(X, y), slope(X, y)
y = residuals(a, b, X, y)
ax = pd.DataFrame(np.array([X, y]).T).plot.scatter(0, 1, s=12)
s = pd.Series(range(150,210))
df = pd.DataFrame( {0:s, 1:s.map(constantly)} )
df.plot(0, 1, legend=False, grid=True, ax=ax)
plt.xlabel('Рост, см.')
plt.ylabel('Остатки')
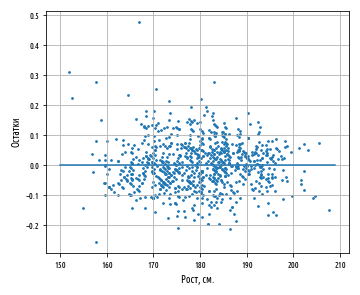
plt.show()График остатков — это график, который показывает остатки на оси Y и независимую переменную на оси X. Если точки на графике остатков разбросаны произвольно по обе стороны от горизонтальной оси, то линейная модель хорошо подогнана к нашим данным:
За исключением нескольких выбросов на левой стороне графика, график остатков, по-видимому, показывает, что линейная модель хорошо подогнана к данным. Построение графика остатков имеет важное значение для получения подтверждения, что линейная модель применима. В линейной модели используются некоторые допущения относительно данных, которые при их нарушении делают не валидными модели, которые вы строите.
Допущения
Первостепенное допущение линейной регрессии состоит в том, что, безусловно, существует линейная зависимость между зависимой и независимой переменной. Кроме того, остатки не должны коррелировать друг с другом либо с независимой переменной. Другими словами, мы ожидаем, что ошибки будут иметь нулевое среднее и постоянную дисперсию по отношению к зависимой и независимой переменной. График остатков позволяет быстро устанавливать, является ли это действительно так.
Левая сторона нашего графика имеет более крупные значения остатков, чем правая сторона. Это соответствует большей дисперсии веса среди более низкорослых спортсменов. Когда дисперсия одной переменной изменяется относительно другой, говорят, что переменные гетероскедастичны, т.е. их дисперсия неоднородна. Этот факт представляет в регрессионном анализе проблему, потому что делает не валидным допущение в том, что модельные ошибки не коррелируют и нормально распределены, и что их дисперсии не варьируются вместе с моделируемыми эффектами.
Гетероскедастичность остатков здесь довольно мала и особо не должна повлиять на качество нашей модели. Если дисперсия на левой стороне графика была бы более выраженной, то она привела бы к неправильной оценке дисперсии методом наименьших квадратов, что в свою очередь повлияло бы на выводы, которые мы делаем, основываясь на стандартной ошибке.
Качество подгонки и R-квадрат
Хотя из графика остатков видно, что линейная модель хорошо вписывается в данные, т.е. хорошо к ним подогнана, было бы желательно количественно измерить качество этой подгонки. Коэффициент детерминации R2, или R-квадрат, варьируется в интервале между 0 и 1 и обозначает объяснительную мощность линейной регрессионной модели. Он вычисляет объясненную долю изменчивости в зависимой переменной.
Обычно, чем ближе R2 к 1, тем лучше линия регрессии подогнана к точкам данных и больше изменчивости в Y объясняется независимой переменной X. R2 можно вычислить с помощью следующей ниже формулы:
Здесь var(ε) — это дисперсия остатков и var(Y) — дисперсия в Y. В целях понимания смысла этой формулы допустим, что вы пытаетесь угадать чей-то вес. Если вам больше ничего неизвестно об испытуемых, то наилучшей стратегией будет угадывать среднее значение весовых данных внутри популяции в целом. Таким путем средневзвешенная квадратичная ошибка вашей догадки в сравнении с истинным весом будет var(Y), т.е. дисперсией данных веса в популяции.
Но если бы я сообщил вам их рост, то в соответствии с регрессионной моделью вы бы предположили, что a + bx. В этом случае вашей средневзвешенной квадратичной ошибкой было бы или дисперсия остатков модели.
Компонент формулы var(ε)/var(Y) — это соотношение средневзвешенной квадратичной ошибки с объяснительной переменной и без нее, т. е. доля изменчивости, оставленная моделью без объяснения. Дополнение R2 до единицы — это доля изменчивости, объясненная моделью.
Как и в случае с r, низкий R2 не означает, что две переменные не коррелированы. Просто может оказаться, что их связь не является линейной.
Значение R2 описывает качество подгонки линии регрессии к данным. Оптимально подогнанная линия — это линия, которая минимизирует значение R2. По мере удаления либо приближения от своих оптимальных значений R2 всегда будет расти.
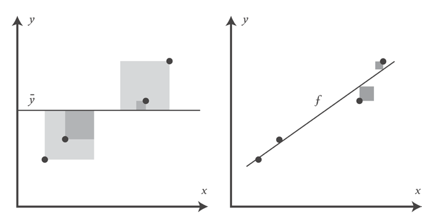
Левый график показывает дисперсию модели, которая всегда угадывает среднее значение для , правый же показывает меньшие по размеру квадраты, связанные с остатками, которые остались необъясненными моделью f. С чисто геометрической точки зрения можно увидеть, как модель объяснила большинство дисперсии в y. Приведенный ниже пример вычисляет R2 путем деления дисперсии остатков на дисперсию значений y:
def r_squared(a, b, xs, ys):
'''Рассчитать коэффициент детерминации (R-квадрат)'''
r_var = residuals(a, b, xs, ys).var()
y_var = ys.var()
return 1 - (r_var / y_var)
def ex_3_15():
'''Рассчитать коэффициент R-квадрат
на примере данных роста и веса'''
df = swimmer_data()
X = df['Рост, см'].apply( jitter(0.5) )
y = df['Вес'].apply(np.log)
a, b = intercept(X, y), slope(X, y)
return r_squared(a, b, X, y)0.75268223613272323В результате получим значение 0.753. Другими словами, более 75% дисперсии веса пловцов, выступавших на Олимпийских играх 2012 г., можно объяснить ростом.
В случае простой регрессионной модели (с одной независимой переменной), связь между коэффициентом детерминации R2 и коэффициентом корреляции r является прямолинейной:
Коэффициент корреляции r может означать, что половина изменчивости в переменной Y объясняется переменной X, но фактически R2 составит 0.52, т.е. 0.25.
Множественная линейная регрессия
Пока что в этой серии постов мы видели, как строится линия регрессии с одной независимой переменной. Однако, нередко желательно построить модель с несколькими независимыми переменными. Такая модель называется множественной линейной регрессией.
Каждой независимой переменной потребуется свой собственный коэффициент. Вместо того, чтобы для каждой из них пытаться подобрать букву в алфавите, зададим новую переменную β (бета), которая будет содержать все наши коэффициенты:
Такая модель эквивалентна двухфакторной линейно-регрессионной модели, где β1 = a и β2 = b при условии, что x1 всегда гарантированно равен 1, вследствие чего β1 — это всегда константная составляющая, которая представляет наше пересечение, при этом x1 называется (постоянным) смещением уравнения регрессии, или членом смещения.
Обобщив линейное уравнение в терминах β, его легко расширить на столько коэффициентов, насколько нам нужно:
Каждое значение от x1 до xn соответствует независимой переменной, которая могла бы объяснить значение y. Каждое значение от β1 до βn соответствует коэффициенту, который устанавливает относительный вклад независимой переменной.
Простая линейная регрессия преследовала цель объяснить вес исключительно с точки зрения роста, однако объяснить вес людей помогает много других факторов: их возраст, пол, питание, тип телосложения. Мы располагаем сведениями о возрасте олимпийских пловцов, поэтому мы смогли бы построить модель, которая учитывает и эти дополнительные данные.
До настоящего момента мы предоставляли независимую переменную в виде одной последовательности значений, однако при наличии двух и более параметров нам нужно предоставлять несколько значений для каждого x. Мы можем воспользоваться функциональностью библиотеки pandas, чтобы выбрать два и более столбцов и управлять каждым как списком, но есть способ получше: матрицы.
Примеры исходного кода для этого поста находятся в моем репо на Github. Все исходные данные взяты в репозитории автора книги.
Темой следующего поста, поста №3, будут матричные операции, нормальное уравнение и коллинеарность.
Определение линейной зависимости
Линейная связь описывает отношение между двумя различными переменными — x и y в виде прямой линии на графике. При представлении линейной зависимости через уравнение значение y выводится через значение x, отражая их корреляцию.
Линейные отношения применяются в повседневных ситуациях, когда один фактор зависит от другого, например, повышение цены на товары снижает спрос на них. В любом случае для получения результата учитываются только две переменные.
Оглавление
- Определение линейной зависимости
- Что такое линейная зависимость?
- Уравнение линейной связи с графиком
- Линейная функция/уравнение
- Форма пересечения наклона
- Стандартная/общая форма
- Примеры
- Линейные и нелинейные отношения
- Графическое представление
- Изменение переменных
- Области применения
- Рекомендуемые статьи
- Линейная связь — это связь, в которой две переменные имеют прямую связь, что означает, что если значение x изменяется, y также должно изменяться в той же пропорции.
- Это статистический метод, позволяющий получить прямые или коррелированные значения двух переменных с помощью графика или математической формулы.
- Количество переменных, рассматриваемых в линейном уравнении, никогда не превышает двух.
- Корреляция двух переменных в повседневной жизни может быть понята с помощью этой концепции.
Что такое линейная зависимость?
Он лучше всего описывает взаимосвязь между двумя переменными (независимой и зависимой), обычно представленными x и y. В области статистики это одна из самых простых концепций для понимания.
Для линейной зависимости переменные должны образовывать прямую линию на графике каждый раз, когда значения x и y складываются вместе. С помощью этого метода можно понять, как различия между двумя факторами могут повлиять на результат и как они соотносятся друг с другом.
Возьмем реальный пример продуктового магазина, где его бюджет является независимой переменной. Независимая переменная. цель), которая измеряется в математическом, статистическом или финансовом моделировании. Читать далее, а товары, подлежащие хранению, являются зависимой переменной. Предположим, что бюджет составляет 2000 долларов США, а продуктовые товары включают 12 брендов закусок (1–2 доллара за упаковку), 12 брендов прохладительных напитков (2–4 доллара за бутылку), 5 брендов хлопьев (5–7 долларов за упаковку) и 40 брендов средств личной гигиены. ($3-$30 за продукт). Из-за бюджетных ограничений и различных цен покупка большего количества одного товара потребует покупки меньшего количества другого.
Уравнение линейной связи с графиком
Будь то графически или математически, значение y зависит от x, что дает прямую линию на графике. Вот краткая формула для понимания линейной корреляции. КорреляцияКорреляция — это статистическая мера между двумя переменными, которая определяется как изменение одной переменной, соответствующее изменению другой. Он рассчитывается как (x(i)-среднее(x))*(y(i)-среднее(y)) / ((x(i)-среднее(x))2 * (y(i)-среднее( y))2. перевод между переменными.
у = мх + б
В формуле m обозначает уклон. В то же время b является точкой пересечения оси Y или точкой на графике, пересекающей ось y с координатой x, равной нулю. Если значения m, x и b заданы, можно легко получить значение y. Можно графически изобразить то же самое, чтобы показать линейную зависимость. Давайте поймем процесс, когда значения для переменных x и y предполагаются следующим образом в сумме ниже:
- х = 2, 4, 6, 8
- у = 7, 13, 19, 25
Чтобы вычислить m, начните с поиска разности между значениями x и y, а затем представите их в виде дроби.
Следовательно, m = y2 – y1/x2 – x1
Помещая значения из значений x и y в приведенное выше уравнение,
мы получаем,
- м = 13-7/4-2
- м = 6/2
- м = 3
Следующий шаг — найти гипотетическое число (b), которое нужно добавить или вычесть в формуле, чтобы получить значение y. Как таковой,
у = мх + б
- у = 3*2 + 1
- у = 7.
Аналогично, подсчитав остальные точки, получим следующий график.
График линейной зависимости будет выглядеть так:
Практическим примером линейного уравнения может быть приготовление домашней пиццы. Здесь две переменные — это количество людей, которых нужно обслужить (постоянная или независимая переменная), и ингредиенты для пиццы (зависимая переменная). Например, предположим, что есть рецепт пиццы на четверых, но его едят только два человека. Чтобы вместить двух человек, сокращение количества ингредиентов наполовину уменьшит производительность вдвое.
Линейные и нелинейные отношения
Хотя линейные и нелинейные отношения описывают отношения между двумя переменными, обе они различаются по своему графическому представлению и тому, как переменные коррелируют.
Графическое представление
Линейная связь всегда будет отображать на графике прямую линию, отображающую отношения между двумя переменными. С другой стороны, нелинейная зависимость может создать кривую линию на графике с той же целью.

В линейной зависимости изменение независимой переменной изменит зависимую переменную. Но это не относится к нелинейным отношениям, поскольку любые изменения одной переменной не повлияют на другую.
Области применения
Линейная зависимость лучше всего описывает ситуации, когда переменные взаимозависимы, например, физические упражнения и потеря веса. Здесь упражнения x раз в день значительно уменьшат любое количество веса.
Не существует линейной связи между переменными в нелинейной зависимости, такой как эффективность лекарства и продолжительность приема. Это связано с тем, что может быть несколько промежуточных факторов, влияющих на эффективность препарата, например:
- Если пациент принимает лекарства вовремя?
- Было ли оно принято в установленном порядке?
- Посещал ли пациент врача для периодического осмотра, как это было предложено в рецепте?
Следовательно, эффективность препарата определяется несколькими факторами, а не только продолжительностью приема, что делает зависимость нелинейной. Было проведено множество исследований, чтобы оценить жизнеспособность изучения ситуаций с точки зрения линейной корреляции. Этот Гарвардское исследование сосредоточил внимание на некоторых проблемных областях в этом отношении. Он также говорил о том, как много ситуаций неизбежно нелинейны.
Рекомендуемые статьи
В этом исчерпывающем руководстве по линейной зависимости обсуждались уравнения, примеры и отличия от нелинейная связь, вместе с ключевыми выводами. Чтобы узнать больше о его использовании в финансах, прочитайте следующие статьи:
- Регрессия
- Линейная регрессия в Excel
- Нелинейная регрессия в Excel
Зависимость переменной и от переменной с записывается формулой и = 2с-3.
Зависимость одной переменной у от другой х, при которой каждому значению переменной х из определенного множества D соответствует единственное значение переменной у, называется функциональной зависимостью или функцией переменной X.
Если переменная у является функцией переменной х, то переменную х называют независимой переменной или аргументом, а переменную у — зависимой переменной.
Множество тех значений, которые может принимать аргумент функции, называется областью определения функции, а множество тех значений, которые может получать зависимая переменная,— областью значений функции.
Например, площадь S квадрата является функцией длины а его стороны. Областью определения этой функции является множество положительных действительных чисел.
Масса т медной шпильки является функцией ее объема V. Область определения этой функции — также множество положительных действительных чисел.
Переменная и из примера 3 является функцией переменной с. Ее область определения — множество всех действительных чисел.
Функции могут задаваться различными способами. Часто это делают с помощью формулы. Мы уже указывали на функциональные зависимости, заданные формулами
S = a2, т = 8,96V, с = 2u — 3.
Формула дает возможность для любого значения аргумента из области определения найти соответствующее значение функции.
Пример. Найдем значения функции S для значений аргумента а, равных 7 и 32:
если а = 7, то S = 72 = 49; если а = 32, то S = 322 = 1024.
Результаты подобных вычислений удобно оформлять таблицей. Составим таблицу значений функции S = а2 для значений а из промежутка [0; 2] с шагом 0,2.
|
а |
0 |
0,2 |
0,4 |
0,6 |
0,8 |
1 |
1,2 |
1,4 |
1,6 |
1,8 |
2 |
|
S |
0 |
0,04 |
0,16 |
0,36 |
0,64 |
1 |
1,44 |
1,96 |
2,56 |
3,24 |
4 |
Задание функции формулой позволяет находить значения аргумента, которым соответствует данное значение функции.
Простая линейная регрессия — это статистический метод, который можно использовать для понимания связи между двумя переменными, x и y.
Одна переменная x известна как предикторная переменная .
Другая переменная, y , известна как переменная ответа .
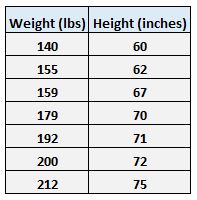
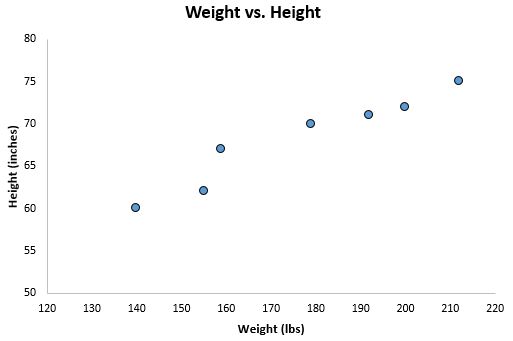
Например, предположим, что у нас есть следующий набор данных с весом и ростом семи человек:
Пусть вес будет предикторной переменной, а рост — переменной отклика.
Если мы изобразим эти две переменные с помощью диаграммы рассеяния с весом по оси x и высотой по оси y, вот как это будет выглядеть:
Предположим, нам интересно понять взаимосвязь между весом и ростом. На диаграмме рассеяния мы ясно видим, что по мере увеличения веса рост также имеет тенденцию к увеличению, но для фактической количественной оценки этой взаимосвязи между весом и ростом нам нужно использовать линейную регрессию.
Используя линейную регрессию, мы можем найти линию, которая лучше всего «соответствует» нашим данным. Эта линия известна как линия регрессии наименьших квадратов, и ее можно использовать, чтобы помочь нам понять взаимосвязь между весом и ростом. Обычно вы должны использовать программное обеспечение, такое как Microsoft Excel, SPSS или графический калькулятор, чтобы найти уравнение для этой линии.
Формула линии наилучшего соответствия записывается так:
ŷ = б 0 + б 1 х
где ŷ — прогнозируемое значение переменной отклика, b 0 — точка пересечения с осью y, b 1 — коэффициент регрессии, а x — значение переменной-предиктора.
Связанный: 4 примера использования линейной регрессии в реальной жизни
Поиск «Линии наилучшего соответствия»
Для этого примера мы можем просто подключить наши данные к калькулятору линейной регрессии Statology и нажать « Рассчитать »:
Калькулятор автоматически находит линию регрессии методом наименьших квадратов :
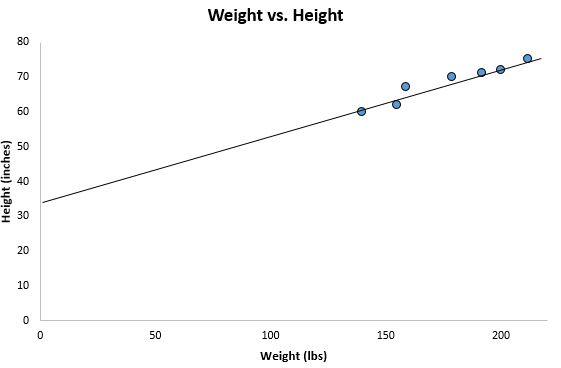
ŷ = 32,7830 + 0,2001x
Если мы уменьшим масштаб нашей диаграммы рассеяния и добавим эту линию на диаграмму, вот как это будет выглядеть:
Обратите внимание, как наши точки данных близко разбросаны вокруг этой линии. Это потому, что эта линия регрессии методом наименьших квадратов лучше всего подходит для наших данных из всех возможных линий, которые мы могли бы нарисовать.
Как интерпретировать линию регрессии методом наименьших квадратов
Вот как интерпретировать эту линию регрессии наименьших квадратов: ŷ = 32,7830 + 0,2001x
б0 = 32,7830.Это означает, что когда предикторная переменная веса равна нулю фунтов, прогнозируемый рост составляет 32,7830 дюйма. Иногда может быть полезно знать значение b 0 , но в этом конкретном примере на самом деле нет смысла интерпретировать b 0 , поскольку человек не может весить ноль фунтов.
б 1 = 0,2001.Это означает, что увеличение x на одну единицу связано с увеличением y на 0,2001 единицы. В этом случае увеличение веса на один фунт связано с увеличением роста на 0,2001 дюйма.
Как использовать линию регрессии наименьших квадратов
Используя эту линию регрессии наименьших квадратов, мы можем ответить на такие вопросы, как:
Какого роста мы ожидаем от человека, который весит 170 фунтов?
Чтобы ответить на этот вопрос, мы можем просто подставить 170 в нашу линию регрессии для x и найти y:
ŷ = 32,7830 + 0,2001 (170) = 66,8 дюйма
Какого роста мы ожидаем от человека, который весит 150 фунтов?
Чтобы ответить на этот вопрос, мы можем подставить 150 в нашу линию регрессии для x и найти y:
ŷ = 32,7830 + 0,2001 (150) = 62,798 дюйма
Предупреждение. При использовании уравнения регрессии для ответа на подобные вопросы убедитесь, что вы используете только те значения переменной-предиктора, которые находятся в пределах диапазона переменной-предиктора в исходном наборе данных, который мы использовали для создания линии регрессии методом наименьших квадратов. Например, вес в нашем наборе данных варьировался от 140 до 212 фунтов, поэтому имеет смысл отвечать на вопросы о прогнозируемом росте только тогда, когда вес составляет от 140 до 212 фунтов.
Коэффициент детерминации
Одним из способов измерения того, насколько хорошо линия регрессии наименьших квадратов «соответствует» данным, является использование коэффициента детерминации , обозначаемого как R 2 .
Коэффициент детерминации — это доля дисперсии переменной отклика, которая может быть объяснена предикторной переменной.
Коэффициент детерминации может варьироваться от 0 до 1. Значение 0 указывает на то, что переменная отклика вообще не может быть объяснена предикторной переменной. Значение 1 указывает, что переменная отклика может быть полностью объяснена без ошибок с помощью переменной-предиктора.
R 2 между 0 и 1 указывает, насколько хорошо переменная отклика может быть объяснена переменной-предиктором. Например, R 2 , равный 0,2, указывает, что 20% дисперсии переменной отклика можно объяснить переменной-предиктором; R 2 , равное 0,77, указывает, что 77% дисперсии переменной отклика можно объяснить переменной-предиктором.
Обратите внимание, что в нашем предыдущем выводе мы получили значение R2, равное 0,9311 , что указывает на то, что 93,11% изменчивости роста можно объяснить предикторной переменной веса:
Это говорит нам о том, что вес является очень хорошим предиктором роста.
Предположения линейной регрессии
Чтобы результаты модели линейной регрессии были достоверными и надежными, нам необходимо проверить выполнение следующих четырех допущений:
1. Линейная зависимость. Существует линейная зависимость между независимой переменной x и зависимой переменной y.
2. Независимость: Остатки независимы. В частности, нет корреляции между последовательными остатками в данных временных рядов.
3. Гомоскедастичность: остатки имеют постоянную дисперсию на каждом уровне x.
4. Нормальность: остатки модели нормально распределены.
Если одно или несколько из этих предположений нарушаются, то результаты нашей линейной регрессии могут быть ненадежными или даже вводящими в заблуждение.
Обратитесь к этому сообщению для объяснения каждого предположения, как определить, выполняется ли предположение, и что делать, если предположение нарушается.