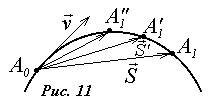
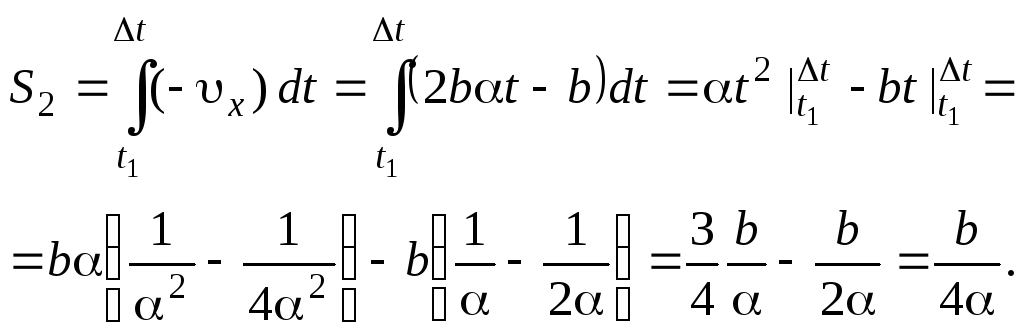Как найти зависимость от времени радиус вектора - Исправление недочетов и поиск решений вместе с Examum.ru

Кинематика
занимается описанием движения без
выяснения его причин.

Материальной
точкой называют физическую модель
такого реального объекта, размерами
которого можно пренебречь в конкретной
задаче.

Прямая
задача кинематики — определить положение
тела в любой момент времени. Если речь
идёт о движении материальной точки, это
означает — определить зависимость
радиус-вектора точки от времени

по известному ускорению
.
Для этого необходимо знать начальные
условия — положение и скорость материальной
точки в начальный момент времени (t = 0).

Существуют
три основных способа описания движения:
векторный, координатный и естественный.

1. Векторный способ

В
этом способе положение материальной
точки задают радиус-вектором
,
проведенным из некоторой неподвижной
точки, называемой началом отсчета.

Рассмотрим
алгоритм решения прямой задачи кинематики
при векторном способе описания движения.

По
известному ускорению материальной
точки, находят скорость точки в
произвольный момент времени

Постоянные
интегрирования определяются, исходя
из начальных условий (см. в примерах).

Определив
,
находят зависимость радиус-вектора от
времени

Если
в задаче требуется определить модуль
скорости тела, то он определяется как:

где

— проекции скорости на оси X,
Y,
Z
соответственно (их также можно называть
составляющими скорости по названным
осям).

Путь,
пройденный телом, определяется из
определения модуля скорости

как
.

Решение задач

1.1.
Положение материальной точки определяется
в момент времени t = 0
радиус-вектором
,
вектором скорости

и постоянным ускорением
,
направленным перпендикулярно скорости
.
Найти временную зависимость радиус-вектора
,
вектора скорости

и модуля скорости точки.

Решение.
Скорость
точки в произвольный момент времени
равна

По
условию задачи
при
t = 0,
следовательно,
.

Поэтому

_{Зависимость

радиус-вектора точки определяется

выражением}

Учитывая,
что по условию
при
t = 0
находим
.
Тогда

Так
как

(рис.1), зависимость от времени модуля
скорости тела определяется выражением

В
разобранной задаче была рассмотрена
прямая задача кинематики — по известному
ускорению и начальным условиям было
найдено местоположение материальной
точки в произвольный момент времени.
Однако, во многих случаях возникает и
обратная задача: по известному закону

определить

и
.
Если прямая задача выполнялась с помощью
математической операции интегрирования,
то обратная требует применения
дифференцирования.

1.2.
Радиус-вектор частицы меняется со
временем по закону
,
где

— постоянный вектор,

— положительная постоянная. Найти:

а)
скорость

и ускорение

частицы в зависимости от времени;

б)
промежуток времени Δt,
по истечении которого частица вернётся
в исходную точку;

в)
путь S,
который она пройдёт при этом.

Решение.
а) По
определению скорость и ускорение в
произвольный момент времени соответственно
равны

б)
По истечении времени Δt
частица
вернется в исходную точку, поэтому
ее радиус-вектор равен нулю:

,
откуда
.

в) Путь, пройденный
частицей, определяется соотношением

Модуль
скорости

— величина всегда положительная. Направим
ось X
вдоль вектора
,
тогда
,

при

и
,

при

и
.

На
промежутке от 0 до t₁:

На
промежутке от t₁
до Δt:

Путь, пройденный
частицей

1.3*.
В момент t = 0
частица вышла из начала координат в
положительном направлении оси
.
Её скорость меняется со временем по
закону
,
где

— начальная скорость,

— некоторая положительная постоянная.
Найти:

а) ускорение и
радиус-вектор;

б)
моменты времени, когда частица проходит
точку, удаленную на расстояние

от начала координат в случае, если
,
где

максимальное удаление точки от начала
отсчета оси
.

Решение.
а)
Продифференцировав

по времени, получим ускорение частицы

Представим
радиус-вектор частицы как

По
условию
при
t = 0,
поэтому

и

б)
Поскольку частица движется вдоль оси
,
то ее положение определяется координатой
,
которая является проекцией вектора
и
равна:

Найдем
максимальную координату
,
приравняв производную

нулю:

и
по условию
.

Покажем,
что найденное значение

действительно является максимумом. Для
этого найдем вторую производную

и сравним ее с нулем

Из
полученного результата видно, что
,
следовательно,

действительно является максимальным
удалением точки от начала отсчета оси
.

Таким
образом, в момент времени

координата частицы равна
,
и частица меняет направление своего
движения на противоположное (рис.2). На
расстоянии

от начала координат частица будет
находиться в моменты времени, когда
,
то есть

Подставив
в это выражение

для определения t,
получим квадратные уравнения

или

Решая уравнения,
получим искомые значения времени

Отметим,
что для существования первых двух корней
необходимо, чтобы
,
то есть
,
что соответствует условию задачи. Один
из полученных корней

является отрицательным и физического
смысла не имеет. Итак, частица проходит
точку, удаленную на расстояние

от начала координат, в момент времени

(до
поворота частицы)

и в моменты времени

(после
поворота частицы).

1.4.
Радиус-вектор меняется со временем по
закону
,

и

— положительные постоянные,

и

— орты осей
X
и Y.
Найти:

а)
уравнение траектории точки y(x);

б)
зависимость от времени скорости
,
ускорения

и модулей этих величин;

в)
зависимость от времени угла

между скоростью и ускорением.

Решение.
а) Спроецируем
вектор

на оси X,
Y
и Z
и получим
зависимости координат от времени

Исключив
из полученной системы уравнений время
,
получим уравнение траектории .

Из
которого видно, что траектория движения
— парабола. График функции y(x)
в плоскости XY
схематично изображен на рис.3.

б) По определению

то есть

, .

поэтому

, .

Модули скорости
и ускорения равны

в)
Как видно из рис.3, угол

между скоростью и ускорением равен в
данной задаче углу между скоростью

и её составляющей по оси Y

Откуда

В
данной задаче угол

между векторами
,
ускорения

можно определить другим, более
универсальным способом, используя
свойство скалярного произведения двух
векторов:

Из которого следует,
что

Откуда

Учитывая,
что согласно вспомогательному
тригонометрическому тождеству
,
приведем полученный результат к виду

что
совпадает с результатом полученным
ранее.

Однако,
этот универсальный способ часто
оказывается достаточно громоздким.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Содержание книги

Предыдующая страница

§2. Кинематическое описание механического движения материальной точки

2.5 Векторные характеристики движения материальной точки

Положение точки в пространстве можно задать с помощью вектора, соединяющего начало координат с данной точкой — такой вектор называется радиус-вектором точки, мы будем обозначать его символом (~vec r). Очевидно, что координаты этого вектора, совпадают с координатами точки (x,y,z) , поэтому мы оставим эти обозначения и для координат радиус-вектора.

Если тело изменяет свое положение в пространстве, то его радиус-вектор будет изменяться с течением времени, то есть станет функцией времени. Зависимость радиус-вектора от времени (~vec r(t)) будет являться законом движения.

Изменение положения в векторной форме удобно описывать с помощью вектора перемещения (~vec S) — вектора, соединяющего начальное (~vec r_0) и конечное положение (~vec r_1) движущейся точки. Вектор перемещения равен разности радиус-векторов конечного и начального положения (см. рис.10)

(~vec S = vec r_1 — vec r_0) . (1)

Отношение изменения радиус-вектора к промежутку времени, за который это изменение произошло, называется средним вектором скорости (или просто средней скоростью):

(~vec upsilon_{cp}= frac{Delta vec r}{Delta t}) . (2)

Если промежуток времени, за который измеряется изменения радиус-вектора, сделать очень малым (предельно малым), то вектор средней скорости перейдет в вектор мгновенной скорости

(~vec upsilon = frac{Delta vec r}{Delta t}) , при Δt → 0 . (3)

Это определение является наиболее общим определением скорости. Заметим, что при постоянном векторе скорости тела его траекторией обязательно является прямая линия.

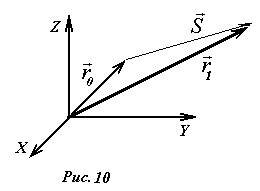
Выясним, как направлен вектор мгновенной скорости по отношению к произвольной траектории движения материальной точки. Пусть тело (которое мы считаем материальной точкой) переместилось за промежуток времени Δt по некоторой траектории из точки A₀ в точку A₁ (см. рис.11). Вектор средней скорости совпадает по направлению с вектором перемещения (~vec S) . При уменьшении рассматриваемого промежутка времени Δt точка A₁ будет находиться все ближе к точке A₀, соответственно, будет изменяться и вектор перемещения, при Δt → 0 вектор перемещения будет стремиться к касательной к траектории, поэтому вектор мгновенной скорости направлен вдоль касательной к траектории.

Вектором ускорения (~vec a) называется отношение изменения вектора скорости к промежутку времени, в течение которого это изменение произошло, при стремлении этого промежутка к нулю:

(~vec a = frac{Delta vec upsilon}{Delta t}) , при Δt → 0 . (4)

Подчеркнем, что в данном определении ускорения фигурирует изменение вектора скорости — а вектор может изменяться как по величине, так и по направлению. Следовательно, непрямолинейное (криволинейное) движение тела обязательно является движением с ускорением (так как изменяется направление вектора скорости).

Простейшие модели движения.

Реальные движения реальных тел, как правило, довольно сложны – разгон, торможения, повороты, скорости, ускорения тел постоянно изменяются. Однако во многих случаях для описания движения можно использовать достаточно простые (конечно, приближенные) модели, к рассмотрению которых мы сейчас и приступим.

Следующая страница

Источник

Равноускоренное движение.

Зависимость скорости от времени.
Закон движения.
Прямолинейное равноускоренное движение.
Свободное падение.
Горизонтальный бросок.
Бросок под углом к горизонту.

Автор — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев

Темы кодификатора ЕГЭ: виды механического движения, скорость, ускорение, уравнения прямолинейного равноускоренного движения, свободное падение.

Равноускоренное движение — это движение с постоянным вектором ускорения vec a . Таким образом, при равноускоренном движении остаются неизменными направление и абсолютная величина ускорения.

к оглавлению ▴

Зависимость скорости от времени.

При изучении равномерного прямолинейного движения вопрос зависимости скорости от времени не возникал: скорость была постоянна в процессе движения. Однако при равноускоренном движении скорость меняется с течением времени, и эту зависимость нам предстоит выяснить.

Давайте ещё раз потренируемся в элементарном интегрировании. Исходим из того, что производная вектора скорости есть вектор ускорения:

$frac{displaystyle dvec{v}}{displaystyle dt}=vec{a}$ . (1)

В нашем случае имеем . Что надо продифференцировать, чтобы получить постоянный вектор vec a ? Разумеется, функцию vec a t . Но не только: к ней можно добавить ещё произвольный постоянный вектор vec c (ведь производная постоянного вектора равна нулю). Таким образом,

. (2)

Каков смысл константы vec c ? В начальный момент времени t=0 скорость равна своему начальному значению: $vec v=vec v_{0}$ . Поэтому, полагая t=0 в формуле (2), получим:

$vec v_{0}=vec c$ .

Итак, константа vec c — это начальная скорость тела. Теперь соотношение (2) принимает свой окончательный вид:

$vec v=vec v_{0}+vec {a}t$ . (3)

В конкретных задачах мы выбираем систему координат и переходим к проекциям на координатные оси. Часто хватает двух осей и прямоугольной декартовой системы координат, и векторная формула (3) даёт два скалярных равенства:

$v_{displaystyle x}=v{displaystyle 0x}+a_{displaystyle x}t$ , (4)

$v_{displaystyle y}=v{displaystyle 0y}+a_{displaystyle y}t$ . (5)

Формула для третьей компоненты скорости, $v_{displaystyle z}$ если она необходима, выглядит аналогично.)

к оглавлению ▴

Закон движения.

Теперь мы можем найти закон движения, то есть зависимость радиус-вектора от времени. Вспоминаем, что производная радиус-вектора есть скорость тела:

$frac{displaystyle dvec{r}}{displaystyle dt}=vec{v}$

Подставляем сюда выражение для скорости, даваемое формулой (3):

$frac{displaystyle dvec{r}}{displaystyle dt}=vec v_{0}+vec {a}t$ (6)

Сейчас нам предстоит проинтегрировать равенство (6). Это несложно. Чтобы получить $vec v_{0}$ , надо продифференцировать функцию $vec v_{0}t$ . Чтобы получить , нужно продифференцировать $vec {a} t^{2} /2$ . Не забудем добавить и произвольную константу vec c :

$vec r=vec c+vec v_{0} t+frac{displaystyle vec a t^{2}}{displaystyle 2}$ .

Ясно, что vec c — это начальное значение $vec r_{0}$ радиус-вектора vec r в момент времени t=0 . В результате получаем искомый закон равноускоренного движения:

$vec r=vec r_{0}+vec v_{0} t+frac{displaystyle vec a t^{2}}{displaystyle 2}$ . (7)

Переходя к проекциям на координатные оси, вместо одного векторного равенства (7) получаем три скалярных равенства:

$x=x_{0}+ v_{displaystyle 0x} t+frac{displaystyle a_{displaystyle x} t^{2}}{displaystyle 2}$ . (8)

$y=y_{0}+ v_{displaystyle 0y} t+frac{displaystyle a_{displaystyle y} t^{2}}{displaystyle 2}$ . (9)

$z=z_{0}+ v_{displaystyle 0z} t+frac{displaystyle a_{displaystyle z} t^{2}}{displaystyle 2}$ . (10)

Формулы (8) — (10) дают зависимость координат тела от времени и поэтому служат решением основной задачи механики для равноускоренного движения.

Снова вернёмся к закону движения (7). Заметим, что $vec r - vec r_{0}=vec s$ — перемещение тела. Тогда
получаем зависимость перемещения от времени:

$vec s= vec v_{0} t+frac{displaystyle vec a t^{2}}{displaystyle 2}$ .

к оглавлению ▴

Прямолинейное равноускоренное движение.

Если равноускоренное движение является прямолинейным, то удобно выбрать координатную ось вдоль прямой, по которой движется тело. Пусть, например, это будет ось . Тогда для решения задач нам достаточно будет трёх формул:

$v_{displaystyle x}=v_{displaystyle 0x}+a_{displaystyle x}t$ ,

$x=x_{0}+ v_{0 displaystyle x} t+frac{displaystyle a_{displaystyle x} t^{2}}{displaystyle 2}$ ,

$s_{x}= v_{0x} t+frac{displaystyle a_{x} t^{2}}{displaystyle 2}$ ,

где $s_{x}= x-x_{0}$ — проекция перемещения на ось .

Но очень часто помогает ещё одна формула, являющаяся их следствием. Выразим из первой формулы время:

$t=frac{displaystyle v_{displaystyle x}-displaystyle v_{displaystyle 0x}}{displaystyle a_{displaystyle x}}$

и подставим в формулу для перемещения:

$s_{x}= v_{0x} frac{displaystyle v_{displaystyle x}-displaystyle v_{displaystyle 0x}}{displaystyle a_{displaystyle x}}+frac{displaystyle a_{x}}{2} (frac{displaystyle v_{displaystyle x}-displaystyle v_{displaystyle 0x}}{displaystyle a_{displaystyle x}})^{2}$ .

После алгебраических преобразований (проделайте их обязательно!) придём к соотношению:

$s_{x}=frac{displaystyle v_{displaystyle x}^{displaystyle 2}-displaystyle v_{displaystyle 0x}^{displaystyle 2}}{displaystyle 2a_{displaystyle x}}$ .

Эта формула не содержит времени и позволяет быстрее приходить к ответу в тех задачах, где время не фигурирует.

к оглавлению ▴

Свободное падение.

Важным частным случаем равноускоренного движения является свободное падение. Так называется движение тела вблизи поверхности Земли без учёта сопротивления воздуха.

Свободное падение тела, независимо от его массы, происходит с постоянным ускорением свободного падения vec g , направленным вертикально вниз. Почти во всех задачах при расчётах полагают g=10 м/с $^{2}$ .

Давайте разберём несколько задач и посмотрим, как работают выведенные нами формулы для равноускоренного движения.

Задача. Найти скорость приземления дождевой капли, если высота тучи h=2 км.

Решение. Направим ось вертикально вниз, расположив начало отсчёта в точке отрыва капли. Воспользуемся формулой

$s_{y}=frac{displaystyle v_{displaystyle y}^{displaystyle 2}-displaystyle v_{displaystyle 0y}^{displaystyle 2}}{displaystyle 2a_{displaystyle y}}$ .

Имеем: $s_{y}=h, v_{y}=v$ — искомая скорость приземления, $v_{0y}=0, a_{y}=g$ . Получаем: $h^{2}=frac{v^{2}}{2g}$ , откуда . Вычисляем: м/с. Это 720 км/ч, порядка скорости пули.

На самом деле капли дождя падают со скоростью порядка нескольких метров в секунду. Почему такое расхождение? Сопротивление воздуха!

Задача. Тело брошено вертикально вверх со скоростью $v_{0}=30$ м/с. Найти его скорость через t=5 c.

Решение. Направим ось вертикально вверх, поместив начало отсчёта на поверхности Земли. Используем формулу

$v_{displaystyle y}=v_{displaystyle 0y}+a_{displaystyle y}t$ .

Здесь $v_{displaystyle 0y}=v_{0}, a_{y}=-g$ , так что $v_{displaystyle y}=v_{displaystyle 0}-gt$ . Вычисляем: $v_{displaystyle y}=30-10 cdot 5=-20$ м/с. Значит, скорость будет равна 20 м/с. Знак проекции указывает на то, что тело будет лететь вниз.

Задача. С балкона, находящегося на высоте h=15 м, бросили вертикально вверх камень со скоростью $v_{0}=10$ м/с. Через какое время камень упадёт на землю?

Решение. Направим ось вертикально вверх, поместив начало отсчёта на поверхности Земли. Используем формулу

$y=y_{0}+ v_{displaystyle 0y} t+frac{displaystyle a_{displaystyle y} t^{2}}{displaystyle 2}$ .

Имеем: $y=0, y_{0} = h, v_{0y}=v_{0}, a_{y}=-g,$ так что $0=h+v_{0}t-frac{displaystyle g t^{2}}{displaystyle 2}=15+10t-5t^{2}$ , или $t^{2}-2t-3=0$ . Решая квадратное уравнение, получим t=3 c.

к оглавлению ▴

Горизонтальный бросок.

Равноускоренное движение не обязательно является прямолинейным. Рассмотрим движение тела, брошенного горизонтально.

Предположим, что тело брошено горизонтально со скоростью $v_{0}$ с высоты . Найдём время и дальность полёта, а также выясним, по какой траектории происходит движение.

Выберем систему координат OXY так, как показано на рис. 1.

Рис. 1. Горизонтальный бросок

Используем формулы:

$x=x_{0}+ v_{displaystyle 0x} t+frac{displaystyle a_{displaystyle x} t^{2}}{displaystyle 2}$

$y=y_{0}+ v_{displaystyle 0y} t+frac{displaystyle a_{displaystyle y} t^{2}}{displaystyle 2}$

В нашем случае $x_{0} = 0, v_{0x}=v_{0}, a_{x}=0, y_{0} = h, v_{0y}=0, a_{y}=-g$ . Получаем:

$x=v_{0}t, y=h-frac{displaystyle g t^{2}}{displaystyle 2}$ . (11)

Время полёта найдём из условия, что в момент падения координата тела обращается в нуль:

$y(T)=0Rightarrow h-frac{displaystyle gT^{displaystyle 2}}{displaystyle 2}=0Rightarrow T=sqrt{frac{displaystyle 2h}{displaystyle g}}$ .

Дальность полёта — это значение координаты в момент времени :

$L=x(T)=v_{0}T=v_{0} sqrt{frac{displaystyle 2h}{displaystyle g}}$ .

Уравнение траектории получим, исключая время из уравнений (11). Выражаем из первого уравнения и подставляем во второе:

$t=frac{displaystyle x}{displaystyle v_{displaystyle 0}}Rightarrow y=h-frac{displaystyle g}{displaystyle 2}(frac{displaystyle x}{displaystyle v_{displaystyle 0}})^{displaystyle 2}=displaystyle h-frac{displaystyle gx^{displaystyle 2}}{displaystyle 2v^{displaystyle 2}_{displaystyle 0}}$ .

Получили зависимость от , которая является уравнением параболы. Следовательно, тело летит по параболе.

к оглавлению ▴

Бросок под углом к горизонту.

Рассмотрим несколько более сложный случай равноускоренного движения: полёт тела, брошенного под углом к горизонту.

Предположим, что тело брошено с поверхности Земли со скоростью $v_{0}$ , направленной под углом alpha к горизонту. Найдём время и дальность полёта, а также выясним, по какой траектории двигается тело.

Выберем систему координат OXY так, как показано на рис. 2.

Рис. 2. Бросок под углом к горизонту

Начинаем с уравнений:

$x=x_{0}+ v_{displaystyle 0x} t+frac{displaystyle a_{displaystyle x} t^{2}}{displaystyle 2}$ ,

$y=y_{0}+ v_{displaystyle 0y} t+frac{displaystyle a_{displaystyle y} t^{2}}{displaystyle 2}$ .

В нашем случае $x_{0} =y_{0}=0, v_{0x}=v_{0}cos alpha, v_{0y}=v_{0}sin alpha , a_{x}=0, a_{y}=-g$ . Получаем:

$x=(v_{0}cos alpha )t, y=(v_{0}sin alpha)t- frac{displaystyle g t^{2}}{displaystyle 2}$ .

Дальше действуем так же, как и в случае горизонтального броска. В результате приходим к соотношениям:

$T=frac{displaystyle 2v_{displaystyle 0}sinalpha }{displaystyle g}$ ,

$L=frac{displaystyle v_{displaystyle 0}^{displaystyle 2}sin2alpha }{displaystyle g}$ ,

$y=x tgalpha -frac{displaystyle gx^{displaystyle 2}}{displaystyle 2v^{displaystyle 2}_{0}cos^{displaystyle 2}alpha }$ .

(Обязательно проделайте эти вычисления самостоятельно!) Как видим, зависимость от снова является уравнением параболы.Попробуйте также показать, что максимальная высота подъёма определяется формулой:

$H=frac{displaystyle v_{displaystyle 0}^{displaystyle 2}sin^{2} alpha }{displaystyle 2g}$ .

Спасибо за то, что пользуйтесь нашими материалами.
Информация на странице «Равноускоренное движение.» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать необходимые и поступить в высшее учебное заведение или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими статьями из данного раздела.

Публикация обновлена:
07.05.2023

Источник

0 / 0 / 0

Регистрация: 16.03.2014

Сообщений: 9

Зависимости радиус – вектора точки от времени

26.03.2014, 01:08. Показов 11108. Ответов 2

Скорость материальной точки, движущейся в плоскости, изменяется по закону V=A*i-2*B*t*j (V,i,j-вектора), где А и В – положительные постоянные. Найти зависимости радиус – вектора точки от времени r(t) (r-вектор), если в начальный момент времени он был равен нулю.

Любитель математики

1476 / 987 / 282

Регистрация: 27.01.2014

Сообщений: 3,275

29.03.2014, 08:32

pasha1999555, имеем $https://www.cyberforum.ru/cgi-bin/latex.cgi?frac{dvec{r}}{dt}=frac{dx}{dt}vec{i}+frac{dy}{dt}vec{j},$ где $https://www.cyberforum.ru/cgi-bin/latex.cgi?frac{dx}{dt}=A,$ $https://www.cyberforum.ru/cgi-bin/latex.cgi?frac{dy}{dt}=-2Bt.$ Нужно проинтегрировать…

2356 / 1463 / 125

Регистрация: 20.12.2011

Сообщений: 2,223

29.03.2014, 14:38

Сообщение от pasha1999555

Найти зависимости радиус – вектора точки от времени r(t)

IT_Exp Эксперт 87844 / 49110 / 22898 Регистрация: 17.06.2006 Сообщений: 92,604	29.03.2014, 14:38
3

Источник