Ускорение свободного падения характеризует то, как быстро будет увеличиваться скорость тела при свободном падении. Свободным падением называется ускоренное движение тела в безвоздушном пространстве, при котором на тело действует только сила тяжести. Из физики известно, что ускорение свободного падения на Земле составляет (9,8)
мс2
.
Вопрос, почему эта величина именно такая, мы рассмотрим в этой теме.
Ускорение свободного падения в упрощённом виде можно рассчитать по формуле
g=Fm
, которая получается из формулы
F=m⋅g
, где (F) — сила тяжести либо вес тела в состоянии покоя или равномерного прямолинейного движения, (m) — масса тела, которое притягивает планета, (g) — ускорение свободного падения.
Сила тяжести, действующая на тело, зависит от массы тела, массы планеты, притягивающей тело, и от расстояния, на котором находится тело от центра массы планеты.
(F) — сила тяжести, Н;
(G) — гравитационная постоянная,
G=6,6720⋅10−11Н⋅м2кг2
;
(R) — расстояние между центрами планеты и объекта в метрах. Если притягиваемое тело находится на поверхности планеты, тогда (R) равен радиусу планеты (если планета имеет сферическую форму);
m1 и
m2
— масса планеты и притягиваемого тела, выраженные в кг.
Обрати внимание!
Если мы объединим обе формулы, тогда получим формулу
g=G⋅mR2
, с помощью которой можно вычислить ускорение свободного падения на любом космическом объекте — на планете или звезде.
Пример:
ускорение свободного падения у поверхности Земли вычисляют таким образом:
, где
(g) — ускорение свободного падения;
(G) — гравитационная постоянная,
G=6,6720⋅10−11Н⋅м2кг2
;
Практически на Земле ускорение свободного падения на полюсах немного больше ((9,832)
мс2
), чем на экваторе ((9,78)
мс2
), так как Земля не имеет форму идеального шара, а на экваторе скорость вращения больше, чем на полюсах. Среднее значение ускорения свободного падения у поверхности Земли равно (9,8)
мс2
.
Ускорение свободного падения у поверхности любого космического тела — на планете или звезде — зависит от массы этого тела и квадрата его радиуса. Таким образом, чем больше масса звезды и чем меньше её размеры, тем больше значение ускорения свободного падения у её поверхности.
При помощи формулы расчёта ускорения свободного падения и измерений, проведённых для удалённых объектов, учёные-физики могут определить величину ускорения свободного падения на любой планете или звезде.
Рис. (1). Планеты Солнечной системы: Меркурий, Венера, Земля, Марс, Юпитер, Сатурн, Уран, Нептун; и карликовые планеты: Церера, Плутон, Эрида ((2003) UB (313))
Таблица (1). Ускорение свободного падения и другие характеристики планет Солнечной системы и карликовых планет
|
Небесное тело |
Ускорение свободного падения, мс2 |
Диаметр, км |
Расстояние до Солнца, миллионы км |
Масса, кг |
Соотношение с массой Земли |
|
Меркурий |
(3,7) |
(4878) |
(58) |
(3,3*) 1023 |
(0,055) |
|
Венера |
(8,87) |
(12103) |
(108) |
(4,9*) 1024 |
(0,82) |
|
Земля |
(9,8) |
(12756,28) |
(150) |
(6,0*) 1024 |
(1) |
|
Марс |
(3,7) |
(6794) |
(228) |
(6,4*) 1023 |
(0,11) |
|
Юпитер |
(24,8) |
(142984) |
(778) |
(1,9*) 1027 |
(317,8) |
|
Сатурн |
(10,4) |
(120536) |
(1427) |
(5,7*) 1026 |
(95,0) |
|
Уран |
(8,87) |
(51118) |
(2871) |
(8,7*) 1025 |
(14,4) |
|
Нептун |
(10,15) |
(49532) |
(4498) |
(1,02*) 1026 |
(17,1) |
|
Плутон |
(0,66) |
(2390) |
(5906) |
(1,3*) 1022 |
(0,0022) |
|
Луна |
(1,62) |
(3473,8) |
(0,3844 ) (до Земли) |
(7,35*) 1022 |
(0,0123) |
|
Солнце |
(274,0) |
(1391000) |
— |
(2,0*) 1030 |
(332900) |
Нейтронные звёзды имеют малый диаметр — порядка десятков километров, — а масса их сопоставима с массой Солнца. Поэтому гравитационное поле у них очень сильное.
Пример:
если диаметр нейтронной звезды равен (20) км, а масса её в (1,4) раза больше массы Солнца, тогда ускорение свободного падения будет в (200000000000) раз больше, чем у поверхности Земли.
Его величина приблизительно равна
2⋅1012 мс2
. Значение ускорения свободного падения для нейтронной звезды может достигать значения
7⋅1012 мс2
.
| Солнце | 273,1 | ||
| Меркурий | 3,68—3,74 | Венера | 8,88 |
| Земля | 9,81 | Луна | 1,62 |
| Церера | 0,27 | Марс | 3,86 |
| Юпитер | 23,95 | Сатурн | 10,44 |
| Уран | 8,86 | Нептун | 11,09 |
| Плутон | 0,61 |
Ускоре́ние свобо́дного паде́ния g (обычно произносится как «Же»), — ускорение, придаваемое телу силой тяжести при исключении из рассмотрения других сил. Сила тяжести складывается из гравитационного притяжения планеты (или другого астрономического тела) и центробежных сил, вызванных её вращением[1][2]. В соответствии со вторым законом Ньютона, ускорение свободного падения численно равно силе тяжести, воздействующей на объект единичной массы.
Содержание
- 1 Величина
- 1.1 Вычисление ускорения свободного падения
- 2 Перегрузки
- 3 См. также
- 4 Примечания
- 5 Литература
Величина [править]
Ускорение свободного падения у поверхности Земли может быть измерено непосредственно, и зависит от широты, времени суток и других факторов. Оно варьируется от 9,780 м/с² на экваторе до 9,832 м/с² на полюсах[3]. Оно может быть вычислено (в м/с²) по эмпирической формуле:
где 

Для приблизительных расчётов, значение ускорения свободного падения на поверхности Земли обычно принимают равным 9,8 или 10 м/с².
Стандартное («нормальное») значение, принятое при построении систем единиц, g = 9,80665 м/с²[5][6], а в технических расчётах обычно принимают g = 9,81 м/с². Стандартное значение g было определено как «среднее» в каком-то смысле ускорение свободного падения на Земле, примерно равно ускорению свободного падения на широте 45,5° на уровне моря.
Вычисление ускорения свободного падения [править]
| h, км | g, м/с2 | h, км | g, м/с2 |
|---|---|---|---|
| 0 | 9,8066 | 20 | 9,7452 |
| 1 | 9,8036 | 50 | 9,6542 |
| 2 | 9,8005 | 80 | 9,5644 |
| 3 | 9,7974 | 100 | 9,505 |
| 4 | 9,7943 | 120 | 9,447 |
| 5 | 9,7912 | 500 | 8,45 |
| 6 | 9,7882 | 1000 | 7,36 |
| 8 | 9,7820 | 10 000 | 1,50 |
| 10 | 9,7759 | 50 000 | 0,125 |
| 15 | 9,7605 | 400 000 | 0,0025 |
Ускорение свободного падения может быть измерено либо непосредственно, либо посредством определения силы тяжести, которая, в частности, придаёт телам вес.
Ускорение свободного падения в системе отсчёта, связанной с поверхностью Земли можно представить как векторную сумму двух слагаемых: гравитационного ускорения и центробежного ускорения. Вторая компонента появляется вследствие отличия этой системы отсчёта от инерциальной (из-за вращения Земли вокруг своей оси).
Значение гравитационного ускорения на поверхности планеты можно приблизительно подсчитать, представив планету однородным шаром массой M и вычислив гравитационное ускорение на расстоянии её радиуса r:
,
где G — гравитационная постоянная (6,6742·10−11 м³с−2кг−1).
Если применить эту формулу для вычисления гравитационного ускорения на поверхности Земли (масса М = 5,9736·1024 кг, радиус r = 6,371·106 м), мы получим
м/с².
Полученное значение лишь приблизительно совпадает с ускорением свободного падения в данном месте. Отличия обусловлены:
- центробежным ускорением, которое присутствует в системе отсчёта, связанной с вращающейся Землёй[7];
- отличием формы Земли от шарообразной (см. геоид);
- неоднородностью Земли, что используется для поиска полезных ископаемых по гравитационным аномалиям (гравиразведка).
Две компоненты ускорения свободного падения g: гравитационная (в первом приближении, если считать Землю однородным шаром, равная GM/r2) и центробежная, равная ω2a, где a — расстояние до земной оси, ω — угловая скорость вращения Земли.
| Город | Долгота | Широта | Высота над уровнем моря, м | Ускорение свободного падения, м/с2 |
|---|---|---|---|---|
| Берлин | 13,40 в.д. | 52,50 с.ш. | 40 | 9,81280 |
| Будапешт | 19,06 в.д. | 47,48 с.ш. | 108 | 9,80852 |
| Вашингтон | 77,01 з.д. | 38,89 с.ш. | 14 | 9,80112 |
| Вена | 16,36 в.д. | 48,21 с.ш. | 183 | 9,80860 |
| Владивосток | 131,53 в.д. | 43,06 с.ш. | 50 | 9,80424 |
| Гринвич | 0,0 в.д. | 51,48 с.ш. | 48 | 9,81188 |
| Каир | 31,28 в.д. | 30,07 с.ш. | 30 | 9,79317 |
| Киев | 30,30 в.д. | 50,27 с.ш. | 179 | 9,81054 |
| Мадрид | 3,69 в.д. | 40,41 с.ш. | 667 | 9,79981 |
| Минск | 27,55 в.д. | 53,92 с.ш. | 220 | 9,81347 |
| Москва | 37,61 в.д. | 55,75 с.ш. | 151 | 9,8154 |
| Нью-Йорк | 73,96 з.д. | 40,81 с.ш. | 38 | 9,80247 |
| Одесса | 30,73 в.д. | 46,47 с.ш. | 54 | 9.80735 |
| Осло | 10,72 в.д. | 59,91 с.ш. | 28 | 9,81927 |
| Париж | 2,34 в.д. | 48,84 с.ш. | 61 | 9,80943 |
| Прага | 14,39 в.д. | 50,09 с.ш. | 297 | 9,81014 |
| Рим | 12,99 в.д. | 41,54 с.ш. | 37 | 9,80312 |
| Стокгольм | 18,06 в.д. | 59,34 с.ш. | 45 | 9,81843 |
| Токио | 139,80 в.д. | 35,71 с.ш. | 18 | 9,79801 |
Исторически масса Земли была впервые определена Генри Кавендишем, исходя из известного ускорения свободного падения и радиуса Земли, и впервые измеренной им гравитационной постоянной.
Перегрузки [править]
«Же» используется в космонавтике, авиации, автоспорте, а также вообще в технике как единица измерения перегрузок — увеличения веса тела, вызванного его движением с ускорением. Допустимое значение перегрузок для гражданских самолетов составляет 4,33 g[источник не указан 203 дня]. Обычный человек может выдерживать перегрузки до 5 g[источник не указан 903 дня]. Тренированные пилоты в антиперегрузочных костюмах могут переносить перегрузки до 9 g. Сопротивляемость к отрицательным, направленным вверх перегрузкам, значительно ниже. Обычно при −2…-3 g в глазах «краснеет» и человек тяжелее переносит такую перегрузку из-за прилива крови к голове.
В этом вопросе существует небольшая терминологическая путаница: к примеру, определение перегрузки выше даёт для стоящего неподвижно человека перегрузку в 0 g, но в таблице ниже этот же случай рассматривается как перегрузка в 1 g. Похожий казус происходит также и при измерении давления: мы говорим — давление 0, подразумевая давление в одну атмосферу вокруг нас, учёный скажет — давление 0, подразумевая полное отсутствие молекул в данном объёме.
| Человек, стоящий неподвижно | 1 g |
| Пассажир в самолете при взлете | 1,5 g |
| Парашютист при приземлении со скоростью 6 м/с | 1,8 g |
| Парашютист при раскрытии парашюта (при изменении скорости от 60 до 6 м/с) | 5,0 g |
| Космонавты при спуске в космическом корабле «Союз» | до 3,0—4,0 g |
| Летчик при выполнении фигур высшего пилотажа | до 5 g |
| Летчик при выведении самолета из пикирования | 8,0—9 g |
| Перегрузка (длительная), соответствующая пределу физиологических возможностей человека | 8,0—10,0 g |
| Наибольшая (кратковременная) перегрузка автомобиля, при которой человеку удалось выжить | 214 g[8] |
См. также [править]
- Гравиметрия
- Гравиразведка
Примечания [править]
- ↑ Сивухин Д.В. Общий курс физики. — М.: Государственное издательство технико-теоретической литературы, 2005. — Т. 1. Механика. — С. 372.
- ↑ Ускорение свободного падения // Физическая энциклопедия / Гл. ред. А. М. Прохоров. — М.: Большая Российская энциклопедия, 1998. — Т. 5 Стробоскопические приборы — Яркость. — С. 245-246. — 760 с. — 20 000 экз. — ISBN 5-85270-101-7
- ↑ «Свободное падение тел. Ускорение свободного падения»
- ↑ g-Extractor на сайте Physikalisch-Technische Bundesanstalt (PTB).
- ↑ Декларация III Генеральной конференции по мерам и весам (1901) (англ.). Международное бюро мер и весов. Проверено 9 апреля 2013.
- ↑ В. М. Деньгуб, В. Г. Смирнов. Единицы величин. Словарь — справочник. М.: Изд-во стандартов, 1990, с. 237.
- ↑ Центробежное ускорение точки, находящейся на расстоянии a от оси вращения и движущейся с тангенциальной скоростью v, равно v2/a и направлено от оси во вращающейся системе отсчёта. На поверхности условной шарообразной Земли a = r cos φ в точке с широтой φ, а скорость v = 2πa/T, где Т — период обращения Земли (звёздные сутки, 86164,1 секунды). Можно подсчитать, что центробежное ускорение меняется от 0 на полюсах до 3,4 см/с2 на экваторе, причём почти везде (кроме полюсов и экватора) оно не сонаправлено с гравитационным ускорением, направленным к центру Земли.
- ↑ Авария Кенни Брака IRL 2003 Texas Chevy 500
Литература [править]
- А. С. Енохович Краткий справочник по физике. — М.: «Высшая школа», 1976. — 288 с.
Ускорение свободного падения
Ускорение свободного падения — движение объекта, который получает ускорение из-за действующей на него силы тяжести; обозначается буквой g и измеряется в м/с². На поверхности Земли ускорение свободного падения примерно равно 9,81 м/с².
На полюсах (Южном и Северном) ускорение свободного падения будет больше, а на экваторе — меньше. Это происходит из-за двух фактов:
- Земля — не идеальный круг, а приплюснутый шар и её радиус на полюсах меньше, чем на экваторе (ускорение зависит от радиуса),
- центробежные силы (при вращении Земли) минимально компенсируют гравитацию больше на экваторе, чем на полюсах.
В вакууме тела падают с одинаковой скоростью потому, что ускорение свободного падения не зависит от массы.
Таблица ускорения свободного падения небесных тел
| Небесное тело | g (в м/с²) |
|---|---|
| Луна | 1,62 |
| Солнце | 274 |
| Меркурий | 3,72 |
| Венера | 8,87 |
| Земля | 9,81 |
| Марс | 3,711 |
| Юпитер | 24,79 |
| Сатурн | 10,44 |
| Уран | 8,87 |
| Нептун | 11,15 |
От чего зависит ускорение свободного падения?
Ускорение свободного падения зависит от массы планеты и радиуса планеты — чем она тяжелее, тем сильнее притягивает тела (т.е. масса тела не влияет на ускорение).
Возможно для будущих вычислений нужны будут эти данные:
- Масса Земли = 5,98 × (10^24) кг (или 5,972E24 кг)
- Радиус Земли = 6 371 км = 6,37×(10^6) м.
Как найти ускорение свободного падения?
Формула ускорения свободного падения

g — ускорение свободного падения
G — гравитационная постоянная
M — масса планеты
R — радиус планеты
Гравитационная постоянная («G», не путайте с «g») — это фундаментальная физическая константа, которая примерно равна
и связывает силы гравитационного притяжения между двумя телами (G) с их массами (m1 и m2) и расстоянием между ними (R) в формуле:
Пример расчёта ускорения свободного падения (для Земли):
Вспомним формулу:

G — гравитационная постоянная
M — масса планеты
R — радиус планеты
Как узнать время падения тела?
Формула времени свободного падения (когда тело падает вертикально):
t = V / g = √(2h/g)
Где:
- t — время
- V — скорость тела
- g — ускорение ≈ 9,8 м/с²
- h — расстояние
Пример:
Высота (h) = 20 м
Нужно найти скорость и время падения.
Решение:
Формула скорости:
V0 = 0
g ≈ 9,8 м/с²
h = 20 м
V² = 0² + 2 × 9,8 м/с² × 20 м ⇔ V = √392 м/с ≈ 19,8 м/с
Зная скорость, применяем эту формулу:
t = V / g = (19,8 м/с) / (9,8 м/с²) ≈ 2,02 с
Либо используя только высоту и ускорение:
t = √(2h/g) = √(2 × 20 м / 9,8 м/с²) ≈ 2,02 с
Где нужны знания о свободном падении?
Они могут понадобиться:
- в авиации,
- в космонавтике,
- при поиске полезных ископаемых (там, где есть залежи тяжёлых ископаемых, g меняется),
- при разработке новых лыжных трамплинов и полос приземления,
- при разработке новых автомобилей (рассчитываются наилучшие показатели для экономии топлива).
Узнайте также про Закон сохранения энергии, Силу Архимеда, Законы Ньютона и Космологию.
Выберем тело, например, камень. Расположим его не некотором расстоянии от поверхности земли. Расстояние от центра Земли до камня равно ( R = left( r + h right) ), как представлено на рисунке 1.
Рис. 1. Камень (черная точка), притягивается к планете (центральная окружность).
Пусть на камень действует только сила, с которой Земля притягивает его, а других сил нет (нет, например, силы сопротивления воздуха).
Свободное падение – это движение тела под действием только одной силы — силы притяжения.
Из законов Ньютона известно: если на тело действует сила, то тело получает ускорение.
Ускорение свободного падения – это ускорение, с которым движется тело, когда на него действует только сила тяжести.
Формула для расчета ускорения свободного падения
Ускорение свободного падения можно посчитать по формуле:
[ large boxed { g = G cdot frac{M}{left( r + h right)^{2}} }]
( g left( frac{text{м}}{c^{2}} right) ) (метры, деленные на секунду в квадрате) – ускорение свободного падения
( M left( text{кг} right) ) (килограммы) — масса планеты, которая притягивает
( r left( text{м} right) ) (метры) – радиус планеты
( h left( text{м} right) ) (метры) — расстояние от поверхности планеты до тела
(G = 6{,}67 cdot 10^{-11} left( text{Н} cdot frac{text{м}^2}{text{кг}^2} right)) — гравитационная постоянная
Интересные факты
У разных планет ускорение свободного падения различается.
- чем больше масса планеты (или звезды), тем больше будет ускорение свободного падения рядом с такой планетой (или звездой);
- чем дальше от планеты, тем меньше ускорение свободного падения;
- на полюсах ускорение свободного падения больше, чем на экваторе планеты;
Важно!
Все тела под действием силы тяжести падают с одинаковым ускорением! Это ускорение не зависит от массы тела.
Из житейского опыта мы знаем: чем больше площадь тела, тем больше времени ему нужно, чтобы упасть с какой-либо высоты. При своем падении тело опирается на воздух, поэтому, к примеру, лист бумаги будет падать дольше, чем шарик из пластилина, или гирька.
В безвоздушном пространстве опираться не на что. Поэтому гирька, лист бумаги, птичье перо и пластилиновый шарик, стартовав с одной и той же высоты одновременно, упадут на поверхность планеты тоже одновременно.
Ускорение свободного падения у поверхности некоторых небесных тел
- у поверхности Земли ( g = 9{,}8 left( frac{text{м}}{c^{2}} right) )
- у поверхности Луны ( g = 1{,}68 left( frac{text{м}}{c^{2}} right) )
- у поверхности Марса ( g = 3{,}86 left( frac{text{м}}{c^{2}} right) )
- у поверхности Солнца ( g = 273{,}1 left( frac{text{м}}{c^{2}} right) )
- у поверхности Юпитера ( g = 23{,}95 left( frac{text{м}}{c^{2}} right) )
Как вывести формулу ускорения свободного падения
Рассмотрим камень, находящийся на некотором расстоянии от Земли.
Земля и камень притягиваются, запишем закон притяжения между планетой и камнем
[ F = G cdot frac{mcdot M}{left( r + h right)^{2}} ]
С другой стороны, у камня есть вес, так как на него действует сила тяжести.
[ F_{text{тяж}} = m cdot g ]
Мы можем записать эти уравнения в виде системы.
[ begin{cases} displaystyle F = G cdot frac{mcdot M}{( r + h)^{2}} \ displaystyle F_{text{тяж}} = m cdot g end{cases} ]
Земля и камень притягиваются, благодаря этому на камень действует сила тяжести. На языке математики это запишется так:
[ F = F_{text{тяж}} ]
А если равны левые части уравнений, то будут равны и правые:
[ G cdot frac{mcdot M}{left( r + h right)^{2}} = m cdot g ]
Масса ( m ) камня встречается в обеих частях уравнения. Поделим обе части уравнения на массу камня.
[ G cdot frac{M}{ left( r + h right)^{2}} = g ]
Все)
Вам будет интересно почитать:
Закон всемирного тяготения
Законы Ньютона
Первая космическая скорость
Вторая космическая скорость
Кикоин А.К. Вращение Земли и ускорение свободного падения //Квант. — 1984. — № 1. — С. 32-34.
По специальной договоренности с редколлегией и редакцией журнала «Квант»
В учебнике «Физика 8» на странице 104 сказано: «Вращение Земли приводит к тому, что ускорение свободного падения, измеренное относительно какого-либо тела на поверхности Земли, на разных широтах различно». Выясним причины этого различия.
Относительность движения состоит, как известно, в том, что движение одного и того же тела, но относительно разных систем отсчета, движущихся друг относительно друга, выглядит по-разному. Различны траектории движения, скорости, ускорения.
Если одна из систем отсчета движется относительно другой с постоянной скоростью (без ускорения), то скорость (~vec upsilon) тела относительно одной из систем отсчета, условно принятой за неподвижную, равна (~vec upsilon_1 + vec upsilon_2), где (~vec upsilon_1) — скорость тела относительно подвижной системы и (~vec upsilon_2) — скорость подвижной системы относительно неподвижной. Ускорение тела относительно обеих систем в таком случае одно и то же (оно, как говорят, абсолютно).
Иное дело, если одна из систем отсчета движется относительно другой с ускорением. Тогда не только скорость, но и ускорение тоже относительно: ускорение (~vec a) тела относительно неподвижной системы отсчета равно сумме ускорений (~vec a_1) и (~vec a_2), где (~vec a_1) — ускорение тела относительно подвижной системы и (~vec a_2) — ускорение подвижной системы относительно неподвижной, то есть
(~vec a = vec a_1 + vec a_2) . (1)
Одним из примеров именно такого случая служит свободное падение тел на Землю. Поскольку Земля вращается вокруг своей оси, система отсчета, связанная с любой точкой на ее поверхности, движется с ускорением. Поэтому ускорение падающего тела относительно неподвижной системы должно равняться сумме ускорения тела относительно подвижной системы и ускорения подвижной системы относительно неподвижной.
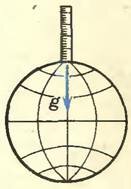
Неподвижная система отсчета может быть связана с каким-нибудь неземным телом, например с Солнцем. Но можно поступить и проще, не покидая Землю. Ведь и на поверхности Земли есть точки, не участвующие в ее вращении. Это — полюсы Земли, через которые проходит ось вращения. Следовательно, чтобы найти значение ускорения падающего тела относительно неподвижной системы отсчета, нужно измерить ускорение свободного падения на земном полюсе. Для этого на полюсе можно установить линейку с делениями (рис. 1) и, например, с помощью стробоскопического метода, измерить ускорение падающего вдоль линейки тела. Линейка и связанная с ней система координат и будут для нас неподвижной системой отсчета.
Рис. 1
Так как свободное падение — движение прямолинейное, достаточно одной координатной оси, которую естественно направить вдоль линейки, то есть вдоль оси вращения Земли.
Результат такого измерения легко предсказать. Согласно второму закону Ньютона и закону всемирного тяготения,
(~mg = G frac{mM}{R^2}) ,
где m — масса тела, g — ускорение падающего тела, G — гравитационная постоянная, М — масса Земли и R — ее радиус. Отсюда можно найти значение ускорения падающего тела относительно неподвижной системы отсчета:
(~g = G frac{M}{R^2}) .
Его мы и получим, если выполним описанный опыт.
Такой же опыт можно провести в любом другом месте на Земле. Для этого надо опять установить вертикальную линейку и с ней связать систему отсчета. Но теперь это будет система отсчета, движущаяся с ускорением относительно неподвижной системы.
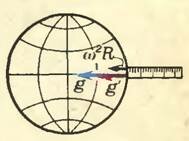
Рис. 2
Расположим, например, линейку на экваторе (рис. 2). Здесь наша система отсчета (линейка) движется вместе с Землей по окружности экватора с центростремительным ускорением, равным ω2R, где ω — угловая скорость вращения Земли и R — ее радиус. Направлено это ускорение к центру Земли, как и ускорение g, сообщаемое телу силой притяжения[1]. Измеренное на экваторе ускорение g’ будет несколько иным по сравнению с ускорением на полюсе. Согласно формуле (1), мы можем написать[2]
(~g = g’ + omega^2 R) . (2)
Эта формула и указывает на то, что ускорение падающего тела относительно неподвижной системы отсчета (g) равно сумме ускорений тела относительно подвижной системы (g’) и подвижной системы относительно неподвижной (ω2R). Из формулы (2) видно, что ускорение g’ свободного падения тела на экваторе не равно значению ускорения g, измеренному на полюсе. Оно меньше g на величину ω2R:
(~g’ = g — omega^2 R) .
На сколько же численно отличается значение g’ от g? Чтобы это узнать, нужно, очевидно, вычислить значение величины ω2R. Угловую скорость о вращения Земли можно найти, зная период вращения Земли Т = 24 ч = 86400 с:
(~omega = frac{2pi}{T} approx 7,3 cdot 10^{-5} c^{-1}) .
Радиус Земли на экваторе R = 6378 км ≈ 6,38·106 м. Значит,
(~omega^2 R approx (7,3 cdot 10^{-5})^2 cdot 6,38 cdot 10^6 m/c^2 approx 3,4 cdot 10^{-2} m/c^2) .
На столько и отличается измеренное ускорение свободного падения на экваторе от того ускорения, которое наблюдалось бы, если бы Земля не совершала суточного вращения и система отсчета, связанная с ней, не двигалась бы ускоренно.
В большинстве случаев этим небольшим различием в значениях ускорения свободного падения пренебрегают. Но обнаружить его можно сравнительно просто. Так, например, часы с маятником (период колебаний маятника зависит от ускорения свободного падения) на экваторе отстают от таких же часов на полюсе приблизительно на 3 минуты за сутки.
Заметим в заключение, что различие в значениях ускорения свободного падения не означает, что и сила притяжения тела к Земле различна в разных местах на Земле. Эта сила определяется законом всемирного тяготения
(~F = G frac{mM}{R^2}) ,
и на нее вращение Земли не оказывает никакого влияния.
Иначе обстоит дело с величиной, называемой весом тела. Вес тела — это сила, с которой тело вследствие притяжения к Земле действует на опору или подвес. Если опора или подвес покоятся относительно Земли или движутся относительно нее без ускорения, то вес численно равен силе тяжести. Но весы, при помощи которых измеряется вес тела, в любом месте Земли, кроме ее полюсов, движутся с ускорением. Поэтому везде, кроме полюсов, вес тела не равен силе тяжести. Наименьшим вес тела будет на экваторе. Впрочем, значения веса на экваторе и на полюсе различаются так же мало, как и значения ускорения свободного падения.
Примечания
- ↑ Мы пренебрегли различием в силе притяженмн на экваторе и на полюсе, вызванным нестрогой сферичностью Земли.
- ↑ Мы здесь не пользуемся векторными обозначениями, так как все три ускорения направлены вдоль координатной оси и их модули равны проекциям на эту ось.



 ,
, м/с².
м/с².