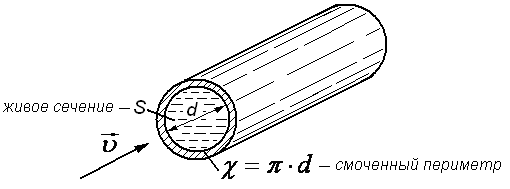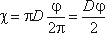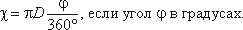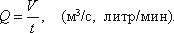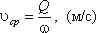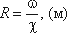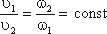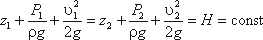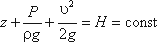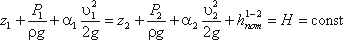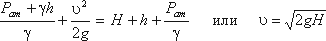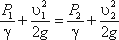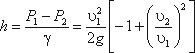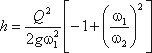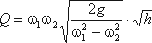В
гидравлических расчётах для характеристики
размеров и формы поперечного сечения
потока вводят понятие о живом
сечении и его элементах: смоченном
периметре и гидравлическом радиусе.
Живым
сечением
называется поверхность в пределах
потока, проведённая нормально к линиям
тока.
Для
круглого трубопровода, когда всё
поперечное сечение заполнено жидкостью,
живым сечение является площадь круга:

Рис.
3.6. Элементы потока
Смоченным
периметром
называют ту часть периметра живого
сечения, по которой жидкость соприкасается
со стенками трубопровода (рис.3.6).
Смоченный периметр обычно обозначают
греческой
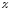
заполненной жидкостью смоченный периметр
равен длине окружности:

Гидравлическим
радиусом
называют отношение живого сечения к
смоченному периметру, т.е. величину

Эта
величина характеризует удельную, т.е.
приходящуюся на единицу длины смоченного
периметра, площадь живого сечения. Легко
сделать вывод, что поток с наибольшим
гидравлическим радиусом при прочих
равных условиях имеет минимальную силу
трения, приложенную к смоченной
поверхности.
Для
круглых труб, полностью заполненных
жидкостью, гидравлический радиус равен
четверти диаметра:

Введение
гидравлического радиуса как характерного
размера позволяет сравнивать по критерию
подобия (Re)
потоки с разными формами живого сечения.
Рассмотренные
основные понятия позволяют решать самые
различные практические задачи гидравлики.
Пример
3.1. Определить
скорость потока в трубопроводе. Диаметр
расход воды (несжимаемой жидкости) —
Решение.
Искомая скорость
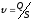
Определим
площадь живого сечения:

Скорость
потока:

3.6. Уравнение количества движения для потока жидкости
Гидравлика
– это техническая механика жидкости,
в которой часто используются упрощённые
методы для решения инженерных задач.
Во многих случаях при решении практических
задач гидравлики удобно применять такие
центральные понятия механики, как
количество движения (уравнение импульсов)
и кинетическая энергия.
В
связи с этим необходимо рассмотреть
возможность вычисления количества
движения и кинетическую энергию потока
жидкости по средней скорости, а не по
действительным местным скоростям. Это
позволит существенно упростить
гидравлические расчёты.
Для
материального тела массой
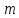
движущегося со скоростью
изменение количества движения за время


где
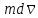
обусловленное импульсом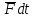
Жидкость
представляет собой материальную систему,
поэтому основной закон механики может
быть приложен к любой выделенной из неё
массе.
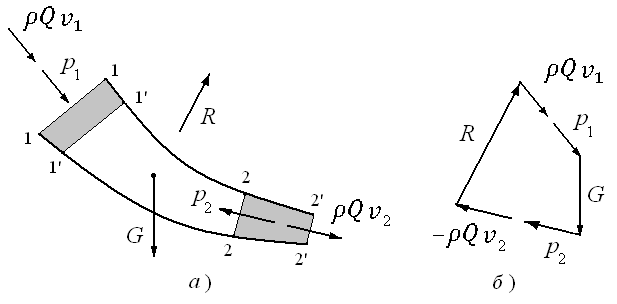
Применим
эту теорему механики к участку потока
жидкости с расходом

участок заштрихован). Ограничимся
рассмотрением только установившегося
движения жидкости (рис. 3.7).
За
время

определяемое сечениями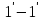

Объёмы этих элементов
а, следовательно, и их массы
движения будет равно

Это
приращение количества движения
обусловлено импульсом всех внешних
сил, действующих на объём жидкости между
сечениями 1-1 и 2-2. Внешними силами,
приложенными к выделенному объёму,
являются сила тяжести всего объёма
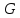
силы давления в первом и втором сечениях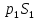

внутрь объёма), а также реакции стенок
трубы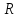
которая складывается из сил давления
и трения, распределённых по боковой
поверхности объёма.
Рис.
3.7. Применение уравнения количества
движения
к
потоку жидкости
Уравнение
импульсов (3.7) для рассматриваемого
случая можно записать в виде
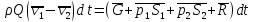
После
сокращения на

Составив
проекции этого векторного уравнения
на три координатные оси, получим три
алгебраических уравнения с тремя
неизвестными —
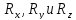
Л.
Эйлер предложил удобный графический
способ нахождения силы

Перенося в формуле (3.?) все слагаемые в
одну сторону, можно представить его в
виде суммы векторов:

0, (3.10)
где
вектор

обратный действительному). В соответствии
с этим выражением (3.10) силу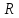
многоугольник сил, как это показано на
рис. 3.7,а.
Анализ
показывает, что при вычислении количества
движения и кинетической энергии по
средней скорости допускается ошибка,
которую можно учесть с помощью двух
коэффициентов:
—
коэффициента Буссинеска


—
коэффициента Кориолиса
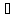
кинетической энергии
Величина
обоих коэффициентов зависит от характера
распределения скоростей в поперечном
сечении потока жидкости. На практике
при турбулентном режиме движения
коэффициент Кориолиса


Поэтому обычно полагают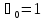
Однако встречаются отдельные случаи,
когда
пренебрежение им может привести к
значительным погрешностям.
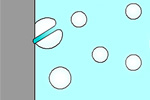
Пример
3.2. Определить
силу воздействия потока жидкости на
преграду. Пусть жидкость вытекает в
атмосферу и наталкивается на безграничную
стенку, установленную нормально к
потоку. В результате жидкость растекается
по стенке, изменяя направление своего
течения на 900
(рис.
3.8). Известны площадь сечения потока

скорость истечения
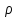
Рис. 3.8. Воздействие
струи на преграду
Для
решения данной задачи берём фиксированный
объём, показанный штриховой линией, и
применяем теорему Эйлера. Так как
давление внутри струи и по поверхности
жидкости равно атмосферному, т.е.
избыточное давление равно нулю, уравнение,
выражающее теорему Эйлера, для направления,
совпадающего с вектором скорости
истечения
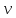
будет иметь вид

или 
Это
и есть сила воздействия потока жидкости
на преграду. При другом угле установке
стенки или других её форме и размерах
в правую формулы (3.11) вводится безразмерный
коэффициент, отличный от единицы, но
пропорциональность силы
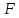

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
2018-03-27
Живое сечение, гидравлический радиус и смоченный периметр в гидравлике
Содержание:
- Живое сечение
- Смоченный периметр
- Гидравлический радиус
- Гидравлический радиус для круглой трубы
- Гидравлический диаметр
Живое сечение
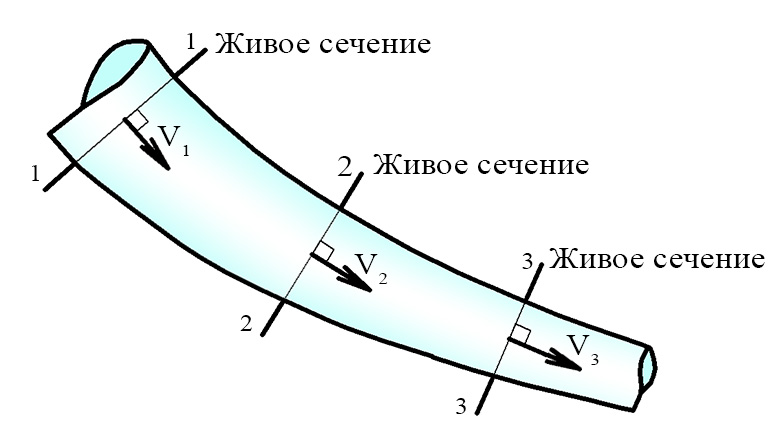
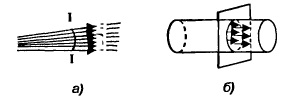
Живым или нормальным называют сечение потока перпендикулярное направлению скорости течения (линиям тока).
На рисунке изображен поток жидкости, в произвольных точках выбраны перпендикулярные направлениям скоростей живые сечения 1-1, 2-2, 3-3.
Смоченный периметр
Периметр контакта жидкости в данном живом сечении называют смоченным периметром (П, м).
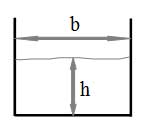
Рассмотрим пример:
Для представленного сечения смоченный периметр можно определить по формуле:
П=2h+b
Гидравлический радиус
Отношение площади живого сечения (А, м2) к смоченному периметру (П, м) называют гидравлическим радиусом.
Rг=А/П, м
Гидравлический радиус для круглой трубы
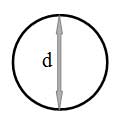
Рассмотрим трубу с внутренним диаметром d, полностью заполненную жидкостью.
П=π d
A=π d2/4
Rг=d/4, м
Гидравлический диаметр
Для заполненной круглой трубы гидравлический диаметр можно определить по формуле:
Dг=4Rг, м
Читайте также:
Все новости
Как делаются вычисления?
Как известно, труба – это цилиндр. Следовательно, площадь её сечения рассчитывается по простым формулам, известным нам из курса геометрии. Основная задача – вычислить площадь круга, диаметр которого равен наружному диаметру изделия. При этом толщина стенок вычитается для получения истинного значения.
Как мы знаем из курса общеобразовательной школы, площадь круга равна произведению числа π на квадрат радиуса:
- R – радиус вычисляемой окружности. Он равен половине её диаметра;
- Π – постоянная равная 3,14;
- S – вычисляемая площадь поперечного сечения трубы.
Приступаем к расчёту
Так как задача – найти истинную площадь, то из полученного значения необходимо вычесть величину толщины стенки. Следовательно, формула приобретает вид:
- S = π • (D/2 – N) 2 ;
- В этой записи D – внешний диаметр окружности;
- N – толщина стенки трубы.
Чтобы вычисления были максимально точными, следует вписать больше знаков после запятой в числе π (пи).
К примеру, требуется рассчитать сечение трубы, внешний диаметр которой 1 метр. Толщина её стенок 10 мм. (или 0,01 м.). Следовательно, нам известно:
Для упрощения возьмём π = 3,14. Подставляем значения в формулу:
S = π • (D/2 – N) 2 = 3,14 • (1/2 – 0,01) 2 = 0,754 м 2 .
Некоторые физические особенности
От площади сечения трубы зависит скорость движения жидкостей и газов, которые по ней транспортируются. Надо выбрать оптимальный диаметр. Не менее важным является и внутреннее давление. Именно от его величины зависит целесообразность выбора сечения.
При расчёте учитывается не только давление, но и температура среды, её характер и свойства. Знание формул не освобождает от необходимости изучения теории. Расчёт труб канализации, водоснабжения, газоснабжения и отопления опирается на информацию справочников. Важно, чтобы выполнялись все необходимые условия при выборе сечения. Его величина также зависит и от характеристик используемого материала.
О чём стоит помнить?
Площадь сечения трубы – один из важных параметров, который следует учитывать при расчёте системы. Но наравне с тем высчитываются параметры прочности, определяется, какой материал выбрать, изучаются свойства системы в целом и пр.
Источник
ОСНОВНЫЕ ОПРЕДЕЛЕНИЯ
Возьмем любую точку в потоке жидкости. Через эту точку протекает жидкость, имеющая определенное направление и скорость движения. Если во всех точках потока направление и скорость движения жидкости не изменяются в течение времени – движение установившееся
.
Если это условие не выполняется – движение неустановившееся
.
Рассмотрим движущуюся в потоке жидкость. Возьмем любую произвольную точку и отложим вектор скорости. На небольшом расстоянии от нее, на векторе скорости, отложим следующую точку (строго говоря, это расстояние должно быть бесконечно малым
). Но в этой точке и направление движения и скорость будут иными, по сравнению с первой точкой. Если мы попытаемся повторить процедуру, аналогичную получению первого отрезка, то мы увидим, что второй отрезок не будет продолжением первого. Это построение можно продолжать, в результате чего мы получим нарисованную выше кривую. Эта кривая будет называться
линией тока
.
Линия тока
– линия, касательные к которой совпадают с векторами скорости.
Следует отличать линию тока от траектории
частицы жидкости. Линия тока является мгновенной фотографией потока. Если движение установившееся, то частица в точности пройдет по линии тока. А если нет? В следующий момент времени, когда частица подойдет к очередной точке, вектор скорости в ней будет уже другим и частица продолжит путь в другом направлении и с другой скоростью.
Живое сечение
– сечение, проведенное перпендикулярно вектору скорости и лежащее внутри потока. В общем случае живое сечение в потоке является криволинейной поверхностью, однако в практических расчетах, если поток изменяется плавно, сечение считают плоским.
Выше приведены примеры живых сечений, где стрелками отмечены векторы скорости, а пунктирными линями – живые сечения.
Представим себе поток жидкости, проведем живое сечение, в котором выделим элементарную площадку dw. Через все точки площадки проведем линии тока.
Живое
сечение
Элементарная струйка
Элементарная
площадка dw
Поток жидкости состоит из совокупности элементарных струек.
Понятие элементарной струйки позволяет получить основные зависимостидля расчета параметров движущейся жидкости. Упростить задачу оказалось возможным благодаря следующим свойствам элементарной струйки
:
1.Так как площадка dw является элементарной, то величины скорости и давления для всех точек элементарного поперечного сечения струйки можно считать одинаковыми. Это свойство позволяет не учитывать в пределах живого сечения элементарной струйки сложного характера изменения скорости и давления
.
2.Так как боковая поверхность струйки образована линиями тока, вдоль которых скользят другие частицы, то проникновение через боковую поверхность других частиц жидкости невозможно. Элементарная струйка как бы заключена в водонепроницаемые стенки, не имеющие толщины. Это свойство позволяет легко реализовать в расчетах законы сохранения массы и энергии не усложняя решение учетом массообменных процессов
.
Расход.
Расходом жидкости называется объем жидкости, проходящий в единицу времени через живое сечение.
Q= L3t, [м3/с]
Так как скорости в различных точках потока различны, расход в общем случае находят как:
Как отмечалось выше, скорости по живому сечению потока различны и их определение является достаточно сложной задачей. Практические расчеты, как правило, выполняются по интегральным показателям и производятся для всего объекта (в данном случае потока жидкости) в целом без уточнения микроструктуры. Среди таких показателей в курсе гидравлики наиболее часто используется средняя скорость.
Средняя скорость
– это средняя для данного живого сечения скорость течения и находится как:
V = Qw
В упрощенном понимании это график изменения скорости по сечению. Ниже представлен пример подобной эпюры.
vҐ
v4
v3
v2
v1
v
Как рассчитать площадь сечения трубы – простые и проверенные способы
Произвести расчет сечения трубы довольно просто, ведь для этого есть ряд стандартных формул, а также многочисленные калькуляторы и сервисы в интернете, которые могут выполнить ряд простых действий. В данном материале мы расскажем о том, как рассчитать площадь сечения трубы самостоятельно, ведь в некоторых случаях нужно учитывать ряд конструкционных особенностей трубопровода.
Формулы вычислений
При проведении вычислений нужно учитывать, что по существу трубы имеют форму цилиндра. Поэтому для нахождения площади их сечения можно воспользоваться геометрической формулой площади окружности. Зная внешний диаметр трубы и значение толщины его стенок, можно найти показатель внутреннего диаметра, который понадобится для вычислений.
Стандартная формула площади окружности такова:
π – постоянное число, равное 3,14;
S – площадь сечения трубы, вычисленная для внутреннего диаметра.
Восходящий поток – жидкость
Восходящий поток жидкости из скважины поднимается по промывочным трубам, проходит через отводную головку, шланги далее попадает в приемный чан.
Снаряд с гидроциклонным шламоулавливателем.
Восходящий поток жидкости проходит по специальному каналу, расположенному в переходнике параллельно шламо-проводящей трубе и в непосредственной близости от нее.
Промывочная головка конструкции б. ЦИСОН для обратной промывки.| Отводная головка для обратной промывки.
Восходящий поток жидкости из скважины поднимается по промывочным трубам, проходит через отвод, шланг и попадает в приемный чан.
Принципиальная схема вискозиметра с падающим шариком.
Восходящим потоком жидкости шарик 1 поднимается в верхнее положение. В момент касания шарика с верхней ограничивающей сеткой 6 насос отключается, а шарик свободно падает в неподвижной сроде.
Скорость восходящего потока жидкости в кольцевом пространстве должна быть меньше скорости оседания песка в этой же жидкости.
В восходящем потоке жидкости от забоя до устья скважины объемная доля песка по высоте имеет различное значение, как и доля мелких частиц песка и глины. Можно предположить, что плотность песчаной пробки при появлении воды будет наибольшей в той части ствола скважины, где в момент прекращения притока жидкости и, следовательно, при скорости вертикального потока, равной нулю, содержалась наиболее высокая концентрация мелких частиц глины и песка.
В этом случае восходящий поток жидкости поддерживает твердые частицы во взвешенном состоянии, препятствуя их осаждению.
В этом случае восходящий поток жидкости поддерживает твердые частицы во взвешенном состояния, препятствуя их осаждению.
В этом случае восходящий поток жидкости поддерживает твердые частицы во взвешенном состоянии, препятствуя их осаждению.
Клапаны поддерживаются открытыми восходящим потоком жидкости, движущейся относительно труб; закрытие клапанов, очевидно, должно произойти в тот момент (), когда относительная скорость w станет равной нулю.
В фильтрах с восходящим потоком жидкости крупность загрузки рекомендуется та же, что и при нисходящем потоке жидкости, а промывка может быть водяной или во-довоздушной.
Твердая частица в восходящем потоке жидкости двигается вверх, если скорость восходящего потока жидкости больше скорости оседания твердой частицы относительно, жидкости в восходящем потоке.
Виды сечений труб.
Для прокладки водопровода или канализации в строительстве применяют трубы различных форм и сечений. Для классического водопровода могут использоваться круглые, квадратные, прямоугольные, треугольные, эллипсовидные и прочие трубы. Для канализации используют трубы круглой, полукруглой, эллиптической, полуэллиптической, яйцевидной, прямоугольной, трапецеидальной и прочих форм и сечений.
Наибольшей популярностью пользуются трубы с круглой формой поперечного сечения. Изготовление таких труб малозатратно, они обладают хорошими техническими характеристиками, а также рядом отличных технических и эксплуатационных качеств.
Для расчета веса трубы, либо длины трубы вы можете воспользоваться трубным калькулятором.
Виды сечений трубопровода могут быть различными:
- а) — Круглые;
- б) — Квадратные;
- в) — Прямоугольные;
- г) — Треугольные;
- д) — Эллипсовыидные;
- е) — Кольчатые;
- а,b — Линейные размеры.
Далее представлены формы поперечных сечений самотечных труб и каналов, такие как:
- а) — Круглое,
- б) — Полукруглое,
- в) — Шатровое,
- г) — Банкетное,
- д) — Яйцевидное (овондальное),
- е) — Эллиптическое,
- ж) — Полукруглое с прямыми вставками;
- э) — Яйцевидное перевернутое,
- и) — Лотковое,
- к) — Пятиугольное,
- л) — Прямоугольное,
- м) — Трапецеидальное
Расчет сечения трубопровода.
Формула площади поперечного сечения трубы будет зависеть от того, какова форма этого сечения. Для расчета сечения трубопровода необходимо вычислить площадь круга с диаметром, который равен наружному диаметру трубы, после чего вычесть толщину ее стенок.
Площадь круга рассчитывается по формуле: S = Pi*(R^2) или S=Pi*(D/2-N)^2,
- R — радиус круга, равный половине ее внутреннего диаметра;
- S — искомое значение;
- Pi — число «пи», которое обычно округляют до 3,14.
- D и N- наружный диаметр и толщина стенки трубы.
Особенности труб с различными сечениями.
Трубы круглого сечения очень просто очищаются от образовавшегося осадка гидравлическим способом с использованием шаров и цилиндров
По мере того увеличения диаметра трубы круглого сечения, давление грунта и временной внешней нагрузки стремительно увеличиваются. Для уменьшения усилия в стенках труб, своду придают полуэллиптическое сечение.
Иногда может использоваться яйцевидная форма сечения, труба такого сечения способна высокие статические и динамические нагрузки, но такая трубы имеет и недостатки: для монтажа труб с таким сечением необходима большая высота канала и глубина заложения, чем для труб круглого сечения при одинаковой пропускной способности.
Кроме этого, в трубах эллиптического сечения намного быстрее образуется осадок, который отлаживается на стенках. В тех местах, где присутствуют плывуны и грунт очень влажный, могут использоваться трубы лотковой формы. Это позволяет прокладывать канализационные сети на меньшей глубине.
Источник
Потенциальный поток – идеальная жидкость
Потенциальный поток идеальной жидкости, плавно обтекающий какое-либо тело, обусловливает такое распределение местных нормальных давлений по поверхности тела, что результирующая этих давлений не дает составляющей в направлении вектора скорости Кос. Парадокс Эйлера противоречит повседневному опыту, указывая одновременно, что гипотеза о потенциальности и безотрывности обтекания не учитывает важных явлений при течениях реальной жидкости.
Рассмотрим потенциальный поток идеальной жидкости в колене, показанном на рис. XIV.6. Частицы жидкости, движущиеся по криволинейным траекториям, находятся под влиянием центробежных сил инерции.
Итак, если потенциальный поток идеальной жидкости, имеющий скорость на бесконечности, равную Vw, плавно обтекает некоторый контур, причем циркуляция скорости вокруг этого контура равна Г, то подъемная сила контура равна по величине произведению плотности жидкости на циркуляцию и на скорость потока в бесконечности. Чтобы определить направление подъемной силы, достаточно повернуть вектор скорости потока в бесконечнсти на 90 против направления течения, обусловленного присоединенным вихрем.
В этом случае потенциальный поток идеальной жидкости вне пограничного слоя не может моделироваться как картина плавного обтекания и должен быть заменен какой-либо другой схемой, отвечающей той или иной задаче.
Заметим, что сила сопротивления при потенциальном потоке идеальной жидкости равна нулю не только при обтекании круглого цилиндра, но и для любого другого тела, независимо от его формы.
Отсутствие силы сопротивления для тел, обтекаемых потенциальным потоком идеальной жидкости, в гидродинамике называется паоадоксом Эйлера-Даламбера.
Отсутствие силы сопротивления для тел, обтекаемых потенциальным потоком идеальной жидкости, в гидродинамике называется парадоксом Эйлера – Даламбгра.
Это распределение можно найти, решив задачу обтекания тела потенциальным потоком идеальной жидкости. Ввиду того, что пограничный слой очень тонок, найденное распределение скорости можно отнести к внешней границе слоя.
Рассмотрим обтекание цилиндра радиуса г1 с двумя симметрично расположенными вихрями потенциальным потоком идеальной жидкости. Центры симметрично расположенных вихрей возьмем в том положении, когда небольшое изменение циркуляции ведет к отрыву одного из вихрей.
Пусть имеется бесконечно глубокий потенциальный поток идеальной жидкости, движущийся над дном ( осью х) со скоростью V в – оо; пусть в этот поток со дна ( у точки х 0) втекает струя со скоростью Vz, направленная под углом а к дну, и требуется определить, как эта струя будет двигаться.
Итак, для случая сходящегося течения в диффузоре течение при больших числах Рейнольдса очень мало отличается от потенциального течения идеальной жидкости. Только вблизи стенок происходит очень быстрое изменение скорости от значений, соответствующих потенциальному потоку идеальной жидкости, до нулевых значений, требуемых условиями прилипания вязкой жидкости к стенкам
Обратим внимание на то, что сходящееся течение в диффузоре происходит в направлении падения давления. В то время, как при малых числах Рейнольдса сходящееся и расходящееся течения в диффузоре имеют одинаковый характер, при больших числах Рейнольдса течения носят совершенно различный характер, а именно, сходящееся течение всюду, кроме непосредственной близости стенок, мало отличается от потенциального течения, расходящееся же течение резко отличается от потенциального течения.
Первая попытка построить вихревую теорию сопротивления давления принадлежит Th. Набегающий потенциальный поток идеальной жидкости плавно обтекает переднюю ( лобовую) часть контура ( на фиг.
Первый – непосредственно прилегает к обтекаемому телу и обычно называется пограничным слоем. Это очень тонкий слой, в котором сосредоточено все влияние вязкости. Второй участок – след за обтекаемым телом, третий – вся остальная область, в которой влияние вязкости не сказывается, и, следовательно, ее можно рассматривать как область потенциального потока идеальной жидкости.
Первый – непосредственно прилегает к обтекаемому телу и обычно называется пограничным слоем. Это очень тонкий слой, в котором сосредоточено все влияние вязкости. Второй участок – след за обтекаемым телом, третий – вся остальная область, – в которой влияние вязкости не сказывается, и, следовательно, ее можно рассматривать как область потенциального потока идеальной жидкости.
Площадь живого сечения трубы формула
Труба — это длинное пустотелое промышленное изделие на основе полого профиля постоянного сечения, предназначенная для транспортировки жидкостей или газов.
Сечение трубы — это изображение фигуры, образованной рассечением трубы плоскостью в поперечном направлении.
Формула для расчета площади поперечного сечения трубы:
Dн — наружный диаметр трубы; Dв — внутренний диаметр трубы.
Быстро выполнить эту математическую операцию можно с помощью нашей онлайн программы. Для этого необходимо в соответствующее поле ввести исходное значение и нажать кнопку.
На этой странице представлен самый простой онлайн калькулятор расчета площади поперечного сечения трубы, если известны наружный и внутренний диаметр трубы. С помощью этого калькулятора вы в один клик сможете рассчитать площадь поперечного сечения трубы.
В гидравлических расчётах для характеристики размеров и формы поперечного сечения потока вводят понятие о живом сечении и его элементах: смоченном периметре и гидравлическом радиусе.
Живым сечением называется поверхность в пределах потока, проведённая нормально к линиям тока.
Для круглого трубопровода, когда всё поперечное сечение заполнено жидкостью, живым сечение является площадь круга:
(рис.3.6).
Смоченным периметром называют ту часть периметра живого сечения, по которой жидкость соприкасается со стенками трубопровода
(рис.3.6)
.
Смоченный периметр обычно обозначают греческой
(хи). Для круглой трубы полностью заполненной жидкостью смоченный периметр равен длине окружности: .
Гидравлическим радиусом называют отношение живого сечения к смоченному периметру, т.е. величину
.
Эта величина характеризует удельную, т.е. приходящуюся на единицу длины смоченного периметра, площадь живого сечения. Легко сделать вывод, что поток с наибольшим гидравлическим радиусом при прочих равных условиях имеет минимальную силу трения, приложенную к смоченной поверхности.
Когда это может пригодиться
Тестеры качества тормозной жидкости
Начать следует с определения случаев, когда подобные расчеты могут пригодиться:
Они могут быть полезны при необходимости рассчитать теплоотдачу через трубопровод. Всё это считается на основе площади поверхности, которая отдает окружающей среде тепловую энергию от теплоносителя. Часто необходимо определить потери тепловой энергии по пути к прибору отопления. Все это позволит определить необходимые число и габариты радиаторов. Для этого необходимо знать, сколько калорий находится в нашем распоряжении. Расчет производится также на основе площади соответствующей поверхности трубопровода, по которому теплоноситель транспортируется от узла элеватора.
С целью определить требуемый объем теплоизоляционного материала, следует также определить площадь внешней поверхности. В таком случае, чем точнее расчет, тем выше экономия средств на приобретение материала. Так как длина теплотрассы может быть равна нескольким километрам, то такая экономия может составить большую сумму.
Также расчет будет полезен при определении затрат, связанных с приобретением окрашивающего материала. Определение площади трубопровода под покраску наряду с расчётом расходования краски на один кв. м. позволяют точно получить величину суммарных затрат. Интересное предложение для новичков. У нас вы можете получить самый выгодный на сегодня промокод 1xbet абсолютно бесплатно при регистрации в компании. Просто перейдите с нашего портала на 1xbet и заведите новый аккаунт. Вам дадут действующий на сегодня промокод 1хбет при регистрации которому на ваш базовый счет начислят до 6500 рублей. Размер бонуса равняется 100% внесенной на первый депозит суммы. Если вы положили на счет 100 рублей, то по коду вам дадут столько же. Промокод 1xBet ‒ удачная возможность сделать бесплатную ставку. Узнайте как получить промокод и использовать его по назначению делая ставки в зеркале 1хБет!
Определение площади внутренней поверхности трубопровода окажется полезным при расчете её максимальной проходимости. Это позволит избежать превышения произведенных затрат на приобретение труб над требуемыми. При проектировании больших сетей коммуникаций это позволит снизить сумму затрачиваемых средств.
Формулы вычислений
При проведении вычислений нужно учитывать, что по существу трубы имеют форму цилиндра. Поэтому для нахождения площади их сечения можно воспользоваться геометрической формулой площади окружности. Зная внешний диаметр трубы и значение толщины его стенок, можно найти показатель внутреннего диаметра, который понадобится для вычислений.
Стандартная формула площади окружности такова:
π – постоянное число, равное 3,14;
S – площадь сечения трубы, вычисленная для внутреннего диаметра.
Лезем в стандарты
Признаться, есть способ избежать сколь-нибудь сложных расчетов в принципе. Дело в том, что масса погонного метра трубы прописана в таблице сортамента, которая, в свою очередь, является частью стандарта на каждый из видов труб.
Так, стальные прямоугольные трубы производятся по ГОСТ 8645-68. Заветная труба размерами 180х145х20 миллиметров находится в самом конце таблицы (она в приложении к статье), в разделе «специальные размеры». И что мы там видим?
Погонный метр трубы весит 84,1 кг. Соответственно, 18 километров трубы будут иметь массу 18000*84,1=1513800 кг, или 1513,8 тонны.
Налицо расхождение с обоими результатами. Рвем волосы на организме и бьемся головой об стену в отчаянии.
Он тоже посчитал массу трубы разными способами
Порядок расчета
Поскольку главная задача – это найти площадь проходного сечения трубы, основная формула будет несколько видоизменена.
В результате вычисления производятся так:
D – значение внешнего сечения трубы;
Примите к сведению, что, чем больше знаков в числе π вы подставите в расчеты, тем точнее они будут.
Приведем числовой пример нахождения поперечного сечения трубы, с наружным диаметром в 1 метр (N). При этом стенки имеют толщину в 10 мм (D). Не вдаваясь в тонкости, примем число π равным 3,14.
Итак, расчеты выглядят следующим образом:
S=π×(D/2-N) 2 =3,14×(1/2-0,01) 2 =0,754 м 2 .
Выводы
Их, собственно, несколько.
- Разные методики расчета дают довольно заметный разброс результатов. Если при расчете прочности металлоконструкций запас прочности в любом случае покроет с избытком отклонения от расчетного веса, то при закупке большого количества труб реальны шансы ошибиться в большую или меньшую сторону, что приведет к повторной закупке или перерасходу бюджета;
- При закупке труб разумнее опираться на цифры из ГОСТ. Исключительно потому, что в спорной ситуации ваша позиция будет более аргументированной: если согласно ГОСТ в тонне трубы должно быть 100 метров, а там оказалось 110 — значит, производитель трубы ради экономии отступил от стандартов.
- Если докупить трубу не будет большой проблемой — лучше ориентироваться на минимальное из рассчитанных значений. Просто из соображений экономии.
Удачи!
Приложение
Понравилась статья? Подписывайтесь на наш канал Яндекс.Дзен
Поток жидкости — это часть неразрывно движущейся жидкости, ограниченная твердыми деформируемыми или недеформируемыми стенками, образующими русло потока. Потоки, имеющие свободную поверхность, называются безнапорными. Потоки, не имеющие свободной поверхности, называются напорными
Поток жидкости характеризуется такими параметрами как площадь живого сечения S, расход жидкости Q(G), средняя скорость движения v.
Живое сечение потока — это сечение, которое перпендикулярно в каждой точке скорости частиц потока жидкости.
Векторы скорости частиц имеют некоторое расхождение в потоке жидкости.
Живым сечением потока жидкости называется сечение, которое перпендикулярно в каждой точке скорости частиц потока жидкости.
Рис. Векторы скорости потока жидкости (а) и живое сечение потока (б)
Поэтому живое сечение потока — криволинейная плоскость (рис. а, линия I—I) В виду незначительного расхождения векторов скорости в гидродинамике за живое сечение принимается плоскость, расположенная перпендикулярно скорости движения жидкости в средней точке потока.
Расход жидкости — это количество жидкости, протекающей через живое сечение потока в единицу времени. Расход может определяться в массовых долях G и объемных Q.
Средняя скорость движения жидкости — это средняя скорость частиц в живом сечении потока.
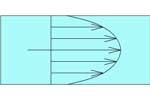
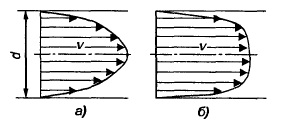
Если в живом сечении потока, движущегося, например, в трубе, построить векторы скорости частиц и соединить концы этих векторов, то получится график изменения скоростей (эпюра скоростей).
Рис. Распределение скоростей движения жидкости в живом сечении трубы при течении: а — турбулентном; б — ламинарном
Если площадь такой эпюры разделить на диаметр данной трубы, то получится значение средней скорости движения жидкости в данном сечении:
Vcр = Sэ/d,
где Sэ — площадь эпюры местных скоростей; d — диаметр трубы
Объемный расход жидкости рассчитывается по формуле:
Q = Sэ*Мср,
где Q — площадь живого сечения потока.
Параметры потока жидкости определяют характер движения жидкости. При этом оно может быть установившимся и неустановившимся, равномерным и неравномерным, неразрывным и кавитационным, ламинарным и турбулентным.
Если параметры потока жидкости не изменяются во времени, то ее движение называется установившимся.
Равномерным называется движение, при котором параметры потока не изменяются по длине трубопровода или канала. Например, движение жидкости по трубе постоянного диаметра является равномерным.
Неразрывным называется движение жидкости, при котором она перемещается сплошным потоком, заполняющим весь объем трубопровода.
Отрыв потока от стенок трубопровода или от обтекаемого предмета приводит к возникновению кавитации.
Кавитацией называется образование в жидкости пустот, заполненных газом, паром или их смесью.
Кавитация возникает в результате местного уменьшения давления ниже критического значения pкр при данной температуре (для воды ркр= 101,3 кПа при Т= 373 К или ркр= 12,18 кПа при Т= 323 К и т. д.). При попадании таких пузырьков в зону, где давление выше критического, в эти пустоты устремляются частицы жидкости, что приводит к резкому возрастанию давления и температуры. Поэтому кавитация неблагоприятно отражается на работе гидротурбин, жидкостных насосов и других элементов гидравлических устройств.
Ламинарное движение — это упорядоченное движение жидкости без перемешивания между ее соседними слоями. При ламинарном течении скорость и силы инерции, как правило, невелики, а силы трения значительны. При увеличении скорости до некоторого порогового значения ламинарный режим течения переходит в турбулентный.
Турбулентное движение — это течение жидкости, при котором ее частицы совершают неустановившееся беспорядочное движение по сложным траекториям. При турбулентном течении скорость жидкости и ее давление в каждой точке потока хаотически изменяется, при этом происходит интенсивное перемешивание движущейся жидкости.
Для определения режима движения жидкости существуют условия, согласно которым скорость потока может быть больше или меньше той критической скорости, когда ламинарное движение переходит в турбулентное и наоборот.
Однако установлен и более универсальный критерий, который называют критерием или числом Рейнольдса:
Re = vd/V,
где Re — число Рейнольдса; v — средняя скорость потока; d — диаметр трубопровода; V — кинематическая вязкость жидкости.
Опытами было установлено, что в момент перехода ламинарного режима движения жидкости в турбулентный Re = 2320.
Число Рейнольдса, при котором ламинарный режим переходит в турбулентный, называется критическим. Следовательно, при Re < 2320 движение жидкости — ламинарное, а при Re > 2320 — турбулентное. Отсюда критическая скорость для любой жидкости:
vкр = 2320v/d
Главная страница
Содержание
Введение
Основы гидростатики
Основы гидродинамики
Гидравлические сопротивления
Истечние жидкости из отверстий, насадков и из-под затворов
Гидравлический расчет простых трубопроводов
Гидравлические машины
Лекция 3. ОСНОВЫ ГИДРОДИНАМИКИ
Гидродинамика — раздел гидравлики, в котором изучаются законы движения жидкости и ее взаимодействие
с неподвижными и подвижными поверхностями.
Если отдельные частицы абсолютно твердого тела жестко связаны между собой, то в движущейся жидкой среде
такие связи отсутствуют. Движение жидкости состоит из чрезвычайно сложного перемещения отдельных молекул.
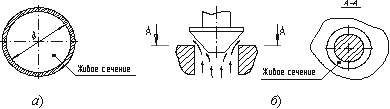
Живым сечением ω (м²) называют площадь поперечного сечения потока, перпендикулярную
к направлению течения. Например, живое сечение трубы — круг (рис.3.1, б); живое сечение клапана — кольцо с
изменяющимся внутренним диаметром (рис.3.1, б).
Рис. 3.1. Живые сечения: а — трубы, б — клапана
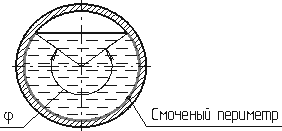
Смоченный периметр χ («хи») — часть периметра живого сечения, ограниченное твердыми
стенками (рис.3.2, выделен утолщенной линией).
Рис. 3.2. Смоченный периметр
Для круглой трубы
если угол в радианах, или
Расход потока Q — объем жидкости V, протекающей за единицу времени t через живое
сечение ω.
Средняя скорость потока υ — скорость движения жидкости, определяющаяся отношением расхода
жидкости Q к площади живого сечения ω
Поскольку скорость движения различных частиц жидкости отличается друг от друга, поэтому скорость движения
и усредняется. В круглой трубе, например, скорость на оси трубы максимальна, тогда как у стенок трубы она
равна нулю.
Гидравлический радиус потока R — отношение живого сечения к смоченному периметру
Течение жидкости может быть установившимся и неустановившимся. Установившимся движением называется
такое движение жидкости, при котором в данной точке русла давление и скорость не изменяются во времени
υ = f(x, y, z)
P = φ f(x, y, z)
Движение, при котором скорость и давление изменяются не только от координат пространства, но и от времени,
называется неустановившимся или нестационарным
υ = f1(x, y, z, t)
P = φ f1(x, y, z, t)
Линия тока (применяется при неустановившемся движении) это кривая, в каждой точке которой вектор
скорости в данный момент времени направлены по касательной.
Трубка тока — трубчатая поверхность, образуемая линиями тока с бесконечно малым поперечным сечением.
Часть потока, заключенная внутри трубки тока называется элементарной струйкой.
Рис. 3.3. Линия тока и струйка
Течение жидкости может быть напорным и безнапорным. Напорное течение наблюдается в закрытых руслах
без свободной поверхности. Напорное течение наблюдается в трубопроводах с повышенным (пониженным давлением).
Безнапорное — течение со свободной поверхностью, которое наблюдается в открытых руслах (реки, открытые
каналы, лотки и т.п.). В данном курсе будет рассматриваться только напорное течение.
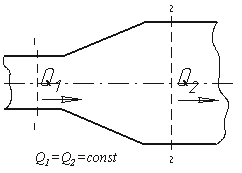
Рис. 3.4. Труба с переменным диаметром при постоянном расходе
Из закона сохранения вещества и постоянства расхода вытекает уравнение неразрывности течений.
Представим трубу с переменным живым сечением (рис.3.4). Расход жидкости через трубу в любом ее сечении
постоянен, т.е. Q1=Q2= const, откуда
ω1υ1 = ω2υ2
Таким образом, если течение в трубе является сплошным и неразрывным, то уравнение неразрывности примет вид:
Уравнение Даниила Бернулли, полученное в 1738 г., является фундаментальным уравнением гидродинамики. Оно
дает связь между давлением P, средней скоростью υ и пьезометрической высотой z
в различных сечениях потока и выражает закон сохранения энергии движущейся жидкости. С помощью этого
уравнения решается большой круг задач.
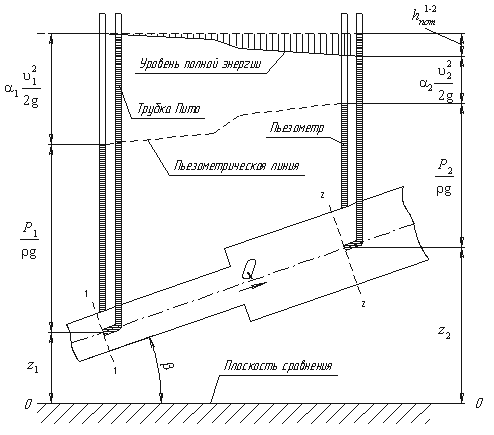
Рассмотрим трубопровод переменного диаметра, расположенный в пространстве под углом
β (рис.3.5).
Рис.3.5. Схема к выводу уравнения Бернулли для идеальной жидкости
Выберем произвольно на рассматриваемом участке трубопровода два сечения: сечение 1-1 и
сечение 2-2. Вверх по трубопроводу от первого сечения ко второму движется жидкость, расход которой
равен Q.
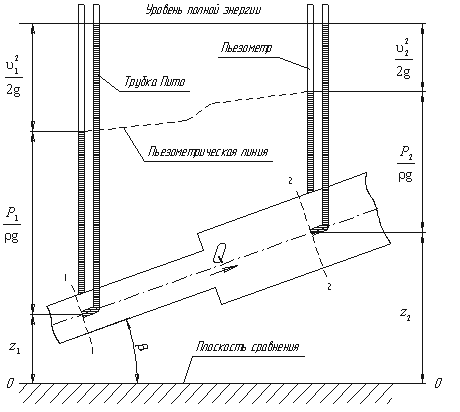
Для измерения давления жидкости применяют пьезометры — тонкостенные стеклянные трубки, в которых
жидкость поднимается на высоту 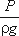
пьезометры, в которых уровень жидкости поднимается на разные высоты.
Кроме пьезометров в каждом сечении 1-1 и 2-2 установлена трубка, загнутый конец которой
направлен навстречу потоку жидкости, которая называется трубка Пито. Жидкость в трубках Пито также
поднимается на разные уровни, если отсчитывать их от пьезометрической линии.
Пьезометрическую линию можно построить следующим образом. Если между сечением 1-1 и 2-2
поставить несколько таких же пьезометров и через показания уровней жидкости в них провести кривую, то мы
получим ломаную линию (рис.3.5).
Однако высота уровней в трубках Пито относительно произвольной горизонтальной прямой 0-0, называемой
плоскостью сравнения, будет одинакова.
Если через показания уровней жидкости в трубках Пито провести линию, то она будет горизонтальна, и будет
отражать уровень полной энергии трубопровода.
Для двух произвольных сечений 1-1 и 2-2 потока идеальной жидкости уравнение Бернулли имеет
следующий вид:
Так как сечения 1-1 и 2-2 взяты произвольно, то полученное уравнение можно переписать иначе:
и прочитать так: сумма трех членов уравнения Бернулли для любого сечения потока идеальной жидкости есть
величина постоянная.
С энергетической точки зрения каждый член уравнения представляет собой определенные виды энергии:
z1 и z2 — удельные энергии положения, характеризующие потенциальную энергию в сечениях 1-1 и
2-2;
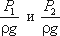
энергию давления в тех же сечениях;
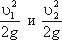
Следовательно, согласно уравнению Бернулли, полная удельная энергия идеальной жидкости в любом сечении
постоянна.
Уравнение Бернулли можно истолковать и чисто геометрически. Дело в том, что каждый член уравнения имеет
линейную размерность. Глядя на рис.3.5, можно заметить, что z1 и z2 — геометрические высоты сечений 1-1
и 2-2 над плоскостью сравнения; 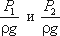
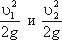
В этом случае уравнение Бернулли можно прочитать так: сумма геометрической, пьезометрической и скоростной
высоты для идеальной жидкости есть величина постоянная.
Уравнение Бернулли для потока реальной жидкости несколько отличается от уравнения
Дело в том, что при движении реальной вязкой жидкости возникают силы трения, на преодоление которых
жидкость затрачивает энергию. В результате полная удельная энергия жидкости в сечении 1-1 будет больше
полной удельной энергии в сечении 2-2 на величину потерянной энергии (рис.3.6).
Рис.3.6. Схема к выводу уравнения Бернулли для реальной жидкости
Потерянная энергия или потерянный напор обозначаются 
Уравнение Бернулли для реальной жидкости будет иметь вид:
Из рис.3.6 видно, что по мере движения жидкости от сечения 1-1 до сечения 2-2 потерянный
напор все время увеличивается (потерянный напор выделен вертикальной штриховкой). Таким образом, уровень
первоначальной энергии, которой обладает жидкость в первом сечении, для второго сечения будет складываться
из четырех составляющих: геометрической высоты, пьезометрической высоты, скоростной высоты и потерянного
напора между сечениями 1-1 и 2-2.
Кроме этого в уравнении появились еще два коэффициента α1 и α2, которые
называются коэффициентами Кориолиса и зависят от режима течения жидкости ( α = 2 для ламинарного
режима, α = 1 для турбулентного режима ).
Потерянная высота 
жидкости, и потерь, вызванных местными сопротивлениями (изменениями конфигурации потока)

С помощью уравнения Бернулли решается большинство задач практической гидравлики. Для этого выбирают два
сечения по длине потока, таким образом, чтобы для одного из них были известны величины Р, ρ,
g, а для другого сечения одна или величины подлежали определению. При двух неизвестных для второго
сечения используют уравнение постоянства расхода жидкости υ1ω
1 = υ2ω2.
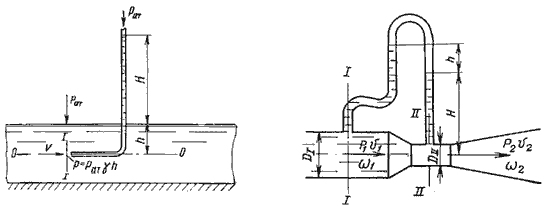
Для измерения скорости в точках потока широко используется работающая на принципе уравнения Бернулли трубка
Пито (рис.3.7), загнутый конец которой направлен навстречу потоку. Пусть требуется измерить скорость жидкости
в какой-то точке потока. Поместив конец трубки в указанную точку и составив уравнение Бернулли для сечения
1-1 и сечения, проходящего на уровне жидкости в трубке Пито получим
где Н — столб жидкости в трубке Пито.
Рис. 3.7. Трубка Пито и pасходомер Вентури
Для измерения расхода жидкости в трубопроводах часто используют расходомер Вентури, действие которого
основано так же на принципе уравнения Бернулли. Расходомер Вентури состоит из двух конических насадков с
цилиндрической вставкой между ними (рис.3.7). Если в сечениях I-I и II-II поставить пьезометры,
то разность уровней в них будет зависеть от расхода жидкости, протекающей по трубе.
Пренебрегая потерями напора и считая z1 = z2 , напишем уравнение Бернулли для сечений I-I и
II-II:
или
Используя уравнение неразрывности
Q = υ1ω1 = υ2ω2
сделаем замену в получено выражении:
Решая относительно Q, получим
Выражение, стоящее перед 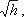
водомера Вентури.
Из полученного уравнения видно, что h зависит от расхода Q. Часто эту зависимость строят в
виде тарировочной кривой h от Q, которая имеет параболический характер.
Проверить себя ( Тест )
Наверх страницы