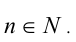Download Article
Download Article
Calculating fractions are one of the most useful math skills to develop. Before you begin working with them, learn how to identify parts and types of fractions. Then you can move on to adding and subtracting them. For more complex calculations, learn how to multiply and divide them. In most cases, you’ll also need to simplify or reduce the fraction.
-
1
Find a fraction. Fractions are written as 1 number placed over a dividing line with 1 number below it.
-
2
Identify the numerator. The number on top is called the numerator and it tells you how many parts of the fraction there are.[1]
- For example, in the fraction 1/5, 1 is the numerator.
Advertisement
-
3
Locate the denominator. The number on the bottom is called the denominator. This number tells you how many parts make up the whole number.[2]
- For example, in the fraction 1/5, 5 is the denominator so there should be 5 parts in the fraction.
-
4
Determine if the fraction is proper or improper. If the numerator is less than the denominator, the fraction is proper. For an improper fraction, the numerator is greater than the denominator.[3]
- For example, 3/4 is a proper fraction and 5/3 is an improper fraction.
- If you have a whole number with a fraction, it’s called a mixed fraction. For example, 1 1/2 is a mixed fraction.
Advertisement
-
1
Identify fractions with like denominators. If you need to add or subtract fractions, they need to have common denominators before you make your calculations. Look at the denominator on the fractions to see if they’re the same (like).
-
2
Find a common denominator if the denominators are unlike. If your denominators aren’t the same, you’ll need to change the fractions so they have the same denominators. To find a common denominator, multiply each part of a fraction by the denominator of the other fraction.[4]
- For example, to find a common denominator for 1/3 + 2/5, multiply the 1 and 3 by 5 and multiply the 2 and 5 by 3. You should get 5/15 + 6/15. Then you can calculate the fractions.
-
3
Add or subtract the numerators to calculate the fractions. Once you’ve found a common denominator and multiplied the numerators if necessary, you’re ready to add or subtract. Add or subtract the numerators and place the result over a dividing line. Put the common denominator below the line.[5]
- For example, 3/6 — 2/6 = 1/6.
- Avoid adding or subtracting denominators.
-
4
Simply the sum if necessary. If you’ve had to find a common denominator, you may end up with a large fraction that can be simplified. For example, if you added 8/32 +12/32, you’d get 20/32. This can be reduced to 5/8.[6]
Advertisement
-
1
Turn mixed fractions or whole numbers into improper fractions. To make it easier to multiply, you’ll need to work with proper or improper fractions. If you have a whole number or mixed fraction that you want to multiply, turn it into its fraction.
- For example, to multiply 2/5 by 7, turn 7 into a fraction. Then you can multiply 2/5 by 7/1.
- If you have a mixed fraction such as 1 1/3, turn it into an improper fraction, 4/3 before you multiply.
-
2
Multiply the numerators and denominators. Instead of adding the numerators, multiply both of them and write the result over your dividing line. You’ll also need to multiply the denominators and put the result under the line.[7]
- For example, to multiply 1/3 by 3/4, multiply 1 by 3 to get the numerator. Multiply 3 by 4 to get the denominator. Your answer will be 3/12.
-
3
Simplify your result. In many cases, you’ll need to reduce the result to a simplified fraction, especially if you started with improper fractions.Identify the greatest common factor and use it to simplify the numerator and denominator.[8]
- For example, if your answer is 3/12, 3 is the greatest common factor. Reduce the fraction by 3 to get 1/4.
Advertisement
-
1
Invert the second fraction. The simplest way to divide fractions, even those with unlike denominators, is to flip the second fraction before you calculate the sum.
- For example, with 5/4 ÷ 1/2 you should flip the 1/2 fraction so it appears as 2/1.
-
2
Multiply the numerators and denominators. Multiply the fractions straight across to multiply the numerators. Put the result over a dividing line and multiply the denominators. Put the result under the dividing line.[9]
- To continue the example, you’d multiply 5/4 by 2/1 to get 10/4.
-
3
Simplify the results, if needed. If your answer is an improper fraction or can be reduced, simplify the fraction. Use the greatest common factor to reduce the fraction.[10]
- For example, the greatest common factor for 10/4 is 2 so your simplified answer is 5/2.
- Since this is an improper fraction, turn it into a whole number with a fraction. 5/2 becomes 2 1/2.
Advertisement
Add New Question
-
Question
What is 5/8 times 16?
To multiply a fraction by a whole number, multiply the numerator by the whole number to get the new numerator. The denominator remains unchanged. (5/8)(16) = 80/8 = 10.
-
Question
How do I calculate 2/3 × -5/6?
(2/3)(-5/6) = [(2)(-5)] / [(3)(6)] = -10/18 = -5/9.
Ask a Question
200 characters left
Include your email address to get a message when this question is answered.
Submit
Advertisement
Video
-
Always write your fractions neatly to reduce your risk for calculation errors.
-
If you’re working with complex fractions, you’ll need to take a few extra steps to simplify them, but that’s still a necessary part of the process.
Advertisement
References
About This Article
Article SummaryX
To calculate fractions by adding or subtracting, start by finding a common denominator of the two numbers. Simply multiply the fraction by the denominator of the other fraction to make the denominators the same. For example, to find a common denominator for 1/3 + 2/5, multiply the 1 and 3 by 5 and multiply the 2 and 5 by 3 to get 5/15 + 6/15. Then, add or subtract the numerators, and use the common denominator as the denominator for your answer. For example, 5/15 + 6/15 would be 11/16. Be sure to simplify your answer if possible! If you want to learn how to multiply fractions together, keep reading the article!
Did this summary help you?
Thanks to all authors for creating a page that has been read 91,615 times.
Reader Success Stories
-
Pavithra Poojani
Mar 19, 2020
«Thanks for the explanation, it helped me to be successful.»
Did this article help you?
Содержание материала
- Понятие алгебраической дроби
- Видео
- Алгебраические дроби и их решение
- Умножение и деление дробей
- Сложение и вычитание дробей
- Наибольший общий делитель (НОД) и наименьшее общее кратное (НОК)
- Более сложные случаи сложения и вычитания дробей
- Сложные дроби
- Все действия с дробями. Расположенные многочлены в числителе и знаменателе дроби. Выделение целой части из неправильной дроби
Понятие алгебраической дроби
Начнем с определения. Под алгебраической дробью понимается выражения P/Q, где P является числителем, а Q – знаменателем. Под буквенной записью может скрываться число, числовое выражение, численно-буквенное выражение.
Прежде чем задаваться вопросом, как решать алгебраические дроби, для начала нужно понимать, что подобное выражение – часть целого.
Как правило, целое – это 1. Число в знаменателе показывает, на сколько частей разделили единицу. Числитель необходим для того, чтобы узнать, сколько элементов взято. Дробная черта соответствует знаку деления. Допускается запись дробного выражения в качестве математической операции «Деление». В таком случае числитель – делимое, знаменатель – делитель.
Алгебраические дроби и их решение
Если алгебраическое выражение, составленное из букв и чисел, содержит, кроме трех первых действий— сложения, вычитания и умножения, — также еще и деление (на буквенное выражение), то такое выражение называют дробным. Примером могут служить выражения: 





Если последнее действие, указываемое выражением, есть деление, то такое выражение называется просто «дробью (алгебраической дробью). При этом, если, кроме этого последнего действия, делений больше производить не нужно, дробь называется простой, в противном случае — сложной. Так, среди предыдущих примеров только последний нельзя назвать дробью (это сумма двух дробей); предпоследний есть сложная дробь, четыре предыдущих — простые дроби.
К сложным дробям мы обратимся несколько позднее; сначала же будем заниматься только простыми.
Простая алгебраическая дробь есть отношение двух целых алгебраических выражений, являющихся числителем и знаменателем дроби.
Мы знаем, что существует число, которое ни в коем случае не может быть знаменателем дроби: это — нуль; поэтому, если знаменатель про стой алгебраической дроби оказывается тождественное равным нулю, то сама дробь не имеет смысла ни при каких значениях входящих букв. Примером служит дробь 
Иногда это отмечают и в явной форме: например, 
В дальнейшем, говоря о данной дроби, мы всегда будем подразумевать, что буквам даются лишь такие значения, которые не обращают знаменатель в нуль. Что касается числителя дроби, то исключать из рассмотрения те случаи, когда он обращается в нуль, излишне. Напомним, что если числитель дроби равен нулю, то и сама дробь равна нулю. Обратно, если дробь равна нулю, то непременно числитель равен нулю. Итак, простая алгебраическая дробь обращается в нуль при тех и только при тех значениях входящих букв, при которых ее числитель обращается в нуль.
Из арифметики отлично известно основное свойство дроби (частного); дробь (частное) не изменяется, если числитель (делимое) и знаменатель (делитель) умножить или разделить на одно и то же число 



Число 





В виде формулы основное свойство дроби записывается следующим образом: 
Основное свойство дроби можно выразить следующими словами; если некоторое выражение входит множителем в числитель и в знаменатель алгебраической дроби, то при условии, что оно не равно нулю, можно на него «сократить» данную дробь: значение дроби при этом не меняется. И, напротив, можно умножить числитель и знаменатель алгебраической дроби на произвольное выражение при условии, что оно не обращается в нуль.
Примечание:
Равенство (1), выражающее основное свойство дроби, считается тождеством, несмотря на то, что его левая часть теряет смысл при 

Вообще за равенством двух алгебраических выражений принято сохранять наименование тождества и в том случае, если одно из этих выражений или оба теряют смысл при некоторых исключительных значениях входящих букв. Такое расширенное понимание тождества, между прочим, позволяет относить сокращение дроби на буквенное выражение к числу тождественных преобразований.
Руководствуясь основным свойством дроби, можно сокращать алгебраическую дробь (как и арифметическую) на буквенные или числовые множители, входящие одновременно в ее числитель и в ее знаменатель.
Если таких множителей нет, дробь называют несократимой.
Например, дробь 


Левая и правая часть равенства тождественно равны (хотя левая теряет смысл при 

Мы переходим дальше к изучению действий над алгебраическими дробями — сложения, вычитания, умножения и деления. Выполнить одно из этих действий над данными простыми дробями — значит не только соединить эти дроби соответственным знаком, но также и произвести над полученным выражением тождественные преобразования, целью которых является представить это выражение в виде простой дроби (или целого выражения). Производя действия над дробями, стараются вместе с тем сокращать дробь на общие множители числителя и знаменателя.
При изучении действий над дробями мы начнем с более легких — умножения и деления, а затем перейдем к более трудным — сложению и вычитанию. Те случаи, когда какие-нибудь из данных выражений оказываются целыми, мы не будем рассматривать отдельно, так как всякое целое выражение можно представить в виде дробного, именно, подписывая под ним в качестве знаменателя единицу.
Умножение и деление дробей
Правило умножения арифметических дробей выражается формулой: 
Написанная выше формула справедлива не только в том случае, если входящие буквы имеют целые положительные значения, но и в том случае, если эти значения — дробные; она справедлива также и в том случае, если некоторые из входящих букв имеют отрицательные значения. Значение нуль, конечно, исключено для знаменателей, но не исключено для числителей.
Но раз равенство (*) имеет место при всех значениях входящих букв (кроме тех исключительных, при которых знаменатели дробей обращаются в нуль), то оно является тождеством.
Таким образом, правило умножения алгебраических дробей выражается той же формулой и формулируется теми же словами, что и правило умножения арифметических дробей.
В алгебре вместо того, чтобы вычесть некоторое число, можно прибавить число, противоположное по знаку: 
Таким же образом вместо того, чтобы разделить на некоторое число (не равное нулю), достаточно умножить на величину, обратную этому числу: 
Действительно, следуя правилу умножения, мы получаем: 
Так как величина, обратная дроби 


Чтобы разделить на дробь, достаточно умножить на величину, ей обратную («разделить на числитель и умножить на знаменатель).
Сложение и вычитание дробей
Сложить две алгебраические дроби означает — представить их сумму в виде одной алгебраической дроби; то же — для вычитания.
Если данные дроби имеют один и тот же знаменатель, то, чтобы сложить их — в алгебре, как и в арифметике, — достаточно составить дробь с тем же знаменателем и с числителем, равным сумме числителей: 
Это — распределительный закон деления, справедливый при любом 
Если же складываемые дроби имеют различные знаменатели, то в алгебре, как и в арифметике, необходимо предварительно привести дроби к общему знаменателю. При этом пользуются основным свойством дроби — основным тождеством (*) , в котором мы теперь поменяем местами правую и левую части: 
Желая сложить две дроби 






Подобным же образом, ссылаясь на распределительный закон деления и на основное свойство дроби, выведите общую формулу вычитания дробей: 
При действиях с дробями часто приходится пользоваться важным частным случаем основного свойства дроби (*) 



Таким образом, значение дроби не меняется при одновременном изменении знаков числителя и знаменателя.
Так как 
Отсюда следует: если мы меняем знак знаменателя, то, чтобы значение дроби не изменилось, достаточно еще изменить знак, или числителя или самой дроби; если мы меняем знак числителя, то, чтобы значение дроби не изменилось, достаточно еще изменить знак или знаменателя или самой дроби. Например,
Наибольший общий делитель (НОД) и наименьшее общее кратное (НОК)
В арифметике указывается правило для нахождения наибольшего общего делителя (НОД) и наименьшего общего кратного (НОК) нескольких целых чисел.
Пусть даны числа 





Составим новое число из данных чисел следующим образом: возьмем каждый встречающийся множитель в наименьшей из степеней, в которых он встречается, и затем перемножим: 
Полученное число 


Составим другое число из данных чисел, отбирая каждый встречающийся множитель в наибольшей из степеней, в которых он встречается, и перемножая: 



Таким же образом можно составлять НОД и НОК алгебраических одночленных выражений с целыми коэффициентами, обращаясь при этом с буквами как с целыми числами (хотя буквы могут иметь какие угодно, в том числе и дробные, значения). Так, если даны выражения 










Наибольший общий делитель двух чисел может быть полезен в арифметике при сокращении дробей: найдя НОД числителя и знаменателя и сократив на него, мы сразу получаем несократимую дробь. При этом нахождение НОД стоит некоторого труда, так как не всегда очевидно с первого взгляда, каковы простые множите ли данного числа и в каких степенях они входят.
В алгебре же такого рода применение НОД излишне, так как буквенные множители выписываются явно.
Если, например, дана дробь 




Зато в алгебре НОД приносит больше пользы при вынесении за скобку общих множителей много членных выражений. Пусть дано выражение 
Мы видим сразу, что НОД всех членов равен 

Что касается наименьшего общего кратного, то мы увидим дальше, что в алгебре, как и в арифметике, оно позволяет значительно упрощать записи при сложении и вычитании дробей.
Более сложные случаи сложения и вычитания дробей
При сложении и вычитании дробей удобно пользоваться приемом составления общего знаменателя посредством перемножения знаменателей данных дробей только в том случае, если каждые два, попарно взятые, знаменателя не имеют общих — ни буквенных, ни числовых — множителей. В других случаях употребление этого приема, хотя и дает верный результат, однако, ни коим образом не может быть рекомендовано, так как ведет к лишним записям и потере времени. Общее правило таково: в качестве общего знаменателя нескольких дробей следует брать НОК знаменателей всех данных дробей. Предварительно необходимо каждый знаменатель представить как про изведение отдельных множителей; в частности, если данный знаменатель — многочлен, нужно общие числовые и буквенные множители его членов выносить за скобку. Если встречаются многочленные множители, отличающиеся только знаком, то знак нужно менять, пользуясь уже известными приемами.
После того как общий знаменатель найден, необходимо выяснить, на какой один и тот же «дополнительный множитель» придется умножить знаменатель и числитель каждой дроби для того, чтобы ее знаменатель стал равным выбранному общему знаменателю.
Дальше, раз уже дроби приведены к общему знаменателю, сделать сложение или вычитание не представляет труда.
Пример:
Произведение знаменателей равно 







Итак,
Пример:

HOK знаменателей равно 



Пример:
Принимая во внимание, что 


Теперь ясно, что наименьшее общее кратное знаменателей равно 






Сложные дроби
Если приходится выполнять деление над выражениями, уже содержащими дроби, то, записывая частное в виде дроби (с чертой), мы получаем сложную дробь. Для облегчения записи в таких случаях иногда пользуются знаком двоеточия, но смысл получаемого от этого, конечно, не изменяется. Например, если 



Сложную дробь всегда можно преобразовать в простую. Для этого достаточно выполнить все действия в том порядке, как они указаны: сначала числитель и знаменатель сложной дроби записать в виде простых дробей и затем разделить дробь на дробь, согласно правилу деления. Так, в нашем примере мы получим:
Однако такой способ преобразования сложной дроби в простую практически менее удобен, чем следующий. Пользуясь основным свойством дроби, умножим в нашем примере числитель и знаменатель на 

В качестве множителя, на который умножаются и числитель и знаменатель данной сложной дроби, следует, конечно, выбирать НОК знаменателей всех дробей, содержащихся в числителе и знаменателе данной дроби.
Всякое дробное алгебраическое выражение содержит лишь конечное число делений. Поэтому, сколько бы ни было «этажей» о сложной дроби, такую дробь всегда можно преобразовать в простую, постепенно уничтожая «этажи». Отсюда следует, что дробное алгебраическое выражение всегда может быте представлено в виде отношения двух целых алгебраических выражений.
Все действия с дробями. Расположенные многочлены в числителе и знаменателе дроби. Выделение целой части из неправильной дроби
Выполняя указанные действия над данными, простыми или сложными, алгебраическими дробями, мы получаем в результате простую алгебраическую дробь.
Если числители и знаменатели данных дробей — многочлены, расположенные по степеням одной и той же буквы, то числитель и знаменатель дроби, получающейся в результате выполнения действий, также представляются в виде многочленов, расположенных по степеням той же буквы.
После этого, если удастся в числителе и знамена теле обнаружить общие множители, на них следует сокращать полученную дробь.
Простая дробь, у которой числитель и знаменатель — многочлены, расположенные по степеням одной и той же буквы, называется: правильной, если степень числителя меньше, чем степень знаменателя; неправильной, если степень числителя больше или равна степени знаменателя.
Если дробь — неправильная, то ее всегда можно представить в виде суммы многочлена и правильной дроби. Это делается посредством деления числителя на знаменатель.
Неправильная дробь равна сумме: 1) частного, получающегося при делении числителя на знаменатель, и 2) правильной дроби, у которой числитель равен остатку при этом делении, а знаменатель — знаменателю данной дроби.
Например, деля многочлен 



Описанное выше преобразование напоминает выделение целой части из неправильной арифметической дроби; сравните хотя бы с таким примером:
По указанной причине это преобразование называется выделением целой части из неправильной алгебраической дроби.
Видео
Теги
В данной публикации мы рассмотрим, каким образом можно найти дробь от целого числа и наоборот – как найти число, если известно, чему равна определенная дробь от него. Также разберем примеры решения задач для лучшего понимания и закрепления теоретического материала.
- Нахождение дроби от числа
- Нахождение числа по значению дроби
Нахождение дроби от числа
Чтобы найти часть от целого числа n, которая представлена дробью, нужно умножить эту дробь (например, a/b) на данное число n.
Дробь от числа = n ⋅
a/b
=
n ⋅ a/b
Пример 1
Решение
5/12
⋅ 24 =
5 ⋅ 24/12
=
120/12
= 10
Пример 2
Решение
4/9
⋅ 7 =
4 ⋅ 7/9
=
28/9
=3
1/9
Таким образом, результат нахождения дроби числа не всегда бывает целым числом.
Примечание: если дробь является смешанной, сперва ее следует представить в виде неправильной и только потом выполнять умножение.
Нахождение числа по значению дроби
Если известно сколько число n занимает в числе m, и эта доля выражена в виде дроби, то для нахождения числа m используется формула:
Пример:
Один ряд кинозала вмещает 20 кресел, что составляет
2/5
от всей вместимости зала. Определите, сколько всего посадочных мест в зале.
Решение
Общее количество кресел равняется:
20 :
2/5
= 20 ⋅
5/2
=
20 ⋅ 5/2
= 50
Арифметическая (обыкновенная) дробь — это число, составленное из целого числа долей единицы. Дробь изображается символом p/q, где р — числитель дроби, он показывает число взятых долей единицы и делится на столько долей, сколько показывает (знаменует) знаменатель q. Дробь можно рассматривать как частное от деления одного (целого) числа р на другое (натуральное) q .
В старину в России дроби назывались ломаными числами (например, в «Арифметике» Магницкого и в «Недоросле» Фонвизина).
Обыкновенная дробь р /q называется правильной, если её числитель по модулю меньше знаменателя, или |p/q| < 1, и неправильной в противном случае (понятие модуля будет введено в разделе 2). Неправильная дробь может быть представлена в виде суммы целого числа и правильной дроби (смешанная дробь). Для этого надо числитель разделить (с остатком) на знаменатель. Например,
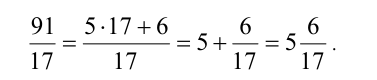
Обыкновенную дробь называют сократимой, если существует такое отличное от единицы натуральное число n , что 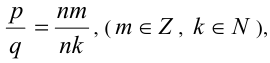
Две дроби называют равными, если их несократимые представления совпадают. Например, дроби 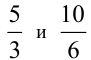
Это даёт возможность любые две дроби привести к общему знаменателю, т.е. найти соответственно равные им дроби, знаменатели которых совпадают. При этом наименьшим общим знаменателем для двух данных дробей будет, очевидно, наименьшее общее кратное их знаменателей (в несократимых представлениях). Аналогичным образом можно приводить к общему знаменателю три дроби и более.
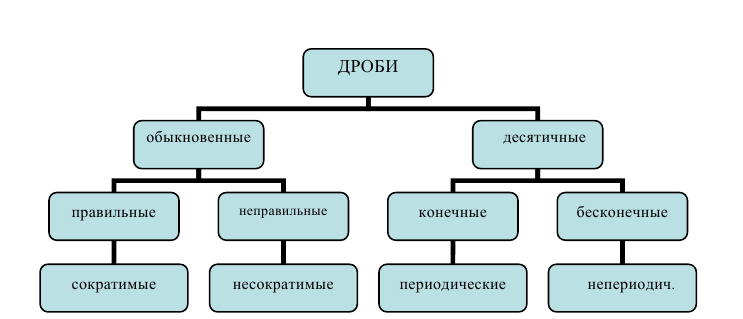
Дробь p/q называется десятичной, если её знаменатель q является натуральной степенью числа 10. Для десятичной дроби используется запись
(черту сверху часто опускают), где 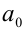
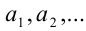
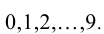
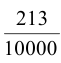
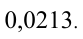
Бесконечные десятичные дроби разбиваются на два класса: периодические, когда, начиная с некоторого момента, одна и та же группа цифр неограниченно повторяется, и непериодические, если не существует такой бесконечно повторяющейся группы цифр после запятой. Повторяющуюся группу цифр после запятой называют периодом и заключают в круглые скобки. Например, вместо 0,2353535… пишут 0,2(35). Читается: «ноль целых, две десятых и тридцать пять в периоде».
Если число 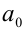
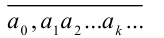
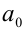
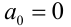
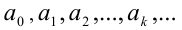
Операции над дробями встречаются уже в древнеегипетском папирусе Ахмеса (ок. 2000 г. до н.э.). У древних индийцев, по-видимому, впервые зародилось современное обозначение дробей. Термин «дробь» вошел в европейскую математику от арабов через Леонардо Пизанского (1202), термины «числитель» и «знаменатель» встречаются у Максима Плануда (конец XIII века). Однако изложение обыкновенных дробей в учебниках арифметики европейских школ произошло только в XVIII в. Дроби усваивались учениками с огромными трудностями. Например, в предисловии к 16-му изданию «Арифметики» Уингейта (Англия) сказано, что в этом издании «изложение арифметики целых чисел, необходимой для денежных расчётов, для торговли и других приложений, даётся раньше, чем открывается доступ к крутым и трудным путям дробей, при одном виде которых некоторые учащиеся приходят в такое уныние, что останавливаются и восклицают: ради бога, не дальше!». Даже в знаменитой Итонской школе для аристократов, существующей с 1446 г., арифметика стала обязательным предметом преподавания только в 1851 г.
Пример. Доказать, что дробь 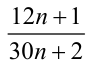
Доказательство. 1-й способ (по определению сократимой дроби). Предположим, от противного, что данная дробь сократима на некоторое натуральное число р , отличное от единицы. Тогда найдутся такие натуральные числа m и k , что 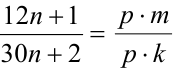
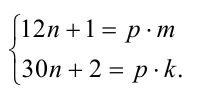
Исключим из уравнений системы величину n. Для этого умножим первое равенство на 5, второе на 2 и вычтем из первого второе:
Проанализируем полученное равенство. В правой его части стоит произведение двух целочисленных множителей: р и 5m — 2k, а слева — единица. Понятно, что в этой ситуации р может принимать только значение, равное единице. Полученное противоречие означает, что предположение о сократимости дроби было неверным.
2-й способ. При этом способе решения используются два очевидных утверждения: во-первых, дроби 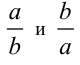
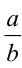
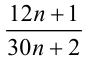
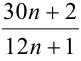
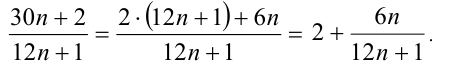
Тогда дробь 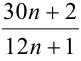
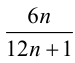
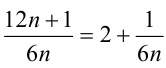
3-й способ. Используя последовательно свойство «Если 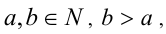
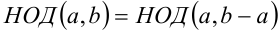
Таким образом, числитель и знаменатель дроби являются взаимно простыми числами, следовательно, данная дробь несократима.
Эта лекция взята со страницы, где размещён подробный курс лекций по предмету математика:
Предмет математика
Эти страницы возможно вам будут полезны: