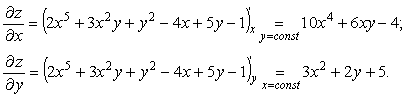Как найти значение частной производной в точке

Частная производная функции в точке

Как найти значение?

Постановка задачи

Найти значение частной производной функции $ u(x,y,z) $ в точке $ M(x_0,y_0,z_0) $

План решения

Частная производная в точке обозначается и вычисляется по формуле:

$$ frac{partial u}{partial x} bigg |_{M(x_0,y_0,z_0)} = frac{partial u}{partial x} (x_0,y_0,z_0) $$

$$ frac{partial u}{partial y} bigg |_{M(x_0,y_0,z_0)} = frac{partial u}{partial y} (x_0,y_0,z_0) $$

$$ frac{partial u}{partial z} bigg |_{M(x_0,y_0,z_0)} = frac{partial u}{partial z} (x_0,y_0,z_0) $$

1. Находим частные производные, к примеру первого порядка:
   $$ frac{partial u}{partial x}; frac{partial u}{partial y}; frac{partial u}{partial z} $$
2. Подставляем координаты $ x_0,y_0,z_0 $ точки $ M $ в полученные частные производные вместо $ x,y,z $:
   $$ frac{partial u}{partial x} (x_0,y_0,z_0); frac{partial u}{partial y} (x_0,y_0,z_0); frac{partial u}{partial z} (x_0,y_0,z_0) $$
3. Вычисляем выражения и записываем ответ

Примеры решений 

Пример 1

Найти частную производную $ u = xy + ln(y^3+z^3) $ в точке $ M(1,2,3) $

Решение

Берем частные производные первого порядка: $$ frac{partial u}{partial x} = y $$ $$ frac{partial u}{partial y} = x + frac{3y^2}{y^3+z^3} $$ $$ frac{partial u}{partial z} = frac{3z^2}{y^3+z^3} $$ Подставляем координаты точки $ M $ вместо $ x,y,z $ в полученные выражения и находим значения частных производных в точке: $$ frac{partial u}{partial x} (1,2,3) = 2 $$ $$ frac{partial u}{partial y} (1,2,3) = 1 + frac{3 cdot 4}{8+27} = 1 + frac{12}{35} = 1.34 $$ $$ frac{partial u}{partial z} (1,2,3) = frac{3 cdot 9}{8+27} = frac{27}{35} = 0.77 $$ Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение онлайн. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя!

Ответ

$$ frac{partial u}{partial x} (1,2,3) = 2; frac{partial u}{partial y} (1,2,3) = 1.34; frac{partial u}{partial z} (1,2,3) = 0.77 $$

ЛЕКЦИЯ
2.
ЧАСТНЫЕ
ПРОИЗВОДНЫЕ И
ПОЛНЫЙ ДИФФЕРЕНЦИАЛ ФУНКЦИИ
ДВУХ ПЕРЕМЕННЫХ

Частные
производные функции двух переменных.
Зафиксируем значение одной из переменных
функции

,
тогда

становится функцией этой одной переменной
и по ней можно брать производную или
дифференциал (если они существуют).
Такие производные и дифференциалы
называются частными.

Определение
2.1.
Частной
производной первого порядка
функции

по переменной

(
)
в точке

называется
предел отношения приращения функции
по

(
)
к приращению самой переменной при
стремлении последнего к нулю:

(
).

Таким образом,
частной
производной по аргументу

функции

является производная этой функции по

при постоянном

,
а частной
производной по аргументу

– производная этой функции при постоянном

.

Обозначения:

,

,

,

.

Частная производная
функции

по переменной

выражает скорость изменения функции в
данном направлении (
),
или скорость изменения функции

одной
переменной

.

Определение
2.2.
Частными
производными второго порядка
функции

называются частные производные от её
частных производных первого порядка.

Они обозначаются:

,

,

,

,

,

,

,

.

Частные производные

,

называются смешанными
частными производными второго порядка.

Отметим, что
смешанные частные производные второго
порядка равны между собой. Это замечание
справедливо для смешанных производных
любого порядка.

Таким образом,
частная производная

-го
порядка функции

есть первая частная производная от её
частной производной

-го
порядка.

Аналогично
определяются и вычисляются частные
производные второго и высших порядков
от функции трёх и большего числа
переменных.

► Пример.
Найти
частные производные второго порядка
функций:

а)

;

б)

;

в)

в точке

.

Решение.
а) Найдем
частные производные первого порядка:

;

.

Найдем частные
производные второго порядка:

;

;

;

.

Действительно,

.
◄

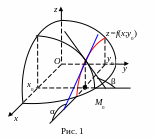
Геометрический
смысл частных производных функции двух
переменных.
Графиком функции

является некоторая поверхность (рис.
1). Уравнение

задаёт плоскость, параллельную
координатной плоскости

.
Линию пересечения функции

и плоскости

описывает функция

или

(функция одной переменной).
Её
производная в точке

имеет
вид:

.

Геометрический
смысл этой
производной:

,

где

– угол между осью

и касательной к кривой

в точке

.

Аналогично,

,
где

– угол между осью

и касательной к кривой

в точке

.

Полное приращение
и полный дифференциал функции двух
переменных

Определение
2.3.
Полным
приращением функции
двух переменных называется изменение
функции при заданных приращениях всех
переменных.

В частности, полным
приращением функции

в точке

является разность

.

Представим эту
разность следующим образом:

.

Рассмотрим частную
производную функции

в точке


по переменной

:

.
По определению 2.1 частных производных

.

Тогда

,

где

при

.

Преобразуем
последнее равенство:

,

где

при

,

при

.

Далее

,

где

при

,

.

В итоге получаем

,

где

при

,

.

Аналогично

,

где

при

,

.

Запишем полное
приращение функции

в точке

с учетом проведённых преобразований:

,

где

,

при

,

.

Сумма первых двух
слагаемых в последнем равенстве
представляет собой главную
часть приращения функции.

Определение
2.4.
Полным
дифференциалом

в точке

функции

называется главная линейная относительно

и

часть полного приращения функции в этой
точке:

.

Дифференциалы
независимых переменных равны их
приращениям:

,

,

поэтому полный
дифференциал функции

находится по формуле:

,

где

– частный дифференциал функции

по переменной

,

– частный дифференциал функции

по переменной

.

Аналогично
определяется полный дифференциал
функции любого числа переменных. Функция,
имеющая полный дифференциал в данной
точке, называется дифференцируемой
в этой точке.
Таким образом, если в данной точке и
некоторой её окрестности частные
производные функции непрерывны, то
функция дифференцируема в этой точке
(обратное также верно).

Полным дифференциалом
второго порядка функции

называется полный дифференциал её
полного дифференциала:

.

Таким образом,
получаем

.

► Пример.
Найти
полные дифференциалы первого и второго
порядков функции

.

Решение.
Находим
частные производные первого порядка:

,

.

Полный дифференциал
первого порядка данной функции имеет
вид:

.

Находим частные
производные второго порядка:

,

,

.

Полный дифференциал
второго порядка данной функции имеет
вид:

.◄

При достаточно
малых

и

для дифференцируемой в точке

функции

верно приближенное равенство

или

,

откуда

Последняя формула
для приближенных вычислений значения
функции

в точке

.

► Пример.
Найти
изменение объема конуса с высотой 30 см
и радиусом основания 10 см при увеличении
этих измерений на 3 мм и на 1 мм
соответственно.

Решение.
Объем конуса

есть функция двух переменных

и

.
Для решения задачи используем приближенное
равенство:

или

.

Найдем значения
частных производных

и

в точке

:

,

;

,

.

Так
как

см и

см, то

(см³).
◄

5

Соседние файлы в предмете Высшая математика

• #
• #
• #
• #
• #
• #
• #

Частные производные

Частной производной по x функции z = f(x,y) в точке A(x₀,y₀) называется предел отношения частного приращения по x функции в точке A к приращению ∆x при стремлении ∆x к нулю.

Частные производные функции z(x,y) находятся по следующим формулам:

Вторые частные производные функции z(x,y) находятся по формулам:



Смешанные частные производные функции z(x,y) находятся по формулам:

Назначение сервиса. Сервис используется для нахождения частных производных функции (см. пример). Решение производится в онлайн режиме и оформляется в формате Word.

• Решение онлайн
• Видеоинструкция
• Также решают

Правила ввода функции, заданной в явном виде

1. 
   
2. 
   
3. 
   

Примеры

x2+xy ≡ x^2+x*y.

cos2(2x+y) ≡ (cos(2*x+y))^2

≡ (x-y)^(2/3)

Правила ввода функции, заданной в неявном виде

1. Все переменные выражаются через x,y,z
2. 
   
3. 
   

Примеры

≡ x^2/(z+y)

cos2(2x+zy) ≡ (cos(2*x+z*y))^2

≡ z+(x-y)^(2/3)

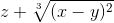
Частные производные используются, например, при нахождении полного дифференциала и экстремумов функции.

Частные производные функции нескольких переменных

Ели одному из аргументов функции z = f(x,y) придать приращение, а другой аргумент не изменять, то функция получит частное приращение по одному из аргументов: Δxz=f(x+Δx,y)-f(x,y) – это частное приращение функции z по аргументу x; Δyz=f(x,y+Δy)-f(x,y) – это частное приращение функции z по аргументу у.

Частной производной функции нескольких переменных по одному из её аргументов называется предел отношения частного приращения функции по этому аргументу к соответствующему приращению аргумента при условии, что приращение аргумента стремится к нулю:

– это частная производная функции z по аргументу x;

– это частная производная функции z по аргументу у.

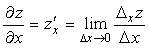
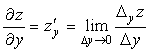
Чтобы вычислить частную производную ФНП по одному из её аргументов, нужно все другие её аргументы считать постоянными и проводить дифференцирование по правилам дифференцирования функции одного аргумента.

Пример 1. z=2x5+3x2y+y2–4x+5y-1

Пример 2. Найти частные производные функции z = f(x;y) в точке A(x₀;y₀).



Находим частные производные:





Найдем частные производные в точке А(1;1)





Находим вторые частные производные:

Найдем смешанные частные производные:

Задать свои вопросы или оставить замечания можно внизу страницы в разделе Disqus.
Можно также оставить заявку на помощь в решении своих задач у наших проверенных партнеров (здесь или здесь).

Частные производные для функции от нескольких переменных

21 сентября 2015

Рассмотрим функцию от двух переменных:

[f=fleft( x,y right)]

Поскольку переменные $x$ и $y$ являются независимыми, для такой функции можно ввести понятие частной производной:

Частная производная функции $f$ в точке $M=left( {{x}_{0}};{{y}_{0}} right)$ по переменной $x$ — это предел

[{{{f}’}_{x}}=underset{Delta xto 0}{mathop{lim }},frac{fleft( {{x}_{0}}+Delta x;{{y}_{0}} right)}{Delta x}]

Аналогично можно определить частную производную по переменной $y$ :

[{{{f}’}_{y}}=underset{Delta yto 0}{mathop{lim }},frac{fleft( {{x}_{0}};{{y}_{0}}+Delta y right)}{Delta y}]

Другими словами, чтобы найти частную производную функции нескольких переменных, нужно зафиксировать все остальные переменные, кроме искомой, а затем найти обычную производную по этой искомой переменной.

Отсюда вытекает основной приём для вычисления таких производных: просто считайте, что все переменные, кроме данной, являются константой, после чего дифференцируйте функцию так, как дифференцировали бы «обычную» — с одной переменной. Например:

$begin{align}& {{left( {{x}^{2}}+10xy right)}_{x}}^{prime }={{left( {{x}^{2}} right)}^{prime }}_{x}+10ycdot {{left( x right)}^{prime }}_{x}=2x+10y, \& {{left( {{x}^{2}}+10xy right)}_{y}}^{prime }={{left( {{x}^{2}} right)}^{prime }}_{y}+10xcdot {{left( y right)}^{prime }}_{y}=0+10x=10x. \end{align}$

Очевидно, что частные производные по разным переменным дают разные ответы — это нормально. Куда важнее понимать, почему, скажем, в первом случае мы спокойно вынесли $10y$ из-под знака производной, а во втором — вовсе обнулили первое слагаемое. Всё это происходит из-за того, что все буквы, кроме переменной, по которой идёт дифференцирование, считаются константами: их можно выносить, «сжигать» и т.д.

Что такое «частная производная»?

Сегодня мы поговорим о функциях нескольких переменных и о частных производных от них. Во-первых, что такое функция нескольких переменных? До сих пор мы привыкли считать функцию как $yleft( x right)$ или $tleft( x right)$, или любую переменную и одну-единственную функцию от нее. Теперь же функция у нас будет одна, а переменных несколько. При изменении $y$ и $x$ значение функции будет меняться. Например, если $x$ увеличится в два раза, значение функции поменяется, при этом если $x$ поменяется, а $y$ не изменится, значение функции точно так же изменится.

Разумеется, функцию от нескольких переменных, точно так же как и от одной переменной, можно дифференцировать. Однако поскольку переменных несколько, то и дифференцировать можно по разным переменным. При этом возникают специфические правила, которых не было при дифференцировании одной переменной.

Прежде всего, когда мы считаем производную функции от какой-либо переменной, то обязаны указывать, по какой именно переменной мы считаем производную — это и называется частной производной. Например, у нас функция от двух переменных, и мы можем посчитать ее как по $x$, так и по $y$ — две частных производных у каждой из переменных.

Во-вторых, как только мы зафиксировали одну из переменных и начинаем считать частную производную именно по ней, то все остальные, входящие в эту функцию, считаются константами. Например, в $zleft( xy right)$, если мы считаем частную производную по $x$, то везде, где мы встречаем $y$, мы считаем ее константой и обращаемся с ней именно как с константой. В частности при вычислении производной произведения мы можем выносить $y$ за скобку (у нас же константа), а при вычислении производной суммы, если у нас где-то получается производная от выражения, содержащего $y$ и не содержащего $x$, то производная этого выражения будет равна «нулю» как производная константы.

На первый взгляд может показаться, что я рассказываю о чем-то сложном, и многие ученики по началу путаются. Однако ничего сверхъестественного в частных производных нет, и сейчас мы убедимся в этом на примере конкретных задач.

Задачи с радикалами и многочленами

Задача № 1

Чтобы не терять время зря, с самого начала начнем с серьезных примеров.

[zleft( x,y right)=sqrt{frac{y}{x}}]

Для начала напомню такую формулу:

[{{left( sqrt{x} right)}^{prime }}_{x}=frac{1}{2sqrt{x}}]

Это стандартное табличное значение, которое мы знаем из стандартного курса.

В этом случае производная $z$ считается следующим образом:

[{{{z}’}_{x}}={{left( sqrt{frac{y}{x}} right)}^{prime }}_{x}=frac{1}{2sqrt{frac{y}{x}}}{{left( frac{y}{x} right)}^{prime }}_{x}]

Давайте еще раз, поскольку под корнем стоит не $x$, а некое другое выражение, в данном случае $frac{y}{x}$, то сначала мы воспользуемся стандартным табличным значением, а затем, поскольку под корнем стоит не $x$, а другое выражение, нам необходимо домножить нашу производную на еще одну из этого выражения по той же самой переменной. Давайте для начала посчитаем следующее:

[{{left( frac{y}{x} right)}^{prime }}_{x}=frac{{{{{y}’}}_{x}}cdot x-ycdot {{{{x}’}}_{x}}}{{{x}^{2}}}=frac{0cdot x-ycdot 1}{{{x}^{2}}}=-frac{y}{{{x}^{2}}}]

Возвращаемся к нашему выражению и записываем:

[{{{z}’}_{x}}={{left( sqrt{frac{y}{x}} right)}^{prime }}_{x}=frac{1}{2sqrt{frac{y}{x}}}{{left( frac{y}{x} right)}^{prime }}_{x}=frac{1}{2sqrt{frac{y}{x}}}cdot left( -frac{y}{{{x}^{2}}} right)]

В принципе, это все. Однако оставлять ее в таком виде неправильно: такую конструкцию неудобно использовать для дальнейших вычислений, поэтому давайте ее немного преобразуем:

[frac{1}{2sqrt{frac{y}{x}}}cdot left( -frac{y}{{{x}^{2}}} right)=frac{1}{2}cdot sqrt{frac{x}{y}}cdot frac{y}{{{x}^{2}}}=]

[=-frac{1}{2}cdot sqrt{frac{x}{y}}cdot sqrt{frac{{{y}^{2}}}{{{x}^{4}}}}=-frac{1}{2}sqrt{frac{xcdot {{y}^{2}}}{ycdot {{x}^{4}}}}=-frac{1}{2}sqrt{frac{y}{{{x}^{3}}}}]

Ответ найден. Теперь займемся $y$:

[{{{z}’}_{y}}={{left( sqrt{frac{y}{x}} right)}^{prime }}_{y}=frac{1}{2sqrt{frac{y}{x}}}cdot {{left( frac{y}{x} right)}^{prime }}_{y}]

Выпишем отдельно:

[{{left( frac{y}{x} right)}^{prime }}_{y}=frac{{{{{y}’}}_{y}}cdot x-ycdot {{{{x}’}}_{y}}}{{{x}^{2}}}=frac{1cdot x-ycdot 0}{{{x}^{2}}}=frac{1}{x}]

Теперь записываем:

[{{{z}’}_{y}}={{left( sqrt{frac{y}{x}} right)}^{prime }}_{y}=frac{1}{2sqrt{frac{y}{x}}}cdot {{left( frac{y}{x} right)}^{prime }}_{y}=frac{1}{2sqrt{frac{y}{x}}}cdot frac{1}{x}=]

[=frac{1}{2}cdot sqrt{frac{x}{y}}cdot sqrt{frac{1}{{{x}^{2}}}}=frac{1}{2}sqrt{frac{x}{ycdot {{x}^{2}}}}=frac{1}{2sqrt{xy}}]

Все сделано.

Задача № 2

[zleft( x,y right)=frac{xy}{{{x}^{2}}+{{y}^{2}}+1}]

Этот пример одновременно и проще, и сложней, чем предыдущий. Сложнее, потому что здесь больше действий, а проще, потому что здесь нет корня и, кроме того, функция симметрична относительно $x$ и $y$, т.е. если мы поменяем $x$ и $y$ местами, формула от этого не изменится. Это замечание в дальнейшем упростит нам вычисление частной производной, т.е. достаточно посчитать одну из них, а во второй просто поменять местами $x$ и $y$.

Приступаем к делу:

[{{{z}’}_{x}}={{left( frac{xy}{{{x}^{2}}+{{y}^{2}}+1} right)}^{prime }}_{x}=frac{{{left( xy right)}^{prime }}_{x}left( {{x}^{2}}+{{y}^{2}}+1 right)-xy{{left( {{x}^{2}}+{{y}^{2}}+1 right)}^{prime }}_{x}}{{{left( {{x}^{2}}+{{y}^{2}}+1 right)}^{2}}}]

Давайте посчитаем:

[{{left( xy right)}^{prime }}_{x}=ycdot {{left( x right)}^{prime }}=ycdot 1=y]

Однако многим ученикам такая запись непонятна, поэтому запишем вот так:

[{{left( xy right)}^{prime }}_{x}={{left( x right)}^{prime }}_{x}cdot y+xcdot {{left( y right)}^{prime }}_{x}=1cdot y+xcdot 0=y]

Таким образом, мы еще раз убеждаемся в универсальности алгоритма частных производных: каким бы мы образом их не считали, если все правила применяются верно, ответ будет один и тот же.

Теперь давайте разберемся еще с одной частной производной из нашей большой формулы:

[{{left( {{x}^{2}}+{{y}^{2}}+1 right)}^{prime }}_{x}={{left( {{x}^{2}} right)}^{prime }}_{x}+{{left( {{y}^{2}} right)}^{prime }}_{x}+{{{1}’}_{x}}=2x+0+0]

Подставим полученные выражения в нашу формулу и получим:

[frac{{{left( xy right)}^{prime }}_{x}left( {{x}^{2}}+{{y}^{2}}+1 right)-xy{{left( {{x}^{2}}+{{y}^{2}}+1 right)}^{prime }}_{x}}{{{left( {{x}^{2}}+{{y}^{2}}+1 right)}^{2}}}=]

[=frac{ycdot left( {{x}^{2}}+{{y}^{2}}+1 right)-xycdot 2x}{{{left( {{x}^{2}}+{{y}^{2}}+1 right)}^{2}}}=]

[=frac{yleft( {{x}^{2}}+{{y}^{2}}+1-2{{x}^{2}} right)}{{{left( {{x}^{2}}+{{y}^{2}}+1 right)}^{2}}}=frac{yleft( {{y}^{2}}-{{x}^{2}}+1 right)}{{{left( {{x}^{2}}+{{y}^{2}}+1 right)}^{2}}}]

По $x$ посчитано. А чтобы посчитать $y$ от того же самого выражения, давайте не будем выполнять всю ту же последовательность действий, а воспользуемся симметрией нашего исходного выражения — мы просто заменим в нашем исходном выражении все $y$ на $x$ и наоборот:

[{{{z}’}_{y}}=frac{xleft( {{x}^{2}}-{{y}^{2}}+1 right)}{{{left( {{x}^{2}}+{{y}^{2}}+1 right)}^{2}}}]

За счет симметрии мы посчитали это выражение гораздо быстрее.

Нюансы решения

Для частных производных работают все стандартные формулы, которые мы используем для обычных, а именно, производная частного. При этом, однако, возникают свои специфические особенности: если мы считаем частную производную $x$, то когда мы получаем ее по $x$, то рассматриваем ее как константу, и поэтому ее производная будет равна «нулю».

Как и в случае с обычными производными, частную (одну и ту же) можно посчитать несколькими различными способами. Например, ту же конструкцию, которую мы только что посчитали, можно переписать следующим образом:

[{{left( frac{y}{x} right)}^{prime }}_{x}=ycdot {{left( frac{1}{x} right)}^{prime }}_{x}=-yfrac{1}{{{x}^{2}}}]

Далее мы точно таким же образом считаем еще две конструкции, а именно:

[{{left( xy right)}^{prime }}_{x}=ycdot {{{x}’}_{x}}=ycdot 1=y]

Вместе с тем, с другой стороны, можно использовать формулу от производной суммы. Как мы знаем, она равна сумме производных. Например, запишем следующее:

[{{left( {{x}^{2}}+{{y}^{2}}+1 right)}^{prime }}_{x}=2x+0+0=2x]

Теперь, зная все это, давайте попробуем поработать с более серьезными выражениями, поскольку настоящие частные производные не ограничиваются одними лишь многочленами и корнями: там встречаются и тригонометрия, и логарифмы, и показательная функция. Сейчас этим и займемся.

Задачи с тригонометрическими функциями и логарифмами

Задача № 1

[zleft( x,y right)=sqrt{x}cos frac{x}{y}]

Запишем следующие стандартные формулы:

[{{left( sqrt{x} right)}^{prime }}_{x}=frac{1}{2sqrt{x}}]

[{{left( cos x right)}^{prime }}_{x}=-sin x]

Вооружившись этими знаниями, попробуем решить:

[{{{z}’}_{x}}={{left( sqrt{x}cdot cos frac{x}{y} right)}^{prime }}_{x}={{left( sqrt{x} right)}^{prime }}_{x}cdot cos frac{x}{y}+sqrt{x}cdot {{left( cos frac{x}{y} right)}^{prime }}_{x}=]

Отдельно выпишем одну переменную:

[{{left( cos frac{x}{y} right)}^{prime }}_{x}=-sin frac{x}{y}cdot {{left( frac{x}{y} right)}^{prime }}_{x}=-frac{1}{y}cdot sin frac{x}{y}]

Возвращаемся к нашей конструкции:

[=frac{1}{2sqrt{x}}cdot cos frac{x}{y}+sqrt{x}cdot left( -frac{1}{y}cdot sin frac{x}{y} right)=frac{1}{2sqrt{x}}cdot cos frac{x}{y}-frac{sqrt{x}}{y}cdot sin frac{x}{y}]

Все, по $x$ мы нашли, теперь давайте займемся вычислениями по $y$:

[{{{z}’}_{y}}={{left( sqrt{x}cdot cos frac{x}{y} right)}^{prime }}_{y}={{left( sqrt{x} right)}^{prime }}_{y}cdot cos frac{x}{y}+sqrt{x}cdot {{left( cos frac{x}{y} right)}^{prime }}_{y}=]

Опять же посчитаем одно выражение:

[{{left( cos frac{x}{y} right)}^{prime }}_{y}=-sin frac{x}{y}cdot {{left( frac{x}{y} right)}^{prime }}_{y}=-sin frac{x}{y}cdot xcdot left( -frac{1}{{{y}^{2}}} right)]

Возвращаемся к исходному выражению и продолжаем решение:

[=0cdot cos frac{x}{y}+sqrt{x}cdot frac{x}{{{y}^{2}}}sin frac{x}{y}=frac{xsqrt{x}}{{{y}^{2}}}cdot sin frac{x}{y}]

Все сделано.

Задача № 2

[zleft( x,y right)=ln left( x+ln y right)]

Запишем необходимую нам формулу:

[{{left( ln x right)}^{prime }}_{x}=frac{1}{x}]

Теперь посчитаем по $x$:

[{{{z}’}_{x}}={{left( ln left( x+ln y right) right)}^{prime }}_{x}=frac{1}{x+ln y}.{{left( x+ln y right)}^{prime }}_{x}=]

[=frac{1}{x+ln y}cdot left( 1+0 right)=frac{1}{x+ln y}]

По $x$ найдено. Считаем по $y$:

[{{{z}’}_{y}}={{left( ln left( x+ln y right) right)}^{prime }}_{y}=frac{1}{x+ln y}.{{left( x+ln y right)}^{prime }}_{y}=]

[=frac{1}{x+ln y}left( 0+frac{1}{y} right)=frac{1}{yleft( x+ln y right)}]

Задача решена.

Нюансы решения

Итак, от какой бы функции мы не брали частную производную, правила остаются одними и теми же, независимо от того, работаем ли мы с тригонометрией, с корнями или с логарифмами.

Неизменными остаются классические правила работы со стандартными производными, а именно, производная суммы и разности, частного и сложной функции.

Последняя формула чаще всего и встречается при решении задач с частными производными. Мы встречаемся с ними практически везде. Ни одной задачи еще не было, чтобы там нам она не попадалась. Но какой бы мы формулой не воспользовались, нам все равно добавляется еще одно требование, а именно, особенность работы с частными производными. Как только мы фиксируем одну переменную, все остальные оказываются константами. В частности, если мы считаем частную производную выражения $cos frac{x}{y}$ по $y$, то именно $y$ и является переменной, а $x$ везде остается константой. То же самое работает и наоборот. Ее можно выносить за знак производной, а производная от самой константы будет равна «нулю».

Все это приводит к тому, что частные производные от одного и того же выражения, но по разным переменным могут выглядеть совершенно по-разному. Например, посмотрим такие выражения:

[{{left( x+ln y right)}^{prime }}_{x}=1+0=1]

[{{left( x+ln y right)}^{prime }}_{y}=0+frac{1}{y}=frac{1}{y}]

Задачи с показательными функциями и логарифмами

Задача № 1

[zleft( x,y right)={{e}^{x}}{{e}^{frac{x}{y}}}]

Для начала запишем такую формулу:

[{{left( {{e}^{x}} right)}^{prime }}_{x}={{e}^{x}}]

Зная этот факт, а также производную сложной функции, давайте попробуем посчитать. Я сейчас решу двумя различными способами. Первый и самый очевидный — это производная произведения:

[{{{z}’}_{x}}={{left( {{e}^{x}}cdot {{e}^{frac{x}{y}}} right)}^{prime }}_{x}={{left( {{e}^{x}} right)}^{prime }}_{x}cdot {{e}^{frac{x}{y}}}+{{e}^{x}}cdot {{left( {{e}^{frac{x}{y}}} right)}^{prime }}_{x}=]

[={{e}^{x}}cdot {{e}^{frac{x}{y}}}+{{e}^{x}}cdot {{e}^{frac{x}{y}}}cdot {{left( frac{x}{y} right)}^{prime }}_{x}=]

Давайте решим отдельно следующее выражение:

[{{left( frac{x}{y} right)}^{prime }}_{x}=frac{{{{{x}’}}_{x}}cdot y-x.{{{{y}’}}_{x}}}{{{y}^{2}}}=frac{1cdot y-xcdot 0}{{{y}^{2}}}=frac{y}{{{y}^{2}}}=frac{1}{y}]

Возвращаемся к нашей исходной конструкции и продолжаем решение:

[={{e}^{x}}cdot {{e}^{frac{x}{y}}}+{{e}^{x}}cdot {{e}^{frac{x}{y}}}cdot frac{1}{y}={{e}^{x}}cdot {{e}^{frac{x}{y}}}left( 1+frac{1}{y} right)]

Все, по $x$ посчитано.

Однако как я и обещал, сейчас постараемся посчитать эту же частную производную другим способом. Для этого заметим следующее:

[{{e}^{x}}cdot {{e}^{frac{x}{y}}}={{e}^{x+frac{x}{y}}}]

В этом запишем так:

[{{left( {{e}^{x}}cdot {{e}^{frac{x}{y}}} right)}^{prime }}_{x}={{left( {{e}^{x+frac{x}{y}}} right)}^{prime }}_{x}={{e}^{x+frac{x}{y}}}cdot {{left( x+frac{x}{y} right)}^{prime }}_{x}={{e}^{x+frac{x}{y}}}cdot left( 1+frac{1}{y} right)]

В результате мы получили точно такой же ответ, однако объем вычислений оказался меньшим. Для этого достаточно было заметить, что при произведении показатели можно складывать.

Теперь посчитаем по $y$:

[{{{z}’}_{y}}={{left( {{e}^{x}}cdot {{e}^{frac{x}{y}}} right)}^{prime }}_{y}={{left( {{e}^{x}} right)}^{prime }}_{y}cdot {{e}^{frac{x}{y}}}+{{e}^{x}}cdot {{left( {{e}^{frac{x}{y}}} right)}^{prime }}_{y}=]

[=0cdot {{e}^{frac{x}{y}}}+{{e}^{x}}cdot {{e}^{frac{x}{y}}}cdot {{left( frac{x}{y} right)}^{prime }}_{y}=]

Давайте решим одно выражение отдельно:

[{{left( frac{x}{y} right)}^{prime }}_{y}=frac{{{{{x}’}}_{y}}cdot y-xcdot {{{{y}’}}_{y}}}{{{y}^{2}}}=frac{0-xcdot 1}{{{y}^{2}}}=-frac{1}{{{y}^{2}}}=-frac{x}{{{y}^{2}}}]

Продолжим решение нашей исходной конструкции:

[={{e}^{x}}cdot {{e}^{frac{x}{y}}}cdot left( -frac{x}{{{y}^{2}}} right)=-frac{x}{{{y}^{2}}}cdot {{e}^{x}}cdot {{e}^{frac{x}{y}}}]

Разумеется, эту же производную можно было бы посчитать вторым способом, ответ получился бы таким же.

Задача № 2

[zleft( x,y right)=xln left( {{x}^{2}}+y right)]

Посчитаем по $x$:

[{{{z}’}_{x}}={{left( x right)}_{x}}cdot ln left( {{x}^{2}}+y right)+xcdot {{left( ln left( {{x}^{2}}+y right) right)}^{prime }}_{x}=]

Давайте посчитаем одно выражение отдельно:

[{{left( ln left( {{x}^{2}}+y right) right)}^{prime }}_{x}=frac{1}{{{x}^{2}}+y}cdot {{left( {{x}^{2}}+y right)}^{prime }}_{x}=frac{2x}{{{x}^{2}}+y}]

Продолжим решение исходной конструкции: $$

[1cdot ln left( {{x}^{2}}+y right)+xcdot frac{2x}{{{x}^{2}}+y}=ln left( {{x}^{2}}+y right)+frac{2{{x}^{2}}}{{{x}^{2}}+y}]

Вот такой ответ.

Осталось по аналогии найти по $y$:

[{{{z}’}_{y}}={{left( x right)}^{prime }}_{y}.ln left( {{x}^{2}}+y right)+xcdot {{left( ln left( {{x}^{2}}+y right) right)}^{prime }}_{y}=]

Одно выражение посчитаем как всегда отдельно:

[{{left( {{x}^{2}}+y right)}^{prime }}_{y}={{left( {{x}^{2}} right)}^{prime }}_{y}+{{{y}’}_{y}}=0+1=1]

Продолжаем решение основной конструкции:

[xcdot frac{1}{{{x}^{2}}+y}cdot 1=frac{x}{{{x}^{2}}+y}]

Все посчитано. Как видите, в зависимости от того, какая переменная берется для дифференцирования, ответы получаются совершенно разные.

Нюансы решения

Вот яркий пример того, как производную одной и той же функции можно посчитать двумя различными способами. Вот смотрите:

[{{{z}’}_{x}}=left( {{e}^{x}}cdot {{e}^{frac{x}{y}}} right)={{left( {{e}^{x}} right)}^{prime }}_{x}cdot {{e}^{frac{x}{y}}}+{{e}^{x}}cdot {{left( {{e}^{frac{x}{y}}} right)}^{prime }}_{x}=]

[={{e}^{x}}cdot {{e}^{frac{x}{y}}}+{{e}^{x}}cdot {{e}^{frac{x}{y}}}cdot frac{1}{y}={{e}^{x}}cdot {{e}^{^{frac{x}{y}}}}left( 1+frac{1}{y} right)]

[{{{z}’}_{x}}={{left( {{e}^{x}}.{{e}^{frac{x}{y}}} right)}^{prime }}_{x}={{left( {{e}^{x+frac{x}{y}}} right)}^{prime }}_{x}={{e}^{x+frac{x}{y}}}.{{left( x+frac{x}{y} right)}^{prime }}_{x}=]

[={{e}^{x}}cdot {{e}^{^{frac{x}{y}}}}left( 1+frac{1}{y} right)]

При выборе разных путей, объем вычислений может быть разный, но ответ, если все выполнено верно, получится одним и тем же. Это касается как классических, так и частных производных. При этом еще раз напоминаю: в зависимости от того, по какой переменной идет взятие производной, т.е. дифференцирование, ответ может получиться совершенно разный. Посмотрите:

[{{left( ln left( {{x}^{2}}+y right) right)}^{prime }}_{x}=frac{1}{{{x}^{2}}+y}cdot {{left( {{x}^{2}}+y right)}^{prime }}_{x}=frac{1}{{{x}^{2}}+y}cdot 2x]

[{{left( ln left( {{x}^{2}}+y right) right)}^{prime }}_{y}=frac{1}{{{x}^{2}}+y}cdot {{left( {{x}^{2}}+y right)}^{prime }}_{y}=frac{1}{{{x}^{2}}+y}cdot 1]

В заключение для закрепления всего этого материала давайте попробуем посчитать еще два примера.

Задачи с тригонометрической функция и функцией с тремя переменными

Задача № 1

[zleft( x,y right)={{3}^{xsin y}}]

Давайте запишем такие формулы:

[{{left( {{a}^{x}} right)}^{prime }}={{a}^{x}}cdot ln a]

[{{left( {{e}^{x}} right)}^{prime }}={{e}^{x}}]

Давайте теперь решать наше выражение:

[{{{z}’}_{x}}={{left( {{3}^{xsin y}} right)}^{prime }}_{x}={{3}^{x.sin y}}cdot ln 3cdot {{left( xcdot sin y right)}^{prime }}_{x}=]

Отдельно посчитаем такую конструкцию:

[{{left( xcdot sin y right)}^{prime }}_{x}={{{x}’}_{x}}cdot sin y+x{{left( sin y right)}^{prime }}_{x}=1cdot sin y+xcdot 0=sin y]

Продолжаем решать исходное выражение:

[={{3}^{xsin y}}cdot ln 3cdot sin y]

Это окончательный ответ частной переменной по $x$. Теперь посчитаем по $y$:

[{{{z}’}_{y}}={{left( {{3}^{xsin y}} right)}^{prime }}_{y}={{3}^{xsin y}}cdot ln 3cdot {{left( xsin y right)}^{prime }}_{y}=]

Решим одно выражение отдельно:

[{{left( xcdot sin y right)}^{prime }}_{y}={{{x}’}_{y}}cdot sin y+x{{left( sin y right)}^{prime }}_{y}=0cdot sin y+xcdot cos y=xcdot cos y]

Решаем до конца нашу конструкцию:

[={{3}^{xcdot sin y}}cdot ln 3cdot xcos y]

Задача № 2

[tleft( x,y,z right)=x{{e}^{y}}+y{{e}^{z}}]

На первый взгляд этот пример может показаться достаточно сложным, потому что здесь три переменных. На самом деле, это одна из самых простых задач в сегодняшнем видеоуроке.

Находим по $x$:

[{{{t}’}_{x}}={{left( x{{e}^{y}}+y{{e}^{z}} right)}^{prime }}_{x}={{left( xcdot {{e}^{y}} right)}^{prime }}_{x}+{{left( ycdot {{e}^{z}} right)}^{prime }}_{x}=]

[={{left( x right)}^{prime }}_{x}cdot {{e}^{y}}+xcdot {{left( {{e}^{y}} right)}^{prime }}_{x}=1cdot {{e}^{y}}+xcdot o={{e}^{y}}]

Теперь разберемся с $y$:

[{{{t}’}_{y}}={{left( xcdot {{e}^{y}}+ycdot {{e}^{z}} right)}^{prime }}_{y}={{left( xcdot {{e}^{y}} right)}^{prime }}_{y}+{{left( ycdot {{e}^{z}} right)}^{prime }}_{y}=]

[=xcdot {{left( {{e}^{y}} right)}^{prime }}_{y}+{{e}^{z}}cdot {{left( y right)}^{prime }}_{y}=xcdot {{e}^{y}}+{{e}^{z}}]

Мы нашли ответ.

Теперь остается найти по $z$:

[{{{t}’}_{z}}={{left( xcdot {{e}^{y}}+{{y}^{z}} right)}^{prime }}_{z}={{left( xcdot {{e}^{y}} right)}^{prime }}_{z}+{{left( ycdot {{e}^{z}} right)}^{prime }}_{z}=0+ycdot {{left( {{e}^{z}} right)}^{prime }}_{z}=ycdot {{e}^{z}}]

Мы посчитали третью производную, на чем решение второй задачи полностью завершено.

Нюансы решения

Как видите, ничего сложного в этих двух примерах нет. Единственное, в чем мы убедились, так это в том, что производная сложной функции применяется часто и в зависимости от того, какую частную производную мы считаем, мы получаем разные ответы.

В последней задаче нам было предложено разобраться с функцией сразу от трех переменных. Ничего страшного в этом нет, однако в самом конце мы убедились, что все они друг от друга существенно отличаются.

Ключевые моменты

Окончательные выводы из сегодняшнего видеоурока следующие:

1. Частные производные считаются так же, как и обычные, при этом, чтобы считать частную производную по одной переменной, все остальные переменные, входящие в данную функцию, мы принимаем за константы.
2. При работе с частными производными мы используем все те же стандартные формулы, что и с обычными производными: сумму, разность, производную произведения и частного и, разумеется, производную сложной функции.

Конечно, просмотра одного этого видеоурока недостаточно, чтобы полностью разобраться в этой теме, поэтому прямо сейчас на моем сайте именно к этому видео есть комплект задач, посвященных именно сегодняшней теме — заходите, скачивайте, решайте эти задачи и сверяйтесь с ответом. И после этого никаких проблем с частными производными ни на экзаменах, ни на самостоятельных работах у вас не будет. Конечно, это далеко не последний урок по высшей математике, поэтому заходите на наш сайт, добавляйтесь ВКонтакте, подписывайтесь на YouTube, ставьте лайки и оставайтесь с нами!

Смотрите также:

1. Производная параметрической функции
2. Системы линейных уравнений: основные понятия
3. Сравнение дробей
4. Четырехугольная пирамида в задаче C2
5. Задача B5: вычисление площади методом обводки
6. Задача B4: вклад в банке и проценты

Частные производные, дифференциал, производная по направлению, градиент.

Список литературы:

2. Б. П. Демидович. Сборник задач и упражнений по математическому анализу 624 стр. М.: «ЧеРо», 1997

Пусть $(x_1, …, x_k, .., x_n) -$  произвольная фиксированная точка из области определения функции $u=f(x_1, …, x_n).$ Придавая значению переменной $x_k,,, (k=1, 2, …, n)$ приращение $delta x_k,$ рассмотрим предел $$limlimits_{delta x_krightarrow 0}frac{f(x_1,…,x_k+delta x_k,…,x_n)-f(x_1,…,x_k,…,x_n)}{delta x_k}.$$

Этот предел называется частной производной (1-го порядка) данной функции по переменной $x_k$ в точке $(x_1, …, x_n)$ и обозначается $frac{partial u}{partial x_k}$ или $f’_{x_k}(x_1, …, x_n).$

Частные производные вычисляются по обычным правилам и формулам дифференцирования (при этом все переменные, кроме $x_k,$ рассматриваются как постоянные).

Частными производными 2-го порядка функции $u=f(x_1, x_2, …, x_n)$ называются частные производные от ее частных производных первого порядка. Производные второго порядка обозначаются следующим образом: $$frac{partial}{partial x_k}left(frac{partial u}{partial x_k}right)=frac{partial^2u}{partial x^2_k}=f»_{x_kx_k}(x_1, x_2, …, x_k, …, x_n).$$ $$frac{partial}{partial x_l}left(frac{partial u}{partial x_k}right)=frac{partial^2u}{partial x_kpartial x_l}=f»_{x_kx_l}(x_1, x_2, …, x_k, …, x_l, …, x_n).$$ и т. д.

Аналогично определяются и обозначаются частные производные порядка выше второго.

Примеры:

Найти  частные производные 1-го и 2-го порядков от заданных функций:

7.55. $z=x^5+y^5-5x^3y^3.$

Решение.

$$z’_x=(x^5+y^5-5x^3y^3)’_x=5x^4-15x^2y^3;$$

$$z’_y=(x^5+y^5-5x^3y^3)’_y=5y^4-15x^3y^2;$$

$$z’_{xx}=(5x^4-15x^2y^3)’_x=20x^3-30xy^3;$$

$$z’_{xy}=(5x^4-15x^2y^3)’_y=-45x^2y^2;$$

$$z’_{yy}=(5y^4-15x^3y^2)’_y=20y^3-30x^3y;$$

$$z’_{yx}=(5y^4-15x^3y^2)’_x=-45x^2y^2.$$

Ответ: $z’_x=5x^4-15x^2y^3;$ $z’_y=5y^4-15x^3y^2;$ $z’_{xx}=20x^3-30xy^3;$ $z’_{xy}=-45x^2y^2;$ $z’_{yy}=20y^3-30x^3y;$ $z’_{yx}=-45x^2y^2.$

7.57. $z=frac{xy}{sqrt{x^2+y^2}}.$

Решение.

$$z’_x=left(frac{xy}{sqrt{x^2+y^2}}right)’_x=frac{ysqrt{x^2+y^2}-xyfrac{2x}{2sqrt{x^2+y^2}}}{x^2+y^2}=frac{y(x^2+y^2)-x^2y}{(x^2+y^2)sqrt{x^2+y^2}}=$$ $$=frac{y^3}{(x^2+y^2)sqrt{x^2+y^2}};$$

$$z’_y=left(frac{xy}{sqrt{x^2+y^2}}right)’_y=frac{xsqrt{x^2+y^2}-xyfrac{2y}{2sqrt{x^2+y^2}}}{x^2+y^2}=frac{x(x^2+y^2)-xy^2}{(x^2+y^2)sqrt{x^2+y^2}}=$$ $$=frac{x^3}{(x^2+y^2)sqrt{x^2+y^2}};$$

$$z’_{xx}=left(frac{y^3}{(x^2+y^2)^{3/2}}right)’_x=-frac{3}{2}y^32x(x^2+y^2)^{-5/2}=-3y^3x(x^2+y^2)^{-5/2};$$

$$z’_{xy}=left(frac{y^3}{(x^2+y^2)^{3/2}}right)’_y=frac{3y^2(x^2+y^2)^{3/2}-frac{3}{2}y^3(x^2+y^2)^{1/2}cdot 2y}{(x^2+y^2)^3}=$$ $$=frac{3y^2(x^2+y^2)-3y^4}{(x^2+y^2)^{5/2}}=frac{3y^2x^2}{(x^2+y^2)^{5/2}};$$

$$z’_{yy}=left(frac{x^3}{(x^2+y^2)^{3/2}}right)’_y=-frac{3}{2}x^32y(x^2+y^2)^{-5/2}=-3x^3y(x^2+y^2)^{-5/2};$$

$$z’_{yx}=left(frac{x^3}{(x^2+y^2)^{3/2}}right)’_x=frac{3x^2(x^2+y^2)^{3/2}-frac{3}{2}x^3(x^2+y^2)^{1/2}cdot 2x}{(x^2+y^2)^3}=$$ $$=frac{3x^2(x^2+y^2)-3x^4}{(x^2+y^2)^{5/2}}=frac{3x^2y^2}{(x^2+y^2)^{5/2}}.$$

Ответ: $z’_x=frac{y^3}{(x^2+y^2)sqrt{x^2+y^2}};$ $z’_y=frac{x^3}{(x^2+y^2)sqrt{x^2+y^2}};$ $z’_{xx}=-3y^3x(x^2+y^2)^{-5/2};$ $z’_{xy}=frac{3y^2x^2}{(x^2+y^2)^{5/2}};$ $z’_{yy}=-3x^3y(x^2+y^2)^{-5/2};$ $z’_{yx}=frac{3x^2y^2}{(x^2+y^2)^{5/2}}.$

7.61.$z=ln(x^2+y^2).$

Решение.

$$z’_x=left(ln(x^2+y^2)right)’_x=frac{2x}{x^2+y^2};$$

$$z’_y=left(ln(x^2+y^2)right)’_y=frac{2y}{x^2+y^2};$$

$$z’_{xx}=left(frac{2x}{x^2+y^2}right)’_x=frac{2(x^2+y^2)-2xcdot 2x}{x^2+y^2}=frac{2(-x^2+y^2)}{x^2+y^2};$$

$$z’_{xy}=left(frac{2x}{x^2+y^2}right)’_y=2xcdot 2yfrac{-1}{(x^2+y^2)^2}=frac{-4xy}{(x^2+y^2)^2};$$

$$z’_{yy}=left(frac{2y}{x^2+y^2}right)’_x=frac{2(x^2+y^2)-2ycdot 2y}{x^2+y^2}=frac{2(x^2-y^2)}{x^2+y^2};$$

$$z’_{yx}=left(frac{2y}{x^2+y^2}right)’_x=2ycdot 2xfrac{-1}{(x^2+y^2)^2}=frac{-4xy}{(x^2+y^2)^2}.$$

Ответ: $z’_x=frac{2x}{x^2+y^2};$ $z’_y=frac{2y}{x^2+y^2};$ $z’_{xx}=frac{2(-x^2+y^2)}{x^2+y^2};$ $z’_{xy}=frac{-4xy}{(x^2+y^2)^2};$ $z’_{yy}=frac{2(x^2-y^2)}{x^2+y^2};$ $z’_{yx}=frac{-4xy}{(x^2+y^2)^{2}}.$

7.66. Найти $f’_x(3, 2),, f’_y(3, 2),$ $f’_{xx}(3, 2),, f’_{xy}(3, 2),$ $f’_{yy}(3, 2),$ если $f(x, y)=x^3y+xy^2-2x+3y-1.$

Решение.

Найдем частные производные:

$$f’_x=left(x^3y+xy^2-2x+3y-1right)’_x=3x^2y+y^2;$$

$$f’_y=left(x^3y+xy^2-2x+3y-1right)’_y=x^3+2xy+3;$$

$$f’_{xx}=left(3x^2y+y^2right)’_x=6xy;$$

$$f’_{xy}=left(3x^2y+y^2right)’_y=3x^2+2y;$$

$$f’_{yy}=left(x^3+2xy+3right)’_x=2x.$$

Теперь найдем значения частных производных в точке $(3, 2):$

$$f’_x(3, 2)=(3x^2y+y^2)|_{(3,2)}=54+4=58;$$

$$f’_y(3, 2)=(x^3+2xy+3)|_{(3,2)}=27+12+3=42;$$

$$f’_{xx}(3, 2)=6xy|_{(3,2)}=36;$$

$$f’_{xy}(3, 2)=(3x^2+2y)|_{(3,2)}=27+4=31;$$

$$f’_{yy}(3, 2)=2x|_{(3,2)}=6.$$

Ответ: $f’_x(3, 2)=58,, f’_y(3, 2)=42,$ $f’_{xx}(3, 2)=36,, f’_{xy}(3, 2)=31,$ $f’_{yy}(3, 2)=4.$

7.79. Показать, что $left(frac{partial z}{partial x}right)^2+frac{partial z}{partial y}+x+z=0,$ если $z=4e^{-2y}+(2x+4y-3)e^{-y}-x-1.$

Решение.

Найдем частные производные:

$$frac{partial z}{partial x}=(4e^{-2y}+(2x+4y-3)e^{-y}-x-1)’_x=2e^{-y}-1;$$

$$frac{partial z}{partial y}=(4e^{-2y}+(2x+4y-3)e^{-y}-x-1)’_y=-8e^{-2y}+4e^{-y}-(2x+4y-3)e^{-y}.$$

$$left(frac{partial z}{partial x}right)^2+frac{partial z}{partial y}+x+z=$$ $$=left(2e^{-y}-1right)^2+left(-8e^{-2y}+4e^{-y}-(2x+4y-3)e^{-y}right)+$$ $$+x+4e^{-2y}+(2x+4y-3)e^{-y}-x-1=$$ $$=4e^{-2y}-4e^{-y}+1-8e^{-2y}+4e^{-y}-2xe^{-y}-4ye^{-y}+3e^{-y}+$$ $$+4e^{-2y}+2xe^{-y}+4ye^{-y}-3e^{-y}-1=0.$$ 

Ответ: доказано.

Для дифференциала функции $u=f(x_1, x_2,…,x_n)$ справедлива формула $$du=frac{partial u}{partial x_1}dx_1+frac{partial u}{partial x_2}dx_2+…+frac{partial u}{partial x_n}dx_n.$$

Функции $u, , v$ нескольких переменных подчиняются обычным правилам дифференцирования: $$d(u+v)=du+dv,$$ $$d(uv)=vdu+udv,$$ $$dleft(frac{u}{v}right)=frac{vdu-udv}{v^2}.$$

При достаточно малом $rho=sqrt{Delta x_1^2+Delta x_2^2+…+Delta x_n^2}$ для дифференцируемой функции $u=f(x_1, x_2, …, x_n)$ имеют место приближенные равенства $$Delta uapprox du,$$ $$f(x_1+Delta x_1,, x_2+Delta x_2,…,, x_n+Delta x_n)approx f(x_1, x_2, …, x_n)+df(x_1, x_2, …, x_n).$$

Примеры:

Найти дифференциалы функций:

7.89. $z=ln(y+sqrt{x^2+y^2}).$

Решение.

$$dz=z’_xdx+z’_ydy.$$

$$z’_x=(ln(y+sqrt{x^2+y^2}))’_x=frac{1}{y+sqrt{x^2+y^2}}(y+sqrt{x^2+y^2})’_x=frac{1}{y+sqrt{x^2+y^2}}frac{1}{2sqrt{x^2+y^2}}(x^2+y^2)’_x=$$ $$=frac{1}{y+sqrt{x^2+y^2}}frac{1}{2sqrt{x^2+y^2}}2x=frac{x}{ysqrt{x^2+y^2}+x^2+y^2}.$$

$$z’_y=(ln(y+sqrt{x^2+y^2}))’_y=frac{1}{y+sqrt{x^2+y^2}}(y+sqrt{x^2+y^2})’_y=$$ $$=frac{1}{y+sqrt{x^2+y^2}}left(1+frac{1}{2sqrt{x^2+y^2}}(x^2+y^2)’_yright)=$$ $$=frac{1}{y+sqrt{x^2+y^2}}left(1+frac{1}{2sqrt{x^2+y^2}}2yright)=frac{1}{y+sqrt{x^2+y^2}}+frac{y}{sqrt{x^2+y^2}(y+sqrt{x^2+y^2})}=$$ $$=frac{sqrt{x^2+y^2}+y}{(y+sqrt{x^2+y^2})sqrt{x^2+y^2}}=frac{1}{sqrt{x^2+y^2}}.$$

$$dz=frac{x}{ysqrt{x^2+y^2}+x^2+y^2}dx+frac{1}{sqrt{x^2+y^2}}dy.$$

Ответ: $dz=frac{x}{ysqrt{x^2+y^2}+x^2+y^2}dx+frac{1}{sqrt{x^2+y^2}}dy.$

7.91. $z=lncosfrac{x}{y}.$

Решение.

$$dz=z’_xdx+z’_ydy.$$

Найдем частные производные:

$$z’_x=(lncosfrac{x}{y})’_x=frac{1}{cosfrac{x}{y}}(cosfrac{x}{y})’_x=-frac{1}{cosfrac{x}{y}}sinfrac{x}{y}(frac{x}{y})’_x=$$ $$=-frac{1}{cosfrac{x}{y}}sinfrac{x}{y}frac{1}{y}.$$

$$z’_y=(lncosfrac{x}{y})’_y=frac{1}{cosfrac{x}{y}}(cosfrac{x}{y})’_y=-frac{1}{cosfrac{x}{y}}sinfrac{x}{y}(frac{x}{y})’_y=$$ $$=frac{1}{cosfrac{x}{y}}sinfrac{x}{y}frac{x}{y^2}.$$

$$dz=left(-frac{1}{cosfrac{x}{y}}sinfrac{x}{y}frac{1}{y}right)dx+left(frac{1}{cosfrac{x}{y}}sinfrac{x}{y}frac{x}{y^2}right)dy=-frac{tgfrac{x}{y}}{y}dx+frac{xtgfrac{x}{y}}{y^2}.$$

Ответ: $dz=-frac{tgfrac{x}{y}}{y}dx+frac{xtgfrac{x}y{}}{y^2}dy.$

7.95. Вычислить приближенно $(2,01)^{3,03}.$

Решение.

Искомое число будем рассматривать как значение функции $f(x, y)=x^y$ при $x=x_0+Delta x, y=y_0+Delta y,$ если $x_0=2, y_0=3,$ $Delta x=0,01,$ $Delta y=0,03.$  Имеем:

$$f(2, 3)=2^3=8,$$

$$Delta f(x, y)approx d f(x, y)=yx^{y-1}dx+x^yln xdy$$

$$Delta f(2, 3)approx 3cdot 2^{3-1}cdot 0,01+2^3ln 2cdot0,03approx 0,06+0,17=0,23.$$

Следовательно, $(2,01)^{3,03}approx 8+0,23=8,23.$

Ответ: $8,23.$

 Производная в данном направлении.

Если направление $l$ в пространстве $Oxyz$ характеризуется направляющими косинусами ${cosalpha, cosbeta, cosgamma}$ и функция $u=f(x, y, z)$ дифференцируема, то производная по направлению $l$ вычисляется по формуле 

$$frac{partial u}{partial l}=frac{partial u}{partial x}cosalpha+frac{partial u}{partial y}cosbeta+frac{partial u}{partial z}cos gamma.$$

Скорость наибольшего роста функций в данной точке, по величине и направлению, определяется вектором — градиентом функции: 

$$grad u=frac{partial u}{partial x}i+frac{partial u}{partial y}j+frac{partial u}{partial z}k,$$ величина которого равна

$$|grad u|=sqrt{left(frac{partial u}{partial x}right)^2+left(frac{partial u}{partial y}right)^2+left(frac{partial u}{partial z}right)^2}.$$

Примеры: (Демидович)

3341. Найти производную функции $z=x^2-y^2$ в точке $M(1, 1)$ в направлении $l,$ составляющем угол $alpha=pi/3$ с положительным направлением оси $Ox.$

Решение.

Направление $l$ характеризуется направляющими косинусами $cosalpha=cospi/3=1/2;$

$cosbeta=cos(pi/2-pi/3)=cospi/6=sqrt{3}/2.$

Производную по направлению ищем по формуле $$frac{partial z}{partial l}=frac{partial z}{partial x}cosalpha+frac{partial z}{partial y}cosbeta.$$

$$z’_x=2x;$$

$$z’_y=-2y;$$ 

$$frac{partial z}{partial l}=2xcdotfrac{1}{2}-2ycdotfrac{sqrt 3}{2}.$$

$$frac{partial z}{partial l}=2cdot 1cdotfrac{1}{2}-2cdot 1cdotfrac{sqrt 3}{2}=1-sqrt 3.$$

Ответ: $1-sqrt 3.$

3345. Найти производную функции $u=xyz$ в точке $M(1, 1, 1)$ в направлении $l(cosalpha, cosbeta, cosgamma).$ Чему равна величина градиента функции в этой точке?

Решение.

Направление $l$ характеризуется направляющими косинусами 

Производную по направлению ищем по формуле $$frac{partial u}{partial l}=frac{partial u}{partial x}cosalpha+frac{partial u}{partial y}cosbeta+frac{partial u}{partial z}cos gamma.$$

$$u’_x=yz;$$

$$u’_y=xz;$$

$$u’_z=xy,$$ $$frac{partial u}{partial l}=yzcosalpha+xzcosbeta+xycos gamma.$$

$$frac{partial u}{partial l}|_{M(1, 1, 1)}=cosalpha+cosbeta+cos gamma.$$

$$grad u=(yz, xz, xy);$$

$$grad u|_{M(1, 1, 1)}=(1, 1, 1);$$

$$|grad u| _{M(1, 1, 1)}=sqrt{1+1+1}=sqrt 3$$

Ответ: $frac{partial u}{partial l}=cosalpha+cosbeta+cosgamma; |grad u|=sqrt{3}.$