Воскресенье, 18 декабря, 2011
В задании B14 из ЕГЭ по математике требуется найти наименьшее или наибольшее значение функции одной переменной. Это достаточно тривиальная задача из математического анализа, и именно по этой причине научиться решать её в норме может и должен каждый выпускник средней школы. Разберём несколько примеров, которые школьники решали на диагностической работе по математике, прошедшей в Москве 7 декабря 2011 года.
В зависимости от промежутка, на котором требуется найти максимальное или минимальное значение функции, для решения этой задачи используется один из следующих стандартных алгоритмов.
I. Алгоритм нахождения наибольшего или наименьшего значения функции на отрезке:
- Найти область определения функции.
- Найти производную функции.
- Определить точки, подозрительные на экстремум (те точки, в которых производная функции обращается в ноль, и точки, в которых не существует двухсторонней конечной производной).
- Выбрать из точек, подозрительных на экстремум, те, которые принадлежат данному отрезку и области определения функции.
- Вычислить значения функции (не производной!) в этих точках.
- Среди полученных значений выбрать наибольшее или наименьшее, оно и будет искомым.
Пример 1. Найдите наименьшее значение функции
y = x3 – 18x2 + 81x + 23 на отрезке [8; 13].
Решение: действуем по алгоритму нахождения наименьшего значения функции на отрезке:
- Область определения функции не ограничена: D(y) = R.
- Производная функции равна: y’ = 3x2 – 36x + 81. Область определения производной функции также не ограничена: D(y’) = R.
- Нули производной: y’ = 3x2 – 36x + 81 = 0, значит x2 – 12x + 27 = 0, откуда x = 3 и x = 9, в наш промежуток входит только x = 9 (одна точка, подозрительная на экстремум).
- Находим значение функции в точке, подозрительной на экстремум и на краях промежутка. Для удобства вычислений представим функцию в виде: y = x3 – 18x2 + 81x + 23 = x(x-9)2+23:
- y(8) = 8 · (8-9)2+23 = 31;
- y(9) = 9 · (9-9)2+23 = 23;
- y(13) = 13 · (13-9)2+23 = 231.
Итак, из полученных значений наименьшим является 23. Ответ: 23.
II. Алгоритм нахождения наибольшего или наименьшего значения функции:
- Найти область определения функции.
- Найти производную функции.
- Определить точки, подозрительные на экстремум (те точки, в которых производная функции обращается в ноль, и точки, в которых не существует двухсторонней конечной производной).
- Отметить эти точки и область определения функции на числовой прямой и определить знаки производной (не функции!) на получившихся промежутках.
- Определить значения функции (не производной!) в точках минимума (те точки, в которых знак производной меняется с минуса на плюс), наименьшее из этих значений будет наименьшим значением функции. Если точек минимума нет, то у функции нет наименьшего значения.
- Определить значения функции (не производной!) в точках максимума (те точки, в которых знак производной меняется с плюса на минус), наибольшее из этих значений будет наибольшим значением функции. Если точек максимума нет, то у функции нет наибольшего значения.
Пример 2. Найдите наибольшее значение функции:
.
Решение: действуем по алгоритму нахождения наибольшего значения функции:
- Область определения функции задается неравенством:
, которое выполняется при любом x, поскольку ветви соответствующей параболы направлены вверх, а дискриминант соответствующего квадратного трехчлена отрицателен: D(y) = R.
- Производная функции равна:
,
область определения которой также не ограничена, поскольку по указанной выше причине x2 – 6x + 10 > 0, и знаменатель дроби нигде не обращается в ноль: D(y’) = R. - Нули производной: 2x — 6 = 0, откуда x = 3 (одна точка, подозрительная на экстремум).
- Отмечаем область определения функции и точки, подозрительные на экстремум, на числовой прямой, определяем знаки производной в получившихся промежутках:
x = 3 — точка максимума, поскольку в ней возрастание функции (плюс производной) сменяется убыванием (минусом производной). Следовательно, максимального значения функция достигает в этой точке.
- Находим это значение:
.
Итак, наибольшее значение функции равно -1. Ответ: -1.
Репетитор по математике
Сергей Валерьевич
30 марта 2012
Все
задачи B14, которые встречаются в ЕГЭ
по математике, делятся на два типа:
-
Задачи
на поиск максимального
или минимального значения функции
на отрезке. Иногда отрезок не задан —
в этом случае работаем на всей
числовой прямой; -
Задачи на точку
максимума/минимума.
Решаются чуть проще, зато функции здесь
намного разнообразнее.
У
каждого из них свои алгоритмы решения,
которые будут рассмотрены ниже. Но в любом
случае, чтобы решить задачу B14, учитесь
считать производную — см. «Производная».
Без производных здесь делать нечего.
Задачи на максимальное/минимальное значение
Если
в задаче B14 требуется найти максимальное
или минимальное
значениефункции f (x) на отрезке [a; b], выполняем
следующие действия:
-
Найти
производную функции: f ′(x); -
Решить
уравнение f ′(x)
= 0. Если корней нет,
пропускаем третий шаг и переходим
сразу к четвертому; -
Из
полученного набора корней вычеркнуть все,
что лежит за пределами
отрезка[a; b]. Оставшиеся
числа обозначим x1, x2,
…, xn — их,
как правило, будет немного; -
Подставим
концы отрезка [a; b] и точки x1, x2,
…, xn в исходную
функцию. Получим набор
чисел f (a), f (b), f (x1), f (x2),
…, f (xn), из которого
выбираем наибольше или наименьшее
значение — это и будет ответ.
Небольшое
пояснение по поводу вычеркивания
корней, когда они совпадают с концами
отрезка. Такое вполне может встретиться
на настоящем экзамене. Эти точки
можно вычеркнуть, поскольку на четвертом
шаге концы отрезка все равно
подставляются в функцию — даже
если уравнение f ′(x)
= 0 не имело
решений.
Также
следует внимательно читать условие
задачи. Когда требуется найти значение
функции (максимальное
или минимальное), концы отрезка
и точки x1, x2,
…, xnподставляются
именно в
функцию, а не в ее производную.
Задача
Найдите
наибольшее значение функции на отрезке [−5;
0]:
y = x3 +
3x2 −
9x −
7
Решение
Для
начала найдем производную:
y′
= (x3 +
3x2 −
9x −
7)′ = 3x2 +
6x −
9
Затем
приравняем ее к нулю:
y′
= 0;
3x2 +
6x −
9 = 0;
…
x1 =
−3; x2 =
1.
Вычеркиваем
корень x =
1, поскольку
он не принадлежит отрезку [−5;
0]. Осталось
вычислить значение функции на концах
отрезка и в точке x =
−3. Имеем:
y(−5)
= (−5)3 +
4 · (−5)2 −
9 · (−5) − 7 = −12;
y(−3)
= (−3)3 +
4 · (−3)2 −
9 · (−3) − 7 = 20;
y(0)
= 03 +
4 · 02 −
9 · 0 − 7 = −7.
Очевидно,
что наибольшее значение равно 20 —
оно достигается в точке x =
−3.
Ответ
20
Задачи на точки максимума/минимума
Теперь
рассмотрим случай, когда требуется
найти точку
максимума
или минимумафункции f (x) на отрезке [a; b]. Если отрезок
не задан, функция рассматривается
на своей области определения. В любом
случае, схема решения такова:
-
Найти
производную функции: f ′(x); -
Решить
уравнение f ′(x)
= 0. Если
производная — дробно-рациональная
функция, дополнительно выясняем,
когда ее знаменатель равен нулю.
Полученные корни обозначим x1, x2,
…, xn; -
Отметить x1, x2,
…, xn на координатной
прямой и расставить знаки, которые
принимает производная между этими
числами. Если задан отрезок [a; b], отмечаем
его и вычеркиваем все, что лежит
за его пределами; -
Среди
оставшихся точек ищем ту, где знак
производной меняется с минуса на плюс
(это точка минимума) или с плюса
на минус (точка минимума). Такая
точка должна быть только одна —
это и будет ответ.
В
целом, задачи на точки максимума/минимума
считаются даже проще,
чем задачи на поиск наименьшего/наибольшего
значения. Это происходит хотя бы
из-за того, что здесь не надо считать
значение функции в конкретных точках.
Статистика свидетельствует, что именно
на этом шаге ученики допускают больше
всего ошибок.
Вдумчивый
читатель наверняка заметит, что
для некоторых функций этот алгоритмне
работает. Действительно,
существует целый класс функций,
для которых нахождение точек экстремума
требует более сложных выкладок. Однако
такие функции в ЕГЭ по математике
не встречаются.
Внимательно
отнеситесь к расстановке знаков
между точками x1, x2,
…, xn. Помните:
при переходе через корень четной
кратности знак
производной не меняется.
Когда ищутся точки экстремума, знаки
читают слева направо, т.е.
по направлениючисловой оси.
Задача
Найдите
точку максимума функции на отрезке [−10;
−1]:
Решение
Найдем
производную:
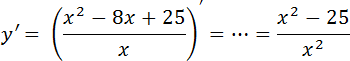
Поскольку
это дробно-рациональная функция,
приравниваем к нулю числитель:
y′
= 0;
x2 −
25 = 0;
…
x1 =
5; x2 =
−5.
Получили
два корня. Теперь приравниваем к нулю
знаменатель:
x2 =
0;
x =
0.
Получили x =
0 — корень
второй кратности. При переходе
через него знак производной не меняется.
Осталось отметить точки x =
−5; x =
0; x =
5 на координатной
прямой, а затем расставить знаки
и границы. Имеем:

Очевидно,
что внутри отрезка останется лишь
одна точка x =
−5, в которой
знак производной меняется с плюса
на минус. Это и есть точка
максимума.
Ответ
−5
Еще
раз поясню, чем отличаются точка
экстремума от самого экстремума.Точка
экстремума — это значение
переменной,
при которой
функция
принимает наибольшее или наименьшее
значение. Экстремум — этозначение
самой функции,
максимальное или минимальное
в некоторой окрестности.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
15.08.2019119.81 Кб0B6.doc
- #
- #
- #
Skip to content
Home » ЕГЭ » B14 » Найдите наименьшее значение функции ЕГЭ по математике B14
Найдите наименьшее значение функции y=4cosx+13x+9 на отрезке от [0;3π/2]
Решение:
Нужно найти производную, чтобы выяснить есть ли на отрезке [0;3π/2] максимальное или минимальное значение кроме концов отрезка.
Формулы производных:
(cosx )’=-sinx
(x)’=1
C’=0
y’=(4 cosx+13x+9)’= — 4sinx+13
Приравниваем производную к 0 чтобы найти точки экстремума.
Точки экстремума — это точки максимума или минимума функции.
-4 sinx+13=0
-4 sinx=-13
sinx=13/4>1
Нет решения этого уравнения так как -1≤sinx≤1
Так как дополнительные точки не нашли,
подставляем концы отрезка в функцию y=4cosx+13x+9.
y(0) = 4cos(0)+13•0+9 = 4•1+0+9 = 13
y(3π/2) = 4cos(3π/2)+13•(3π/2)+9 = 4•0+19,5π+9≈19,5•3,14+9 = 70,23
Ответ: 13
Видео вебинара, где рассмотрено решение части B1-B14.
Кликните СЮДА, чтобы посмотреть видео.
Подписывайтесь на канал на YOUTUBE и смотрите видео, подготавливайтесь к экзаменам по математике и геометрии с нами.
|
Найдите наибольшее значение функции $$ y=2^{-37-12x-x^2} $$
[посмотреть решение] |
|
Найдите наибольшее значение функции $$ y=log_7 (-42-14x-x^2)-6 $$
[посмотреть решение] |
|
Найдите наибольшее значение функции на отрезке $[?3;0]$ $$ y=(x+2)^2(x-1)+1 $$
[посмотреть решение] |
|
Найдите точку минимума функции $$ y=-frac{x}{x^2+9} $$
[посмотреть решение] |
|
Найдите точку максимума функции принадлежащую промежутку $(0;frac{pi}{2})$ $$ y=(4x-6)cos x-4sin x+14 $$
[посмотреть решение] |
|
Найдите наибольшее значение функции на отрезке [2;32] $$ y=(x-33)^2e^{x-31} $$
[посмотреть решение] |
|
Найдите наибольшее значение функции на отрезке $[?22;?0.5]$ $$ y=x+frac{121}{x}+18 $$
[посмотреть решение] |
|
Найдите наименьшее значение функции на отрезке $[0;frac{pi}{4}]$ $$ y=28operatorname{tg} x-28x+44 $$
[посмотреть решение] |
|
Найдите точку максимума функции $$ y=1.5x^2-42x+135cdotln x-4 $$
[посмотреть решение] |
|
Найдите наименьшее значение функции $$ y=sqrt{x^2+2x+65} $$
[посмотреть решение] |
1. Прототипы В 14 Исследование сложной функции, содержащей показательную, логарифмическую функции и функцию квадратный корень
ПРОТОТИПЫ В 14
ИССЛЕДОВАНИЕ СЛОЖНОЙ
ФУНКЦИИ, СОДЕРЖАЩЕЙ
ПОКАЗАТЕЛЬНУЮ,
ЛОГАРИФМИЧЕСКУЮ
ФУНКЦИИ И ФУНКЦИЮ
КВАДРАТНЫЙ КОРЕНЬ
2. Проверяемые требования (умения): уметь выполнять действия с функциями.
Умения по КТ
• Вычислять производные и
первообразные
элементарных функций
• Исследовать в
простейших случаях
функции на
монотонность,
находить наибольшие
и наименьшие
значения функций
3. Содержание задания В14 по КЭС
Начала математического анализа
• 4.1 Производная
4.1.1 Понятие о производной функции, геометрический смысл производной
4.1.2 Физический смысл производной, нахождение скорости для процесса,
заданного формулой или графиком
4.1.3 Уравнение касательной к графику функции
4.1.4 Производные суммы, разности, произведения, частного
4.1.5 Производные основных элементарных функций
4.1.6 Вторая производная и ее физический смысл
• 4.2 Исследование функций
4.2.1 Применение производной к исследованию функций и построению
графиков
4.2.2 Примеры использования производной для нахождения наилучшего
решения в прикладных, в том числе социально-экономических, задачах
4. Памятка ученику
• Задание B14 — на нахождение с
помощью производной точек
экстремума функции или
вычисление наибольшего
(наименьшего) значения функции на
отрезке. Для успешного решения
задачи ученик должен уметь
вычислять производные
элементарных функций и в
простейших случаях исследовать
функцию на монотонность.
5.
f ‘ (x)
формулы
С’
0
(x)’
1
(xa)’
ax a 1
sin’x
cos x
сos’x
tg’x
ctg’x
при a≠1
sin x
1
cos 2 x
1
sin 2 x
(ex)’
ex
(ax)’
a x ln a
ln’x
1
x
loga’x
1
x ln a
(f+g)’
f ‘ g’
(f∙g)’
f ‘ g fg ‘
(cf)’
cf ‘
f
‘
g
(f(kx+b)) ‘
(f(g(x))) ‘
( f ‘ g fg ‘ )
g2
kf ‘ ( kx b)
f ‘ ( g( x )) g’ ( x )
6.
7.
8.
9.
10.
11.
12.
13.
14. Алгоритм нахождения наименьшего (наибольшего) значения на данном отрезке. Первый способ (традиционный) предполагает
использование алгоритмов и
1)
2)
3)
4)
знание формул.
использование алгоритмов и знание формул. Найти
производную функции.
Приравнять производную к нулю и решить полученное
уравнение.
Найти значение функции на краях числового
промежутка и в нулях производной, входящих в
данный числовой промежуток.
Выбрать среди полученных значений функции
значение, соответствующее вопросу задачи
(наибольшее или наименьшее)
Важно: промежуток может быть не указан, но
очевиден: область определения.
15. Прототип задания B14
• Найдите наименьшее значение
x 7
y
(
x
8
)
e
функции
на отрезке [6;8].
Найдем y'(x). Производная произведения равна
(uv) u v v u
y ( x 

Приравняем к нулю:
exx 77 ( x 7) 0
e
0- нет корней;
[6;8]
7
x 7, 0 x- принадлежит
Найдём наименьшее значение функции:
y (6) (6 
y(7) (7 
y(8) (8 
Решение
20
27
Ответ: -1 — наименьшее значение функции на отрезке
[6;8].
16. Задания для самостоятельного решения
• Задание B14
Найдите наименьшее значение функции
y ( x 6)e x 5 на отрезке [4;6].
• Задание B14
Найдите наименьшее значение функции
y ( x 17)e x 16 на отрезке [15;17].
Проверка
Ответ: -1
Ответ: -1
17. Прототип задания B14
• Найдите наибольшее значение
функции y 12 cos x 6 3 x 2 3π 6
на отрезке
0; 2
Найдем y'(x). Производная функции равна
y 12 sin x 6 3
Приравняем к нулю:
3 — принадлежит
x
12 sin x 6 3 0 sin x
3
2
0; 2
Найдём наибольшее значение функции:
y (0) 12 1 6 3 0 2 3 6 12 2 3 6 7,12
1
y 12 6 3 2 3 6 6 2 3 2 3 6 12
2
3
3
y 0 6 3 2 3 6 3 3 2 3 6 3 6 11,4
2
2
Ответ: 12 — наибольшее значение функции на отрезке
Решение
0; 2 .
18. Задания для самостоятельного решения
Задание B14
Найдите наибольшее значение функции
на отрезке
0.;
y 12 2 cos x 12 x 3 9
Задание B14
Найдите наибольшее значение функции
.
на отрезке
0;
7
y 7 2 cos x 7 x
9
4
Проверка
2
2
Ответ: 21
Ответ: 16
19. Прототип задания B14
• Найдите наименьшее значение функции
3
на
отрезке
2 ;0
y 5 cos x 6 x 4
Найдем y'(x). Производная функции равна
y 5 sin x 6
Приравняем к нулю:
6
sin x — нет корней
5 функции:
Найдём наименьшее значение
5 sin 6 0
y (
Решение
3
3 3
) 5 cos
6
4 27 4 31
2
2 2
y (0) 5 4 9
Ответ: 9 — наименьшее значение функции на отрезке
3 .
;0
2
20. Задания для самостоятельного решения
Задание B14
Найдите наименьшее значение функции y 7 cos x 13x 9
на отрезке
.
Задание B14
Найдите наименьшее значение функции y 5 cos x 9 x 3 на отрезке
.
3
2 ;0
3
2 ;0
Проверка
Ответ: 16
Ответ: 8
21. Алгоритм нахождения наибольшего (наименьшего) значения функции без указания числового промежутка:
1) Найти производную функции.
2) Приравнять производную к нулю и решить
полученное уравнение.
3) Провести исследование на экстремумы в
области определения функции. Если
экстремум один, то именно в нем достигается
наибольшее (наименьшее) значение
функции.
22. Алгоритм нахождения точек экстремума.
Найти производную функции.
Приравнять производную к нулю и решить полученное уравнение.
На числовой прямой отметить нули производной и точки, в которых
производная не определена.
Соотнести поведение производной с поведением функции и ответить на
вопрос.
Например:
f (x )
f (x )
-3
Ответ:
3
т. max
23.
Формулы:
Дифференцирование показательной функции:
Дифференцирование логарифмической функции:
Дифференцирование сложной функции:
17.12.2017
a a
x
x
ln a
1
log a х
x ln a
f g x f g g x
23
24. Найдите наибольшее значение функции
y log 5 4 2 x x 2 3
Решение:
Промежуток не указан. Очевидно, что необходимо исследовать функцию
на всей области определения.
1
2
y
(
4
2
x
x
)
2
(4 2 х x ) ln 5
D f : 4 2 x x 0
2
x 1 5; 1 5
Конечно, страшновато, но
уже ясно, что краев у
числового промежутка нет,
а, следовательно в них не будет
достигаться наибольшее или
наименьшее значение.
y
1
( 2 2 x )
2
(4 2 х x ) ln 5
y 0
при x 1
Убедимся, что это значение наибольшее
f (x )
f (x )
1
т. max
Ответ:
17.12.2017
4
Точка максимума одна, следовательно в ней и будет
наибольшее значение.
yнаиб. y( 1) 4
24
25. Найдите наибольшее значение функции
7 6 x x 2
Решение:
y 3
y 3
x
Промежуток не указан. Очевидно, что необходимо исследовать функцию
на всей области определения.
D f : R
y 3
7 6 x x 2
7 6 x x 2
3
yнаиб. y ( 3) 9
ln 3 ( 6 2 x)
ln 3 ( 6 2 x) 0
Убедимся, что это наибольшее значение:
Разделим на первый и второй множители,
не равные нулю:
6 2x 0
17.12.2017
f (x )
3
т. max
Точка максимума одна, следовательно в ней и будет
наибольшее значение.
x 3
Ответ:
f (x )
9
25
26. Не очень просто. Тем более, что некоторые программы не предусматривают использование формул дифференцирования показательной и
логарифмической функции в общем виде.
Попробуем иначе. Без использования
алгоритма и формул.
27. В случае, если мы имеем дело со сложной функцией f(g(x)), где f – монотонная функция, то достаточно исследовать функцию g(x).
28. Найдите наибольшее значение функции
7 6 x x 2
y 3
Решение:
Функция
y 3xвозрастает на R, следовательно наибольшее значение
принимает при наибольшем значении аргумента (аргументом в данном случае
является функция, находящаяся в показателе).
Исследуем на наибольшее значение функцию, находящуюся в
показателе.
f ( x) 7 6 x x
f ( x ) 6 2 x
6 2x 0
x 3
2
f (x )
f (x )
3
т. max
Следовательно f ( x )наиб. f ( 3) 2
2
y
3
9
Следовательно
наиб.
Ответ:
17.12.2017
9
28
29.
Можно и совсем обойтись без производной.
Используем простые графические
соображения.
17.12.2017
29
30. Найдите наименьшее значение функции
y 2
Решение:
x 2 2 x 5
Функция y 2 возрастает на R, следовательно наименьшее значение
принимает при наименьшем значении аргумента (функции, находящейся в
показателе).
x
Исследуем на наибольшее значение функцию, находящуюся в
показателе.
f ( x) x 2 2 x 5
График – парабола, ветви направлены
вверх.
b
1
2a
у0 4
Следовательно
f ( x )наим.
4
x0
Ответ:
17.12.2017
yнаиб. 2 4 16
1 6
30
31. Найдите наибольшее значение функции
Решение:
y log 5 4 2 x x 2 3
3
Функция y log 5 x возрастает
на всей области определения , следовательно
наибольшее значение принимает при наибольшем значении значении аргумента
(функции, находящейся под знаком логарифма).
Исследуем на наибольшее значение функцию, находящуюся под знаком
2
логарифма.
D f : 4 2 x x 0
f ( x) 4 2 x x 2
x 1 5; 1 5
График – парабола, ветви направлены
вниз.
x0
у0 5
5
f ( x )наиб.
b
1
2a
Ответ: 4
Следовательно yнаиб. log 5 5 3 4
31
32.
Решим таким же способом задания,
связанные с исследованием сложной
функции, содержащей квадратичную
функцию под знаком квадратного корня.
17.12.2017
32
33. Найдите точку минимума функции
y x 2 6 x 11
Решение:
Функция
y x возрастает на всей области определения, следовательно
ведет себя так же, как подкоренная функция на области определения.
Подкоренное выражение больше нуля при любом значении х. D(y):R.
Исследуем функцию, находящуюся под знаком корня.
f ( x ) x 2 6 x 11
График – парабола, ветви направлены
вверх.
x0
b
3
2a
Ответ: 3
т. min
3
33
34. Найдите наибольшее значение функции
y 5 4 x x2
Решение:
Функция
y x возрастает на всей области определения, следовательно
принимает наибольшее значение в той же точке, что и подкоренная функция с
учетом области определения.
D(y):[-5;1].
Исследуем функцию, находящуюся под знаком корня.
f ( x) 5 4 x x 2
График – парабола, ветви направлены
вниз.
b
2
2a
y0 9
9
f ( x )наиб.
x0
Ответ: 3
Следовательно yнаиб. 9 3
34
35. Реши самостоятельно любым способом:
• Найдите точку минимума функции
• Найдите точку максимума функции
• Найдите наименьшее значение функции
• Найдите наименьшее значение функции
17.12.2017
35
36. Задания для домашнего (или дополнительного) решения
• Задание B14
Найдите наименьшее значение функции
.
на отрезке
0; 2
• Задание B14
Найдите наименьшее значение функции
на отрезке 0; .
2
Проверка
Ответ: 0
y 4
y 11
4 3
4 3 x 8 cos x
3
7 3 7 3
14 3
x
cos x
18
3
3
Ответ: 4
37. Задания для домашнего (или самостоятельного) решения
Задание B14
Найдите наибольшее значение функции
2 ;0
Задание B14
Найдите наибольшее значение функции
2 ;0
Проверка
Ответ: 3
y 11xна
9отрезке
sin x 3
на отрезке
y 12 x 8 sin x 6
Ответ: 6

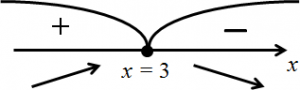 x = 3 — точка максимума, поскольку в ней возрастание функции (плюс производной) сменяется убыванием (минусом производной). Следовательно, максимального значения функция достигает в этой точке.
x = 3 — точка максимума, поскольку в ней возрастание функции (плюс производной) сменяется убыванием (минусом производной). Следовательно, максимального значения функция достигает в этой точке.