Как найти значение функции по графику прямой

В новой 9 задаче профильного ЕГЭ много заданий на линейные функции. Самое сложное, что нужно сделать, решая эти задачи – определить формулу линейной функции, т.е. найти (k) и (b) по графику. Примеры таких заданий (решения будут внизу статьи):

В статье я расскажу про два простых способа найти (k) и (b), если известен график линейной функции.

Способ 1

Первый способ основывается на трех фактах:

1. Линейная функция пересекает ось (y) в точке (b).
   Примеры:

   

   Но не советую определять так (b), если прямая пересекает ось не в целом значении или если точка пересечения вообще не видна на графике. Для таких случаев пользуйтесь вторым способом.

   Примеры:

   

2. Если функция возрастает, то знак коэффициента (k) плюс, если убывает – минус, а если постоянна, то (k=0).

   Примеры:

   

3. Чтоб конкретнее определить (k) надо построить на прямой прямоугольный треугольник так, чтобы гипотенуза лежала на графике функции, а вершины треугольника совпадали с вершинами клеточек. Далее, чтоб определить (k) нужно вертикальную сторону треугольника поделить на горизонтальную и поставить знак согласно возрастанию/убыванию функции.

   Примеры:

   

Пример (ЕГЭ)

Давайте пока что не будем искать формулу иррациональной функции, сосредоточимся только на линейной функции.

(b=3) – это сразу видно. Функция идет вниз, значит (k<0).

Достроим прямую до прямоугольного треугольника. Вершинами будут жирные точки, которые нам дали в задаче.

(k=-frac{AC}{BC}=-frac{1}{3}). Получается (g(x)=-frac{1}{3}x+3).

Способ 1 быстрее способа 2, но не во всех ситуациях помогает. Поэтому важно владеть и вторым способом тоже.

Способ 2

Вы обращали внимание, что в задачах ЕГЭ на прямых всегда жирно выделяют 2 точки? Так вот, чтобы найти формулу линейной функции, достаточно подставить координаты этих точек в формулу (f(x)=kx+b) и решить получившуюся систему уравнений.

Пример (ЕГЭ)

Обозначим жирные точки какими-нибудь буквами и найдем их координаты.

(A(-2;2)) и (B(2;-5)) подставим эти значения вместо (x) и (f(x)) в формулу (f(x)=kx+b):

Получим:

(begin{cases}2=-2k+b\-5=2k+bend{cases})

Теперь найдем (k) и (b), решив эту систему.

Для этого сложим уравнения друг с другом, чтобы исчезло (k):

(2+(-5)=-2k+b+2k+b)
(-3=2b)
(b=-1,5)

Теперь подставим найденное (b) во второе уравнение системы и найдем (k):

(-5=2k-1,5)
(-5+1,5=2k)
(-3,5=2k)
(k=-1,75)

Получается (f(x)=-1,75x-1,5). Остается последний шаг – вычислим при каком иксе функция, то есть (f(x)), равна (16):

(16=-1,75x-1,5)
(17,5=-1,75x)
(x=-10).

Ответ: (-10).

Пример (ЕГЭ)

Чтоб решить задачу, нам понадобятся формулы каждой из двух функций. Давайте формулу нижней функции найдем с помощью способа 1, а формулу верхней с помощью способа 2. Начнем с нижней функции.

Функция (f(x)) возрастает, значит (k>0). (k=+frac{AC}{BC}=frac{4}{4}=1,b=1). (f(x)=x+1).

Теперь перейдем к функции (g(x)). Найдем координаты точек (D) и (E): (D(-2;4)), (E(-4;1)). Можно составить систему:

(begin{cases}4=-2k+b\1=-4k+bend{cases})

Вычтем второе уравнение из первого, чтоб убрать (b):

(4-1=-2k+b-(-4k+b))
(3=2k)
(k=1,5)

Найдем (b):

(4=-2cdot 1,5+b)
(4=-3+b)
(b=7)

(g(x)=1,5x+7). Обе функции найдены, теперь можно найти абсциссу (икс) точки пересечения. Приравняем (f(x)) и (g(x)).

(x+1=1,5x+7)
(x-1,5x=7-1)
(-0,5x=6)
(x=6:(-0,5))
(x=-12).

Ответ: (-12).

Картинку в хорошем качестве, можно скачать нажав на кнопку «скачать статью».

Смотрите также:
Как определить a, b и c по графику параболы

Скачать статью

График линейной функции, его свойства и формулы

О чем эта статья:

Понятие функции

Функция — это зависимость y от x, где x является независимой переменной или аргументом функции, а y — зависимой переменной или значением функции.

Задать функцию значит определить правило, следуя которому по значениям независимой переменной можно найти соответствующие значения функции. Вот какими способами ее можно задать:

Табличный способ помогает быстро определить конкретные значения без дополнительных измерений или вычислений.

Аналитический способ — через формулы. Компактно, и можно посчитать функцию при произвольном значении аргумента из области определения.

Словесный способ.

Графический способ — наглядно. Его мы и разберем в этой статье.

График функции — это множество точек (x; y), где x — это аргумент, а y — значение функции, которое соответствует данному аргументу.

Понятие линейной функции

Линейная функция — это функция вида y = kx + b, где х — независимая переменная, k, b — некоторые числа. При этом k — угловой коэффициент, b — свободный коэффициент.

Геометрический смысл коэффициента b — длина отрезка, который отсекает прямая по оси OY, считая от начала координат.

Геометрический смысл коэффициента k — угол наклона прямой к положительному направлению оси OX, считается против часовой стрелки.

Если известно конкретное значение х, можно вычислить соответствующее значение у.

Нам дана функция: у = 0,5х — 2. Значит:

если х = 0, то у = -2;

если х = 2, то у = -1;

если х = 4, то у = 0 и т. д.

Для удобства результаты можно оформлять в виде таблицы:

Графиком линейной функции является прямая. Для ее построения достаточно двух точек, координаты которых удовлетворяют уравнению функции.

Угловой коэффициент отвечает за угол наклона прямой, свободный коэффициент — за точку пересечения графика с осью ординат.

k и b — это числовые коэффициенты функции. На их месте могут стоять любые числа: положительные, отрицательные или дроби.

Давайте потренируемся и определим для каждой функций, чему равны числовые коэффициенты k и b.

Функция	Коэффициент k	Коэффициент b
y = 2x + 8	k = 2	b = 8
y = −x + 3	k = −1	b = 3
y = 1/8x − 1	k = 1/8	b = −1
y = 0,2x	k = 0,2	b = 0

Может показаться, что в функции y = 0,2x нет числового коэффициента b, но это не так. В данном случае он равен нулю. Чтобы не поддаваться сомнениям, нужно запомнить: в каждой функции типа y = kx + b есть коэффициенты k и b.

Свойства линейной функции

Область определения функции — множество всех действительных чисел.

Множеством значений функции является множество всех действительных чисел.

График линейной функции — прямая. Для построения прямой достаточно знать две точки. Положение прямой на координатной плоскости зависит от значений коэффициентов k и b.

Функция не имеет ни наибольшего, ни наименьшего значений.

Четность и нечетность линейной функции зависят от значений коэффициентов k и b:

b ≠ 0, k = 0, значит, y = b — четная;

b = 0, k ≠ 0, значит, y = kx — нечетная;

b ≠ 0, k ≠ 0, значит, y = kx + b — функция общего вида;

b = 0, k = 0, значит, y = 0— как четная, так и нечетная функция.

Свойством периодичности линейная функция не обладает, потому что ее спектр непрерывен.

График функции пересекает оси координат:

ось абсцисс ОХ — в точке (−b/k; 0);

ось ординат OY — в точке (0; b).

x = −b/k — является нулем функции.

Если b = 0 и k = 0, то функция y = 0 обращается в ноль при любом значении переменной х.

Если b ≠ 0 и k = 0, то функция y = b не обращается в нуль ни при каких значениях переменной х.

Функция монотонно возрастает на области определения при k > 0 и монотонно убывает при k 0 функция принимает отрицательные значения на промежутке (−∞; −b/k) и положительные значения на промежутке (−b/k; +∞).

При k 0, то этот угол острый, если k

Построение линейной функции

В геометрии есть аксиома: через любые две точки можно провести прямую и притом только одну. Исходя из этой аксиомы следует: чтобы построить график функции вида у = kx + b, достаточно найти всего две точки. А для этого нужно определить два значения х, подставить их в уравнение функции и вычислить соответствующие значения y.

Например, чтобы построить график функции y = 1/3x + 2, можно взять х = 0 и х = 3, тогда ординаты этих точек будут равны у = 2 и у = 3. Получим точки А (0; 2) и В (3; 3). Соединим их и получим такой график:

В уравнении функции y = kx + b коэффициент k отвечает за наклон графика функции:

если k > 0, то график наклонен вправо;

если k 0, то график функции y = kx + b получается из y = kx со сдвигом на b единиц вверх вдоль оси OY;

если b 0, то график функции y = kx + b выглядит так:

0″ src=»https://user84060.clients-cdnnow.ru/uploads/5fc1049363f94987951092.png» style=»height: 600px;»>

Если k > 0 и b > 0, то график функции y = kx + b выглядит так:

0 и b > 0″ src=»https://user84060.clients-cdnnow.ru/uploads/5fc104b2640e6151326286.png» style=»height: 600px;»>

Если k > 0 и b

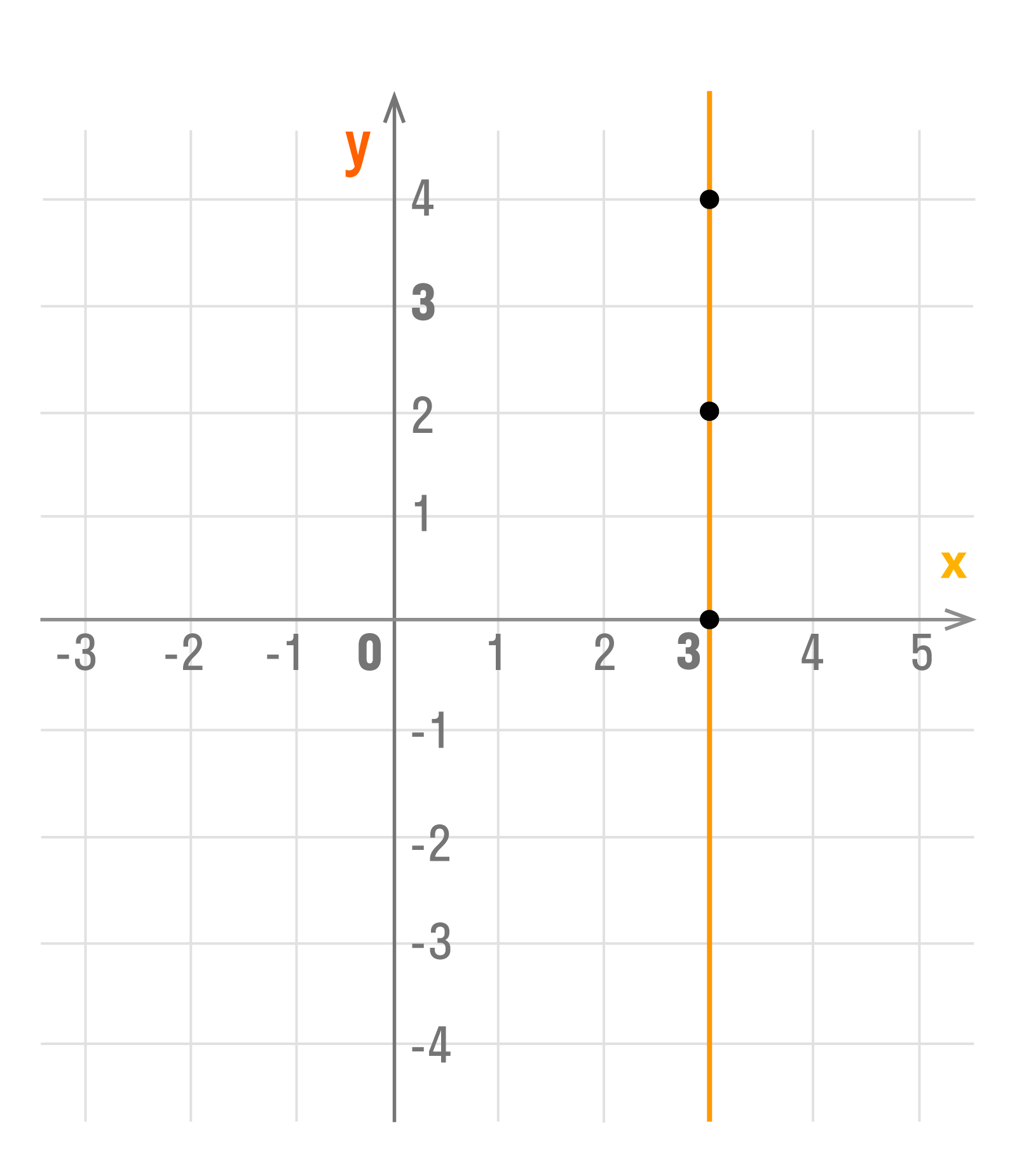
В задачах 7 класса можно встретить график уравнения х = а. Он представляет собой прямую линию, которая параллельна оси ОY все точки которой имеют абсциссу х = а.

Важно понимать, что уравнение х = а не является функцией, так как различным значениям аргумента соответствует одно и то же значение функции, что не соответствует определению функции.

Например, график уравнения х = 3:

Условие параллельности двух прямых:

График функции y = k₁x + b₁ параллелен графику функции y = k₂x + b₂, если k₁ = k₂.

Условие перпендикулярности двух прямых:

График функции y = k₁x + b₁ перпендикулярен графику функции y = k₂x + b₂, если k₁k₂ = −1 или k₁ = −1/k₂.

Точки пересечения графика функции y = kx + b с осями координат:

С осью ОY. Абсцисса любой точки, которая принадлежит оси ОY равна нулю. Поэтому, чтобы найти точку пересечения с осью ОY, нужно в уравнение функции вместо х подставить ноль. Тогда получим y = b.

Координаты точки пересечения с осью OY: (0; b).

С осью ОХ. Ордината любой точки, которая принадлежит оси ОХ равна нулю. Поэтому, чтобы найти точку пересечения с осью ОХ, нужно в уравнение функции вместо y подставить ноль. И получим 0 = kx + b. Значит x = −b/k.

Координаты точки пересечения с осью OX: (−b/k; 0).

Решение задач на линейную функцию

Чтобы решать задачи и строить графики линейных функций, нужно рассуждать и использовать свойства и правила выше. Давайте потренируемся!

Пример 1. Построить график функции y = kx + b, если известно, что он проходит через точку А (-3; 2) и параллелен прямой y = -4x.

В уравнении функции y = kx + b два неизвестных параметра: k и b. Поэтому в тексте задачи нужно найти два условия, которые характеризуют график функции.

Из того, что график функции y = kx + b параллелен прямой y = -4x, следует, что k = -4. То есть уравнение функции имеет вид y = -4x + b.

Осталось найти b. Известно, что график функции y = -4x + b проходит через точку А (-3; 2). Подставим координаты точки в уравнение функции и мы получим верное равенство:

Таким образом, нам надо построить график функции y = -4x — 10

Мы уже знаем точку А (-3; 2), возьмем точку B (0; -10).

Поставим эти точки в координатной плоскости и соединим прямой:

Пример 2. Написать уравнение прямой, которая проходит через точки A (1; 1); B (2; 4).

Если прямая проходит через точки с заданными координатами, значит координаты точек удовлетворяют уравнению прямой y = kx + b.

Следовательно, если координаты точек подставить в уравнение прямой, то получим верное равенство.

Подставим координаты каждой точки в уравнение y = kx + b и получим систему линейных уравнений.

Вычтем из второго уравнения системы первое, и получим k = 3.

Подставим значение k в первое уравнение системы, и получим b = -2.

Ответ: уравнение прямой y = 3x — 2.

Алгоритм определения формулы линейной функции по графику

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

Выполнила учительница математики МБОУ Башкирский лицей № 1 муниципального района Учалинский район Республики Башкортостан Хидиятова Залифа Даутовна

Алгоритм определения формулы линейной функции по графику»

На рисунке представлен график функции у = kx +b.
Записать формулу линейной функции, соответствующей данному графику.

1) Так как ордината точки пересечения графика функции с осью Оy равна 1, следовательно, b=1.
Значит, у = kx+ 1

2) Выбираем на графике произвольную точку, например, А (2;2) и определяем её координаты: если x = 2, то у = 2. Подставим в нашу формулу вместо Х и У и получим уравнение относительно k.
2 = 2k+1
2k=1
k = 0.5 Записываем формулу линейной функции: у = 0,5х + 1.

Написать ФОРМУЛУ линейной функции У= КХ+В, график которой изображен на рисунке :

Это ВПР задание это ответ:

ВНИМАНИЕ : задание на сегодня 16 апреля

Внимание : вот эти следующие задания пока НЕ РЕШАТЬ.

Курс повышения квалификации

Дистанционное обучение как современный формат преподавания

• Сейчас обучается 945 человек из 80 регионов

Курс профессиональной переподготовки

Математика: теория и методика преподавания в образовательной организации

• Сейчас обучается 687 человек из 75 регионов

Курс повышения квалификации

Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО

• Сейчас обучается 315 человек из 69 регионов

Ищем педагогов в команду «Инфоурок»

Дистанционные курсы для педагогов

«Взбодрись! Нейрогимнастика для успешной учёбы и комфортной жизни»

Свидетельство и скидка на обучение каждому участнику

Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:

5 591 467 материалов в базе

Материал подходит для УМК

«Алгебра», Макарычев Ю.Н., Миндюк Н.Г., Нешков К.И. и др. / Под ред. Теляковского С.А.

16. Линейная функция и её график

Самые массовые международные дистанционные

Школьные Инфоконкурсы 2022

33 конкурса для учеников 1–11 классов и дошкольников от проекта «Инфоурок»

«Психологические методы развития навыков эффективного общения и чтения на английском языке у младших школьников»

Свидетельство и скидка на обучение каждому участнику

Другие материалы

• 16.09.2020
• 200
• 11

• 31.03.2020
• 1170
• 30

• 16.03.2020
• 227
• 1

• 16.03.2020
• 191
• 1

• 08.03.2020
• 282
• 6

• 20.02.2020
• 1254
• 72

• 21.01.2020
• 180
• 0

• 09.12.2019
• 424
• 13

Вам будут интересны эти курсы:

Оставьте свой комментарий

Авторизуйтесь, чтобы задавать вопросы.

Добавить в избранное

• 30.09.2020 16211
• DOCX 549.2 кбайт
• 155 скачиваний
• Оцените материал:

Настоящий материал опубликован пользователем Хидиятова Залифа Даутовна. Инфоурок является информационным посредником и предоставляет пользователям возможность размещать на сайте методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайт

Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.

Автор материала

• На сайте: 5 лет и 3 месяца
• Подписчики: 0
• Всего просмотров: 38959
• Всего материалов: 37

Московский институт профессиональной
переподготовки и повышения
квалификации педагогов

Дистанционные курсы
для педагогов

663 курса от 690 рублей

Выбрать курс со скидкой

Выдаём документы
установленного образца!

Учителя о ЕГЭ: секреты успешной подготовки

Время чтения: 11 минут

Университет им. Герцена и РАО создадут портрет современного школьника

Время чтения: 2 минуты

Минобрнауки создаст для вузов рекомендации по поддержке молодых семей

Время чтения: 1 минута

В Курганской области дистанционный режим для школьников продлили до конца февраля

Время чтения: 1 минута

В приграничных пунктах Брянской области на день приостановили занятия в школах

Время чтения: 0 минут

В Белгородской области отменяют занятия в школах и детсадах на границе с Украиной

Время чтения: 0 минут

Курские власти перевели на дистант школьников в районах на границе с Украиной

Время чтения: 1 минута

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.

Как найти k и b по графику линейной функции?

В новой 9 задаче профильного ЕГЭ много заданий на линейные функции. Самое сложное, что нужно сделать, решая эти задачи – определить формулу линейной функции , т.е. найти (k) и (b) по графику. Примеры таких заданий (решения будут внизу статьи):

В статье я расскажу про два простых способа найти (k) и (b), если известен график линейной функции.

Способ 1

Первый способ основывается на трех фактах:

Линейная функция пересекает ось (y) в точке (b).
Примеры:

Но не советую определять так (b), если прямая пересекает ось не в целом значении или если точка пересечения вообще не видна на графике. Для таких случаев пользуйтесь вторым способом.

Если функция возрастает, то знак коэффициента (k) плюс, если убывает – минус, а если постоянна, то (k=0).

Чтоб конкретнее определить (k) надо построить на прямой прямоугольный треугольник так, чтобы гипотенуза лежала на графике функции, а вершины треугольника совпадали с вершинами клеточек. Далее, чтоб определить (k) нужно вертикальную сторону треугольника поделить на горизонтальную и поставить знак согласно возрастанию/убыванию функции.

Давайте пока что не будем искать формулу иррациональной функции, сосредоточимся только на линейной функции.

(b=3) – это сразу видно. Функция идет вниз, значит (k 0). (k=+frac=frac<4><4>=1,b=1). (f(x)=x+1).

Теперь перейдем к функции (g(x)). Найдем координаты точек (D) и (E): (D(-2;4)), (E(-4;1)). Можно составить систему:

Вычтем второе уравнение из первого, чтоб убрать (b):

(g(x)=1,5x+7). Обе функции найдены, теперь можно найти абсциссу (икс) точки пересечения. Приравняем (f(x)) и (g(x)).

Картинку в хорошем качестве, можно скачать нажав на кнопку «скачать статью».

источники:

http://infourok.ru/algoritm-opredeleniya-formuly-linejnoj-funkcii-po-grafiku-4463697.html

http://cos-cos.ru/ege/zadacha203/376/

Как найти функцию по ее графику

Еще в школе мы подробно изучаем функции и строим их графики. Однако читать график функции и находить ее вид по готовому чертежу, нас, к сожалению, практически не учат. На самом деле, это совсем не сложно, если помнить несколько основных видов функций.Задача описания свойств функции по ее графику часто возникает при экспериментальных исследованиях. По графику можно определить промежутки возрастания и убывания функции, разрывы и экстремумы, а также можно видеть асимптоты.

Инструкция

Если графиком является прямая линия, проходящая через начало координат и образующая с осью ОX угол α (угол наклона прямой к положительной полуоси ОХ). Функция, описывающая эту прямую, будет иметь вид y = kx. Коэффициент пропорциональности k равен tg α. Если прямая проходит через 2-ю и 4-ю координатные четверти, то k < 0, и функция является убывающей, если через 1-ю и 3-ю, то k > 0 и функция возрастает.Пусть график представляет собой прямую линию, располагающуюся различным образом относительно осей координат. Это линейная функция, и она имеет вид y = kx + b, где переменные x и y стоят в первой степени, а k и b могут принимать как положительные, так и отрицательные значения или равны нулю. Прямая параллельна прямой y = kx и отсекает на оси ординат |b| единиц. Если прямая параллельна оси абсцисс, то k = 0, если оси ординат, то уравнение имеет вид x = const.

Кривая, состоящая из двух ветвей, располагающихся в разных четвертях и симметричных относительно начала координат, называется гиперболой. Этот график выражает обратную зависимость переменной y от x и описывается уравнением y = k/x. Здесь k ≠ 0 — коэффициент обратной пропорциональности. При этом если k > 0, функция убывает; если же k < 0 — функция возрастает. Таким образом, областью определения функции является вся числовая прямая, кроме x = 0. Ветви гиперболы приближаются к осям координат как к своим асимптотам. С уменьшением |k| ветки гиперболы все больше «вдавливаются» в координатные углы.

Квадратичная функция имеет вид y = ax2 + bx + с, где a, b и c – величины постоянные и a  0. При выполнении условия b = с = 0, уравнение функции выглядит, как y = ax2 (простейший случай квадратичной функции), а ее график является параболой, проходящей через начало координат. График функции y = ax2 + bx + с имеет ту же форму, что и простейший случай функции, однако ее вершина (точка пересечения параболы с осью OY) лежит не в начале координат.

Параболой является также график степенной функции, выраженной уравнением y = xⁿ, если n – любое четное число. Если n — любое нечетное число, график такой степенной функции будет иметь вид кубической параболы.
В случае, если n – любое отрицательное число, уравнение функции приобретает вид. Графиком функции при нечетном n будет гипербола, а при четном n их ветви будут симметричны относительно оси ОУ.

Войти на сайт

или

Забыли пароль?
Еще не зарегистрированы?

Как определить a, b и c по графику параболы

Предположим, вам попался график функции (y=ax^2+bx+c) и нужно по этому графику определить коэффициенты (a), (b) и (c). В этой статье я расскажу 3 простых способа сделать это.

1 способ – ищем коэффициенты на графике

Данный способ хорош, когда координаты вершины и точка пересечения параболы с осью (y) – целые числа. Если это не так, советую использовать способ 2.

Коэффициент (a) можно найти с помощью следующих фактов:

— Если (a>0), то ветви параболы направленных вверх, если (a 1), то график вытянут вверх в (a) раз по сравнению с «базовым» графиком (у которого (a=1)). Вершина при этом остается на месте. Это наглядно видно по выделенным точкам.

Ищем 3 точки с целыми координатами, принадлежащие параболе.
Пример:

Выписываем координаты этих точек и подставляем в формулу квадратичной функции: (y=ax^2+bx+c). Получится система с тремя уравнениями.

Решаем систему.
Пример:

Вычтем из второго уравнения первое:

Подставим (9a) вместо (b):

Первое и второе уравнения совпали (это нормально для точек, симметричных относительно прямой проходящей через вершину – как точки (A) и (B) в нашем случае), но нас это не остановит – мы вычтем из второго уравнение третье:

Подставим в первое уравнение (a):

Получается квадратичная функция: (y=-x^2-9x-15).

Сразу заметим, что по графику можно сразу определить, что (c=4). Это сильно облегчит нашу систему – нам хватит 2 точек. Выберем их на параболе: (C(-1;8)), (D(1;2)) (на самом деле, если присмотреться, то можно заметить, что эти точки выделены жирно на изначальной картинке – это вам подсказка от авторов задачи).

Таким образом имеем систему:

Сложим 2 уравнения:

Подставим во второе уравнение:

Теперь найдем точки пересечения двух функций:

Теперь можно найти ординату второй точки пересечения:

3 способ – используем преобразование графиков функций

Этот способ быстрее первого и более универсальный, в частности он может пригодится и в задачах на другие функции.

Главный недостаток этого способа — вершина должна иметь целые координаты.

Сам способ базируется на следующих идеях:

График (y=-x^2) симметричен относительно оси (x) графику (y=x^2).

– Если (a>1) график (y=ax^2) получается растяжением графика (y=x^2) вдоль оси (y) в (a) раз.
– Если (a∈(0;1)) график (y=ax^2) получается сжатием графика (y=x^2) вдоль оси (y) в (a) раз.

– График (y=a(x+d)^2) получается сдвигом графика (y=ax^2) влево на (d) единиц.
— График (y=a(x-d)^2) получается сдвигом графика (y=ax^2) вправо на (d) единиц.

График (y=a(x+d)^2+e) получается переносом графика (y=a(x+d)^2) на (e) единиц вверх.
График (y=a(x+d)^2-e) получается переносом графика (y=a(x+d)^2) на (e) единиц вниз.

У вас наверно остался вопрос — как этим пользоваться? Предположим, мы видим такую параболу:

Сначала смотрим на её форму и направленность её ветвей. Видим, что форма стандартная, базовая и ветви направлены вверх, поэтому (a=1). То есть она получена перемещениями графика базовой параболы (y=x^2).

А как надо было перемещать зеленый график чтоб получить оранжевый? Надо сдвинуться вправо на пять единиц и вниз на (4).

То есть наша функция выглядит так: (y=(x-5)^2-4).
После раскрытия скобок и приведения подобных получаем искомую формулу:

Чтобы найти (f(6)), надо сначала узнать формулу функции (f(x)). Найдем её:

Парабола растянута на (2) и ветви направлены вниз, поэтому (a=-2). Иными словами, первоначальной, перемещаемой функцией является функция (y=-2x^2).

Парабола смещена на 2 клеточки вправо, поэтому (y=-2(x-2)^2).

Парабола поднята на 4 клеточки вверх, поэтому (y=-2(x-2)^2+4).

График линейной функции, его свойства и формулы

О чем эта статья:

Понятие функции

Функция — это зависимость y от x, где x является независимой переменной или аргументом функции, а y — зависимой переменной или значением функции.

Задать функцию значит определить правило, следуя которому по значениям независимой переменной можно найти соответствующие значения функции. Вот какими способами ее можно задать:

Табличный способ помогает быстро определить конкретные значения без дополнительных измерений или вычислений.

Аналитический способ — через формулы. Компактно, и можно посчитать функцию при произвольном значении аргумента из области определения.

Словесный способ.

Графический способ — наглядно. Его мы и разберем в этой статье.

График функции — это множество точек (x; y), где x — это аргумент, а y — значение функции, которое соответствует данному аргументу.

Понятие линейной функции

Линейная функция — это функция вида y = kx + b, где х — независимая переменная, k, b — некоторые числа. При этом k — угловой коэффициент, b — свободный коэффициент.

Геометрический смысл коэффициента b — длина отрезка, который отсекает прямая по оси OY, считая от начала координат.

Геометрический смысл коэффициента k — угол наклона прямой к положительному направлению оси OX, считается против часовой стрелки.

Если известно конкретное значение х, можно вычислить соответствующее значение у.

Нам дана функция: у = 0,5х — 2. Значит:

если х = 0, то у = -2;

если х = 2, то у = -1;

если х = 4, то у = 0 и т. д.

Для удобства результаты можно оформлять в виде таблицы:

Графиком линейной функции является прямая. Для ее построения достаточно двух точек, координаты которых удовлетворяют уравнению функции.

Угловой коэффициент отвечает за угол наклона прямой, свободный коэффициент — за точку пересечения графика с осью ординат.

k и b — это числовые коэффициенты функции. На их месте могут стоять любые числа: положительные, отрицательные или дроби.

Давайте потренируемся и определим для каждой функций, чему равны числовые коэффициенты k и b.

Функция	Коэффициент k	Коэффициент b
y = 2x + 8	k = 2	b = 8
y = −x + 3	k = −1	b = 3
y = 1/8x − 1	k = 1/8	b = −1
y = 0,2x	k = 0,2	b = 0

Может показаться, что в функции y = 0,2x нет числового коэффициента b, но это не так. В данном случае он равен нулю. Чтобы не поддаваться сомнениям, нужно запомнить: в каждой функции типа y = kx + b есть коэффициенты k и b.

Свойства линейной функции

Область определения функции — множество всех действительных чисел.

Множеством значений функции является множество всех действительных чисел.

График линейной функции — прямая. Для построения прямой достаточно знать две точки. Положение прямой на координатной плоскости зависит от значений коэффициентов k и b.

Функция не имеет ни наибольшего, ни наименьшего значений.

Четность и нечетность линейной функции зависят от значений коэффициентов k и b:

b ≠ 0, k = 0, значит, y = b — четная;

b = 0, k ≠ 0, значит, y = kx — нечетная;

b ≠ 0, k ≠ 0, значит, y = kx + b — функция общего вида;

b = 0, k = 0, значит, y = 0— как четная, так и нечетная функция.

Свойством периодичности линейная функция не обладает, потому что ее спектр непрерывен.

График функции пересекает оси координат:

ось абсцисс ОХ — в точке (−b/k; 0);

ось ординат OY — в точке (0; b).

x = −b/k — является нулем функции.

Если b = 0 и k = 0, то функция y = 0 обращается в ноль при любом значении переменной х.

Если b ≠ 0 и k = 0, то функция y = b не обращается в нуль ни при каких значениях переменной х.

Функция монотонно возрастает на области определения при k > 0 и монотонно убывает при k 0 функция принимает отрицательные значения на промежутке (−∞; −b/k) и положительные значения на промежутке (−b/k; +∞).

При k 0, то этот угол острый, если k

Построение линейной функции

В геометрии есть аксиома: через любые две точки можно провести прямую и притом только одну. Исходя из этой аксиомы следует: чтобы построить график функции вида у = kx + b, достаточно найти всего две точки. А для этого нужно определить два значения х, подставить их в уравнение функции и вычислить соответствующие значения y.

Например, чтобы построить график функции y = 1/3x + 2, можно взять х = 0 и х = 3, тогда ординаты этих точек будут равны у = 2 и у = 3. Получим точки А (0; 2) и В (3; 3). Соединим их и получим такой график:

В уравнении функции y = kx + b коэффициент k отвечает за наклон графика функции:

если k > 0, то график наклонен вправо;

если k 0, то график функции y = kx + b получается из y = kx со сдвигом на b единиц вверх вдоль оси OY;

если b 0, то график функции y = kx + b выглядит так:

0″ src=»https://user84060.clients-cdnnow.ru/uploads/5fc1049363f94987951092.png» style=»height: 600px;»>

Если k > 0 и b > 0, то график функции y = kx + b выглядит так:

0 и b > 0″ src=»https://user84060.clients-cdnnow.ru/uploads/5fc104b2640e6151326286.png» style=»height: 600px;»>

Если k > 0 и b

В задачах 7 класса можно встретить график уравнения х = а. Он представляет собой прямую линию, которая параллельна оси ОY все точки которой имеют абсциссу х = а.

Важно понимать, что уравнение х = а не является функцией, так как различным значениям аргумента соответствует одно и то же значение функции, что не соответствует определению функции.

Например, график уравнения х = 3:

Условие параллельности двух прямых:

График функции y = k₁x + b₁ параллелен графику функции y = k₂x + b₂, если k₁ = k₂.

Условие перпендикулярности двух прямых:

График функции y = k₁x + b₁ перпендикулярен графику функции y = k₂x + b₂, если k₁k₂ = −1 или k₁ = −1/k₂.

Точки пересечения графика функции y = kx + b с осями координат:

С осью ОY. Абсцисса любой точки, которая принадлежит оси ОY равна нулю. Поэтому, чтобы найти точку пересечения с осью ОY, нужно в уравнение функции вместо х подставить ноль. Тогда получим y = b.

Координаты точки пересечения с осью OY: (0; b).

С осью ОХ. Ордината любой точки, которая принадлежит оси ОХ равна нулю. Поэтому, чтобы найти точку пересечения с осью ОХ, нужно в уравнение функции вместо y подставить ноль. И получим 0 = kx + b. Значит x = −b/k.

Координаты точки пересечения с осью OX: (−b/k; 0).

Решение задач на линейную функцию

Чтобы решать задачи и строить графики линейных функций, нужно рассуждать и использовать свойства и правила выше. Давайте потренируемся!

Пример 1. Построить график функции y = kx + b, если известно, что он проходит через точку А (-3; 2) и параллелен прямой y = -4x.

В уравнении функции y = kx + b два неизвестных параметра: k и b. Поэтому в тексте задачи нужно найти два условия, которые характеризуют график функции.

Из того, что график функции y = kx + b параллелен прямой y = -4x, следует, что k = -4. То есть уравнение функции имеет вид y = -4x + b.

Осталось найти b. Известно, что график функции y = -4x + b проходит через точку А (-3; 2). Подставим координаты точки в уравнение функции и мы получим верное равенство:

Таким образом, нам надо построить график функции y = -4x — 10

Мы уже знаем точку А (-3; 2), возьмем точку B (0; -10).

Поставим эти точки в координатной плоскости и соединим прямой:

Пример 2. Написать уравнение прямой, которая проходит через точки A (1; 1); B (2; 4).

Если прямая проходит через точки с заданными координатами, значит координаты точек удовлетворяют уравнению прямой y = kx + b.

Следовательно, если координаты точек подставить в уравнение прямой, то получим верное равенство.

Подставим координаты каждой точки в уравнение y = kx + b и получим систему линейных уравнений.

Вычтем из второго уравнения системы первое, и получим k = 3.

Подставим значение k в первое уравнение системы, и получим b = -2.

Ответ: уравнение прямой y = 3x — 2.

Алгоритм определения формулы линейной функции по графику

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

Выполнила учительница математики МБОУ Башкирский лицей № 1 муниципального района Учалинский район Республики Башкортостан Хидиятова Залифа Даутовна

Алгоритм определения формулы линейной функции по графику»

На рисунке представлен график функции у = kx +b.
Записать формулу линейной функции, соответствующей данному графику.

1) Так как ордината точки пересечения графика функции с осью Оy равна 1, следовательно, b=1.
Значит, у = kx+ 1

2) Выбираем на графике произвольную точку, например, А (2;2) и определяем её координаты: если x = 2, то у = 2. Подставим в нашу формулу вместо Х и У и получим уравнение относительно k.
2 = 2k+1
2k=1
k = 0.5 Записываем формулу линейной функции: у = 0,5х + 1.

Написать ФОРМУЛУ линейной функции У= КХ+В, график которой изображен на рисунке :

Это ВПР задание это ответ:

ВНИМАНИЕ : задание на сегодня 16 апреля

Внимание : вот эти следующие задания пока НЕ РЕШАТЬ.

Курс повышения квалификации

Дистанционное обучение как современный формат преподавания

• Сейчас обучается 924 человека из 80 регионов

Курс профессиональной переподготовки

Математика: теория и методика преподавания в образовательной организации

• Сейчас обучается 686 человек из 75 регионов

Курс повышения квалификации

Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО

• Сейчас обучается 309 человек из 69 регионов

Ищем педагогов в команду «Инфоурок»

Дистанционные курсы для педагогов

«Взбодрись! Нейрогимнастика для успешной учёбы и комфортной жизни»

Свидетельство и скидка на обучение каждому участнику

Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:

5 580 470 материалов в базе

Материал подходит для УМК

«Алгебра», Макарычев Ю.Н., Миндюк Н.Г., Нешков К.И. и др. / Под ред. Теляковского С.А.

16. Линейная функция и её график

Самые массовые международные дистанционные

Школьные Инфоконкурсы 2022

33 конкурса для учеников 1–11 классов и дошкольников от проекта «Инфоурок»

Другие материалы

• 16.09.2020
• 199
• 11

• 31.03.2020
• 1166
• 30

• 16.03.2020
• 227
• 1

• 16.03.2020
• 191
• 1

• 08.03.2020
• 282
• 6

• 20.02.2020
• 1246
• 71

• 21.01.2020
• 180
• 0

• 09.12.2019
• 420
• 13

Вам будут интересны эти курсы:

Оставьте свой комментарий

Авторизуйтесь, чтобы задавать вопросы.

Добавить в избранное

• 30.09.2020 16045
• DOCX 549.2 кбайт
• 155 скачиваний
• Оцените материал:

Настоящий материал опубликован пользователем Хидиятова Залифа Даутовна. Инфоурок является информационным посредником и предоставляет пользователям возможность размещать на сайте методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайт

Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.

Автор материала

• На сайте: 5 лет и 3 месяца
• Подписчики: 0
• Всего просмотров: 38689
• Всего материалов: 37

Московский институт профессиональной
переподготовки и повышения
квалификации педагогов

Дистанционные курсы
для педагогов

663 курса от 690 рублей

Выбрать курс со скидкой

Выдаём документы
установленного образца!

Учителя о ЕГЭ: секреты успешной подготовки

Время чтения: 11 минут

Профессия педагога на третьем месте по популярности среди абитуриентов

Время чтения: 1 минута

В Ростовской и Воронежской областях организуют обучение эвакуированных из Донбасса детей

Время чтения: 1 минута

Инфоурок стал резидентом Сколково

Время чтения: 2 минуты

Минпросвещения упростит процедуру подачи документов в детский сад

Время чтения: 1 минута

Количество бюджетных мест в вузах по IT-программам вырастет до 160 тыс.

Время чтения: 2 минуты

В Швеции запретят использовать мобильные телефоны на уроках

Время чтения: 1 минута

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.