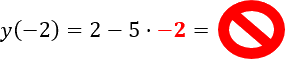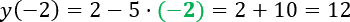Прежде чем перейти к разбору решения задач с функциями обязательно прочитайте урок
«Что такое функция в математике».
После того, как вы действительно поймете, что такое функция
(возможно, придется прочитать урок не один раз) вы с бóльшей уверенностью сможете решать задания с функциями.
В этом уроке мы разберем, как решать основные типы задач на функцию и графики функций.
Как получить значение функции
Рассмотрим задание.
Функция задана формулой «y = 2x − 1»
- Вычислить «y» при «x = 15»
- Найти значение «x», при котором
значение «y» равно «−19».
Для того, чтобы вычислить «y» при
«x = 15» достаточно подставить в функцию вместо «x»
необходимое числовое значение.
Запись решения выглядит следующим образом.
y(15) = 2 · 15 − 1 = 30 − 1 = 29
Для того, чтобы найти «x»
по известному «y», необходимо подставить вместо
«y» в формулу функции числовое значение.
То есть теперь наоборот, для поиска «x»
мы подставляем в функцию «y = 2x − 1» вместо
«y» число «−19» .
−19 = 2x − 1
Мы получили линейное уравнение с неизвестным «x»,
которое решается по правилам решения линейных уравнений.
Запомните!
Не забывайте про правило переноса в уравнениях.
При переносе из левой части уравнения в правую (и наоборот) буква или число меняет знак на
противоположный.
−19 = 2x − 1
0 = 2x − 1 + 19
−2x = −1 + 19
−2x = 18
Как и при решении линейного уравнения, чтобы найти неизвестное, сейчас
требуется умножить и левую, и правую часть на «−1» для смены знака.
−2x = 18 | · (−1)
2x = −18
Теперь разделим и левую, и правую часть на «2», чтобы найти «x» .
2x = −18 | (: 2)
x = −9
Как проверить верно ли равенство для функции
Рассмотрим задание.
Функция задана формулой «f(x) = 2 − 5x».
Верно ли равенство
«f(−2) = −18»?
Чтобы проверить верно ли равенство, нужно подставить в функцию «f(x) = 2 − 5x»
числовое значение «x = −2» и сопоставить с тем, что получится при расчетах.
Важно!
Когда подставляете отрицательное число вместо «x», обязательно заключайте его в скобки.
Не забывайте использовать
правило знаков.
Неправильно
Правильно
С помощью расчетов мы получили
«f(−2) = 12».
Это означает, что «f(−2) = −18»
для функции «f(x) = 2 − 5x» не является верным равенством.
Как проверить, что точка принадлежит графику функции
Рассмотрим функцию «y = x2 −5x + 6»
Требуется выяснить, принадлежит ли графику этой функции точка с координатами
(1; 2).
Для этой задачи нет необходимости, строить график заданной функции.
Запомните!
Чтобы определить, принадлежит ли точка функции,
достаточно подставить её координаты в функцию (координату по оси
«Ox» вместо
«x» и координату по оси «Oy»
вместо «y»).
Если получится верное равенство, значит, точка принадлежит функции.
Вернемся к нашему заданию. Подставим в функцию «y = x2 − 5x + 6»
координаты точки (1; 2).
Вместо «x» подставим «1».
Вместо «y» подставим «2».
2 = 12 − 5 · 1 + 6
2 = 1 − 5 + 6
2 = −4 + 6
2 = 2 (верно)
У нас получилось верное равенство, значит, точка с координатами
(1; 2) принадлежит заданной функции.
Теперь проверим точку с координатами (0; 1).
Принадлежит ли она
функции «y = x2 − 5x + 6»?
Вместо «x» подставим «0».
Вместо «y» подставим «1».
1 = 02 − 5 · 0 + 6
1 = 0 − 0 + 6
1 = 6 (неверно)
В этом случае мы не получили верное равенство.
Это означает, что точка с координатами (0; 1) не принадлежит функции
«y = x2 − 5x + 6»
Как получить координаты точки функции
С любого графика функции можно снять координаты точки. Затем необходимо убедиться, что при подстановке координат
в формулу функции получается верное равенство.
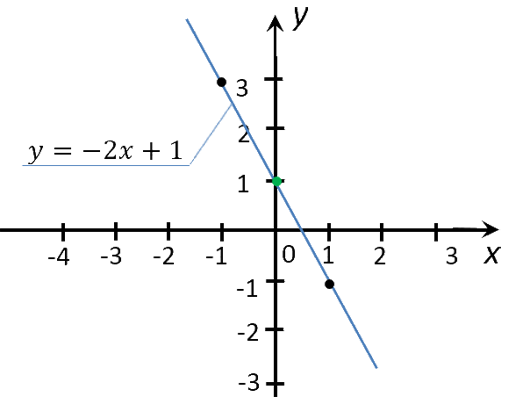
Рассмотрим функцию «y(x) = −2x + 1». Её график
мы уже
строили
в предыдущем уроке.
Найдем на графике функции «y(x) = −2x + 1», чему равен «y»
при x = 2.
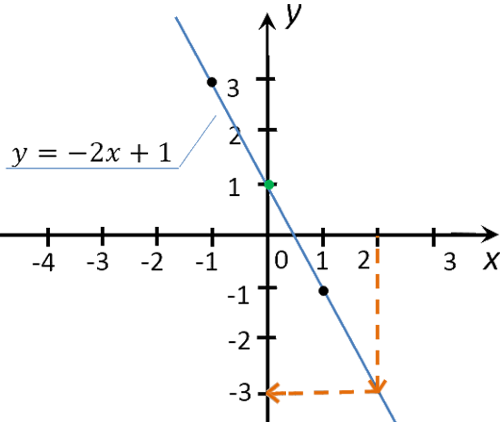
Для этого из значения «2» на оси «Ox» проведем перпендикуляр к графику функции.
Из точки пересечения перпендикуляра и графика функции проведем еще один перпендикуляр к оси «Oy».
Полученное значение «−3» на оси «Oy» и будет искомым значением «y».
Убедимся, что мы правильно сняли координаты точки для x = 2
в функции «y(x) = −2x + 1».
Для этого мы подставим x = 2 в формулу функции
«y(x) = −2x + 1». Если мы правильно
провели перпендикуляр, мы также должны получить в итоге y = −3.
y(2) = −2 · 2 + 1 = −4 + 1 = −3
При расчетах мы также получили y = −3.
Значит, мы правильно получили координаты с графика функции.
Важно!
Все полученные координаты точки с графика функции обязательно проверяйте
подстановкой значений «x» в функцию.
При подстановке числового значения «x» в функцию в результате должно получиться
то же значение «y», которое вы получили на графике.
При получении координат точек с графика функции высока вероятность, что вы ошибетесь, т.к. проведение перпендикуляра к осям выполняется «на глазок».
Только подстановка значений в формулу функции дает точные результаты.
Ваши комментарии
Важно!
Чтобы оставить комментарий, вам нужно войти на наш сайт при помощи
«ВКонтакте».

Оставить комментарий:
11 ноября 2018 в 15:46
Веточка Сакуры
Профиль
Благодарили: 0
Сообщений: 1
Веточка Сакуры
Профиль
Благодарили: 0
Сообщений: 1
Функция y=f(x) является нечётной и при x ⩽0 задаётся формулой y= — x² — 8x.Найдите значение фун. в т. минимума (y min).
0
Спасибо
Ответить
12 ноября 2018 в 3:25
Ответ для Веточка Сакуры
Евгений Фёдоров
Профиль
Благодарили: 0
Сообщений: 60
Евгений Фёдоров
Профиль
Благодарили: 0
Сообщений: 60
ymin = y(4) = -16.
0
Спасибо
Ответить
17 сентября 2018 в 13:28
Alesger Mammedov
Профиль
Благодарили: 0
Сообщений: 1
Alesger Mammedov
Профиль
Благодарили: 0
Сообщений: 1
Добрый день помогите пожалуйста с задачкой
f(x2-3x)=3x2+5x-4
f(3)=?
0
Спасибо
Ответить
17 сентября 2018 в 23:01
Ответ для Alesger Mammedov
Евгений Фёдоров
Профиль
Благодарили: 0
Сообщений: 60
Евгений Фёдоров
Профиль
Благодарили: 0
Сообщений: 60
f(3) = 26 ± 7√21
0
Спасибо
Ответить
13 ноября 2016 в 6:43
Роман Безбородов
Профиль
Благодарили: 0
Сообщений: 1
Роман Безбородов
Профиль
Благодарили: 0
Сообщений: 1
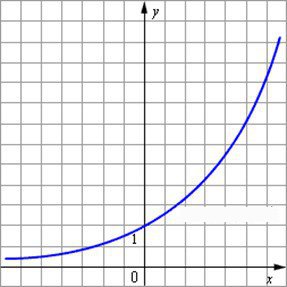
0
Спасибо
Ответить
14 ноября 2016 в 17:30
Ответ для Роман Безбородов
Евгений Фёдоров
Профиль
Благодарили: 0
Сообщений: 60
Евгений Фёдоров
Профиль
Благодарили: 0
Сообщений: 60
y = ax; a > 1.
0
Спасибо
Ответить
7 сентября 2016 в 22:08
Иван Баранов
Профиль
Благодарили: 0
Сообщений: 3
Иван Баранов
Профиль
Благодарили: 0
Сообщений: 3
у=Х2+2Х-3 найдите значение функции, если значение аргумента равно -2
у=3х-5 при каком значении аргумента значение функции раво 10
0
Спасибо
Ответить
8 сентября 2016 в 15:26
Ответ для Иван Баранов
Юлия Анарметова
Профиль
Благодарили: 0
Сообщений: 11
Юлия Анарметова
Профиль
Благодарили: 0
Сообщений: 11
аргумент это х значит у=(-2)2+2 · (-2)-3=4-4-3=-3
у=3х-5 значит 10=3х-5
10+5=3х
15=3х
х=15:3=5
0
Спасибо
Ответить
Как найти значение функции по значению аргумента
Как найти значение функции по значению аргумента? Это можно сделать с помощью формулы, задающей функцию.
Если функция задана формулой y=f(x), чтобы найти значение функции по данному значению аргумента, надо в формулу функции вместо каждого икса подставить это значение и вычислить значение y.
Пример.
1) Линейная функция задана формулой y=10x-7.
Найти значение функции, соответствующее значению аргумента, равному 3; -2,5; 1,4; 0.
Решение:
При x=3
при x=-2,5
при x=1,4
при x=0
2) Функция задана формулой
Найти значение функции при x, равном 10; -2; 1; 0.
Решение:
При x=10
при x=-2
при x=1
при x=0
Значение функции по данному значению аргумента можно найти также по графику. Как это сделать, мы рассмотрим в следующий раз.
Как по значению аргумента найти соответствующее значение функции. ?
Как по значению аргумента найти соответствующее значение функции?
Аргумент — х, значение функции — y.
Нам известно некоторое значение аргумента, например, х = 2. Чтобы найти соответствующее ему значение функции нужно в формулу у = 6х + 12 вместо х подставить его значение, в нашем примере это число 2. Получаем:
у = 6*2 + 12 = 12 + 12 = 24
Итак, значению аргумента х = 2 соответствует значение функции у = 24.
Правило: чтобы по значению аргумента найти значение функции надо в формулу данной функции вместо х подставить его числовое значение.
б) Как найти значение аргумента, которому соответствует указанное значение функции?
Нам задано значение функции — y, например y = 6.
Чтобы найти значение аргумента, которому соответствует указанное значение функции нужно в формулу у = 6х + 12 вместо y подставить его значение, в нашем примере это число 6. Получаем уравнение:
Итак, значению функции y = 6 соответствует значение аргумента х = -1.
Правило: чтобы по значению функции найти значение аргумента надо в формулу данной функции вместо y подставить его числовое значение.
Найти значение функции – Как найти значение функции по значению аргумента
Как найти значение функции по значению аргумента? Это можно сделать с помощью формулы, задающей функцию.
Если функция задана формулой y=f(x), чтобы найти значение функции по данному значению аргумента, надо в формулу функции вместо каждого икса подставить это значение и вычислить значение y.
1) Линейная функция задана формулой y=10x-7.
Найти значение функции, соответствующее значению аргумента, равному 3; -2,5; 1,4; 0.
2) Функция задана формулой
Найти значение функции при x, равном 10; -2; 1; 0.
Значение функции по данному значению аргумента можно найти также по графику. Как это сделать, мы рассмотрим в следующий раз.
Как найти значение аргумента по значению функции
Как найти значение аргумента по значению функции? Это можно сделать с помощью формулы функции.
Если формула задана формулой вида y=f(x), чтобы найти значение аргумента по значению функции, надо в формулу вместо y подставить заданное значение функции и решить получившееся уравнение относительно икса.
1) Линейная функция задана формулой y=5x-8. Найти значение аргумента, при котором значение функции равно 7; -38;0.
Поменяем местами левую и правую часть, чтобы запись выглядела в привычном виде (знаки при этом менять не надо):
Это — линейное уравнение. Неизвестное — в одну сторону, известные — в другую (при переносе слагаемых из одной части в другую знаки меняются на противоположные):
Обе части уравнения делим на число, стоящее перед иксом:
2) При каком значении аргумента значение функции
Решаем квадратное уравнение.
При y=0 x=3 и x=0,5.
Это — неполное квадратное уравнение. Общий множитель x выносим за скобки
и решаем уравнение типа «произведение равно нулю»:
При y=3 x=0 и x=3,5.
Значение аргумента по заданному значению функции можно также найти с помощью графика. О том, как это сделать, мы будем говорить в следующий раз.
Как по значению аргумента найти соответствующее значение функции. ?
Как по значению аргумента найти соответствующее значение функции? Аргумент — х, значение функции — y. Нам известно некоторое значение аргумента, например, х = 2. Чтобы найти соответствующее ему значение функции нужно в формулу у = 6х + 12 вместо х подставить его значение, в нашем примере это число 2. Получаем: у = 6*2 + 12 = 12 + 12 = 24 Итак, значению аргумента х = 2 соответствует значение функции у = 24. Правило: чтобы по значению аргумента найти значение функции надо в формулу данной функции вместо х подставить его числовое значение. б) Как найти значение аргумента, которому соответствует указанное значение функции? Нам задано значение функции — y, например y = 6. Чтобы найти значение аргумента, которому соответствует указанное значение функции нужно в формулу у = 6х + 12 вместо y подставить его значение, в нашем примере это число 6. Получаем уравнение: 6 = 6х + 12 6х = -6 х = -1 Итак, значению функции y = 6 соответствует значение аргумента х = -1. Правило: чтобы по значению функции найти значение аргумента надо в формулу данной функции вместо y подставить его числовое значение.
подставляй найденный аргумент в условие и останется только одна переменная
Функцыя задана формулой y=5x-1.Найти значение функции, если значение аргумента равно -1.
Что такое алгебра?! Функция и аргумент в алгебре.
Один из разделов математики это алгебра, которая подразумевает выполнение различных операций с числами, так как сложение, умножение и т.д. Можно сказать, что алгебра это нечто вроде расширения арифметики до более высокого уровня. Понять, что такое алгебра и откуда она взялась, помогут исторические факты. Первые предпосылки алгебры появились в разных уголках мира, людям нужна была алгебра для того, чтобы решить определенные уравнения. Например, в Древней Греции впервые об уравнениях заговорил Диофант, это был 2-3 век нашей эры.
В Китае примерно 2 тысячи лет до нашей времени уже было умение решать квадратные уравнения и уравнения первой степени. Также некоторые предпосылки алгебры встречались у индийского народа и жителей арабских стран. Согласно историческому прошлому, также отличилось издание «Алгебра» аль-Хваризми, которое стало популярным в 12-ом веке благо переводу на латинском языке. Человечество нуждалось в проведение расчетов, так появилась алгебра. Что такое алгебра для вас и нужна или нет, каждый решает сам. Потребность в алгебре появилась, как необходимость решать однотипные задачи. В школе алгебра всегда была и остается обязательным предметом.
Когда начинают учить алгебру в школе?
Разделение математики на несколько областях определило для алгебры решение определенных уравнений, под названием алгебраические уравнения. Что такое алгебра как предмет можно узнать только в 7-ом классе. Именно тогда вместе привычной математики появляется два отдельных предмета: алгебра и геометрия. Изучение начинается с простых понятий, также как и в случае других учебных процессов, все строится от простого материала к сложному.
7 класс оптимальное время для того, чтобы узнать, что такое алгебра. Вместо обычных операций с числами осуществляется переход на переменные. Так проще понять общие законы арифметики, научиться работать с неизвестными и функциями. Алгебру можно разделить на 5 отдельных категорий:
Школьная программа подразумевает изучение исключительно элементарной категории. Элементарная алгебра занимается изучением операций с вещественными числами. Перемененные и постоянные обозначены в алгебре символами в виде букв. С их помощью происходит преображение уравнений и математических выражений на основе четких правил.
Функция в алгебре
Понимание алгебры как предмет требует знание определенных элементов, так как функция, аргумент и определение. Что такое функция в алгебре и чем она определена? Функция является одним из основных понятий и определяет зависимость между переменными с неодинаковой величиной.
Что такое функция?:
Функция в алгебре представляет собой сопоставимость между двумя множествами. Согласно этому каждый элемент множества соответствует по одному единственному элементу другого множества.
Функция задается различным образом:
— согласно словесной формулировке (описание словами)
— аналитическим образом (используя формулу).
Школьная алгебра всецело сосредоточена над изучением числовых функций. Функция и аргумент указаны в виде чисел. Пример: y=f(x), где x перемена независимого типа, а y функция наоборот зависимая. У функции есть еще такие параметры как: область определения (D) и область значения (E). Первый параметр представляет собой совокупность значений для переменной «х», в то время как второй обозначает множество значений для «у».
Аргумент в алгебре
Что такое аргумент в алгебре? Это не что иное, как перемена х, от которой зависит у, то есть функция. Аргумент функции в алгебре это независимая перемена с помощью которой определяется значение функции.
Значение аргумента можно определить по значению функции. Для определения аргумента по функции y=f(x), надо заменить y заданным значением. Остается только решить уравнение относительно x для того, чтобы значение стало известным. Существует возможность определения данного параметра и по графику функции.
Определение алгебры и ее практическая польза
Определение, что такое алгебра, позволяет понять какая от нее практическая польза. Только понимая область деятельности этой части математики, появляется стремление ее изучать. Благодаря алгебре, можно шагать на более высокий уровень познания математики. Алгебра это та простая ступень, которая позволяет делать прогресс в процессе изучения современной математики. Благодаря ней, появилась возможность взглянуть иначе на множества.
Постепенно элементарные значения алгебры перешли в более сложные понятия. Так появилась универсальная алгебра, которая стала основой для развития топологии. Алгебра это ступень, которая позволяет ступать дальше, и без нее не быть некоторым явлений прогресса. Знания некоторых людей, может завершиться на элементарных основ дисциплины, но в определенных областях глубокое изучение обязательно.
Определение понятия функции. Переменные.
Определение
Зависимость переменной у от переменной х, при которой любому значению переменной х соответствует единственное значение переменной у, называют функцией.
- х – это независимая переменная, ее называют аргумент.
- у – это зависимая переменная.
Ключевое слово, которое нужно запомнить в определении функции – это зависимость.
Например, человек идет на деловую встречу, но чувствует, что он опаздывает. Он ускоряет свой шаг, потому что от его скорости зависит время. Чем быстрее он двигается, тем меньше времени уйдет у него на дорогу. То есть время зависит от скорости.
Или, например, спортсмен метает ядро на дальнее расстояние. Чем сильнее будет бросок, тем дальше полетит ядро. Скорость полета зависит от силы толчка. Здесь опять прослеживается зависимость.
Функцию коротко записывают так: y = f(x). Вместо буквы f может быть использована и другая буква. Чтение данной записи следующее: “у равно f от х”.
Например, функция задана формулой у = – 3х2 – 7. Равносильная ей запись такая: f(x)= – 3х2 – 7.
Пример 1. Найти значение функции f(x)= – 3х2 – 7 для значений аргумента, равных –5 и 4.
Подставим в формулу вместо х значения, сначала (-5), а затем 4
f (–5) = – 3.(–5)2 – 7 = –75–7 = –82
f (4) = – 3.(4)2 – 7 = – 48 – 7 = –55
Пример 2. Найти значение х, при котором функция, заданная формулой f (х) = 3х+2, принимает значение равное 5.
Так как дано, что значение равно 5, то значит f (х) = 5, составим и решим уравнение: 5=3х + 2
выполним перенос слагаемого 2 в левую часть, изменяя при этом знак: 5 – 2 = 3х
приведем подобные слагаемые в левой части уравнения: 3 = 3х
найдем неизвестный множитель делением: х = 1
Ответ: х=1.
Области определения и значения функции
Определение
Все возможные значения независимой переменной (х) называют областью определения функции.
Все значения, которые принимает зависимая переменная (у) называют областью значений функции.
Если какая-либо функция у=f(x) задана формулой, а при этом ее область определения не указана, то считается, что она состоит из любых значений переменной, при которых выражение имеет смысл.
Области определения и значений школьных функций
1. Для линейной функции областью определения будет являться любое число.
Если у такой функции k≠0, то областью ее значений также будет являться любое число.
При k=0 область значений этой функции состоит из единственного числа b.
Например, функция задана формулой у = 7. Тогда ее область значения — это число 7, а область определения – любое число.
2. Гипербола задается формулой вида y = k/x.
Область определения такой функции – любое число, кроме нуля.
Область значений такой функции – аналогичная.
3. Функция, заданная формулой y= |x|, имеет область определения – любое число.
4. У функций у = х2 и у = х3 область определения – любое число.
Для того чтобы понимать, как находится область определения функции и рассмотреть примеры заданий на нахождение области определения функции, вспомним правила, при которых существуют ограничения и выражение не имеет смысл: нельзя делить на нуль; нельзя извлекать квадратный корень из отрицательного числа.
Пример 3. Рассмотрим, как находится область определения функций, которые заданы следующими формулами:
- у = 5х + 2
Данное выражение будет иметь смысл при любом значении х, так как все действия здесь выполнимы. Например, подставив нуль, получим, что 5×0 + 2 = 2. Также при любых отрицательных или положительных значениях х выражение будет иметь смысл.
- у = – 8х2 – 4
Данное выражение содержит степень. Все действия здесь так же выполнимы при любом значении х.
- у = 87/(х + 11)
В знаменателе этого выражения содержится переменная х, поэтому надо проверить, при каком значении он может быть равным нулю и исключить это значение из области определения, так как на знаменатель делят, а на нуль делить нельзя.
Итак, имеем знаменатель х + 11. Приравниваем его к нулю, получаем х + 11 = 0. Решаем простое уравнение на нахождение неизвестного слагаемого и получаем х= – 11. Это число исключаем из области определения функции.
- у = √х
Выражение содержит квадратный корень из переменной х. Знаем, что он может извлекаться только из положительного или равного нулю числа. Поэтому область определения будет х≥0.
Ответ: (1) и (2) – множество всех чисел; (3) – любое число, кроме (-11) или х ≠ – 11; (4) х ≥0.
Нахождение области определения функции
- Если выражение целое и не содержит квадратного корня, то оно имеет смысл при любом значении независимой переменной. Следовательно, областью определения будет являться множество всех чисел.
- Если выражение дробное, то необходимо исключить те значения, которые обращают знаменатель в нуль. Для этого знаменатель дроби приравнять к нулю и решить полученное уравнение. Областью определения будут являться все числа, кроме тех, которые получились при решении уравнения.
Даниил Романович | Просмотров: 13.7k
План урока:
Что такое функция
Способы задания функции
Построение графика функции
Линейная функция
Степенная функция с натуральным показателем
Что такое функция
Нередко в жизни можно наблюдать взаимосвязь между различными величинами. Предположим, что на входе в зоопарк указана информация о стоимости билетов. Для детей до 7 лет проход бесплатен, для детей от 8 до 18 лет билет стоит 100 рублей, а взрослым он обойдется в 200 рублей. Таким образом, стоимость билета определяется возрастом его покупателя. Математики в таком случае говорят, что цена билета является функцией от возраста посетителя.
Пусть есть выражение 2s + 5. Обозначим его значение переменной d. Для любого значения s мы можем вычислить значение d, которое будет ему соответствовать. При s = 5 получаем
d = 2*5 + 2 = 15
а при s = 10 имеем
d = 2*10 + 2 = 25
Получается, что значение переменной d однозначно определяется s, то есть d является функцией от s.
Попробуем дать строгое определение функции. Как и многие другие определения в математике, оно использует понятие множества.
Обозначим буквой D множество всех тех чисел, которые можно подставить в функцию вместо величины d. Очевидно, что это множество всех действительных чисел. Аналогично буквой S обозначим множество всех тех значений, которые может принимать величина s. Получается, что функция
d = 2s + 5
задает правило, по которому каждому элементу множества D ставится в соответствие один из элементов множества S. В связи с этим можно сформулировать определение:
Множество S называют областью определения функции, а множество D – областью значений функции. Величину s называют независимой величиной, независимой переменной, либо просто аргументом, ведь мы можем по своему усмотрению придавать ей любое значение. Для величины d используют термин зависимая величина, зависимая переменная, либо просто функция, ведь ее значение ЗАВИСИТ от того, какое значение будет выбрано для аргумента. Другими словами, аргумент и функция – это две величины, одна из которых (независимая) определяет другую (зависимую). Иногда встречается запись:
d(s) = 2s + 5
Буква s в скобках означает, что d зависит именно от переменной s. Другой пример: запись u(t)обозначает некую функцию, где t выступает в роли независимой величины, а u – в роли зависящей от аргумента функции.
Иногда необходимо указать значение функции при конкретном значении аргумента. В этом случае этот аргумент пишут в скобках:
d(3) = 2*3 + 5 = 11
d(8) = 2*8 + 5 = 21
d(-100) = 2*(-100) + 5 = -195
То есть, если нам надо указать значение какой-то функции y(х) при х равном, например, 7, то мы просто пишем у(7).
Сделаем несколько уточнений. Во-первых, множества, между которыми устанавливается соответствие, не обязательно должны быть числовыми. Например, если стоимость чехла для телефона зависит от его цвета (синий, желтый, красный), то эту стоимость можно считать функцией от цвета, который не описывается числом. Если для каждого кассира, работающего в магазине, можно указать кассу, где он трудится, то касса является функцией от имени кассира. Впрочем, в основном математика, а особенно алгебра,изучает именно числовые функции.
Во-вторых, принципиально важно, чтобы для каждого значения аргумента функция задавала ровно 1 значение зависимой величины.
Например, пусть числу n соответствует такое число m, чтобы выполнялось условие:
m2=n
Тогда числу 4 мы можем поставить в соответствие как 2, так и – 2:
(-2)2=4
22 = 4
Значит, это соответствие не является функцией.
Однако допускается обратная ситуация, когда при разных аргументах функция имеет одинаковое значение:
Здесь на рисунке разным аргументам, 2 и (– 2), соответствует одно и тоже число, 4.
В-третьих, данное определение подходит только для функций, зависящих от одной переменной. Существуют и более сложные функции, зависящие от двух и более переменных. Например, в медицине используется индекс массы тела, который рассчитывается как отношение массы тела к квадрату роста. Таким образом, этот индекс зависит от двух переменных – от роста человека и его веса. В рамках школьного курса математики функции нескольких переменных не изучаются, однако они используются при решении многих практических задач.
Наконец, надо понимать, что фраза «переменная d зависит от s» не всегда означает наличия причинно-следственной связи между этими параметрами. Классический пример – цены на нефть на мировых биржах. Для каждого прошедшего момента времени можно указать, сколько именно тогда стоила нефть. Тем самым, с математической точки зрения, задается функция, где цена товара зависит от времени. Однако любой экономист скажет, что на самом деле стоимость продукции зависит отнюдь не от времени, а от спроса и предложения на товар, а также себестоимости его производства. Другими словами, в математике словосочетание «a зависит от b» правильнее понимать как «a соответствует b».
Способы задания функции
Самый простой способ задания какой-либо зависимости – описательный, или словесный. Вот пример такого описания: «каждому нечетному числу x соответствует число y, равное его наименьшему делителю (не считая единицы)». Такая формулировка значит, что, например, числу 15 соответствует число 3, ведь 15 делится только на 3 и 5, а тройка меньше пятерки. Числу 91 соответствует 7, так как 91 делится на 7 и 13. А какое число соответствует, скажем, 12? Никакое, ведь в описании функции указано, что аргументом должно быть нечетное число, а 12 – четное.
Чаще всего в алгебре применяют аналитический способ задания функции. Он подразумевает, что записывается формула, позволяющая по значению независимой величины вычислить величину зависимую:
Этим записям аналогична другая, где аргумент прямо указывается в скобках после зависимой величины:
Иногда функция может быть представлена в виде алгоритма. Например: «для вычисления значения g(х) необходимо сложить все десятичные цифры, из которых состоит натуральное число x». Тогда для аргумента 135 функция будет равна 9:
g(135) = 1 + 3 + 5 = 9
Вот ещё несколько значений этой функции:
g(89) = 8 + 9 =17
g(5656) = 5 + 6 + 5 +6 = 22
Подобный подход нередко встречается в некоторых языках программирования.
Если область определения функции не содержит бесконечное число чисел, то ее можно задать таблицей.В ней указывают все возможные значения независимой величины, а также соответствующие её значения зависимой величины. Вот пример табличной функции, задающей соответствие между размерами европейскими и английскими размерами мужских пальто:
А вот ещё одна табличная функция, которая каждому натуральному числу n от 1 до 5 ставит в соответствие число, равное 2n + 3:
По приведенной таблице легко определить, что
y(1) = 5
y(2) = 7
y(3) = 9
y(4) = 11
y(5) = 13
Очень распространен графический способ задания функции. Он предполагает, что нарисован график (линия или набор линий на координатной плоскости), с помощью которого можно по аргументу определить зависимую величину. Этот график может выглядеть так:
На координатной плоскости показана горизонтальная ось, по которой откладывают значение независимой переменной (в этом примере это х), и вертикальная ось, где отмечают зависимую переменную (у). Сам график показан синей линией. Покажем, как с его помощью находить значение y. Пусть надо узнать y(2), то есть значение y при x = 2. Находим на горизонтальной оси x (ее ещё называют осью абсцисс) число 2 и проводим с нее вертикальную линию до пересечения графика:
После этого от полученной точки проводится уже горизонтальная линия до пересечения с вертикальной осью y (другое ее название – ось ординат):
Далее смотрим, где именно горизонтальная линия пересекла ось у. В рассматриваемом случае получили, что у(2) = – 2,5.
Можно сформулировать определение графика функции:
Надо понимать, что не любая линия задает какую-нибудь функцию. Дело в том, что ни одна вертикальная линия не должна пересекаться с графиком в 2 и более точках, ведь тогда одному значению аргумента будет соответствовать несколько значений функции.Такая ситуация показана на рисунке:
Здесь можно видеть, что для x = 3 можно указать два значения для y. Однако по определению значению независимой величины в соответствие ставится лишь одно значение зависимой переменной. Поэтому синяя линия здесь не является графиком функции (приведен как пример того, что не всякая линия может являться графиком функции). Нередко полностью построить график невозможно. Например, зависимость
y = x + 2
определена и при x = 1, и при x =1000000000000000000. Поэтому иногда график строят частично, чтобы наглядно были видны его особенности.
Примерами графических функций являются кардиограммы, фиксирующие работу сердца, а также показания сейсмографа – прибора, измеряющего силу землетрясений.
Построение графика функции
Одну и ту же зависимость возможно порою задать как аналитически, так и графически. Графики помогают при решении многих сложных задач, ведь они наглядно иллюстрируют поведение функций. Посмотрим, как построить график функции, если для нее известна формула, ее описывающая.
Пусть дана зависимость
y(x) = 0.5x(4 — x)
Будем строить для нее график при значениях x от – 2 до 6. Для этого запишем в таблице все возможные целые значения х и вычислим для них величину y.Покажем несколько примеров расчета:
y(-2) = 0.5*(-2)(4-(-2)) = -6
y(-1) = 0.5*(-1)(4-(-1)) = -2.5
y(0) = 0.5*0*(4-0) = 0
Таким образом заполняется вся таблица:
Получили координаты 9 точек, которые отметим на плоскости (для первых двух точек пунктирами показано, как нашли их местоположение):
Они уже «намечают» некоторую линию. Конечно, отметить все возможные точки невозможно. Однако при необходимости можно «уплотнить» точки на графике, вычислив у ещё при некоторых дробных значениях x, например:
y(-1.5) = 0.5*(-1.5)(4-(-1.5)) = 4.125
y(-0.5) = 0.5*(-0.5)(4-(-0.5)) = 1.125
Отложим эти и ещё несколько дополнительных точек на графике:
С помощью современной компьютерной техники можно почти мгновенно вычислить местоположение миллионов таких точек. Соединив их все плавной линией, получим график:
Линейная функция
Можно представить огромное количество разных функций, однако есть некоторые, которые имеют особое значение как в математике, так и в естественных науках. Знакомство с основными функциями мы начнем с простейшей и одновременно важнейшей из них –линейной функции. Сначала познакомимся с ее частным случаем – прямой пропорциональностью.
Пусть автомобиль едет со скоростью 15 м/с. Обозначим за t время поездки в секундах, а за s – пройденное расстояние в метрах. Так как путь равен произведению скорости и времени, то можно записать:
s = 15t
Увеличение времени поездки, например, вдвое ведет также к удвоению пройденного расстояния. Сокращение времени в три раза приведет и к уменьшению пути втрое. В таком случае математики говорят, что величина s прямо пропорциональна величине t.
Периметр квадрата p зависит от длины его стороны a и вычисляется по формуле:
p = 4a
Величины p и a также прямо пропорциональны друг другу.
Зависимость, связывающая такие величины, называется прямой пропорциональностью. Она имеет вид
y = kx
где x – независимая величина, y – зависимая величина, а k – произвольное число (константа), которое не равно нулю.
Число k называют коэффициентом пропорциональности. Он показывает, во сколько раз зависимая переменная больше аргумента.
Легко заметить, что при x = 0 и y = 0, причем это правило будет выполняться независимо от значения коэффициента пропорциональности. Это значит, что график у = kх обязательно проходит через начало координат точку O (0;0).
Построим график прямой пропорциональности на примере
y = 0.5x
Выше мы уже строили график функции, находя несколько ее значений и занося их в таблицу. Здесь поступим также:
Теперь можно отметить найденные точки, соединить их и получить график:
Оказывается, что все точки лежат строго на одной прямой! И это будет верно для любой зависимости, которая является прямой пропорциональностью. Для наглядности покажем на графике функции:
- y = x (синий цвет);
- y = 2x (зеленый цвет);
- y = 3x (красный цвет).
Из курса геометрии известно, что для построения прямой достаточно двух ее точек. Поэтому, чтобы получить график заданной прямой пропорциональности, достаточно найти одну точку, относящуюся к этому графику, и соединить ее прямой с началом координат.
На координатной плоскости принято выделять координатные четверти, которые ещё называют квадрантами. Их использование упрощает анализ графиков:
По четверти, в которой располагается точка, можно сразу определить знак ее координат:
- в I четверти координаты х и у положительны;
- во II четверти х отрицателен, а у положителен;
- в III четверти обе координаты отрицательны;
- в IV четверти х положителен, а у отрицателен.
Все примеры графиков прямой пропорциональности, которые мы рассматривали до этого, проходили через I и III четверть. Это было связано с тем, что коэффициент пропорциональности в них был положительным числом. Теперь попробуем построить графики функций
y = -0.5x
y = -x
y = -2x
На графике они показаны соответственно синим, зеленым и красным цветом:
Видно, что при отрицательных значениях коэффициента пропорциональности прямая проходит через II и IV четверти.
Также можно заметить, что наклон графика зависит от k. Чем больше этот коэффициент (по модулю, то есть без учета знака), тем ближе прямая к вертикальной линии. Чем меньше k, тем ближе прямая к горизонтальной линии. Убедимся в этом, построив графики y = 10x и y = 0,1x:
Теперь рассмотрим собственно линейную функцию. Она отличается от прямой пропорциональности добавлением свободного коэффициента в правой части. Примерами линейной функции являются:
s = 8t + 2
d = 0.27b — 7.5
y = 19x + 0.001
Приведем пример из реальной жизни. Пусть есть бидон для молока, который весит 5 кг. Масса 1 литра молока равна 0,9 кг. Тогда масса бидона (обозначим ее как m), в который залили молоко, зависит от объема молока в нем (обозначим этот объем как p). Эту зависимость можно описать так:
m = 5 + 0.9p
Говорят, что масса бидона линейно зависит от объема молока в нем.
По сути, линейная функция – это такая же прямая пропорциональность. Отличие только в том, что при аргументе, равном нулю, сама зависимая переменная нулю может и не равняться. В данном примере при отсутствии молока в емкости у нее всё равно остается собственная масса.
Отдельно отметим два момента. Во-первых, прямая пропорциональность тоже является линейной функцией, если принять b = 0, а k≠ 0, то будет: у = kx. Во-вторых, в отличие от прямой пропорциональности, у линейной функции коэффициент k может быть и равным нулю.
Каковы особенности линейной функции и ее графика? До этого мы строили график
y = 0.5x
Теперь построим график линейной зависимости
y = 0.5x + 3
Будем сравнивать в таблице значения этих двух выражений:
Видно, что при любом значении x функция y = 0,5x + 3 имеет значение, которое на 3 больше значения y = 0,5x. Поэтому все точки графика можно получить, «подняв» на 3 единицы точки графика без коэффициента b (а это прямая пропорциональность):
Получается, что график линейной зависимости – это также прямая, которая, однако, может и не проходить через точку О (0; 0).
Если в зависимость
y = kx + b
подставить значение аргумента, равное нулю, то получим
y = k*0 + b
y = b
Это значит, что график линейной функции проходит через точку с координатами (0, b), в которой он и пересекает вертикальную ось у. С другой стороны, график линейной зависимости у = kх + b параллелен графику y = kx:
Так как коэффициент k определяет наклон прямой, его именуют угловым коэффициентом.
Через любые две точки проходит только одна прямая, а потому для построения графика линейной зависимости достаточно вычислить ее значение в двух точках, отметить их и соединить прямой линией.
Пусть необходимо построить график зависимости
y = 2x/3 + 2
Вычислим значение функции в двух точках. Удобнее всего взять значения х, равные 0 и 3:
y(0) = 2/3*0 + 2 = 2
y(3) = 2/3*3 + 2 = 2 + 2 = 4
Отметим эти точки на координатной плоскости и проведем прямую:
Рассмотрим отдельно ситуацию, когда число k = 0. В этом случае одночлен с переменной x можно опустить:
y = 0*x + b = b
Примерами подобных функций являются
y = 1
y = 5
y = 8.37
y = -3.23
Хотя в записи этих выражений аргумент не указан (нет переменной x), их всё равно можно считать функциями, ведь определить значение зависимой величины можно. Просто при любом значении независимой величины значение y остается одним и тем же.
Графиками подобных зависимостей являются горизонтальные прямые, пересекающие ось ординат в точке с координатами (0;b):
Если на плоскости построены два разных графика с одинаковым угловым коэффициентом, то они будут параллельны друг другу. В противном случае они пересекутся. Любые две прямые пересекаются только в одной точке. Покажем, как ее найти.
Пусть надо найти точку пересечения графиков
y = -3x + 1
и
y = x — 3
Ясно, что их общая точка должна иметь такие координаты, которые при подставлении в каждую из функций дают верное равенство. Обозначим ее координаты как x0 и y0. Тогда можно записать два равенства:
y0 = -3x0 + 1
y0 = x0 — 3
У этих двух уравнений равны левые части, значит, должны равняться и правые:
-3x0 + 1 = x0 — 3
Решим его:
-4x0 = -4
x0 = 1
Найдя значение x0, можно подставить его в любую из функций, чтобы вычислить и значение y0:
y0 = x0 — 3 = 1 — 3 = -2
Получили точку (1; – 2). Данный способ нахождения точки пересечения графиков функции называют аналитическим. Проверим себя, используя графический способ, то есть просто построим эти графики:
Степенная функция с натуральным показателем
Если обозначить сторону квадрата как a, то его площадь будет являться функцией:
S = a2
Для вычисления объема куба с ребром a необходимо возводить число уже в третью степень:
V = a3
Эти выражения являются примерами степенных функций с натуральным показателем. Таковой будет являться любое уравнение y = xs, где s – это какое-то натуральное число.
При s = 1 степенная функция обращается в зависимость у = х, то есть в прямую пропорциональность. Независимая величина х может принимать любые значения, а вот область значений зависит от четности или нечетности показателя s (этот вопрос будет рассмотрен подробнее чуть позже).
Рассмотрим функцию y = x2. Ясно, что при х, равном нулю, зависимая переменная также обращается в нуль:
y(0) = 02 = 0
Следовательно, ее график проходит через точку О (0;0). Это характерное свойство степенных функций с любым натуральным показателем.
Квадрат любого числа не может быть отрицательным числом, а потому график лежит в I и II четвертях. Следовательно, областью значений будет являться всё множество неотрицательных действительных чисел.
Заметим, что противоположным значениям х соответствуют одинаковые значения y:
y(-x) = (-x)2 = x2 = y(x)
Из-за этого график обладает симметрией относительно оси у.
Найдем несколько точек, по которым можно построить график степенной функции:
Полученную фигуру называют параболой, а точку О (0;0) – вершиной параболы. Видно, что точки параболы располагаются симметрично относительно оси ординат.
Заметим, что у степенных функций с четным показателем графики похожи. Они все симметричны относительно оси у, а также у них есть три общие точки:
- (0;0);
- (1;1);
- (– 1;1).
Они определены на множестве всех неотрицательных чисел. Чем выше показатель степени, тем более плотно график «прижимается» к горизонтальной оси при малых х и тем более резко он поднимается вверх при больших х:
Далее изучим те степенные функции, показатель которых – нечетное число. Одной из них является
y = x3
Её график также пересекает начало координат. При положительном значении аргумента куб числа также положителен, а при отрицательном значении аргумента он будет отрицательным числом. Следовательно, график должен проходить через I и III четверти. Построим график по точкам:
Полученный график называют кубической параболой. Графики других степенных функций (x5, x7, x9 и т.д.) похожи на этот:
Они проходят через точки (0;0), (1;1) и (– 1; –1), лежат в I и III четвертях. У всех этих функций и в область значений, и область определений попадают все действительные числа.