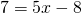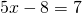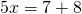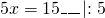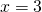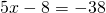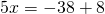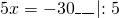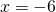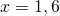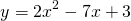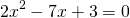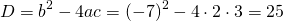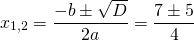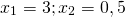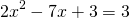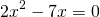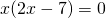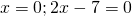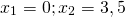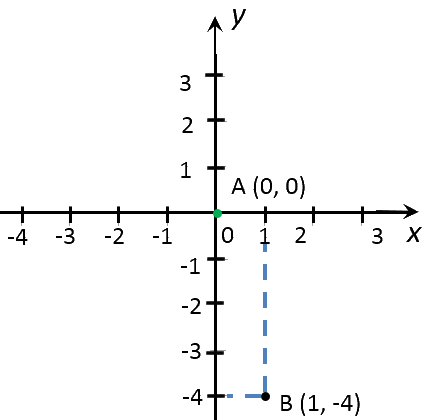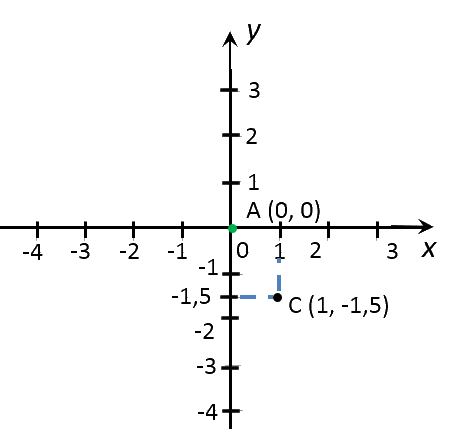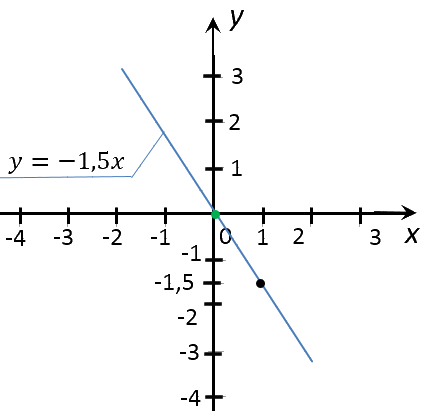Как найти значение игрек соответствующее значению икс

Как найти значение аргумента по значению функции? Это можно сделать с помощью формулы функции.

Если формула задана формулой вида y=f(x), чтобы найти значение аргумента по значению функции, надо в формулу вместо y подставить заданное значение функции и решить получившееся уравнение относительно икса.

1) Линейная функция задана формулой y=5x-8. Найти значение аргумента, при котором значение функции равно 7; -38;0.

Поменяем местами левую и правую часть, чтобы запись выглядела в привычном виде (знаки при этом менять не надо):

Это — линейное уравнение. Неизвестное — в одну сторону, известные — в другую (при переносе слагаемых из одной части в другую знаки меняются на противоположные):

Обе части уравнения делим на число, стоящее перед иксом:

2) При каком значении аргумента значение функции

Решаем квадратное уравнение.

При y=0 x=3 и x=0,5.

Это — неполное квадратное уравнение. Общий множитель x выносим за скобки

При y=3 x=0 и x=3,5.

Значение аргумента по заданному значению функции можно также найти с помощью графика. О том, как это сделать, мы будем говорить в следующий раз.

В прошлый раз мы находили значение функции по значению аргумента с помощью формулы.

Рассмотрим, как по данному графику функции найти y по x.

1) Пользуясь графиком линейной функции, изображенной на рисунке 1, найдите значение функции,если значение аргумента равно 1; 3; -3, -1; 0.

Аргумент — это x, функция — y.

Найти значение функции по значению аргумента — значит, по данному значению x найти, чему равен y.

Начнём с x=1. На оси абсцисс Ox находим x=1. Чтобы найти соответствующее значение y, надо из точки на Ox идти либо вверх, либо вниз, чтобы попасть на график.

От x=1 идём вверх. От полученной точки на графике надо двигаться либо влево, либо вправо, чтобы попасть на ось Oy. В данном случае идем влево и попадаем с ординатой y=2 (стрелочки помогают увидеть направление движения).

Следовательно, при x=1 y=2.

Аналогично, если x=3, идем вверх до пересечения с графиком, затем влево до пересечения с осью ординат Oy.

Получаем, что при x=3 y=4.

Если x=-3, чтобы попасть на график функции, нужно идти вниз, затем — вправо, до пересечения с осью Oy.

При x=-1 ни вверх, ни вниз двигаться не надо — эта точка уже на графике функции. Следовательно, y=0.

Записываем: при x=-1 y=0.

При x=0 идем до графика вверх и попадаем в точку с ординатой y=2.

2) На рисунке 2 изображен график функции y=f(x).

Пользуясь графиком, найдите значение функции, если значение аргумента равно 1; 3; 5; 7; -1; -5.

Чтобы по графику функции найти y по x, сначала надо от точки с данной абсциссой попасть на график, двигаясь вверх либо вниз, а затем от точки на графике идти к оси Oy, двигаясь влево или вправо.

При x=1 идем до графика функции вверх, затем влево — на ось Oy. Попадаем в точку с ординатой y=2.

Пишем: при x=1 y=2.

При x равном -1 и -5 идем сначала вверх, затем — вправо.

При иксах равных 3; 5 и 7 идём вниз и влево.

Обратите внимание: различным значениям икса может соответствовать одно значение y:

Дана следующая функция y=f(x) :
y = 2x – 10, если x > 0
y = 0, если x = 0
y = 2 * |x| – 1, если x

Требуется найти значение функции по переданному x .

1. Получить с клавиатуры значение x .
2. Если x больше 0, то вычислить выражение 2*x-10 , результат присвоить переменной y .

1. Иначе если x равен 0, то присвоить y значение 0.

1. Иначе присвоить y результат выражения 2*|x|-1 .

Вывести значение y на экран.

var x , y : integer ;
begin
readln ( x ) ;
if x > 0 then y : = 2 * x – 10
else
if x = 0 then y : = 0
else y : = 2 * abs ( x ) – 1 ;

writeln ( y ) ;
end .

main ( ) <
int x , y ;
scanf ( «%d» , & x ) ;
if ( x > 0 ) y = 2 * x – 10 ;
else
if ( x == 0 ) y = 0 ;
else
y = 2 * abs ( x ) – 1 ;

printf ( «%d
» , y ) ;
>

x = input ( )
x = int ( x )

if x > 0 :
y = 2 *x – 10
elif x == 0 :
y = 0
else :
y = 2 * abs ( x ) – 1

В КуМир функция взятия модуля от числа возвращает вещественное значение. Поэтому используется функция int(), чтобы привести к целому, иначе присвоение невозможно.

Разберем определение подробнее:

— Что значит «…зависимость переменной (y) от переменной (x)…»?

Наглядный пример: предположим, вы пришли в магазин купить конфеты, которые продаются вразвес и стоят по (100) рублей килограмм. Вопрос – сколько денег вы заплатите? Ответ: смотря сколько конфет купим! Действительно, купим два килограмма – заплатим (200) рублей, купим четыре с половиной – заплатим (450) рублей. То есть, цена покупки зависит от количества килограмм. Или, иначе говоря, цена покупки есть функция от количества купленных килограмм.

И если количество килограмм обозначить за (x), а цену покупки — за (y), то можно записать: (y=100x). Фактически, эта запись и есть функция. При этом понятно, что (x) изменяется по нашему желанию. Поэтому:

Игрек же меняется автоматически, не сам по себе, а потому что изменился (x). Поэтому:

                            

Эту связь между иксом и игреком можно пояснить такой аналогией: игрек – это телевизор, а икс – пульт от него. И если вы хотите, например, увеличить звук — вы не лезете внутрь телевизора и не пытаетесь вручную поменять напряжение в его резисторах, а просто нажимаете кнопку на пульте – и звук меняется. То есть звук поменялся не сам по себе, а потому что вы нажали кнопку. При этом с самим телевизором вы ничего не делали.

— Что значит «…каждому значению (x) соответствует только одно значение (y)»?
Если мы в полученную выше функцию (y=100x) поставим вместо икса, например, тройку, то получим, что игрек равен (100·3=300). И сколько бы раз мы не подставляли вместо икса тройку – мы всегда будем получать, что игрек равен (300). Мы никак не сможем получить другое значение игрека, если будем подставлять один и тот же икс. В этом и заключается смысл записи «каждому значению икса – только одно значение игрека».

Отметим, что игрек может быть одинаков для нескольких иксов. Например, функция (y=x^2-6x+9) имеет одинаковые значения игрека для икса равного (1) и для икса равного (5).

(x=1)      (y=1^2-6·1+9=4)
(x=5)      (y=5^2-6·5+9=4)

Однако это никак не противоречит сказанному выше: сколько бы мы не подставляли вместо икса (1) или (5) – мы всегда будем получать только «игрек равен (4)».

Вообще понятие функции гораздо шире рассмотренного выше, потому что функцией можно назвать не только «вычисления по формуле», но и любую зависимость элементов. При этом обязательно должно выполняться требование «одному иксу – один игрек». Для ясности приведем еще несколько примеров из жизни.

Например, зависимость типа «человек» — «рост человека» вполне можно считать функцией, потому что для каждого «икса» (то есть каждого отдельного человека) есть свой «игрек» (рост этого человека). Причем значение игрека (роста) определяется тем, какой икс (то есть какого именно человека) мы взяли, и это значение — только одно.

А вот зависимость типа «человек» — «хобби человека» уже не функция! Потому что требование «одному иксу – один игрек» здесь не выполняется, ведь у человека (икса) может быть и два, и три, и десять разных хобби (игреков).

Еще пример: вы шли по улице и нашли (100) рублей. Значит ли это, что пройдя по этой улице (10) раз, вы найдете (1000) рублей? Нет, не значит, потому что здесь нет зависимости между прогулкой и найденной суммой. Это случайность, а не функция.

Способы задания функции

Функция может задаваться:
— аналитически (в виде «формулы»):
например,          (y=100x) или (y=x^2-6x+9)

— таблично (таблица значений «икса» и соответствующих ему значений «игрека»):

например,

Имя ученика: Средний балл по математике: Васильева Татьяна 4,83 Сухарев Андрей 5,0 Якунин Василий 4,75

— графически (в виде графика):
например,
                                      

Зачастую одну и ту же функцию можно задать разными способами. Например, при построении графика мы как раз функцию, заданную аналитически, представляем в графическом виде.

Обратите внимание: на график функции требование «одному иксу – один игрек» также распространяется!

Это график функции, здесь каждому иксу соответствует свой игрек. Например, при (x=-5) игрек равен (-2), а при (x=6), игрек равен (4). Аналогично и для всех остальных значений икса.
А это не функция, а просто рисунок, так как здесь есть иксы, которым соответствует более одного игрека. Например, при (x=2), игрек равен сразу четверке, единице и минус трем.

Виды функций

В школьном курсе подробно изучаются следующие виды функций:

— Линейная (имеет график — прямая) —  все функции, приводимые к виду (y=kx+b), где (k) и (b) – числа. В этих функциях икс только в первой степени и нет переменных в знаменателях.		(y=2x+1)
— Квадратичная  (график — парабола) – функция имеет вид (y=ax^2+bx+c). Здесь обязательно есть икс в квадрате. А вот икс в первой степени или свободные члены (c) – могут отсутствовать.		(y=x^2-2)
— Обратной пропорциональности (график — гипербола) – задается формулой (y=) (frac{k}{x}), причем (k≠0).		(y=)(frac{3}{x})

В старших классах также изучается степенная, показательная, логарифмическая и тригонометрические функции.

Смотрите также:
Как  построить  график функции
Виды графиков функций

Что такое значение функции? Как найти значение функции?

Рассмотрим значение функции в математике на примере.

Значение функции в математике

Значение функции – это значение зависимой переменной.

Часто функцию в общем виде записывают как

y = f(x)

здесь игрек представляет значение функции.

Примеры значений функции

Простой пример значения функции:

y = x + 5

Что такое значение в этой функции?

Значение в этой функции представлено игреком.

Как узнать, что именно игрек, а не икс и не число пять, в этой функции покажет её значение?

Значение функции есть значение зависимой переменной.

Значение функции есть значение переменной, которое получается в результате математического действия.

В нашем случае к переменной икс прибавляется 5. Значит икс есть аргумент.

Значение же игрека получается в результате данного математического действия. Игрек и будет представлять значение функции.

Значение функции – это то, чему равна функция.

Пример. Пусть дана функция:

y = 5x

Функцией здесь является игрек. Чтоб найти значение функции, т.е. значение игрека, нужно подставить допустимое значение аргумента x. Так и сделаем. Пусть икс равен 4, тогда

20 = 5 * 4

откуда получаем, что значение функции при икс = 4 будет равно 20-ти.

Итак, значение функции это х или у? Значение функции это y.

График линейной функции, его свойства и формулы

О чем эта статья:

Понятие функции

Функция — это зависимость y от x, где x является независимой переменной или аргументом функции, а y — зависимой переменной или значением функции.

Задать функцию значит определить правило, следуя которому по значениям независимой переменной можно найти соответствующие значения функции. Вот какими способами ее можно задать:

Табличный способ помогает быстро определить конкретные значения без дополнительных измерений или вычислений.

Аналитический способ — через формулы. Компактно, и можно посчитать функцию при произвольном значении аргумента из области определения.

Словесный способ.

Графический способ — наглядно. Его мы и разберем в этой статье.

График функции — это множество точек (x; y), где x — это аргумент, а y — значение функции, которое соответствует данному аргументу.

Понятие линейной функции

Линейная функция — это функция вида y = kx + b, где х — независимая переменная, k, b — некоторые числа. При этом k — угловой коэффициент, b — свободный коэффициент.

Геометрический смысл коэффициента b — длина отрезка, который отсекает прямая по оси OY, считая от начала координат.

Геометрический смысл коэффициента k — угол наклона прямой к положительному направлению оси OX, считается против часовой стрелки.

Если известно конкретное значение х, можно вычислить соответствующее значение у.

Нам дана функция: у = 0,5х — 2. Значит:

если х = 0, то у = -2;

если х = 2, то у = -1;

если х = 4, то у = 0 и т. д.

Для удобства результаты можно оформлять в виде таблицы:

Графиком линейной функции является прямая. Для ее построения достаточно двух точек, координаты которых удовлетворяют уравнению функции.

Угловой коэффициент отвечает за угол наклона прямой, свободный коэффициент — за точку пересечения графика с осью ординат.

k и b — это числовые коэффициенты функции. На их месте могут стоять любые числа: положительные, отрицательные или дроби.

Давайте потренируемся и определим для каждой функций, чему равны числовые коэффициенты k и b.

Функция	Коэффициент k	Коэффициент b
y = 2x + 8	k = 2	b = 8
y = −x + 3	k = −1	b = 3
y = 1/8x − 1	k = 1/8	b = −1
y = 0,2x	k = 0,2	b = 0

Может показаться, что в функции y = 0,2x нет числового коэффициента b, но это не так. В данном случае он равен нулю. Чтобы не поддаваться сомнениям, нужно запомнить: в каждой функции типа y = kx + b есть коэффициенты k и b.

Свойства линейной функции

Область определения функции — множество всех действительных чисел.

Множеством значений функции является множество всех действительных чисел.

График линейной функции — прямая. Для построения прямой достаточно знать две точки. Положение прямой на координатной плоскости зависит от значений коэффициентов k и b.

Функция не имеет ни наибольшего, ни наименьшего значений.

Четность и нечетность линейной функции зависят от значений коэффициентов k и b:

b ≠ 0, k = 0, значит, y = b — четная;

b = 0, k ≠ 0, значит, y = kx — нечетная;

b ≠ 0, k ≠ 0, значит, y = kx + b — функция общего вида;

b = 0, k = 0, значит, y = 0— как четная, так и нечетная функция.

Свойством периодичности линейная функция не обладает, потому что ее спектр непрерывен.

График функции пересекает оси координат:

ось абсцисс ОХ — в точке (−b/k; 0);

ось ординат OY — в точке (0; b).

x = −b/k — является нулем функции.

Если b = 0 и k = 0, то функция y = 0 обращается в ноль при любом значении переменной х.

Если b ≠ 0 и k = 0, то функция y = b не обращается в нуль ни при каких значениях переменной х.

Функция монотонно возрастает на области определения при k > 0 и монотонно убывает при k 0 функция принимает отрицательные значения на промежутке (−∞; −b/k) и положительные значения на промежутке (−b/k; +∞).

При k 0, то этот угол острый, если k

Построение линейной функции

В геометрии есть аксиома: через любые две точки можно провести прямую и притом только одну. Исходя из этой аксиомы следует: чтобы построить график функции вида у = kx + b, достаточно найти всего две точки. А для этого нужно определить два значения х, подставить их в уравнение функции и вычислить соответствующие значения y.

Например, чтобы построить график функции y = 1/3x + 2, можно взять х = 0 и х = 3, тогда ординаты этих точек будут равны у = 2 и у = 3. Получим точки А (0; 2) и В (3; 3). Соединим их и получим такой график:

В уравнении функции y = kx + b коэффициент k отвечает за наклон графика функции:

если k > 0, то график наклонен вправо;

если k 0, то график функции y = kx + b получается из y = kx со сдвигом на b единиц вверх вдоль оси OY;

если b 0, то график функции y = kx + b выглядит так:

0″ src=»https://user84060.clients-cdnnow.ru/uploads/5fc1049363f94987951092.png» style=»height: 600px;»>

Если k > 0 и b > 0, то график функции y = kx + b выглядит так:

0 и b > 0″ src=»https://user84060.clients-cdnnow.ru/uploads/5fc104b2640e6151326286.png» style=»height: 600px;»>

Если k > 0 и b

В задачах 7 класса можно встретить график уравнения х = а. Он представляет собой прямую линию, которая параллельна оси ОY все точки которой имеют абсциссу х = а.

Важно понимать, что уравнение х = а не является функцией, так как различным значениям аргумента соответствует одно и то же значение функции, что не соответствует определению функции.

Например, график уравнения х = 3:

Условие параллельности двух прямых:

График функции y = k₁x + b₁ параллелен графику функции y = k₂x + b₂, если k₁ = k₂.

Условие перпендикулярности двух прямых:

График функции y = k₁x + b₁ перпендикулярен графику функции y = k₂x + b₂, если k₁k₂ = −1 или k₁ = −1/k₂.

Точки пересечения графика функции y = kx + b с осями координат:

С осью ОY. Абсцисса любой точки, которая принадлежит оси ОY равна нулю. Поэтому, чтобы найти точку пересечения с осью ОY, нужно в уравнение функции вместо х подставить ноль. Тогда получим y = b.

Координаты точки пересечения с осью OY: (0; b).

С осью ОХ. Ордината любой точки, которая принадлежит оси ОХ равна нулю. Поэтому, чтобы найти точку пересечения с осью ОХ, нужно в уравнение функции вместо y подставить ноль. И получим 0 = kx + b. Значит x = −b/k.

Координаты точки пересечения с осью OX: (−b/k; 0).

Решение задач на линейную функцию

Чтобы решать задачи и строить графики линейных функций, нужно рассуждать и использовать свойства и правила выше. Давайте потренируемся!

Пример 1. Построить график функции y = kx + b, если известно, что он проходит через точку А (-3; 2) и параллелен прямой y = -4x.

В уравнении функции y = kx + b два неизвестных параметра: k и b. Поэтому в тексте задачи нужно найти два условия, которые характеризуют график функции.

Из того, что график функции y = kx + b параллелен прямой y = -4x, следует, что k = -4. То есть уравнение функции имеет вид y = -4x + b.

Осталось найти b. Известно, что график функции y = -4x + b проходит через точку А (-3; 2). Подставим координаты точки в уравнение функции и мы получим верное равенство:

Таким образом, нам надо построить график функции y = -4x — 10

Мы уже знаем точку А (-3; 2), возьмем точку B (0; -10).

Поставим эти точки в координатной плоскости и соединим прямой:

Пример 2. Написать уравнение прямой, которая проходит через точки A (1; 1); B (2; 4).

Если прямая проходит через точки с заданными координатами, значит координаты точек удовлетворяют уравнению прямой y = kx + b.

Следовательно, если координаты точек подставить в уравнение прямой, то получим верное равенство.

Подставим координаты каждой точки в уравнение y = kx + b и получим систему линейных уравнений.

Вычтем из второго уравнения системы первое, и получим k = 3.

Подставим значение k в первое уравнение системы, и получим b = -2.

Ответ: уравнение прямой y = 3x — 2.

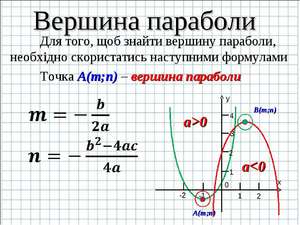
Как найти вершину параболы: три формулы

Парабола присутствует в мире математики, физики и других наук. По траектории параболы передвигаются искусственные спутники, которые стремятся покинуть пределы Солнечной системы, мяч при игре в волейбол тоже описывает её траекторию. Нужно уметь строить параболу. А чтобы это не составляло труда, надо знать, как найти вершину параболы.

Нахождение вершины параболы: способы, примеры, советы

График функции y = ax 2 + bx + c, где a — первый коэффициент, b — второй коэффициент, c — свободный член, называется параболой. Но обратите внимание на тот факт, что a ≠0.

У каждой точки параболы есть симметричная ей, кроме одной точки, и эта точка называется вершиной. Для того чтобы найти точку, которая является вершиной, нужно определиться, что такое точка на графике. Точка на графике – это определённая координата по оси абсцисс и по оси ординат. Она обозначается как (x; y). Давайте разбираться, как найти заветные числа.

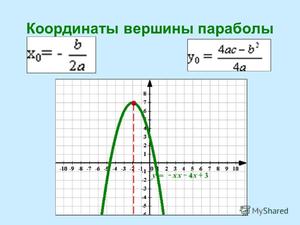
Первый способ

Если вы хотите знать, как необходимо правильно вычислять координаты вершины, то нужно только выучить формулу x0 = -b/2a. Подставляя полученное число в функцию, получим y0.

Например, y =x 2 –8 x +15;

находим первый, второй коэффициенты и свободный член;

подставляем значения a и b в формулу;

вычисляем значения y;

Значит, вершина находится в точке (4;-1).

Ветви параболы симметричны относительно оси симметрии, которая идёт через вершину параболы. Зная корни уравнения, можно без особых трудностей посчитать абсциссу вершины параболы. Предположим, что k и n — корни квадратичного уравнения. Тогда точка x0 равноудалена от точек k и n, и её можно вычислить по формуле: x0 = (k + n)/2.

Рассмотрим на примере y =x 2 –6x+5

1) Приравниваем к нулю:

2) Находим дискриминант, используя формулу: D = b 2 –4 ac:

3) Находим корни уравнения по формуле (-b±√ D)/2a:

• 1 — первый корень;
• 5 — второй корень.

Второй способ

Дополнение до полного квадрата – отличный способ узнать, где располагается вершина. Используя этот способ, вы сможете вычислить точки x и y одновременно, без нужды подставлять x в начальный пример. Рассмотрим этот метод на примере функции: y=x 2 +8 x +10.

1. Сначала нужно приравнять выражение с переменной к 0. Потом перенести c в правую сторону с противоположным знаком, то есть у нас получается выражение x 2 + 8x = -10.

2. Теперь в левой части нужно сделать полный квадрат. Для этого посчитайте (b/2) 2 и увеличьте обе части уравнения результат. В этом случае нужно подставит 8 вместо b.

У нас получается 16. Теперь прибавьте это число к обеим частям уравнения:

3. Видно, что полученное выражение – полный квадрат. Его можно представить в форме: (x + 4) 2 = 6.

4. Используйте это выражение для поиска координат вершины параболы. Чтобы посчитать x, нужно приравнять его к 0. Получаем, x =-4. Координата y равна тому, что находится в правой части, то есть y =6. Вершина параболы этого уравнения (-4, 6).

Третий способ

Если вы знаете, что такое производная, то для вас есть другая формула. Несмотря на то, куда смотрят «рога» параболы, её вершина — точка экстремума. Для этого способа надо применить следующий алгоритм:

1. Нахождение первой производной по формуле f'(x) = (ax² + bx + c)’ = 2ax + b.

2. Приравнивание производной к 0. В итоге вы получите 0 = 2ax + b, отсюда можно найти то, что нас интересует.

Рассмотрим этот способ подробнее.

Дана функция y = 4x²+16x-17;

• Записываем производную и приравниваем к нулю.

f'(x) = (4x²+16x-17)’ = 8x+16 =0

Построение параболы

Самое трудное при построении – это верно найти точки функции. Для подробного построения нужно просчитать 5–7 точек (для школьного курса хватит этого). Для этого выбираем какое-либо значение x и подставляем его в данную функцию. Итогом подсчётов будет число точки по оси ординат. После этого ставим на координатную плоскость полученные нами точки. В итоге у нас получается парабола.

Рассмотрим подробнее вопрос о нахождении точек, которые нужно отметить. Для примера возьмём функцию y =-x 2 +11 x -24 с вершиной в точке (5,5;-6,25).

1) Строим таблицу

2) Заполняем таблицу

Так как парабола имеет осевую симметрию, то можно считать только значения справа или слева от вершины. Лучше считать те значения, которые ближе к 0, так удобнее. В нашем случае эти значения 4 и 5.

X	4	5	5,5	6	7
Y	-4	-6	-6,25	-6	-4

Советы

Правильно находите коэффициенты.

Пишите промежуточные вычисления на бумаге. Это не только облегчит нахождение вершины, но и поможет найти свои ошибки.

Делайте всё поэтапно. Следуйте алгоритму.

Обратите ваше внимание на то, что:

• Нужно проверять правильно ли ваше решение.
• Необходимо успокоиться. Решение любых задач по математике требует опыта. Просто нужно отработать данную тему, и тогда непременно у вас всё получится.

Видео

Это видео поможет вам научиться находить вершину параболы

Прямые на координатной плоскости

Линейная функция

Линейной функцией называют функцию, заданную формулой

где k и b – произвольные (вещественные) числа.

При любых значениях k и b графиком линейной функции является прямая линия .

Число k называют угловым коэффициентом прямой линии (1), а число b – свободным членом .

График линейной функции

При k > 0 линейная функция (1) возрастает на всей числовой прямой, а её график ( прямая линия ) имеет вид, изображенный на рис. 1, 2 и 3.

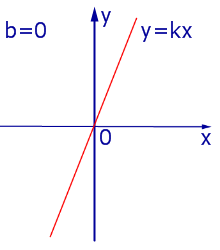Рис.1

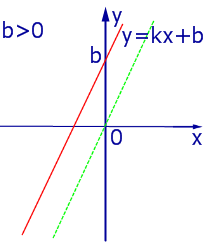Рис.2

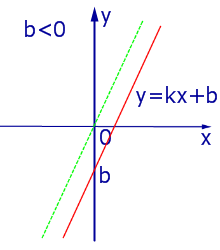Рис.3

При k = 0 линейная функция (1) принимает одно и тоже значение y = b при всех значениях x , а её график представляет собой прямую линию, параллельную оси абсцисс, и изображен на рис. 4, 5 и 6.

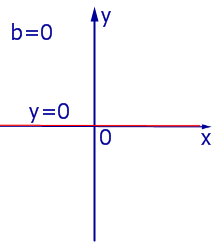Рис.4

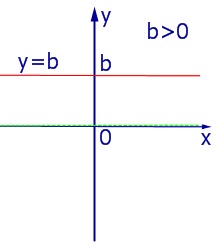Рис.5

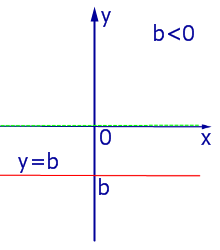Рис.6

При k линейная функция (1) убывает на всей числовой прямой, а её график ( прямая линия ) имеет вид, изображенный на рис. 7, 8 и 9.

k y = kx + b₁ и y = kx + b₂ ,

имеющие одинаковые угловые коэффициенты и разные свободные члены , параллельны .

имеющие разные угловые коэффициенты , пересекаются при любых значениях свободных членов.

y = kx + b₁ и

перпендикулярны при любых значениях свободных членов.

Угловой коэффициент прямой линии

равен тангенсу угла φ , образованному (рис. 10) при повороте положительной полуоси абсцисс против часовой стрелки вокруг начала координат до прямой (2).

Рис.10

Рис.11

Рис.12

Прямая (1) пересекает ось Oy в точке, ордината которой (рис. 11) равна b .

При прямая (1) пересекает ось Ox в точке, абсцисса которой (рис. 12) вычисляется по формуле

Прямые, параллельные оси ординат

Прямые, параллельные оси Oy , задаются формулой

где c – произвольное число, и изображены на рис. 13, 14, 15.

Рис.13

Рис.14

Рис.15

Замечание 1 . Из рис. 13, 14, 15 вытекает, что зависимость, заданная формулой (3), функцией не является, поскольку значению аргумента x = c соответствует бесконечное множество значений y .;

Уравнение вида px + qy = r . Параллельные прямые. Перпендикулярные прямые

где p, q, r – произвольные числа.

В случае, когда уравнение (4) можно переписать в виде (1), откуда вытекает, что оно задаёт прямую линию .

что и требовалось.

В случае, когда получаем:

откуда вытекает, что уравнение (4) задает прямую линию вида (3).

В случае, когда q = 0, p = 0, уравнение (4) имеет вид

и при r = 0 его решением являются точки всей плоскости:

В случае, когда уравнение (5) решений вообще не имеет.

Замечание 2 . При любом значении r₁ , не совпадающем с r прямая линия, заданная уравнением

параллельна прямой, заданной уравнением (4) .

Замечание 3 . При любом значении r₂ прямая линия, заданная уравнением

перпендикулярна прямой, заданной уравнением (4) .

Пример . Составить уравнение прямой, проходящей через точку с координатами (2; – 3) и

1. параллельной к прямой
2. перпендикулярной к прямой (8).

В соответствии с формулой (6), будем искать уравнение прямой, параллельной прямой (8), в виде

где r₁ – некоторое число. Поскольку прямая (9) проходит через точку с координатами (2; – 3), то справедливо равенство

Итак, уравнение прямой, параллельной к прямой

В соответствии с формулой (7), будем искать уравнение прямой, перпендикулярной прямой (8), в виде

где r₂ – некоторое число. Поскольку прямая (10) проходит через точку с координатами (2; – 3), то справедливо равенство

источники:

http://liveposts.ru/articles/education-articles/matematika/kak-najti-vershinu-paraboly-tri-formuly

http://www.resolventa.ru/spr/algebra/degree1.htm

Прежде чем перейти к изучению функции «y = kx»
внимательно изучите урок
«Что такое функция в математике»
и
«Как решать задачи на функцию».

Функция «y = kx» — это первый тип функции, который изучается в математике.

Другими словами, можно сказать, что «y = kx» — это семейство всевозможных функций, где вместо
«k» стоит число.

Примеры функций вида «y = kx».

• y = 4x
• y = −1,5x
• y = x

Давайте определим для каждой из функций выше, чему в них равен числовый коэффициент
«k».

Функция	Коэффициент «k»
y = 4x	k = 4
y = −1,5x	k = −1,5
y = 1 2 x	k = 1 2

Как построить график функции «y = kx»

Из геометрии вспомним аксиому (утверждение, которое не требует доказательства),
что через любые две точки можно провести прямую и притом только одну.

Исходя из этой аксиомы, что
чтобы построить график функции вида «у = kx» нам будет достаточно найти всего
две точки.

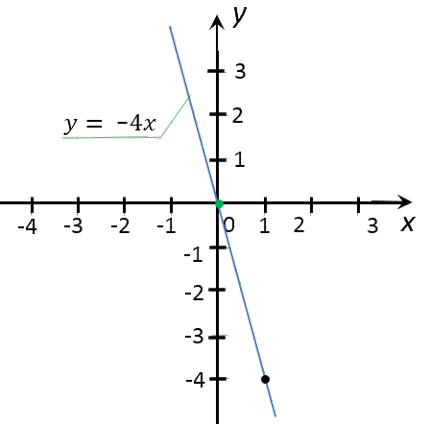
Для примера построим график функции «y = −4x».

Найдем значение функции «y» для двух произвольных значений «x».
Подставим, например, вместо «x» числа «0» и «1».

x	Расчет «y»
0	y(0) = −4 · 0 = 0
1	y(1) = −4 · 1 = −4

Полученные значения «x» и «y» — это координаты точек графика

функции «y = −4x».

Запишем полученные координаты точек «y = −4x» в таблицу.

Точка	Координата по оси «Оx» (абсцисса)	Координата по оси «Оy» (ордината)
(·)A	0	0
(·)B	1	−4

Отметим полученные точки на системе координат.

Теперь проведем прямую через отмеченные точки. Эта прямая и будет
являться графиком функции «y = −4x».

После построения не забудьте подписать график функции.

Как решать задачи на функцию «y = kx»

Рассмотрим задачу.

---

Построить график функции «y = −1,5x». Найти по графику:

1. значение «y» соответствующее значению «x» равному 1; 0; 2; 3;
2. значение «x», если значение «y» равно
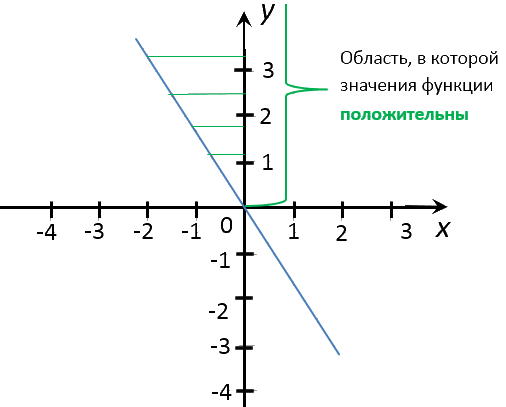
   −3; 4,5; 6;
3. несколько целых значений «x», при которых значения
   «y» положительны (отрицательны).

---

Вначале построим график функции «y = −1,5x».

Используем правила, по которым мы строили график функции выше.
Для построения графика функции «y = −1,5x» достаточно найти всего две точки.

Выберем два произвольных числовых значения для «x». Для удобства расчетов выберем числа
«0» и «1».

Выполним расчеты и запишем их результаты в таблицу.

Точка	Координата по оси «Оx»	Координата по оси «Оy»
(·)A	0	y(0) = −1,5 · 0 = 0
(·)B	1	y(1) = −1,5 · 1 = −1,5

Отметим полученные точки на прямоугольной системе координат.

Соединим полученные точки прямой. Проведенная прямая будет являться графиком функции
«y = −1,5x».

---

Теперь работаем с построенным графиком функции «y = −1,5x».

Требуется найти значение «y»,
соответствующее значению «x» равному 1; 0; 2; 3.

---

Тему
«Как получить координаты точки функции» с графика функции
мы уже подробно рассматривали в уроке
«Как решать задачи на функцию».

В этому уроке для решения задачи выше вспомним только основные моменты.

По правилам выше найдем на построенном ранее графике функции «y = −1,5x»
необходимые значения функции «y» для
«x» равным 1; 0; 2; 3.

Запишем полученные результаты в таблицу.

Заданное значение «x»	Полученное с графика значение «y»
0	0
1	−1,5
2	−3
3	−4,5

---

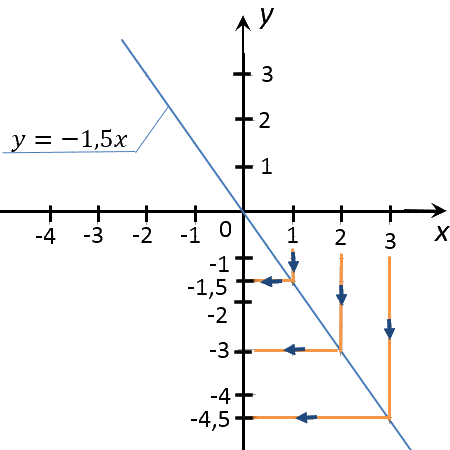
Переходим ко второму заданию задачи. Требуется найти значение «x»,
если значение «y» равно −3; 4,5; 6.

---

Выполним те же действия, что и при решении предыдущего задания.
Разница будет лишь в том, что изначально мы будем проводить перпендикуляры
от оси «Oy».

Запишем полученные результаты в таблицу.

Заданное значение «y»	Полученное с графика значение «x»
−3	2
4,5	−3
6	−4

---

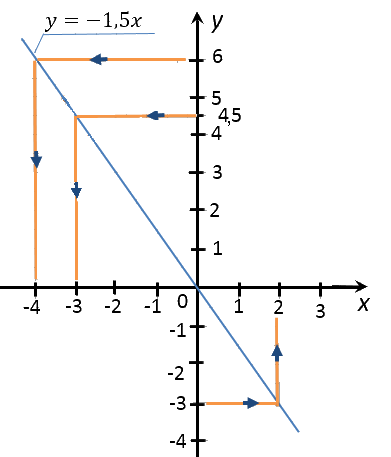
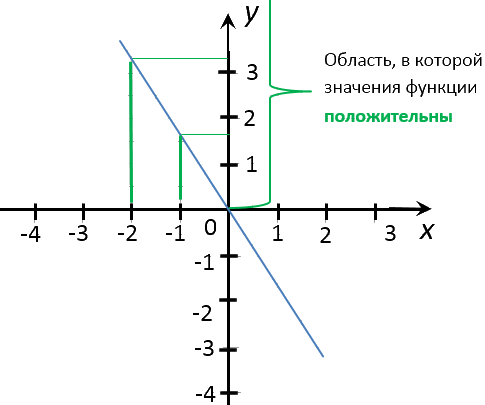
Перейдем к последнему заданию. Нас просят найти несколько целых значений «x»,
при которых значения «y» положительны (отрицательны).

Для решения этой задачи необходимо внимательно изучить
график функции
«y = −1,5x».

Отметим область на оси
«Oy», где значения «y» для графика функции «y = −1,5x»
положительны.

Из этой области проведем от графика функции несколько перпендикуляров
к оси «Ox».

Помните, что по заданию, нас просят найти несколько «целых» значений «x».
Поэтому перпендикуляры мы будем проводить к оси «Ox» в целые числовые значения.

Запишем ответ. При x = −2; x = −1 значения
y > 0.

---

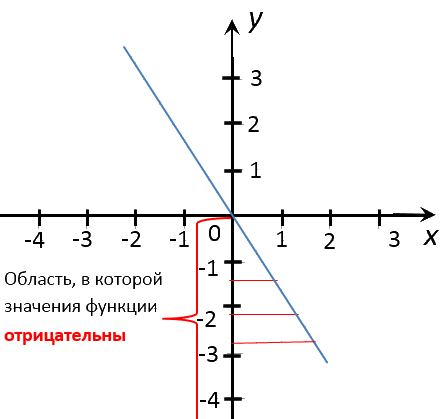
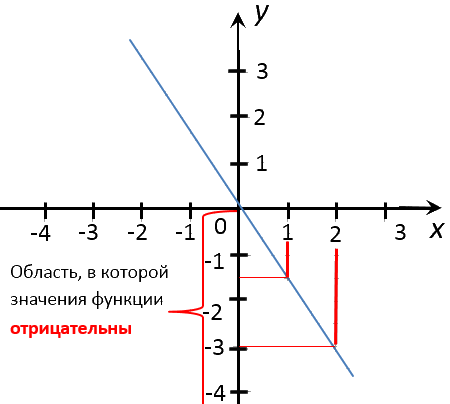
Теперь найдем при каких «x», значения
«y» отрицательны.
Отметим область на оси «Oy», где значения
«y» на графике функции отрицательны.

Проведем перпендикуляры из отмеченной области к оси «Ox» в
целые числовые значения «x».

Запишем ответ. При x = 1; x = 2 значения
y < 0.

---

Рассмотрим другую задачу.

Какие из точек A(5; −3), D(2; 1)
принадлежат графику функции, заданной
формулой
«y = x»?

---

Подробный разбор задачи «Как проверить, что точка принадлежит графику функции» мы приводили в уроке
«Как решать задачи на функцию».

В этом уроке мы вспомним только основные моменты решения подобных задач.

Подставим в функцию
«y = x»
координаты точки (·)A(5; −3).

−3 = · 5

              
−3 = (неверно)

Это означает, что точка (·)А(5; −3)
не принадлежит графику функции «y = x»

Проверим точку (·)D(2; 1).
Также подставим её координаты в функцию «y = x».

1 = ·2

1 =

            
1 = 1(верно)

Это означает, что точка (·)D(2; 1)
принадлежит графику функции «y = x».

---

Ваши комментарии

Оставить комментарий:

---