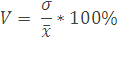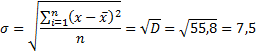Как найти значение коэффициента вариации - Исправление недочетов и поиск решений вместе с Examum.ru

Коэффициент вариации

Из
всех показателей вариации среднеквадратическое
отклонение в наибольшей степени
используется для проведения других
видов статистического анализа. Однако
среднеквадратическое отклонение дает
абсолютную оценку меры разбросанности
значений и чтобы понять, насколько она
велика относительно самих значений,
требуется относительный показатель.
Такой показатель называется он коэффициент
вариации.

Формула
коэффициента вариации:

Данный
показатель измеряется в процентах (если
умножить на 100%).

В
статистике принято, что, если коэффициент
вариации

меньше
10%, то степень рассеивания данных
считается незначительной,

от
10% до 20% — средней,

больше
20% и меньше или равно 33% — значительной,

значение
коэффициента вариации не превышает
33%, то совокупность считается однородной,

если
больше 33%, то – неоднородной.

Средние,
рассчитанные для однородной совокупности
– значимы, т.е. действительно характеризуют
эту совокупность, для неоднородной
совокупности – незначимы, не характеризуют
совокупность из-за значительного
разброса значений признака в совокупности.

Возьмем
пример с расчетом среднего линейного
отклонения.

И
график для напоминания

По
этим данным рассчитаем: среднее значение,
размах вариации, среднее линейное
отклонение, дисперсию и стандартное
отклонение.

Среднее
значение – это обычная средняя
арифметическая.

Размах
вариации – разница между максимумом и
минимумом:

Среднее
линейное отклонение считается по
формуле:

Дисперсия
считается по формуле:

Среднеквадратическое
отклонение – квадратный корень из
дисперсии:

Расчет
сведем в табличку.

Вариация
показателя отражает изменчивость
процесса или явления. Ее степень может
измеряться с помощью нескольких
показателей.

Размах
вариации –
разница между максимумом и минимумом.
Отражает диапазон возможных значений.
Среднее
линейное отклонение –
отражает среднее из абсолютных (по
модулю) отклонений всех значений
анализируемой совокупности от их
средней величины.
Дисперсия –
средний квадрат отклонений.
Среднеквадратическое
отклонение –
корень из дисперсии (среднего квадрата
отклонений).
Коэффициент
вариации –
наиболее универсальных показатель,
отражающий степень разбросанности
значений независимо от их масштаба и
единиц измерения. Коэффициент вариации
измеряется в процентах и может быть
использован для сравнения вариации
различных процессов и явлений.

Таким
образом, в статистическом анализе
существует система показателей,
отражающих однородность явлений и
устойчивость процессов. Часто показатели
вариации не имеют самостоятельного
смысла и используются для дальнейшего
анализа данных. Исключением является
коэффициент вариации, который характеризует
однородность данных, что является ценной
статистической характеристикой.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Коэффициент вариации — это статистическая метрика, которая может помочь специалистам зарегистрировать изменения в данных с течением времени. Эта метрика также может быть эффективным методом расчета финансового риска и вознаграждения за инвестиционную деятельность. Вы можете рассчитать коэффициент вариации с помощью простой формулы.

В этой статье мы обсудим, что такое коэффициент вариации и как его рассчитать, а также приведем несколько примеров применения этого статистического измерения к различным инвестиционным сценариям.

Основные выводы:

Коэффициент вариации — это эффективная метрика для быстрой оценки относительной дисперсии точек данных вокруг среднего значения выборки.
Финансовые аналитики и инвесторы могут часто оценивать коэффициент вариации для анализа риска и волатильности в зависимости от ожидаемой доходности инвестиций.
Более низкое соотношение между стандартным отклонением и средним значением может указывать на более высокий коэффициент доходности, в то время как более высокое соотношение может указывать на более низкий коэффициент доходности.

Что такое коэффициент вариации?

Коэффициент вариации (CV) измеряет разброс точек данных вокруг среднего значения. Отношение стандартного отклонения к среднему значению делает CV ценным ресурсом при сравнении вариаций одного ряда данных с другим. Он показывает, насколько сильно варьируются данные в выборке по сравнению со средним значением популяции.

Когда вы оцениваете CV, вы можете представить значение в процентах, где более низкий процент может указывать на более низкий CV, а более высокий процент может означать более высокий CV. В финансовом и инвестиционном анализе, где волатильность и риск могут влиять на потенциальную доходность, более низкий CV означает более низкое соотношение риска и доходности, что указывает на лучший компромисс между потенциальной доходностью и риском, присущим конкретному инвестиционному инструменту.

Какова формула для коэффициента вариации?

Формула CV использует стандартное отклонение и среднее значение данных вашей выборки для расчета коэффициента, отражающего дисперсию ваших значений вокруг среднего. В статистическом анализе основной формулой для расчета коэффициента вариации является:

CV = стандартное отклонение выборочного среднего x 100

При применении формулы в бизнесе, например, в финансовых расчетах, многие специалисты упрощают формулу CV, чтобы она соответствовала таким финансовым показателям, как доходность инвестиций, прирост капитала, риск и волатильность инвестиций. Поэтому многие аналитики могут также использовать следующую формулу для расчета CV с точки зрения финансового риска и вознаграждения:

CV = прогнозируемая доходность волатильности x 100

Использование коэффициента вариации

Вы можете использовать КВ для определения соотношения риска и доходности, а также для определения того, превышает ли вознаграждение риск инвестиций. КВ также иногда может привести к неточному или непригодному для использования значению. Например, вычисление отрицательного значения или нуля может указывать на то, что измерение коэффициента неточно отражает ваш коэффициент. Нахождение коэффициента вариации в данных относится не только к сфере бизнеса и финансов.

Например, биологи и исследователи часто используют его в своих наблюдениях для расчета повторяемости результатов данных. Педагоги также могут применять CV для сравнения методик преподавания, выясняя, что приводит к повышению среднего балла. Метеорологи используют его для измерения временной изменчивости осадков. Однако существуют некоторые споры относительно точности CV в этих ситуациях. При широком диапазоне переменных и условий возрастает вероятность неточности.

Как рассчитать коэффициент вариации

Чтобы рассчитать коэффициент вариации, выполните следующие шаги, используя вышеупомянутую формулу:

1. Определите волатильность

Чтобы найти волатильность или стандартное отклонение, вычтите среднюю цену за период из каждой ценовой точки. Чтобы преобразовать разницу в дисперсию, возведите в квадрат, просуммируйте и усредните ответ. Квадратный корень из дисперсии становится приемлемым процентом для волатильности.

2. Определение ожидаемой доходности

Чтобы найти ожидаемую доходность, умножьте потенциальные исходы или доходность на вероятность их наступления. Сумма всех собранных ответов становится ожидаемой доходностью. На данном этапе оба показателя готовы для формулы.

3. Разделить

Рассчитав показатели волатильности и ожидаемой доходности, разделите их друг на друга. Большинство ответов дается в виде десятичных дробей. Вы также можете преобразовать CV в проценты.

4. Умножить на 100

Чтобы перевести в проценты, умножьте десятичные числа на 100. При этом десятичный знак сдвигается на две цифры, создавая либо целое число, либо десятичный процент. Окончательный ответ — коэффициент вариации.

Как рассчитать коэффициент вариации в электронной таблице

Некоторые предприятия и частные лица используют электронные таблицы для записи больших объемов данных за длительные периоды времени. Они выбирают электронные таблицы не только для того, чтобы успевать за огромным количеством собранных данных, но и для того, чтобы легко рассчитать коэффициент вариации в своих данных. Электронные таблицы могут записывать расчеты вместе с данными и продолжать их по мере добавления новых данных. Вы можете рассчитать коэффициент вариации с помощью электронной таблицы, выполнив следующие три шага:

1. Используйте функцию стандартного отклонения для набора данных

Программы для работы с электронными таблицами должны иметь определенную функцию для стандартного отклонения. Для того чтобы расчет работал, набор данных должен содержать эту функцию. Во многих распространенных программах электронных таблиц для вычисления стандартного отклонения можно ввести команду =STDEVP. Введите формулу в пустую ячейку рядом с соответствующим набором данных, который вы оцениваете.

2. Рассчитайте среднее значение

Вычисление среднего значения в электронных таблицах требует специальных формул. Например, в большинстве приложений электронных таблиц вы можете использовать =AVERAGE для применения программной функции. При вводе команды среднего значения поместите его в ячейку рядом с соответствующим набором данных, чтобы легче его увидеть.

3. Разделите стандартное отклонение на среднее значение

Разделите ячейки, содержащие стандартное отклонение и среднее значение. Например, чтобы разделить стандартное отклонение в ячейке A3 и среднее значение в ячейке A5, вы можете использовать функцию =A3A5 в пустой ячейке для вычисления коэффициента и отображения коэффициента вариации.

Некоторые программы обработки электронных таблиц могут вычислять коэффициент вариации с помощью команды =STDEV.P, что устраняет необходимость в нескольких шагах. В зависимости от программы, вы можете просто ввести команду в пустую ячейку и обозначить диапазон данных, которые вы хотите рассчитать. После этого в выбранной ячейке появится значение CV.

Пример расчета

Чтобы принять обоснованное решение между акциями и облигациями, Джамиля применяет формулу коэффициента вариации для определения соотношения риска и доходности для обоих инвестиционных инструментов. Сначала она оценивает инвестиции в акции, волатильность которых составляет 5%, а прогнозируемая доходность — 13%. Используя эти значения в формуле, Джамиля находит:

CV = среднее стандартное отклонение выборки x 100 =
CV = прогнозируемая доходность волатильности x 100 =
CV = (0.05) (0.13) x 100 = 0.38 x 100 = 38%

Чтобы рассчитать коэффициент вариации облигации для сравнения, Джамиля делит волатильность в 3% на прогнозируемую доходность в 15%. Используя формулу, она оценивает:

CV = стандартное отклонение выборочного среднего x 100 =
CV = прогнозируемая доходность волатильности x 100 =
CV = (0.03) (0.15) x 100 = 0.2 = 20%

Джамиля сравнивает инвестиции в облигации и акции и приходит к выводу, что CV инвестиций в облигации в размере 20% указывает на более низкое соотношение риска и доходности, чем CV акций в размере 38%. Теперь, когда Джамиля понимает, какой инвестиционный инструмент представляет наименьшее соотношение риска и доходности, она может выбрать наиболее подходящий вариант для достижения своих финансовых целей.

Источник

Понятие вариации используется в целом ряде академических дисциплин, коммерции и искусстве:

В математике для оценки изменчивости переменной или функции,
В статистике термин используется для обозначения отклонений в определенной совокупности данных,
Музыкальная вариация подразумевает изменение основной темы произведения,
В финансах для определения соотношения между риском и доходностью внедряемого проекта,
В биологии изменчивость основного вида популяции,
Астрономия рассматривает вариации возмущения движения Луны, которое происходит в результате притяжения солнца,
Страхование рассматривает совокупность равнозначных объектов с различием в определенном конкретном признаке.

Таким образом, вариация – это изменение или отклонение от основного ожидаемого или рассчитанного значения.

Коэффициент вариации можно вычислить только для количественных показателей, полученных в результате измерений, расчетов или сбора данных.

Что такое коэффициент вариации

При сборе данных получают совокупность результатов, которые отображают состояние исследуемого объекта в определенный временной интервал. Данные могут отличаться от прогнозируемого значения или среднестатистической выборки. Чтобы проанализировать и сделать выводы о стабильности полученных результатов, ожидаемых прогнозов и возможности внесения корректировок, используют коэффициент вариации. Он характеризует степень колебания показателей относительно среднего значения выборки.

Применяют этот показатель при теоретическом расчете планируемых прогнозов поведения исследуемых величин и при практическом анализе полученных данных. Ведь при вычислении среднего показателя, данные могут быть равные, а отклонение составлять десятки процентов. Поэтому для получения детальных прогнозов и результатов учитывают процент разброса или вариацию исследуемого объекта.

По результатам отклонений от модели вправо или влево числового ряда, судят о стабильности или изменчивости совокупности показателей. Изучаемую область определяют как однородную или неоднородную.

Так, при анализе товарооборота предприятия и выявления резкого отклонения в определенных периодах, говорит о недостаточной работе с товарными запасами, наличии большого процента сезонных товаров, устаревшем ассортименте, отсутствии ходовых позиций и не взвешенной организации работы по ценообразованию. При показателе рассеивания данных до 10% говорят о незначительном отклонении, что приравнивается к норме, от 10 до 20 % – средний показатель, который предупреждает о назревающих проблемах. На этом этапе предпринимаются меры по его стабилизации. От 20 до 33% считается значительным, но допустимым, если продажи зависят от сезонности. А при увеличении расхождения более 33% –вариация недопустима и требует пересмотра работы всех структурных подразделений.

При производстве точных деталей и узлов показатель вариации более 33% говорит о большом количестве брака при производстве, хотя средняя величина отклонений может быть в норме и соответствовать требованиям стандартов.

Этот показатель используется для расчета начальной стоимости контракта при заключении сделки.

При анализе работы предприятия анализируют отклонения данных в уровне квалификации сотрудников, выполнения плановых заданий, стоимости контрактов, цен на выпускаемую продукцию, ее качество.

При расчете уровня безопасности инвестиционного проекта показатель риска больше 33% предупреждает о неоправданном риске доходности данного инструмента инвестиции. Чем меньше показатель CV, тем оправданным является соотношение риска для достижения максимальной доходности проекта.

Правила расчета

Коэффициент вариантности (CV или coefficient of variation) рассчитывается по формуле

К_в = σ/х,

где

Ϭ – среднеквадратичное отклонение в выборке данных

х – среднеарифметическое значение всех показателей исследуемой выборки.

Пример расчета

Чтобы проиллюстрировать, что такое коэффициент вариации, приведем пример расчета на основе данных товарооборота предприятия.

Квартал	Значение,Х	(Х_і– Х_ср)²
I	16,54	2,9
II	12,41	0,02
III	18,03	4,36
IV	19,58	6,7
Итого	66,56	13,98

Рассчитаем Х_ср = 16,64

Среднее значение выборки Ϭ = = 1,87

CV=1,87/16,64ӿ100% = 11,23%

Полученный результат показывает однородность исследуемых значений, поквартальное колебание в норме и составляет 11,23%.

Коэффициент вариации можно рассчитать в Excel, Open Office или с помощью онлайн калькулятора для расчета колебаний выборки.

Источник

Онлайн калькулятор для расчета коэффициента вариации, коэффициент вариации – это величина равная отношению стандартного (среднеквадратичного) отклонения случайной величины к ее математическому ожиданию, выражается в процентах.

В статистике принято, что:
— при коэффициенте вариации меньше 10%, степень рассеивания данных считается незначительной;
— если коэффициент от 10% до 20% — средней;
— больше 20% и меньше или равно 33% — значительной.

Совокупность считается однородной если коэффициент не превышает 33%, а если больше 33%, то – неоднородной.

Одно из основных применений коэффициента вариации — оценка инвестиционных рисков, например для расчет начальной максимальной цены контракта (НМЦК).

Источник