Как найти значение корня 8 класс алгебра

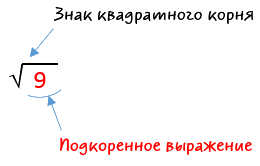
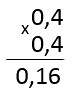Читается: квадратный корень из (a).

Число (a) называется подкоренным числом.

Часто используемые квадраты целых чисел:

Примеры:

Как извлечь квадратный корень из числа?

Чтобы извлечь квадратный корень из числа, надо задать себе вопрос: какое число в квадрате даст выражение под корнем?

Например. Извлеките корень: а)(sqrt{2500}); б) (sqrt{frac{4}{9}}); в) (sqrt{0,001}); г) (sqrt{1frac{13}{36}})

а) Какое число в квадрате даст (2500)?

(sqrt{2500}=50)

б) Какое число в квадрате даст (frac{4}{9})?

(sqrt{frac{4}{9}})(=)(frac{2}{3})

в) Какое число в квадрате, даст (0,0001)?

(sqrt{0,0001}=0,01)

г) Какое число в квадрате даст (sqrt{1frac{13}{36}})? Чтобы дать ответ на вопрос, нужно перевести смешанную дробь в неправильную.

(sqrt{1frac{13}{36}}=sqrt{frac{49}{16}}=frac{7}{6})

Замечание: Хотя (-50), (-frac{2}{3}), (-0,01),(- frac{7}{6}), тоже отвечают на поставленные вопросы, но их не учитывают, так как квадратный корень – всегда положителен.

Главное свойство корня

Как известно, в математике у любого действия есть обратное. У сложения – вычитание, у умножения – деление. Обратное действие возведению в квадрат — извлечение квадратного корня. Поэтому эти действия компенсируют друг друга:

((sqrt{a})^2=a)

Это и есть главное свойства корня, которое чаще всего используется (в том числе и в ОГЭ)

Пример. (задание из ОГЭ). Найдите значение выражения (frac{(2sqrt{6})^2}{36})

Решение: (frac{(2sqrt{6})^2}{36}=frac{4 cdot (sqrt{6})^2}{36}=frac{4 cdot 6}{36}=frac{4}{6}=frac{2}{3})

Пример. (задание из ОГЭ). Найдите значение выражения ((sqrt{85}-1)^2)

Решение:

Ответ: (86-2sqrt{85})

Конечно, при работе с квадратным корнем нужно использовать и другие свойства. 

Пример. (задание из ОГЭ). Найдите значение выражения (5sqrt{11} cdot 2sqrt{2}cdot sqrt{22}) 
Решение:

(5sqrt{11} cdot 2sqrt{2}cdot sqrt{22}=)		Перемножим числа без корня, а числа с корнем запишем под одним знаком, по свойству: (sqrt{a}cdot sqrt{b}=sqrt{a cdot b})
(=10 sqrt {11 cdot 2 cdot 22}=10sqrt{(22)^2} )

Ответ: (220)

4 правила про которые всегда забывают

Пример: (sqrt{2}),(sqrt{53}),(sqrt{200}),(sqrt{0,1}) и т.д. – извлечь корень из числа не всегда возможно и это нормально!

Не надо относится к (sqrt{2}), (sqrt{53}), как-то особенно. Это числа, да не целые, да иррациональные, но не все в нашем мире измеряется в целых числах.

Поэтому в учебниках вы не увидите вот таких записей (sqrt{-23}),(sqrt{-1}),и т.п.

Примеры:

                                  

Вместо этого нужно преобразовать выражение так, чтобы под корнями были одинаковые числа, тогда их можно будет складывать, и вычитать, как подобные слагаемые.

Примеры:

Смотрите также:   Свойства арифметического квадратного корня

Скачать статью

Поурочное планирование по алгебре для 8 класса. Ориентировано на работу с УМК Макарычев. Алгебра 8 класс. Просвещение. Глава 2. КВАДРАТНЫЕ КОРНИ (19 ч). § 5. Арифметический квадратный корень (5 ч). Урок 28. Нахождение приближенных значений квадратного корня. Вернуться к Списку уроков Тематического планирования.

---

Цель: сформировать представление о приближенном вычислении квадратного корня.
Планируемые результаты: научиться вычислять приближенное значение корня из числа.
Тип урока: урок–исследование.

Ход урока

I. Сообщение темы и цели урока

II. Повторение и закрепление пройденного материала

1. Ответы на вопросы по домашнему заданию (разбор нерешенных задач).
2. Контроль усвоения материала (самостоятельная работа).

Вариант 1

1. Решите уравнение: а) x² – 0,04 = 0,6; б) (2х – З)² = 16;    в) (3х + а)² = 81.
2. Определите число корней уравнения x² – 4х = а.

Вариант 2

1. Решите уравнение: а) x² + 0,05 = 0,3; б) (Зх + 2)² = 36;    в) (2х – а)² = 49.
2. Определите число корней уравнения –x² + 6х = а.

III. Работа по теме урока

На предыдущих занятиях мы узнали, что √a может быть целым числом (например, √0 = 0, √9 = 3 и т. д.), обыкновенной дробью (например, 

десятичной дробью (например, 

и иррациональным числом (например, 

Так как иррациональное число является бесконечной десятичной непериодической дробью, то при практических вычислениях возникает вопрос о вычислении приближенного значения арифметического квадратного корня.

Пример 1. Найдем приближенное значение √3 с двумя знаками после запятой.

Оценим подкоренное выражение 3 сначала в целых числах. Так как 1 < 3 < 4, то √1 < √3 < √4 или 1 < √3 < 2. Поэтому десятичная запись числа √З начинается с цифры 1, т. е. √3 ≈ 1,… (рис. а).

Найдем теперь цифру десятых. Для этого будем возводить в квадрат десятичные дроби 1,1; 1,2; 1,3… до тех пор, пока вновь не оценим такими числами подкоренное выражение 3. Имеем 1,1² = 1,21; 1,2² = 1,44; 1,3² = 1,69; 1,4² = 1,96; 1,5² = 2,25; 1,6² = 2,56; 1,7² = 2,89; 1,8² = 3,24. Так как 2,89 < 3 < 3,24 или 1,7² < 3 < 1,8², то 1,7 < √З < 1,8. Значит, √3 ≈ 1,7… (рис. б).

Чтобы найти цифру сотых, будем последовательно возводить в квадрат десятичные дроби 1,71; 1,72; 1,73…, вновь оценивая подкоренное выражение 3. Имеем: 1,71² = 2,9241; 1,72² = 2,9584; 1,73² = 2,9929; 1,74² = 3,0276. Так как 1,73² < 3 < 1,74², то 1,73 < √3 < 1,74 (рис. в). Поэтому √3 ≈ 1,73.

Аналогичным образом можно найти приближенное значение арифметического квадратного корня с любой заданной точностью.

При практических расчетах для нахождения приближенных значений квадратных корней используют специальные таблицы или вычислительную технику.

Пример 2. С помощью калькулятора найдем .

Введем в калькулятор число 27,4 и нажмем клавишу √. На экране появится число 5,234500931 — приближенное значение . Полученный результат округляют до требуемого количества знаков. Округлим, например, этот результат до сотых и получим  ≈ 5,23.

IV. Задания на уроке

№ 336 (а, г); 338 (б); 339 (а); 340 (б); 344 (а, б); 345 (а); 348 (б, г).

V. Подведение итогов урока

Домашнее задание: № 336 (в, е); 338 (а); 339 (б); 340 (а); 344 (в, г); 345 (б); 348 (а, в).

---

Вы смотрели: Поурочное планирование по алгебре для 8 класса. УМК Макарычев (Просвещение). Глава 2. КВАДРАТНЫЕ КОРНИ (19 ч). § 5. Арифметический квадратный корень (5 ч). Урок 28. Нахождение приближенных значений квадратного корня.

Вернуться к Списку уроков Тематического планирования.

В уроке «Степень числа»
мы проходили, что возвести в квадрат число означает умножить число на само себя.
Кратко запись числа в квадрате выглядит следующим образом:

3 · 3 = 3² = 9

Но как быть, если нам нужно получить обратный результат?
Например, узнать, какое число при возведении в квадрат дало бы число «9»?

У квадратного корня есть специальный знак.
Исходя из вычислений выше, нетрудно догадаться, что число, которое в квадрате дает «9»,
это число «3». Запись извлечения квадратного корня из числа «9» выглядит так:

√9 = 3

Читаем запись: «Арифметический квадратный корень из девяти». Можно опустить слово «арифметический».
Словосочетания «арифметический квадратный корень» и «квадратный корень» полностью равнозначны.

Число под знаком корня называют подкоренным выражением.

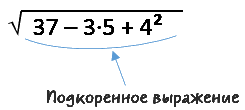
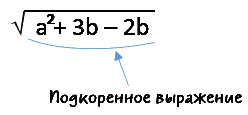
Подкоренное выражение может быть представлено не только одним числом.
Всё, что находится под знаком корня, называют подкоренным выражением. Оно может сожержать как числа, так и буквы.

---

• 
  √−9
  = … нельзя извлекать квадратный корень из отрицательного числа;
• 
  √64 = 8
  
• 
  √−1,44
  
  = … нельзя извлекать квадратный корень из отрицательного числа;

• 
  √256 = 16
  

Квадратный корень из нуля

Квадратный корень из единицы

Как найти квадратный корень из числа

Квадратные корни из целых чисел, чьи квадраты известны, вычислить довольно просто.
Для этого достаточно выучить таблицу квадратов.

Чаще всего в задачах школьного курса математики требуется найти квадратный корень из квадратов чисел от
1 до 20.

Решение примеров с квадратными корнями

Разбор примера

Вычислить арифметический квадратный корень из числа.

• √81 = 9
• √64 = 8
• √100 = 10

Как найти квадратный корень из десятичной дроби

Более подробно разберем на примере ниже.

Разбор примера

Вычислить квадратный корень из десятичной дроби «0,16».

√0,16 =

По первому пункту правила забудем про запятую в десятичной дроби и представим ее в виде целого числа «16».

Нетрудно вспомнить, какое число в квадрате дает «16». Это число
«4».

√16 = 4

√0,16 = …

Вспомним правило умножения десятичных дробей.
Количество знаков после запятой в результате умножения десятичных дробей равняется сумме количества знаков после запятой каждой
дроби.

Т.е., например, при умножении «0,15» на
«0,3» в полученном произведении будет десятичная дробь с тремя знаками после запятой.

0,15 · 0,3 = 0,045

Значит, при вычислении квадратного корня
√0,16

нам нужно найти десятичную дробь, у которой был бы только один знак после запятой.

Мы исходим из того, что в результате умножения десятичной дроби на саму себя в результате должно было получиться
два знака после запятой, как у десятичной дроби «0,16».

Получается, что ответ — десятичная дробь «0,4».

√0,16 = 0,4

Убедимся, что квадрат десятичной дроби
«0,4²» дает
«0,16».

Умножим в столбик «0,4» на

«0,4».

---

Рассмотрим другой пример вычисления квадратного корня из десятичной дроби. Вычислить:

√1,44 =

Представим вместо десятичной дроби «1,44» целое число
«144». Какое число в квадрате даст «144»?
Ответ — число «12».

12² = 144

√144 = 12

√1,44 = …

Так как в десятичной дроби «1,44» — два знака после запятой, значит в десятичной дроби,
которая дала в квадрате «1,44» должен быть один знак после запятой.

√1,44 = 1,2

Убедимся, что «1,2²» дает в квадрате «1,44».

1,2² = 1,2 · 1,2 = 1,44

Квадратные корни из чисел

√2,
√3,
√5,
√6,

и т.п.

Не из всех чисел удается легко извлечь квадратный корень. Например, совершенно неочевидно, чему равен

√2

или

√3

и т.п.

В самом деле, какое число в квадрате даст «2»? Или число «3»?
Такое число не будет целым. Более того, оно представляет из себя
непериодическую десятичную дробь
и входит в
множество иррациональных чисел.

Что делать, когда в ответе остаются подобные квадратные корни? Как, например, в примере ниже:

√15 − 2 · 4 =
√15 − 8 =
√7

Нет такого целого числа, которое бы дало в квадрате число «7».
Поэтому, перед завершением задачи внимательно читайте её условие.

Если в задаче дополнительно ничего не сказано об обязательном вычислении всех квадратных корней, тогда ответ можно
оставить с корнем.

√15 − 2 · 4 =
√15 − 8 =
√7

Если в задании сказано, что необходимо вычислить все квадратные корни с помощью микрокалькулятора,
то после вычисления квадратного корня на калькуляторе
округлите результат до необходимого количества знаков.

Текст задания в таком случае может быть написан следующим образом:

«Вычислить. Квадратные корни найти с помощью калькулятора и округлить с точностью до
«0,001».

√15 − 2 · 4 =
√15 − 8 =
√7 ≈ 2,646

---

Ваши комментарии

Оставить комментарий:

---

План урока:

Арифметический квадратный корень

Вычисление квадратного корня

Функция квадратного корня

Свойства арифметического квадратного корня

Преобразование выражений с квадратными корнями

Арифметический квадратный корень

Рассмотрим задачу. Нам известно, что длина квадрата равна 14 см. Какова площадь этого квадрата? Из курса геометрии мы знаем, что для ответа на вопрос надо просто умножить сторону саму на себя, то есть возвести ее в квадрат:

S = 14•14 = 196 см²

Теперь рассмотрим обратную задачу. Известно, что площадь квадрата равна 196 см². Чему равна длина его стороны? Очевидно, что она составляет 14 см. Для нахождения ответа мы произвели действие, обратное возведению во вторую степень. В математике оно называется извлечением квадратного корня, а само число 14 – квадратным корнем из 196.

Так, 5 – это квадратный корень из числа 25, так как

5² = 25

Очень часто квадратный корень является не целым, а дробным числом. Так, корень из 2 примерно равен 1,414213562 (способы вычисления значения корня будут рассмотрены в этом же уроке, но позже).

Отметим, что порою можно указать для числа не один, а сразу два квадратных корня. Они будут отличаться своим знаком, но совпадать по абсолютной величине (модулю). Так число (–5) также является квадратным корнем из 25:

(– 5)² = – 5•(– 5) = 25

Вообще у любого положительного числа есть 2 квадратных корня, у любого отрицательного числа их вообще нет, и только у нуля есть единственное значение корня – сам нуль. Докажем это.

Пусть есть произвольное число а, для которого надо вычислить квадратный корень. Обозначим этот корень как х. Тогда по определению можно составить уравнение:

х² = а

Попробуем решить его с помощью графиков. Для этого построим отдельные графики для левой и правой части равенства. Оба графика, и у = а, и у = х², мы уже строили в 7 классе. В итоге получаем три случая:

Видно, что при а> 0 графики пересекаются в 2 точках, то есть существует два квадратных корня, которые отличаются лишь своими знаками.

Для определенности математики ввели понятие арифметического квадратного корня.

Ещё раз уточним, что у числа может быть два квадратных корня. Например, у числа 25 это –5 и 5:

(– 5)² = 25

5² = 25

Арифметическим же называют тот квадратный корень, у которого НЕТ знака минус.

Существует специальный символ для арифметического квадратного корня, который именуют знаком радикала, или просто знаком корня. Выглядит он так:

Если надо показать, что, например, арифметический квадратный корень (часто говорят просто корень) из 25 равен 5, то получается такая запись:

Под знаком радикала может стоять и выражение, содержащее переменные величины. Для его обозначения используют термин подкоренное выражение. Так, в записи

выражением х² + 2х + 2 является подкоренным.

Мы уже поняли, что из отрицательного числа невозможно извлечь квадратный корень, ведь каждое действительное число при умножении на само себя становится неотрицательным. Поэтому если под знаком радикала находится отрицательное число, то говорят, что выражение не имеет смысла (так же как и дробное выражение, у которого в знаменателе стоит ноль). Так, бессмысленны выражения:

Если под корнем находиться переменная, то при одних ее значениях выражение с корнем имеет смысл, а при других нет. Так, выражение

при х = 9 имеет значение, равное двум:

Но если х = 4, то получаем бессмысленное выражение:

Изучая понятие иррационального числа, мы уже сталкивались с корнями. Исторически именно корень из 2 стал первым числом, для которого была доказана его иррациональность. Числа, чей квадратный корень является целым числом, называются полными квадратами. Примерами полных квадратов являются:

• 4 (потому что 2² = 4);
• 9 (3² = 9);
• 16 (4² = 16).

Для всех натуральных чисел, не являющихся полными квадратами, можно доказать, что их квадратные корни – это иррациональные числа.

Стоит отметить, что открытие иррациональностей корней изменило представления древних греков о числах и сыграло огромную роль в развитии математики.

Теперь рассмотрим порядок действий в выражениях с корнями. Сначала всегда производятся операции в скобках, потом под знаком радикала, далее происходит возведение в степень, и лишь потом другие арифметические операции. Например, есть выражение

Покажем последовательность действий, выделяя их красным цветом:

Если в ходе вычислений получили корень не из полного квадрата, то его следует оставить как есть, и продолжать вычисления, например:

Одинаковые корни можно складывать и вычитать друг с другом:

Из определения квадратного корня следует очевидное тождество:

Приведем пример с конкретными числами:

Однако здесь важно учитывать, что под знаком радикала не может находиться отрицательное число. Так, некорректной будет запись

так как под радикалом слева стоит отрицательное число. Но допускается такая запись:

потому что под знаком радикала слева стоит положительная величина (– 3)•( – 3) = 9.

Напомним, что модулем числа называется его величина, взятая без учета знака. Для обозначения модуля используются квадратные скобки:

Можно записать следующее тождество, связывающее модуль числа с его корнем:

Например:

Вычисление квадратного корня

Ранее для выполнения арифметических операций мы использовали метод «столбика». А как производить вычисление квадратного корня? Существует несколько приемов, мы рассмотрим простейший из них.

Очевидно, что чем больше число, тем больше и его квадрат. Например, 5 > 4, поэтому и 5²> 4². Значит, справедливо и обратное утверждение: чем больше число, тем больше и его квадратный корень.

Убедиться в этом можно и с помощью графика функции у = х². Будем отмечать на нем числа и их квадратные корни:

Видно, что чем выше на оси Оу располагается число, тем правее на оси Ох находится его квадратный корень.

Зная это свойство, легко оценить значение корня из любого числа. Продемонстрируем это на примере вычисления значение корня из 2. Нам известно, что

1 < 2 < 4

Значит, можно записать следующие неравенства:

Нам удалось определить, что корень из двух находится между единицей и двойкой, то есть

Теперь определим первую цифру после запятой для корня из двух. Будем возводить в квадрат десятичные дроби 1,1; 1,2; 1,3 и т. д, до тех пор пока не получим выражение, большее 2:

1,1² = 1,21

1,2² = 1,44

1,3² = 1,69

1,4² = 1,96

1,5² = 2,25

Теперь мы можем записать неравенства:

Получается, что корень имеет значение, находящееся между 1,4 и 1,5, то есть

Попытаемся определить ещё одну цифру после запятой:

1,41² = 1,999396

1,42² = 2,002225

Отсюда следует, что:

Продолжая подобные вычисления, можно вычислить любое количество знаков после запятой:

Конечно, на практике все вычисления выполняются компьютером, а не вручную. Однако программисты стремятся написать программы так, чтобы они работали как можно быстрее, то есть получали результат, выполняя меньшее количество вычислений. Поэтому на практике чаще используется метод бисекции (деления надвое), который отличается большей эффективностью. Для начала нужно найти очевидную оценку корня, например:

Получили, что корень из 2 находится между 1 и 2. Теперь найдем среднее арифметическое этих двух значений:

(1 + 2)/2 = 1,5

Возведем среднее арифметическое в квадрат:

1,5² = 2,25

Теперь мы можем записать неравенство

То есть искомое нами значение находится между 1 и 1,5. Снова найдем среднее этих двух оценок и возведем его в квадрат:

(1 + 1,5)/2 = 1,25

1,25² = 1,5625

Зная это, можем записать:

На каждом следующем шаге вычислений мы будем всё точнее определять оценки корня, при этом вычислений мы делаем не очень много.

Периодически могут встречаться задания, в которых надо грубо оценить значение квадратного корня.

Пример. Сколько целых чисел на координатной прямой располагается между

Решение: Ближайшие к числу 60 полные квадраты – это 64 и 49, поэтому можно записать:

Также можно оценить и корень из 140:

Получаем, что между корнями располагается четыре числа: 8, 9, 10 и 11:

Ответ: 4

Функция квадратного корня

Каждому числу соответствует не более чем 1 арифметический квадратный корень. Поэтому формула

задает функцию. Исследуем ее.

Так как под знаком радикала может находиться лишь неотрицательное число, то областью определения корня является множество всех неотрицательных чисел. Такова же и область допустимых значений.

Построим график квадратного корня по точкам. Для этого вычислим ее значения в нескольких точках (указана точность до 0,1):

График функции квадратного корня будет выглядеть так:

Отметим, что полученная линия чем-то напоминает обычную параболу функции у = х², которую «положили набок», то есть повернули против часовой стрелки на 90°, а после убрали одну из ветвей:

И это не случайность. Дело в том, что две эти функции являются обратными друг другу. Действительно, пусть с помощью графика параболы мы хотим найти значение величины а². Стрелки показывают последовательность действий:

Мы должны найти а на оси Ох, построить от найденной точки вертикальную линию до пересечения с графиком, а потом провести горизонтальную линию. Но если нам надо вычислить корень из положительного числа b, то мы должны действовать в обратном порядке: найти b на вертикальной оси, провести горизонтальную линию до пересечения с параболой, и потом опустить перпендикуляр на горизонтальную ось:

Получается, для вычисления обеих функций можно использовать один график! Но, так как традиционно аргумент функции обозначают буквой х, а саму функцию как у, а также ось Ох располагают горизонтально, то для получения графика обратной функции надо буквально повернуть график основной функции так, чтобы оси Ох и Оу поменялись местами:

Действительно, в результате поворота получили уже знакомый график функции корня из х. Осталось лишь правильно переименовать оси и повернуть цифры в привычное положение.

Взаимное расположение этих графиков можно описать и иначе. Они симметричны относительно прямой линии, которую задает график у = х. Ведь если точка имеет координаты (а; b) принадлежит параболе у = х², то, по определению корня, точка с обратными координатами (b; а) должна лежать на графике корня. Однако две такие точки будут симметричны относительно линии у = х:

Соответственно, симметричны относительно этой прямой и графики обратных функций:

Исключительно для большей наглядности (чтобы была очевидна симметрия, о которой идет речь), повернем эту картинку на 45°:

Свойства арифметического квадратного корня

Для упрощения некоторых выражений необходимо использовать особые правила работы с корнями. Сформулируем первое из них:

Математически это правило записывается так:

Например:

Тождество работает для любого количества множителей, а также в обратную сторону:

Однако следующее преобразование недопустимо:

Дело в том, что под знаком радикала не может быть отрицательное число! Слева под двумя радикалами стоят отрицательные числа, а справа под корнем находится уже положительная величина (– 2)•(– 32) = 64. В результате выражение слева не имеет смысл, а справа – имеет, поэтому знака равенства между ними быть не может.

Докажем это правило. Для этого возведем во вторую степень выражение

Получили, что по определению корня можно записать:

Следующее свойство касается дробей:

Символически это выглядит так:

Приведем примеры использования этого свойства:

Теперь докажем это правило. Можно записать, что

Значит, по определению верно равенство

Третье правило помогает извлекать корень из числа, возведенного в степень:

где а –действительное число (в том числе и отрицательное), а k – натуральное число.

Это тождество помогает выполнить следующие действия:

Стоит обратить внимание, что в последнем случае под корнем НЕ стоит отрицательное число, так как на самом деле (– 2)¹⁰ – это положительное число. Вообще при возведении любого числа в четную степень получается неотрицательное число.

Для доказательства этого факта используем то, что

Зная это, можно выполнить преобразования:

Преобразование выражений с квадратными корнями

Изученные правила помогают преобразовывать некоторые выражения. Так, можно вынести множитель из-под знака корня:

Это действие может использоваться для сложения корней, у которых, казалось бы, стоят разные числа под знаком радикала:

Обратное действие называют внесением множителя под знак корня:

Пример. Какое число больше

Решение. Внесем множитель под знак корня:

Из двух корней больше тот, у которого больше подкоренное выражение, поэтому

Из этого следует, что

Заметим, что под знак радикала может быть внесен исключительно неотрицательный множитель! Знак минуса должен остаться перед радикалом:

Принято считать, что с дробью, содержащей радикал, проще работать, когда этот радикал находится в числителе, а не знаменателе. В связи с этим стремятся избавиться от иррациональности в знаменателе. В простейшем случае дробь просто домножают на квадратный корень:

Как видим, корень «переехал» из знаменателя в числитель. Несколько сложнее производится освобождение от иррациональности, если в знаменателе стоит сумма или разность корней. В этом случае помогает формула разности квадратов:

Рассмотрим несколько задач.

Пример. Найдите наибольшее значение выражения

Решение. По формуле разности квадратов можно записать:

Зная это, заменим знаменатель дроби:

Эта дробь принимает наибольшее значение тогда, когда ее числитель, наоборот, принимает минимальное значение. Это произойдет при а = 0, так как арифметический квадратный корень не может быть отрицательным. Тогда наибольшее значение дроби будет составлять

Пример. Упростите выражение

Довольно тяжелым является случай, когда под знаком корня находится другой корень. Выражения вида

называют двойным радикалом.

Существует формула двойного радикала, с помощью которой его можно иногда упростить:

Для доказательства справедливости этого тождества возведем его правую часть в квадрат, используя формулу квадрата суммы (х ± у)² = х² ± 2ху + у²:

Принципиально важно, что величина а² – b должна быть неотрицательной. Рассмотрим преобразование двойных радикалов на примере. Пусть надо освободиться от внешнего радикала в выражении

Для этого сначала внесем двойку под знак внутреннего радикала, а потом воспользуемся формулой:

Заметим, что формула двойного радикала полезна в том случае, если выражение а² – b является полным квадратом.