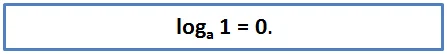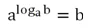Многие школьники считают логарифмы сложной темой в курсе математики. Но если разобрать, что такое логарифм подробно, от простого к сложному, то на ЕГЭ вы не станете их опасаться.
Часто у учеников возникает путаница, где аргумент, а где основание логарифма. И что же нужно возвести в степень, чтобы этот логарифм, наконец, посчитать.
В этой статье мы откроем секрет, как легче запомнить принцип решения логарифма.
Итак, давайте разбираться, что такое логарифм.
- Что такое логарифм и как его посчитать
- Зачем логарифмам специальные обозначения
- Основные свойства логарифмов — все формулы в одном месте
- 10 примеров логарифмов с решением
Что такое логарифм и как его посчитать
Логарифм имеет следующий вид:
где a – это основание логарифма,
b – это аргумент логарифма
Чтобы узнать значение логарифма приравняем его к X.и преобразовываем в
Запомните, что именно основание (оно выделено красным) возводится в степень.
Чтобы было легче, можно запоминать так – основание всегда остается внизу (и в первом, и во втором выражении a внизу)!
Приведем пример:
Чтобы вычислить данный логарифм, необходимо приравнять его к X и воспользоваться правилом, описанным выше:

Еще примеры:

Логарифмы со специальным обозначением
Для некоторых логарифмов в математике введены специальные обозначения. Это связано с тем, что такие логарифмы встречаются особенно часто. К таким логарифмам относятся десятичный логарифм и натуральный логарифм. Для этих логарифмов справедливы все правила, что и для обычных логарифмов.
Десятичный логарифм
Десятичный логарифм обозначается lg и имеет основание 10, т.е.
Чтобы вычислить десятичный логарифм, нужно 10 возвести в степень X.
Например, вычислим lg100
Натуральный логарифм
Натуральный логарифм обозначается ln и имеет основание e, то есть
Чтобы вычислить данный логарифм нужно число е возвести в степень x. Некоторые из вас спросят, что это за число такое е? Число е – это иррациональное число, т.е. точное его значение вычислить невозможно. е = 2,718281…
Сейчас не будем подробно разбирать, зачем это число нужно, просто запомним, что
И вычислить его можно таким образом:
Основные свойства логарифмов
Логарифмы можно преобразовывать, но для этого необходимо знать правила, которые называются основными свойствами логарифмов. Данные свойства обязательно нужно знать каждому ученику! Без знания этих свойств невозможно решить ни одну серьезную логарифмическую задачу. Вот эти свойства:
Совет – тренируйтесь применять эти свойства в обе стороны, то есть как слева направо, так и справа налево!
Рассмотрим свойства логарифмов на примерах.
Логарифмический ноль и логарифмическая единица
Это следствия из определения логарифма. И их нужно обязательно запомнить. Эти простейшие свойства нередко вводят учеников в ступор.
Запомните, что логарифм от a по основанию а всегда равен единице:
loga a = 1 – это логарифмическая единица.
Если же в аргументе стоит единица, то такой логарифм всегда равен нулю независимо от основания, так как a0 = 1:
loga 1 = 0 – логарифмический ноль.
Основное логарифмическое тождество
В первой формуле число m становится степенью, которая стоит в аргументе. Данное число может быть любым. Некоторые выражения могут быть решены только с помощью этого тождества.
Вторая формула по сути является просто переформулированным определением логарифма
Разберем применение тождества на примере:
Необходимо найти значение выраженияСначала преобразуем логарифм
Вернемся к исходному выражению и применим правило умножения степеней с одинаковым основанием:
Теперь применим основное логарифмическое тождество и получим:
Сумма логарифмов. Разница логарифмов
Логарифмы с одинаковыми основаниями можно складывать:Логарифмы с одинаковыми основаниями можно вычитать:
Мы видим, что исходные выражения состояли из логарифмов, которые по отдельности не вычисляются, а при применении свойств логарифмов у нас получились нормальные числа. Поэтому повторим, что основные свойства логарифмов нужно знать обязательно!
Обратите внимание, что формулы суммы и разности логарифмов верны только для логарифмов с одинаковыми основаниями! Если основания разные, то данные свойства применять нельзя!
Вынесение показателя степени из логарифма
Вынесение показателя степени из логарифма:
Переход к новому основанию

Такие формулы чаще всего нужны при решении логарифмических уравнений и неравенств.
Разберем на примере.
Необходимо найти значение такого выраженияДля начала преобразуем каждый логарифм с помощью свойства вынесения показателя степени из логарифма:
Теперь применим переход к новому основанию для второго логарифма:Подставим полученные результаты в исходное выражение:
10 примеров логарифмов с решением
1. Найти значение выражения




Сначала найдем значение
Для этого приравняем его к Х:

7. Найти значение выражения
Преобразуем наше выражение:
Теперь воспользуемся свойством вынесения показателя степени из логарифма и получим:
8. Найти значение выражения
Так как основания логарифмов одинаковые, воспользуемся свойством разности логарифмов:

Так как основания логарифмов разные, применять свойство суммы логарифмов нельзя. Поэтому решаем каждый логарифм по отдельности:

4 + 3 = 7
10. Найти значение выраженияОбращаем внимание, что данное выражение – это не произведение логарифмов. У логарифма по основанию 4 подлогарифным выражением является log216. Поэтому сначала найдем значение log216, а затем подставим полученный результат в log4:
Надеюсь, теперь вы разобрались, что такое логарифм. Больше видео уроков вы можете найти
1.11. Определение логарифма
10.
Логарифмом
числа b
по основанию b
называется показатель степени, в которую
нужно возвести число a,
чтобы получить b,
обозначается
и
20.
Десятичный логарифм — это логарифм по
основанию 10:
.
30.
Натуральный логарифм — это логарифм
по основанию
:
.
1.12. Основное
логарифмическое тождество:
Например,
1.13. Свойства логарифмов
-
Сумма логарифмов
есть логарифм произведения
-
Разность
логарифмов есть логарифм дроби
-
Число, стоящее
перед логарифмом ставим в показатель
степени выражения, стоящего после знака
логарифма
-
Переход к новому
основанию
Следствия:
|
5. |
6. |
7. |
8. |
-
Любое число
представимо в виде логарифма -
Любое число k>0
представимо в виде степени
Пример. Вычислить
a)
если
;
б)
►а) перейдём в
к основанию 2. Воспользуемся свойством
4:
.
б) заменим корни
степенями и воспользуемся свойством
6:
.◄
1.14. Логарифмирование и потенцирование
Если некоторое
выражение
составлено из положительных чисел с
помощью операций умножения, деления и
возведение в степень, то, используя
свойства логарифмов, можно выразить
через логарифмы входящих в выражение
чисел. Такое преобразование называется
логарифмированием.
Обратная задача: нахождение выражения
по его логарифму, называется потенцированием.
Пример 1.
Прологарифмировать по основанию
выражение
.
►
◄
Пример 2. Найти
,
если
►
◄
1.15. Теория многочленов
Многочленом степени
называется целая рациональная функция
|
(3) |
|
Многочлен |
|
|
Многочлен |
|
|
Многочлен |
|
|
Многочлен |
|
|
Многочлен |
Например,
есть многочлен
—
степени, 2 есть многочлен
—
степени.
Деление
многочленов:
1.16. Выделение целой части из дроби
Дробь называется
неправильной, если в числителе стоит
многочлен степени не ниже степени
многочлена знаменателя.
Тогда дробь можно
представить в виде:
,
где
— частное от деления
на
(целая
часть),
— полученный при этом остаток.
Пример. Выделить
целую часть из дроби
.
►Дробь неправильная,
делим числитель на знаменатель столбиком:
Целая
часть
(под уголком), а остаток
(в конце деления). Поэтому дробь будет
иметь вид:
◄
2. Алгебраические уравнения
Элементарная математика
|
Сканави М. Книга представляет собой повторительный курс элементарной математики и рассчитана на тех, кто хочет пополнить, укрепить и систематизировать свои знания. Как и в первом издании, содержание ориентировано на программы вступительных экзаменов в технические вузы и, в особенности, на программы подготовительных отделений при высших учебных заведениях, для учащихся которых, как мы надеемся, книга окажется полезной. (Книга включает в себя Ч1 — Арифметика, алгебра и элементарные функции и Ч2 — Геометрия. Каждый раздел включает в себя теоретическую часть и большое количество задач с решениями.) |
|
Оглавление
ВВЕДЕНИЕ
Часть первая. АРИФМЕТИКА, АЛГЕБРА И ЭЛЕМЕНТАРНЫЕ ФУНКЦИИ
Глава I. ДЕЙСТВИТЕЛЬНЫЕ И КОМПЛЕКСНЫЕ ЧИСЛА
2. Простые и составные числа. Признаки делимости.
3. Наибольший общий делитель и наименьшее общее кратное.
4. Целые числа. Рациональные числа.
5. Десятичные дроби. Представление рациональных чисел десятичными дробями.
6. Иррациональные числа. Действительные числа.
7. Действия с приближенными числами.
8. Числовая ось. Координаты точки на плоскости.
§ 2. Степени и корни
9. Степени с натуральными показателями.
10. Степени с целыми показателями.
11. Корни.
12. Степени с рациональными показателями. Степени с действительными показателями.
13. Алгоритм извлечения квадратного корня.
§ 3. Комплексные числа
14. Основные понятия и определения.
15. Рациональные действия с комплексными числами.
16. Геометрическое изображение комплексных чисел. Тригонометрическая форма комплексного числа.
17. Действия с комплексными числами, заданными в тригонометрической форме. Формула Муавра.
18. Извлечение корня из комплексного числа.
Глава II. ТОЖДЕСТВЕННЫЕ ПРЕОБРАЗОВАНИЯ
19. Алгебраические выражения. Одночлены и многочлены.
20. Формулы сокращенного умножения.
41. Обратная пропорциональная зависимость. Степенная функция с рациональным показателем степени.
42. Показательная функция.
43. Логарифмическая функция.
§ 3. Преобразование графиков
44. Параллельный сдвиг графика.
45. График квадратного трех члена.
46. График дробно-линейной функции.
47. Преобразование симметрии. Сжатие и растяжение графика.
48. Построение графиков функций.
49. Сложение графиков.
§ 4. Некоторые сведения о рациональных функциях
50. Целые и дробные рациональные функции. Деление многочленов.
51. Схема Горнера. Теорема Безу.
52. Нули многочлена. Разложение многочлена на множители.
Глава V. УРАВНЕНИЯ
53. Уравнение. Корни уравнения.
54. Равносильные уравнения.
55. Системы уравнений.
56. Графическое решение уравнений.
§. 2. Алгебраические уравнения с одной неизвестной
57. Число и кратность корней.
58. Уравнения первой степени (линейные уравнения).
59. Уравнения второй степени (квадратные уравнения).
60. Формулы Виета. Разложение квадратного трехчлена на множители.
61. Исследование квадратного уравнения.
62. Уравнения высших степеней. Целые корни.
63. Двучленные уравнения.
64. Уравнения, сводящиеся к квадратным.
65. Возвратные уравнения.
§ 3. Системы алгебраических уравнений
66. Линейные системы.
67. Определители второго порядка. Исследование линейных систем двух уравнений с двумя неизвестными.
68. Системы, состоящие из уравнения второй степени и линейного уравнения.
69. Примеры систем двух уравнений второй степени. Системы уравнений высших степеней.
§ 4. Иррациональные, показательные и логарифмические уравнения
70. Иррациональные уравнения.
71. Показательные уравнения.
72. Логарифмические уравнения.
73. Разные уравнения. Системы уравнений.
Глава VI. НЕРАВЕНСТВА
74. Свойства неравенств. Действия над неравенствами.
75. Алгебраические неравенства.
§ 2. Решение неравенств
76. Множество решений неравенства.
77. Графическое решение неравенств.
79. Квадратные неравенства.
80. Неравенства высших степеней. Неравенства, содержащие дробные рациональные функции от х.
81. Иррациональные, показательные и логарифмические неравенства.
82. Неравенства с двумя неизвестными.
Глава VII. ПОСЛЕДОВАТЕЛЬНОСТИ
83. Числовая последовательность.
84. Предел числовой последовательности.
85. Бесконечно малые. Правила предельного перехода.
§ 2. Арифметическая прогрессия
86. Арифметическая прогрессия. Формула общего члена.
87. Свойства арифметической прогрессии.
88. Формула для суммы n членов арифметической прогрессии.
§ 3. Геометрическая прогрессия
89. Геометрическая прогрессия. Формула общего члена.
90. Свойства геометрической прогрессии.
91. Формулы для суммы n членов геометрической прогрессии.
92. Бесконечно убывающая геометрическая прогрессия.
Глава VIII. ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ УГЛА (ДУГИ)
93. Вектор, проекция вектора.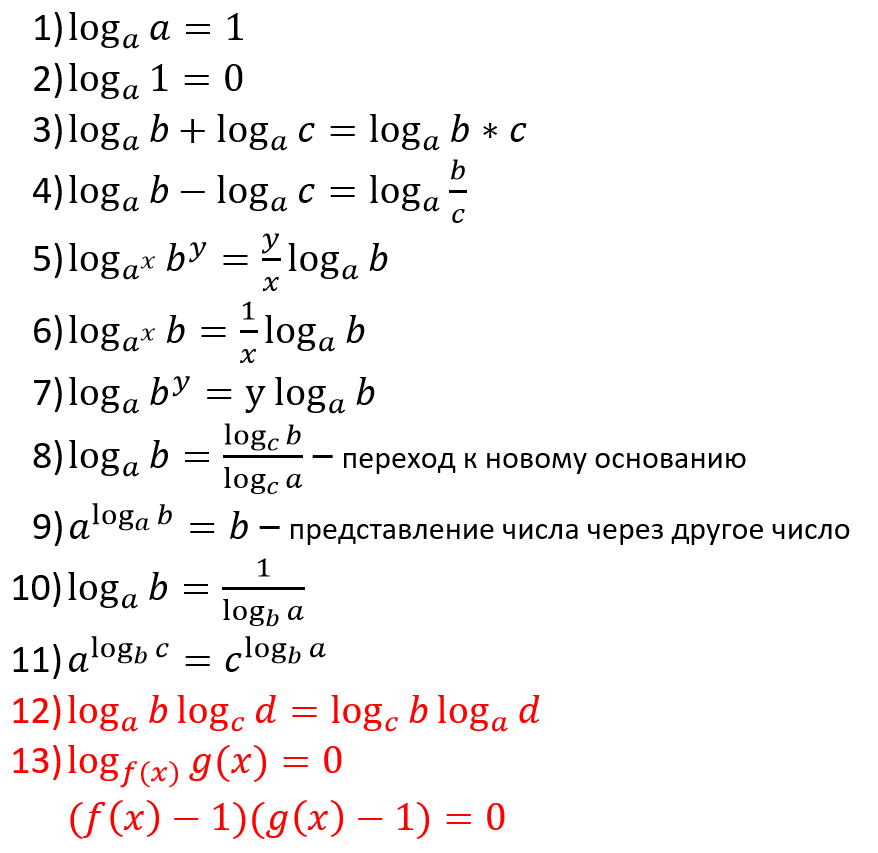
94. Положительные углы и дуги, меньшие 360°.
95. Углы и дуги, большие 360°.
96. Отрицательные углы. Сложение и вычитание углов.
§ 2. Тригонометрические функции произвольного угла
97. Определение основных тригонометрических функций.
98. Изменение основных тригонометрических функций при изменении угла от 0 до 2pi.
§ 3. Соотношения между тригонометрическими функциями одного и того же угла
99. Основные тригонометрические тождества.
100. Вычисление значений тригонометрических функций по значению одной из них.
101. Значения тригонометрических функций некоторых углов.
§ 4. Четность, нечетность и периодичность тригонометрических функций
102. Четность и нечетность.
103. Понятие периодической функции.
104. Периодичность тригонометрических функций.
§ 5. Формулы приведения
105. Зависимость между тригонометрическими функциями дополнительных углов.
106. Формулы приведения.
Глава IX. ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ ЧИСЛОВОГО АРГУМЕНТА И ИХ ГРАФИКИ
§ 1.
108. Области определения и области изменения значений тригонометрических функций.
109. Некоторые неравенства и их следствия.
§ 2. Графики тригонометрических функций
110. Первоначальные сведения о таблицах тригонометрических функций.
111. Основные графики.
112. Примеры построения графиков некоторых других тригонометрических функций.
113. Дальнейшие примеры построения графиков функций.
Глава X. ПРЕОБРАЗОВАНИЕ ТРИГОНОМЕТРИЧЕСКИХ ВЫРАЖЕНИЙ
114. Расстояние между двумя точками на плоскости.
115. Косинус суммы и разности двух аргументов.
116. Синус суммы и разности двух аргументов.
117. Тангенс суммы и разности двух аргументов.
118. О формулах сложения для нескольких аргументов.
§ 2. Формулы для двойного и половинного аргумента. Выражение sin na и cos na через степени sin a и cos a
119. Тригонометрические функции двойного аргумента.
120. Выражение sin na и cos na через степени sin a и cos a при натуральном числе n.
121. Тригонометрические функции половинного аргумента.
122. Выражение основных тригонометрических функций аргумента а через tg(a/2).
§ 3. Преобразование в сумму выражений вида sina•cosb, cosa•cosb и sinа•sinb
§ 4. Преобразование в произведение сумм вида
§ 5. Преобразование некоторых выражений в произведения с помощью введения вспомогательного аргумента
127. Преобразование в произведение выражения a•sina + b•cosa.
128. Преобразование в произведение выражений a•sina+b и a•cosa+b
129. Преобразование в произведение выражения a•tga+b.
Глава XI. ОБРАТНЫЕ ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ И ИХ ГРАФИКИ
130. Функция у = arcsin x (арксинус).
131. Функция y = arccos x (арккосинус).
132. Функция y = arctg x (арктангенс).
133. Функция y = arcctg x (арккотангенс).
134. Пример.
§ 2. Операции над обратными тригонометрическими функциями
135. Тригонометрические операции.
136. Операции сложения (вычитания).
§ 3. Обратные тригонометрические операции над тригонометрическими функциями
137.
138. Функция y = arctg (tg x).
Глава XII. ТРИГОНОМЕТРИЧЕСКИЕ УРАВНЕНИЯ И НЕРАВЕНСТВА
139. Уравнение sin х = а.
140. Уравнение cos х = a.
141. Уравнение tg x = a.
142. Уравнение ctg x = a.
143. Некоторые дополнения.
§ 2. Способ приведения к одной функции одного и того же аргумента
145. Некоторые типы уравнений, приводящихся к уравнениям относительно функции одного аргумента.
146. Способ разложения на множители.
147. Решение рациональных тригонометрических уравнений с помощью универсальной тригонометрической подстановки tg(x/2) = t.
§ 3. Некоторые частные приемы решения тригонометрических уравнений и систем
148. Введение вспомогательного аргумента.
149. Преобразование произведения в сумму или разность.
150. Переход к функциям удвоенного аргумента.
151. Решение уравнения типа…
152. Применение подстановок sinx ± соsx = y.
§ 4. Решение тригонометрических неравенств
154. Простейшие тригонометрические неравенства.
155. Примеры тригонометрических неравенств, сводящихся к простейшим.
Часть вторая. ГЕОМЕТРИЯ
156. Точка. Прямая. Луч. Отрезок.
157. Плоскость. Фигуры и тела.
160. Равенство фигур. Движение.
161. Равенство тел.
§ 2. Измерение геометрических величин
162. Сложение отрезков. Длина отрезка.
163. Общая мера двух отрезков.
164. Сравнительная длина отрезков и ломаных.
165. Измерение углов.
166. Радианная мера угла.
167. Измерение площадей.
168. Площадь прямоугольника. Объем прямоугольного параллелепипеда.
Глава XIV. ПЕРПЕНДИКУЛЯРНЫЕ И ПАРАЛЛЕЛЬНЫЕ ПРЯМЫЕ. ЗАДАЧИ НА ПОСТРОЕНИЕ
169. Перпендикуляр и наклонные.
170. Свойство перпендикуляра, проведенного к отрезку в его середине.
171. Параллельные прямые.
172. Углы, образованные двумя параллельными прямыми и секущей.
173. Углы с параллельными или перпендикулярными сторонами.
§ 2. Геометрические места точек. Окружность
174. Геометрическое место точек.
175. Свойство биссектрисы угла.
176. Окружность.
177. Взаимное расположение прямой и окружности. Касательная и секущая.
178. Хорда и диаметр. Сектор и сегмент.
179. Взаимное расположение двух окружностей.
§ 3. Основные задачи на построение
181. Деление отрезка пополам. Построение перпендикуляров.
182. Построение углов.
183. Другие задачи на построение.
Глава XV. ТРЕУГОЛЬНИКИ, ЧЕТЫРЕХУГОЛЬНИКИ
184. Стороны и углы треугольника.
185. Биссектрисы треугольника. Вписанная окружность.
186. Оси симметрии сторон треугольника. Описанная окружность.
187. Медианы и выcоты треугольника.
188. Равенство треугольников.
189. Построение треугольников.
190. Равнобедренные треугольники.
191. Прямоугольные треугольники.
§ 2. Параллелограммы
192. Четырехугольники.
193. Параллелограмм и его свойства.
194. Прямоугольник.
§ 3. Трапеция
196. Трапеция.
197. Средняя линия треугольника.
198. Средняя линия трапеции.
199. Деление отрезка на равные части.
§ 4. Площади треугольников и четырехугольников
200. Площадь параллелограмма.
201. Площадь треугольника.
202. Площадь трапеции.
Глава XVI. ПОДОБИЕ ГЕОМЕТРИЧЕСКИХ ФИГУР
203. Пропорциональные отрезки.
204. Свойства биссектрис внутреннего и внешнего углов треугольника.
§ 2. Подобное преобразование фигур (гомотетия)
205. Определение гомотетичных фигур.
206. Свойства преобразования подобия.
§ 3. Общее подобное соответствие фигур
207. Подобные фигуры.
208. Периметры и площади подобных треугольников.
209. Применение подобия к решению задач на построение.
Глава XVII. МЕТРИЧЕСКИЕ СООТНОШЕНИЯ В ТРЕУГОЛЬНИКЕ И КРУГЕ
210. Углы с вершиной на окружности.
211. Углы с вершиной внутри и вне круга.
212. Угол, под которым виден данный отрезок.
213. Четырехугольники, вписанные в окружность.
214. Пропорциональные отрезки в круге.
215. Задачи на построение.
§ 2. Метрические соотношения в треугольнике
216. Пропорциональные отрезки в прямоугольном треугольнике.
218. Теорема синусов. Формула Герона.
217. Квадрат стороны, лежащей против острого или тупого утла и треугольнике. Теорема косинусов.
218. Теорема синусов. Формула Герона.
219. Радиусы вписанной и описанной окружностей.
§ 3. Решение треугольников
220. Таблицы функций.
221. Решение треугольников. Сводка основных формул.
222. Решение прямоугольных треугольников.
223. Решение косоугольных треугольников.
Глава XVIII. ПРАВИЛЬНЫЕ МНОГОУГОЛЬНИКИ. ДЛИНА окружности И ПЛОЩАДЬ КРУГА
224. Выпуклые многоугольники.
225. Правильные многоугольники.
226. Соотношения между стороной, радиусом и апофемой.
227. Периметр и площадь правильного n-угольника.
228. Удвоение числа сторон правильного многоугольника.
§ 2. Длина окружности. Площадь круга и его частей
229. Длина окружности.
230. Площадь круга и его частей.
Глава XIX. ПРЯМЫЕ И ПЛОСКОСТИ В ПРОСТРАНСТВЕ
231. Взаимное расположение двух прямых в пространстве.
232. Взаимное расположение прямой линии и плоскости.
233. Взаимное расположение двух плоскостей.
234. Свойства параллельных прямых и плоскостей.
235. Построения в стереометрии.
§ 2. Перпендикулярность прямых и плоскостей
236. Перпендикуляр к плоскости.
237. Перпендикуляр и наклонные.
238. Угол между прямой и плоскостью.
239. Связь между перпендикулярностью и параллельностью прямых и плоскостей.
240. Общий перпендикуляр двух скрещивающихся прямых.
§ 3. Двугранные и многогранные углы
241. Двугранный угол.
242. Взаимно перпендикулярные плоскости.
243. Трехгранные углы.
244. Многогранные углы.
§ 4. Многогранники
245. Многогранники.
246. Правильные многогранники.
Глава XX. МНОГОГРАННИКИ И КРУГЛЫЕ ТЕЛА
247. Цилиндры и призмы.
248. Параллелепипеды.
249. Объемы призм и цилиндров.
250. Площадь боковой поверхности призмы.
251. Площадь поверхности цилиндра.
§ 2. Пирамида. Конус
252. Свойства пирамиды и конуса.
253. Объем пирамиды и конуса.
254. Площадь боковой поверхности правильной пирамиды и конуса.
255. Усеченный конус и усеченная пирамида.
§ 3. Шаровая поверхность. Шар
256. Шар и шаровая поверхность.
257. Объем шара и его частей.
258. Площадь поверхности шара и ее частей.
259. Понятие телесного угла.
Ответы к упражнениям
Приложения
логарифмов | nool
Перейти к основному содержанию
Домашняя страница Технологического института Онтарио
nool
Функция f(x) = 2 x называется экспоненциальной функцией, потому что переменная x является показателем степени. В общем случае показательные функции имеют вид f(x) = a x , где a — положительная константа.
В науке важно уметь оценивать логарифмические функции, поскольку они встречаются во многих приложениях. Чтобы вычислить логарифм (по основанию 10) числа, введите число в свой калькулятор, затем нажмите клавишу [log]. Некоторые калькуляторы немного отличаются; поэтому важно, чтобы учащиеся были знакомы с собственным калькулятором. Также во многих ситуациях важно уметь определять антилогарифмическое значение логарифмического значения. Чтобы вычислить антилогарифм числа, введите число в калькулятор и нажмите [10 x ].
Пример: Найдите x в каждом из следующих уравнений: x = log 10 3,6 и log 10 x = 6,75.
Решение:
x = log 10 3,6
x = 0,556 x= 5,62×10 6
Пример: 90]10 .0009 -3 М до pH.
Решение :
PH = -LOG [H + ]
PH = -LOG [3,5 x 10 -3 ]
PH = 2,4
Пример: . Какое значение [H +] соответствует рН 4,3?
Решение :
PH = -LOG [H+]
4,3 = -LOG [H+]
-4,3 = log [H+]
[H+] = 10 -4,3
[H+] = = = = 10 -4,3
[H+] = = = 5,0 x 10 -5 M
Пример:
Объяснение и примеры, показатели, доказательства
Законы логарифмов — это правила, которые можно применять для упрощения и решения сложных логарифмических уравнений.
Основные законы бревен
Формула изменения закона находится в буклете с формулами, который вам дадут на экзамене.
Доказательство закона логарифмов
Не обязательно уметь доказывать каждый закон логарифма для экзамена, но важно понимать каждый шаг и почему он происходит.
Закон произведения (сложения)
1. Если и , то можно переписать логарифмы в виде экспоненциальной функции.
Для , основание равно x, показатель степени равен c , ответ на показатель степени равен a .
Следовательно, это можно записать как
Для , основание равно x, показатель степени равен d , а ответ на показатель степени равен b.
Следовательно, это можно записать как
2. Таким образом, используя наше экспоненциальное (индексное) правило,
3.
4. Поскольку включает как экспоненту с основанием x , так и логарифм с основанием x (), они компенсируют друг друга, чтобы стать просто c + d.
Этот шаг связан с тем, что логарифмы и экспоненты являются обратными функциями друг друга. Подумайте о том, когда мы компенсируем +4 и -4 в x +4 -4 = 10 — это тот же принцип.
5. Мы определили c и d в части 1. и
Следовательно,
Правило частных
1. Если и , то можно переписать логарифмы в виде экспоненциальной функции.
Ибо, основание равно x, показатель степени равен c, и ответ на показатель степени равен a .
Следовательно, это можно записать как
Для , основание равно x, показатель степени равен d, и ответ на показатель степени равен б.
Следовательно, это можно записать как
2.
3. Возьмем журнал обеих сторон.
4. Поскольку включает экспоненту с основанием x и логарифм с основанием x , они компенсируют друг друга и становятся просто c — d .
5. Мы определили c и d в части 1 где и :
Изменение основания
1. Пусть, где основание a , показатель степени равен k, и x экспоненциальный ответ на x .
Следовательно, его можно переписать в экспоненциальном виде:
2. Возьмите логарифм обеих сторон
3. Используйте степенное правило для упрощения
, которое затем можно подставить обратно в уравнение
4. Перестроить, чтобы получить k самостоятельно путем деления на
5. Поскольку k уже определено, его можно подставить в уравнение как использование наших экспоненциальных правил с негативами.
Журнал базы
- Набор, где база а, 9Показатель степени 0012 равен x, , а ответ на экспоненту равен a . Поэтому его можно записать как.
- В соответствии с экспоненциальными правилами, если ответ экспоненты равен основанию, то показатель степени должен быть равен 1.
Логарифм 1
- Набор, где основание равно a, показатель степени равен x, и ответ на экспоненту равен 1. Следовательно, это можно записать как.
- В соответствии с экспоненциальными правилами, если ответ экспоненты равен 1, то показатель степени должен быть равен 0.
Упрощение и решение с использованием законов бревен
Здесь мы рассмотрим несколько примеров упрощения ряда законов бревен.
Упрощение и решение с использованием 1 логарифмического закона
Показать логарифм (6) + логарифм (4) = логарифм (24)
логарифм (6) + логарифм (4) = логарифм (6 x 4) = логарифм (24)
Лог решения (14) — Лог (7)
Лог (14) — Лог (7) = Лог (14/7) = Лог (2) = 0,301 (3 ст.
Упростить 2логарифм (9), сохранить точная форма
Решить
Упрощение и решение с использованием законов множественных журналов
Возможно, будет полезно использовать правила, которые упрощают отдельные журналы, перед выполнением законов упрощения множественных журналов.
Решить
Упростить
Доказать, где
1. Используя правило степени, .
Следовательно,
2. Используя правило отношения,
3. Когда вы хотите удалить логарифм, вам нужно преобразовать его в экспоненту. Это работает так же, как обычно — просто убедитесь, что вы пометили каждую часть.
Основание равно 2; показатель степени равен 3; ответ на экспоненциальный
4. Решите как обычное уравнение являются законом продукта, частным законом, изменением основного закона и правилом силы.

Все знакомы, что такое степень числа (если нет, то вам сюда). В таблице приведены различные степени числа 2. Глядя на таблицу, ясно, что, например, число 32 – это 2 в пятой степени, то есть двойка, умноженная на саму себя пять раз.
Теперь при помощи этой таблицы введем понятие логарифма.
Логарифм от числа 32 по основанию 2 ((log_{2}(32))) – это в какую степень нужно возвести двойку, чтобы получить 32. Из таблицы видно, что 2 нужно возвести в пятую степень. Значит наш логарифм равен 5:
$$ log_{2}(32)=5;$$
Аналогично, глядя в таблицу получим, что:
$$log_{2}(4)=2;$$
$$log_{2}(8)=3;$$
$$log_{2}(16)=4;$$
$$log_{2}(64)=6;$$
$$log_{2}(128)=7.$$
Естественно, логарифм бывает не только по основанию 2, а по любым основаниям больших 0 и неравных 1. Можете так же создавать таблицы для разных чисел. Но, конечно, со временем вы это будете делать в уме.
Теперь дадим определение логарифма в общем виде:
Логарифмом положительного числа (b) по основанию положительно числа (a) называется степень (c), в которую нужно возвести число (a), чтобы получить (b)
$$log_{a}(b)=c;$$
$$a^{c}=b.$$
Будьте внимательны! В первое время обычно путают, что такое основание и то, что стоит под логарифмом (аргумент). Логарифм — это всегда функция, зависящая от двух переменных. Чтобы их не путать, помните определение логарифма – это степень, в которую нужно возвести основание, чтобы получить аргумент.
Но, конечно, вы часто будете сталкиваться не с такими простыми логарифмами, как в примерах с двойкой, а очень часто будет, что логарифм нельзя в уме посчитать. Действительно, что скажете про логарифм пяти по основанию два:
$$log_{2}(5)=???$$
Как его посчитать? При помощи калькулятора. Он нам покажет, что такой логарифм равен иррациональному числу:
$$log_{2}(5)=2,32192809…$$
Или логарифм шести по основанию 4:
$$log_{4}(6)= 1.2924812…$$
На уроках математики пользоваться калькулятором нельзя, поэтому на экзаменах и контрольных принято оставлять такие логарифмы в виде логарифма – не считая его, это не будет ошибкой!
Но иногда можно столкнуться с заданием, где нужно примерно оценить значение логарифма – это очень просто! Давайте для примера оценим логарифм (log_{4}(6)). Необходимо подобрать слева и справа от 6 такие ближайшие числа, логарифм от которых мы сможем посчитать, другими словами, надо найти степени 4-ки ближайшие к 6-ке:
$$ log_{4}(4) lt log_{4}(6) lt log_{4}(16);$$
$$ 1 lt log_{4}(6) lt 2. $$
Значит (log_{4}(6)) принадлежите промежутку от 1 до 2:
$$ log_{4}(6) in (1;2). $$
Как посчитать логарифм
Перед тем, как научиться считать логарифмы, нужно ввести несколько ограничений. Дело в том, что функция логарифма (log_{a}(b)) существует только при положительных значениях основания (a) и аргумента (b). И кроме этого на основание накладывается условие, что оно не должно быть равно (1).
$$ log_{a}(b) quad существует,;при quad a gt 0; ;b gt 0 ;a neq 1.$$
Почему так? Это следует из определения показательной функций. Показательная функция не может быть (0). А основание не равно (1), потому что тогда логарифм теряет смысл – ведь (1) в любой степени это будет (1).
При этих ограничениях логарифм существует.
В дальнейшем при решении различных логарифмических уравнений и неравенств вам это пригодится для ОДЗ.
Обратите внимание, что само значение логарифма может быть любым. Это же степень, а степень может быть любой – отрицательной, рациональной, иррациональной и т.д.
$$log_{3}(frac{1}{3})=-1;$$
Так как (вспоминайте определение отрицательной степени)
$$3^{-1}=frac{1}{3};$$
Теперь давайте разберем общий алгоритм вычисления логарифмов:
- Во-первых, постарайтесь представить основание и аргумент (то, что стоит под логарифмом) в виде степеней с одинаковым основанием. Параллельно с этим избавляемся от всех десятичных дробей – переводим их в обыкновенные.
- Разобраться в какую степень (x) нужно возвести основание, чтобы получить аргумент. Когда у вас там и там степени с одинаковым основанием, это сделать довольно просто.
- (x) и будет искомым значением логарифма.
Давайте разберем на примерах.
Пример 1. Посчитать логарифм (9) по основанию (3): (log_{3}(9))
- Сначала представим аргумент и основание в виде степени тройки:
$$ 3=3^1, qquad 9=3^2;$$ - Теперь надо разобраться в какую степень (x) нужно возвести (3^1), чтобы получить (3^2)
$$ (3^1)^x=3^2, $$
$$ 3^{1*x}=3^2, $$
$$ 1*x=2,$$
$$ x=2.$$ - Вот мы и решили:
$$log_{3}(9)=2.$$
Пример 2. Вычислить логарифм (frac{1}{125}) по основанию (5): (log_{5}(frac{1}{125}))
- Представим аргумент и основание в виде степени пятерки:
$$ 5=5^1, qquad frac{1}{125}=frac{1}{5^3}=5^{-3};$$ - В какую степень (x) надо возвести (5^1), чтобы получить (5^{-3}):
$$ (5^1)^x=5^{-3}, $$
$$ 5^{1*x}=5^{-3},$$
$$1*x=-3,$$
$$x=-3.$$ - Получили ответ:
$$ log_{5}(frac{1}{125})=-3.$$
Пример 3. Вычислить логарифм (4) по основанию (64): (log_{64}(4))
- Представим аргумент и основание в виде степени двойки:
$$ 64=2^6, qquad 4=2^2;$$ - В какую степень (x) надо возвести (2^6), чтобы получить (2^{2}):
$$ (2^6)^x=2^{2}, $$
$$ 2^{6*x}=2^{2},$$
$$6*x=2,$$
$$x=frac{2}{6}=frac{1}{3}.$$ - Получили ответ:
$$ log_{64}(4)=frac{1}{3}.$$
Пример 4. Вычислить логарифм (1) по основанию (8): (log_{8}(1))
- Представим аргумент и основание в виде степени двойки:
$$ 8=2^3 qquad 1=2^0;$$ - В какую степень (x) надо возвести (2^3), чтобы получить (2^{0}):
$$ (2^3)^x=2^{0}, $$
$$ 2^{3*x}=2^{0},$$
$$3*x=0,$$
$$x=frac{0}{3}=0.$$ - Получили ответ:
$$ log_{8}(1)=0.$$
Пример 5. Вычислить логарифм (15) по основанию (5): (log_{5}(15))
- Представим аргумент и основание в виде степени пятерки:
$$ 5=5^1 qquad 15= ???;$$
(15) в виде степени пятерки не представляется, поэтому этот логарифм мы не можем посчитать. У него значение будет иррациональное. Оставляем так, как есть:
$$ log_{5}(15).$$
Внимание!
Как понять, что некоторое число (a) не будет являться степенью другого числа (b). Это довольно просто – нужно разложить (a) на простые множители.
$$16=2*2*2*2=2^4,$$
(16) разложили, как произведение четырех двоек, значит (16) будет степенью двойки.
$$ 48=6*8=3*2*2*2*2,$$
Разложив (48) на простые множители, видно, что у нас есть два множителя (2) и (3), значит (48) не будет степенью.
Теперь поговорим о наиболее часто встречающихся логарифмах. Для них даже придумали специально названия – десятичный логарифм и натуральный логарифм. Давайте разбираться.
Десятичный логарифм
На самом деле, все просто. Десятичный логарифм – это любой обыкновенный логарифм, но с основанием 10. Обозначается — (lg(a)).
Пример 6
$$ log_{10}(100)= lg(100)=2;$$
$$log_{10}(1000)=lg(1000)=3;$$
$$log_{10}(10)=lg(10)=1.$$
Натуральный логарифм
Натуральным логарифмом называется логарифм по основанию (e). Обозначение — (ln(x)). Что такое (e)? Так обозначают экспоненту, число-константу, равную, примерно, (2,718281828459…). Это число известно тем, что используется в многих математических законах. Просто запомните, что логарифмы с основанием (e) часто встречаются, и поэтому им придумали специальное название – натуральный логарифм.
Пример 7
$$ log_{e}(e^2)=ln(e^2)=2;$$
$$ log_{e}(e)=ln(e)=1;$$
$$ log_{e}(e^5)=ln(e^5)=5.$$
Натуральные и десятичные логарифмы подчиняются тем же самым свойствам и правилам, что и обыкновенные логарифмы.
У логарифмов есть несколько свойств, по которым можно проводить преобразования и вычисления. Кроме этих свойств, никаких операций с логарифмами делать нельзя.
Свойства логарифмов
$$1. ; log_{a}(1)=0;$$
$$2. ; log_{a}(a)=1;$$
$$3. ; log_{a}(b*c)=log_{a}(b)+ log_{a}(c);$$
$$4. ; log_{a}(frac{b}{c})= log_{a}(b)- log_{a}(c);$$
$$5. ; log_{a}(b^m)= m*log_{a}(b);$$
$$6. ; log_{a^m}(b)=frac{1}{m}* log_{a}(b);$$
$$ 7. ; log_{a}(b)=frac{ log_{c}(b)}{ log_{c}(a)}, ; b gt 0; ; c gt 0; ; c neq 1; $$
$$ 8. ; log_{a}(b)=frac{1}{log_{b}(a)};$$
$$ 9. ; a^{ log_{a}(b)}=b.$$
Давайте разберем несколько примеров на свойства логарифмов.
Пример 8. Воспользоваться формулой (3). Логарифм от произведения – это сумма логарифмов.
$$log_{a}(b*c)=log_{a}(b)+ log_{a}(c);$$
$$ log_{3}(12)=log_{3}(3*4)=log_{3}(3)+log_{3}(4)=1+log_{3}(4);$$
$$ log_{3}(2.7)+log_{3}(10)=log_{3}(2.7*10)=log_{3}(27)=3;$$
Пример 9. Воспользоваться формулой (4). Логарифм от частного – это разность логарифмов.
$$ log_{a}(frac{b}{c})= log_{a}(b)- log_{a}(c);$$
$$ log_{7}(98)-log_{7}(2)=log_{7}(frac{98}{2})=log_{7}(49)=2;$$
Пример 10. Формула (5,6). Свойства степени.
$$log_{a}(b^m)= m*log_{a}(b);$$
$$log_{a^m}(b)=frac{1}{m}* log_{a}(b);$$
Логично, что будет выполняться и такое соотношение:
$$log_{a^m}(b^n)=frac{n}{m}* log_{a}(b);$$
И если (m=n), то:
$$log_{a^m}(b^m)=frac{m}{m}* log_{a}(b);=log_{a}(b)$$
$$log_{4}(9)=log_{2^2}(3^2)=log_{2}(3);$$
Пример 11. Формулы (7,8). Переход к другому основанию.
$$ log_{a}(b)=frac{ log_{c}(b)}{ log_{c}(a)}, ; b gt 0;c gt 0;c neq 1; $$
$$ log_{a}(b)=frac{1}{log_{b}(a)};$$
$$log_{4}(5)=frac{1}{log_{5}(4)};$$
$$log_{4}(5)=frac{log_{7}(5)}{log_{7}(4)};$$
План урока:
Понятие логарифма
Ограничения, связанные с логарифмом
Основные свойства логарифмов
Функция логарифма
Три основных вида логарифмов
Преобразования логарифмических выражений
Переход к новому основанию алгоритма
Использование логарифма для вычислений
Логарифмическая функция в природе и науке
Понятие логарифма
Великий ученый Пьер-Симон Лаплас говорил, что изобретение логарифмов продлило жизнь астрономов вдвое, ведь с их помощью астрономические расчеты, которые ранее занимали несколько месяцев, стало возможно выполнять за считанные дни. Что же представляют собой логарифмы и как они так сильно упрощают вычисления? Для ответа на этот вопрос сначала следует вспомнить показательные уравнения.
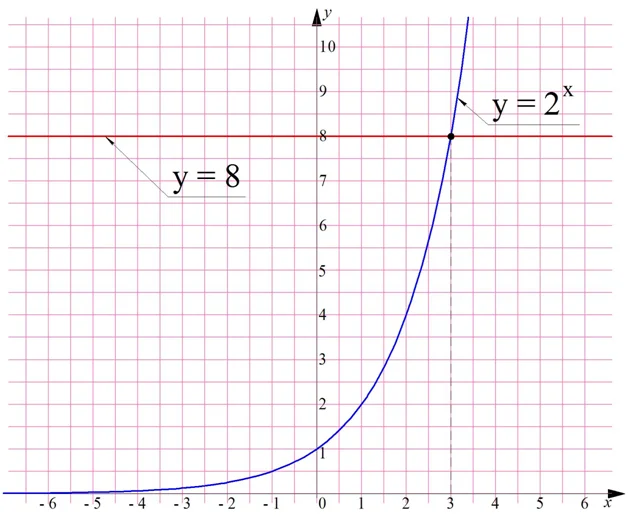
Рассмотрим простейшее показательное уравнение 2х = 4. Так как 22 =4, то, очевидно, оно имеет единственный корень, равный 2. Найти его можно не только аналитически, но и графически:
Далее посмотрим на уравнение 2х = 8. Так как восьмерка – это двойка в кубе (23 = 8), то единственным корнем ур-ния будет число 3. Также проиллюстрируем это с помощью графика:
Однако если мы попытаемся решить уравнение 2х = 6, то мы столкнемся с проблемами. Представить шестерку как какую-то степень двойки не получается. Графический метод показывает, что у этого ур-ния есть единственный корень, который лежит между числами 2 и 3, но точно определить его значение не получается:
Можно доказать (мы не будем этого делать), что искомый нами корень невозможно выразить с помощью дробей и даже корней n-ой степени. Поэтому возникает необходимость ввести какое-то новое обозначение, чтобы записывать корни таких уравнений. Математики придумали для такого числа обозначение log2 6, которое читается как «логарифм шести по основанию два».
Рассмотрим теперь более общий случай. Пусть есть некоторое ур-ние
Если число b положительно, то уравнение имеет корень, и при том единственный. Для его обозначения используется запись logab. Покажем, как графически показать значение величины logab. Для этого надо построить показательную функцию у = ах и горизонтальную линию у = b. Они пересекутся в единственной точке (если b положительно). Абсцисса (координата х) этой точки и будет равна logab:
Дадим строгое определение логарифма:
Задание. Какое число является решением показательного уравнения
Задача. Слиток радиоактивного изотопа, чей период полураспада (его обозначают буквой Т) составляет 10 минут, имеет начальную массу (m0), равную 1 кг. Через сколько минут его вес уменьшится до 300 грамм (0,3 кг)? Масса радиоактивного изотопа изменяется по закону
m(t) = m0•2–t/T
Решение. Подставим исходные данные в формулу, и получим уравнение с неизвестной величиной t:
0,2 = 1•2–t/10
0,3 = 2–t/10
Получили простейшее показательное уравнение, однако его левую часть (число 0,3) нельзя представить как степень двойки. Однако с помощью определения логарифма мы можем записать, что
– t/10 = log2 0,3
Умножаем ур-ние на (– 10) и получаем:
t = – 10 log2 0,3
С помощью калькулятора или компьютера можно узнать, что
log2 0,3 ≈ – 1,737
Тогда искомое нами время примерно равно
t = – 10 log2 0,3 ≈ – 10•(– 1,737) ≈ 17,37 минут ≈ 17 минут 22 секунды
Ответ: – 10 log2 0,3 минут ≈ 17 минут 22 секунды.
Из задачи видно, что с логарифмы используются и при решении некоторых практических задач.
Иногда бывает удобнее использовать иное определение, которое по своей сути почти не отличается от первого:
Вычислим для примера несколько простейших логарифмов:
Ограничения, связанные с логарифмом
Заметим, что сам логарифм может оказаться любым вещественным числом, ведь мы умеем возводить числа и в отрицательные, и в дробные, и даже в иррациональные степени. Однако для логарифма logab некоторые ограничения накладываются на значение числа а (оно называется основанием логарифма) и на значение числа b (будем называть его аргументом логарифма).
Напомним, что при определении показательной функции у = ах было введено ограничение, согласно которому основание степени (число а) должно быть строго положительным числом и при этом НЕ может равняться единице. Из-за этого и основание логарифма должно также соответствовать этому ограничению. Основание логарифма и основание показательной функции даже специально обозначают одной буквой а, чтобы связь этих двух понятий была очевидней.
Также напомним, что показательное уравнение ах = b имеет решение только при положительных значениях b. Это решение и представляет собой logab. Если же число b отрицательно, то корня у уравнения нет, а значит и вычислить logab невозможно. Поэтому аргумент логарифма не может быть отрицательным.
Сформулируем эти ограничения в виде одного правила:
Ранее мы уже сталкивались с тремя случаями, когда выражения не имеют смысла. Во-первых, это происходит при делении на ноль (или нахождении нуля в знаменателе дроби, что, по сути, одно и то же). Во-вторых, выражения бессмысленны, если под корнем четной степени находится отрицательное число. В-третьих, не имеют смысла выражения, в которых отрицательные числа возводятся в дробную степень, ведь возведение в дробную степень можно заменить извлечением корня
а отрицательное число не должно оказываться под знаком корня
Сейчас мы узнали четвертый подобный случай, связанный с понятием логарифма. Больше в рамках школьного не будут рассматриваться никакие другие ситуации, в которых выражение может потерять смысл.
Основные свойства логарифмов
Любое число, возведенной в первую степень, равно самому себе. То есть справедливо равенство
а1 = а
Из него, пользуясь определением логарифма, получаем первое важное его свойство: logаa = 1.
Продемонстрируем использование этого правила:
Любое число при возведении в нулевую степень равно единице:
Из этого следует второе важное правило: логарифм единицы по любому основанию равен нулю:
Покажем несколько примеров использования этого тривиального правила:
Для получения третьего свойства логарифма запишем очевидно справедливое равенство:
Пользуясь определением логарифма, мы можем записать, что logaac = c.
Продемонстрируем, как работает это свойство логарифмов:
Это правило можно применить для вычисления некоторых простейших логарифмов:
Логарифм logab, согласно одному из своих определений, это та степень, в которую нужно возвести а, чтобы получилось b. Это определение можно представить в виде формулы:
Данное равенство называют основным логарифмическим тождеством.
В силу этого тождества справедливы следующие равенства:
Функция логарифма
Арифметическое действие, в ходе которого находят логарифм какого-либо числа, называется логарифмированием. Это действие является обратным по отношению к возведению в степень. Проиллюстрируем это табличкой, в которой слева будет показана операция возведения в степень, а справа – логарифмирование:
Теперь подумаем о функции у = logax. Так как логарифмирование является обратным действием для возведения в степень, то и ф-ция у = logax должна быть обратной для показательной ф-ции у = ах.
В свою очередь это означает, что графики этих двух функций должны быть симметричны относительно прямой, задаваемой уравнением у = х.
Напомним, что на вид показательной функции у = ах влияет значение основания степени а. Если оно больше единицы, то функция оказывается возрастающей. Тогда и обратная ей логарифмическая функция также окажется возрастающей. Для примера построим графики у = 2х и у = log2x.
Полученный график логарифмической функции называют логарифмической кривой, однако понятно, что она представляет собой всё ту же экспоненту, которую отобразили симметрично относительно оси Ох.
График у = log2x можно и построить иначе, по точкам, просто вычислив ее значение в нескольких «удобных» для вычисления точках:
Видно, что в обоих случаях получился один и тот же график. Похожим будет и график любой функции у =logax, если число а будет больше единицы.
Ситуация меняется в том случае, когда а < 1, ведь при таком основании показательная функция у = ах будет убывающей. Тогда убывающим окажется и логарифмическая функция. Для примера построим график ф-ции = 0,5х и график обратной ей функции у = log0,5x:
Возможно, вы заметили, что графики у = log2x и у = log0,5xчем-то похожи друг на друга. И действительно, если построить их на одной плоскости, то мы увидим, что они симметричны относительно оси Ох:
Причиной такой симметрии является то, что их основания, числа 2 и 0,5, являются обратными числами, то есть при перемножении дают единицу (2•0,5 = 1).
Аналогично такой же симметрией будут обладать любые две логарифмические кривые с обратными основаниями. Это свойство логарифмов мы докажем чуть позднее.
Далее построим ещё несколько графиков, чтобы лучше понять свойства логарифмических функции:
Анализируя полученные графики, мы можем заметить следующие свойства функции логарифма:
Область определения логарифмической функции – это множество всех положительных чисел, то есть промежуток (0; + ∞). Действительно, выражение logаb имеет смысл только тогда, когда число b> 0.
Областью значения логарифмической функции является множество всех действительных чисел, то есть промежуток(– ∞; + ∞).
Логарифмическая функция является строго монотонной. При этом при основании а > 1 она возрастает, а при основании 0 <a< 1 она убывает.
График каждой логарифмической функции проходит через точку (1; 0). Это связано с тем, что для любого основания справедливо равенство loga 1 = 0.
Три основных вида логарифмов
Математика изучает логарифмы с любыми положительными основаниями. Однако на практике наиболее распространены три их вида.
Первым из них является десятичный логарифм, основание которого равно 10. Дело в том, что его помощью до изобретения калькуляторов и компьютеров можно было быстро и с высокой точностью перемножать большие числа, используя такой прибор, как логарифмическая линейка. История понятия логарифма начиналась в XVI-XVII веках и была связана именно с необходимостью выполнения сложных арифметических действий с большими числами. Для обозначения десятичных логарифмов используют специальный символ lg, то есть
Сегодня из-за развития электроники десятичные логарифмы используются значительно реже по сравнению с 50-60 г. XX века. Но, так как почти вся вычислительная техника построена на использовании двоичной системы счета, возросла значимость двоичного логарифма log2b. Для его обозначения не используются никакие специальные символы, однако в работах, посвященным информатике и оценке сложности алгоритмов, он используется особенно часто.
Наконец, самым важным является натуральный логарифм. Это логарифм, основанием которого является число e, примерно равное 2,71828… Для его обозначения используют символ ln, то есть
Свойства натурального логарифма, которые отличают его от других логарифмов, будут изучены нами позднее, в 11 классе. Заметим лишь, что многие физические формулы содержат именно натуральный логарифм.
Преобразования логарифмических выражений
Для работы с логарифмическими выражениями надо знать несколько основных свойств логарифмов. Первое из них помогает вычислять логарифм произведения.
Для доказательства этого правила введем обозначения. Пусть
Тогда нам надо доказать, что z = x + у. По определению логарифма мы можем записать что
Теперь подставим (1) и (2) в (3):
Получили, что az = ax+y. В этом равенстве в обеих частях стоят степени с совпадающим основанием а. Значит, должны совпадать и их степени, то есть
что и мы и пытались доказать.
Убедимся в справедливости этого правила на простейшем примере. Очевидно, что
log2 4 = 2, ведь 22 = 4
log2 8 = 3, ведь 23 = 8
log2 32 = 5, ведь 25 = 32
С одной стороны, так как
2 + 3 = 5
то и
log2 4 + log2 8 = log2 32
С другой стороны, число 32 можно представить как произведение 4•8, то есть
log2 32 = log2 (4•8)
С учетом этого получаем, что
log24 + log28 = log232 = log2(4•8)
Покажем несколько примеров использования только что доказанного правила:
Отдельно отметить, что правило сложения логарифмов действует и в том случае, когда складываются не два, а большее количество логарифмов:
Второе правило используют для определения логарифма от степени какого-либо числа.
Грубо говоря, показатель степени можно перенести и записать перед знаком логарифма. Сначала для наглядности приведем доказательство только для случая, когда r– целая степень. Тогда число br можно представить как произведение r множителей, равных b. Однако логарифм такого произведения можно заменить на сумму r логарифмов:
Однако более строгое доказательство должно рассматривать и случай, когда r – это отрицательное или даже дробное число. Поэтому, как и в ситуации с доказательством первого правила, введем переменные. Пусть
Получается, что нам доказать, что у = r•x. Из определения логарифма следуют следующие формулы:
Подставляя первую формулу во вторую, получаем:
И снова, если у двух равных степеней равны основания, то и показатели обязательно будут равными:
Это равенство мы и пытались доказать.
Продемонстрируем, как работает это свойство логарифмов:
Правило работает и в обратную сторону:
Задание. Чему равна дробь
Третье правило помогает вычислять логарифм от частного или дроби.
Для доказательства этого свойства логарифмов воспользуемся уже доказанными нами двумя правилами. Но предварительно напомним, что произвольное число с в степени (– 1) представляет собой дробь 1/с:
Тогда доказательство будет записываться в две строчки:
С помощью полученной формулы возможно выполнить следующие преобразования:
Заметим, что все полученные формулы справедливы только в том случае, когда под знаком логарифма стоят исключительно положительные числа. Например, вполне допустимо преобразование
но ошибочной будет такая запись:
ведь в левой части стоит выражение, имеющее смысл, а в правой – выражение, смысла не имеющее.
Но что делать в случае, если необходимо упростить выражение с переменными, которые могут принимать как положительные, так и отрицательные значения? Получается, что запись
не является корректной. Действительно, если и х, и у являются отрицательными числами, то их произведение ху положительно. Но тогда получается, что при некоторых значениях переменных левая часть равенства имеет смысл, а правая – нет. Это значит, что оно не является тождеством.
Здесь может помочь использование модуля числа. Запись
уже будет корректной при любых допустимых значениях х и у. Если же хоть одна из переменных будет равна нулю, то обе части равенства одновременно потеряют смысл. Таким образом, данное равенство можно считать тождеством.
Аналогично и формулу разности логарифмов можно представить в более общем случае, при котором допускаются отрицательные значения переменных:
Можно ли записать равенство logaх2 = 2logaх, если допускается, что х может быть и отрицательным? Нет, нельзя, ведь при отрицательных х выражение левая часть равенства будет иметь смысл, а правая нет. Однако использование модуля поможет и в этом случае. Можно написать, что
Аналогичным образом можно упростить и любые другие логарифмы, аргументы которых возведены в четную степень:
Ещё раз уточним, что эти правила используются при упрощении выражений с переменными, если те могут принимать отрицательные значения. Если же известно, что числа b и c положительны, то лучше использовать формулы, не содержащие модулей.
Переход к новому основанию алгоритма
До этого мы рассматривали преобразования, в ходе которых не менялось основание логарифма. Однако иногда возникает необходимость сложить или вычесть логарифмы с различными основаниями. Пусть надо вычислить значение выражения
Так как основания двух логарифмов различны, то мы не можем использовать выведенную нами формулу разности логарифмов. Однако можно попытаться привести один из логарифмов к новому основанию. Для такой операции существует специальная формула.
Докажем это утверждение. Для этого введем новые переменные:
Тогда по определению логарифма можно записать равенства
Отсюда следует, что ax = cy. Подставим в это равенство вместо а выражение cz и получим:
Отсюда следует, что zx = у, или х = y/z. Теперь заменим х, у и z на логарифмы и получим то самое тождество, которые необходимо доказать:
Вернемся к примеру
Теперь мы можем произвести эти вычисления, но для этого сначала приведем log259 к основанию 5:
Теперь можно вычислить, чему равна искомая разность:
Формула перехода к новому основанию позволяет иначе взглянуть на графики логарифмических функций. Пусть дана функция у =log4x. Попытаемся привести ее к показателю 2:
Выходит, что график у = log4x можно получить из графика у = log2x его сжатием в 2 раза. Убедимся в этом, построив оба графика в одной плоскости:
Заметим, что и более общем случае графики функций у = logax и у = logbx могут быть получены друг из друга растяжением или сжатием в некоторое число раз. Действительно, формулу перехода к новому основанию можно переписать в таком виде:
Теперь подставим вместо числа b переменную х и получим соотношение, связывающее любые две логарифмические функции:
В данном случае logсx и logax – это логарифмические функции, а logca – некоторое число. В результате можно заключить, что график функции у = logсx может быть получен из графика logax его растяжением в logca раз.
Попытаемся привести логарифм logab к обратному основанию, то есть к основанию 1/а:
Итак, logab = – log1/аb. Именно из-за этого графики логарифмов с обратными основаниями (например, 2 и 0,5) симметричны относительно оси Ох:
Покажем примеры использования этой формулы:
А что будет, если мы попробуем logab привести к основанию b? Сделаем это:
Получили ещё одну замечательную логарифмическую формулу.
Её работу иллюстрируют следующие примеры:
Ещё одна логарифмическая формула позволяет возводить основание логарифма и его аргумент в одинаковую степень:
Докажем это тождество в «обратном порядке», то есть из правой части выведем левую. Для этого просто перейдем к основанию а:
Проиллюстрируем, как это свойство можно применять на практике:
Использование логарифма для вычислений
Исторически развитие теории логарифмов было связано с необходимостью выполнять громоздкие вычисления. Например, пусть надо возвести число 7 в пятисотую степень, то есть вычислить величину 7500. Сделать напрямую это довольно затруднительно. Однако в силу основного логарифмического тождества мы можем записать, что
Напомним, что десятичный логарифм обозначают символом lg, поэтому перепишем это равенство в более привычном виде:
Степень из-под знака логарифма можно вынести:
Значение числа lg 7 можно узнать с помощью калькулятора, в древности же использовали специальные таблицы, в которых были указаны десятичные логарифмы всех чисел от 1 до 10 (с маленьким шагом, равным, например, 0,001). Так или иначе, можно узнать, что
Получили число, записанное в стандартном виде. При этом наши расчеты были относительно простыми, если сравнить их с необходимостью умножить число 7 само на себя 500 раз. Аналогично и многие другие сложные операции выполняются значительно быстрее, если используются логарифмы. Поэтому долгое время знание теории логарифмов было необходимо для выполнения сложных инженерных расчетов. Но сегодня развитие компьютерной техники позволило избавиться от необходимости использования логарифмических линеек и таблиц.
Логарифмическая функция в природе и науке
Логарифм – это не просто инструмент для выполнения сложных операций. Например, в теории вероятностей существуют логарифмическое и логнормальное (от слов «логарифм» и «нормальное») распределение случайных величин, которые используются в генетике и физике. Так, размеры астероидов в Солнечной системе описываются логарифмическим распределением, а размеры градин во время града – логнормальным.
В компьютерной технике многие величин можно вычислить с использованием логарифмов. Например, ясно, что чем больше телефонных номеров находится в базе данных, тем дольше компьютер будет искать требуемый необходимый номер в ней. Зависимость времени поиска от количества номеров в базе данных описывается логарифмической функцией.
Огромное значение логарифмы имеют в астрономии. Так, яркость звезд на небе характеризуется таким параметром, как «видимая звездная величина». Однако в физике для оценки яркости света используют величину «освещенность», измеряемую в люксах. Зависимость между освещенностью звезд и их видимой величиной также является логарифмической.
Используются логарифмы и в термодинамике для вычисления такой характеристики систем, как энтропия. При расчете количества топлива, необходимого ракете для набора определенной скорости, используется формула Циолковского, содержащая натуральный логарифм:
В биологии давно замечено, что зависимость человеческих ощущений от силы воздействующих на них факторов окружающей среды носит логарифмический характер. В связи с этим для измерения громкости звуков используется специальная шкала децибелов, которая является логарифмической.
В строении ряда организмов можно обнаружить логарифмические кривые. Классическим примером является форма некоторых ракушек.
Логарифмом положительного числа (c) по основанию (a) ((a>0, aneq1)) называется показатель степени (b), в которую надо возвести основание (a), чтобы получить число (c) ((c>0)), т.е.
(a^{b}=c) (Leftrightarrow) (log_{a}{c}=b)
Объясним проще. Например, (log_{2}{8}) равен степени, в которую надо возвести (2), чтоб получить (8). Отсюда понятно, что (log_{2}{8}=3).
|
Примеры: |
(log_{5}{25}=2) |
т.к. (5^{2}=25) |
||
|
(log_{3}{81}=4) |
т.к. (3^{4}=81) |
|||
|
(log_{2})(frac{1}{32})(=-5) |
т.к. (2^{-5}=)(frac{1}{32}) |
Аргумент и основание логарифма
Любой логарифм имеет следующую «анатомию»:

Аргумент логарифма обычно пишется на его уровне, а основание — подстрочным шрифтом ближе к знаку логарифма. А читается эта запись так: «логарифм двадцати пяти по основанию пять».
Как вычислить логарифм?
Чтобы вычислить логарифм — нужно ответить на вопрос: в какую степень следует возвести основание, чтобы получить аргумент?
Например, вычислите логарифм: а) (log_{4}{16}) б) (log_{3})(frac{1}{3}) в) (log_{sqrt{5}}{1}) г) (log_{sqrt{7}}{sqrt{7}}) д) (log_{3}{sqrt{3}})
а) В какую степень надо возвести (4), чтобы получить (16)? Очевидно во вторую. Поэтому:
(log_{4}{16}=2)
б) В какую степень надо возвести (3), чтобы получить (frac{1}{3})? В минус первую, так как именно отрицательная степень «переворачивает дробь» (здесь и далее пользуемся свойствами степени).
(log_{3})(frac{1}{3})(=-1)
в) В какую степень надо возвести (sqrt{5}), чтобы получить (1)? А какая степень делает любое число единицей? Ноль, конечно!
(log_{sqrt{5}}{1}=0)
г) В какую степень надо возвести (sqrt{7}), чтобы получить (sqrt{7})? В первую – любое число в первой степени равно самому себе.
(log_{sqrt{7}}{sqrt{7}}=1)
д) В какую степень надо возвести (3), чтобы получить (sqrt{3})? Из свойств степени мы знаем, что корень – это дробная степень, и значит квадратный корень — это степень (frac{1}{2}).
(log_{3}{sqrt{3}}=)(frac{1}{2})
Пример: Вычислить логарифм (log_{4sqrt{2}}{8})
Решение:
|
(log_{4sqrt{2}}{8}=x) |
Нам надо найти значение логарифма, обозначим его за икс. Теперь воспользуемся определением логарифма: |
|
|
((4sqrt{2})^{x}=8) |
Что связывает (4sqrt{2}) и (8)? Двойка, потому что и то, и другое число можно представить степенью двойки: |
|
|
({(2^{2}cdot2^{frac{1}{2}})}^{x}=2^{3}) |
Слева воспользуемся свойствами степени: (a^{m}cdot a^{n}=a^{m+n}) и ((a^{m})^{n}=a^{mcdot n}) |
|
|
(2^{frac{5}{2}x}=2^{3}) |
Основания равны, переходим к равенству показателей |
|
|
(frac{5x}{2})(=3) |
Умножим обе части уравнения на (frac{2}{5}) |
|
|
(x=1,2) |
Получившийся корень и есть значение логарифма |
Ответ: (log_{4sqrt{2}}{8}=1,2)
Зачем придумали логарифм?
Чтобы это понять, давайте решим уравнение: (3^{x}=9). Просто подберите (x), чтобы равенство сработало. Конечно, (x=2).
А теперь решите уравнение: (3^{x}=8).Чему равен икс? Вот в том-то и дело.
Самые догадливые скажут: «икс чуть меньше двух». А как точно записать это число? Для ответа на этот вопрос и придумали логарифм. Благодаря ему, ответ здесь можно записать как (x=log_{3}{8}).
Хочу подчеркнуть, что (log_{3}{8}), как и любой логарифм — это просто число. Да, выглядит непривычно, но зато коротко. Потому что, если бы мы захотели записать его в виде десятичной дроби, то оно выглядело бы вот так: (1,892789260714…..)
Пример: Решите уравнение (4^{5x-4}=10)
Решение:
|
(4^{5x-4}=10) |
(4^{5x-4}) и (10) никак к одному основанию не привести. Значит тут не обойтись без логарифма.
Воспользуемся определением логарифма: |
|
|
(log_{4}{10}=5x-4) |
Зеркально перевернем уравнение, чтобы икс был слева |
|
|
(5x-4=log_{4}{10}) |
Перед нами линейное уравнение. Перенесем (4) вправо. И не пугайтесь логарифма, относитесь к нему как к обычному числу. |
|
|
(5x=log_{4}{10}+4) |
Поделим уравнение на 5 |
|
|
(x=)(frac{log_{4}{10}+4}{5}) |
Вот наш корень. Да, выглядит непривычно, но ответ не выбирают. |
Ответ: (frac{log_{4}{10}+4}{5})
Десятичный и натуральный логарифмы
Как указано в определении логарифма, его основанием может быть любое положительное число, кроме единицы ((a>0, aneq1)). И среди всех возможных оснований есть два встречающихся настолько часто, что для логарифмов с ними придумали особую короткую запись:
Натуральный логарифм: логарифм, у которого основание — число Эйлера (e) (равное примерно (2,7182818…)), и записывается такой логарифм как (ln{a}).
То есть, (ln{a}) это то же самое, что и (log_{e}{a}), где (a) — некоторое число.
Десятичный логарифм: логарифм, у которого основание равно 10, записывается (lg{a}).
То есть, (lg{a}) это то же самое, что и (log_{10}{a}), где (a) — некоторое число.
Основное логарифмическое тождество
У логарифмов есть множество свойств. Одно из них носит название «Основное логарифмическое тождество» и выглядит вот так:
Это свойство вытекает напрямую из определения. Посмотрим как именно эта формула появилась.
Вспомним краткую запись определения логарифма:
если (a^{b}=c), то (log_{a}{c}=b)
То есть, (b) – это тоже самое, что (log_{a}{c}). Тогда мы можем в формуле (a^{b}=c) написать (log_{a}{c}) вместо (b). Получилось (a^{log_{a}{c}}=c) – основное логарифмическое тождество.
Остальные свойства логарифмов вы можете найти здесь. С их помощью можно упрощать и вычислять значения выражений с логарифмами, которые «в лоб» посчитать сложно.
Пример: Найдите значение выражения (36^{log_{6}{5}})
Решение:
|
(36^{log_{6}{5}}=) |
Сразу пользоваться свойством (a^{log_{a}{c}}=c) мы не можем, так как в основании степени и в основании логарифма – разные числа. Однако мы знаем, что (36=6^{2}) |
|
|
(=(6^{2})^{log_{6}{5}}=) |
Зная формулу ((a^{m})^{n}=a^{mcdot n}), а так же то, что множители можно менять местами, преобразовываем выражение |
|
|
(=6^{2cdotlog_{6}{5}}=6^{log_{6}{5}cdot2}=(6^{log_{6}{5}})^{2}=) |
Вот теперь спокойно пользуемся основным логарифмическим тождеством. |
|
|
(=5^{2}=25) |
Ответ готов. |
Ответ: (25)
Как число записать в виде логарифма?
Как уже было сказано выше – любой логарифм это просто число. Верно и обратное: любое число может быть записано как логарифм. Например, мы знаем, что (log_{2}{4}) равен двум. Тогда можно вместо двойки писать (log_{2}{4}).
Но (log_{3}{9}) тоже равен (2), значит, также можно записать (2=log_{3}{9}) . Аналогично и с (log_{5}{25}), и с (log_{9}{81}), и т.д. То есть, получается
(2=log_{2}{4}=log_{3}{9}=log_{4}{16}=log_{5}{25}=log_{6}{36}=log_{7}{49}…)
Таким образом, если нам нужно, мы можем где угодно (хоть в уравнении, хоть в выражении, хоть в неравенстве) записывать двойку как логарифм с любым основанием – просто в качестве аргумента пишем основание в квадрате.
Точно также и с тройкой – ее можно записать как (log_{2}{8}), или как (log_{3}{27}), или как (log_{4}{64})… Здесь мы как аргумент пишем основание в кубе:
(3=log_{2}{8}=log_{3}{27}=log_{4}{64}=log_{5}{125}=log_{6}{216}=log_{7}{343}…)
И с четверкой:
(4=log_{2}{16}=log_{3}{81}=log_{4}{256}=log_{5}{625}=log_{6}{1296}=log_{7}{2401}…)
И с минус единицей:
(-1=) (log_{2})(frac{1}{2})(=) (log_{3})(frac{1}{3})(=) (log_{4})(frac{1}{4})(=) (log_{5})(frac{1}{5})(=) (log_{6})(frac{1}{6})(=) (log_{7})(frac{1}{7})(…)
И с одной третьей:
(frac{1}{3})(=log_{2}{sqrt[3]{2}}=log_{3}{sqrt[3]{3}}=log_{4}{sqrt[3]{4}}=log_{5}{sqrt[3]{5}}=log_{6}{sqrt[3]{6}}=log_{7}{sqrt[3]{7}}…)
И так далее.
Любое число (a) может быть представлено как логарифм с основанием (b): (a=log_{b}{b^{a}})
Пример: Найдите значение выражения (frac{log_{2}{14}}{1+log_{2}{7}})
Решение:
|
(frac{log_{2}{14}}{1+log_{2}{7}})(=) |
Превращаем единицу в логарифм с основанием (2): (1=log_{2}{2}) |
|
|
(=)(frac{log_{2}{14}}{log_{2}{2}+log_{2}{7}})(=) |
Теперь пользуемся свойством логарифмов: |
|
|
(=)(frac{log_{2}{14}}{log_{2}{(2cdot7)}})(=)(frac{log_{2}{14}}{log_{2}{14}})(=) |
В числителе и знаменателе одинаковые числа – их можно сократить. |
|
|
(=1) |
Ответ готов. |
Ответ: (1)
Смотрите также:
Логарифмические уравнения
Логарифмические неравенства














 И. Элементарная математика. 2-е изд., перераб. и доп., М.: 1974г. — 592с.
И. Элементарная математика. 2-е изд., перераб. и доп., М.: 1974г. — 592с.