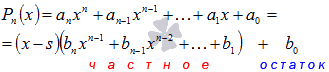
Как найти значение многочлена по схеме горнера - Исправление недочетов и поиск решений вместе с Examum.ru

Схема Горнера

11 июля 2022

Схема Горнера — это алгоритм для быстрого (счёт идёт на секунды) вычисления значения многочлена

[Pleft( x right)={{a}_{n}}{{x}^{n}}+{{a}_{n-1}}{{x}^{n-1}}+ldots +{{a}_{1}}x+{{a}_{0}}]

в точке $x=a$. Также схема Горнера позволяет быстро (быстрее, чем столбиком) делить многочлен $Pleft( x right)$ на линейные двучлены вида $x-a$, искать остатки от деления и многое другое.

Содержание

Описание Схемы Горнера
Вычисление значения многочлена
Деление многочлена с остатком
Перебор корней уравнения
Разложение на множители
Разложение по степеням
Как всё это работает

1. Описание схемы Горнера

Итак, рассмотрим многочлен

[Pleft( x right)= color{blue}{{a}_{n}}{{x}^{n}}+color{blue}{{a}_{n-1}}{{x}^{n-1}}+ldots +color{blue}{{a}_{1}}x+color{blue}{{a}_{0}}]

Для наглядности коэффициенты выделены синим цветом. Распишем схему Горнера для многочлена $Pleft( x right)$ в точке $x=color{red}{a}$. Для этого заполним таблицу

[begin{array}{c|c|c|c|c|c|c} {} & color{blue}{{a}_{n}} & color{blue}{{a}_{n-1}} & color{blue}{{a}_{n-2}} & ldots & color{blue}{{a}_{1}} & color{blue}{{a}_{0}} \ hlinecolor{red}{a} & {} & {} & {} & {} & {} & {} \ end{array}]

В первой строке мы видим коэффициенты многочлена $Pleft( x right)$ в порядке убывания степеней. Таких коэффициентов всегда на один больше, чем степень многочлена: для квадратного многочлена всего 3 коэффициента, для кубического — уже 4, и т.д.

Во второй строке таблицы мы вписываем лишь число $color{red}{a}$ в самой левой клетке. Остальные клетки заполняются последовательно по следующему алгоритму.

В первую свободную клетку мы переносим элемент из верхней строки без изменений. Назовём этот элемент ${{b}_{n-1}}$ — дальше вы поймёте, зачем нужна такая нумерация:

Вторая клетка — элемент ${{b}_{n-2}}$ — считается по формуле ${{b}_{n-2}}={{b}_{n-1}}cdot color{red}{a}+color{blue}{{a}_{n-1}}$. Другими словами, берём элемент слева, умножаем на число $a$ и добавляем элемент сверху:

Далее находим элемент ${{b}_{n-3}}$ по аналогичной формуле: ${{b}_{n-3}}={{b}_{n-2}}cdot color{red}{a}+color{blue}{{a}_{n-2}}$. Заносим результат в третью клетку:

Аналогично находим элементы ${{b}_{n-4}}$, ${{b}_{n-5}}$ и далее. Берём элемент слева, умножаем на исходное число $color{red}{a}$, добавляем элемент сверху, результат записываем в клетку:

[{{b}_{k-1}}={{b}_{k}}cdotcolor{red}{a}+color{blue}{{a}_{k}}]

В какой-то момент мы доберёмся до элемента ${{b}_{0}}$, который находится в клетке под коэффициентом $color{blue}{{a}_{1}}$:

Элемент в последней клетке считается по той же схеме: ${{b}_{0}}cdot color{red}{a}+color{blue}{{a}_{0}}$. Обозначим его буквой $r$:

Итак, мы заполнили все клетки и получили таблицу:

Схема заполнения этой таблицы как раз и называется схемой Горнера. Найденные элементы ${{b}_{n-1}}$, …, ${{b}_{0}}$ и $r$ позволяют переписать исходный многочлен $Pleft( x right)$ в виде

[Pleft( x right)=left( {{b}_{n-1}}{{x}^{n-1}}+ldots +{{b}_{1}}x+{{b}_{0}} right)left( x-color{red}{a} right)+r]

Такая запись оказывается грозным оружием для решения задач с многочленами, если знать её свойства. И сегодня мы изучим все эти свойства, но сначала немного практики.

Пример 1. Простой многочлен

Заполните таблицу по схеме Горнера для многочлена

[Pleft( x right)=2{{x}^{4}}-7{{x}^{3}}+{{x}^{2}}+2x-3]

в точке $x=3$.

Решение. Для начала аккуратно запишем коэффициенты исходного многочлена. Для наглядности они вновь помечены синим:

[Pleft( x right)= color{blue}{2}cdot {{x}^{4}}+left( color{blue}{-7} right)cdot {{x}^{3}}+color{blue}{1}cdot {{x}^{2}}+color{blue}{2} cdot x+left( color{blue}{-3} right)]

Составим таблицу. Поскольку степень многочлена $deg Pleft( x right)=4$, в таблице будет пять основных столбцов и один дополнительный столбец слева, в котором мы запишем число $x=color{red}{3}$:

[begin{array}{c|c|c|c|c|c} {} & color{blue}{2} & color{blue}{-7} & color{blue}{1} & color{blue}{2} & color{blue}{-3} \ hlinecolor{red}{3} & {} & {} & {} & {} & {} \ end{array}]

Заполняем пустые клетки во второй строке. В первую клетку переносим без изменений элемент сверху:

[begin{array}{c|c|c|c|c|c} {} & color{blue}{2} & color{blue}{-7} & color{blue}{1} & color{blue}{2} & color{blue}{-3} \ hlinecolor{red}{3} & 2 & {} & {} & {} & {} \ end{array}]

Элемент во второй клетке считается по формуле $2cdot color{red}{3}+left( color{blue}{-7} right)=-1$:

[begin{array}{c|c|c|c|c|c} {} & color{blue}{2} & color{blue}{-7} & color{blue}{1} & color{blue}{2} & color{blue}{-3} \ hlinecolor{red}{3} & 2 & -1 & {} & {} & {} \ end{array}]

Третью и четвёртую клетку заполняем аналогично: сначала $-1cdot color{red}{3}+color{blue}{1}=-2$, затем $-2cdot color{red}{3}+color{blue}{2}=-4$:

[begin{array}{c|c|r|r|r|c} {} & color{blue}{2} & color{blue}{-7} & color{blue}{1} & color{blue}{2} & color{blue}{-3} \ hlinecolor{red}{3} & 2 & -1 & -2 & -4 & {} \ end{array}]

Наконец, последняя клетка: $-4cdot color{red}{3}+left( color{blue}{-3} right)=-15$:

[begin{array}{c|c|r|r|r|r} {} & color{blue}{2} & color{blue}{-7} & color{blue}{1} & color{blue}{2} & color{blue}{-3} \ hlinecolor{red}{3} & 2 & -1 & -2 & -4 & -15 \ end{array}]

Готово! Мы заполнили таблицу по схеме Горнера.

Пример 2. Пропущенные коэффициенты

Заполните таблицу по схеме Горнера для многочлена

[Pleft( x right)={{x}^{4}}+3{{x}^{3}}-4]

в точке $x=1$.

Решение. Обратите внимание: в записи многочлена отсутствуют одночлены ${{x}^{2}}$ и $x$. Другими словами, коэффициенты в этих двух одночленах равны нулю:

[Pleft( x right)= color{blue}{1}cdot {{x}^{4}}+color{blue}{3}cdot {{x}^{3}}+color{blue}{0}cdot {{x}^{2}}+color{blue}{0} cdot x+left( color{blue}{-4} right)]

Для наглядности мы вновь отметили коэффициенты синим цветом — всего их снова пять, т.е. на один больше степени многочлена. И все они переносятся в таблицу. Пропуск нулевых коэффициентов будет грубой ошибкой:

[begin{array}{c|c|c|c|c|c} {} & color{blue}{1} & color{blue}{3} & color{blue}{0} & color{blue}{0} & color{blue}{-4} \ hlinecolor{red}{1} & {} & {} & {} & {} & {} \ end{array}]

Заполняем таблицу по схеме Горнера. Первый элемент переносим сверху:

[begin{array}{c|c|c|c|c|c} {} & color{blue}{1} & color{blue}{3} & color{blue}{0} & color{blue}{0} & color{blue}{-4} \ hlinecolor{red}{1} & 1 & {} & {} & {} & {} \ end{array}]

Второй, третий и четвёртый элемент считаем по формуле: $1cdot color{red}{1}+color{blue}{3}=4$; $4cdot color{red}{1}+color{blue}{0}=4$; $4cdot color{red}{1}+color{blue}{0}=4$:

[begin{array}{c|c|c|c|c|c} {} & color{blue}{1} & color{blue}{3} & color{blue}{0} & color{blue}{0} & color{blue}{-4} \ hlinecolor{red}{1} & 1 & 4 & 4 & 4 & {} \ end{array}]

Наконец, последний элемент таблицы: $4cdot color{red}{1}+left( color{blue}{-4} right)=0$:

[begin{array}{c|c|c|c|c|r} {} & color{blue}{1} & color{blue}{3} & color{blue}{0} & color{blue}{0} & color{blue}{-4} \ hlinecolor{red}{1} & 1 & 4 & 4 & 4 & 0 \ end{array}]

Готово! Таблица заполнена, последний элемент оказался равен нулю. И это не случайно. Скоро узнаем почему.:)

2. Вычисление значения многочлена

Чтобы понять, зачем нужна схема Горнера, давайте вкратце повторим всю цепочку рассуждений. Берём произвольный многочлен

[Pleft( x right)= color{blue}{{a}_{n}}{{x}^{n}}+color{blue}{{a}_{n-1}}{{x}^{n-1}}+ldots +color{blue}{{a}_{1}}x+color{blue}{{a}_{0}}]

и произвольную точку $x=color{red}{a}$. Составляем таблицу:

Найденные коэффициенты ${{b}_{n-1}}$, …, ${{b}_{0}}$, $r$ позволяют переписать многочлен $Pleft( x right)$ в новом виде:

[Pleft( x right)=left( {{b}_{n-1}}{{x}^{n-1}}+ldots +{{b}_{1}}x+{{b}_{0}} right)left( x-color{red}{a} right)+r]

Но чем так примечательна эта запись? В ближайших четырёх пунктах мы детально разберём все её свойства. И начнём с самого простого. Подставим в эту новую запись число $x=color{red}{a}$, т.е. вычислим $Pleft( color{red}{a} right)$:

[Pleft( color{red}{a} right)=left( {{b}_{n-1}}{color{red}{a}^{n-1}}+ldots +{{b}_{1}}color{red}{a}+{{b}_{0}} right)left( color{red}{a}-color{red}{a} right)+r=r]

Итак, последнее число $r$ в таблице — это значение многочлена $Pleft( x right)$ в точке $x=color{red}{a}$:

[Pleft( color{red}{a} right)=r]

А это значит, что благодаря схеме Горнера можно считать значения многочленов быстро (нет операции возведения в степень) и надёжно (в сложении мы ошибаемся реже, чем в умножении).

Так, из Примера 1 следует, что значение многочлена

[Pleft( x right)=2{{x}^{4}}-7{{x}^{3}}+{{x}^{2}}+2x-3]

в точке $x=3$ равно

[Pleft( 3 right)=r=-15]

Сравните это с прямой подстановкой $x=3$ в многочлен:

[begin{align} Pleft( 3 right) &=2cdot {{3}^{4}}-7cdot {{3}^{3}}+{{3}^{2}}+2cdot 3-3= \ &=2cdot 81-7cdot 27+left( 9+6-3 right)= \ &=162-189+12= \ &=-15 end{align}]

Результат один и тот же, но объём вычислений вырос на порядок.

Пример 3. «Некрасивые» значения

С помощью схемы Горнера найдите значение многочлена

[Pleft( x right)=8{{x}^{4}}-12{{x}^{3}}-24{{x}^{2}}+11x+7]

в точке $x=2,5$.

Решение. Выделим коэффициенты многочлена

[Pleft( x right)= color{blue}{8}cdot {{x}^{4}}+left( color{blue}{-12} right)cdot {{x}^{3}}+left( color{blue}{-24} right)cdot {{x}^{2}}+color{blue}{11} cdot x+color{blue}{7}]

и заполним таблицу для $x=color{red}{2,5}$:

[begin{array}{c|c|c|c|c|c} {} & color{blue}{8} & color{blue}{-12} & color{blue}{-24} & color{blue}{11} & color{blue}{7} \ hlinecolor{red}{2,5} & 8 & 8 & -4 & 1 & 9,5 \ end{array}]

Итого значение многочлена $Pleft( color{red}{2,5} right)=9,5$. Точно такое же значение можно получить прямой подстановкой, но вычисления будут настолько громоздкими, что мы не будем приводить их.

3. Деление многочлена с остатком

Напомню, что разделить многочлен $color{blue}{Pleft( x right)}$ на многочлен $color{red}{Aleft( x right)}$ с остатком — значит найти многочлены $Qleft( x right)$ и $Rleft( x right)$ такие, что

[color{blue}{Pleft( x right)}=Qleft( x right)cdot color{red}{Aleft( x right)}+Rleft( x right)]

причём степень многочлена $Rleft( x right)$ строго меньше степени делителя $color{red}{Aleft( x right)}$:

[deg Rleft( x right) lt deg color{red}{Aleft( x right)}]

Многочлен $Qleft( x right)$ называют неполным частным, $Rleft( x right)$ — остатком от деления. Можно показать, что $Qleft( x right)$ и $Rleft( x right)$ определены однозначно для исходных многочленов $color{blue}{Pleft( x right)}$ и $color{red}{Aleft( x right)}$.

3.1. Случай линейного делителя

Пусть $Aleft( x right)=x- color{red}{a}$ — линейный двучлен. Очевидно, его степень $deg Aleft( x right)=1$.

Рассмотрим произвольный многочлен

[Pleft( x right)= color{blue}{{a}_{n}}{{x}^{n}}+color{blue}{{a}_{n-1}}{{x}^{n-1}}+ldots +color{blue}{{a}_{1}}x+color{blue}{{a}_{0}}]

и составим таблицу для $x=color{red}{a}$ по схеме Горнера:

Получим новую запись многочлена $Pleft( x right)$:

[Pleft( x right)=left( {{b}_{n-1}}{{x}^{n-1}}+ldots +{{b}_{1}}x+{{b}_{0}} right)left( x-color{red}{a} right)+r]

где $r$ — обычное число, т.е. $deg r=0 lt deg Aleft( x right)$. Но тогда многочлен

[Qleft( x right)={{b}_{n-1}}{{x}^{n-1}}+{{b}_{n-2}}{{x}^{n-1}}+ldots +{{b}_{1}}x+{{b}_{0}}]

является неполным частным при делении $Pleft( x right)$ на двучлен $x-color{red}{a}$, а число $r$ — остаток этого деления:

[Pleft( x right)=Qleft( x right)cdot left( x-color{red}{a} right)+r]

Итак, схема Горнера позволяет быстро находить неполное частное и остаток от деления произвольного многочлена $Pleft( x right)$ на двучлен $x-color{red}{a}$.

Пример 4. Деление с остатком

Найдите частное и остаток при делении многочлена

[{{x}^{4}}-2{{x}^{3}}+4{{x}^{2}}-6x+10]

На многочлен $x-1$.

Решение. Выделим синим цветом коэффициенты исходного многочлена:

[color{blue}{1}cdot {{x}^{4}}+left( color{blue}{-2} right)cdot {{x}^{3}}+color{blue}{4}cdot {{x}^{2}}+left( color{blue}{-6} right)cdot x+color{blue}{10}]

Заполним таблицу по схеме Горнера для $x=color{red}{1}$:

[begin{array}{c|c|r|c|r|c} {} & color{blue}{1} & color{blue}{-2} & color{blue}{4} & color{blue}{-6} & color{blue}{10} \ hlinecolor{red}{1} & 1 & -1 & 3 & -3 & 7 \ end{array}]

Первые четыре числа — это коэффициенты многочлена-частного. Отметим их зелёным цветом:

[begin{array}{c|c|r|c|r|c} {} & color{blue}{1} & color{blue}{-2} & color{blue}{4} & color{blue}{-6} & color{blue}{10} \ hlinecolor{red}{1} & color{#green}{1} & color{#green}{-1} & color{#green}{3} & color{#green}{-3} & 7 \ end{array}]

Остаток от деления равен $r=7$. Составим многочлен-частное:

[Qleft( x right)= color{#green}{1}cdot {{x}^{3}}+left( color{#green}{-1} right)cdot {{x}^{2}}+color{#green}{3}cdot x+left( color{#green}{-3} right)]

Очевидно, при делении на линейный двучлен степень частного должна быть на единицу меньше степени исходного многочлена. Так и получилось:

[deg Qleft( x right)=4-1=3]

Пример 5. Проверка делимости

Убедитесь, что многочлен

[{{x}^{5}}-6{{x}^{4}}+16{{x}^{2}}-33{{x}^{2}}+44x-28]

делится на двучлен ${{left( x-2 right)}^{2}}$.

Решение. Многочлен делится без остатка на ${{left( x-2 right)}^{2}}$, если сначала он делится на двучлен $x-2$, а затем частное вновь делится на $x-2$. Следовательно, решение состоит из двух шагов.

Первый шаг: выделим коэффициенты исходного многочлена

[color{blue}{1}cdot {{x}^{5}}+left( color{blue}{-6} right)cdot {{x}^{4}}+color{blue}{16}cdot {{x}^{2}}+left( color{blue}{-33} right)cdot {{x}^{2}}+color{blue}{52} cdot x+left( color{blue}{-36} right)]

[begin{align}color{blue}{1}cdot {{x}^{5}} &+left( color{blue}{-6} right)cdot {{x}^{4}}+color{blue}{16}cdot {{x}^{2}}+ \ &+left( color{blue}{-33} right)cdot {{x}^{2}}+color{blue}{52} cdot x+left( color{blue}{-36} right) \ end{align}]

Составим таблицу для $x=color{red}{2}$. В ней будет 6 основных столбцов:

[begin{array}{c|c|c|c|c|c|c} {} & color{blue}{1} & color{blue}{-6} & color{blue}{16} & color{blue}{-33} & color{blue}{52} & color{blue}{-36} \ hlinecolor{red}{2} & {} & {} & {} & {} & {} & {} \ end{array}]

Заполним все пустые клетки по схеме Горнера:

[begin{array}{c|c|c|c|r|c|c} {} & color{blue}{1} & color{blue}{-6} & color{blue}{16} & color{blue}{-33} & color{blue}{52} & color{blue}{-36} \ hlinecolor{red}{2} & color{green}{1} & color{green}{-4} & color{green}{8} & color{green}{-17} & color{green}{18} & 0 \ end{array}]

Получили остаток $r=0$, поэтому исходный многочлен действительно делится на $x-color{red}{2}$, а частное равно

[Qleft( x right)= color{green}{1}cdot {{x}^{4}}+left( color{green}{-4} right)cdot {{x}^{3}}+color{green}{8}cdot {{x}^{2}}+left( color{green}{-17} right) cdot x+color{green}{18}]

Следовательно, исходный многочлен можно представить так:

[begin{align} & {{x}^{5}}-6{{x}^{4}}+16{{x}^{2}}-33{{x}^{2}}+44x-28= \ = & left( {{x}^{4}}-4{{x}^{3}}+8{{x}^{2}}-17x+18 right)cdot left( x-color{red}{2} right) \ end{align}]

Второй шаг: выделяем коэффициенты и заполняем ту же самую таблицу, но уже для многочлена $Qleft( x right)$.

[Qleft( x right)= color{blue}{1}cdot {{x}^{4}}+left( color{blue}{-4} right)cdot {{x}^{3}}+color{blue}{8}cdot {{x}^{2}}+left( color{blue}{-17} right) cdot x+color{blue}{18}]

Но все коэффициенты в нужном количестве уже присутствуют в таблице, которую мы получили на предыдущем шаге. А потому достаточно приписать к этой таблице ещё одну строку и вновь заполнить её для $x=color{red}{2}$:

[begin{array}{c|c|c|c|r|c|c} {} & 1 & -6 & 16 & -33 & 52 & -36 \ hlinecolor{red}{2} & color{blue}{1} & color{blue}{-4} & color{blue}{8} & color{blue}{-17} & color{blue}{18} & 0 \ hlinecolor{red}{2} & color{green}{1} & color{green}{-2} & color{green}{4} & color{green}{-9} & 0 & {} \ end{array}]

Остаток от деления равен нулю, поэтому многочлен $Qleft( x right)$ делится на $x-color{red}{2}$, и его можно переписать так:

[Qleft( x right)=left( color{green}{1}cdot {{x}^{3}}+left( color{green}{-2} right){{x}^{2}}+color{green}{4} cdot x+left( color{green}{-9} right) right)cdot left( x-color{red}{2} right)]

Возвращаясь к исходному многочлену, получим

[begin{align} & {{x}^{5}}-6{{x}^{4}}+16{{x}^{2}}-33{{x}^{2}}+44x-28= \ = & left( {{x}^{3}}-2{{x}^{2}}+4x-9 right)cdot {{left( x-color{red}{2} right)}^{2}} \ end{align}]

Такая запись, как и приведённая выше таблица, доказывает, что исходный многочлен делится на ${{left( x-color{red}{2} right)}^{2}}$.

Обратите внимание: на каждом следующем шаге количество коэффициентов уменьшается на единицу:

В первой строке мы выписали все 6 коэффициентов исходного многочлена.
Во второй строке осталось лишь 5 коэффициентов, а последнее число — остаток.
Третья срока — 4 коэффициента и вновь остаток.

Всё это пригодится нам в следующем пункте.

4. Перебор корней уравнения

До сих пор мы применяли схему Горнера для некоторой точки $x=color{red}{a}$, которая была прямо указана в условии задачи. Но что если найти такую точку — как раз и есть условие задачи?

Рассмотрим уравнение

[color{blue}{{a}_{n}}{{x}^{n}}+color{blue}{{a}_{n-1}}{{x}^{n-1}}+ldots +color{blue}{{a}_{1}}x+color{blue}{{a}_{0}}=0]

Число $x=color{red}{a}$ будет корнем этого уравнения, если $Pleft( color{red}{a} right)=0$. Это значит, что последний элемент в схеме Горнера должен быть равен нулю:

Следовательно, мы можем быстро проверить, является ли число $x=color{red}{a}$ корнем уравнения. Достаточно просто подставить его в таблицу и найти последний элемент.

Кроме того, мы знаем, что последний элемент — это остаток $r$. При $r=color{green}{0}$ исходное уравнение примет вид

[left( {{b}_{n-1}}{{x}^{n-1}}+ldots +{{b}_{1}}x+{{b}_{0}} right)left( x-color{red}{a} right)=0]

Произведение равно нулю тогда и только тогда, когда хотя бы один из множителей равен нулю. Откуда либо $x-color{red}{a}=0$ (этот случай мы уже разобрали), либо

[color{blue}{{b}_{n-1}}{{x}^{n-1}}+ldots +color{blue}{{b}_{1}}x+color{blue}{{b}_{0}}=0]

Получили новое уравнение — меньшей степени, чем исходное. Коэффициенты этого уравнения уже занесены в таблицу, и к нему вновь применима схема Горнера для перебора кандидатов в корни.

Более того: этот перебор можно ускорить. Но об этом чуть позже. Сначала рассмотрим пару простых примеров.

Пример 6. Уравнение третьей степени

Решите уравнение:

[{{x}^{3}}+9{{x}^{2}}+23x+15=0]

Решение. Заметим, что все коэффициенты многочлена положительны, поэтому уравнение не имеет положительных корней. Иначе, если $x gt 0$, левая часть равенства представляет собой сумму положительных чисел, которая никогда не равна нулю.

Рассмотрим отрицательные числа. Начнём с $x=color{red}{-1}$:

[begin{array}{c|c|c|c|c} {} & color{blue}{1} & color{blue}{9} & color{blue}{23} & color{blue}{15} \ hlinecolor{red}{-1} & 1 & 8 & 15 & color{green}{0} \ end{array}]

Получили $r=color{green}{0}$. Следовательно, $x=color{red}{-1}$ — корень, и всё уравнение можно переписать так:

[left( {{x}^{2}}+8x+15 right)left( x+1 right)=0]

Далее уравнение разделяется на линейное $x+1=0$, которое мы уже решили, и квадратное

[{{x}^{2}}+x+15=0]

Такое уравнение можно решить через дискриминант или по теореме Виета. Получим корни $x=-3$ и $x=-5$.

Окончательный ответ: $x=-1$, $x=-3$, $x=-5$.

Впрочем, с тем же успехом мы могли продолжить решение по схеме Горнера:

[begin{array}{r|c|c|c|c} {} & color{blue}{1} & color{blue}{9} & color{blue}{23} & color{blue}{15} \ hlinecolor{red}{-1} & 1 & 8 & 15 & color{green}{0} \ hlinecolor{red}{-3} & 1 & 5 & color{green}{0} & {} \ hlinecolor{red}{-5} & 1 & color{green}{0} & {} & {} \ end{array}]

При этом уравнение примет вид

[left( x+3 right)left( x+5 right)left( x+1 right)=0]

По сути, мы получили разложение на множители. И чуть ниже об этом будет отдельный пункт.

Пример 7. Ещё одно уравнение

Решите уравнение:

[2{{x}^{3}}-{{x}^{2}}-5x-2=0]

Решение. В этот раз мы видим, что корни вполне могут быть положительными. Начнём с $x=color{red}{1}$:

[begin{array}{c|c|r|r|r} {} & color{blue}{2} & color{blue}{-1} & color{blue}{-5} & color{blue}{-2} \ hlinecolor{red}{1} & 2 & 1 & -4 & color{red}{-6} \ end{array}]

Получили $r=color{red}{-6}ne 0$. Следовательно, $x=color{red}{1}$ не является корнем. Проверим $x=color{red}{2}$:

[begin{array}{c|c|r|r|r} {} & color{blue}{2} & color{blue}{-1} & color{blue}{-5} & color{blue}{-2} \ hlinecolor{red}{1} & 2 & 1 & -4 & color{red}{-6} \ hlinecolor{red}{2} & 2 & 3 & 1 & color{green}{0} \ end{array}]

Обратите внимание: при заполнении третьей строки таблицы мы игнорируем вторую строку, где нас постигла неудача. И если бы мы могли стирать строки, то схема Горнера выглядела бы так:

[begin{array}{c|c|r|r|r} {} & color{blue}{2} & color{blue}{-1} & color{blue}{-5} & color{blue}{-2} \ hlinecolor{red}{2} & 2 & 3 & 1 & color{green}{0} \ end{array}]

В любом случае мы получили $r=color{green}{0}$, поэтому $x=color{red}{2}$ — корень, и уравнение примет вид

[left( 2{{x}^{2}}+3x+1 right)left( x-2 right)=0]

Далее можно решить квадратное уравнение через дискриминант, а можно продолжить заполнять таблицу. Например, для $x=color{red}{-1}$:

[begin{array}{r|c|r|r|r} {} & 2 & -1 & -5 & -2 \ hline1 & 2 & 1 & -4 & -6 \ hline2 & color{blue}{2} & color{blue}{3} & color{blue}{1} & color{green}{0} \ hline-1 & 2 & 1 & color{green}{0} & {} \ end{array}]

Вновь получили ноль в последней клетке, поэтому $x=color{red}{-1}$ — тоже корень, а уравнение примет вид

[left( 2x+1 right)left( x+1 right)left( x-2 right)=0]

Теперь ответ очевиден: $x=2$, $x=-1$, $x=-0,5$.

Помните: «неудачные» строки — это нормально. Их бывает много. Главное при переборе корней — игнорировать такие строки и заполнять таблицу так, будто этих строк не существует.

4.1. Теорема Безу

Теорема Безу и следствия из неё позволяет значительно сузить круг потенциальных корней.

Теорема Безу. Остаток от деления многочлена

[Pleft( x right)={{a}_{n}}{{x}^{n}}+{{a}_{n-1}}{{x}^{n-1}}+ldots +{{a}_{1}}x+{{a}_{0}}]

на двучлен $x-a$ равен $Pleft( a right)$.

Несложно заметить, что схема Горнера и следующая из неё запись многочлена

[Pleft( x right)=left( {{b}_{n-1}}{{x}^{n-1}}+ldots +{{b}_{1}}x+{{b}_{0}} right)left( x-color{red}{a} right)+r]

является прямым доказательством этой теоремы. Действительно, если подставить в эту запись значение $x=color{red}{a}$, мы получим

[Pleft( color{red}{a} right)=left( {{b}_{n-1}}color{red}{{a}^{n-1}}+ldots +{{b}_{1}}color{red}{a}+{{b}_{0}} right)left( color{red}{a}-color{red}{a} right)+r=r]

У теоремы Безу огромное количество полезных приложений — см. урок «Теорема Безу». Сейчас же нас интересует не сама теорема, а следствие из неё, связанное с корнями многочлена.

Пусть $x=color{red}{a}$ — корень многочлена $Pleft( x right)$. Распишем многочлен по схеме Горнера для $x=color{red}{a}$:

[Pleft( x right)=left( {{b}_{n-1}}{{x}^{n-1}}+ldots +{{b}_{1}}x+{{b}_{0}} right)left( x-color{red}{a} right)]

Поскольку $x=color{red}{a}$ — корень, остаток $r=0$, и мы получили разложение многочлена $Pleft( x right)$ на множители. А теперь выполним обратную операцию — раскроем скобки и приведём подобные слагаемые:

[Pleft( x right)={{b}_{n-1}}{{x}^{n}}+ldots -color{red}{a}cdot {{b}_{0}}]

Получается, что корень $x=color{red}{a}$ является делителем свободного члена $Pleft( x right)$. Более того, можно показать, что в многочлене

[Pleft( x right)= color{blue}{{a}_{n}}{{x}^{n}}+color{blue}{{a}_{n-1}}{{x}^{n-1}}+ldots +color{blue}{{a}_{1}}x+color{blue}{{a}_{0}}]

с целыми коэффициентами $color{blue}{{a}_{n}}$, …, $color{blue}{{a}_{0}}$ все рациональные корни имеют вид

[x=frac{m}{n}]

где $min mathbb{Z}$ — делитель свободного члена $color{blue}{{a}_{0}}$, а $nin mathbb{N}$ — делитель старшего коэффициента $color{blue}{{a}_{n}}$.

И хоть при первом взгляде на все эти рассуждения они могут показаться сложными, на практике теорема Безу значительно упрощает поиск корней. Взгляните на примеры.:)

Пример 8. Сплошной перебор

Решите уравнение:

[{{x}^{5}}+8{{x}^{4}}+24{{x}^{3}}+35{{x}^{2}}+28x+12=0]

Решение. Слева от знака равенства стоит многочлен пятой степени. Старший коэффициент многочлена ${{a}_{5}}=color{blue}{1}$, свободный член ${{a}_{0}}=color{blue}{12}$. Если такой многочлен имеет рациональные корни вида

[x=frac{m}{n}]

то $n=1$ — это единственный натуральный делитель для ${{a}_{5}}=color{blue}{1}$. А вот число $m$ будем искать среди делителей числа ${{a}_{0}}=color{blue}{12}$:

[m=pm 1, pm 2, pm 3, pm 4, pm 6, pm 12.]

Итого 12 вариантов. Далее заметим, что все коэффициенты исходного многочлена положительны, поэтому достаточно проверить лишь отрицательные корни. Начнём с $x=color{red}{-1}$, затем $x=color{red}{-2}$, $x=color{red}{-3}$ и т.д.:

[begin{array}{r|c|c|c|c|c|c} {} & color{blue}{1} & color{blue}{8} & color{blue}{24} & color{blue}{35} & color{blue}{28} & color{blue}{12} \ hline color{red}{-1} & 1 & 7 & 17 & 18 & 10 & color{red}{2} \ hline color{red}{-2} & 1 & 6 & 12 & 11 & 6 & color{green}{0} \ hline color{red}{-3} & 1 & 3 & 3 & 2 & color{green}{0} & {} \ end{array}]

Как видим, вариант $x=color{red}{-1}$ не подошёл, поэму строку с проверкой этого числа можно вычеркнуть. Зато $x=color{red}{-2}$ и $x=color{red}{-3}$ — корни. Более того: можно повторно проверить $x=color{red}{-2}$. Получим интересный результат:

[begin{array}{r|c|c|c|c|c|c} {} & color{blue}{1} & color{blue}{8} & color{blue}{24} & color{blue}{35} & color{blue}{28} & color{blue}{12} \ hline color{red}{-2} & 1 & 6 & 12 & 11 & 6 & color{green}{0} \ hline color{red}{-3} & 1 & 3 & 3 & 2 & color{green}{0} & {} \ hline color{red}{-2} & 1 & 1 & 1 & color{green}{0} & {} & {} \ end{array}]

Другими словами, исходное уравнение можно переписать так:

[left( {{x}^{2}}+x+1 right){{left( x+2 right)}^{2}}left( x+1 right)=0]

Число $x=color{red}{-2}$ оказалось корнем второй кратности, а квадратное уравнение

[{{x}^{2}}+x+1=0]

не имеет корней. Поэтому окончательный ответ: $x=-2$, $x=-3$.

Пример 9. Дробные корни

Решите уравнение:

[3{{x}^{4}}+5{{x}^{3}}-{{x}^{2}}-5x-2=0]

Решение. По теореме Безу получаем, что рациональные корни вида

[x=frac{m}{n}]

должны быть составлены из чисел $min left{ pm 1, pm 2 right}$ и $nin left{ 1,3 right}$. Всего существует восемь таких комбинаций:

[xin left{ pm 1; pm 2; pm frac{1}{3}; pm frac{2}{3} right}]

Рассмотрим самые простые корни: $x=color{red}{1}$ и $x=color{red}{-1}$. Причём на каждом шаге будем проверять возможную кратность:

[begin{array}{r|c|c|c|c|c} {} & color{blue}{3} & color{blue}{5} & color{blue}{-1} & color{blue}{-5} & color{blue}{-2} \ hline color{red}{1} & 3 & 8 & 7 & 2 & color{green}{0} \ hline color{red}{1} & 3 & 11 & 18 & color{red}{20} & {} \ hline color{red}{-1} & 3 & 5 & 2 & color{green}{0} & {} \ hline color{red}{-1} & 3 & 2 & color{green}{0} & {} & {} \ end{array}]

Получили корень $x=color{red}{1}$ (первой кратности) и $x=color{red}{-1}$ (как минимум второй кратности), а само уравнение можно переписать так:

[left( 3x+2 right){{left( x+1 right)}^{2}}left( x-1 right)=0]

Теперь очевидно, что всего уравнение имеет три корня: $x=1$, $x=-1$ и $x=-{2}/{3};$.

4.2. Учёт кратности корней

Как видим, схема Горнера позволяет не просто перебирать корни, но и определять их кратность. Это особенно важно при решении неравенств и задач с параметрами.

Чтобы определить кратность корня $x=color{red}{a}$, достаточно подставлять его в таблицу до тех пор, пока не появится остаток, отличный от нуля. Либо пока исходный многочлен не будет полностью разложен на множители.

Пример 10. Корень четвёртой кратности

Решите уравнение и определите кратность корней:

[{{x}^{5}}-10{{x}^{3}}-20{{x}^{2}}-15x-4=0]

Решение. Слева стоит многочлен с целыми коэффициентами. Выпишем потенциальные корни по теореме Безу:

[xin left{ pm 1; pm 2; pm 4 right}]

Начнём с самых простых чисел: $x=color{red}{1}$ и $x=color{red}{-1}$. Проверим их по схеме Горнера:

[begin{array}{r|c|r|r|r|r|r} {} & color{blue}{1} & color{blue}{0} & color{blue}{-10} & color{blue}{-20} & color{blue}{-15} & color{blue}{-4} \ hlinecolor{red}{1} & 1 & 1 & -9 & -29 & -44 & color{red}{-48} \ hlinecolor{red}{-1} & 1 & -1 & -9 & -11 & -4 & color{green}{0} \ hlinecolor{red}{-1} & 1 & -2 & -7 & -4 & color{green}{0} & {} \ hlinecolor{red}{-1} & 1 & -3 & -4 & color{green}{0} & {} & {} \ hlinecolor{red}{-1} & 1 & -4 & color{green}{0} & {} & {} & {} \ end{array}]

Перепишем исходное уравнение:

[{{left( x+1 right)}^{4}}left( x-1 right)left( x-4 right)=0]

Итого уравнение имеет три различных корня: $x=-1$ (четвёртой кратности), $x=1$ (первой кратности) и $x=4$ (тоже первой кратности).

Ключевая мысль: с помощью схемы Горнера можно решать даже уравнения высших степеней. Поэтому если при решении текстовой задачи (и особенно задачи с параметром) возникло уравнение 3-й степени и выше, это вовсе не означает, что вы где-то ошиблись. Вполне возможно, что составители задачи хотят проверить, умеете ли вы решать уравнения высших степеней.

5. Разложение на множители

Схему Горнера часто применяют для разложения многочлена на множители. Мы знаем, что для всякого $x=color{red}{a}$ такого, что последний элемент таблицы $r=color{green}{0}$, можно переписать исходный многочлен $Pleft( x right)$ в виде

[Pleft( x right)=left( x-color{red}{a} right)cdot Qleft( x right)]

Коэффициенты многочлена $Qleft( x right)$ будут также даны в таблице, и к нему тоже применима схема Горнера.

Пример 11. Простой многочлен

Разложите на множители многочлен

[{{x}^{4}}+2{{x}^{3}}+4{{x}^{2}}+3x-10]

Решение. Рассмотрим многочлен

[Pleft( x right)= color{blue}{1}cdot {{x}^{4}}+color{blue}{2}cdot {{x}^{3}}+color{blue}{4}cdot {{x}^{2}}+color{blue}{3}cdot x+left( color{blue}{-10} right)]

Будем выделять из него двучлены вида $left( x-color{red}{a} right)$, где $x=color{red}{a}$ — корни многочлена $Pleft( x right)$. Рассмотрим в качестве таких корней делители свободного члена ${{a}_{0}}=color{blue}{-10}$. Начнём с $x=color{red}{1}$ и $x=color{red}{-1}$:

[begin{array}{r|c|c|c|c|c} {} & color{blue}{1} & color{blue}{2} & color{blue}{4} & color{blue}{3} & color{blue}{-10} \ hlinecolor{red}{1} & 1 & 3 & 7 & 10 & color{green}{0} \ hlinecolor{red}{-1} & 1 & 2 & 5 & color{red}{5} & {} \ hlinecolor{red}{-2} & 1 & 1 & 5 & color{green}{0} & {} \ end{array}]

Итого одна неудачная попытка и две удачных. Получили разложение многочлена

[Pleft( x right)=left( x-1 right)left( x+2 right)left( {{x}^{2}}+x+5 right)]

Квадратный трёхчлен в третьей скобке всегда положителен:

[{{x}^{2}}+x+5 gt 0]

Его нельзя разложить на множители, поэтому указанное разложение $Pleft( x right)$ — окончательное.

Пример 12. Сложный многочлен

Разложите на множители многочлен

[{{x}^{5}}-6{{x}^{4}}+2{{x}^{3}}+36{{x}^{2}}-27x-54]

Решение. Рассмотрим многочлен

[Pleft( x right)= color{blue}{1}cdot {{x}^{5}}+left( color{blue}{-6} right)cdot {{x}^{4}}+color{blue}{2}cdot {{x}^{3}}+color{blue}{36}cdot {{x}^{2}}+left( color{blue}{-27} right)cdot x+left( color{blue}{-54} right)]

[begin{align}Pleft( x right)= color{blue}{1}cdot {{x}^{5}} &+left( color{blue}{-6} right)cdot {{x}^{4}}+color{blue}{2}cdot {{x}^{3}}+ \ &+color{blue}{36}cdot {{x}^{2}}+left( color{blue}{-27} right) cdot x+left( color{blue}{-54} right) \ end{align}]

Проверим делители свободного члена ${{a}_{0}}=color{blue}{-54}$. Таких делителей очень много, поэтому начнём с самых простых: $x=color{red}{1}$ и $x=color{red}{-1}$:

[begin{array}{r|c|c|c|c|c|c} {} & color{blue}{1} & color{blue}{-6} & color{blue}{2} & color{blue}{36} & color{blue}{-27} & color{blue}{-54} \ hlinecolor{red}{1} & 1 & -5 & -3 & 33 & 6 & color{red}{-48} \ hlinecolor{red}{-1} & 1 & -7 & 9 & 27 & -54 & color{green}{0} \ hlinecolor{red}{-1} & 1 & -8 & 17 & 10 & color{red}{-64} & {} \ hlinecolor{red}{2} & 1 & -5 & -1 & 25 & color{red}{-4} & {} \ hlinecolor{red}{-2} & 1 & -9 & 27 & -27 & color{green}{0} & {} \ hlinecolor{red}{3} & 1 & -6 & 9 & color{green}{0} & {} & {} \ hlinecolor{red}{3} & 1 & -3 & color{green}{0} & {} & {} & {} \ hlinecolor{red}{3} & 1 & color{green}{0} & {} & {} & {} & {} \ end{array}]

Получили три неудачных попытки и пять удачных. В целом многочлен привет вид

[Pleft( x right)=left( x+1 right)left( x+2 right){{left( x-3 right)}^{3}}]

Это и есть искомое разложение на множители.

Обратите внимание: после проверки корня $x=color{red}{-2}$ в таблице возникла формула сокращённого умножения — куб разности:

[{{x}^{3}}-9{{x}^{2}}+27x-27={{left( x-3 right)}^{3}}]

С этим замечанием дальше можно было вообще не заполнять таблицу, поскольку многочлен сразу примет вид

[Pleft( x right)=left( x+1 right)left( x+2 right){{left( x-3 right)}^{3}}]

6. Разложение по степеням

Наконец, ещё одно применение схемы Горнера — это разложение многочлена по степеням двучлена $left( x-color{red}{a} right)$. Для этого достаточно составлять таблицу с указанным $x=color{red}{a}$ до тех пор, пока не закончатся столбцы с коэффициентами.

Полученные остатки будут коэффициентами искомого разложения. Взгляните на примеры.

Пример 13. Разложение многочлена

Разложите по степеням $left( x-1 right)$ многочлен

[{{x}^{4}}-6{{x}^{3}}+16{{x}^{2}}-17x-5]

Решение. Выделим коэффициенты многочлена:

[Pleft( x right)= color{blue}{1}cdot {{x}^{4}}+left( color{blue}{-6} right)cdot {{x}^{3}}+color{blue}{16}cdot {{x}^{2}}+left( color{blue}{-17} right)cdot x+left( color{blue}{-5} right)]

[begin{align}Pleft( x right)= color{blue}{1}cdot {{x}^{4}} &+left( color{blue}{-6} right)cdot {{x}^{3}}+color{blue}{16}cdot {{x}^{2}}+ \ &+left( color{blue}{-17} right) cdot x+left( color{blue}{-5} right) \ end{align}]

Занесём эти коэффициенты в таблицу и будем заполнять её по схеме Горнера для $x=color{red}{1}$ до тех пор, пока не вычеркнем все столбцы:

[begin{array}{c|c|c|c|c|c} {} & color{blue}{1} & color{blue}{-6} & color{blue}{16} & color{blue}{-17} & color{blue}{-5} \ hlinecolor{red}{1} & 1 & -5 & 11 & -6 & color{green}{-11} \ hlinecolor{red}{1} & 1 & -4 & 7 & color{green}{1} & {} \ hlinecolor{red}{1} & 1 & -3 & color{green}{4} & {} & {} \ hlinecolor{red}{1} & 1 & color{green}{-2} & {} & {} & {} \ hlinecolor{red}{1} & color{green}{1} & {} & {} & {} & {} \ end{array}]

Числа, выделенные зелёным — это остатки от деления в каждой новой строке. Они и будут коэффициентами разложения в порядке возрастания степеней. Внизу таблицы находится старший коэффициент, а в первой строке — свободный член:

[Pleft( x right)= color{green}{1}cdot {{left( x-1 right)}^{4}}+left( color{green}{-2} right)cdot {{left( x-1 right)}^{3}}+color{green}{4}cdot {{left( x-1 right)}^{2}}+color{green}{1}cdot left( x-1 right)+left( color{green}{-11} right)]

[begin{align}Pleft( x right) &=color{green}{1}cdot {{left( x-1 right)}^{4}}+left( color{green}{-2} right)cdot {{left( x-1 right)}^{3}}+ \ &+color{green}{4}cdot {{left( x-1 right)}^{2}}+color{green}{1}cdot left( x-1 right)+left( color{green}{-11} right) \ end{align}]

Представим эту запись более компактно:

[Pleft( x right)={{left( x-1 right)}^{4}}-2{{left( x-1 right)}^{3}}+4{{left( x-1 right)}^{2}}+left( x-1 right)-11]

[begin{align}Pleft( x right) &={{left( x-1 right)}^{4}}-2{{left( x-1 right)}^{3}}+ \ &+4{{left( x-1 right)}^{2}}+left( x-1 right)-11 \ end{align}]

Это и есть искомое разложение.

Пример 14. Финал

Разложите по степеням $left( x-2 right)$ многочлен

[{{x}^{4}}-8{{x}^{3}}+24{{x}^{2}}-50x+48]

Решение. В раз не будем переписывать многочлен с выделением коэффициентов, а сразу составим таблицу:

[begin{array}{c|c|c|c|c|c} {} & color{blue}{1} & color{blue}{-8} & color{blue}{24} & color{blue}{-50} & color{blue}{48} \ hlinecolor{red}{2} & 1 & -6 & 12 & -26 & color{green}{-4} \ hlinecolor{red}{2} & 1 & -4 & 4 & color{green}{-18} & {} \ hlinecolor{red}{2} & 1 & -2 & color{green}{0} & {} & {} \ hlinecolor{red}{2} & 1 & color{green}{0} & {} & {} & {} \ hlinecolor{red}{2} & color{green}{1} & {} & {} & {} & {} \ end{array}]

Запишем найденное разложение в порядке убывания степеней:

[color{green}{1}cdot {{left( x-2 right)}^{4}}+color{green}{0}cdot {{left( x-2 right)}^{3}}+color{green}{0}cdot {{left( x-2 right)}^{2}}+left( color{green}{-18} right)cdot left( x-2 right)+left( color{green}{-4} right)]

[begin{align}color{green}{1}cdot {{left( x-2 right)}^{4}}&+color{green}{0}cdot {{left( x-2 right)}^{3}}+color{green}{0}cdot {{left( x-2 right)}^{2}}+ \ &+left( color{green}{-18} right)cdot left( x-2 right)+left( color{green}{-4} right) \ end{align}]

То же самое разложение, но более компактно:

[{{left( x-2 right)}^{4}}-18left( x-2 right)-4]

Это окончательный ответ.

7. Как работает Схема Горнера

Очень просто. Вернёмся к исходному многочлену:

[Pleft( x right)= color{blue}{{a}_{n}}{{x}^{n}}+color{blue}{{a}_{n-1}}{{x}^{n-1}}+ldots +color{blue}{{a}_{1}}x+color{blue}{{a}_{0}}]

Вынесем за скобки множитель $x$ из всех слагаемых, кроме последнего:

[Pleft( x right)=left( color{blue}{{a}_{n}}{{x}^{n-1}}+color{blue}{{a}_{n-1}}{{x}^{n-2}}+ldots +color{blue}{{a}_{1}} right)cdot x+color{blue}{{a}_{0}}]

В скобках стоит новый многочлен. Вновь вынесем за скобки $x$. Сделаем так много раз и в какой-то момент получим запись вида

[Pleft( x right)=left( ldots left( left( color{blue}{{a}_{n}} right)cdot x+color{blue}{{a}_{n-1}} right)cdot x+ldots +color{blue}{{a}_{1}} right)cdot x+color{blue}{{a}_{0}}]

Мы видим множество скобок. Обозначим элемент в самой внутренней скобке через ${{b}_{n-1}}$:

[{{b}_{n-1}}=color{blue}{{a}_{n}}]

Элемент в предыдущей скобке обозначим ${{b}_{n-2}}$:

[{{b}_{n-2}}={{b}_{n-1}} cdot x+color{blue}{{a}_{k}}]

И так далее по уже известной формуле

[{{b}_{k-1}}={{b}_{k}} cdot x+color{blue}{{a}_{k}}]

В какой-то момент мы находим ${{b}_{0}}$ и $r$:

[begin{align} {{b}_{0}} &={{b}_{1}}cdot x+color{blue}{{a}_{1}} \ r &={{b}_{0}}cdot x+color{blue}{{a}_{0}} end{align}]

Собираем все найденные значения в таблицу:

[begin{array}{c|c|c|c|c|c|c} {} & color{blue}{{a}_{n}} & color{blue}{{a}_{n-1}} & color{blue}{{a}_{n-2}} & ldots & color{blue}{{a}_{1}} & color{blue}{{a}_{0}} \ hline x & {{b}_{n-1}} & {{b}_{n-2}} & {{b}_{n-3}} & ldots & {{b}_{0}} & r \ end{array}]

Легко показать, что $r=Pleft( x right)$. Кроме того, согласно теореме Безу, при подстановке $x=color{red}{a}$ найденное число $r=Pleft( color{red}{a} right)$ есть остаток от деления многочлена $Pleft( x right)$ на двучлен $x-color{red}{a}$:

[Pleft( x right)=Qleft( x right)cdot left( x-color{red}{a} right)+r]

В частности, при $r=0$ деление выполнено без остатка, поэтому многочлен $Pleft( x right)$ раскладывается на множители:

[Pleft( x right)=Qleft( x right)cdot left( x-color{red}{a} right)]

Далее по индукции или прямым вычислением можно показать, что коэффициенты $Qleft( x right)$ — это те самые числа ${{b}_{n-1}}$, …, ${{b}_{0}}$ из таблицы. Поскольку $deg Qleft( x right)=n-1$, на каждом шаге степень этого многочлена будет уменьшаться.

В какой-то момент окажется, что $Qleft( x right)= color{blue}{{a}_{n}}$ — константа, и дальнейшее заполнение таблицы по схеме Горнера невозможно. Вот и всё.:)

Смотрите также:

Бином Ньютона
Теорема Безу и корни многочленов
Решение задач B12: №448—455
Задача B3 — работа с графиками
Пример решения задачи 15
Задача B15: частный случай при работе с квадратичной функцией

Источник

Вычисление значения многочлена. Все ли тривиально в этом вопросе?

Время на прочтение
5 мин

Количество просмотров 46K

Вычисление значения многочлена в точке является одной из простейших классических задач программирования.
При проведении различного рода вычислений часто приходится определять значения многочленов при заданных значениях аргументов. Часто приближенное вычисление функций сводится к вычислению аппроксимирующих многочленов.
Рядового читателя Хабрахабр нельзя назвать неискушенным в применении всяческих извращений. Каждый второй скажет, что многочлен надо вычислять по правилу Горнера. Но всегда есть маленькое «но», всегда ли схема Горнера является самой эффективной?

Я не ставлю цель точно описать алгоритмы для вычисления многочленов, а лишь показать, что в некоторых случаях можно (нужно) применять схемы отличные правила Горнера. Для тех, кого заинтересует материал, в конце статьи приведен список литературы, с которой можно ознакомиться для более детального изучения вопроса.
Кроме того, иногда становиться обидно, что фамилии наших русских математиков остаются малоизвестными. К тому же мне просто приятно рассказать о работах наших математиков.

Схема Горнера

При вычислении значений многочленов очень широкое применение получило правило Горнера. Метод назван в честь британского математика Уильяма Джорджа Горнера.
В соответствии с этим правилом многочлен n-й степени:

${{P}_{n}}(x)={{a}_{0}}{{x}^{n}}+{{a}_{1}}{{x}^{n-1}}+...+{{a}_{n-1}}x+{{a}_{n}}$

представляется в виде

${{P}_{n}}(x)=(...(({{a}_{0}}x+{{a}_{1}})x+{{a}_{2}})x+...+{{a}_{n-1}})x+{{a}_{n}}.$

Вычисление значения многочлена производится в порядке, определяемом скобками. Что имеем? Чтобы вычислить многочлен ${{P}_{n}}(x)$ по схеме Горнера, надо выполнить n умножений и n-k сложений (здесь k – число коэффициентов многочлена, равных 0). Если ${{a}_{0}}=1$ , то умножений будет n-1.
Можно показать, что для вычисления многочленов, общего вида нельзя построить схему более экономичную по числу операций, чем схема Горнера.
Самая большая привлекательность схемы Горнера состоит в простоте алгоритма для вычисления значения многочлена.

Исключения

При вычислении многочленов специального вида может потребоваться меньшее число операций, чем при применении универсальной схемы Горнера. Например, вычисление степени ${{x}^{n}}$ по схеме Горнера означает последовательное перемножение n множителей и требует n-1 умножение. Однако каждый первый читатель скажет, что для вычисления, например, ${{x}^{8}}$ нужно последовательно вычислить ${{x}^{2}}=xcdot x$ , ${{x}^{4}}={{x}^{2}}cdot {{x}^{2}}$ , ${{x}^{8}}={{x}^{4}}cdot {{x}^{4}}$ , т.е. выполнить всего 3 умножения вместо 7.

А есть что-то еще, ведь схема Горнера самая экономичная?

На самом деле все решают объемы вычислений. Если надо вычислить одно значение многочлена, то лучше схемы Горнера ничего не придумано. Но если значения многочлена вычисляются во многих точках, то появляется возможность сэкономить большое число операций умножения за счет предварительных вычислений, выполняемых ровно один раз. Это может значительно ускорить работу программы.

В некоторых случаях для получения значений полиномов целесообразно использовать двухэтапные схемы. На первом этапе выполняются действия только над коэффициентами многочлена, он преобразуется к специальному виду. На втором же этапе вычисляют уже значение самого многочлена при заданных значениях аргумента. При этом может оказаться, что количество операций, выполняемых на втором этапе будет меньше, чем при вычислениях по схеме Горнера.

Снова замечу, что такие методы вычислений целесообразны при вычислении значений многочлена ${{P}_{n}}(x)$ для большого числа значений x. Выигрыш получается, за счет того, что первый этап для многочлена выполняется лишь один раз. Примером может послужить вычисление элементарных функций, где приближающий многочлен готовиться заранее.

В дальнейших рассуждениях, говоря о количестве операций для вычисления ${{P}_{n}}(x)$ , я буду иметь в виду сложность второго этапа вычислений.

Схема Дж.Тодта для многочленов 6 степени

Имеем следующий многочлен:

${{P}_{6}}(x)={{x}^{6}}+A{{x}^{5}}+B{{x}^{4}}+C{{x}^{3}}+D{{x}^{2}}+Ex+F.$

Для вычислений используем следующие вспомогательные многочлены:

${{p}_{1}}(x)=x(x+{{b}_{1}})$ ,

${{p}_{2}}(x)=({{p}_{1}}+x+{{b}_{2}})({{p}_{1}}+{{b}_{3}})$ ,

${{p}_{3}}(x)=({{p}_{2}}+{{b}_{4}})({{p}_{1}}+{{b}_{5}})+{{b}_{6}}$ .

Коэффициенты ${{b}_{j}}$ определяются методом неопределенных коэффициентов исходя из условия ${{p}_{3}}(x)equiv {{P}_{6}}(x)$ . Из последнего условия составляем систему уравнений, приравнивая коэффициенты при равных степенях многочленов.

Саму систему, здесь приводить не буду. Но она легко решается методом подстановок, при этом приходится решать квадратные уравнения. Коэффициенты могут получиться комплексными, но если коэффициенты оказываются действительными, то вычисления требуют трех умножений и семи сложений вместо пяти умножений и шести сложений по схеме Горнера.

Говорить об универсальности данной схемы не приходится, но зато читатель наглядно может оценить уменьшение числа операций по сравнению со схемой Горнера.

Схема Ю.Л. Кеткова

Наконец-то, добрался и до наших математиков.

Ю.Л. Кетков дал общее представление многочлена n-й степени для n>5, всегда приводящее к действительным выражениям и требующее для вычисления многочлене n-й степени выполнения [(n+1)/2]+[n/4] умножений и n+1 сложений.

Например, при n=2k схема Кеткова сводится к нахождению многочленов:

${{N}_{2}}(x)=x({{b}_{0}}+x),$

${{N}_{4}}(x)=({{N}_{2}}+{{b}_{1}}+x)({{N}_{2}}+{{b}_{2}})+{{b}_{3}},$

${{N}_{6}}(x)={{N}_{2}}{{N}_{4}}+{{b}_{4}}x+{{b}_{5}},$

${{N}_{2k}}(x)=({{N}_{2}}+{{s}_{k}}{{b}_{2k-2}}){{N}_{2k-2}}+{{r}_{k}}{{b}_{2k-2}}x+{{b}_{2k-1}},$

где ${{r}_{k}}=0$ , ${{s}_{k}}=1$ при k –четном, и ${{r}_{k}}=1$ , ${{s}_{k}}=0$ , если k нечетное (k>2).

Все неизвестные коэффициенты находятся из равенства ${{P}_{n}}(x)={{N}_{2k}}$ . В работах Кеткова для решения получающихся систем дается метод, дающий всегда действительные коэффициенты ${{b}_{j}}$ .

Схемы В.Я. Пана

Э. Белага в своих работах дал строгое доказательство невозможности построения схемы вычисления произвольных многочленов n-й степени, использующей на втором этапе меньше, чем [(n+1)/2]+1 умножений и n сложений.

В.Я. Пан занимался вопросами оптимального вычисления многочленов. В частности, им предложено несколько схем для вычисления действительных многочленов, которые весьма близко подобрались к оценкам Э. Белаги. Приведу некоторые схемы Пана для действительных многочленов.
1. Схема для вычисления многочленов четвертой степени.
Рассматривается многочлен ${{P}_{4}}(x)={{a}_{0}}{{x}^{4}}+{{a}_{1}}{{x}^{3}}+{{a}_{2}}{{x}^{2}}+{{a}_{3}}x+{{a}_{4}}$ .

Представим ${{P}_{4}}(x)$ в виде:

$g(x)=x(x+{{lambda }_{1}}),$

${{P}_{4}}(x)equiv {{a}_{0}}left( left( g(x)+{{lambda }_{2}} right)left( g(x)+x+{{lambda }_{3}} right)+{{lambda }_{4}} right),$

где

${{lambda }_{1}}=frac{{{a}_{1}}-{{a}_{0}}}{2{{a}_{0}}},{{lambda }_{2}}=frac{{{a}_{3}}}{{{a}_{0}}}-{{lambda }_{1}}frac{{{a}_{2}}}{{{a}_{0}}}+({{lambda }_{1}}+1)lambda _{1}^{2},$

${{lambda }_{3}}=frac{{{a}_{2}}}{{{a}_{0}}}-{{lambda }_{1}}({{lambda }_{1}}+1)-{{lambda }_{2}},{{lambda }_{4}}=frac{{{a}_{4}}}{{{a}_{0}}}-{{lambda }_{2}}{{lambda }_{3}}.$

2. Схема для вычисления ${{P}_{n}}(x)$ , nge 5 .
Строим вспомогательные многочлены g(x) , h(x) , ${{p}_{s}}(x)$ :

$g(x)=x(x+{{lambda }_{1}}),h(x)=g(x)+x,{{p}_{0}}(x)=x,$

${{p}_{s}}(x)={{p}_{s-1}}(x)left( (g(x)+{{lambda }_{4s-2}})(h(x)+{{lambda }_{4s-1}})+{{lambda }_{4s}} right)+{{lambda }_{4s+1}}$ , s=1,2,…,k.

Для вычисления значения многочлена используем выражения:

${{P}_{n}}(x)equiv {{a}_{0}}{{p}_{k}}(x)$ , при n=4k+1 ,

${{P}_{n}}(x)equiv {{a}_{0}}x{{p}_{k}}(x)+{{lambda }_{n}}$ , при n=4k+2 ,

${{P}_{n}}(x)equiv {{a}_{0}}left( {{p}_{k}}(x)(g(x)+{{lambda }_{n-1}})+{{lambda }_{n}} right)$ , при n=4k+3 ,

${{P}_{n}}(x)equiv {{a}_{0}}xleft( {{p}_{k}}(x)(g(x)+{{lambda }_{n-2}})+{{lambda }_{n-1}} right)+{{lambda }_{n}}$ , при n=4k+4 ,

Эта схема на втором этапе требует [n/2]+2 умножения и n+1 сложения.

Особенностью данной схемы является то, что коэффициенты ${{lambda }_{j}}$ всегда существуют при nge 5 и действительных коэффициентах исходного многочлена.

У В.Я. Пана существуют и другие схемы для вычисления многочленов, в том числе и для комплексных.

Заключение

Резюмируя сказанное, замечу, что вычисление одного или нескольких значений полинома бесспорно нужно проводить с использованием схемы Горнера.

Однако, если число значений полинома, которые потребуется вычислить велико, а производительность очень важна, то имеет смысл рассмотреть применение специальных методов вычисления многочленов.

Некоторые читатели скажут, что возиться с применением схем, отличных от схемы Горнера, сложно, муторно и не стоит с этим связываться. Однако в реальной жизни встречаются задачи, в которых требуется вычислять просто огромное число значений многочленов с большими степенями (например, на их вычисление могут уходить месяцы), и уменьшение числа умножений в два раза даст существенный выигрыш во времени, даже если вам придется потратить пару дней на реализацию конкретной схемы для вычисления многочленов.

Литература

Кетков Ю.Л. Об одном способе вычисления полиномов на математических машинах. // Известия ВУЗ’ов. Радиофизика, т.1., № 4, 1958
В. Я. Пан, “Вычисление многочленов по схемам с предварительной обработкой коэффициентов и программа автоматического нахождения параметров”, Ж. вычисл. матем. и матем. физ., 2:1 (1962), 133–140
В. Я. Пан, “О способах вычисления значений многочленов”, УМН, 21:1(127) (1966), 103–134
В. Я. Пан, “О вычислении многочленов пятой и седьмой степени с вещественными коэффициентами”, Ж. вычисл. матем. и матем. физ., 5:1 (1965), 116–118
Пан В. Я. Некоторые схемы для вычисления значений полиномов с вещественными коэффициентами. Проблемы кибернетики. Вып. 5. М.: Наука, 1961, 17–29.
Белага Э. Г. О вычислении значений многочлена от одного переменного с предварительной обработкой коэффициентов. Проблемы кибернетики. Вып. 5. М.: Физматгиз, 1961, 7–15.

Источник

Поскольку большинство методов
аппроксимации функций сводится к
замене этих функций многочленами, то
одной из важнейших задач является
отыскание удобного способа вычисления
значения многочлена в произвольной
точке. Одним из критериев удобства
является уменьшение числа сложений и
умножений, необходимых для вычисления
многочлена.

Рассмотрим многочлен

ой
степени

.
(2.2)

Если непосредственно вычислить значение
этого многочлена в произвольной точке

,
то потребуется

арифметических действий. При этом
возникает потеря точности за счет
погрешности вычисления.

Вычисление многочлена

удобнее производить следующим образом.
Представим его в виде

.
(2.3)

Отсюда, последовательно
вычисляя числа

(2.4)

находим

.

Описанный метод вычисления значения
многочлена в заданной точке носит
название схемы Горнера. Она позволяет
сократить число сложений и умножений
до

операций, при этом повышается точность
вычисления.

Пример. Вычислить значение многочлена

при

.

Решение. Имеем

Последовательное применение формулы
(2.4) дает

Следовательно,

Практически схему Горнера удобно
реализовывать в виде следующей таблицы

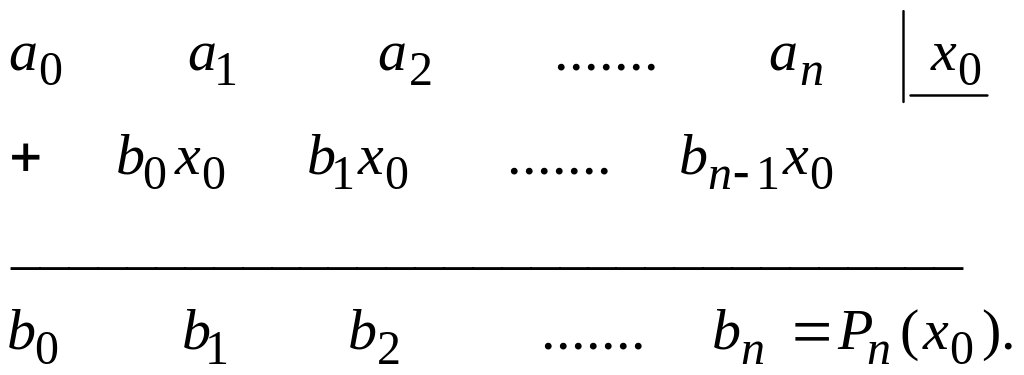
Тогда рассмотренный пример будет иметь
вид

2.3. Интерполяционный многочлен Лагранжа

Будем искать многочлен

степени не выше

,
имеющий в заданных узлах интерполяции
те же значения, что и функция

.
Запишем этот многочлен в виде (2.2).
Неизвестные коэффициенты

,

,
…,

можно найти из условия

.
Это условие приводит к системе линейных
уравнений

(2.5)

Определитель
этой системы

называется
определителем Ван-дер-Монда. Он отличен
от нуля, так как все узлы интерполирования
различны. Следовательно, система (2.5)
имеет единственное решение и
интерполяционный многочлен

определяется единственным образом.
Однако, для большого числа узлов
интерполяции, решать эту систему
сложно. Многочлен

можно построить
другим способом:
строятся

многочленов

таких, что

Так как искомый
многочлен обращается в нуль в

точках

,
то он имеет вид

,
(2.6)

где

— постоянный коэффициент. Полагая

в формуле (2.6) и учитывая, что

,
получим

Отсюда

Подставив это
значение в формулу (2.6), будем иметь

.
(2.7)

Тогда, многочлен

,
удовлетворяющий условиям

,
имеет вид

. (2.8)

Подставив в
формулу (2.8) значение

из (2.7), получим

.
(2.9)

Многочлен

,
определяемый по формуле (2.9) , называется
интерполяционным многочленом Лагранжа.
Очевидно, что степень многочлена Лагранжа
не превышает числа

.
Часто многочлен Лагранжа записывают
виде

При

имеем две точки, и формула Лагранжа
представляет в этом случае уравнение
прямой

,
проходящей через две заданные точки

где

— абсциссы этих точек.

При

получим уравнение параболы

,
проходящей через три точки

Пример. Для функции

построить интерполяционный многочлен
Лагранжа, выбрав узлы

Решение. Многочлен Лагранжа для
трех узлов интерполирования запишется
так

Вычисляем
соответствующие значения функции

Применяя
формулу Лагранжа, получим

или

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Схема Горнера

Схема Горнера – способ деления многочлена

$$P_n(x)=sumlimits_{i=0}^{n}a_{i}x^{n-i}=a_{0}x^{n}+a_{1}x^{n-1}+a_{2}x^{n-2}+ldots+a_{n-1}x+a_n$$

на бином $x-a$. Работать придётся с таблицей, первая строка которой содержит коэффициенты заданного многочлена (они выделены для наглядности синим цветом). Первым элементом второй строки будет число $a$, взятое из бинома $x-a$:

$$
P_n(x)=normblue{a_{0}}x^{n}+normblue{a_{1}}x^{n-1}+normblue{a_{2}}x^{n-2}+ldots+normblue{a_{n-1}}x+normblue{a_n}\
$$
$$
begin{array} {c|c|c|c|c|c|c|c}
& normblue{a_0} & normblue{a_1} & normblue{a_2} & normblue{a_3} & ldots & normblue{a_{n-1}} & normblue{a_n} \
hline a & & & & & & &
end{array}
$$

Вторая строка таблицы заполняется постепенно. Второй элемент этой строки (обозначим его $b_0$) равен $a_0$, т.е., по сути, мы просто переносим вниз число $a_0$:

$$
begin{array} {c|c|c|c|c|c|c|c}
& a_0 & a_1 & a_2 & a_3 & ldots & a_{n-1} & a_n \
hline a & b_0=a_0 & & & & & &
end{array}
$$

Следующий элемент второй строки, который мы обозначим как $b_1$, получается по такой формуле: $b_1=acdot{b_0}+a_1$:

$$
begin{array} {c|c|c|c|c|c|c|c}
& a_0 & a_1 & a_2 & a_3 & ldots & a_{n-1} & a_n \
hline a & b_0 & b_1=acdot{b_0}+a_1 & & & & &
end{array}
$$

Далее находим элемент $b_2$ по формуле $b_2=acdot{b_1}+a_2$:

$$
begin{array} {c|c|c|c|c|c|c|c}
& a_0 & a_1 & a_2 & a_3 & ldots & a_{n-1} & a_n \
hline a & b_0 & b_1 & b_2=acdot{b_1}+a_2 & & & &
end{array}
$$

Аналогично вычисляем и элемент $b_3=acdot{b_2}+a_3$:

$$
begin{array} {c|c|c|c|c|c|c|c}
& a_0 & a_1 & a_2 & a_3 & ldots & a_{n-1} & a_n \
hline a & b_0 & b_1 & b_2 & b_3=acdot{b_2}+a_3 & & &
end{array}
$$

Далее находим $b_4$, $b_5$ и так далее. В целом, общая формула для вычисления $b_i$, где $ige{1}$, будет такой:

$$
b_i = acdot{b_{i-1}}+a_i
$$

В конечном итоге, мы вычислим последний элемент $b_n = acdot{b_{n-1}}+a_n$, и на этом работа будет закончена. Заполненная таблица будет иметь такой вид:

$$
begin{array} {c|c|c|c|c|c|c|c}
& a_0 & a_1 & a_2 & a_3 & ldots & a_{n-1} & a_n \
hline a & b_0 & b_1 & b_2 & b_3 & ldots & b_{n-1} & b_n
end{array}
$$

После деления исходного многочлена n-ой степени $P_n(x)$ на бином $x-a$, получим многочлен, степень которого на единицу меньше исходного, т.е. равна $n-1$. Последнее число второй строки, т.е. $b_n$, есть остаток от деления $P_n(x)$ на $x-a$:

$$
a_{0}x^{n}+a_{1}x^{n-1}+a_{2}x^{n-2}+ldots+a_{n-1}x+a_n
=(x-a)cdotleft(b_{0}x^{n-1}+b_{1}x^{n-2}+ldots+b_{n-1}right)+b_n
$$

Если вспомнить теорему Безу, то можно сформулировать и так: число $b_n$ равно значению многочлена $P_n(x)$ при $x=a$, т.е. $b_n = P_n (a)$.

Если $b_n=0$, то исходный многочлен делится на бином $x-a$ нацело, т.е. число $a$ является корнем этого многочлена. Непосредственное применение схемы Горнера проще всего показать на примерах.

Пример №1

Разделить $5x^4+5x^3+x^2-11$ на $x-1$, используя схему Горнера.

Решение

Для сокращения записи обозначим заданный многочлен как $P(x)$, т.е. $P(x)=5x^4+5x^3+x^2-11$. Для начала составим таблицу из двух строк. В первой строке запишем коэффициенты многочлена $P(x)$, расположенные по убыванию степеней переменной $x$. Заметьте, что данный многочлен не содержит $x$ в первой степени, т.е. коэффициент перед $x$ в первой степени равен 0:

$$
normblue{5}cdot{x^4}+normblue{5}cdot{x^3}+normblue{1}cdot{x^2}+normblue{0}cdot{x}+normblue{(-11)}\
$$

Так как мы делим на $x-normred{1}$, то в первой ячейке второй строки запишем число $normred{1}$. Таблица, с которой мы будем работать, имеет такой вид:

$$
begin{array} {c|c|c|c|c|c}
& normblue{5} & normblue{5} & normblue{1} & normblue{0} & normblue{-11} \
hline normred{1} & & & & &
end{array}
$$

Начнём заполнять пустые ячейки во второй строке. Во вторую ячейку второй строки запишем число $5$, просто перенеся его вниз из второй ячейки первой строки:

$$
begin{array} {c|c|c|c|c|c}
& normgreen{5} & 5 & 1 & 0 & -11 \
hline 1 & normgreen{5} & & & &
end{array}
$$

Следующую ячейку заполним по такому принципу: $normred{1}cdotnormgreen{5}+normpurple{5}=normblue{10}$:

$$
begin{array} {c|c|c|c|c|c}
& 5 & normpurple{5} & 1 & 0 & -11 \
hline normred{1} & normgreen{5} & normblue{10} & & &
end{array}
$$

Аналогично заполним и четвертую ячейку второй строки: $normred{1}cdotnormgreen{10}+normpurple{1}=normblue{11}$:

$$
begin{array} {c|c|c|c|c|c}
& 5 & 5 & normpurple{1} & 0 & -11 \
hline normred{1} & 5 & normgreen{10} & normblue{11} & &
end{array}
$$

Для пятой ячейки получим: $normred{1}cdotnormgreen{11}+normpurple{0}=normblue{11}$:

$$
begin{array} {c|c|c|c|c|c}
& 5 & 5 & 1 & normpurple{0} & -11 \
hline normred{1} & 5 & 10 & normgreen{11} & normblue{11} &
end{array}
$$

И, наконец, для последней, шестой ячейки, имеем: $normred{1}cdotnormgreen{11}+normpurple{(-11)}=normblue{0}$:

$$
begin{array} {c|c|c|c|c|c}
& 5 & 5 & 1 & 0 & normpurple{-11} \
hline normred{1} & 5 & 10 & 11 & normgreen{11} &normblue{0}
end{array}
$$

Числа, расположенные во второй строке (между единицей и нулём), есть коэффициенты многочлена, полученного после деления $P(x)$ на $x-1$. Последнее число во второй строке (ноль) равно остатку от деления многочлена $P(x)$ на $x-1$. Остаток равен нулю, т.е. многочлен $P(x)$ делится на $x-1$ нацело. Для наглядности я запишу полученный результат, выделив коэффициенты разными цветами:

$$
begin{array} {c|c|c|c|c|c}
& 5 & 5 & 1 & 0 & -11 \
hline normred{1} & normblue{5} & normblue{10} & normblue{11} & normblue{11} &normgreen{0}
end{array}
$$

$$
P(x)
=(x-normred{1})cdotleft(normblue{5}cdot{x^4}+normblue{10}cdot{x^3}+normblue{11}cdot{x^2}+normblue{11}cdot{x}right)+normgreen{0}
=(x-1)left(5x^3+10x^2+11x+11right)
$$

Естественно, что так как степень исходного многочлена $P(x)$ равнялась четырём, то степень многочлена $5x^3+10x^2+11x+11$ на единицу меньше, т.е. равна трём.

Полученный нами результат можно ещё охарактеризовать так: значение многочлена $P(x)$ при $x=1$ равно нулю. Так как значение многочлена $P(x)$ при $x=1$ равно нулю, то единица является корнем многочлена $P(x)$.

Ответ: $5x^4+5x^3+x^2-11 = (x-1)left(5x^3+10x^2+11x+11right)$.

Пример №2

Разделить многочлен $x^4+3x^3+4x^2-5x-47$ на $x+3$ по схеме Горнера.

Решение

Для сокращения записи обозначим заданный многочлен как $P(x)$, т.е. $P(x)=x^4+3x^3+4x^2-5x-47$. Сразу оговорим, что выражение $x+3$ нужно представить в форме $x-(-3)$. В схеме Горнера будет учавствовать именно $-3$. Выполняем преобразования, аналогичные сделанным в примере №1:

$$
begin{array} {c|c|c|c|c|c}
& 1 & 3 & 4 & -5 & -47 \
hline -3 & 1 & 0 & 4 & -17 & 4
end{array}
$$

Так как степень исходного многочлена $P(x)$ равна четырём, то в результате деления получим многочлен третьей степени.

$$P(x)=(x+3)left(x^3+0cdot x^2 +4x-17right)+4=(x+3)left(x^3+4x-17right)+4$$

Полученный результат означает, что многочлен $P(x)$ делится на бином $x+3$ не нацело. Остаток от деления $P(x)$ на $x+3$ равен $4$. Этот же результат означает, что значение многочлена $P(x)$ при $x=-3$ равно $4$, т.е. $P(-3)=4$. Кстати, это несложно перепроверить непосредственной подстановкой $x=-3$ в заданный многочлен:

$$
x^4+3x^3+4x^2-5x-47=(-3)^4+3 cdot (-3)^3-5 cdot (-3)-47=4.
$$

Т.е. схему Горнера можно также использовать, если необходимо найти значение многочлена при заданном значении переменной.

Ответ: $x^4+3x^3+4x^2-5x-47=(x+3)left(x^3+4x-17right)+4$.

Если наша цель – найти все корни многочлена, то схему Горнера можно применять несколько раз подряд, – до тех пор, пока мы не исчерпаем все корни, как рассмотрено в примере №3.

Пример №3

Найти все целочисленные корни многочлена $x^6+2x^5-21x^4-20x^3+71x^2+114x+45$, используя схему Горнера.

Решение

Для сокращения записи обозначим заданный многочлен как $P(x)$, т.е.

$$P(x)=x^6+2x^5-21x^4-20x^3+71x^2+114x+45$$

Коэффициенты рассматриваемого многочлена есть целые числа, а коэффициент перед старшей степенью переменной (т.е. перед $x^6$) равен единице. В этом случае целочисленные корни многочлена нужно искать среди делителей свободного члена, т.е. среди делителей числа 45. Для заданного многочлена такими корнями могут быть числа $45; ; 15; ; 9; ; 5; ; 3; ; 1$ и $-45; ; -15; ; -9; ; -5; ; -3; ; -1$. Проверим, к примеру, число $1$:

Табл. №1

$$
begin{array} {c|c|c|c|c|c|c|c}
& 1 & 2 & -21 & -20 & 71 & 114 & 45 \
hline 1 & 1 & 3 & -18 & -38 & 33 & 147 & 192
end{array}
$$

Как видите, значение многочлена $P(x)$ при $x=1$ равно $192$ (последнее число в второй строке), а не $0$, посему единица не является корнем данного многочлена. Так как проверка для единицы окончилась неудачей, проверим значение $x=-1$. Новую таблицу составлять не будем, а продолжим использование табл. №1, дописав в нее новую (третью) строку. Вторую строку, в которой проверялось значение $1$, выделим красным цветом и в дальнейших рассуждениях использовать её не будем.

Можно, конечно, просто переписать таблицу заново, но при заполнении вручную это займет немало времени. Тем более, что чисел, проверка которых окончится неудачей, может быть несколько, и каждый раз записывать новую таблицу затруднительно. При вычислении «на бумаге» красные строки можно просто вычёркивать.

Табл. №2

Итак, значение многочлена $P(x)$ при $x=-1$ равно нулю, т.е. $P(-1)=0$. Это значит, что число $-1$ есть корень многочлена $P(x)$. После деления многочлена $P(x)$ на бином $x-(-1)=x+1$ получим многочлен $x^5+x^4-22x^3+2x^2+69x+45$, коэффициенты которого взяты из третьей строки табл. №2. Результат вычислений можно также представить в такой форме:

$$
begin{equation}
P(x)=(x+1)left(x^5+x^4-22x^3+2x^2+69x+45right)
end{equation}
$$

Продолжим поиск целочисленных корней. Теперь уже нужно искать корни многочлена $x^5+x^4-22x^3+2x^2+69x+45$. Опять-таки, целочисленные корни этого многочлена ищут среди делителей его свободного члена, – числа $45$. Попробуем ещё раз проверить число $-1$. Новую таблицу составлять не будем, а продолжим использование предыдущей табл. №2, т.е. допишем в нее еще одну строку:

Итак, число $-1$ является корнем многочлена $x^5+x^4-22x^3+2x^2+69x+45$. Этот результат можно записать так:

$$
begin{equation}
x^5+x^4-22x^3+2x^2+69x+45=(x+1)left(x^4-22x^2+24x+45right)
end{equation}
$$

Учитывая равенство (2), равенство (1) можно переписать в такой форме:

$$
begin{equation}
P(x)=(x+1)left(x^5+x^4-22x^2+2x^2+69x+45right)=\
=(x+1)(x+1)left(x^4-22x^2+24x+45right)
=(x+1)^2left(x^4-22x^2+24x+45right)
end{equation}
$$

Теперь уже нужно искать корни многочлена $x^4-22x^2+24x+45$, – естественно, среди делителей его свободного члена (числа $45$). Проверим еще раз число $-1$:

Число $-1$ является корнем многочлена $x^4-22x^2+24x+45$. Этот результат можно записать так:

$$
begin{equation}
x^4-22x^2+24x+45=(x+1)left(x^3-x^2-21x+45right)
end{equation}
$$

С учетом равенства (4), равенство (3) перепишем в такой форме:

$$
begin{equation}

P(x)=(x+1)^2left(x^4-22x^3+24x+45right)=\
=(x+1)^2(x+1)left(x^3-x^2-21x+45right)
=(x+1)^3left(x^3-x^2-21x+45right)

end{equation}
$$

Теперь ищем корни многочлена $x^3-x^2-21x+45$. Проверим еще раз число $-1$:

$$
begin{array} {c|c|c|c|c|c|c|c}
& 1 & 2 & -21 & -20 & 71 & 114 & 45 \
hline normred{1} & normred{1} & normred{3} & normred{-18} & normred{-38} & normred{33} & normred{147} & normred{192}\
hline -1 & 1 & 1 & -22 & 2 & 69 & 45 & 0 \
hline -1 & 1 & 0 & -22 & 24 & 45 & 0 & \
hline -1 & 1 & -1 & -21 & 45 & 0 & & \
hline -1 & 1 & -2 & -19 & 64 & & &
end{array}
$$

Проверка окончилась неудачей. Выделим шестую строку красным цветом и попробуем проверить иное число, например, число $3$:

В остатке ноль, посему число $3$ – корень рассматриваемого многочлена. Итак,

$$x^3-x^2-21x+45=(x-3)left(x^2+2x-15right)$$

Теперь равенство (5) можно переписать так:

$$
begin{equation}
P(x)=(x+1)^3left(x^3-x^2-21x+45right)
=(x+1)^3(x-3)left(x^2+2x-15right)
end{equation}
$$

Проверим ещё раз число $3$:

Полученный результат можно записать так (это продолжение равенства (6)):

$$
begin{equation}
P(x)=(x+1)^3(x-3)left(x^2+2x-15right)
=(x+1)^3(x-3)(x-3)(x+5)
=(x+1)^3(x-3)^2(x+5)
end{equation}
$$

Из последней скобки видно, что число $-5$ также является корнем данного многочлена. Можно, конечно, формально продолжить схему Горнера, проверив значение $x=-5$, но необходимости в этом нет. Итак,

$$ P(x)=(x+1)^3(x-3)left(x^2+2x-15right)=(x+1)^3(x-3)^2(x+5)$$

Числа $-1$, $3$, $-5$ – корни данного многочлена. Причем, так как скобка $(x+1)$ в третьей степени, то $-1$ – корень третьего порядка; так как скобка $(x-3)$ во второй степени, то $3$ – корень второго порядка; так как скобка $(x+5)$ в первой степени, то $x=-5$ – корень первого порядка (простой корень).

Вообще, обычно оформление таких примеров состоит из таблицы, в которой перебираются возможные варианты корней, и ответа:

Из таблицы следует вывод, полученный нами ранее с подробным решением:

$$ P(x)=(x+1)^3(x-3)left(x^2+2x-15right)=(x+1)^3(x-3)^2(x+5)$$

Ответ: $-1$, $3$, $-5$.

Пример №4

Убедиться, что числа $2$ и $-5$ являются корнями многочлена $3x^6+9x^5-28x^4+6x^3-30x^2-30x+100$. Разделить заданный многочлен на биномы $x-2$ и $x+5$.

Решение

Как и ранее, для сокращения записи обозначим заданный многочлен как $P(x)$, т.е.

$$P(x)=3x^6+9x^5-28x^4+6x^3-30x^2-30x+100$$

Степень многочлена $P(x)$ равна $6$. После деления на два заданных бинома степень заданного многочлена уменьшится на $2$, т.е. станет равна $4$.

$$
begin{array} {c|c|c|c|c|c|c|c}
& 3 & 9 & -28 & 6 & -30 & -30 & 100 \
hline normblue{2} & 3 & 15 & 2 & 10 & -10 & -50 & 0 \
hline normpurple{-5} & normgreen{3} & normgreen{0} & normgreen{2} & normgreen{0} & normgreen{-10} & 0 &
end{array}
$$

$$
P(x)=(x-normblue{2})cdot(x-(normpurple{-5}))cdotleft(normgreen{3}cdot{x^4}+normgreen{0}cdot{x^3}+normgreen{2}cdot{x^2} + normgreen{0}cdot{x} + (normgreen{-10})right)
=(x-2)(x+5)left(3x^4+2x^2-10right)
$$

Конечно, данный метод подбора малоэффективен в общем случае, когда корни не являются целыми числами, но для целочисленных корней метод довольно-таки неплох.

Источник

На чтение 13 мин Просмотров 9 Опубликовано 11 апреля 2023 Обновлено 11 апреля 2023

Содержание

Схема Горнера
Найти производные многочлена по схеме горнера
Схема Горнера

Схема Горнера

Схема Горнера – способ деления многочлена

на бином $x-a$. Работать придётся с таблицей, первая строка которой содержит коэффициенты заданного многочлена. Первым элементом второй строки будет число $a$, взятое из бинома $x-a$:

После деления многочлена n-ой степени на бином $x-a$, получим многочлен, степень которого на единицу меньше исходного, т.е. равна $n-1$. Непосредственное применение схемы Горнера проще всего показать на примерах.

Разделить $5x^4+5x^3+x^2-11$ на $x-1$, используя схему Горнера.

Составим таблицу из двух строк: в первой строке запишем коэффициенты многочлена $5x^4+5x^3+x^2-11$, расположенные по убыванию степеней переменной $x$. Заметьте, что данный многочлен не содержит $x$ в первой степени, т.е. коэффициент перед $x$ в первой степени равен 0. Так как мы делим на $x-1$, то во второй строке запишем единицу:

Начнем заполнять пустые ячейки во второй строке. Во вторую ячейку второй строки запишем число $5$, просто перенеся его из соответствующей ячейки первой строки:

Следующую ячейку заполним по такому принципу: $1cdot 5+5=10$:

Аналогично заполним и четвертую ячейку второй строки: $1cdot 10+1=11$:

Для пятой ячейки получим: $1cdot 11+0=11$:

И, наконец, для последней, шестой ячейки, имеем: $1cdot 11+(-11)=0$:

Задача решена, осталось только записать ответ:

Как видите, числа, расположенные во второй строке (между единицей и нулём), есть коэффициенты многочлена, полученного после деления $5x^4+5x^3+x^2-11$ на $x-1$. Естественно, что так как степень исходного многочлена $5x^4+5x^3+x^2-11$ равнялась четырём, то степень полученного многочлена $5x^3+10x^2+11x+11$ на единицу меньше, т.е. равна трём. Последнее число во второй строке (ноль) означает остаток от деления многочлена $5x^4+5x^3+x^2-11$ на $x-1$. В нашем случае остаток равен нулю, т.е. многочлены делятся нацело. Этот результат ещё можно охарактеризовать так: значение многочлена $5x^4+5x^3+x^2-11$ при $x=1$ равно нулю.

Можно сформулировать вывод и в такой форме: так как значение многочлена $5x^4+5x^3+x^2-11$ при $x=1$ равно нулю, то единица является корнем многочлена $5x^4+5x^3+x^2-11$.

Разделить многочлен $x^4+3x^3+4x^2-5x-47$ на $x+3$ по схеме Горнера.

Сразу оговорим, что выражение $x+3$ нужно представить в форме $x-(-3)$. В схеме Горнера будет учавствовать именно $-3$. Так как степень исходного многочлена $x^4+3x^3+4x^2-5x-47$ равна четырём, то в результате деления получим многочлен третьей степени:

Полученный результат означает, что

$$x^4+3x^3+4x^2-5x-47=(x+3)(x^3+0cdot x^2 +4x-17)+4=(x+3)(x^3+4x-17)+4$$

В этой ситуации остаток от деления $x^4+3x^3+4x^2-5x-47$ на $x+3$ равна $4$. Или, что то самое, значение многочлена $x^4+3x^3+4x^2-5x-47$ при $x=-3$ равно $4$. Кстати, это несложно перепроверить непосредственной подстановкой $x=-3$ в заданный многочлен:

$$x^4+3x^3+4x^2-5x-47=(-3)^4+3 cdot (-3)^3-5 cdot (-3)-47=4.$$

Т.е. схему Горнера можно использовать, если необходимо найти значение многочлена при заданном значении переменной. Если наша цель – найти все корни многочлена, то схему Горнера можно применять несколько раз подряд, – до тех пор, пока мы не исчерпаем все корни, как рассмотрено в примере №3.

Найти все целочисленные корни многочлена $x^6+2x^5-21x^4-20x^3+71x^2+114x+45$, используя схему Горнера.

Как видите, значение многочлена $x^6+2x^5-21x^4-20x^3+71x^2+114x+45$ при $x=1$ равно $192$ (последнее число в второй строке), а не $0$, посему единица не является корнем данного многочлена. Так как проверка для единицы окончилась неудачей, проверим значение $x=-1$. Новую таблицу для этого составлять не будем, а продолжим использование табл. №1, дописав в нее новую (третью) строку. Вторую строку, в которой проверялось значение $1$, выделим красным цветом и в дальнейших рассуждениях использовать её не будем.

Итак, значение многочлена $x^6+2x^5-21x^4-20x^3+71x^2+114x+45$ при $x=-1$ равно нулю, т.е. число $-1$ есть корень этого многочлена. После деления многочлена $x^6+2x^5-21x^4-20x^3+71x^2+114x+45$ на бином $x-(-1)=x+1$ получим многочлен $x^5+x^4-22x^3+2x^2+69x+45$, коэффициенты которого взяты из третьей строки табл. №2 (см. пример №1). Результат вычислений можно также представить в такой форме:

Итак, число $-1$ является корнем многочлена $x^5+x^4-22x^3+2x^2+69x+45$. Этот результат можно записать так:

Учитывая равенство (2), равенство (1) можно переписать в такой форме:

Число $-1$ является корнем многочлена $x^4-22x^2+24x+45$. Этот результат можно записать так:

С учетом равенства (4), равенство (3) перепишем в такой форме:

Теперь ищем корни многочлена $x^3-x^2-21x+45$. Проверим еще раз число $-1$:

В остатке ноль, посему число $3$ – корень рассматриваемого многочлена. Итак, $x^3-x^2-21x+45=(x-3)(x^2+2x-15)$. Теперь равенство (5) можно переписать так:

Полученный результат можно записать так (это продолжение равенства (6)):

Числа $-1; ; 3; ; 5$ – корни данного многочлена. Причем, так как скобка $(x+1)$ в третьей степени, то $-1$ – корень третьего порядка; так как скобка $(x-3)$ во второй степени, то $3$ – корень второго порядка; так как скобка $(x+5)$ в первой степени, то $x=-5$ – корень первого порядка (простой корень).

Из таблицы следует вывод, полученный нами ранее с подробным решением:

Степень многочлена $3x^6+9x^5-28x^4+6x^3-30x^2-30x+100$ равна $6$. После деления на два заданных бинома степень заданного многочлена уменьшится на $2$, т.е. станет равна $4$.

Заметили ошибку, опечатку, или некорректно отобразилась формула? Отпишите, пожалуйста, об этом в данной теме на форуме (регистрация не требуется).

Источник

Найти производные многочлена по схеме горнера

1. Разделить 5 x 4 + 5 x 3 + x 2 − 11 на x − 1 , используя схему Горнера.

Составим таблицу из двух строк: в первой строке запишем коэффициенты многочлена 5x 4 +5x 3 +x 2 −11, расположенные по убыванию степеней переменной x. Заметьте, что данный многочлен не содержит x в первой степени, т.е. коэффициент перед x в первой степени равен 0. Так как мы делим на x−1, то во второй строке запишем единицу:

Начнем заполнять пустые ячейки во второй строке. Во вторую ячейку второй строки запишем число 5 , просто перенеся его из соответствующей ячейки первой строки:

Следующую ячейку заполним по такому принципу: 1 ⋅ 5 + 5 = 10 :

Аналогично заполним и четвертую ячейку второй строки: 1 ⋅ 10 + 1 = 11 :

Для пятой ячейки получим: 1 ⋅ 11 + 0 = 11 :

И, наконец, для последней, шестой ячейки, имеем: 1 ⋅ 11 + ( −11) = 0 :

Задача решена, осталось только записать ответ:

Как видите, числа, расположенные во второй строке (между единицей и нулём), есть коэффициенты многочлена, полученного после деления 5x 4 +5x 3 +x 2 −11 на x−1. Естественно, что так как степень исходного многочлена 5x 4 +5x 3 +x 2 −11 равнялась четырём, то степень полученного многочлена 5x 3 +10x 2 +11x+11 на единицу меньше, т.е. равна трём. Последнее число во второй строке (ноль) означает остаток от деления многочлена 5x 4 +5x 3 +x 2 −11 на x−1.
В нашем случае остаток равна нулю, т.е. многочлены делятся нацело. Этот результат ещё можно охарактеризовать так: значение многочлена 5x 4 +5x 3 +x 2 −11 при x=1 равно нулю.
Можно сформулировать вывод и в такой форме: так как значение многочлена 5x 4 +5x 3 +x 2 −11 при x=1 равно нулю, то единица является корнем многочлена 5x 4 +5x 3 +x 2 −11.

2. Найдите неполное частное, остаток от деления многочлена

Источник

Схема Горнера

В этой статье мы расскажем об удобной схеме решения примеров на деление многочленов. Если нам нужно вычислить коэффициент частного P n ( x ) = a n a n + a n — 1 x n — 1 + . . . + a 1 x + a 0 и остаток от деления многочлена на линейный двучлен x — s , то удобно будет воспользоваться схемой (методом) Горнера.

Она заключается в создании особой таблицы и занесении в нее исходных данных:

s i	коэффициенты многочленов
a n	a n — 1	a n — 2	. . .	a 0
s	a n = b n	a n — 1 + b n · s = b n — 1	a n — 2 + b n — 1 · s = b n — 2	. . .	a 0 + b 1 · s = b 0

Числа b n , b n — 1 , b n — 2 , . . . , b 1 и будут нужными нам коэффициентами от деления P n ( x ) = a n a n + a n — 1 x n — 1 + . . . + a 1 x + a 0 на x — s . Остаток обозначен здесь как b 0 . Иначе можно записать решение так:

Теперь покажем , как именно применять эту схему на практике.

Условие: разделите многочлен 2 x 4 — 3 x 3 — x 2 + 4 x + 13 на линейный двучлен х — 1 , используя схему Горнера.

Заполним таблицу. У нас есть s , равный единице, и коэффициенты a 4 = 2 , a 3 = — 3 , a 2 = — 1 , a 1 = 4 , a 0 = 13 .

s i	коэффициенты многочленов
a 4 = 2	a 3 = — 3	a 2 = 1	a 1 = 4	a 0 = 13
s = 1	a 4 = 2 = b 4	a 3 + b 4 · s = = — 3 + 2 · 1 = = — 1 = b 3	a 2 + b 3 · s = = — 1 + ( — 1 ) · 1 = = — 2 = b 2	a 1 + b 2 · s = 4 + ( — 2 ) · 1 = = 2 = b 1	a 0 + b 1 · s = = 13 + 2 · 1 = = 15 = b 0

Ответ: получили частное, равное b 4 x 3 + b 3 x 2 + b 2 x + b 1 = 2 x 3 — x 2 — 2 x + 2 , и остаток b 0 = 15 .

Во второй задаче мы обойдемся без подробных комментариев.

Условие: определите, можно ли разделить многочлен 2 x 3 — 11 x 2 + 12 x + 9 на двучлен x + 1 2 без остатка. Вычислите частное.

Заполним таблицу согласно схеме Горнера.

s i	коэффициенты многочленов
2	— 11	12	9
— 1 2	2	— 11 + 2 · — 1 2 = — 12	12 + — 12 · — 1 2 = 18	9 + 18 · — 1 2 = 0

В последней ячейке мы видим нулевой остаток, следовательно, разделить исходный многочлен на двучлен можно.

Ответ: частное будет представлять из себя многочлен 2 x 2 — 12 x + 18 .

Если b 0 = 0 , то можно говорить о делимости многочлена P n ( x ) = a n a n + a n — 1 x n — 1 + . . . + a 1 x + a 0 на двучлен x — s , и мы имеем корень исходного многочлена, равный s . Используя следствие из теоремы Безу, можем представить этот многочлен в виде произведения:

P n ( x ) = a n a n + a n — 1 x n — 1 + . . . + a 1 x + a 0 = = x — s ( b n x n + 1 + b n — 1 x n — 2 + . . . + b 1 )

Благодаря этому схема Горнера хорошо подходит для тех случаев, когда нужно отыскать целые корни уравнений высших степеней, имеющих целые коэффициенты, или же разложить многочлен на простые множители.

Условие: решите уравнение x 3 — 7 x — 6 = 0 . Разложите многочлен слева на отдельные множители.

Мы знаем, что целые корни уравнения (если они есть) нужно искать среди делителей свободного члена. Запишем их отдельно 1 , — 1 , 2 , — 2 , 3 , — 3 , 6 , — 6 и проверим, используя схему Горнера.

x i	коэффициенты многочленов
a 3 = 1	a 2 = 0	a 1 = — 7	a 0 = — 6
1	1	0 + 1 · 1 = 1	— 7 + 1 · 1 = — 6	— 6 + — 6 · 1 = — 12

Из данных таблицы видно, что единица не будет входить в число корней данного уравнения.

Дополним таблицу еще одним возможным корнем.

x i	коэффициенты многочленов
a 3 = 1	a 2 = 0	a 1 = — 7	a 0 = — 6
1	1	0 + 1 · 1 = 1	— 7 + 1 · 1 = — 6	— 6 + — 6 · 1 = — 12
— 1	1	0 + 1 · ( — 1 ) = — 1	— 7 + — 1 · — 1 = — 6	— 6 + ( — 6 ) · ( — 1 ) = 0

А вот — 1 подходит, значит, мы можем представить исходный многочлен как x 3 — 7 x — 6 = ( x + 1 ) ( x 2 — x — 6 ) .

Проверяем делители дальше. Начнем с — 1 , поскольку возможно повторение корней, но в качестве коэффициентов будем брать значения последней строки:

x i	коэффициенты многочленов
a 3 = 1	a 2 = 0	a 1 = — 7	a 0 = — 6
1	1	0 + 1 · 1 = 1	— 7 + 1 · 1 = — 6	— 6 + — 6 · 1 = — 12
— 1	1	0 + 1 · ( — 1 ) = — 1	— 7 + — 1 · — 1 = — 6	— 6 + ( — 6 ) · ( — 1 ) = 0
— 1	1	— 1 + 1 · — 1 = — 2	— 6 + — 2 · — 1 = — 4

Из этого следует, что — 1 не будет кратным (повторяющимся) корнем. Берем следующий вариант и вычисляем:

x i	коэффициенты многочленов
a 3 = 1	a 2 = 0	a 1 = — 7	a 0 = — 6
1	1	0 + 1 · 1 = 1	— 7 + 1 · 1 = — 6	— 6 + — 6 · 1 = — 12
— 1	1	0 + 1 · ( — 1 ) = — 1	— 7 + — 1 · — 1 = — 6	— 6 + ( — 6 ) · ( — 1 ) = 0
— 1	1	— 1 + 1 · — 1 = — 2	— 6 + — 2 · — 1 = — 4
2	1	— 1 + 1 · 2 = 1	— 6 + 1 · 2 = — 4

Число 2 не входит в число корней уравнения. Дополним таблицу Горнера для х = — 2 :

x i	коэффициенты многочленов
a 3 = 1	a 2 = 0	a 1 = — 7	a 0 = — 6
1	1	0 + 1 · 1 = 1	— 7 + 1 · 1 = — 6	— 6 + — 6 · 1 = — 12
— 1	1	0 + 1 · ( — 1 ) = — 1	— 7 + — 1 · — 1 = — 6	— 6 + ( — 6 ) · ( — 1 ) = 0
— 1	1	— 1 + 1 · — 1 = — 2	— 6 + — 2 · — 1 = — 4
2	1	— 1 + 1 · 2 = 1	— 6 + 1 · 2 = — 4
— 2	1	— 1 + 1 · — 2 = — 3	— 6 + — 3 · — 2 = 0

Минус два будет корнем исходного уравнения. Мы можем записать многочлен так:

x 3 — 7 x — 6 = ( x + 1 ) ( x 2 — x — 6 ) = = ( x + 1 ) ( x + 2 ) ( x — 3 )

Третий и последний корень уравнения будет равен трем. Закончим заполнение таблицы, взяв значения последней полученной строки в качестве коэффициентов:

x i	коэффициенты многочленов
a 3 = 1	a 2 = 0	a 1 = — 7	a 0 = — 6
1	1	0 + 1 · 1 = 1	— 7 + 1 · 1 = — 6	— 6 + — 6 · 1 = — 12
— 1	1	0 + 1 · ( — 1 ) = — 1	— 7 + — 1 · — 1 = — 6	— 6 + ( — 6 ) · ( — 1 ) = 0
— 1	1	— 1 + 1 · — 1 = — 2	— 6 + — 2 · — 1 = — 4
2	1	— 1 + 1 · 2 = 1	— 6 + 1 · 2 = — 4
— 2	1	— 1 + 1 · — 2 = — 3	— 6 + — 3 · — 2 = 0
3	1	— 3 + 1 · 3 = 0

Из этого можно сделать вывод, что последняя полученная таблица, заполненная по методу Горнера, и будет решением нашего примера. Эту задачу можно было решить и делением многочлена на линейный двучлен столбиком, однако показанная здесь схема нагляднее и проще.

Ответ: х = — 1 , х = — 2 , х = 3 , x 3 — 7 x — 6 = ( x + 1 ) ( x + 2 ) ( x — 3 ) .

Источник