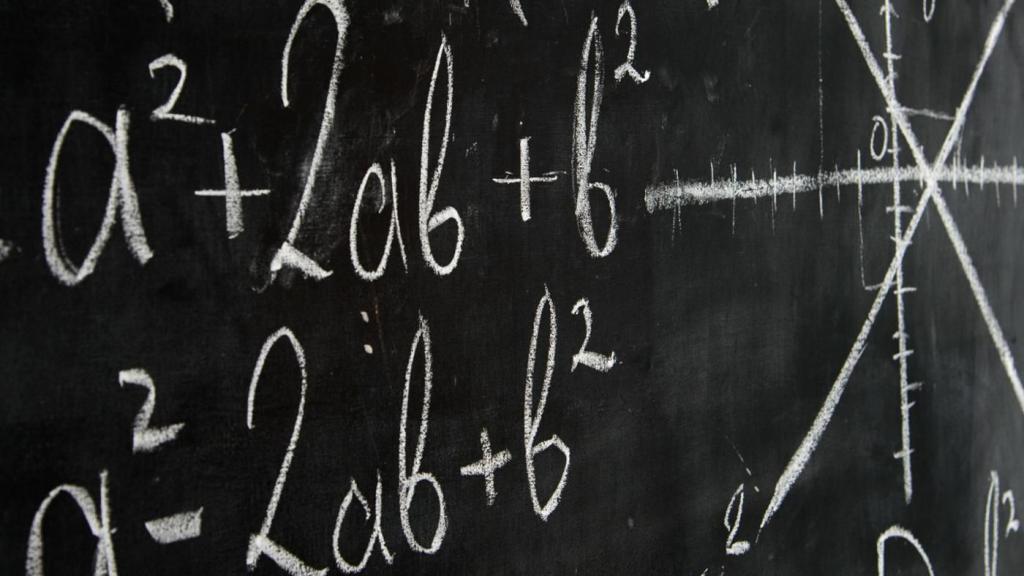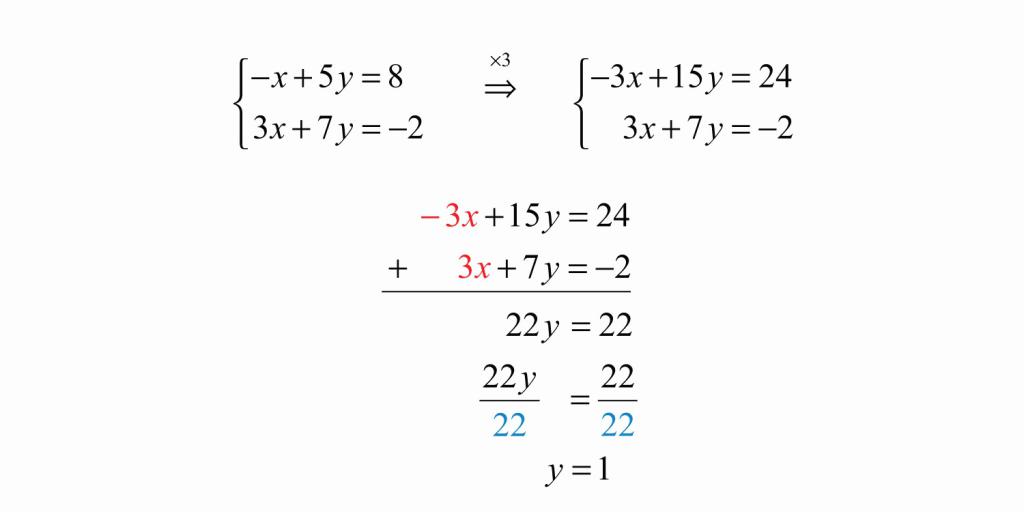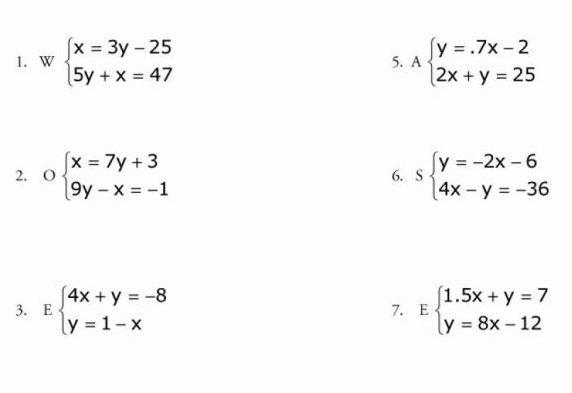Как найти значение переменной в математике

Что такое переменная величина в математике

Первое, что дети начинают изучать в школьном курсе алгебры – это переменные и числа. Содержащиеся в уравнениях неизвестные величины обычно обозначают произвольной буквой. При решении такой задачи необходимо найти значение этой переменной.

Основным показателем переменной является то, что она записывается не числом, а буквой. Под условным обозначением чаще всего скрывается определенное значение. Переменная получила свое название благодаря тому, что ее значение меняется в зависимости от уравнения. Как правило, любая буква алфавита может быть использована в качестве обозначения для такого элемента. Например, если вы знаете, что у вас есть 5 рублей и вы хотите купить яблоки, которые стоят 35 копеек, конечное количество яблок, которые можно купить, обозначается буквой (например «С»).

Если есть переменная, которая была выбрана по вашему усмотрению, необходимо составить алгебраическое уравнение. Оно будет связывать между собой известные и неизвестные величины, а также показывать связь между ними. Это выражение будет включать в себя цифры, переменные и одну алгебраическую операцию. Важно отметить, что выражение будет содержать знак равенства.

Полное уравнение содержит значение выражения в целом. Оно отделено от остального уравнения знаком равенства. В предыдущем примере с яблоками 0.35 или 35 копеек, умноженные на «С», является выражением. Для того чтобы создать полное уравнение, необходимо записать следующее:

0.35*С = 5.00

Существуют две основные классификации выражений: одночлены и многочлены. Мономы являются единичной переменной, числом или произведением переменной и числа. Кроме того, выражение из нескольких переменных или выражений с показателями также является мономом. Например, число 7, переменная х, и произведение 7*x — это моном. Выражения с показателями, в том числе x^2 или 3x^2y^3 также одночлены.

Полиномы являются выражениями, которые включают комбинацию из сложения или вычитания двух или более одночленов. Любой тип одночленов, в том числе цифр, отдельных переменных или выражений с числами и неизвестными, могут быть включены в полином. Например, выражение х+7 является многочленом, который складывают вместе моном х и моном 7. 3x^2 — также многочлен. 10x+3xy-2y^2 – это пример многочлена, который сочетает три одночлена с использованием сложения и вычитания.

В математике независимыми переменными являются неизвестные, которые определяют другие части уравнения. Они стоят отдельно в выражениях и не изменяются вместе с другими переменными.

Значения зависимых переменных определяются с помощью независимых. Их значения зачастую определяются эмпирически.

Рассмотрим такую задачу: «Денис старше Матвея на $2$ года. Сколько лет будет Денису, когда Матвею будет $10$ лет?» Решить ее можно следующим образом:

$10 + 2 = 12$.

А интересно, сколько лет будет Денису, когда Матвею будет $11$ лет? Решение в этом случае выглядит так:

$11 + 2 = 13$.

А если Матвею будет $12$ лет? — Тогда так:

$12 + 2 = 14$.

Спрашивается, нельзя ли как-нибудь на все подобные вопросы ответить раз и навсегда в виде какого-нибудь правила? Оказывается можно:

(возраст Дениса) = (возраст Матвея) + $2$.

Правила, записанные в виде равенств, называются формулами. Математикам очень часто приходится исписывать целые страницы разными равенствами и формулами, поэтому они стремятся делать их, по возможности, краткими. Математик предпочел бы написать следующим образом:

Д = М + $2$,

а потом отдельно пояснить, что Д означает возраст Дениса, а М — возраст Матвея. Но и это не принесло бы ему полного удовлетворения. Математики предпочитают пользоваться буквами самого распространенного в мире алфавита — латинского. Вот запись, которая удовлетворила бы математика полностью:

$d = m + 2$.

Разумеется, как и ранее, к этой формуле необходимо еще приложить пояснения, что $d$ — это возраст Дениса, а $m$ — это возраст Матвея.

Итак, скажите мне, сколько лет Матвею, — и, глядя на эту формулу, я вам быстро отвечу, сколько лет Денису. Принято говорить: если $m$ принимает значение $10$, то $d$ принимает значение $12$. Или: если ${m = 10}$, то ${d = 12}$. Буквы, которые входят в математические выражения и которые могут принимать разные численные значения, называются переменными.

Мы уже довольно давно занимаемся математикой и успели за это время сделать кое-какие важные математические открытия. С помощью формул мы можем теперь эти открытия грамотно записать. Например, мы однажды заметили, что если поменять местами слагаемые, то значение суммы не изменится. В виде формулы это записывается следующим образом:

$a + b = b + a$,

где $a$ и $b$ — любые числа. Школьные учителя называют это «переместительным свойством сложения». Лично мне такое словосочетание режет слух. Это примерно то же самое, что сказать: «оранжевое свойство апельсина». Переместительным является, конечно, не свойство, а само сложение. А профессиональные математики используют тут и вовсе другое слово. Они говорят: сложение коммутативно.

Равенства, которые остаются верными при любых значениях входящих в них переменных, называются тождествами. Вот еще пример тождества:

$a + (b + c) = (a + b) + c$,

или, что то же самое,

$a + (b + c) = a + b + c$.

Это знакомое нам правило, по которому можно изменять порядок действий, или, как мы еще говорили, раскрывать скобки. У школьных учителей это называется «сочетательным свойством сложения». Грамотные же люди говорят: сложение ассоциативно.

Но, разумеется, не всякое равенство является тождеством. Зададимся вопросом: коммутативно ли вычитание? Можно ли написать так:

$a − b = b − a$?

Ну, написать-то так, пожалуй, можно: бумага, говорят, все вытерпит. Но вычитание, конечно же, некоммутативно, а значит, данное равенство не является тождеством. Убедиться в этом очень просто. Пусть, например, $a = 2$ и $b = 1$. Подставляем эти значения в равенство и получаем: ${2 − 1 = 1 − 2}$. Ерунда какая-то! Но, с другой стороны, пусть ${a = 5}$ и ${b = 5}$. В этом случае равенство принимает вид: ${5 − 5 = 5 − 5}$. Ну, что ж, спорить нечего, так оно и есть. Равенство, которые становятся верными лишь при некоторых значениях переменных, называются уравнениями.

Уравнениями очень удобно пользоваться при решении всевозможных математических задач. Вернемся к задаче про Дениса и Матвея: «Денис старше Матвея на $2$ года. Каков будет возраст Дениса, $d$, когда Матвею будет $m$ лет?» Мы твердо знаем, что Денис всегда останется старше Матвея на одно и то же число лет. Поэтому мы можем составить следующее уравнение:

$d − m = 2$.

Здесь две переменные, а именно $d$ и $m$. Следует отметить, что роль этих переменных неодинакова. Предполагается, что численное значение переменной $m$ нам известно. Если даже мы не знаем этого значения сейчас, то, вероятно, нам назовут его когда-нибудь потом. И уж, во всяком случае, его нахождение не входит в нашу задачу. Такие переменные называются параметрами. В противоположность этому, о численном значении переменной $d$ нам никто никогда не собирается сообщать. Наша задача как раз и заключается в том, чтобы его найти. Такие переменные называются неизвестными.

Решить уравнение — это значит выписать формулу, по которой можно вычислить значение неизвестной, если нам скажут численное значение параметра. В данном случае решение — это

$d = m + 2$.

Давайте посмотрим, как мы пришли от исходного уравнения

$d − m = 2$.

к его решению. Ну, мы пристально посмотрели на уравнение, что-то прикинули в уме и выписали результат. Так делать, конечно, можно. Однако в математике разработаны особые методы, которые позволяют решать уравнения без особенного умственного напряжения. Тут очень удобно воспользоваться одним простеньким приемом.

Но сперва — небольшое отступление. Допустим, у Дениса в брюках есть два кармана, один слева, другой справа. В этих карманах лежат конфеты. Точное количество конфет нам неизвестно, но мы знаем, что в левом и правом карманах конфет поровну. Введем обозначения. Пусть $L$ — это число конфет в левом кармане, а $P$ — это число конфет в правом кармане. На основе имеющихся у нас сведений, мы можем составить уравнение:

$L = P$.

Далее события развиваются так. Денис положил в левый карман еще одну конфету и в правый карман еще одну конфету. Ясно, что в обоих карманах конфет снова оказалось поровну:

$L + 1 = P + 1$.

А что было бы, если бы Денис положил в каждый карман не по одной конфете, а по двум или трем или десяти? Ну, наши рассуждения тогда не сильно бы изменились. Просто в новом уравнении вместо «$1$» мы написали бы «$2$» или «$3$» или «$10$». Рассмотрим ситуацию, как говорят математики, в общем виде. Пусть Денис положил в каждый карман по $k$ конфет. В обоих карманах конфет как было, так и осталось поровну. Значит,

$L + k = P + k$.

Заметим, что параметр $k$ может даже быть отрицательным (то есть Денис не кладет конфеты, а, наоборот, берет их).

Тут напрашивается очень важный вывод. Оказывается, что если у нас есть какое-то уравнение, то к обеим его частям можно одновременно прибавить одно и то же число, и тогда уравнение, по своей сути, не изменится. Если при каких-то значениях переменных первое уравнение обращается в верное равенство, то при тех же самых значениях переменных обратится в верное равенство и второе уравнение. И наоборот, если обратилось в верное равенство второе уравнение, то и с первым уравнением случилось то же самое. Иными словами, оба уравнения имеют одинаковые решения. Профессиональные математики в этом случае говорят, что уравнения эквивалентны.

Вернемся теперь к задаче про возраст Дениса и Матвея. Мы получили уравнение

$d — m = 2$.

Давайте преобразуем это уравнение, прибавив к обеим его частям параметр $m$:

$d — m + m = 2 + m$.

После очевидных упрощений новое уравнение принимает вид:

$d = m + 2$.

Вот и всё! Решение получено.

Рассмотрим теперь другую, но очень похожую задачу, в которой вопрос поставлен несколько по-другому: «Денис старше Матвея на $2$ года. Каков будет возраст Матвея, $m$, когда Денису будет $d$ лет?» Уравнение, которое можно составить по этому условию, оказывается по виду точно таким же, как и прежде:

$d — m = 2$.

Однако, на этот раз переменная $d$ является параметром, а переменная $m$ — неизвестной. В таких случаях еще говорят, что уравнение требуется решить относительно переменной $m$. Такое решение находится лишь ненамного труднее предыдущего. Приобразуем уравнение, прибавив к обеим его частям вначале $m$, а потом $(-2)$:

$d — m + m — 2 = 2 + m — 2$.

После упрощений получаем:

$d — 2 = m$.

Тут стоит обратить внимание вот на что. В исходном уравнении переменная $m$ была в левой части, и перед ней стоял знак минус. В конечном уравнении эта же переменная находится в правой части, и подразумевается, что перед ней стоит знак плюс. Говорят, что слагаемые в уравнениях можно переносить из одной части в другую с противоположным знаком (то есть минус следует менять на плюс, а плюс — на минус). В данном случае, справедливость этого правила можно также проследить на числе $2$. Вначале двойка стояла справа, и перед ней подразумевался знак плюс. А в конце она оказалась слева со знаком минус.

Теперь вспомним о задаче, которую мы решаем. В полученном уравнении осталось только поменять местами левую и правую часть — и ответ готов:

$m = d — 2$.

После того, как уравнение решено, полезно сделать так называемую проверку, то есть подставить найденное решение в исходное уравнение и посмотреть, что получится. Например, в данном случае, в исходном уравнении,

$d — m = 2$,

надо $m$ заменить на ${(d — 2)}$:

$d — (d — 2) = 2$.

И что же получилось? Ну, конечно, тождество! Если бы мы не получили тождества, это бы означало, что уравнение решено неверно.

Подобные же рассуждения применимы и к неравенствам. Рассмотрим, для примера, такую задачу. Сколько лет должно пройти, чтобы Матвею можно было официально смотреть фильмы для взрослых? Поскольку человек считается взрослым с $18$ лет, мы должны записать:

$m + x geqslant 18$,

где $m$ обозначает нынешний возраст Матвея, а $x$ — это число лет, которые ему надо подождать, чтобы его стали пускать в кинотеатр на сеансы для взрослых. Значок «$geqslant$» у математиков заменяет слова «больше или равно». Ясно, что если прибавить (или отнять) от обеих частей неравенства одно и то же число, то оно оcтанется по сути тем же самым. Или, говоря точнее, оно превратится в эквивалентное неравенство, которое имеет в точности то же самое решение, что и первоначальное. Отнимаем от обеих частей нашего неравенства число $m$ и получаем:

$x geqslant 18 — m$.

Если Матвею сейчас, допустим, $12$ лет, то

$x geqslant 18 — m = 18 — 12 = 6$,

или, окончательно:

$x geqslant 6$.

Таким образом, для того чтобы Матвей мог официально смотреть фильмы для взрослых, должно пройти $6$ лет или больше.

Точно так же, нам может приготиться понятие «меньше или равно», которые обозначается значком «$leqslant$». Допустим, мы в составе группы из $a$ человек дожидаемся лифта в многоэтажном доме. Грузоподъемность лифта ограничена $12$ человеками, но, когда он подойдет, может оказаться, что в нем уже есть $x$ человек. Спрашивается, каково должно быть значение $x$, чтобы вся наша группа зараз поместилась в лифте? Записываем:

$a + x leqslant 12$,

и, применив наш обычный трюк, получаем:

$x leqslant 12 — a$.

Отметим заодно, что вся эта задача имеет смысл, только если численность нашей группы меньше или равна $12$ человек:

$a leqslant 12$.

Посмотрим теперь, как ведут себя переменные в примерах на умножение и деление. Пусть требуется найти неизвестную переменную $x$ в уравнении:

$x / 3 = 4$.

По условию нашей задачи, $x/3$ и $4$ — это одно и то же число, просто записанное двумя разными способами. Умножим-ка мы это число на $3$. И результат тоже запишем по-разному:

$(x / 3) cdot 3 = 4 cdot 3$.

Здесь деление и умножение на тройку, конечно же, взаимно отменяют друг друга. С учетом этого получаем:

$x = 12$.

Решение уравнения найдено.

А теперь, пусть дано такое уравнение (опять-таки относительно $x$):

$5 cdot x = 20$.

Сможем ли мы его решить? Разумеется, сможем. Только вначале — небольшое замечание. Знак умножения «$cdot$» перед переменной ставить не принято. Когда мы берем переменную $x$ пять раз, то мы пишем просто $5x$, точно также как мы пишем $5$ карандашей или $5$ копеек. Поэтому наше уравнение следует переписать так:

$5x = 20$.

После деления обеих частей на $5$ получаем:

$x = 4$.

А как насчет такого уравнения?

$21 / x = 3$.

Это уравнение решается в два действия. Вначале умножаем обе его части на $x$:

$21 = 3 x$.

А потом делим на $3$:

$7 = x$.

Теперь остается только для большей красоты поменять местами левую и правую части этого равенства:

 $x = 7$,

и решение окончательно готово.

Если после всего этого нам встретится неравенство с неизвестным, такое, например, как

$2 x > 10$,

то мы, конечно, не растеряемся и тоже сможем легко найти его решение

$x > 10 / 2$,

потому что оно находится с помощью всё тех же самых трюков, что и в случае уравнений. Впрочем, тут надо сделать одну важную оговорку. Хотя мы уже и познакомились с отрицательными числами, умножением и делением на них мы пока еще не занимались. Покуда мы делим и умножаем только на положительные числа, все рассмотренные тут трюки прекрасно работают в одинаковой степени как для равенств, так и для неравенств. Но когда мы перейдем к умножению и делению на отрицательные числа, тогда у неравенств обнаружатся кое-какие особенности, о которых мы будем еще говорить отдельно. Что же касается умножения и деления на ноль, то, как мы знаем, делить на ноль вообще нельзя, а умножать на ноль обе части равенств или неравенств не имеет смысла, потому что при умножении любого числа на ноль получается ноль. Если в обеих частях уравнения или неравенства у нас окажутся нули, то толку от этого ровным счетом никакого не будет.

Конспект

1. Рассмотрим задачу:

Денис старше Матвея на два года. Найти возраст Дениса, если известен возраст Матвея.

Ее условие можно переписать в виде уравнения

$d — m = 2$,

где $d$ — это переменная, означающая возраст Дениса, а $m$ — переменная, означающая возраст Матвея. Считается, что значение переменной $m$ нам известно. Такая переменная называется параметром. Напротив, значение переменной $d$ требуется найти. Такая переменная называется неизвестной. Чтобы ответить на вопрос задачи, решаем уравнение относительно переменной $d$ и получаем формулу

$d = m + 2$,

позволяющую рассчитать возраст Дениса, если дан возраст Матвея. Пусть, например Матвею $10$ лет. Подставляем $10$ в формулу вместо $m$ и получаем

$d = 10 + 2 = 12$ — столько лет Денису.

2. Свойства сложения, записанные в виде формул:

$a + b = b + a$  — переместительное (коммутативность);

$a + (b + c) = (a + b) + c$  — сочетательное (ассоциативность).

Эти равенства являются тождествами: они верны при любых значениях переменных.

3. В отличие от тождеств, уравнения — это равенства, которые становятся верны только при некоторых значениях переменных. Решить уравнение относительно входящей в него переменной $x$ — это значит найти такое значение $x$, при котором уравнение обращается в верное равенство. Уравнения решаются с помощью преобразований, позволяющие получать более простые, но эквивалентные уравнения (то есть уравнения с теми же самыми решениями). Правила преобразований: (1) к обеим частям уравнения можно прибавлять одно и то же число (в том числе отрицательное), (2) обе части можно умножать или делить на одно и то же число (пока только натуральное). Следствие правила (1): слагаемые можно переносить из одной части уравнения в другое с противоположным знаком.

4. Неравенства также могут содержать неизвестную переменную. Они решаются с помощью таких же преобразований, как и уравнения.

Задачи

2.4.1. Определить, какие из следующих равенств являются тождествами, а какие — уравнениями. Особо отметить уравнения, не имеющие решений (то есть такие равенства, которые не становятся верными ни при каких значениях переменных).

$x — y = 5$;
$x — 5 = 5$;
$-(-x) = x$;
$-(-x) = -x$;
$-(x — y) = -(y — x)$;
$-(x — y) = y — x$;
$x + 2 = x$;
$x — (y + z) = x — y — z$;
$x — 2 = x$.

2.4.2. Для каждого выражения из левого столбца найти тождественное выражение из правого столбца. (Два выражения называются тождественными, если при постановке между ними знака равенства получается тождество.)

$x$		$-(x — 1)$
$1 — x$	$- y + x$
$x — x$	$5 + x — 5$
$x — y$	$-y — x$
$-(x + y)$	$3 — 3$

2.4.3. Раскрыть скобки:

$a + (b + c)$;
$a — (b + c)$;
$a + (b — c)$;
$a — (b — c)$;
$a + (-b + c)$;
$a — (-b + c)$;
$a + (-b — c)$;
$a — (-b — c)$.

2.4.4. Для каждого уравнения из левого столбца подобрать эквивалентное ему уравнение из правого столбца.

$x — y = 0$		$1 = y$
$x — 3 = y$	$y = x$
$x — y = -y — x$	$x — y + 1 = 4$
$1 — x = y — x$	$x + x = 0$

2.4.5. Решить уравнения и сделать проверку ($x$ — неизвестная, $a$ — параметр):

$x + 531 = 273$;
$x — 531 = 273$;
$344 — x = 118$;
$a — x = 37$;
$a — x = a$;
и т.п.

2.4.6. Старшему брату $a$ лет, а младшему брату $b$ лет. Каков будет возраст старшего брата, $x$, когда младшему будет $y$ лет? Решить задачу в общем виде и получить численный ответ при следующих значениях параметров: ${a = 11}$, ${b = 5}$, ${y = 18}$. Каков будет возраст младшего брата, $y$, когда старшему будет $x$ лет? Дать ответ в общем виде и получить его численное значение при ${a = 11}$, ${b = 5}$, ${x = 18}$.

2.4.7. Один брат старше другого на $a$ лет. Через $b$ лет старшему брату будет $c$ лет. Найти нынешний возраст старшего брата, $x$, и младшего брата, $y$. Вычислить ответ при ${a = 3}$, ${b = 10}$, ${c = 25}$.

2.4.8. У Дениса было какое-то количество конфет, и у Матвея было какое-то количество конфет. После того как Денис дал Матвею $a$ конфет, у них стало конфет поровну. На сколько конфет было у Дениса больше первоначально? Вычислить ответ при ${a = 3}$.

Из «бесконечного» сборника типовых упражнений

Простейшие уравнения, неравенства и подстановки (натуральные числа)

Простейшие уравнения, неравенства и подстановки (целые числа)

Простейшие задачи с параметрами (натуральные числа)

Простейшие задачи с параметрами (целые числа)

Поиск значений выражений — основное математическое действие. Им сопровождается каждый пример, задача. Поэтому чтобы вам было проще работать с различными математическими выражениями, подробно разберем способы и правила их решения в данной статье. Правила представлены в порядке увеличения сложности: от простейших выражений до выражений с функциями. Для лучшего понимания каждый пункт сопровождается подробным пояснением и расписанными примерами.

Поиск значения числовых выражений

Числовые выражения представляют собой математические задачи, состоящие, преимущественно, из чисел. Они подразделяются на несколько групп в зависимости от своей сложности: простейшие, со скобками, корнями, дробями и т.д. Каждый тип выражений подразумевает свои правила нахождения значения, порядок действий. Рассмотрим каждый случай подробнее.

Простейшие числовые выражения. К простейшим числовым выражениям относятся примеры, состоящие из двух элементов:

• Числа (целые, дробные и т.д.);
• Знаки: «+», «—», «•» и «÷».

Чтобы найти значение выражения в данном случае, необходимо выполнить все арифметические действия (которые подразумевают конкретные знаки). В случае отсутствия скобок решение примера производится слева направо. Первыми выполняются действия деления и умножения. Вторыми — сложение и вычитание.

Пример 1. Решение числового выражения

Задача. Решить:

20 — 2 • 10 ÷ 5 — 4 = ?

Решение. Чтобы решить выражение, нам необходимо выполнить все арифметические действия в соответствии с установленными правилами. Поиск значения начинается с решения деления и умножения. В первую очередь находим произведение цифр 2 и 10 (если рассматривать с левой стороны, данное действие является первым по значимости). Получаем 20. Теперь это число делим на 5. Итог — 4. Когда известно значение основных действий, можем подставить его в наш пример:

20 — 4 — 4 = ?

Упрощенный пример также решаем слева направо: 20 — 4 = 16. Второе действие: 16 — 4 = 12. Ответ 12.

Решение без пояснений. 20 — 2 • 10 ÷ 5 — 4 = 20 — (2 • 10 ÷ 5) — 4 = 20 — 4 — 4 = 12.

Ответ. 12

Пример 2. Решение числового выражения

Задача. Решить:

0,2 — 5 • (— 4) + 1/2 • 5 • 4 = ?

Решение. Начинаем решение с умножения и деления. Умножая 5 на (— 4) получаем (— 20), т.к. производное сохраняет знак множителя. Далее умножаем 1/2 на 5. Для этого преобразуем дробь: 1/2 = 5/10 = 0,5. 0,5 умножаем на 5. Ответ — 2,5. Далее умножаем полученное число на 4. 2,5 • 4 = 10. Получаем следующее выражение:

0,2 — (— 20) + 10

Теперь нам остается решить сложение и вычитание. В первую очередь раскрываем скобку и получаем:

0,2 + 20 + 10 = 30,2

Решение без пояснений. 0,2 — 5 • (— 4) + 1/2 • 5 • 4 = 0,2 — (— 20) + 10 = 0,2 + 20 + 10 = 30,2

Ответ. 30,2

Находим значение выражения со скобками

Скобки определяют порядок действий при решении примера. Выражения, находящиеся внутри скобок «()» имеют первостепенную значимость, независимо от того, какое математическое действие в них выполняется.

Пример 3. Значение числового выражения со скобками

Задача. Решить:

5 + (7 — 2 • 3) • (6 — 4) ÷ 2 = ?

Решение. Начинаем нахождение значения выражения с решения скобок. Порядок действий определяется слева направо. При этом не забываем, что после раскрытия скобок в первую очередь решаем умножение и деление и лишь потом — вычитание и сложение:

• 7 — 2 • 3 = 7 — 6 = 1
• 6 — 4 = 2

Когда скобки решены, подставляем полученные значения в наш пример:

5 + 1 • 2 ÷ 2

Снова решаем все по порядку, не забывая о том, что деление и умножение выполняется в первую очередь:

• 1 • 2 = 2
• 2 ÷ 2 = 1

Упрощенное выражение выглядит следующим образом:

5 + 1 = 6

Решение без пояснений. 5 + (7 — 2 • 3) • (6 — 4) ÷ 2 = 5 + (7 — 6) • 2 ÷ 2 = 5+ 1 • 2 ÷ 2 = 5 + 1 = 6

Ответ. 6

Значение числового выражения со скобками

Задача. Решить:

4 + (3 + 1 + 4 • (2+3)) = ?

Решение. Подобные примеры решаются поэтапно. Помним, что поиск выражения со скобками начинается с решения скобок. Поэтому в первую очередь решаем:

3 + 1 + 4 • (2+3)

В уже упрощенном примере снова встречаются скобки. Их будем решать в первую очередь:

2 + 3 = 5

Теперь можем подставить определенное значение в общую скобку:

3 + 1 + 4 • 5

Начинаем решение с умножения и далее слева направо:

• 4 • 5 = 20
• 3 + 1 = 4
• 4 + 20 = 24

Далее подставляем полученный ответ вместо большой скобки и получаем:

4 + 24 = 28

Решение без пояснений. 4 + (3 + 1 + 4 • (2+3)) = 4 + (3 + 1 + 4 • 5) = 4 + (3 + 1 + 20) = 4 + 24 = 28

Ответ. 28

Важно: Чтобы правильно определить значение числового выражения с множественными скобками, необходимо выполнять все действия постепенно. Скобки читаются слева направо. Приоритет в решении внутри скобок остается за делением и умножением.

Поиск значения выражения с корнями

Часто алгебраические задания основываются на нахождении значений из-под корня. И если определить √4 несложно (напомним, это будет 2), то с примерами, которые полностью расположены под корнем, возникает ряд вопросов. На самом деле в таких заданиях нет ничего сложного. В данном случае порядок действий следующий:

• Решаем все выражение, которое находится под корнем (не забываем о правильной последовательности: сперва скобки, деление и умножение, а лишь потом — сложение и вычитание);
• Извлекаем корень из числа, которое получили в результате решения обычного примера.

Если же и под корнем имеется корень (например: √ 4 + 8 — √4), то начинаем решение примера с его извлечения (в нашем примере это будет: √ 4 + 8 — 2). Если подкоренные числа возведены во вторую степень, то их квадратный корень будет равняться модулю подкоренного выражения.

Значение числового выражения с корнями

Задача. Решить:

√ 2² • 2² • 3² = ?

Решение. Все действия под корнем одинаковы — умножение. Это дает нам право разделить выражение на множители. Получаем:

√2² • √2² • √3² = ?

Т.к. под квадратным корнем у нас числа, возведенные во вторую степень, получаем:

2 • 2 • 3 = 12

Решение без пояснений. √ 2² • 2² • 3² = √2² • √2² • √3² = 2 • 2 • 3 = 12

Ответ. 12

Находим значение числовых выражений со степенями

Следующий математический знак, который имеет приоритет в процессе решения, — степени. Они представляют собой результат многократного умножения числа на себя. Само число является основанием степени. А количество операций умножения — ее показателем. Причем выражен он может быть не только целым числом, но и дробью, полноценным числовым выражением.

Начинается решение выражения со степенями с вычисления самих степеней. Если они представляют собой полноценное выражение (например: [3^{3 cdot 4-10}]), то его необходимо решить в нашем примере это будет: [3^{12-10}=3^{2}=9].

Задача. Решите:

[ 3^{1 / 3} cdot 7^{1 / 3} cdot 21^{2 / 3}=? ]

Решение. Чтобы решить это выражение со степенями, воспользуемся равенством:

[(a cdot b)^{r}=a^{r} cdot b^{r}]

Рассматривая пример слева направо, видим, что у первых двух множителей одинаковые степени. Это позволяет нам упростить выражение:

[ (3 cdot 7)^{1 / 3} cdot 21^{2 / 3}=21^{1 / 3} cdot 21^{2 / 3} ]

Зная, что при умножении степени с одинаковыми показателями складываются, получаем следующее выражение:

[ 21^{1 / 3} cdot 21^{2 / 3}=21^{1 / 3+2 / 3}=21^{1}=21 ]

Решение без пояснений: [3^{1 / 3} cdot 7^{1 / 3} cdot 21^{2 / 3}=(3 cdot 7)^{1 / 3} cdot 21^{2 / 3}=21^{1 / 3} cdot 21^{2 / 3}=21^{1 / 3+2 / 3}=21^{1}=21]

Ответ. 21

Интересно: Этот же пример можно решить и другим способом, преобразовав число 21 в степени ⅔ в два множителя. В данном случае решение будет выглядеть следующим образом:

[3^{1 / 3} cdot 7^{1 / 3} cdot 21^{2 / 3}=3^{1 / 3} cdot 7^{1 / 3} cdot(3 cdot 7)^{2 / 3}=3^{1 / 3} cdot 7^{1 / 3} cdot 3^{2 / 3} cdot 7^{2 / 3}=3^{1 / 3+2 / 3} cdot 7^{1 / 3+2 / 3}=3^{1}+7^{1}=21]

Ответ. 21

Задача. Решить:

[ 2^{-2 sqrt{5}} cdot 4^{sqrt{5}-1}+left((sqrt{3})^{1 / 3}right)^{6} ]

Решение. В данном случает получить точные числовые значения показателей степеней не удастся. Поэтому искать значение выражения с дробями в виде степени будем снова через упрощение:

Ответ. 3,25

Выражения с дробями

Поиск значения выражения дробей начинается с их приведения к общему виду. В большинстве случаев проще представить все значения в виде обыкновенной дроби с числителем и знаменателем. После преобразования всех чисел необходимо привести все дроби к общему знаменателю.

Важно: Прежде чем найти выражение дробей, необходимо провести вычисления в их знаменателе и числителе отдельно. В данном случае действуют стандартные правила решения.

Когда дроби приведены к единому знаменателю можно переходить к решению. Вычисление значений верхней строки (числителя) и нижней (знаменателя) производятся параллельно.

Задача. Решить:

[ 6 frac{2}{13}+4 frac{1}{13}=? ]

Решение. Действуя по главному правилу, прежде чем найти значение числового выражения, преобразуем всего его части в простую дробь. Получаем:

[ frac{6 cdot 13+2}{13}+frac{4 cdot 13+1}{13} ]

Теперь выполняем вычисления в знаменателе и числителе и находим ответ:

[ frac{6 cdot 13+2}{13}+frac{4 cdot 13+1}{13}=frac{80}{13}+frac{53}{13}=frac{133}{13}=10 frac{3}{13} ]

Ответ. [10 frac{3}{13}]

Примеры(2):

Задача. Решить:

[ frac{2}{sqrt{5}-1}-frac{2 sqrt{5}-7}{4}-3=? ]

Решение. В данном примере мы не можем извлечь корень из пятерки. Но мы можем воспользоваться формулой разложения корней:

[ frac{2}{sqrt{5}-1}=frac{2(sqrt{5}+1)}{(sqrt{5}-1)(sqrt{5}+1)}=frac{2(sqrt{5}+1)}{5-1}=frac{2 sqrt{5}+2}{4} ]

Теперь можем придать нашему первоначальному выражению следующий вид:

[ frac{2 sqrt{5}+2}{4} frac{2 sqrt{5}-7}{4}-3=frac{2 sqrt{5}+2-2 sqrt{5}+7}{4}-3=frac{9}{4} 3=-frac{3}{4} ]

Ответ. [-frac{3}{4}].

Выражения с логарифмами

Как и степени, логарифмы (log), имеющиеся в выражении, вычисляются (если это возможно) в первую очередь. К примеру, зная, что [log _{2} 4=2] мы можем сразу упростить выражение  [log _{2} 4+5 cdot 6] до простого и понятного 2 + 5*6 = 32.

Со степенями логарифмы объединяет и порядок выполнения действий. Прежде чем искать значение выражения логарифмов, необходимо вычислить его основание (если оно представлено математическим выражением).

В случаях, когда полное вычисление логарифма невозможно, производится упрощение примера.

Задача. Решить:

[log _{27} 81+log _{27} 9=?]

Решение. Чтобы найти логарифм выражения, воспользуемся свойствами логарифмов и представим значение логарифмов со степенями:

Это позволит нам решить пример следующим образом:

Ответ. 2

Решаем выражения с тригонометрической функцией

Часто в выражениях встречаются тригонометрические функции. Всего их в математике шесть:

• Синус;
• Косинус;
• Котангенс;
• Тангенс;
• Секанс;
• Косеканс.

Изучение тригонометрии начинается в 9-м классе, когда ученики уже подготовлены к сложным задачам. Большинство заданий представляются с sin и cos. Остальные функции встречаются значительно реже.

В математических примерах, которые содержат sin, cos, tg и др. функции, вычисление тригонометрической функции производится в первую очередь. Если это невозможно — осуществляется упрощение выражения до получения краткой формулы.

Задача. Решить:

[ frac{24}{sin ^{2} 127+1+sin ^{2} 217} ]

Решение. Разложим 217 на 90 и 127. Т.к. по формуле приведения sin(90 + a) = cosa, получаем:

sin217 — sin (90 + 127) = cos127

Теперь заменяем полученной формулой наше слагаемое в знаменателе дроби:

[ frac{24}{sin ^{2} 127+cos ^{2} 127+1} ]

Вспоминаем, что по тригонометрическому тождеству sin²a+ cos² a= 1 (независимо от значения угла a). Поэтому одну часть слагаемого знаменателя (sin²127+ cos²127) преобразуем в единицу и получаем:

[ frac{24}{sin ^{2} 127+cos ^{2} 127+1}=frac{24}{1+1}=frac{24}{2}=2 ]

Ответ. 2

Задача. Решить:

[ sqrt{4} 8-sqrt{1} 92 sin ^{2} frac{19 pi}{12}=? ]

Решение. Начинаем решение с разбора второй дроби. Обращаем внимание, что 192 = 48 • 2. А значит, корень этого числа можно представить в виде 2√48. Зная это и используя формулу косинуса двойного угла, преобразим наше выражение:

Теперь по формуле приведения решаем наш пример:

[ sqrt{4} 8 cos left(3 pi+frac{pi}{6}right)=sqrt{4} 8left(-cos frac{pi}{6}right)=-sqrt{4} 8 cdot frac{sqrt{3}}{2}=-4 sqrt{3} cdot frac{sqrt{3}}{2}=-6 ]

Ответ. — 6.

Общий случай: находим значения выражений с дробями, функциями, степенями и не только

Самым сложным считается поиск числовых выражений общих случаев. Они представляют собой тригонометрические примеры, которые могут содержать:

• Степени;
• Скобки;
• Корни;
• Функции и т.д.

Общие числовые выражения сложны только длительностью решения. В остальном же они ничуть не сложнее, чем решение каждого примера (со скобкой, степенями, функциями и т.д.) по отдельности.

Чтобы найти значение выражения с логарифмами, тригонометрическими функциями, скобками и/или другими действиями, необходимо помнить три основных правила:

• Упрощение. Прежде чем приступать к решению внимательно изучите выражение. Особенно — его степени, корни, логарифмы, функции. В большинстве случаев их можно сократить или заменить простым числовым значением еще до решения.
• Скобки. Независимо от типа выражения, действий, начинать решение всегда необходимо со скобок. Часто именно игнорирование этого правила приводит к получению неверного ответа или отсутствию решения в принципе.
• Общий вид. Старайтесь привести выражение к общему виду. Особенно это касается дробей. Смешанные и десятичные дроби преобразуйте в обычные.
• Последовательность. Действия в скобках и действия после их решения выполняются слева направо. В первую очередь необходимо совершать умножение и деление. Когда все произведения и частные найдены, можно переходить к сложению и вычитанию.

Для удобства решения и устранения возможных ошибок рекомендуем расставлять порядок действий непосредственно над математическими знаками.

Задача. Решить:

[ -frac{sqrt{2} sin left(frac{pi}{6}+2left(frac{2 pi}{5}+frac{3 pi}{5}right)right)+3}{operatorname{Ln} e^{2}}+left(1+3^{sqrt{9}}right)=? ]

Решение. Чтобы решить этот пример, сначала найдем значение выражения числителя дроби, а точнее — подкоренного выражения. Для этого необходимо вычислить значение sin и общего выражения. Начинаем с раскрытия скобок в числителе:

Полученное значение можем подставить в подкоренное выражение для вычисления числителя дроби:

[ sqrt{2} sin cdotleft(frac{pi}{6}+2left(frac{2 pi}{5}+frac{3 pi}{5}right)+3=sqrt{4}=2right. ]

Со знаменателем дела обстоят куда проще:

[ ln e^{2}=2 ]

Числитель и знаменатель у нас одинаковые, что позволяет нам их сократить:

Теперь остается решить следующее выражение:

Ответ. 27

Как видите, при последовательном решении примеров с большим количеством действий нет ничего сложного. Главное — верно обозначить последовательность шагов и четко ей следовать.

Как найти значение выражения числителя дроби, подкорневого значения рационально?

Независимо от типа выражения решать его необходимо последовательно, руководствуясь стандартными правилами (описаны ранее). Но не стоит забывать, что во многих случаях поиск ответа может быть значительно упрощен за счет рационального подхода к решению. Основывается он на нескольких правилах.

Правило 1. Когда произведение равно нулю

Производное равно нулю в том случае, если хотя бы один из его сомножителей равен нулю. Если вы решаете пример из нескольких сомножителей, одним из которых является «0», то проводить многочисленные вычислительные действия не стоит.

Например, выражение [3 cdotleft(451+4+frac{18}{3}right)left(1-sin left(frac{3 pi}{4}right)right) cdot 0] будет равняться нулю.

Правило 2. Группировка и вынесение чисел

Ускорить процесс поиска ответа можно за счет группировки множителей, слагаемых или вынесения единого множителя за скобки. Также не стоит забывать о возможности сокращения дроби.

Например, выражение [frac{left(451+4+frac{18}{3}right)}{4left(451+4+frac{18}{3}right)}] решать не надо. Достаточно сократить скобки, чтобы получить ответ [=frac{1}{4}]

Решение примеров с переменными

Примеры с переменными отличаются от числовых только формой предоставления. В данном случае значения предоставляются дополнительно к выражению.

Пример задания: Найдите значение выражения 2x — y, если x = 2,5, а y = 2. В данном случае решение будет выглядеть следующим образом:

2x — y = 2 • 2,5 — 2 = 3

При этом в таких примерах сохраняются все описанные выше правила. Касается это и советов по рациональному решению примеров. Так, решать дробь [frac{sqrt{y}}{sqrt{y}}] бессмысленно, т.к. при любых значениях «y» ответ будет одинаковым — 1.

Была ли эта статья полезной?

Значение переменных в математике велико, ведь за время ее существования ученые успели совершить множество открытий в данной области, и, чтобы кратко и ясно изложить ту или иную теорему, мы пользуемся переменными для записи соответствующих формул. Например, теорема Пифагора о прямоугольном треугольнике: a² = b² + c². Чем каждый раз при решении задачи писать: по теореме Пифагора квадрат гипотенузы равен сумме квадратов катетов — мы записываем это формулой, и все сразу становится понятно.

Итак, в этой статье пойдет речь о том, что такое переменные, об их видах и свойствах. Также будут рассмотрены разные математические выражения: неравенства, формулы, системы и алгоритмы их решения.

Понятие переменной

Для начала узнаем, что такое переменная? Это численная величина, которая может принимать множество значений. Она не может быть постоянной, так как в разных задачах и уравнениях для удобства решения мы принимаем за переменную разные числа, то есть, например, z — это общее обозначение для каждой из величин, за которые ее принимают. Обычно их обозначают буквами латинского или греческого алфавита (x, y, a, b и так далее).

Есть разные виды переменных. Ими задаются как некоторые физические величины — путь (S), время (t), так и просто неизвестные значения в уравнениях, функциях и других выражениях.

Например, есть формула: S = Vt. Здесь переменными обозначаются определенные величины, имеющие отношение к реальному миру — путь, скорость и время.

А есть уравнение вида: 3x — 16 = 12x. Здесь уже за x принимается абстрактное число, которое имеет смысл в данной записи.

Виды величин

Под величиной имеется в виду то, что выражает свойства определенного предмета, вещества или явления. К примеру, температура воздуха, масса животного, процентное содержание витаминов в таблетке — это все величины, числовые значения которых можно вычислить.

Для каждой величины есть свои единицы измерения, которые все вместе образуют систему. Ее называют системой исчисления (СИ).

Что такое переменные и постоянные величины? Рассмотрим их на конкретных примерах.

Возьмем прямолинейное равномерное движение. Точка в пространстве движется с одинаковой скоростью на каждом промежутке времени. То есть изменяются время и расстояние, а скорость остается одинаковой. В данном примере время и расстояние — переменные величины, а скорость — постоянная.

Или, например, “пи”. Это иррациональное число, которое продолжается без повторяющейся последовательности цифр и не может быть записано полностью, поэтому в математике оно выражается общепринятым символом, который принимает только значение данной бесконечной дроби. То есть “пи” — это постоянная величина.

История

История обозначения переменных начинается в семнадцатом веке с ученого Рене Декарта.

Известные величины он обозначил первыми буквами алфавита: a, b и так далее, а для неизвестных предложил использовать последние буквы: x, y, z. Примечательным является то, что такие переменные Декарт считал неотрицательными числами, а при столкновении с отрицательными параметрами ставил знак минус перед переменной или, если было неизвестно, каким по знаку является число, многоточие. Но со временем наименованиями переменных стали обозначать числа любого знака, и началось это с математика Иоганна Худде.

С переменными вычисления в математике решаются проще, ведь как, например, сейчас мы решаем биквадратные уравнения? Вводим переменную. Например:

x⁴ + 15x² + 7 = 0

За x² принимаем некое k, и уравнение приобретает понятный вид:

x² = k, при k ≥ 0

k² + 15k + 7 = 0

Вот какую пользу в математику несет введение переменных.

Неравенства, примеры решения

Неравенство представляет собой запись, в которой два математических выражения или два числа связаны знаками сравнения: <, >, ≤, ≥. Они бывают строгими и обозначаются знаками < и > или нестрогими со знаками ≤, ≥.

Впервые эти знаки ввел Томас Гарриот. После смерти Томаса вышла его книга с этими обозначениями, математикам они понравились, и со временем их стали повсеместно употреблять в математических вычислениях.

Существует несколько правил, которые нужно соблюдать при решении неравенств с одной переменной:

1. При переносе числа из одной части неравенства в другую меняем его знак на противоположный.
2. При умножении или делении частей неравенства на отрицательное число их знаки меняются на противоположные.
3. Если умножить или разделить обе части неравенства на положительное число, то получится неравенство, равное исходному.

Решить неравенство — значит найти все допустимые значения переменной.

Пример с одной переменной:

10x — 50 > 150

Решаем, как обычное линейное уравнение — переносим слагаемые с переменной влево, без переменной — вправо и приводим подобные члены:

10x > 200

Делим обе части неравенства на 10 и получаем:

x > 20

Для наглядности в примере решения неравенства с одной переменной изображаем числовую прямую, отмечаем на ней проколотую точку 20, так как неравенство строгое, и данное число не входит в множество его решений.

Решением этого неравенства будет промежуток (20; +∞).

Решение нестрогого неравенства осуществляется так же, как и строгого:

6x — 12 ≥ 18

6x ≥ 30

x ≥ 5

Но есть одно исключение. Запись вида x ≥ 5 нужно понимать так: икс больше или равно пяти, значит число пять входит во множество всех решений неравенства, то есть, записывая ответ, мы ставим квадратную скобку перед числом пять.

x ∈ [5; +∞)

Квадратные неравенства

Если взять квадратное уравнение вида ax² + bx +c = 0 и изменить в нем знак равно на знак неравенства, то соответственно получим квадратное неравенство.

Чтобы решить квадратное неравенство, надо уметь решать квадратные уравнения.

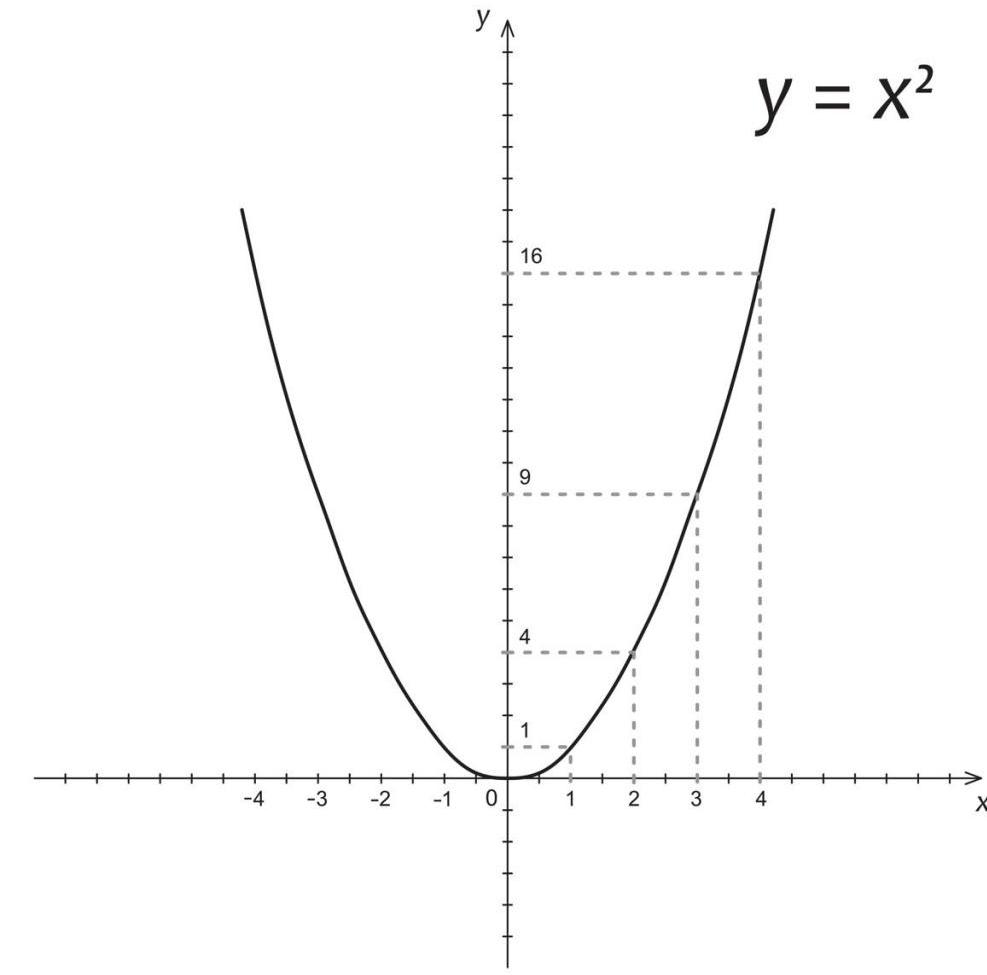
y = ax² + bx + c — это квадратичная функция. Ее мы можем решить с помощью дискриминанта, либо используя теорему Виета. Вспомним, как решаются подобные уравнения:

1) y = x² + 12x + 11 — функция является параболой. Ее ветви направлены вверх, так как знак коэффициента «a» положительный.

2) x² + 12x + 11 = 0 — приравниваем к нулю и решаем с помощью дискриминанта.

a = 1, b = 12, c = 11

D = b² — 4ac= 144 — 44 = 100 > 0, 2 корня

По формуле корней квадратного уравнения получаем:

x₁ = -1, x₂ = -11

Или можно было решить это уравнение по теореме Виета:

x₁ + x₂ = -b/a, x₁ + x₂ = -12

x₁x₂ = c/a, x₁x₂ = 11

Методом подбора получаем такие же корни уравнения.

Парабола

Итак, первый способ решения квадратного неравенства — это парабола. Алгоритм ее решения таков:

1. Определяем, куда направлены ветви параболы.

2. Приравниваем функцию к нулю и находим корни уравнения.

3. Строим числовую прямую, отмечаем на ней корни, проводим параболу и находим нужный нам промежуток в зависимости от того, какой у неравенства знак.

Решим неравенство x² + x — 12 > 0

Выписываем в виде функции:

1) y = x² + x — 12 — парабола, ветви вверх.

Приравниваем к нулю.

2) x² + x -12 = 0

Дальше решаем как квадратное уравнение и находим нули функции:

x₁ = 3, x₂ = -4

3) Изображаем числовую прямую и на ней точки 3 и -4. Парабола пройдет через них, ветвями вверх и ответом к неравенству будет множество положительных значений, то есть (-∞; -4), (3; +∞).

Метод интервалов

Второй способ — это метод интервалов. Алгоритм его решения:

1. Находим корни уравнения, при которых неравенство равно нулю.

2. Отмечаем их на числовой прямой. Таким образом она делится на несколько интервалов.

3. Определяем знак любого интервала.

4. Расставляем знаки у остальных интервалов, меняя их через один.

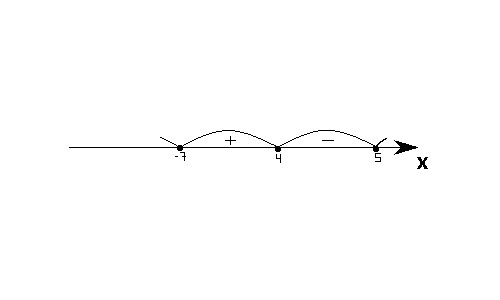
Решим неравенство (x — 4)(x — 5)(x + 7) ≤ 0

1) Нули неравенства: 4, 5 и -7.

2) Изображаем их на числовой прямой.

3) Определяем знаки интервалов.

Ответ: (-∞; -7]; [4; 5].

Решим еще одно неравенство: x²(3x — 6)(x + 2)(x — 1) > 0

1. Нули неравенства: 0, 2, -2 и 1.

2. Отмечаем их на числовой прямой.

3. Определяем знаки интервалов.

Прямая делится на промежутки — от -2 до 0, от 0 до 1, от 1 до 2.

Возьмем значение на первом промежутке — (-1). Подставляем в неравенство. При данном значении неравенство становится положительным, значит и знак на этом промежутке будет +.

Далее, начиная от первого промежутка, расставляем знаки, меняя их через один.

Неравенство больше нуля, то есть надо найти множество положительных значений на прямой.

Ответ: (-2; 0), (1; 2).

Системы уравнений

Системой уравнений с двумя переменными называют два уравнения, объединенных фигурной скобкой, для которых необходимо найти общее решение.

Системы могут являться равносильными, если общее решение одной из них является решением другой, или они обе не имеют решений.

Мы изучим решение систем уравнений с двумя переменными. Есть два способа их решения — метод подстановки или алгебраический метод.

Алгебраический метод

Чтобы решить систему, изображенную на картинке, данным методом, необходимо сначала помножить одну из ее частей на такое число, чтобы потом иметь возможность взаимно уничтожить одну переменную из обеих частей уравнения. Здесь мы умножаем на три, подводим черту под системой и складываем ее части. В итоге иксы становятся одинаковы по модулю, но противоположны по знаку, и мы их сокращаем. Далее получаем линейное уравнение с одной переменной и решаем его.

Игрек мы нашли, но на этом мы не можем остановиться, ведь мы еще не нашли икс. Подставляем игрек в ту часть, из которой удобно будет вывести икс, например:

-x + 5y = 8 , при y = 1

-x + 5 = 8

Решаем получившееся уравнение и находим икс.

-x = -5 + 8

-x = 3

x = -3

Главное в решении системы — правильно записать ответ. Многие школьники делают ошибку и пишут:

Ответ: -3, 1.

Но это неверная запись. Ведь, как уже писалось выше, решая систему уравнений, мы ищем общее решение для его частей. Правильным будет ответ:

(-3; 1)

Метод подстановки

Это, пожалуй, самый простой метод, в котором трудно совершить ошибку. Возьмем систему уравнений номер 1 с этой картинки.

В первой ее части икс уже приведен к нужному нам виду, поэтому нам остается только подставить его в другое уравнение:

5y + 3y — 25 = 47

Переносим число без переменной вправо, приводим подобные слагаемые к общему значению и находим игрек:

8y = 72

y = 9

Затем, как и в алгебраическом методе, подставляем значение игрека в любое из уравнений и находим икс:

x = 3y — 25, при y = 9

x = 27 — 25

x = 2

Ответ: (2; 9).